публикуем рейтинг развития краевых муниципалитетов
14 сентября , 07:16СтатьиФото: СКИА
В правительстве Ставропольского края опубликовали доклад, в котором приведены результаты эффективности деятельности органов местного самоуправления муниципалитетов региона за 2021 год. Какие города и округа заняли лидирующие позиции, а кто отстаёт — в материале «Победы26».
Мониторинг проводился по двум группам: среди 7 городов Ставропольского края и 26 городских округов и муниципальных округов региона. Специалисты сравнили данные по 10 сферам деятельности: «Экономическое развитие», «Развитие малого и среднего предпринимательства», «Дошкольное, общее и дополнительное образование», «Культура», «Физическая культура и спорт», «Жилищное строительство и обеспечение граждан жильем. Жилищно-коммунальное хозяйство», «Выявление и пресечение случаев осуществления строительства без получения соответствующего разрешения», «Безопасность дорожного движения», «Организация муниципального управления», «Энергосбережение и повышение энергетической эффективности».
Разберём более подробно каждую из них.
«Экономическое развитие»
Развитие экономики высчитывали исходя из данных об объёмах инвестиций в основной капитал (за исключением бюджетных средств) в расчёте на одного жителя. В семи муниципальных образованиях Ставрополья эти показатели превысили среднекраевой уровень. Также специалисты проанализировали среднюю зарплату работников крупных, средних предприятий и некоммерческих организаций. Сложив показатели, аналитики получили следующие данные: Ставрополь, Лермонтов и Невинномысск разделили пьедестал в первой группе; Левокумский, Кочубеевский и Будённовский округа заняли почётные места во второй. Аутсайдер первой группы — Ессентуки, второй — Курский округ.
«Развитие малого и среднего предпринимательства»
Как указано в докладе, в 2021 году в среднем по муниципалитетам Ставрополья число субъектов малого и среднего предпринимательства в расчёте на 10 тысяч человек увеличилось, в сравнении с 2020 годом, на 18,5 процента.
Лидером в этой области стала краевая столица, курортные города Пятигорск и Железноводск забрали второе и третье места соответственно. Худший показатель — у Курского округа.
Составители рейтинга также изучили долю среднесписочной численности работников малых и средних предприятий. Она в среднем выросла на 27,9 процента и увеличилась, в сравнении с 2020 годом, на 0,7 процента. Лидирующие позиции в данном пункте заняли города Лермонтов, Ессентуки и Кисловодск. В минус, по сравнению с 2020 годом, ушли Нефтекумский, Предгорный, Курский, Красногвардейский и Новоалександровский округа.
В докладе также отмечают, что в 2021 году в аппарат Уполномоченного по защите прав предпринимателей Ставрополья поступило 204 обращения от бизнесменов, что втрое меньше количества аналогичных жалоб, принятых в 2020 году.
«Дошкольное, общее и дополнительное образование»
В следующем пункте специалисты подсчитали долю детей в возрасте от 1 до 6 лет, состоящих на учёте для определения в детские сады.
Средний показатель в этом пункте составил 5,9 процента и снизился, в сравнении с 2020 годом, на 0,7 процента.
Напомним, что в 2022 году благодаря краевой госпрограмме по развитию образования открыли три дошкольных образовательных учреждения на 420 мест. До конца 2023 года будет создано ещё девять детских садов на 1 180 мест. Реализацию программы по развитию дошкольного образования на Ставрополье лично контролирует губернатор региона Владимир Владимиров.
Наименьшие значения данного показателя отмечены в Благодарненском округе (0,3 процента), в Апанасенковском (0,1 процента) и Степновском (0,5 процента). Самые высокие цифры в Ставрополе (21,0 процента), Пятигорске (15,7 процента) и Шпаковском округе (22,5 процента).
Также аналитики выявили среднюю зарплату учителей и работников дошкольных учреждений. Благодаря этому удалось составить топ муниципалитетов Ставрополья, где активно развивается образование.
«Культура»
Анализируя показатель культурного развития, исследователи подсчитали долю культурных учреждений, которые находятся в аварийном состоянии и нуждаются в капитальном ремонте.
В целом по краю этот показатель снизился на 1,7 процента, по сравнению с 2020 годом. Также аналитики выявили средний показатель зарплаты работников культуры, искусства в муниципалитетах Ставрополья. С помощью этих данных удалось составить список городов и округов, которые лидируют и отстают в области культурного развития.
«Физическая культура и спорт»
В 2021 году доля населения, систематически занимающегося спортом, составила 51,5 процента и увеличилась, в сравнении с 2020 годом, на 3,3 процентных пункта.
Наиболее высокие показатели этого пункта в Лермонтове (56,3 процента), Пятигорске (55,0 процента) и Минераловодском округе (55,3 процента). Самые низкие — в Ессентуках (45,8 процента), Кировском (44,2 процента) и Курском округах (46,6 процента).
Таким образом, исследователи составили список самых «спортивных» муниципалитетов края.
«Жилищное строительство и обеспечение граждан жильем. Жилищно-коммунальное хозяйство»
Оценку ЖКХ проводили, анализируя общую площадь жилых помещений, приходящихся в среднем на одного жителя.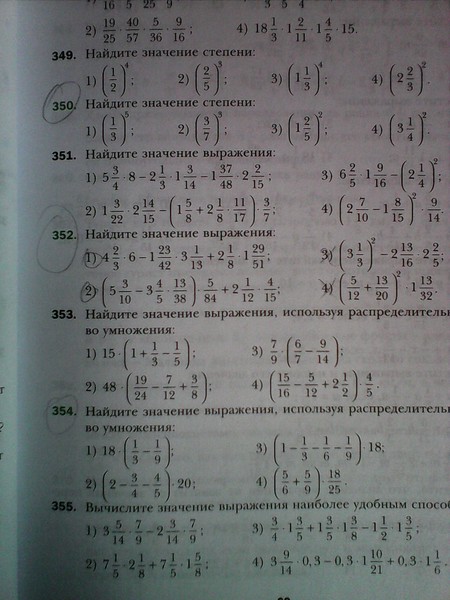
В 2021 году она составила 24,7 квадратного метра, или 102,1 процента к уровню 2020 года. Также исследователи выявили долю населения, получившего жилые помещения и улучшившего жилищные условия, состоящего на учёте в качестве нуждающегося в жилых помещениях.
Самые высокие показатели здесь у Красногвардейского округа (19,3 процента), Новоселицкого округа (27,7 процента) и Шпаковского округа (25,8 процента).
«Выявление и пресечение случаев осуществления строительства без получения соответствующего разрешения»
Не менее важным направлением деятельности органов местного самоуправления является работа по выявлению и пресечению незаконного строительства. В 2021 году на Ставрополье выявили 21 такой объект, что, в сравнении с 2020 годом, в 2,2 раза меньше.
Наибольшее количество объектов, возведённых без разрешения, выявили в Ставрополе, Кисловодске, в Будённовском и Предгорном округах (по три объекта в каждом).
«Безопасность дорожного движения»
В 2021 году удельная величина расходов краевого бюджета на дорожную деятельность составила семь процентов от общих затрат и увеличилась в сравнении с 2020 годом на 0,7 процента.
Наименьшие значения показателя «Удельная величина расходов бюджета на дорожную деятельность в общем объёме расходов» отмечены в Ессентуках (1 процент), Кисловодске (1,5 процента) и Нефтекумском округе (1,3 процента), наибольшие — в Ставрополе (14,5 процента), Минераловодском округе (13,6 процента) и Апанасенковском округе (21,4 процента).
Удельная величина ДТП из-за неудовлетворительных дорожных условий составила 43,7 процента и снизилась за год на 1,9 процента.
Данные этих показателей позволили составить рейтинг муниципалитетов, лидирующих и отстающих по безопасности дорожного движения.
«Организация муниципального управления»
Оценивая организацию муниципального управления, специалисты подсчитали расходы бюджета Ставропольского края на содержание работников органов местного самоуправления в расчёте на одного жителя муниципалитета. Среднее показание по краю — 185,4 рубля, или 132,8 процента к уровню 2020 года.
Также в исследование вошли данные о налоговых и неналоговых доходах местного бюджета в общем объёме собственных доходов бюджета муниципального образования.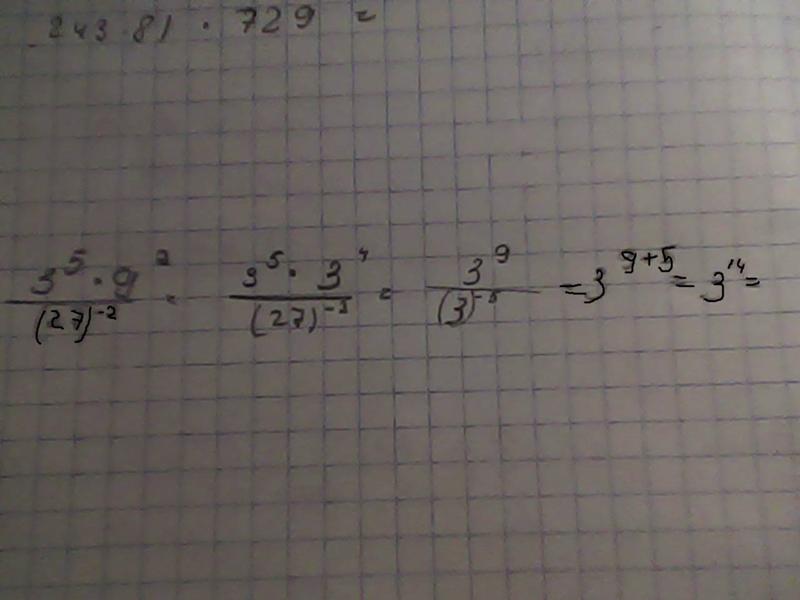
«Энергосбережение и повышение энергетической эффективности»
Заключительный рейтинг составляли исходя из данных удельной величины потребления электричества в многоквартирных домах, которая в сравнении с 2020 годом выросла на два процента и в среднем составила 680,7 кВт/ч на одного проживающего.
Наименьшие значения данного показателя зафиксированы в Ессентуках (416,0 кВт/ч на одного проживающего), Петровском округе (456,7 кВт/ч на одного проживающего) и Туркменском округе (388,9 кВт/ч на одного проживающего).
Самые высокие показатели отмечены в Ставрополе (952,8 кВт/ч на одного проживающего), Кисловодске ( 1 177,4 кВт/ч на одного проживающего) и Курском округе (921,0 кВт/ч на одного проживающего).
Второй показатель, взятый для исследования, — удельная величина потребления холодной воды в многоквартирных домах. В среднем он составил 32 кубических метра на одного проживающего и снизился, в сравнении с 2020 годом, на 3,6 процента.
Самые невысокие значения этого показателя у жителей Курского округа (19,5 кубического метра на одного проживающего в год), Туркменского округа (14,2 кубического метра на одного проживающего) и Шпаковского округа (19,1 кубического метра на одного проживающего).
Наибольшие значения отметили в Невинномысске (51,9 кубического метра на одного проживающего), Ессентуках (50 кубических метров на одного проживающего) и Изобильненском округе (52,7 кубического метра на одного проживающего).
В итоге в числе победителей данного рейтинга свои позиции сохранил Ставрополь, Предгорный и Шпаковский округа.
В I группе 1-е место занял город Ставрополь, 2-е место — город-курорт Пятигорск. Во II группе 1-е место занял Шпаковский муниципальный округ, 2-е место — Кочубеевский муниципальный округ, 3-е место — Предгорный муниципальный округ.
Подготовить сводный доклад удалось благодаря сведениям Управления Федеральной службы государственной статистики по Северо-Кавказскому федеральному округу, органов исполнительной власти и местного самоуправления Ставрополья.
ставропольский краймуниципалитетыаналитикарейтингразвитие ставрополья
Эриксен и Фернандеш – два мозговых центра МЮ. С ними прогрессирует даже МакТоминэй 13.09.2022 читать блог на SOCCER.
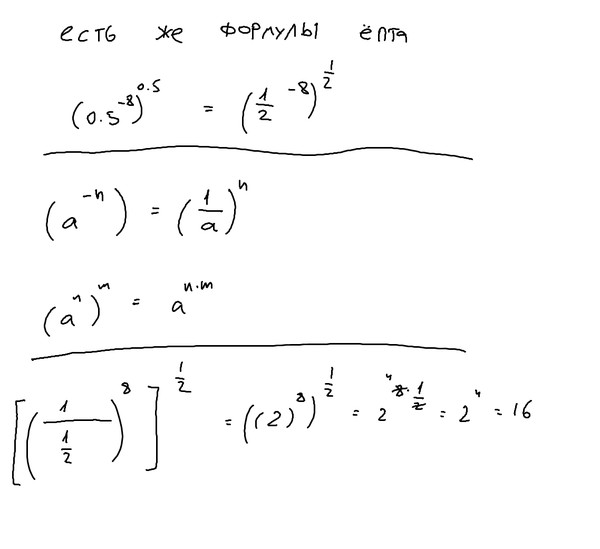RU13 сентября 2022, 19:50
00:00 / 00:00
Главный козырь – центр поля.
После кошмарного старта «Манчестер Юнайтед» в АПЛ казалось, что тен Хаг проработает в клубе недолго – поражения от «Брайтона» и «Брентфорда» не внушали никакого доверия. При этом на уровне задумки приглашение Эрика казалось самым осознанным решением манкунианцев в последние годы. Чтобы все заработало, требовалось как раз доверие – менеджеру только предстояло выстроить цельный коллектив. Еще один минус – покупка Антони за космические 100 миллионов евро. Бразилец этих денег явно не стоил, но, как говорят, настоял главный тренер.
Говорить о включении в чемпионскую гонку точно не стоит – хотя не отметить наметившиеся тенденции невозможно. И прежде всего – значительную роль Кристиана Эриксена, который нашел взаимопонимание с Бруну Фернандешем.
Теперь у
МЮ два креативщика в центре поляКристиан отлично дополняет концепцию нидерландского менеджера и служит мостиком в воплощении его идей на поле – сам тренер считает его правильным игроком для своей концепции. Полузащитник нашел общий язык с тен Хагом еще в ходе переговоров, к тому же мотивирован быть частью этого проекта:
Я смог представить себя в МЮ после прихода тен Хага с идеями, которые у него есть, а также с нашими разговорами с ним. В то же время это очень большой клуб, если не самый большой. У него большая история, приятно чувствовать себя частью чего-то такого значительного. Но я прихожу сюда играть в футбол не только ради эмблемы.
Последнее – довольно важная вводная. К примеру, проблемы с Роналду связаны как раз с тем, что он прежде всего берет в расчет свои амбиции – перетягивает игру с мячом на себя, из-за отсутствия должного, по его мнению, усиления был готов покинуть клуб.
В случае с Эриксеном манкунианцы получили второго игрока в центр поля с отличным видением площадки, первым пасом, умными перемещениями и готовностью играть на благо команды. Кристиан – самый вовлеченный в игру в пас футболист манкунианцев. Схожими качествами обладает Бруну Фернандеш, с которым у датчанина получается огненная связка.
Всегда там, где нужно
Огромную роль играют перемещения Эриксена и Бруну по полю. Причем польза от этого есть даже в начальной стадии атаки. Крайние защитники «Ман Юнайтед», когда «красные дьяволы» владеют мячом, выдвигаются вплоть до финальной трети поля, оставляя центральных вдвоем. На примере матча с «Арсеналом» было видно, как Варану и Мартинесу не хватало третьего для развития атаки – «канониры» перекрывали линии передачи.
Несмотря на то, что номинально МЮ в последних турах играет с парой опорников Эриксен-МакТоминэй, Кристиан по указанию тен Хага может уйти ближе к флангу. Особенно показателен пример с тем же «Арсеналом». «Канониры» всегда активно прессингуют крайних игроков соперника – Сака/Мартинелли давят на защитников, Уайт/Зинченко (или Тирни вместо Александра) – на вингеров. Под плотной опекой у Санчо и Маласии (левый фланг, где чаще оказывался мяч) почти не было вариантов развития атаки. В такой ситуации смещения Эриксена добавляли адресата для передачи. По ситуации туда же смещался Фернандеш.
Главный козырь этих полузащитников – видение поля и пас, навыки, дополняющие друг друга.
Под давлением Кристиан все равно способен найти, кому отдать мяч и обострить – с его паса на Бруну началась атака, завершившаяся голом «Арсеналу» от Антони. Аналогичным образом манкунианцы соорудили и второй гол в ворота «пушкарей», причем Бруну отдал достаточно сильно, чтобы выбежавший из-под защитника Рэшфорд получил мяч на свободном пространстве. Третье взятие ворот – первый пас Фернандеша на Эриксена в окружении четырех игроков соперника.
Страшно представить, насколько бы стали хуже дела с созданием момента этих двоих – именно они пасом создают всю остроту.
С Эриксеном прокачался МакТоминэй
Основная проблема первых матчей «Юнайтед» была в форме основных игроков – Фред и МакТоминэй не справлялись с опорной зоной, Магуайр привычно допускал ошибки. С Кристианом и Фернандешем в связке Скотт стал в разы увереннее и не теряется под прессингом – находит выход за счет расположения, почти не обрезается, сводит время на обработку мяча к минимуму и прикрывает его корпусом.
В отдельных матчах шотландец сам смещается ближе к флангу (встреча с «Лестером») или создает ширину у центрального круга.
Воспитанник «Юнайтед» уже может один оставаться в опорной зоне и справляться с возложенными на него обязанностями, а Эриксен и Бруну помогут найти варианты открываниями.
В степени становления концепции «Манчестер Юнайтед» еще много вводных – не все игроки под нее подходят, в подвешенном состоянии вопрос с перспективами Роналду (пусть и сам тренер говорит, что тот остается), атмосферой в раздевалке. Зато Эриксен и Фернандеш – два столпа, на которые можно опереться в выстраивании командных связей и действиях на поле. Главное, чтобы взаимопонимание улучшалось, а сам проект получал одобрение от боссов, разрастался. В ближайшей перспективе за МЮ следить надо особенно пристально.
Ман Юнайтед Эриксен Кристиан МакТоминэй Скотт Фернандеш Бруну
Источник: Soccer.
RuФото: Официальный сайт «Манчестер Юнайтед»
Отказались от 100 млн евро и скучают по Бензема. У «Реала» семь побед в новом сезоне
14 сентябряВадим Багров в блоге Тактический лабиринт6
Мундиаль уже влияет на еврокубки. «Спортинг» и «Брюгге» не последние очарования
14 сентябряВадим Багров в блоге Забыли спросить4
Холанд покоряет голами АПЛ. Форварды определят исход английского сезона
28 августаВадим Багров в блоге Тактический лабиринт5
Вы удивитесь новой свободе Хави. У «Барселоны» триединый Педри и «дубль вэ»
24 августаВадим Багров в блоге «Соккер» Топ9
«Спартак» нашёл ещё двух футболистов.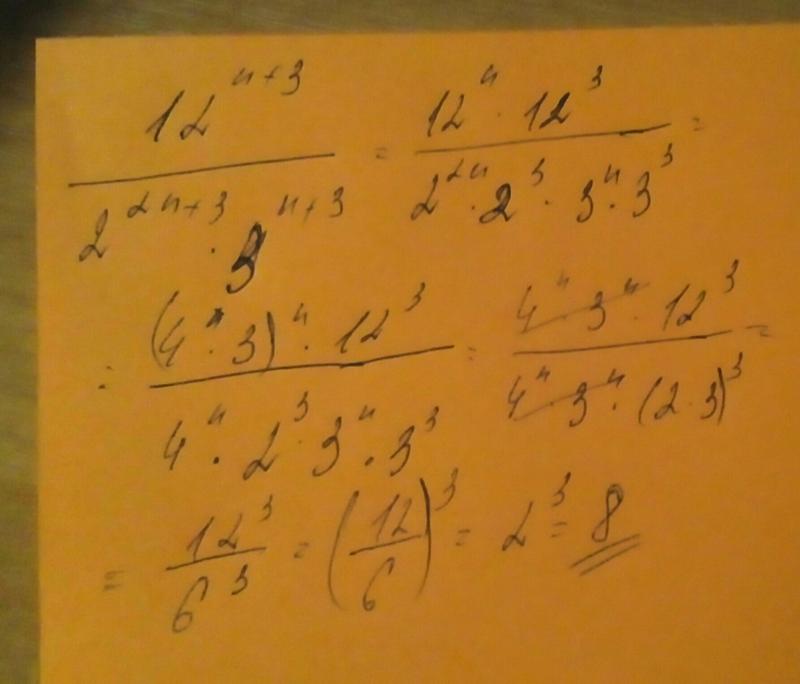
18 августаВадим Багров в блоге Футбольный Скаут5
Мележиков: «Задача „Спартака“ – всегда быть на вершине таблицы»
18 августа
Три правила показателей — Полный курс алгебры
Навыки
в н
A L G E B R A
Содержание | Дом
Назад к Разделу 1
Правило 1. Та же база
Правило 2. Мощность продукта
Правило 3. Сила силы
Правило 1. Та же база
a m a n = a m + n
«Чтобы умножить степени одного и того же основания, сложите показатели степени.»
Например, a 2 a 3 = a 5 .
Зачем мы добавляем показатели степени? Из-за того, что означают символы.
Пример 1. Умножить 3 x 2 · 4 x 5 · 2 x
Решение . Проблема означает (Урок 5): Умножьте числа, затем объедините степени x :
3 x 2 · 4 x 5 · 2 x = 24 x 90
Два фактора x — x 2 — умножить на пять множителей x — x 5 — умножить на один множитель x , всего 1 = 2 + 5 + множителей x : x 8 .
Задача 1. Умножение. Примените правило Та же база.
Чтобы увидеть ответ, наведите указатель мыши на цветную область.
Чтобы снова закрыть ответ, нажмите «Обновить» («Reload»).
Сначала решай проблему сам!
| а) | 5 x 2 · 6 x 4 = 30 x 6 | б) | 7 x 3 · 8 x 6 = 56 x 9 | ||||
| в) | x · 5 x 4 = 5 x 5 | г) | 2 x · 3 x · 4 x = 24 x 3 | ||||
| д) | x 3 · 3 x 2 · 5 x = 15 x 6 | е) | x 5 · 6 x 8 y 2 = 6 x 13 | ||||
| г) | 4 x · y · 5 x 2 · y 3 = 20 x 3 y 4 | ч) | 2 x Y · x 3 Y 5 = 18 x 4 Y 88888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888888889н | ||||
| i) | а 2 б 3 а 3 б 4 = а 5 б 7 | | к) | a 2 bc 3 b 2 ac = a 3 b 3 c 4 | | |||
| к) | x m y n x p y q = x m + p y n + q | л) | a p b q ab = а р + 1 б к + 1 | ||||
Задача 2. Различите следующее:
x · x и x + x .
х · х = х ². х + х = 2 х .
Пример 2. Сравните следующее:
a) x · x 5 b) 2 · 2 5
Решение .
A) x · x 5 = x 6
B) 2 · 2 5 = 2 6 9003
Часть b) имеет ту же форму , что и часть a). Это часть а) с х = 2,
Один множитель 2 умножает пять множителей 2, что дает шесть множителей 2.
2 · 2 = 4 здесь неверно.
Проблема 3. Примените правило «Та же основа».
| а) | x x 7 = x 8 | б) | 3 · 3 7 = 3 8 | в) | 2 · 2 4 · 2 5 = 2 10 | ||
| г) | 10 · 10 5 = 10 6 | д) | 3 x · 3 6 x 6 = 3 7 x 7 | ||||
Проблема 4. Примените правило «Та же основа».
| а) | x n x 2 = x n + 2 | б) | x нет x = x n + 1 | ||||
| в) | x n x n = x 2 n 9 | г) | x n x 1 − n = x | ||||
| д) | x · 2 x n − 1 = 2 x n | е) | x n x м = x n + m 8 | ||||
| г) | x 2 n x 2 − n = x n 8 0 + 9| | | |||||
Правило 2: Степень произведения факторов
( аб ) н = а н б н
«Возвести каждый множитель в ту же степень. »
Например, ( ab ) 3 = a 3 b 3 .
Почему мы можем это делать? Опять же по тому, что означают символы:
( AB ) 3 = AB · AB · AB = AAABBBBBBBBB = A 3 333333333333334 .
Порядок факторов не имеет значения:
аб · аб · аб = аааббб .
Задача 5. Применить правила экспонент.
| а) | ( x y ) 4 = x 4 y 4 | б) | ( шт. ) 5 = p 5 q 5 r 5 | в) | (2 abc ) 3 = 2 3 а 3 б 3 9 23 3 |
| d) x 3 y 2 z 4 5 0 9 5 0 9 0 0028 | = | x 3 y 2 z 4 · x 5 y 5 z 5 Rule 2. |
| = | x 8 y 7 z 9 Та же база. | |
Правило 3: Сила силы
( a m ) n = a mn
«Чтобы взять степень степени, умножьте степени.»
Например, ( a 2 ) 3 = a 2 · 3 = a 6 .
Зачем мы это делаем? Опять же, из-за того, что означают символы:
( a 2 ) 3 = a 2 a 2 a 2 = a 3 · 2 = a 6
Задача 6. Применить правила показателей.
| а) | ( х 2 ) 5 = x 10 | б) | ( a 4 ) 8 = a 32 | в) | (10 7 ) 9 = 10 63 |
Пример 3. Примените правила показателей: (2 x 3 y 4 ) 5
Решение . В скобках указаны три множителя: 2, x 3 и y 4 . По правилу 2 мы должны взять пятую степень каждого из них. Но чтобы взять степень степени, мы умножаем показатели. Следовательно,
(2 x 3 Y 4 ) 5 = 2 5 x 15 Y 20
Задача 7. Применить правила показателей.
| а) | (10 a 3 ) 4 = 10 000 a 12 | б) | (3 x 6 ) 2 = 9 x 12 | |
| в) | (2 и 2 б 3 ) 5 = 32 а 10 б 15 | г) | ( xy 3 z 5 ) 2 = x 2 y 6 z 10 | |
| д) | (5 x 2 y 4 ) 3 = 125 x 6 y 12 | е) | (2 a 4 bc 8 ) 6 = 64 a 24 b 6 c 48 | |
Задача 8. Применить правила показателей.
a) 2 x 5 y 4 (2 x 3 y 6 ) 5 = 2 x 5 y 4 · 2 5 x 15 Y 30 = 2 6 x 20 Y 34
б) абв 9 ( а 2 б 3 с 4 ) 8 = abc 9 · a 16 b 24 c 32 = a 17 b 25 c 41
Задача 9. Используйте правила экспонент, чтобы вычислить следующее.
а) (2 · 10) 4 = 2 4 · 10 4 = 16 · 10 000 = 160 000
б) (4 · 10 2 ) 3 = 4 3 · 10 6 = 64 000 000
c) (9 · 10 4 ) 2 = 81 · 10 8 = 8 100 000 000
В степенях числа 10 столько нулей, сколько в степени 10.
Пример 4. Квадрат x 4 .
Решение . ( х 4 ) 2 = х 8 .
Чтобы возвести в квадрат степень, удвойте показатель степени.
Задача 10. Возведите в квадрат следующее.
| а) | x 5 = x 10 | б) | 8 a 3 b 6 = 64 a 6 b 12 | |
| в) | −6 x 7 = 36 x 14 | г) | x n = x 2 n | |
Часть c) иллюстрирует: Квадрат числа никогда не бывает отрицательным.
(-6)(-6) = +36. Правило знаков.
Задача 11. Применить правило экспоненты — если возможно.
| а) | x 2 x 5 = x 7 , Правило 1. | б) | ( х 2 ) 5 = x 10 , Правило 3. |
| в) | x 2 + x 5 |
| Невозможно. Правила экспоненты применяют только к умножению. |
Итого: Добавьте степени, когда одно и то же основание встречается дважды: x 2 х 4 = х 6 . Умножить степени, когда основание встречается один раз — и в круглых скобках: ( x 2 ) 5 = x 10 .
Задача 12. Применить правила показателей.
| а) | ( x n ) n = x n · n = x n 2 | б) | ( x n ) 2 = x 2 n |
Задача 13. Примените правило степеней или добавьте похожие термины, если это возможно.
а) 2 x 2 + 3 х 4 Невозможно. Это не термина .
б) 2 x 2 · 3 x 4 = 6 x 6 . Правило 1.
c) 2 x 3 + 3 x 3 = 5 х 3 . Как термины. Показатель не меняется.
г) x 2 + г 2 Невозможно. Это не такие термины.
e) x 2 + x 2 = 2 х 2 . Как термины.
f) x 2 · x 2 = х 4 . Правило 1
g) x 2 · y 3 Невозможно. Разные базы.
ч) 2 · 2 6 = 2 7 . Правило 1
i) 3 5 + 3 5 + 3 5 =
3 · 3 5 (При добавлении подобных слагаемых) = 3 6 .
Мы продолжим правила экспонент в Уроке 21.
Следующий урок: умножение. Распределительное правило.
Назад к Разделу 1
Содержание | Главная
Copyright © 2021 Лоуренс Спектор
Вопросы или комментарии?
Электронная почта: [email protected]
Степени двойки
Степени двойкиДля этого курса вы должны уметь конвертировать между следующими степени двойки и их шестнадцатеричные/десятичные эквиваленты. Что то есть не нужно делать никаких расчетов, даже в уме, чтобы перейти от одного к другому.
| Степень двойки | Двоичный | Шестнадцатеричный | Десятичное значение |
|---|---|---|---|
| 2 0 | 0001 | 1 | 1 |
| 2 1 | 0010 | 2 | 2 |
| 2 2 | 0100 | 4 | 4 |
| 2 3 | 1000 | 8 | 8 |
| 2 4 | 0001 0000 | 10 | 16 |
| 2 5 | 0010 0000 | 20 | 32 |
| 2 6 | 0100 0000 | 40 | 64 |
| 2 7 | 1000 0000 | 80 | 128 |
| 2 8 | 0001 0000 0000 | 100 | 256 |
| 2 9 | 0010 0000 0000 | 200 | 512 |
| 2 10 | 0100 0000 0000 | 400 | 1 024 |
| Степень двойки | Двоичный | Десятичное значение | Имя | Префикс |
|---|---|---|---|---|
| 2 10 | 0100 0000 0000 | 1 024 | тысяч | килограмм |
| 2 20 | 0001 0000 0000 0000 0000 0000 | 1 048 576 | миллионов | Мега |
| 2 30 | 0100 0000 0000 0000 0000 0000 0000 0000 | 1 073 741 824 | миллиард | Гига |
| 2 40 | 0001 … (40 нулей) | 1 099 511 627 776 | триллион | Тера |
| 2 50 | 0001 . .. (50 нулей) | 1 125 899 906 842 624 | Квадриллион | Пета |
Обязательно ознакомьтесь с единицами Измерьте веб-страницу для получения информации об альтернативном наборе имен для перечисленные здесь префиксы.
Имея в виду эти две таблицы, вы можете легко построить большие двоичные числа, помня, что вы добавляете показатели степени при умножении чисел с той же базой. Например, память объемом 256 мегабайт имеет 2 8 * 2 20 = 2 28 байт. В двоичном формате это будет единица с 28 нулями.
Число с отрицательным показателем является обратным соответствующее число с положительным показателем. это не так важно запомнить эти значения как положительные, но важно понять закономерность.
| Степень двойки | Двоичный | Сила шестнадцати | Шестнадцатеричный | Десятичное значение |
|---|---|---|---|---|
| 2 -1 | 0,1000 | 8 * 16 -1 | 0,8 | 0,500 |
| 2 -2 | 0,0100 | 4 * 16 -1 | 0,4 | 0,250 |
| 2 -3 | 0,0010 | 2 * 16 -1 | 0,2 | 0,125 |
| 2 -4 | 0,0001 | 1 * 16 -1 | 0,1 | 0,062 500 |
| 2 -5 | 0,0000 1000 | 8 * 16 -2 | 0,08 | 0,031 250 |
| 2 -6 | 0,0000 0100 | 4 * 16 -2 | 0,04 | 0,015 625 |
| 2 -7 | 0,0000 0010 | 2 * 16 -2 | 0,02 | 0,007 812 500 |
| 2 -8 | 0,0000 0001 | 1 * 16 -2 | 0,01 | 0,003 906 250 |
| 2 -9 | 0,0000 0000 1000 | 8 * 16 -3 | 0,008 | 0,001 953 125 |
См. также единицы измерения
веб-страница.
Учебное пособие по степеням десяти
При решении рабочих задач по астрономии вы часто будете сталкиваться с очень большими или очень небольшие числа. Например, количество звезд в нашей галактике Млечный Путь составляет около 100 млрд. Большие числа, такие как 100 миллиардов, обременительны для записи. в обычной форме (100 000 000 000), поэтому ученые используют сокращение обозначения, называемые степенями десяти.
В степенях десяти большие числа записываются с использованием десяти к мощность или экспонента. Показатель степени говорит вам, сколько раз десять должно быть умножить на iteslf, чтобы получить число, которое вы хотите написать. Например, 100 можно записать как 10×10 = 10 2 . 10 000 = 10x10x10x10 = 10 4 . Обратите внимание, что показатель степени десяти — это просто число нули.
1.Что такое 100 миллиардов = 100 000 000 000 в степени десяти?
| A). . 10 6 B)..10 8 C).. 10 9 D)..10 11 E)..10 12 9 |
Многие люди путаются в том, как написать 10 и 1 в этой форме. 10 = 10 1 и 1 = 10 0 .
Очень маленькие числа также могут быть записаны в десятичной степени, но маленькие числа используют отрицательные показатели. Например, 0,01 = 10 -2 . Почему знак минус? Легко понять, почему, если вы сначала запишете 0,01 как 1/100 = 1/10 2 . Тогда становится ясно, что отрицательная сила просто указывает степень десяти знаменателя, когда вы написали число как дробь.
Примечание. Простой способ вычислить степень десяти для небольших чисел — это считать нули после запятой и прибавлять единицу.
Например,
2. Что такое 0,0001 в десятичной степени?
| А)… 10 3 . Б)…10 -4 C). ..10 -3 D)…10 -2 E)…10 -1 |
Другой пример: диаметр атома водорода составляет примерно 0,0000000001 метра.
3.Что это в степенях десяти обозначений?
| А)… 10 -12 . Б)… 10 -10 . С)… 10 -11 . Г)… 10 1/12 . Е)… 10 -13 . |
Как мы используем степени десяти, чтобы записать такие числа, как 475 000 000 или 0,00031?
Здесь хитрость заключается в том, чтобы записать число как ненулевое число, умноженное на степень 10. Например, 475 000 000 = 4,75×100 000 000 = 4,75×10 8 .
Точно так же 0,00031 = 3,1×0,0001 = 3,1×10 -4 .
Обратите внимание, что вы могли бы также написать 475 000 000 как
475×10 6 или 47,5×10 7 . вообще легче читать
число, если написать только одну цифру слева от запятой, но
используйте свое суждение.
4. Что такое 31 600 000 в десятичной степени?
| A)… 3,16 x 10 5 B)… 3,16 x 10 6 C)… 3,16 x 10 7 D)… 3,16 x 10 8 E)… x10 9 |
Теперь, когда у вас есть некоторое представление о том, как записывать числа в десятичной степени, мы должны посмотреть, как умножать и делить такие числа.
Правила просты.
К множественному, добавить степени.
Разделить, вычесть степени.
Например, чтобы умножить: 10 6 x10 4 = 10 6+4 = 10 10 .
Чтобы разделить: 10 5 /10 3 = 10 5-3 = 10 2 .
5. Что такое 10 3 x 10 5 ?
А)…?
Давайте теперь решим немного более сложную задачу. 7. Что такое 3,16×10 7 x 2,99×10 8 ?
До сих пор мы обсуждали только умножение и деление с использованием десятичных степеней. Иногда вам нужно будет возводить числа в степень. В таком случае вы умножить показатели. Например, (10 5 ) 3 = 10 5×3 = 10 15 . В качестве другого примера (10 6 ) 1/2 = 10 6x(1/2) = 10 3 . Обратите внимание, что возведение числа в дробную степень эквивалентно извлечению корня. Вы должны быть осторожны при возведении чисел в степени, чтобы взять все числа, причастные к власти. Например, (3,14x24x10 3 ) 3 = (3,14 3 x 24 3 x (10 3 ) 3 = 31,0×1,38×10 4 x10 3×3 = 4,28×10 1+4+9 = 4,28×10 14 . 8. Что такое (2×10 3 ) 2 ?
Вау! Достаточно?
|
Правила экспоненты — ChiliMath
Правила экспоненты, также известные как «правила экспоненты», являются одними из правил алгебры, с которыми нам необходимо ознакомиться. Овладение этими основными правилами экспоненты вместе с основными правилами логарифмирования (также известными как «логарифмические правила») сделает ваше изучение алгебры очень продуктивным и приятным.
Начнем с изучения частей экспоненциального числа.
Показательное число или выражение состоит из двух частей. Первый компонент с основанием , который «несет» показатель степени , который является вторым компонентом в правом верхнем углу.
Взгляните на рисунок ниже.
Например, как записать 2 \cdot 2 \cdot 2 \cdot 2 \cdot 2 в экспоненциальном представлении?
Число 2 многократно умножается, поэтому оно автоматически становится основанием экспоненциального выражения. Обратите внимание, что это написано пять раз. Это значение указывает количество вхождений основания, поэтому оно должно быть показателем степени.
Читается как «от 2 до 5 степени».
Основой экспоненциального выражения также может быть буква или переменная. Предположим, у нас есть
. Поскольку переменная x умножается сама на себя десять раз, мы можем записать это в компактной форме.
Читается как «x в 10-й степени».
Краткий обзор семи (7) правил экспоненты
Теперь давайте рассмотрим семь (7) основных правил экспоненты.
Описание каждого правила экспоненты с примерами 90} = 1.- Упростите приведенное ниже экспоненциальное выражение.
Каждое выражение со скобками, возведёнными в нулевую степень, 0, встречающееся как в числителе, так и в знаменателе, будет просто заменено на 1. Обязательно уменьшите дробь до наименьшего члена.
ПРАВИЛО 2: Свойство отрицательного показателя степени
Любое ненулевое число, возведенное в отрицательную степень, не соответствует стандартной форме. Нам нужно будет сделать некоторую перестановку. Переместите основание с отрицательным показателем в противоположную часть дроби, а затем сделайте показатель степени положительным. Предположения здесь таковы: b \ne 0, а n — целое число. 9{-\,4}}.
По основанию 2 отрицательный показатель степени равен -4. Это можно исправить, переместив его в знаменатель и изменив знак экспоненты на положительный, используя отрицательное правило экспоненты.
- Упростите экспоненциальное выражение.
На этот раз в знаменателе находится основание с отрицательным показателем степени. Поднимите его до числителя, сделав показатель степени положительным.
- Упростите экспоненциальное выражение.
Оба показателя в числителе и знаменателе отрицательны. Имеет смысл поменять их местами вдоль дробной полосы. Переменная x уменьшается, а переменная y растет! Обязательно измените оба их показателя на положительные. 92}} \справа).
После умножения экспоненциальных выражений с одним и тем же основанием путем сложения их показателей степени мы получаем одну переменную с отрицательным показателем, а другую с нулевым показателем.
Не стесняйтесь применять два предыдущих изученных правила, а именно Правило 1 и Правило 2, чтобы еще больше упростить это выражение.
ПРАВИЛО 4: Частное свойство экспоненты
При делении экспоненциальных выражений с одним и тем же основанием, где основанием является ненулевое действительное число, скопируйте общее основание, а затем вычтите верхний показатель из нижнего показателя. Здесь мы должны предположить, что b \ne 0 и оба m и n принадлежат множеству целых чисел.
Примеры :
- Упростите частное экспоненциальных выражений.
Дробная черта означает, что мы собираемся делить. Имеет смысл применить правило деления экспоненты, то есть скопировать общее основание в числителе и знаменателе и вычесть верхний показатель на меньший показатель.
- Упростите экспоненциальные выражения.
Сравнивая выражения в числителе и знаменателе, я вижу, что есть два общих основания, х и у. Примените правило деления к каждой переменной. После этого переменная x будет содержать отрицательную экспоненту, поэтому используйте отрицательное правило экспоненты, чтобы решить проблему.
- Упростите экспоненциальные выражения.
Один из способов упростить это — пока игнорировать отрицательные показатели степени. Сначала примените правило деления и посмотрите, появятся ли снова отрицательные показатели. Если это так, используйте отрицательное правило экспоненты.
ПРАВИЛО 5: Степень степени Свойство экспоненты
Когда экспоненциальное выражение возводится в степень, скопируйте основание, которое является ненулевым действительным числом, затем умножьте внутренний и внешний показатели степени. Здесь мы предполагаем, что b \ne 0, а m и n — целые числа. 93}.
У этого выражения есть внутренние и внешние показатели. Правило степени в степени позволяет нам копировать основание и умножать показатели степени.
ПРАВИЛО 6: Степень произведения Свойство экспоненты
Когда произведение двух или более множителей возводится в степень, скопируйте каждый множитель, а затем умножьте его показатель степени на внешний показатель степени. Мы должны сделать это для каждого фактора внутри скобок, которые в данном случае являются a и b. Предположения: a \ne 0 или b \ne 0, а n — целое число. 92}.
Эта проблема очень похожа на предыдущую. Единственная разница в том, что есть три (3) множителя с показателями степени. Нам просто нужно распределить внешний показатель на каждый из внутренних показателей.
ПРАВИЛО 7: Степень частного Свойство экспоненты
Когда частное возведено в степень, скопируйте множитель в числитель, затем умножьте его показатель степени на внешний показатель степени. Мы должны сделать то же самое с множителем в знаменателе, где мы копируем его, а затем умножаем его показатель степени на внешний показатель степени. Здесь также нужно предположить, что a \ne 0 или b \ne 0, а m — целое число.
Пример:
- Упростите экспоненциальное выражение.
На самом деле, мы будем использовать здесь одновременно два свойства экспонент, чтобы полностью упростить это. В дополнение к правилу 7 (правило мощности частного) нам нужно будет применить правило 6 (правило мощности продукта). Проще говоря, просто рассматривайте числитель и знаменатель отдельно при распределении путем умножения внутреннего и внешнего показателей для каждого фактора.
Вас также может заинтересовать:
Правила логарифмирования
Отрицательные экспоненты – объяснение и примеры
Экспоненты – это степени или индексы. Показательное выражение состоит из двух частей: основания, обозначаемого как b, и показателя степени, обозначаемого как n. Общая форма экспоненциального выражения: b n . Например, 3 x 3 x 3 x 3 можно записать в экспоненциальной форме как 3 4 , где 3 — основание, а 4 — показатель степени. Они широко используются в алгебраических задачах, и по этой причине важно их выучить, чтобы облегчить изучение алгебры.
Многим учащимся будет трудно понять отрицательные числа и дроби. Обычно это полная катастрофа, когда к уравнениям добавляются отрицательные показатели. Ну не совсем. Изучение отрицательных показателей является основным фундаментом для решения сложных математических выражений. Это связано с тем, что он дает учащимся необходимые навыки и знания для решения сложных проблем в классе и вне его.
Если вы не знаете, с чего начать, не волнуйтесь, эта статья поможет вам превратить курс отрицательных показателей в положительный опыт.
Чтобы помочь вам лучше понять правило отрицательной степени, в этой статье подробно обсуждаются следующие темы правила отрицательной степени:
- Правило отрицательной степени
- Примеры отрицательной степени с отрицательными показателями
- Как умножать отрицательные показатели
- Деление отрицательных показателей
Прежде чем мы приступим к каждой из этих тем, давайте кратко повторим правила возведения в степень.
- Умножение степеней с одинаковым основанием: При умножении одинаковых основ сложите степени вместе.
- Правило отношения степеней: при делении одинаковых оснований степени вычитаются
- Правило степени степеней: умножение степеней вместе при возведении степени в другую степень
- Правило степени произведения: распределение мощности по каждому основанию при возведении нескольких переменных в степени
- Степень частного правила: Распределить мощность по каждому основанию при возведении нескольких переменных в степень
- Правило нулевой степени: Это правило подразумевает, что любое основание, возведенное в нулевую степень, равно единице.
- Правило отрицательного показателя степени: Чтобы преобразовать отрицательный показатель степени в положительный, запишите число в обратное число.
Как решать отрицательные показатели?
Закон отрицательных степеней гласит, что когда число возводится в отрицательную степень, мы делим 1 на основание, возведенное в положительную степень. Общая формула этого правила такова: а -т = 1/а м и (а/б) -n = (б/а) н .
Пример 1
Ниже приведены примеры работы правила отрицательного порядка: 0,125
b -n/m = 1 / b n/m = 1 / ( m √b) n
Отсюда следует, что если основание 2 возвести в отрицательную степень 1/ 2, это эквивалентно 1, деленному на основание 2, возведенному в положительную степень 1/2:
2 -1/2 = 1/2 1/2 = 1/ √ 2 = 0,7071
Вы должны заметить, что дробная отрицательная экспонента аналогична нахождению корня основания.
Дроби с отрицательными показателями
Правило подразумевает, что если дробь a/b возвести в отрицательную степень n, она будет равна 1, деленной на основание a/b, возведенное в положительную степень n:
(a/b) -n = 1 / (a/b) n = 1 / (a n /b n ) = b n /a n
Основание 2/3, возведенное в отрицательную степень числа 2 равно 1, деленному на основание 2/3, возведенное в положительный показатель степени 2. Другими словами, 1 делится на обратную величину основания, возведенного в положительный показатель степени 2
(2/3) -2 = 1 / (2/3) 2 = 1 / (2 2 /3 2 ) = (3/2) 2 = 9/4 = 2.25
Умножение отрицательных показателей
При умножении показателей с одинаковым основанием мы можем сложить показатели: / a n + m
Пример 2
2 -3 x 2 -4 = 2 -(3 + 4) = 2 -7 = 1 / 2 7 = 1 / (2 x 2 x 2 x 2 x 2 x 2 x 2) = 1 / 128 = 0,0078125
В случае разных оснований и общих показателей а и b мы можем перемножить а и b:
a -n ⋅ b -n = (a ⋅ b) -n
9292 Пример.
3 -2 x 4 – 2 = (3 x 4) -2 = 12 -2 = 1 / 12 2 = 1 / 12 2 = 1 / 12 2 = 1 / 12 2 = 0,0069444
In case both the bases and the exponents are different we calculate each exponent separately and then multiply:
a -n ⋅ b -m
Example 4
3 -2 x 4 -3 = (1/9) x (1/64) = 1/576 = 0,0017361
Как делить отрицательные показатели
В случае показателей с одинаковым основанием мы вычитаем показатели степени:
a -n / a – m = a -n + m
Example 5
2 -6 /2 -3 = 2 -6+3
= 2 — 3
= 1/2 3
= 1/8
Положительные дробные показатели и нуль.