| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0. 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Действия с десятичными дробями
Десятичные дроби можно складывать, вычитать, умножать и делить. Также, десятичные дроби можно сравнивать между собой.
Также, десятичные дроби можно сравнивать между собой.
В этом уроке мы рассмотрим каждую из этих операций по отдельности.
Сложение десятичных дробейКак мы знаем, десятичная дробь состоит из целой и дробной части. При сложении десятичных дробей, целые и дробные части складываются по отдельности.
Например, сложим десятичные дроби 3,2 и 5,3. Десятичные дроби удобнее складывать в столбик.
Запишем сначала эти две дроби в столбик, при этом целые части обязательно должны быть под целыми, а дробные под дробными. В школе это требование называют «запятая под запятой».
Запишем дроби в столбик так, чтобы запятая оказалась под запятой:
Складываем дробные части: 2 + 3 = 5. Записываем пятёрку в дробной части нашего ответа:
Теперь складываем целые части: 3 + 5 = 8. Записываем восьмёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 8,5. Значит, выражения 3,2 + 5,3 равно 8,5
Значит, выражения 3,2 + 5,3 равно 8,5
3,2 + 5,3 = 8,5
На самом деле не всё так просто как кажется на первый взгляд. Здесь тоже имеются свои подводные камни, о которых мы сейчас поговорим.
Разряды в десятичных дробях
У десятичных дробей, как и у обычных чисел, есть свои разряды. Это разряды десятых, разряды сотых, разряды тысячных. При этом разряды начинаются после запятой.
Первая цифра после запятой отвечает за разряд десятых, вторая цифра после запятой за разряд сотых, третья цифра после запятой за разряд тысячных.
Разряды в десятичных дробях хранят в себе нéкоторую полезную информацию. В частности, они сообщают сколько в десятичной дроби десятых частей, сотых частей и тысячных частей.
Например, рассмотрим десятичную дробь 0,345
Позиция, где находится тройка, называется разрядом десятых
Позиция, где находится четвёрка, называется разрядом сотых
Позиция, где находится пятёрка, называется разрядом тысячных
Посмотрим на данный рисунок. Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .
Видим, что в разряде десятых располагается тройка. Это говорит о том, что в десятичной дроби 0,345 содержится три десятых .
Смотрим дальше. В разряде сотых располагается четвёрка. Это говорит о том, что в десятичной дроби 0,345 содержится четыре сотых .
Смотрим дальше. В разряде тысячных находится пятёрка. Это говорит о том, что в десятичной дроби 0,345 содержится пять тысячных .
Если мы сложим дроби , и то получим изначальную десятичную дробь 0,345
Сначала мы получили ответ , но перевели его в десятичную дробь и получили 0,345.
При сложении десятичных дробей соблюдаются те же правила что и при сложении обычных чисел. Сложение десятичных дробей происходит по разрядам: десятые части складываются с десятыми частями, сотые с сотыми, тысячные с тысячными.
Поэтому при сложении десятичных дробей требуют соблюдать правило «запятая под запятой». Запятая под запятой обеспечивает тот самый порядок, в котором десятые части складываются с десятыми, сотые с сотыми, тысячные с тысячными.
Пример 1. Найти значение выражения 1,5 + 3,4
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
В первую очередь складываем дробные части 5 + 4 = 9. Записываем девятку в дробной части нашего ответа:
Теперь складываем целые части 1 + 3 = 4. Записываем четвёрку в целой части нашего ответа:
Теперь отделяем запятой целую часть от дробной. Для этого опять же соблюдаем правило «запятая под запятой»:
Получили ответ 4,9. Значит значение выражения 1,5 + 3,4 равно 4,9
1,5 + 3,4 = 4,9
Пример 2. Найти значение выражения: 3,51 + 1,22
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»
В первую очередь складываем дробную часть, а именно сотые части 1+2=3. Записываем тройку в сотой части нашего ответа:
Теперь складываем десятые части 5+2=7. Записываем семёрку в десятой части нашего ответа:
Теперь складываем целые части 3+1=4. Записываем четвёрку в целой части нашего ответа:
Записываем четвёрку в целой части нашего ответа:
Отделяем запятой целую часть от дробной, соблюдая правило «запятая под запятой»:
Получили ответ 4,73. Значит значение выражения 3,51 + 1,22 равно 4,73
3,51 + 1,22 = 4,73
Как и в обычных числах, при сложении десятичных дробей может произойти переполнение разряда. В этом случае в ответе записывается одна цифра, а остальные переносят на следующий разряд.
Пример 3. Найти значение выражения 2,65 + 3,27
Записываем в столбик данное выражение:
Складываем сотые части 5+7=12. Число 12 не поместится в сотой части нашего ответа. Поэтому в сотой части записываем цифру 2, а единицу переносим на следующий разряд:
Теперь складываем десятые части 6+2=8 плюс единица, которая досталась от предыдущей операции, получим 9. Записываем цифру 9 в десятой части нашего ответа:
Теперь складываем целые части 2+3=5. Записываем цифру 5 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 5,92. Значит значение выражения 2,65 + 3,27 равно 5,92
Значит значение выражения 2,65 + 3,27 равно 5,92
2,65 + 3,27 = 5,92
Пример 4. Найти значение выражения 9,5 + 2,8
Записываем в столбик данное выражение
Складываем дробные части 5 + 8 = 13. Число 13 не поместится в дробной часть нашего ответа, поэтому сначала записываем цифру 3, а единицу переносим на следующий разряд, точнее переносим её к целой части:
Теперь складываем целые части 9+2=11 плюс единица, которая досталась от предыдущей операции, получаем 12. Записываем число 12 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 12,3. Значит значение выражения 9,5 + 2,8 равно 12,3
9,5 + 2,8 = 12,3
При сложении десятичных дробей количество цифр после запятой в обеих дробях должно быть одинаковым. Если цифр не хватает, то эти места в дробной части заполняются нулями.
Пример 5. Найти значение выражения: 12,725 + 1,7
Прежде чем записывать в столбик данное выражение, сделаем количество цифр после запятой в обеих дробях одинаковым. В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
В десятичной дроби 12,725 после запятой три цифры, а в дроби 1,7 только одна. Значит в дроби 1,7 в конце нужно добавить два нуля. Тогда получим дробь 1,700. Теперь можно записать в столбик данное выражение и начать вычислять:
Складываем тысячные части 5+0=5. Записываем цифру 5 в тысячной части нашего ответа:
Складываем сотые части 2+0=2. Записываем цифру 2 в сотой части нашего ответа:
Складываем десятые части 7+7=14. Число 14 не поместится в десятой части нашего ответа. Поэтому сначала записываем цифру 4, а единицу переносим на следующий разряд:
Теперь складываем целые части 12+1=13 плюс единица, которая досталась от предыдущей операции, получаем 14. Записываем число 14 в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 14,425. Значит значение выражения 12,725+1,700 равно 14,425
12,725+ 1,700 = 14,425
Вычитание десятичных дробей
При вычитании десятичных дробей нужно соблюдать те же правила что и при сложении: «запятая под запятой» и «равное количества цифр после запятой».
Пример 1. Найти значение выражения 2,5 − 2,2
Записываем в столбик данное выражение, соблюдая правило «запятая под запятой»:
Вычисляем дробную часть 5−2=3. Записываем цифру 3 в десятой части нашего ответа:
Вычисляем целую часть 2−2=0. Записываем ноль в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 0,3. Значит значение выражения 2,5 − 2,2 равно 0,3
2,5 − 2,2 = 0,3
Пример 2. Найти значение выражения 7,353 — 3,1
В этом выражении разное количество цифр после запятой. В дроби 7,353 после запятой три цифры, а в дроби 3,1 только одна. Значит в дроби 3,1 в конце нужно добавить два нуля, чтобы сделать количество цифр в обеих дробях одинаковым. Тогда получим 3,100.
Теперь можно записать в столбик данное выражение и вычислить его:
Получили ответ 4,253. Значит значение выражения 7,353 − 3,1 равно 4,253
7,353 — 3,1 = 4,253
Как и в обычных числах, иногда придётся занимать единицу у соседнего разряда, если вычитание станет невозможным.
Пример 3. Найти значение выражения 3,46 − 2,39
Вычитаем сотые части 6−9. От число 6 не вычесть число 9. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда число 6 обращается в число 16. Теперь можно вычислить сотые части 16−9=7. Записываем семёрку в сотой части нашего ответа:
Теперь вычитаем десятые части. Поскольку мы заняли в разряде десятых одну единицу, то цифра, которая там располагалась, уменьшилась на одну единицу. Другими словами, в разряде десятых теперь не цифра 4, а цифра 3. Вычислим десятые части 3−3=0. Записываем ноль в десятой части нашего ответа:
Теперь вычитаем целые части 3−2=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,07. Значит значение выражения 3,46−2,39 равно 1,07
3,46−2,39=1,07
Пример 4. Найти значение выражения 3−1,2
В этом примере из целого числа вычитается десятичная дробь. Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,2 оказалась под числом 3
Запишем данное выражение столбиком так, чтобы целая часть десятичной дроби 1,2 оказалась под числом 3
Теперь сделаем количество цифр после запятой одинаковым. Для этого после числа 3 поставим запятую и допишем один ноль:
Теперь вычитаем десятые части: 0−2. От нуля не вычесть число 2. Поэтому нужно занять единицу у соседнего разряда. Заняв единицу у соседнего разряда, 0 обращается в число 10. Теперь можно вычислить десятые части 10−2=8. Записываем восьмёрку в десятой части нашего ответа:
Теперь вычитаем целые части. Раньше в целой располагалось число 3, но мы заняли у него одну единицу. В результате оно обратилось в число 2. Поэтому из 2 вычитаем 1. 2−1=1. Записываем единицу в целой части нашего ответа:
Отделяем запятой целую часть от дробной:
Получили ответ 1,8. Значит значение выражения 3−1,2 равно 1,8
3 − 1,2 = 1,8
Умножение десятичных дробей
Умножение десятичных дробей это просто и даже увлекательно. Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Чтобы перемножить десятичные дроби, нужно перемножить их как обычные числа, не обращая внимания на запятые.
Получив ответ, необходимо отделить запятой целую часть от дробной. Чтобы сделать это, надо посчитать количество цифр после запятой в обеих дробях, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Пример 1. Найти значение выражения 2,5 × 1,5
Перемножим эти десятичные дроби как обычные числа, не обращая внимания на запятые. Чтобы не обращать внимания на запятые, можно на время представить, что они вообще отсутствуют:
Получили 375. В этом числе необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в дробях 2,5 и 1,5. В первой дроби после запятой одна цифра, во второй дроби тоже одна. Итого две цифры.
Возвращаемся к числу 375 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 3,75. Значит значение выражения 2,5 × 1,5 равно 3,75
2,5 × 1,5 = 3,75
Пример 2. Найти значение выражения 12,85 × 2,7
Найти значение выражения 12,85 × 2,7
Перемножим эти десятичные дроби, не обращая внимания на запятые:
Получили 34695. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 12,85 и 2,7. В дроби 12,85 после запятой две цифры, в дроби 2,7 одна цифра — итого три цифры.
Возвращаемся к числу 34695 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую:
Получили ответ 34,695. Значит значение выражения 12,85 × 2,7 равно 34,695
12,85 × 2,7 = 34,695
Умножение десятичной дроби на обычное число
Иногда возникают ситуации, когда требуется умножить десятичную дробь на обычное число.
Чтобы перемножить десятичную дробь и обычное число, нужно перемножить их, не обращая внимания на запятую в десятичной дроби. Получив ответ, необходимо отделить запятой целую часть от дробной. Для этого нужно посчитать количество цифр после запятой в десятичной дроби, затем в ответе отсчитать справа столько же цифр и поставить запятую.
Например, умножим 2,54 на 2
Умножаем десятичную дробь 2,54 на обычное число 2, не обращая внимания на запятую:
Получили число 508. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,54. В дроби 2,54 после запятой две цифры.
Возвращаемся к числу 508 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 5,08. Значит значение выражения 2,54 × 2 равно 5,08
2,54 × 2 = 5,08
Умножение десятичных дробей на 10, 100, 1000
Умножение десятичных дробей на 10, 100 или 1000 выполняется таким же образом, как и умножение десятичных дробей на обычные числа. Нужно выполнить умножение, не обращая внимания на запятую в десятичной дроби, затем в ответе отделить целую часть от дробной, отсчитав справа столько же цифр, сколько было цифр после запятой в десятичной дроби.
Например, умножим 2,88 на 10
Умножим десятичную дробь 2,88 на 10, не обращая внимания на запятую в десятичной дроби:
Получили 2880. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дроби 2,88. Видим, что в дроби 2,88 после запятой две цифры.
Возвращаемся к числу 2880 и начинаем двигаться справа налево. Нам нужно отсчитать две цифры справа и поставить запятую:
Получили ответ 28,80. Отбросим последний ноль — получим 28,8. Значит значение выражения 2,88×10 равно 28,8
2,88 × 10 = 28,8
Есть и второй способ умножения десятичных дробей на 10, 100, 1000. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается вправо на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 2,88×10 этим способом. Не приводя никаких вычислений, сразу же смотрим на множитель 10. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 2,88 передвигаем запятую вправо на одну цифру, получим 28,8.
2,88 × 10 = 28,8
Попробуем умножить 2,88 на 100. Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
Сразу же смотрим на множитель 100. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 2,88 передвигаем запятую вправо на две цифры, получаем 288
2,88 × 100 = 288
Попробуем умножить 2,88 на 1000. Сразу же смотрим на множитель 1000. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 2,88 передвигаем запятую вправо на три цифры. Третьей цифры там нет, поэтому мы дописываем ещё один ноль. В итоге получаем 2880.
2,88 × 1000 = 2880
Умножение десятичных дробей на 0,1 0,01 и 0,001
Умножение десятичных дробей на 0,1, 0,01 и 0,001 происходит таким же образом, как и умножение десятичной дроби на десятичную дробь. Необходимо перемножить дроби, как обычные числа, и в ответе поставить запятую, отсчитав столько цифр справа, сколько цифр после запятой в обеих дробях.
Например, умножим 3,25 на 0,1
Умножаем эти дроби, как обычные числа, не обращая внимания на запятые:
Получили 325. В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
В этом числе нужно отделить запятой целую часть от дробной. Для этого необходимо посчитать количество цифр после запятой в дробях 3,25 и 0,1. В дроби 3,25 после запятой две цифры, в дроби 0,1 одна цифра. Итого три цифры.
Возвращаемся к числу 325 и начинаем двигаться справа налево. Нам нужно отсчитать три цифры справа и поставить запятую. Отсчитав три цифры мы обнаруживаем, что цифры закончились. В этом случае нужно дописать один ноль и поставить запятую:
Получили ответ 0,325. Значит значение выражения 3,25 × 0,1 равно 0,325
3,25 × 0,1 = 0,325
Есть и второй способ умножения десятичных дробей на 0,1, 0,01 и 0,001. Этот способ намного проще и удобнее. Он заключается в том, что запятая в десятичной дроби передвигается влево на столько цифр, сколько нулей во множителе.
Например, решим предыдущий пример 3,25 × 0,1 этим способом. Не приводя никаких вычислений сразу же смотрим на множитель 0,1. Нас интересует сколько в нём нулей. Видим, что в нём один ноль. Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
Теперь в дроби 3,25 передвигаем запятую влево на одну цифру. Передвинув запятую на одну цифру влево мы видим, что перед тройкой больше нет никаких цифр. В этом случае дописываем один ноль и ставим запятую. В результате получаем 0,325
3,25 × 0,1 = 0,325
Попробуем умножить 3,25 на 0,01. Сразу же смотрим на множитель 0,01. Нас интересует сколько в нём нулей. Видим, что в нём два нуля. Теперь в дроби 3,25 передвигаем запятую влево на две цифры, получаем 0,0325
3,25 × 0,01 = 0,0325
Попробуем умножить 3,25 на 0,001. Сразу же смотрим на множитель 0,001. Нас интересует сколько в нём нулей. Видим, что в нём три нуля. Теперь в дроби 3,25 передвигаем запятую влево на три цифры, получаем 0,00325
3,25 × 0,001 = 0,00325
Нельзя путать умножение десятичных дробей на 0,1, 0,001 и 0,001 с умножением на 10, 100, 1000. Типичная ошибка большинства людей.
При умножении на 10, 100, 1000 запятая переносится вправо на столько же цифр сколько нулей во множителе.
А при умножении на 0,1, 0,01 и 0,001 запятая переносится влево на столько же цифр сколько нулей во множителе.
Если на первых порах это сложно запомнить, можно пользоваться первым способом, в котором умножение выполняется как с обычными числами. В ответе нужно будет отделить целую часть от дробной, отсчитав справа столько же цифр, сколько цифр после запятой в обеих дробях.
Деление меньшего числа на большее. Продвинутый уровень.
В одном из предыдущих уроков мы сказали, что при делении меньшего числа на большее получается дробь, в числителе которой делимое, а в знаменателе – делитель.
Например, чтобы разделить одно яблоко на двоих, нужно в числитель записать 1 (одно яблоко), а в знаменатель записать 2 (двое друзей). В результате получим дробь . Значит каждому другу достанется по яблока. Другими словами, по половине яблока. Дробь это ответ к задаче «как разделить одно яблоко на двоих»
Оказывается, можно решать эту задачу и дальше, если разделить 1 на 2. Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.
Ведь дробная черта в любой дроби означает деление, а значит и в дроби это деление разрешено. Но как? Мы ведь привыкли к тому, что делимое всегда больше делителя. А здесь наоборот, делимое меньше делителя.
Всё станет ясным, если вспомнить, что дробь означает дробление, деление, разделение. А значит и единица может быть раздроблена на сколько угодно частей, а не только на две части.
При разделении меньшего числа на большее получается десятичная дробь, в которой целая часть будет 0 (нулевой). Дробная часть же может быть любой.
Итак, разделим 1 на 2. Решим этот пример уголком:
Единицу на два просто так нацело не разделить. Если задать вопрос «сколько двоек в единице», то ответом будет 0. Поэтому в частном записываем 0 и ставим запятую:
Теперь как обычно умножаем частное на делитель, чтобы вытащить остаток:
Настал момент, когда единицу можно дробить на две части. Для этого справа от полученной единички дописываем ещё один ноль:
Получили 10. Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Делим 10 на 2, получаем 5. Записываем пятёрку в дробной части нашего ответа:
Теперь вытаскиваем последний остаток, чтобы завершить вычисление. Умножаем 5 на 2, получаем 10
Получили ответ 0,5. Значит дробь равна 0,5
Половину яблока можно записать и с помощью десятичной дроби 0,5. Если сложить эти две половинки (0,5 и 0,5), мы опять получим изначальное одно целое яблоко:
Этот момент также можно понять, если представить, как 1 см делится на две части. Если 1 сантиметр разделить на 2 части, то получится 0,5 см
Пример 2. Найти значение выражения 4 : 5
Сколько пятёрок в четвёрке? Нисколько. Записываем в частном 0 и ставим запятую:
Умножаем 0 на 5, получаем 0. Записываем ноль под четвёркой. Сразу же вычитаем этот ноль из делимого:
Теперь начнём дробить (делить) четвёрку на 5 частей. Для этого справа от 4 дописываем ноль и делим 40 на 5, получаем 8. Записываем восьмёрку в частном.
Завершаем пример, умножив 8 на 5, и получив 40:
Получили ответ 0,8. Значит значение выражения 4 : 5 равно 0,8
Значит значение выражения 4 : 5 равно 0,8
Пример 3. Найти значение выражения 5 : 125
Сколько чисел 125 в пятёрке? Нисколько. Записываем 0 в частном и ставим запятую:
Умножаем 0 на 125, получаем 0. Записываем 0 под пятёркой. Сразу же вычитаем из пятёрки 0
Теперь начнём дробить (делить) пятёрку на 125 частей. Для этого справа от этой пятёрки запишем ноль:
Делим 50 на 125. Сколько чисел 125 в числе 50? Нисколько. Значит в частном опять записываем 0
Умножаем 0 на 125, получаем 0. Записываем этот ноль под 50. Сразу же вычитаем 0 из 50
Теперь делим число 50 на 125 частей. Для этого справа от 50 запишем ещё один ноль:
Делим 500 на 125. Сколько чисел 125 в числе 500. В числе 500 четыре числа 125. Записываем четвёрку в частном:
Завершаем пример, умножив 4 на 125, и получив 500
Получили ответ 0,04. Значит значение выражения 5 : 125 равно 0,04
Деление чисел без остатка
В уроке деление мы научились делить числа с остатком. Например, чтобы разделить 9 на 5, мы поступали следующим образом:
Например, чтобы разделить 9 на 5, мы поступали следующим образом:
и далее говорили, что «девять разделить на пять будет один и четыре в остатке».
Теперь мы получили необходимые знания, чтобы разделить 9 на 5 без остатка. Наша задача раздробить остаток 4 на 5 частей. Другими словами, разделить меньшее число на большее.
Итак, поставим в частном после единицы запятую, тем самым указывая, что деление целых частей закончилось и мы приступаем к дробной части:
Допишем ноль к остатку 4
Теперь делим 40 на 5, получаем 8. Записываем восьмёрку в частном:
Что делать дальше мы уже знаем. Вытаскиваем остаток (если есть). Умножаем восьмёрку на делитель 5, и записываем полученный результат под 40:
40−40=0. Получили 0 в остатке. Значит деление на этом полностью завершено. При делении 9 на 5 получается десятичная дробь 1,8:
9 : 5 = 1,8
Пример 2. Разделить 84 на 5 без остатка
Сначала разделим 84 на 5 как обычно с остатком:
Получили в частном 16 и еще 4 в остатке. Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь разделим этот остаток на 5. Поставим в частном запятую, а к остатку 4 допишем 0
Теперь делим 40 на 5, получаем 8. Записываем восьмерку в частном после запятой:
и завершаем пример, проверив есть ли еще остаток:
Деление десятичной дроби на обычное число
Десятичная дробь, как мы знаем состоит из целой и дробной части. При делении десятичной дроби на обычное число в первую очередь нужно:
- разделить целую часть десятичной дроби на это число;
- после того, как целая часть будет разделена, нужно в частном сразу же поставить запятую и продолжить вычисление, как в обычном делении.
Например, разделим 4,8 на 2
Запишем этот пример уголком:
Теперь разделим целую часть на 2. Четыре разделить на два будет два. Записываем двойку в частном и сразу же ставим запятую:
Теперь умножаем частное на делитель и смотрим есть ли остаток от деления:
4−4=0. Остаток равен нулю. Ноль пока не записываем, поскольку решение не завершено.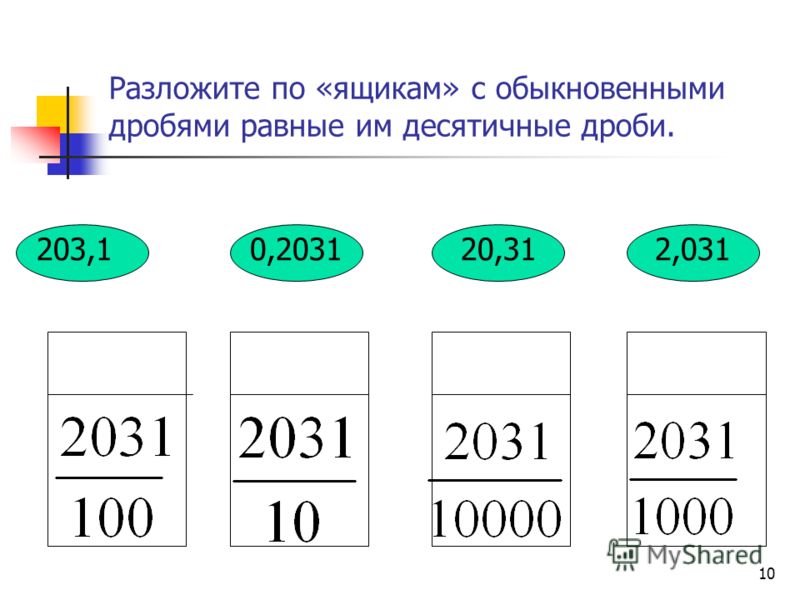 Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
Далее продолжаем вычислять, как в обычном делении. Сносим 8 и делим её на 2
8 : 2 = 4. Записываем четвёрку в частном и сразу умножаем её на делитель:
Получили ответ 2,4. Значение выражения 4,8 : 2 равно 2,4
Пример 2. Найти значение выражения 8,43 : 3
Делим 8 на 3, получаем 2. Сразу же ставим запятую после двойки:
Теперь умножаем частное на делитель 2 × 3 = 6. Записываем шестёрку под восьмёркой и находим остаток:
Далее продолжаем вычислять, как в обычном делении. Сносим 4
Делим 24 на 3, получаем 8. Записываем восьмёрку в частном. Сразу же умножаем её на делитель, чтобы найти остаток от деления:
24−24=0. Остаток равен нулю. Ноль пока не записываем. Сносим последнюю тройку из делимого и делим на 3, получим 1. Сразу же умножаем 1 на 3, чтобы завершить этот пример:
Получили ответ 2,81. Значит значение выражения 8,43 : 3 равно 2,81
Деление десятичной дроби на десятичную дробь
Чтобы разделить десятичную дробь на десятичную дробь, надо в делимом и в делителе перенести запятую вправо на столько же цифр, сколько их после запятой в делителе, и затем выполнить деление на обычное число.
Например, разделим 5,95 на 1,7
Запишем уголком данное выражение
Теперь в делимом и в делителе перенесём запятую вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит мы должны в делимом и в делителе перенести запятую вправо на одну цифру. Переносим:
После перенесения запятой вправо на одну цифру десятичная дробь 5,95 обратилась в дробь 59,5. А десятичная дробь 1,7 после перенесения запятой вправо на одну цифру обратилась в обычное число 17. А как делить десятичную дробь на обычное число мы уже знаем. Дальнейшее вычисление не составляет особого труда:
Запятая переносится вправо с целью облегчить деление. Это допускается по причине того, что при умножении или делении делимого и делителя на одно и то же число, частное не меняется. Что это значит?
Это одна из интересных особенностей деления. Его называют свойством частного. Рассмотрим выражение 9 : 3 = 3. Если в этом выражении делимое и делитель умножить или разделить на одно и то же число, то частное 3 не изменится.
Давайте умножим делимое и делитель на 2, и посмотрим, что из этого получится:
(9 × 2) : (3 × 2) = 18 : 6 = 3
Как видно из примера, частное не поменялось.
Тоже самое происходит, когда мы переносим запятую в делимом и в делителе. В предыдущем примере, где мы делили 5,91 на 1,7 мы перенесли в делимом и делителе запятую на одну цифру вправо. После переноса запятой, дробь 5,91 преобразовалась в дробь 59,1 а дробь 1,7 преобразовалась в обычное число 17. На самом деле здесь происходило умножение на 10. Вот как это выглядело:
5,91 × 10 = 59,1
1,7 × 10 = 17
Поэтому от количества цифр после запятой в делителе зависит то, на что будет умножено делимое и делитель. Другими словами, от количества цифр после запятой в делителе будет зависеть то, на сколько цифр в делимом и в делителе запятая будет перенесена вправо.
Деление десятичной дроби на 10, 100, 1000
Деление десятичной дроби на 10, 100, или 1000 осуществляется таким же образом, как и деление десятичной дроби на обычное число. Например, разделим 2,1 на 10. Решим этот пример уголком:
Например, разделим 2,1 на 10. Решим этот пример уголком:
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится влево на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 2,1 : 10. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 2,1 нужно перенести запятую влево на одну цифру. Переносим запятую влево на одну цифру и видим, что там больше не осталось цифр. В этом случае перед цифрой дописываем ещё один ноль. В итоге получаем 0,21
2,1 : 10 = 0,21
Попробуем разделить 2,1 на 100. В числе 100 два нуля. Значит в делимом 2,1 надо перенести запятую влево на две цифры:
2,1 : 100 = 0,021
Попробуем разделить 2,1 на 1000. В числе 1000 три нуля. Значит в делимом 2,1 надо перенести запятую влево на три цифры:
2,1 : 1000 = 0,0021
Деление десятичной дроби на 0,1, 0,01 и 0,001
Деление десятичной дроби на 0,1, 0,01, и 0,001 осуществляется таким же образом, как и деление десятичной дроби на десятичную дробь. В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
В делимом и в делителе надо перенести запятую вправо на столько цифр, сколько их после запятой в делителе.
Например, разделим 6,3 на 0,1. В первую очередь перенесём запятые в делимом и в делителе вправо на столько же цифр, сколько их после запятой в делителе. В делителе после запятой одна цифра. Значит переносим запятые в делимом и в делителе вправо на одну цифру.
После перенесения запятой вправо на одну цифру, десятичная дробь 6,3 превращается в обычное число 63, а десятичная дробь 0,1 после перенесения запятой вправо на одну цифру превращается в единицу. А разделить 63 на 1 очень просто:
63 : 1 = 63
Значит значение выражения 6,3 : 0,1 равно 63
6,3 : 0,1 = 63
Но есть и второй способ. Он более лёгкий. Суть этого способа в том, что запятая в делимом переносится вправо на столько цифр, сколько нулей в делителе.
Решим предыдущий пример этим способом. 6,3 : 0,1. Смотрим на делитель. Нас интересует сколько в нём нулей. Видим, что там один ноль. Значит в делимом 6,3 нужно перенести запятую вправо на одну цифру. Переносим запятую вправо на одну цифру и получаем 63
Переносим запятую вправо на одну цифру и получаем 63
6,3 : 0,1 = 63
Попробуем разделить 6,3 на 0,01. В делителе 0,01 два нуля. Значит в делимом 6,3 надо перенести запятую вправо на две цифры. Но в делимом после запятой только одна цифра. В этом случае в конце нужно дописать ещё один ноль. В результате получим 630
6,3 : 0,01 = 630
Попробуем разделить 6,3 на 0,001. В делителе 0,001 три нуля. Значит в делимом 6,3 надо перенести запятую вправо на три цифры:
6,3 : 0,001 = 6300
Задания для самостоятельного решения
Задание 1. Выполните сложение:
0,6 + 0,3
Решение:
Показать решение
Задание 2. Выполните сложение:
1,2 + 5,3
Решение:
Показать решение
Задание 3. Выполните сложение:
1,6 + 0,4
Решение:
Показать решение
Задание 4. Выполните сложение:
0,8 + 0,5
Решение:
Показать решение
Задание 5. Выполните вычитание:
0,9 − 0,4
Решение:
Показать решение
Задание 6. Выполните вычитание:
Выполните вычитание:
2 − 0,3
Решение:
Показать решение
Задание 7. Выполните вычитание:
9 − 7,8
Решение:
Показать решение
Задание 8. Выполните вычитание:
4 − 1,8
Решение:
Показать решение
Задание 9. Выполните умножение:
3,2 × 1,8
Решение:
Показать решение
Задание 10. Выполните умножение:
9,3 × 5,8
Решение:
Показать решение
Задание 11. Выполните умножение:
0,23 × 0,07
Решение:
Показать решение
Задание 12. Выполните умножение:
3,14 × 0,25
Решение:
Показать решение
Задание 13. Выполните деление:
9,36 : 6
Решение:
Показать решение
Задание 14. Выполните деление:
0,169 : 13
Решение:
Показать решение
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Десятичная запись дробных чисел / Десятичные дроби / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Десятичные дроби
- Десятичная запись дробных чисел
Среди обыкновенных дробей выделяют дроби, у которых в знаменателе стоит единица с нулями, т. е. 10, 100, 1 000 и т.д., для таких дробей существует специальная форма записи, в которой используют запятую, например, вместо пишут 0,1 (читают: ноль целых одна десятая), пишут 2,34 (читают: две целых тридцать четыре сотых), пишут 25,657 (читают: двадцать пять целых шестьсот пятьдесят семь тысячных). Такую форму записи дробей называют десятичной, а саму дробь — десятичной дробью. Запятая отделяет целую часть от дробной.
е. 10, 100, 1 000 и т.д., для таких дробей существует специальная форма записи, в которой используют запятую, например, вместо пишут 0,1 (читают: ноль целых одна десятая), пишут 2,34 (читают: две целых тридцать четыре сотых), пишут 25,657 (читают: двадцать пять целых шестьсот пятьдесят семь тысячных). Такую форму записи дробей называют десятичной, а саму дробь — десятичной дробью. Запятая отделяет целую часть от дробной.
Обратите внимание: после запятой стоит столько цифр, сколько нулей стоит в записи знаменателя соответствующей обыкновенной дроби.
Поэтому вместо пишут 2,03 (читают: две целых три сотых), т.е. чтобы записать данную дробь в десятичной форме, после запятой перед тем числом, которое стоит в числителе мы дописываем ноль, чтобы после запятой было два знака, т.к. в знаменателе стоит два нуля, а вместо пишут 12,004 (читают: двенадцать целых 4 тысячных), т. е. чтобы записать данную дробь в десятичной форме, после запятой перед тем числом, которое стоит в числителе мы дописываем два нуля, чтобы после запятой было три знака, т.к. в знаменателе стоит три нуля.
е. чтобы записать данную дробь в десятичной форме, после запятой перед тем числом, которое стоит в числителе мы дописываем два нуля, чтобы после запятой было три знака, т.к. в знаменателе стоит три нуля.
Разряды десятичных дробей
Разрядные единицы:
записываются так:
0,1; 0,01; 0,001; 0,0001; 0,00001; … .
| При чтении десятичной дроби сначала называют ее часть, стоящую перед запятой, и добавляют слово «целых»; затем называют часть, стоящую после запятой, и добавляют название последнего разряда. |
Например, в десятичной дроби 8,4567 последний разряд — это десятитысячные. Поэтому читают ее так: 8 целых 4567 десятитысячных.
Чтобы несократимую дробь преобразовать в десятичную, необходимо привести ее к одному из знаменателей 10, 100, 1 000 и т.д. |
Примеры:
Несократимую дробь можно преобразовать в десятичную только тогда, когда разложение знаменателя на простые множители не содержит чисел, отличных от 2 и 5. |
Примеры:
1) ;
2) — нельзя преобразовать в десятичную дробь (в разложении знаменателя на простые множители есть 3).
| Чтобы преобразовать обыкновенную дробь в десятичную, можно ее числитель разделить на знаменатель. |
Пример:
| — | 9 | 0 | 0 | 0 | 0 | 1 | 6 | ||||||
| 8 | 0 | 0 | 5 | 6 | 2 | 5 | |||||||
| — | 0 | 0 | |||||||||||
| 9 | 6 | ||||||||||||
| — | 4 | 0 | |||||||||||
| 3 | 2 | ||||||||||||
| — | 8 | 0 | |||||||||||
| 8 | 0 | ||||||||||||
| 0 |
Не любую обыкновенную дробь можно записать в виде десятичной дроби. Например, дробь обратить в десятичную нельзя. Разделим числитель данной дроби на знаменатель получим:
Например, дробь обратить в десятичную нельзя. Разделим числитель данной дроби на знаменатель получим:
| — | 1 | 3 | 1 | 8 | ||||||||||
| 1 | 2 | 6 | 0 | , | 7 | 2 | 2 | 2 | . | . | . | |||
| — | 4 | 0 | ||||||||||||
| 3 | 6 | |||||||||||||
| — | 4 | 0 | ||||||||||||
| 3 | 6 | |||||||||||||
| — | 4 | 0 | ||||||||||||
| 3 | 6 | |||||||||||||
| 4 |
Мы видим, что деление можно продолжать бесконечно. И результат деления будет 0,72222… . В данном случае точки означают, что цифра 2 периодически повторяется бесконечно много раз.
И результат деления будет 0,72222… . В данном случае точки означают, что цифра 2 периодически повторяется бесконечно много раз.
Число 0,72222… — это бесконечная периодическая десятичная дробь, или периодическая дробь. Данную дробь принято записывать: 0,7(2) и читать: «нуль целых семь десятых и два в периоде». Цифру (2) называют периодом дроби 0,7(2). Записываем так:
При этом полученную периодическую дробь мы можем округлить до любого из разрядов, например, округлим дробь 0,72222… до десятых, получим:
0,7. В данном случае число 0,7 называют десятичным приближением до десятых дроби . Запишем:
0,7.
Чтобы найти десятичное приближение обыкновенной дроби до нужного разряда, надо: 1) выполнить деление до следующего разряда; 2) полученную конечную десятичную дробь или бесконечную периодическую десятичную дробь округлить до нужного разряда. |
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Сравнение десятичных дробей
Сложение и вычитание десятичных дробей
Приближенные значения чисел. Округление чисел
Умножение десятичных дробей
Деление десятичных дробей
Среднее арифметическое
Десятичные дроби
Правило встречается в следующих упражнениях:
5 класс
Задание 1552, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1626, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1697, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Задание 8, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
Номер 810, Мерзляк, Полонский, Якир, Учебник
Номер 2, Мерзляк, Полонский, Якир, Учебник
Номер 826, Мерзляк, Полонский, Якир, Учебник
Номер 835, Мерзляк, Полонский, Якир, Учебник
Номер 1154, Мерзляк, Полонский, Якир, Учебник
6 класс
Номер 547, Мерзляк, Полонский, Якир, Учебник
Номер 568, Мерзляк, Полонский, Якир, Учебник
Номер 611, Мерзляк, Полонский, Якир, Учебник
Задание 245, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 685, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 688, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 856, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1056, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1256, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
Задание 1415, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 24, Мерзляк, Полонский, Якир, Учебник
Номер 149, Мерзляк, Полонский, Якир, Учебник
Номер 150, Мерзляк, Полонский, Якир, Учебник
Номер 160, Мерзляк, Полонский, Якир, Учебник
Номер 162, Мерзляк, Полонский, Якир, Учебник
Номер 297, Мерзляк, Полонский, Якир, Учебник
Номер 470, Мерзляк, Полонский, Якир, Учебник
Номер 528, Мерзляк, Полонский, Якир, Учебник
Номер 586, Мерзляк, Полонский, Якир, Учебник
Номер 636, Мерзляк, Полонский, Якир, Учебник
Математика.
 {-4}&\!\!\!\!=~\phantom{0}1{,}0009. \end{array}$
{-4}&\!\!\!\!=~\phantom{0}1{,}0009. \end{array}$Замечание. Надо признаться, что запятая для этой роли подходит плохо. Как мы теперь будем отличать число $1{,}2$ от перечисления двух чисел, единицы и двойки: ${1, 2}$? Единственное отличие заключается в том, что в перечислении ${1, 2}$ после запятой стоит пробел, а в числе $1{,}2$ такого пробела нет. Но это, прямо скажем, не такое отличие, которое сразу бросается в глаза. Но такова традиция, получившая распространение в европейских странах, и нам придется ей следовать. Во избежание путаницы мы теперь будем использовать при перечислениях не запятую, а точку с запятой: ${1; 2}$. В англоязычной литературе и в языках программирования в качестве десятичного разделителя используют точку, что следует признать более удачным выбором.
Новый вид дробей, в написании которых используется запятая, называются десятичными — для того чтобы отличать их от дробей, с которыми мы имели дело ранее, называемых обыкновенными. {-2}}$) и так далее.
{-2}}$) и так далее.
Сложение и вычитание десятичных дробей делается очень просто, так как они легко приводятся к одному знаменателю. Например,
$\begin{align*} 0{,}432\phantom{.}\!&+ 0{,}1 =\\ 0{,}432\phantom{.}\!&+ 0{,}100 =\\ 0{,}532.\!&\phantom{+} \end{align*}$
Или же:
$\begin{align*} 0{,}432\phantom{.}\!&- 0{,}1 =\\ 0{,}432\phantom{.}\!&- 0{,}100 =\\ 0{,}332.\!&\phantom{+} \end{align*}$
Впрочем, вторые строчки в обеих этих цепочках равенств — совершенно лишние. Приписывать «недостающие» нули можно и мысленно. При сложении и вычитании столбиком запятые у чисел должны находиться одна под другой:
$+$ | $3$ | $2,$ | $1$ |
|
|
| $0,$ | $2$ | $4$ | $6$ | |
| $3$ | $2,$ | $3$ | $4$ | $6$ |
Умножение десятичных дробей на $\boldsymbol{10^n}$
Мы уже знаем, что всякую десятичную дробь с дробной частью, не равной нулю, можно представить как
$a \cdot 10^k$,
где $a$ и $k$ — целые числа, причем ${k
$1234{,}0$. {k+n}$.
{k+n}$.
Если оба показателя степени, $k$ и $n$, больше нуля, то мы приходим к давно известному нам правилу умножения «круглых» чисел: мы отбрасываем поначалу все конечные нули, выполняем умножение без них, а потом к результату приписываем столько нулей, сколько мы раньше отбросили в обоих сомножителях вместе взятых. Например,
$3\underline{00} \cdot 5\underline{0} = 15\underline{000}$;
Это же правило формально действует и в том случае, когда один из показателей степени положителен, а другой равен нулю:
$3\underline{00} \cdot 5 = 15\underline{00}$;
Если оба показателя степени, $k$ и $n$, меньше нуля, то числа $x$ и $y$ являются дробными. Для них правило умножения таково: мы отбрасываем в их записи запятые, выполняем умножение как с целыми числами, а потом в ответе отделяем запятой столько знаков, сколько их было отделено в обоих сомножителях вместе взятых. Например,
$0{,}\underline{03} \cdot 0{,}\underline{5} = 0{,}\underline{015}$;
Это же правило формально действует и в том случае, когда один из показателей степени отрицателен, а другой равен нулю:
$0,\underline{03} \cdot 5 = 0{,}\underline{15}$;
Если же один из показателей степени положителен, а другой отрицателен, тогда мы имеем дело с умножением «круглого» числа на дробное.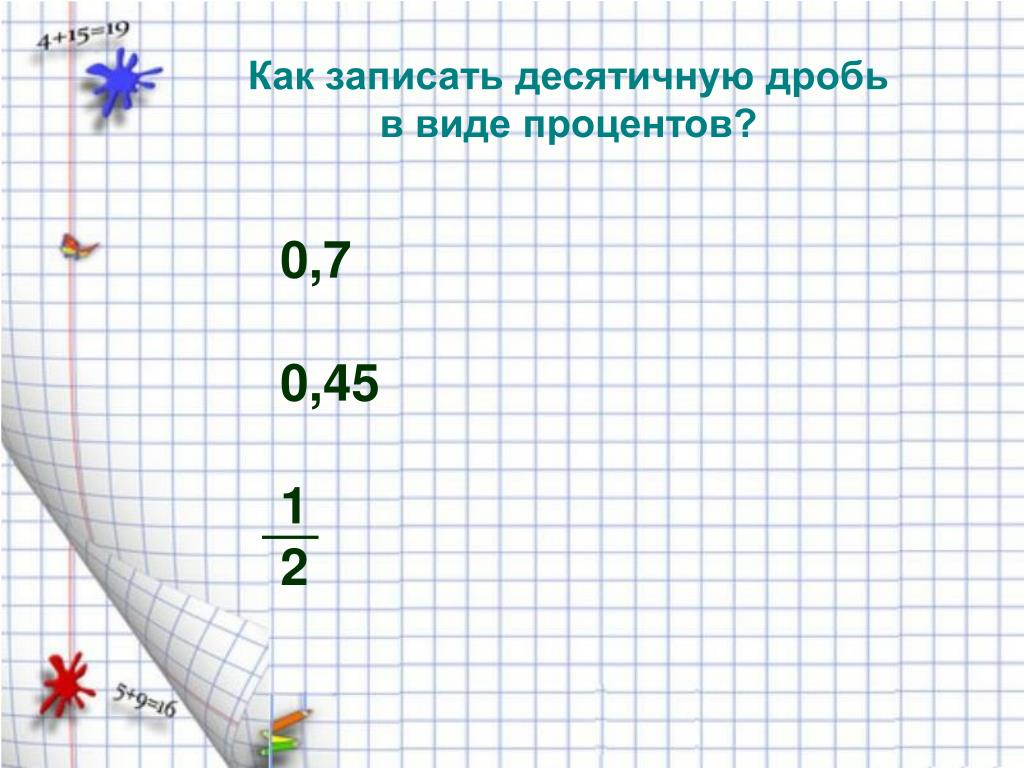 {k-n}}$. В случае когда $a$ делится нацело на $b$ результатом деления $x/y$ является десятичная дробь (возможно, с нулевой дробной частью).
{k-n}}$. В случае когда $a$ делится нацело на $b$ результатом деления $x/y$ является десятичная дробь (возможно, с нулевой дробной частью).
Из «бесконечного» сборника типовых упражнений
Примечание: во всех приведенных ниже примерах деление сводится к делению нацело.
Примеры в два действия с десятичными дробями
Примеры в четыре действия с десятичными дробями
Примеры в семь действий с десятичными дробями («одноэтажная» запись)
То же («многоэтажная» запись, LaTeX)
Примеры с десятичными дробями на сокращение «большой» дроби («одноэтажная запись»)
То же («многоэтажная» запись, LaTeX)
Что такое 1/5 в виде десятичной дроби? (Преобразовать 1/5 в десятичную)
Преобразование 1/5 в десятичную, возможно, является одним из самых простых вычислений, которые вы можете сделать. В этом (очень коротком) руководстве мы покажем вам, как превратить любую дробь в десятичную менее чем за 3 секунды! Вот так!
Хотите быстро узнать или показать учащимся, как преобразовать 1/5 в десятичную дробь? Включи это очень быстрое и веселое видео прямо сейчас!
Прежде всего, если вы не знаете, что такое числитель и знаменатель в дроби, нам нужно повторить это:
1 (числитель) / 5 (знаменатель)
Вот небольшой секрет, с помощью которого можно мгновенно преобразовать любую дробь в десятичную: Просто разделите числитель на знаменатель:
= 1/5
= 1 ÷ 5
= 0,2
3
Вот буквально все! 1/5 в виде десятичной дроби равно 0,2.
Хотел бы я рассказать вам больше о преобразовании дроби в десятичную, но это действительно так просто, и мне больше нечего об этом сказать.
Если вы хотите потренироваться, возьмите ручку и блокнот и попробуйте самостоятельно вычислить некоторые дроби в десятичном формате. Если вы действительно чувствуете себя ленивым , вы можете вместо этого использовать наш калькулятор ниже!
Почему вы хотите преобразовать 1/5 в десятичную дробь?
Отличный вопрос. У нас есть много расчетов на этом сайте о преобразовании дроби в десятичную, но зачем вам вообще это нужно?
Ну, во-первых, это просто хороший способ представить дробь в лучшем виде, который позволяет вам выполнять с ними обычные арифметические действия (такие как сложение, вычитание, деление и умножение).
В реальной жизни мы в основном имеем дело с десятичными дробями (например, с валютой), и, поскольку наш мозг с юных лет приучают понимать и сравнивать десятичные дроби чаще, чем дроби, проще понимать и сравнивать дроби, если они сначала преобразовать в десятичную!
Вот небольшой пример из реальной жизни преобразования дроби в десятичную при использовании количества. Допустим, вы готовите, и обычно вы можете видеть, сколько ингредиента осталось в упаковке. Однако электронные весы измеряют вес в десятичных дробях, а не в долях оставшегося ингредиента. Это делает преобразование между дробями и десятичными дробями полезным навыком в кулинарии.
Допустим, вы готовите, и обычно вы можете видеть, сколько ингредиента осталось в упаковке. Однако электронные весы измеряют вес в десятичных дробях, а не в долях оставшегося ингредиента. Это делает преобразование между дробями и десятичными дробями полезным навыком в кулинарии.
Надеюсь, это руководство помогло вам понять, как преобразовать дробь в десятичное число. Теперь вы можете идти вперед и преобразовывать дроби в десятичные столько, сколько пожелает ваше маленькое сердце!
Процитируйте, дайте ссылку или ссылку на эту страницу
Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большую услугу и используйте приведенный ниже инструмент, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!
«Что такое 1/5 в виде десятичной дроби?».
 VisualFractions.com . По состоянию на 27 сентября 2022 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-5-as-a-decimal/.
VisualFractions.com . По состоянию на 27 сентября 2022 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-5-as-a-decimal/.«Что такое 1/5 в виде десятичной дроби?». VisualFractions.com , http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-5-as-a-decimal/. По состоянию на 27 сентября 2022 г.
Что такое 1/5 в виде десятичной дроби?. VisualFractions.com. Получено с http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-5-as-a-decimal/.
Калькулятор преобразования дроби в десятичную дробь
Дробь в виде десятичной дроби
Введите числитель и знаменатель
Вычисление следующей дроби в десятичную дробь
- Что такое 1/6 в виде десятичной дроби?
Случайные дроби в десятичные числа
Если вы добрались до этого конца страницы, значит, вы ДЕЙСТВИТЕЛЬНО любите преобразовывать дроби в десятичные? Ниже приведена куча случайно сгенерированных вычислений для вашего удовольствия от десятичной любви:
Что такое 510/781 как десятичная
Десятичное число 755/784
Десятичное число 221/566
Десятичное число 197/436
Десятичное число 200/698
Десятичное число 19
Десятичное число 236/278
Десятичное число 940/977
Десятичное число 162/421
Десятичное число 244/728
Десятичное число 4 9
Что такое 289/448 в виде десятичного числа
Что такое 885/996 в виде десятичного числа
Десятичное число 777/861
Десятичное число 454/821
Десятичное число 444/778
Десятичное число 116/296
Десятичное число 6 а
Десятичное число 678/920
Десятичное число 540/726
Десятичное число 41/846
Десятичное число 345/614
Десятичное число 92/37
Что такое 678/809 в виде десятичного числа
Что такое 421/640 в виде десятичного числа
Десятичное число 938/945
Десятичное число 444/491
Десятичное число 343/681
Десятичное число 238/243
Десятичное число 6 а
Десятичное число 799/812
Десятичное число 367/725
Десятичное число 337/382
Десятичное число 382/889
Десятичное число 50
Что такое 600/764 в виде десятичного числа
Что такое 721/829 в виде десятичного числа
Десятичное число 556/774
Десятичное число 586/931
Десятичное число 981/993
Десятичное число 205/605
Десятичное число 9 aДесятичное число 665/893
Десятичное число 862/985
Десятичное число 214/774
Десятичное число 262/816
Десятичное число 14
Что такое 284/680 в виде десятичного числа
Что такое 201/226 в виде десятичного числа
Десятичное число 696/832
Десятичное число 46/958
Десятичное число 164/979
Десятичное число 427/485
Десятичное число 4 а
Десятичное число 44/700
Десятичное число 806/896
Десятичное число 820/914
Десятичное число 72/452
Десятичное число 6 143/55
Что такое 834/925 в виде десятичного числа
Что такое 611/947 в виде десятичного числа
Десятичное число 209/667
Десятичное число 851/934
Десятичное число 74/933
Десятичное число 289/307
Десятичное число 8
Десятичное число 782/795
Десятичное число 650/955
Десятичное число 239/978
Десятичное число 750/905
Десятичное число 9 721/9002
Что такое 341/701 в виде десятичного числа
Что такое 129/389 в виде десятичного числа
Десятичное число 82/447
Десятичное число 424/638
Десятичное число 623/848
Десятичное число 454/833
Десятичное число 796/97
Что такое десятичное число 203/528?
Что такое десятичное число 314/821?
Что такое десятичное число 51/771?
Что такое десятичное число 673/797?
Что такое 848/951 в виде десятичного числа
Что такое 820/834 в виде десятичного числа
Десятичное число 516/895
Десятичное число 140/489
Десятичное число 123/893
Десятичное число 260/503
Десятичное число 119/21
Десятичное число 830/941
Десятичное число 142/506
Десятичное число 432/526
Десятичное число 478/773
Что такое 413/649 в виде десятичного числа
Что такое 101/764 в виде десятичного числа 93-8
Что такое 1 5/32 в десятичной форме
1 5/32 равно 1,15625 в десятичной форме. Используйте наш калькулятор преобразования дробей в десятичные, чтобы преобразовать любую дробь в десятичную и узнать, является ли она завершающей или повторяющейся (повторяющейся) десятичной дробью.
Используйте наш калькулятор преобразования дробей в десятичные, чтобы преобразовать любую дробь в десятичную и узнать, является ли она завершающей или повторяющейся (повторяющейся) десятичной дробью.
Калькулятор / конвертер дробей в десятичные дроби
| Введите значение дроби: Пример: 1/2, 2 1/2, 5/3 и т. д. Обратите внимание, что 2 1/2 означает два с половиной = 2 + 1/2 = 2,5 |
Ответ: |
Пошаговое решение: |
| Цитаты |
См. также:
- Калькулятор дробей
- Калькулятор десятичной дроби
- Калькулятор доли в процентах
- Упрощение/сокращение дробей
- Калькулятор эквивалентных дробей
Таблица преобразования: дробь в десятичные дюймы и эквивалент в миллиметрах
Чтобы преобразовать дроби в десятичные и миллиметры и наоборот, используйте следующую формулу:
1 дюйм = 25,4 мм, то есть . ..
..
Чтобы преобразовать дюймы в миллиметры, умножьте значение в дюймах на 25,4.
Чтобы преобразовать миллиметры в дюймы, разделите значение в миллиметрах на 25,4.
Проще всего это сделать с помощью приведенной ниже таблицы. Как?
Пример 1
Преобразование 1 1/32 дюйма в мм:
Найдите 1 1/32 и прочитайте справа под столбцом мм! Вы найдете 26,1938.
Пример 2
Преобразование 0,875 дюймов после запятой в дюймы (в форме дроби).
Посмотрите вниз по десятичному столбцу, пока не найдете 0,875, затем прочитайте влево, чтобы найти 7/8 дюйма, или переместитесь в правый столбец, чтобы найти значение в миллиметрах!
Практическая фракция до десятичных дюймов и диаграмма конверсии миллиметровых
| Фракция | Десятиц | мм |
|---|---|---|
| 1/64 | 9 | |
| 1/64 | ||
| 1/64 | 999 | |
| 1/64999999 | ||
| 1/64 | ||
| 1/64 | 0.0313 | 0.7938 |
| 3/64 | 0.0469 | 1.1906 |
| 1/16 | 0.0625 | 1.5875 |
| 5/64 | 0.0781 | 1.9844 |
| 3/32 | 0.0938 | 2.3813 |
| 7/64 | 0.1094 | 2.7781 |
| 1/8 | 0.1250 | 3.1750 |
| 9/64 | 0.1406 | 3.5719 |
| 5/32 | 0.1563 | 3.9688 |
| 11/64 | 0.1719 | 4.3656 |
| 3/16 | 0.1875 | 4.7625 |
| 13/64 | 0.2031 | 5.1594 |
| 7/32 | 0.2188 | 5.5563 |
| 15/64 | 0.2344 | 5.9531 |
| 1/4 | 0.2500 | 6.3500 |
| 17/64 | 0. 2656 2656 | 6.7469 |
| 9/32 | 0.2813 | 7.1438 |
| 19/64 | 0.2969 | 7.5406 |
| 5/16 | 0.3125 | 7.9375 |
| 21/64 | 0.3281 | 8.3344 |
| 11/32 | 0.3438 | 8.7313 |
| 23/64 | 0.3594 | 9.1281 |
| 3/8 | 0.3750 | 9.5250 |
| 25/64 | 0.3906 | 9.9219 |
| 13/32 | 0.4063 | 10.3188 |
| 27/64 | 0.4219 | 10.7156 |
| 7/16 | 0.4375 | 11.1125 |
| 29/64 | 0.4531 | 11.5094 |
| 15/32 | 0.4688 | 11.9063 |
| 31/64 | 0.4844 | 12.3031 |
| 1/2 | 0. 5000 5000 | 12.7000 |
| 33/64 | 0.5156 | 13.0969 |
| 17/32 | 0.5313 | 13.4938 |
| 35/64 | 0.5469 | 13.8906 |
| 9/16 | 0.5625 | 14.2875 |
| 37/64 | 0.5781 | 14.6844 |
| 19/32 | 0.5938 | 15.0813 |
| 39/64 | 0.6094 | 15.4781 |
| 5/8 | 0.6250 | 15.8750 |
| 41/64 | 0.6406 | 16.2719 |
| 21/32 | 0.6563 | 16.6688 |
| 43/64 | 0.6719 | 17.0656 |
| 11/16 | 0.6875 | 17.4625 |
| 45/64 | 0.7031 | 17.8594 |
| 23/32 | 0.7188 | 18.2563 |
| 47/64 | 0. 7344 7344 | 18.6531 |
| 3/4 | 0.7500 | 19.0500 |
| 49/64 | 0.7656 | 19.4469 |
| 25/32 | 0.7813 | 19.8438 |
| 51/64 | 0.7969 | 20.2406 |
| 13/16 | 0.8125 | 20.6375 |
| 53/64 | 0.8281 | 21.0344 |
| 27/32 | 0.8438 | 21.4313 |
| 55/64 | 0.8594 | 21.8281 |
| 7/8 | 0.8750 | 22.2250 |
| 57/64 | 0.8906 | 22.6219 |
| 29/32 | 0.9063 | 23.0188 |
| 59/64 | 0.9219 | 23.4156 |
| 15/16 | 0.9375 | 23.8125 |
| 61/ 64 | 0.9531 | 24.2094 |
| 31/32 | 0.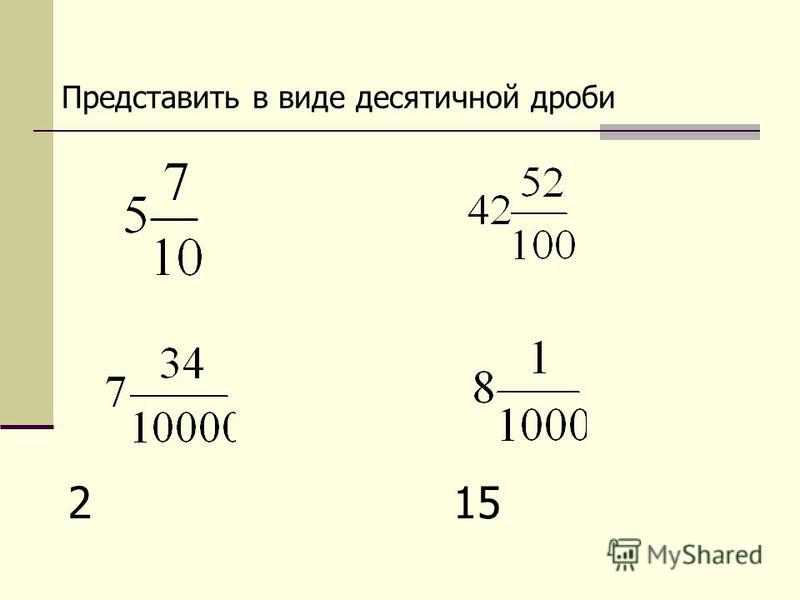 9688 9688 | 24.6063 |
| 63/64 | 0.9844 | 25.0031 |
| 1 | 1.0000 | 25.4000 |
| fraction | decimal | mm |
|---|---|---|
| 1 1/64 | 1.0156 | 25.7969 |
| 1 1/32 | 1.0313 | 26.1938 |
| 1 3/64 | 1.0469 | 26.5906 |
| 1 1/16 | 1.0625 | 26.9875 |
| 1 5/64 | 1.0781 | 27.3844 |
| 1 3/32 | 1.0938 | 27.7813 |
| 1 7/64 | 1.1094 | 28.1781 |
| 1 1/8 | 1.1250 | 28.5750 |
| 1 9 /64 | 1.1406 | 28.9719 |
| 1 5/32 | 1.1563 | 29.3688 |
| 1 11/64 | 1. 1719 1719 | 29.7656 |
| 1 3/16 | 1.1875 | 30.1625 |
| 1 13/64 | 1.2031 | 30.5594 |
| 1 7/32 | 1.2188 | 30.9563 |
| 1 15/64 | 1.2344 | 31.3531 |
| 1 1/4 | 1.2500 | 31.7500 |
| 1 17/64 | 1.2656 | 32.1469 |
| 1 9/32 | 1.2813 | 32.5438 |
| 1 19/64 | 1.2969 | 32.9406 |
| 1 5/16 | 1.3125 | 33.3375 |
| 1 21/64 | 1.3281 | 33.7344 |
| 1 11/32 | 1.3438 | 34.1313 |
| 1 23/64 | 1.3594 | 34.5281 |
| 1 3/8 | 1.3750 | 34.9250 |
| 1 25/64 | 1.3906 | 35. 3219 3219 |
| 1 13/32 | 1.4063 | 35.7188 |
| 1 27/64 | 1.4219 | 36.1156 |
| 1 7/16 | 1.4375 | 36.5125 |
| 1 29 /64 | 1.4531 | 36.9094 |
| 1 15/32 | 1.4688 | 37.3063 |
| 1 31/64 | 1.4844 | 37.7031 |
| 1 1/2 | 1.5000 | 38.1000 |
| 1 33/64 | 1.5156 | 38.4969 |
| 1 17/32 | 1.5313 | 38.8938 |
| 1 35/64 | 1.5469 | 39.2906 |
| 1 9/16 | 1.5625 | 39.6875 |
| 1 37/64 | 1.5781 | 40.0844 |
| 1 19/32 | 1.5938 | 40.4813 |
| 1 39/64 | 1.6094 | 40.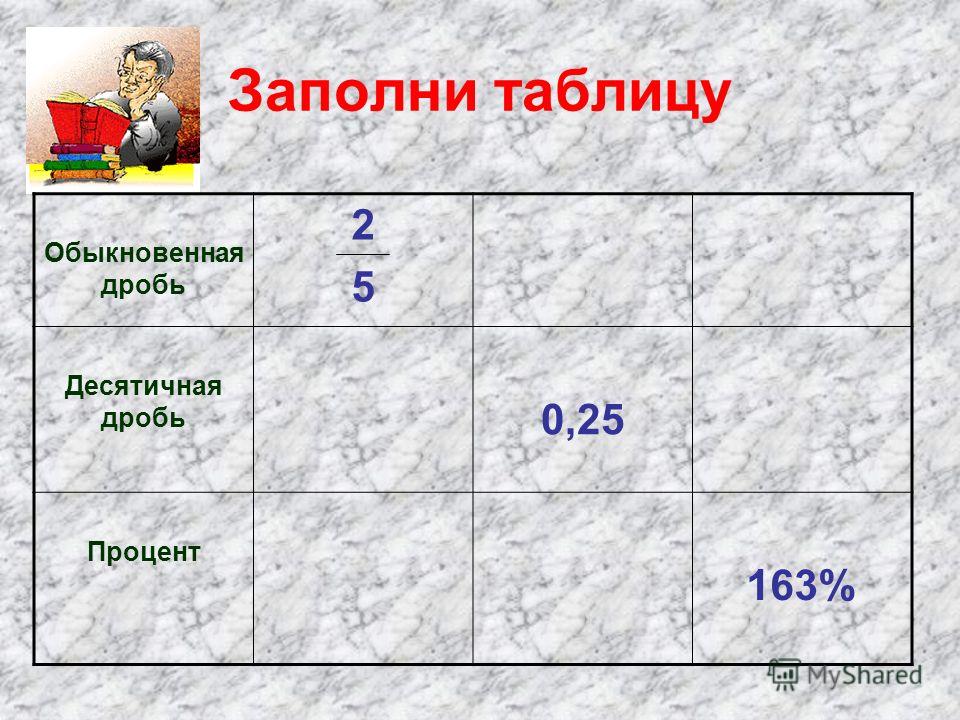 8781 8781 |
| 1 5/8 | 1.6250 | 41.2750 |
| 1 41/64 | 1.6406 | 41.6719 |
| 1 21/32 | 1.6563 | 42.0688 |
| 1 43/64 | 1.6719 | 42.4656 |
| 1 11/16 | 1.6875 | 42.8625 |
| 1 45/64 | 1.7031 | 43.2594 |
| 1 23/32 | 1.7188 | 43.6563 |
| 1 47/64 | 1.7344 | 44.0531 |
| 1 3/4 | 1.7500 | 44.4500 |
| 1 49/64 | 1.7656 | 44.8469 |
| 1 25/32 | 1.7813 | 45.2438 |
| 1 51/64 | 1.7969 | 45.6406 |
| 1 13/16 | 1.8125 | 46.0375 |
| 1 53/64 | 1.8281 | 46. 4344 4344 |
| 1 27/32 | 1.8438 | 46.8313 |
| 1 55/64 | 1.8594 | 47.2281 |
| 1 7/8 | 1.8750 | 47.6250 |
| 1 57/64 | 1.8906 | 48.0219 |
| 1 29/32 | 1.9063 | 48.4188 |
| 1 59/64 | 1.9219 | 48.8156 |
| 1 15/16 | 1.9375 | 49.2125 |
| 1 61/64 | 1.9531 | 49.6094 |
| 1 31/32 | 1.9688 | 50.0063 |
| 1 63/64 | 1.9844 | 50.4031 |
| 2 | 2.0000 | 50.8000 |
| fraction | decimal | mm |
|---|---|---|
| 2 1/64 | 2.0156 | 51.1969 |
| 2 1/32 | 2. 0313 0313 | 51.5938 |
| 2 3/64 | 2.0469 | 51.9906 |
| 2 1/16 | 2.0625 | 52.3875 |
| 2 5/64 | 2.0781 | 52.7844 |
| 2 3/32 | 2.0938 | 53.1813 |
| 2 7/64 | 2.1094 | 53.5781 |
| 2 1/8 | 2.1250 | 53.9750 |
| 2 9/64 | 2.1406 | 54.3719 |
| 2 5/32 | 2.1563 | 54.7688 |
| 2 11/64 | 2.1719 | 55.1656 |
| 2 3/16 | 2.1875 | 55.5625 |
| 2 13/64 | 2.2031 | 55.9594 |
| 2 7/32 | 2.2188 | 56.3563 |
| 2 15/64 | 2.2344 | 56.7531 |
| 2 1/4 | 2.2500 | 57. 1500 1500 |
| 2 17/ 64 | 2.2656 | 57.5469 |
| 2 9/32 | 2.2813 | 57.9438 |
| 2 19/64 | 2.2969 | 58.3406 |
| 2 5/16 | 2.3125 | 58.7375 |
| 2 21/64 | 2.3281 | 59.1344 |
| 2 11/32 | 2.3438 | 59.5313 |
| 2 23/64 | 2.3594 | 59.9281 |
| 2 3/8 | 2.3750 | 60.3250 |
| 2 25/64 | 2.3906 | 60.7219 |
| 2 13/32 | 2.4063 | 61.1188 |
| 2 27/64 | 2.4219 | 61.5156 |
| 2 7/16 | 2.4375 | 61.9125 |
| 2 29/64 | 2.4531 | 62.3094 |
| 2 15/32 | 2.4688 | 62. 7063 7063 |
| 2 31/64 | 2.4844 | 63.1031 |
| 2 1/2 | 2.5000 | 63.5000 |
| 2 33/64 | 2.5156 | 63.8969 |
| 2 17/32 | 2.5313 | 64.2938 |
| 2 35/64 | 2.5469 | 64.6906 |
| 2 9/16 | 2.5625 | 65.0875 |
| 2 37/64 | 2.5781 | 65.4844 |
| 2 19/32 | 2.5938 | 65.8813 |
| 2 39/64 | 2.6094 | 66.2781 |
| 2 5/8 | 2.6250 | 66.6750 |
| 2 41/64 | 2.6406 | 67.0719 |
| 2 21/32 | 2.6563 | 67.4688 |
| 2 43/64 | 2.6719 | 67.8656 |
| 2 11/16 | 2.6875 | 68. 2625 2625 |
| 2 45/64 | 2.7031 | 68.6594 |
| 2 23/32 | 2.7188 | 69.0563 |
| 2 47/64 | 2.7344 | 69.4531 |
| 2 3/4 | 2.7500 | 69.8500 |
| 2 49/64 | 2.7656 | 70.2469 |
| 2 25/32 | 2.7813 | 70.6438 |
| 2 51/64 | 2.7969 | 71.0406 |
| 2 13/16 | 2.8125 | 71.4375 |
| 2 53/64 | 2.8281 | 71.8344 |
| 2 27/32 | 2.8438 | 72.2313 |
| 2 55/64 | 2.8594 | 72.6281 |
| 2 7/8 | 2.8750 | 73.0250 |
| 2 57/64 | 2.8906 | 73.4219 |
| 2 29/32 | 2.9063 | 73. 8188 8188 |
| 2 59/64 | 2.9219 | 74.2156 |
| 2 15/16 | 2.9375 | 74.6125 |
| 2 61/64 | 2.9531 | 75.0094 |
| 2 31/32 | 2.9688 | 75.4063 |
| 2 63/64 | 2.9844 | 75.8031 |
| 3 | 3.0000 | 76.2000 |
Калькулятор дробей
Ссылка на эту страницу! Просто щелкните правой кнопкой мыши на изображении выше, выберите «Скопировать адрес ссылки», а затем вставьте его в HTML-код.
Фракция выборки до десятичных расчетов
- с 1/83 до десятичного десятичного деть.
- с 1/93 до десятичного десятичного детья
- 3 17/32 до десятичного десятичного от
- 4 55/64 до десятичного деть. 51/64 в десятичной системе
- 1 54/29 в десятичной системе
- 3 21/85 до десятичной дроби
- 1 100/7 до десятичной дроби
Отказ от ответственности
Несмотря на то, что мы прилагаем все усилия для обеспечения точности информации, представленной на этом веб-сайте, ни этот веб-сайт, ни его авторы не несут ответственности за какие-либо ошибки или упущения. Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Поэтому содержимое этого сайта не подходит для любого использования, связанного с риском для здоровья, финансов или имущества.
Калькулятор дробей
Этот калькулятор выполняет основные и расширенные операции с дробями, выражения с дробями в сочетании с целыми, десятичными и смешанными числами. Он также показывает подробную пошаговую информацию о процедуре расчета дроби. Калькулятор помогает найти значение из операций с несколькими дробями. Решайте задачи с двумя, тремя и более дробями и числами в одном выражении.
Правила выражений с дробями:
Дроби — для деления числителя на знаменатель используйте косую черту, т.е. для пятисотых введите 5/100 . Если вы используете смешанные числа, оставьте пробел между целой и дробной частями.
Смешанные числа (смешанные числа или дроби) сохраняют один пробел между целым числом и дробью
и используют косую черту для ввода дробей, например, 1 2/3 . Пример отрицательной смешанной дроби: -5 1/2 .
Пример отрицательной смешанной дроби: -5 1/2 .
Поскольку косая черта является одновременно знаком дробной части и деления, используйте двоеточие (:) в качестве оператора деления дробей, т. е. 1/2 : 1/3 .
Decimals (десятичные числа) вводятся с десятичной точкой . и они автоматически преобразуются в дроби — т.е. 1.45 .
Математические символы
| Символ | Название символа | Символ Значение | Пример | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| + | plus sign | addition | 1/2 + 1/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| — | minus sign | subtraction | 1 1/2 — 2/3 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| * | asterisk | multiplication | 2/3 * 3/4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| × | times sign | multiplication | 2/3 × 5/6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| : | division sign | division 91/2 • сложение дробей и смешанных чисел: 8/5 + 6 2/7 • деление целых чисел и дробей: 5 ÷ 1/2 • сложные дроби: 5/8 : 2 2/3 • десятичная дробь: 0,625 • Преобразование дроби в десятичную: 1/4 • Преобразование дроби в процент: 1/8 % • сравнение дробей: 1/4 2/3 • умножение дроби на целое число: 6 * 3/4 • квадратный корень дроби: sqrt(1/16) • уменьшение или упрощение дроби (упрощение) — деление числителя и знаменателя дроби на одно и то же ненулевое число — эквивалентная дробь: 4/22 • выражение со скобками: 1/3 * (1/2 — 3 3/8) • составная дробь: 3/4 от 5/7 • кратные дроби: 2/3 от 3/5 • разделить, чтобы найти частное: 3/5 ÷ 2/3 Калькулятор следует известным правилам для порядка операций .
more math problems »
Как найти десятичный эквивалент дробиВсе математические ресурсы SAT16 диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept ← Предыдущая 1 2 3 Следующая → SAT Math Help » Арифметика » Десятичные » Десятичные дроби » Как найти десятичный эквивалент дроби 0,3 < 1 / 3 4 > √17 1 / 2 < 1 / 8 900| = 6 Какое из приведенных выше утверждений верно? Возможные ответы: 0,3 < 1 / 3 4 > √17 –|–6| = 6 1 / 2 < 1 / 8 Правильный ответ: 0,3 < 1 / 3 Объяснение: Лучший подход к этому уравнению состоит в том, чтобы оценить каждое из уравнений и неравенств. √17 должно быть немного больше, чем √16, равное 4, поэтому «>» должно быть «<». Наконец, дробь 1 / 3 имеет повторяющиеся тройки, что делает его больше, чем 3 / 10 , так что это правда. Сообщить об ошибке Насколько меньше ? Возможные ответы: больше . Правильный ответ: Объяснение: Сообщить об ошибке Людоед под мостом ест пиццу, а остальную пиццу бросает крысам. Крысы едят то, что осталось. Какая часть пиццы останется, когда крысы будут готовы? Возможные ответы: Правильный ответ: Пояснение: 1/5 часть пиццы остается после того, как огр съест свою долю. 1/4 * 1/5 = 1/20 = 5% Сообщить об ошибке Какое из следующих чисел находится между 1/5 и 1/6? Возможные ответы: 0,22 0,25 0,16 0,19 0,13 Правильный ответ: 0,19 Объяснение: Длинное деление показывает, что 1/5 = 0,20 и 1/6 = 0,16666… 0,13 < 0,16 < 1/6 < 0,19 < 1/5 < 0,22 < 0,25. Сообщить об ошибке Тревор, Джеймс и Уилл получили по шоколадному батончику. Тревор съел 7/12 своего, а Уилл съел 20% своего. Если Джеймс съел больше, чем Уилл, и меньше, чем Тревор, сколько Джеймс мог съесть? Возможные ответы: 9/15 8/9 3/5 2/7 1/10 Правильный ответ: 2/7 . Превратите суммы Тревора и Уилла в десятичные дроби, чтобы сравнить: 20 % = 0,20 и 7/12 = 0,5083 с округлением. Когда варианты ответов преобразуются в десятичные числа, 2/7 = 0,2871 является единственным значением между 0,20 и 0,5083. Сообщить об ошибке Возможные ответы: 0,05 0,07 0,10 0,04 0,01 Правильный ответ: 0,07 . Пояснение: Умножьте числитель на другой числитель и умножьте знаменатель на другой знаменатель для умножения. Чтобы разделить дроби, поменяйте местами числитель и знаменатель и считайте это умножением. Ответ 0,07. Сообщить об ошибке Приведите дробь к десятичной и округлите до трех знаков после запятой: Возможные ответы: Правильный ответ: Объяснение: Чтобы вычислить эту дробь, составь пропорцию, где знаменатель равен 100 частям. Крест умножить. Разделите семь на обе стороны. Перепишите пропорцию. Чтобы найти десятичную дробь, просто переместите десятичный разряд числителя на две позиции назад, а знаменатель — на две позиции назад. Ответ: Отчет о ошибке Найдите десятичный эквивалент следующей фракции: Возможные ответы: Правильный ответ: . Пояснение: Чтобы найти десятичный эквивалент дроби, разделите числитель на знаменатель. Поскольку число в числителе меньше числа в знаменателе, после него нужно поставить десятичную точку и добавить нули. Затем выполните длинное деление. Во многих случаях десятичная дробь не заканчивается, поэтому лучше всего делить до четырех знаков после запятой, а затем соответственно округлять. Чтобы выполнить деление в большую сторону, убедитесь, что значение в числителе находится в пределах символа деления. Отсюда, поскольку внутреннее значение меньше внешнего значения, обязательно добавьте десятичную дробь и ноль.
Теперь оцените, сколько раз 7 входит в 50. Поскольку семь умножить на семь равно 49, а это самое близкое значение к 50 без превышения, это первое значение в десятичной дроби. Отсюда из 50 вычтите 49.
Теперь оцените, сколько раз 7 входит в 10. В данном случае это только один раз. Умножьте один на семь и вычтите из 10 этот продукт. не превышая его, и, таким образом, это значение, которое мы выбираем.
Поскольку все варианты ответов ограничиваются тремя цифрами, мы закончили. Следовательно, ответ — Отчет о ошибке Найдите десятичный эквивалент фракции: Возможные ответы: Правильный ответ: . Чтобы найти десятичный эквивалент дроби, разделите числитель на знаменатель. Поскольку число в числителе меньше числа в знаменателе, после него нужно поставить десятичную точку и добавить нули. Затем выполните длинное деление. Во многих случаях десятичная дробь не заканчивается, поэтому лучше всего делить до четырех знаков после запятой, а затем соответственно округлять. Для этого вопроса это будет выглядеть так: Чтобы выполнить деление в длинное число, убедитесь, что значение в числителе находится в символе деления. Отсюда нам нужно добавить десятичную точку и ноль, потому что внутреннее значение меньше внешнего значения.
Теперь оцените, сколько раз 16 входит в число 150. Поскольку 16 умножить на 9 равно 144, а это самое близкое значение к 150 без превышения, это первое значение в десятичной дроби. Отсюда из 150 вычтите 144.
Сейчас оцените, сколько раз 16 переходит в 60. . много раз 16 переходит в 120. Поскольку 16 умножить на 7 равно 112, это самое близкое значение к 120, не превышающее его, что означает, что это значение, которое нам нужно выбрать.
Поскольку все варианты ответов ограничиваются тремя цифрами, мы закончили. Следовательно, ответ — Отчет о ошибке Найдите десятичный эквивалент фракции: Возможные ответы: Правильный ответ: . Пояснение: Чтобы найти десятичный эквивалент дроби, разделите числитель на знаменатель. Поскольку число в числителе меньше числа в знаменателе, после него нужно поставить десятичную точку и добавить нули. Чтобы выполнить деление в большую сторону, убедитесь, что значение в числителе находится в символе деления. Отсюда нам нужно добавить десятичную точку и ноль, потому что внутреннее значение меньше внешнего значения.
Теперь оцените, сколько раз 8 входит в 10. В данном случае это только один раз, поэтому умножьте 1 на 8, чтобы получить 8. Отсюда вычтите 8 из 10. Теперь оцените, сколько раз 8 входит в число 20. Поскольку 2 умножить на 8 равно 16, вычтите это число из 20.
Теперь оцените, сколько раз 8 входит в число 40.
Поскольку наш окончательный ответ после вычитания равен нулю, мы закончили. Следовательно, ответ Сообщить об ошибке ← Предыдущий 1 2 3 Далее → Уведомление об авторских правах Все математические ресурсы SAT16 Диагностические тесты 660 практических тестов Вопрос дня Карточки Learn by Concept Дробь 1 5/100 как десятичнаяДробь 1 5/100 равна 0,15 при преобразовании в десятичную. Ниже подробно описано, как преобразовать дробь 1 5/100 в десятичное значение. Как преобразовать дробь в десятичную?Чтобы легко преобразовать дробь в десятичную, разделите числитель (верхнее число) на знаменатель (нижнее число). Пример 1: Как преобразовать4 / 8 в десятичное число?
Пример 2: Как преобразовать 11 / 3 до десятичной?
Примечание: результат округлен до 2 знаков после запятой. Доли дюймов в десятичные дюймы и миллиметры (мм)
|


 VisualFractions.com . По состоянию на 27 сентября 2022 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-5-as-a-decimal/.
VisualFractions.com . По состоянию на 27 сентября 2022 г. http://visualfractions.com/calculator/fraction-as-decimal/what-is-1-5-as-a-decimal/. 0288 1/32
0288 1/32 Наиболее распространенные мнемоники для запоминания этого порядка операций:
Наиболее распространенные мнемоники для запоминания этого порядка операций:  A
A  Какую часть составляют девочки?
Какую часть составляют девочки? Абсолютное значение –6 равно 6, но значение, противоположное значению, обозначенному знаком «–», равно –6, что не равно 6. 0,5 > 0,125.
Абсолютное значение –6 равно 6, но значение, противоположное значению, обозначенному знаком «–», равно –6, что не равно 6. 0,5 > 0,125. Крысы съедают 3/4 этого количества, так что остается 1/4 от 1/5 пиццы.
Крысы съедают 3/4 этого количества, так что остается 1/4 от 1/5 пиццы. Объяснение:
Объяснение:
 Для этого вопроса это будет выглядеть так:
Для этого вопроса это будет выглядеть так: Пояснение:
Пояснение: Поскольку 3 раза 16 составляет 48, вычитайте это число от 60.
Поскольку 3 раза 16 составляет 48, вычитайте это число от 60. Затем выполните длинное деление. Во многих случаях десятичная дробь не заканчивается, поэтому лучше всего делить до четырех знаков после запятой, а затем соответственно округлять. Для этого вопроса это будет выглядеть так:
Затем выполните длинное деление. Во многих случаях десятичная дробь не заканчивается, поэтому лучше всего делить до четырех знаков после запятой, а затем соответственно округлять. Для этого вопроса это будет выглядеть так:

 1563
1563 1281
1281 2875
2875 4469
4469