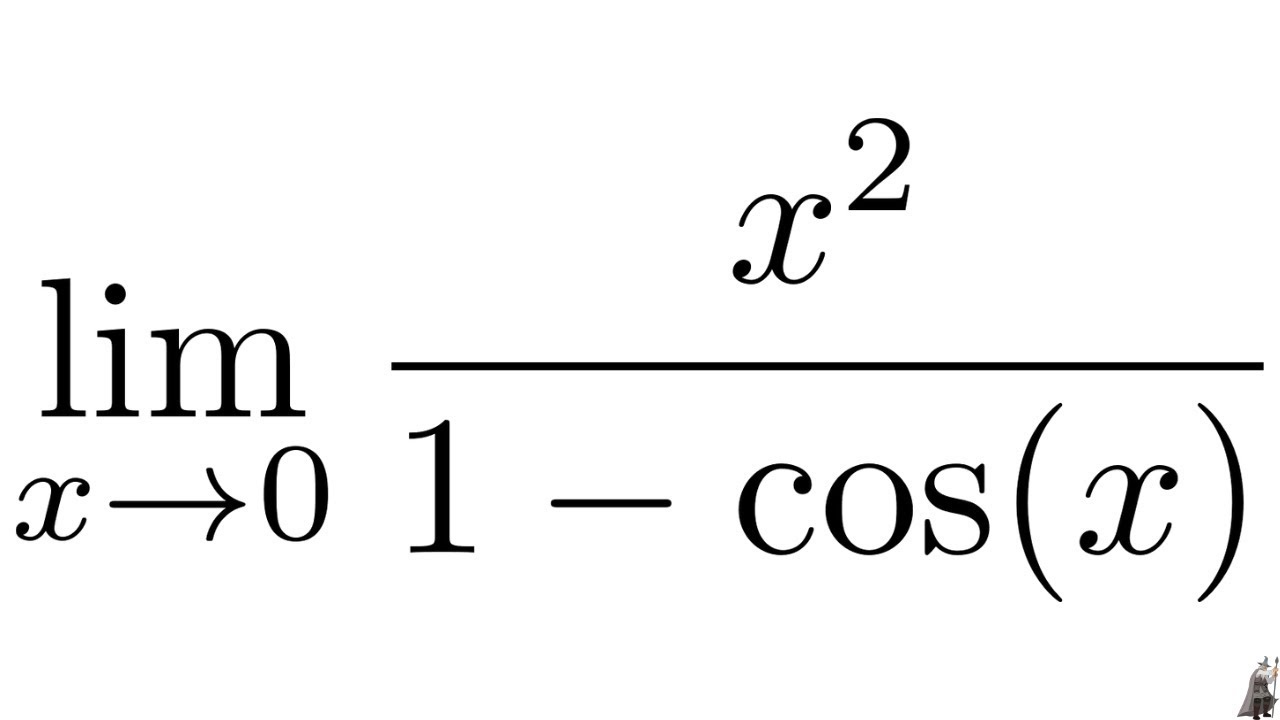y = 1/cos(x)
Графики функций, Построение графиков Работа проверена: Slavikk85 Время решения: 13 мин Сложность: 4.0
Дано$$f{left (x right )} = frac{1}{cos{left (x right )}}$$
График функции
Область определения функции
Точки, в которых функция точно неопределена:
$$x_{1} = 1.5707963267949$$
$$x_{2} = 4.71238898038469$$
Точки пересечения с осью координат X
График функции пересекает ось X при f = 0
значит надо решить уравнение:
$$frac{1}{cos{left (x right )}} = 0$$
Решаем это уравнение
Решения не найдено,
может быть, что график не пересекает ось X
Точки пересечения с осью координат Y
График пересекает ось Y, когда x равняется 0:подставляем x = 0 в 1/cos(x).
$$frac{1}{cos{left (0 right )}}$$
Результат:
$$f{left (0 right )} = 1$$
Точка:
(0, 1)
Экстремумы функции
Для того, чтобы найти экстремумы, нужно решить уравнение(производная равна нулю),
и корни этого уравнения будут экстремумами данной функции:
$$frac{d}{d x} f{left (x right )} = $$
Решаем это уравнение
Корни этого ур-ния
$$x_{1} = 0$$
$$x_{2} = pi$$
Зн.
 {2}} f{left (x right )} = $$
{2}} f{left (x right )} = $$Решаем это уравнение
Решения не найдены,
возможно перегибов у функции нет
Вертикальные асимптоты
Есть:
$$x_{1} = 1.5707963267949$$
$$x_{2} = 4.71238898038469$$
Горизонтальные асимптоты
Горизонтальные асимптоты найдём с помощью пределов данной функции при x->+oo и x->-oo
$$lim_{x to -infty} frac{1}{cos{left (x right )}} = langle -infty, inftyrangle$$
Возьмём предел
значит,
уравнение горизонтальной асимптоты справа:
$$y = langle -infty, inftyrangle$$
Наклонные асимптоты
Наклонную асимптоту можно найти, подсчитав предел функции 1/cos(x), делённой на x при x->+oo и x ->-ooTrue
Возьмём предел
значит,
уравнение наклонной асимптоты справа:
$$y = x lim_{x to infty}left(frac{1}{x cos{left (x right )}}right)$$
Чётность и нечётность функции
Проверим функци чётна или нечётна с помощью соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
$$frac{1}{cos{left (x right )}} = frac{1}{cos{left (x right )}}$$
– Да
$$frac{1}{cos{left (x right )}} = – frac{1}{cos{left (x right )}}$$
– Нет
значит, функция
является
чётной
- Курс
- NCERT
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8 9000 8
- Класс 7
- Класс 6
- IIT JEE
- NCERT
- Экзамен
- JEE MAINS
- JEE ADVANCED
- X BOARDS
- XII BOARDS
- NEET
- Neet Предыдущий год (по годам)
- Физика Предыдущий год
- Химия Предыдущий год
- Биология Предыдущий год
- Нет Все образцы работ
- Образцы работ по биологии
- Образцы работ по физике
- Образцы работ по химии
- Скачать PDF-файлы
- Класс 12
- Класс 11
- Класс 10
- Класс 9
- Класс 8
- Класс 7
- Класс 6
- Экзаменационный уголок
- Онлайн класс 9 0021
- Викторина
- Задать вопрос в Whatsapp
- Поиск Doubtnut
- Английский словарь
- Блог
- Скачать
- Получить приложение
Вычислить: (lim)(nvecoo)n[1/(n a)+1/(n a+1)+1/(n a+2)++1/(n b)]
03:11
- 9 0003 Toppers Talk
Вопрос
Обновлено:30/05/2023ARIHANT MATHS-LIMITS-Exercise For Session 6
5 видеоРЕКЛАМА
Text Solution
Ответ
Правильный ответ =18
Ab Padhai каро бина объявления ке
Khareedo DN Pro и дехо сари видео бина киси объявление ки рукаават ке! Похожие видео (1-cosx) х4.
35782616
03:44
अभिकलित कीजिए limx→0ex-sinx-1x
5484922 0
01:12
Вычислить limx→0xtanx(1−cosx)
61736886
02:12
Если A=limx→0sin−1(sinx)cos−1(cosx) и B=limx→0[|x|]x, то 2 03:41
limx→01−cos(1−cosx)x4 का मान है —
88358092
07:46
limx→01−cos(1−cosx)x4 равно
90 122 46704999807:09
limx→0 √1+cos2xx…….
510442594
01:51
Решить cos-1(cosx)>sin-1(sinx),x∈[0,2π]
642529879 9012 3
01: 18
Вычислить limx→01-cos(1-cosx)x4.
642541068
02:36
Если A=limx→0sin−1(sinx)cos−1(cosx)и B=limx→0[|x|]x, то 0122 03:34
यदि limx→0x(1+acosx)−bsinxx3=1,हो , तो
643235205
06:17
Оценить следующие пределы:
limx→0(1+3x )4/х
643754151
02 :07
Ltx→0(xsinx)cosxx cosecx−1=
643754284
Текст Решение
Если [x] обозначает наибольшую целочисленную функцию, то Ltx→0sin[cosx]1+[cosx]= 9(1/n), is
04:38
- Спросить Unlimited Doubts
- Видеорешения на нескольких языках (включая хинди)
- Видеолекции экспертов
- Бесплатные PDF-файлы (документы за предыдущий год, книжные решения и многое другое)
- Посещение специальных консультационных семинаров для IIT-JEE, NEET и экзаменов Совета
Сомневающийся хочет отправлять вам уведомления. Разрешите получать регулярные обновления!
Разрешите получать регулярные обновления!
5 1 попрактиковаться в тригонометрических тождествах, ключ ответа
www.ecusd4.com › vimages › общие › vnews › рассказы › ПК 5-1 Ключ
Ключ. 5-1. Упражняться. ДАТА. ПЕРИОД. Тригонометрические тождества. Шансы 1-11, 12. EC # 13. Найдите значение каждого выражения, используя данную информацию. 1.
[PDF] 5-1 Учебное пособие и вмешательство — Тригонометрические тождества — г-н Роу
mrrowesroom.weebly.com › загрузки › 5 › 5.1_study_guide.pdf
Тригонометрические тождества — это тождества, включающие тригонометрические функции. Взаимные тождества. Пифагорейские тождества sin θ = 1 csc θ csc θ …
[PDF] 5-1 Тригонометрические тождества
www.nhvweb.net › jfranz › files › 2011/10 › 5-1-1-15-odd -solutions
РЕШЕНИЕ: Используйте Пифагорейскую идентичность, которая включает csc, чтобы найти кроватку. Руководство по eSolutions — разработано Cognero.
5 1 Тригонометрические тождества — YouTube
www.youtube.com › смотреть
12.11.2013 · 4,2K просмотров 9 лет назад Precalculus. Предварительный расчет, … Показать еще. Показать больше. Показывай меньше. 4,261 …
Dauer: 24:26
Прислан: 12.11.2013
Глава 5: Тригонометрические тождества — Математический веб-сайт миссис Пауэрс
site.google.com › asdk12.net › home › pre-calculus
Глава 5: Тригонометрические тождества ; Ċ, 5-2 Ключ к домашнему заданию.pdf. Посмотреть загрузки ; Ċ, 5.2 Примечания.pdf. Посмотреть загрузки ; Ċ, 5.2 Практические ответы.pdf. Посмотреть загрузки ; В, 5,2 …
5 1practice Solutions.pdf — НАЗВАНИЕ ДАТА ПЕРИОД 5-1… — Course Hero
www.coursehero.com › файл › 5-1practice-solutionspdf
Bewertung 5,0 (1) 90 123 ПЕРИОД ______Глава 57 Предварительное исчисление Гленко 5-1 Практика Тригонометрические тождества Найдите значение каждого выражения, используя данную информацию.