Как найти абсциссу точки: Найти абсциссу точки х

alexxlab / / Разное

Найти абсциссу точки х

Бизнес с Oriflame — рост и РАЗВИТИЕ!

ЗАМУЧИЛИ БОЛИ В СПИНЕ?

Александр | 2014-09-11

Найти абсциссу точки. Друзья! В этой статье для вас размещено ещё несколько заданий связанных с координатной плоскостью. Решение данного типа задач, входящих в состав ЕГЭ очень простенькое – решаются они практически сходу в течение минуты. Если вы забыли, что такое абсцисса и ордината, то посмотрите эту статью.

Суть рассматриваемых ниже задач такая – даны фигуры на плоскости, заданы координаты  вершин (не всех), необходимо определить абсциссу или ординату неизвестной вершины. Также имеются задачи на определение длины отрезка. Если у вас развито визуальное (зрительное) представление, то решение вы «увидите» сразу посмотрев на эскиз.

Если есть сложности с визуальным представлением фигур на координатной плоскости, то моя вам «универсальная» рекомендация – постройте фигуру по данным координатам на листе в клетку, далее вы без труда определите координаты (местонахождение)  вершины или оговоренной в условии точки и ответите на поставленный вопрос. Посмотрите, как это будет выглядеть такое построение:

Например, абсцисса и ордината точки Р (точка пересечения диагоналей параллелограмма) определяется без труда, соответственно 3 и 4. Рассмотрим задачи:

27673. Точки O (0;0), A (6;8), C (0;6) и B являются вершинами параллелограмма. Найдите ординату точки B.

Точка В смещена относительно точки О в положительном направлении по оси оУ на 2  единицы (также как и точка А смещена относительно точки С), значит её ордината будет равна  0 + 2 = 2.

Ответ: 2

27674. Точки O (0;0), A (6;8), B (4;2) и C являются вершинами параллелограмма. Найдите ординату точки C.

Ордината точки С равна длине стороны ОС. Известно, что противолежащие стороны параллелограмма равны, то есть ОС = АВ = 8 – 2 = 6.

Ответ: 6

Точки O (0;0), A (6;8), B (6;2), C (0;6) являются вершинами четырехугольника. Найдите абсциссу точки P пересечения его диагоналей.

Обратите внимание на то, что в условии сказано, что дан четырёхугольник, то есть как бы подразумевается, что это возможно это и не параллелограмм.

Но по координатам видно, что это не что иное, как параллелограмм.

*Для убедительности можно построить данную фигуру на координатной плоскости  на листе в клетку.

Известно, что точка пересечения диагоналей равноудалена от противолежащих сторон (лежит посередине). Поэтому абсцисса точки Р будет равна 6:2 = 3.

Ответ: 3

27677. Точки О(0;0), А(10;8), С(2;6) и В являются вершинами параллелограмма. Найдите абсциссу точки В.

Абсцисса точки В на 2 меньше абсциссы точки А (также как абсцисса точки О меньше абсциссы точки С), значит она равна 10 – 2 = 8.

Ответ: 8

27679 (80). Точки O (0;0), A (10;8), B (8;2) и C являются вершинами параллелограмма. Найдите абсциссу и ординату точки C.

Точка С смещена относительно точки О в положительном направлении по оси оХ на 2  единицы (также как и точка А смещена относительно точки В), значит её абсцисса равна  0 + 2 = 2.

Точка С смещена относительно точки О в положительном направлении по оси оУ на 6  единиц (также как и точка А смещена относительно точки В), значит её ордината равна шести.

Ответ: абсцисса равна 2, ордината равна 6.

27681 (2). Точки O (0;0), B (8;2), C (2;6) и A являются вершинами параллелограмма. Найдите абсциссу и  ординату точки A.

Точка А смещена относительно точки С в положительном направлении по оси оХ на 8 единиц (также как и точка В смещена относительно точки О), значит её абсцисса равна 2 + 8 = 10.

Точка А смещена относительно точки В в положительном направлении по оси оУ на 6 единиц (также как и точка С смещена относительно точки О), значит её ордината равна 2 + 6 = 8.

Ответ: Абсцисса точки А равна 10, ордината равна 8.

27683 (4). Точки O(0, 0), A(10, 8), B(8, 2), C(2, 6) являются вершинами четырехугольника. Найдите абсциссу и ординату точки P пересечения его диагоналей.

Можно использовать формулу координат середины отрезка. Формула:

Ответ: абсцисса равна 5, ордината равна 4.

 

27672. Точки O(0;0), B(6;2), C(0;6) и A являются вершинами параллелограмма. Найдите ординату точки A.

Посмотреть решение

27675. Точки O(0;0), A(6;8), B(6;2), C(0;6) являются вершинами четырехугольника. Найдите ординату точки P пересечения его диагоналей.

Посмотреть решение

 

27678. Точки O(0;0), A(10;8), C(2;6) и B являются вершинами параллелограмма. Найдите ординату точки B.

Посмотреть решение

 

27685. Точки О(0;0), А(6;8), В(8;2) являются вершинами треугольника. Найдите длину его средней линии CD, параллельной OA.

Рекомендация!

Можно использовать формулу координат середины отрезка, а затем зная их вычислить длину отрезка  по соответствующей формуле. Но будет проще и быстрее построить фигуру на координатной плоскости на листе в клетку и вычислить длину отрезка по теореме Пифагора.

Посмотреть решение

 

27686. Точки O(0;0), A(10;0), B(8;6), C(2;6) являются вершинами трапеции. Найдите длину ее средней линии DE.

Рекомендация!

Можно использовать формулы координат середины отрезка и затем длины отрезка или построить трапецию н листе в клетку, но в данном случае удобно воспользоваться формулой средней линии трапеции.

Посмотреть решение

На этом всё! Успеха Вам!

С уважением, Александр Крутицких.

P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.


Категория: Коорд плоскость | ЕГЭ-№1

НЕ ОТКЛАДЫВАЙ! Заговори на английском!

ДОЛОЙ обидные ошибки на ЕГЭ!!

Подготовка к ЕГЭ, онлайн-обучение с Фоксворд!

Замучили боль и скованность в мышцах спины?

*Нажимая на кнопку, я даю согласие на рассылку, обработку персональных данных и принимаю политику конфиденциальности.


Прямая параллельна касательной к графику функции

Рассмотрим задания из №7 ЕГЭ, в которых данная прямая параллельна касательной к графику функции.

№1

Прямая y=9x+5 параллельна касательной к графику функции y=x²-5x+54. Найти абсциссу точки касания.

Решение:

Прямые y=k1x+b1 y=k2x+b2 параллельны,если их угловые коэффициенты равны: k1=k2.

y=9x+5, отсюда k1=9.

Угловой коэффициент касательной равен значению производной в точке касания: k2=f'(xo).

f'(x)=(x²-5x+54)’=2x-5;

f'(xo)=2xo-5.

Таким образом, 2xo-5=9; 2xo=14; xo=7.

Ответ: 7.

№2

Прямая y=14-2x является касательной к графику функции y=x³+1,5x²-8x+4. Найти абсциссу точки касания.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(xo).

f'(x)=(x³+1,5x²-8x+4)’=3x²+3x-8;

f'(xo)=3xo²+3xo-8.

По условию, y=14-2x. Отсюда k=-2.

3xo²+3xo-8=-2

3xo²+3xo-6=0

xo²+xo-2=0

xo=1 либо xo=-2.

Точка касания принадлежит и касательной, и графику функции.

xo³+1,5xo²-8xo+4=14-2xo.

Проверяем, выполняется ли равенство при xo=1:

1³+1,5·1²-8·1+4=14-2·1?

-1,5≠12.

При xo=-2:

(-2)³+1,5·(-2)²-8·(-2)+4=14-2·(-2)

18=18.

Абсцисса точки касания равна xo=-2.

Ответ: -2.

№3

Прямая y=11x+8 является касательной к графику функции y=ax²+7x-2. Найти a.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(xo).

f'(x)=(ax²+7x-2)’=2ax+7;

f'(xo)=2axo+7.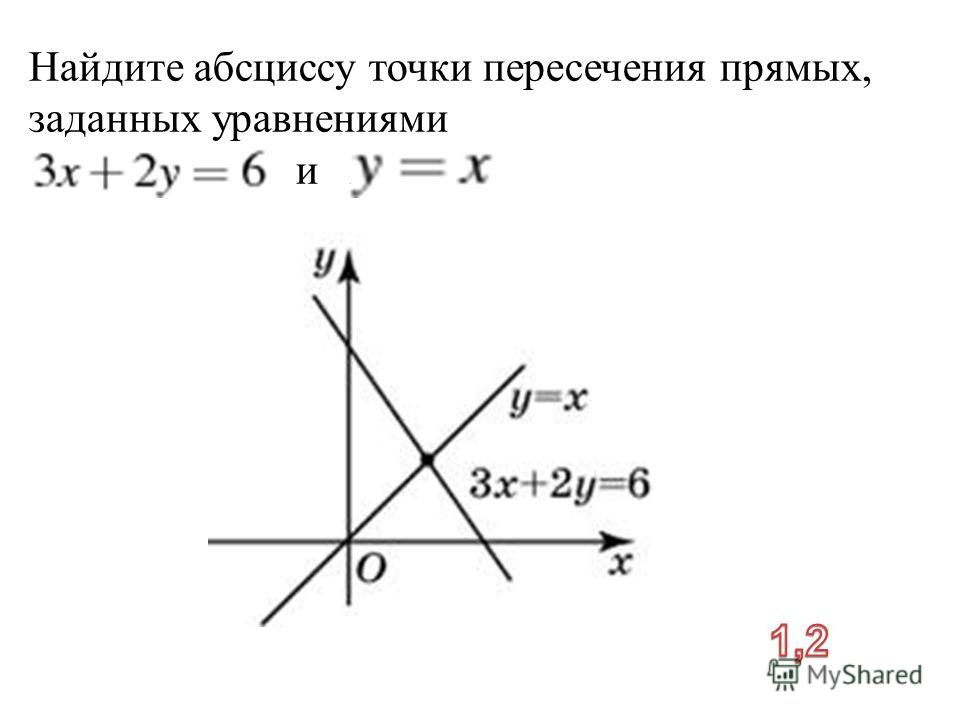

По условию, уравнение касательной y=5x+1, поэтому k=5.

Имеем: 2axo+7=11, откуда axo=2.

Точка касания принадлежит и касательной, и графику функции, поэтому

axo²+7xo-2=11xo+8. Подставив в это равенство axo=2, получим

2xo+7xo-2=11xo+8, откуда xo=-5.

axo=2

-5a=2

a=-0,4.

Ответ: 0,4.

№4

Прямая y=-6x+7 является касательной к графику функции y=6x²+bx+13. Найти b, учитывая, что абсцисса точки касания меньше 0.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(xo).

f'(x)=(6x²+bx+13)’=12x+b;

f'(xo)=12xo+b.

По условию, уравнение касательной y=-6x+7, поэтому k=-6.

Имеем: 12xo+b=-6, откуда b=-12xo-6.

Точка касания принадлежит и касательной, и графику функции.

6xo²+bxo+13=-6xo+7

6xo²+(-12xo-6)xo+13=-6xo+7

6xo²-12xo²-6xo+13+6xo-7=0

-6xo²+6=0

xo=1 либо xo=-1.

По условию, xo<0, следовательно, xo=-1.

b=-12·(-1)-6=6.

Ответ: 6.

№5

Прямая y=2x+4 является касательной к графику функции y=x²-4x+c. Найти c.

Решение:

Угловой коэффициент касательной равен значению производной в точке касания: k=f'(xo).

f'(x)=(x²-6x+c)’=2x-6;

f'(xo)=2xo-6.

По условию, уравнение касательной y=2x+4, поэтому k=2.

Имеем: 2x

o-6=2, откуда xo=4.

Точка касания принадлежит и касательной, и графику функции, поэтому

xo²-4xo+с=2xo+4. Подставив в это равенство xo=4, получим

16-16+с=8+4

с=12.

Ответ: 12.

Ответ: Абсцисса точки равна 3. Если ее…

P Предварительные понятия1 Отношения прямых и углов2 Параллельные прямые3 Треугольники4 Четырехугольники5 Подобные треугольники6 Окружности7 Геометрическое место и пересечение8 Площади многоугольников и окружностей9 Поверхности и тела10 Аналитическая геометрия11 Введение в тригонометриюПриложение

1.1 Ранние определения и постулаты 1.2 Углы и их отношения 1.3 Введение в геометрическое доказательство 1.4 Отношения: перпендикулярные линии 1.5 Формат доказательства теоремы 1.CR Обзорные упражнения 1.CT Test

Задача 1CR: Назовите четыре компонента математической системы. Задача 2CR: Назовите три типа рассуждений. Задача 3CR: Назовите четыре характеристики хорошего определения. Задача 4CR: В повторении упражнений 4–6 назовите проиллюстрирован тип рассуждений. Наблюдая, как кувшин нагревается… Задача 5CR: В повторных упражнениях 4–6 назовите показанный тип рассуждений. Лора уехала в лагерь. О… Задаче 6CR: В повторных упражнениях с 4 по 6 назовите проиллюстрированный тип рассуждения. Сара знает правило Число… Задача 7CR: В повторных упражнениях 7 и 8 сформулируйте гипотезу и вывод для каждого утверждения. Если… Проблема 8CR: В обзорных упражнениях 7 и 8 сформулируйте гипотезу и вывод для каждого утверждения. Диагонали… Задача 9CRЗадача 10CRЗадача 11CRЗадача 12CR: A, B и C — три точки на прямой. АС=8, ВС=4 и АВ=12. Какая точка должна быть между другой… Задача 13CRЗадача 14CR: Фигура MNPQ — ромб. Проведите диагонали MP и QN ромба. Как выглядят MP и QN… Задача 15CR: В повторных упражнениях с 15 по 17 нарисуйте и подпишите описанные фигуры. Точки A, B, C и D… Задача 16CR: В повторении упражнений с 15 по 17 нарисуйте и подпишите описанные фигуры. Прямая l пересекает плоскость X в точке… Задача 17CR: В повторении упражнений с 15 по 17 нарисуйте и подпишите описанные фигуры. Плоскость M содержит пересекающиеся… Задача 18CR: Судя по внешнему виду, какой тип угла показан? Задача 19CR: Основываясь на внешнем виде, какой тип угла показан? Задача 20CR: Дано: BD делит ABC пополам mABD=2x+15 mDBC=3x+5 Найти: mABCЗадача 21CR: Дано: mABD=2x+5 mDBC=3×4 mABC= 86 Найти: mDBCPProblem 22CR: Дано: AM=3×1 MB=4×5 M — середина AB Найти: ABProblem 23CR: Дано: AM=4×4 MB=5x+2 AB=25 Найти: MBProblem 24CR: Дано: D — середина AC ACBC CD=2x+5 BC=x+28 Найти: ACProblem 25CR: Дано: m3=7×21 m4=3x+7 Найти: mFMHProblem 26CR: Дано: mFMH=4x+1 m4=x+4 Найти: m4Problem 27CR: In по фигуре найдите: a KHFJ b MJMH c KMJJMH d MKMH Задача 28CR: Дано: EFG — прямой угол. mHFG=2×6 mEFH=3mHFG Находка: mEFHЗадача 29ЧР: Два угла являются дополнительными. Один угол в 40 раз больше другого. Найдите меры… Задача 30CR: a Напишите выражение для периметра показанного треугольника. ПОДСКАЗКА: сложите длины сторон… Задача 31CR: Сумма мер всех трех углов треугольника в обзорном упражнении 30 равна 180. Если сумма… Задача 32CR: Сьюзан хочет получить 4- ft доска с некоторыми колышками на нем. Она хочет оставить 6 дюймов на каждом конце и 4… Задача 33CR. Укажите, всегда ли предложения в повторных упражнениях с 33 по 37 истинны A, иногда истинны S, или… Задача 34CR. Укажите, являются ли предложения в повторении Упражнения с 33 по 37 всегда верны A, иногда истинны S или… Задача 35CR. Укажите, всегда ли предложения в повторных упражнениях 33–37 истинны A, иногда истинны S или… Задача 36CR. в упражнениях на повторение с 33 по 37 всегда верно A, иногда верно S или… Задача 37CR. Укажите, всегда ли предложения в упражнениях на повторение 33-37 верны A, иногда верно S или. .. Задача 38CR. недостающие утверждения или причины. Дано: 1P 4P VP делит RVO пополам Докажите: TVPMVP Доказательство… Задача 39CR: Напишите доказательства в два столбца для повторных упражнений с 39 по 46. Дано: KFFH JHF является правильным Докажите: KFHJHF Задача 40CR: Напишите доказательства в два столбца для повторных упражнений с 39 по 46. Дано: KHFJ G является серединой KH и. ..Problem 41CRProblem 42CRProblem 43CRProblem 44CRProblem 45CRProblem 46CRProblem 47CR: Дано: VP Конструкция: VW такая, что VW=4VPProblem 48CRProblem 49CRProblem 50CRProblem 51CRProblem 52CR