1 делить на косинус: Найти производную y’ = f'(x) = 1/cos(x) (1 делить на косинус от (х))

alexxlab / / Разное

Mathway | Популярные задачи

1Найти точное значениеsin(30)
2Найти точное значениеsin(45)
3Найти точное значениеsin(30 град. )
4Найти точное значениеsin(60 град. )
5Найти точное значениеtan(30 град. )
6Найти точное значениеarcsin(-1)
7Найти точное значениеsin(pi/6)
8
Найти точное значение		cos(pi/4)
9Найти точное значениеsin(45 град. )
10Найти точное значениеsin(pi/3)
11Найти точное значениеarctan(-1)
12Найти точное значениеcos(45 град. )
13Найти точное значениеcos(30 град. )
14Найти точное значениеtan(60)
15
Найти точное значение		csc(45 град. )
16Найти точное значениеtan(60 град. )
17Найти точное значениеsec(30 град. )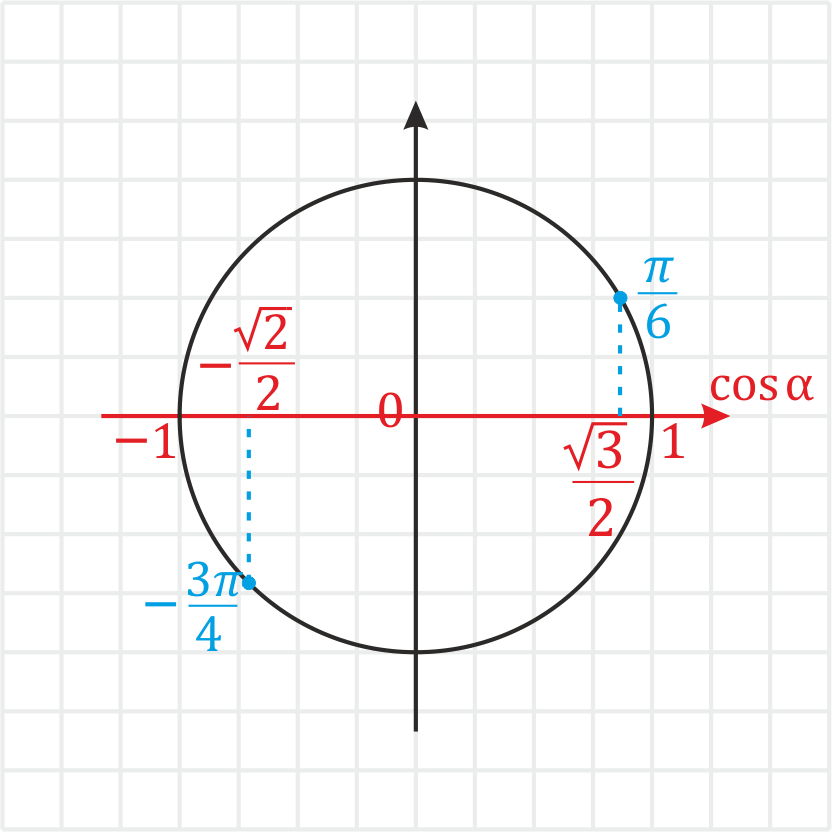
18Найти точное значениеcos(60 град. )
19Найти точное значениеcos(150)
20Найти точное значениеsin(60)
21Найти точное значениеcos(pi/2)
22Найти точное значениеtan(45 град. )
23Найти точное значениеarctan(- квадратный корень из 3)
24Найти точное значениеcsc(60 град. )
25Найти точное значениеsec(45 град. )
26Найти точное значениеcsc(30 град. )
27Найти точное значение sin(0)
28Найти точное значениеsin(120)
29Найти точное значениеcos(90)
30Преобразовать из радианов в градусыpi/3
31Найти точное значениеtan(30)
32Преобразовать из градусов в радианы45
33Найти точное значениеcos(45)
34Упроститьsin(theta)^2+cos(theta)^2
35Преобразовать из радианов в градусыpi/6
36Найти точное значениеcot(30 град. )
37Найти точное значениеarccos(-1)
38Найти точное значениеarctan(0)
39Найти точное значениеcot(60 град. )
40Преобразовать из градусов в радианы30
41Преобразовать из радианов в градусы(2pi)/3
42Найти точное значениеsin((5pi)/3)
43Найти точное значениеsin((3pi)/4)
44Найти точное значениеtan(pi/2)
45Найти точное значениеsin(300)
46Найти точное значениеcos(30)
47Найти точное значениеcos(60)
48Найти точное значениеcos(0)
49Найти точное значениеcos(135)
50Найти точное значениеcos((5pi)/3)
51Найти точное значениеcos(210)
52Найти точное значениеsec(60 град. )
53Найти точное значениеsin(300 град. )
54Преобразовать из градусов в радианы135
55Преобразовать из градусов в радианы150
56Преобразовать из радианов в градусы(5pi)/6
57Преобразовать из радианов в градусы(5pi)/3
58Преобразовать из градусов в радианы89 град.
59Преобразовать из градусов в радианы60
60Найти точное значениеsin(135 град. )
61Найти точное значениеsin(150)
62Найти точное значениеsin(240 град. )
63Найти точное значениеcot(45 град. )
64Преобразовать из радианов в градусы(5pi)/4
65Найти точное значениеsin(225)
66Найти точное значениеsin(240)
67Найти точное значениеcos(150 град. )
68Найти точное значениеtan(45)
69Вычислитьsin(30 град. )
70Найти точное значениеsec(0)
71Найти точное значениеcos((5pi)/6)
72Найти точное значениеcsc(30)
73Найти точное значениеarcsin(( квадратный корень из 2)/2)
74Найти точное значениеtan((5pi)/3)
75Найти точное значениеtan(0)
76Вычислитьsin(60 град. )
77Найти точное значениеarctan(-( квадратный корень из 3)/3)
78Преобразовать из радианов в градусы(3pi)/4
79Найти точное значениеsin((7pi)/4)
80Найти точное значениеarcsin(-1/2)
81Найти точное значениеsin((4pi)/3)
82Найти точное значениеcsc(45)
83Упроститьarctan( квадратный корень из 3)
84Найти точное значениеsin(135)
85Найти точное значениеsin(105)
86Найти точное значениеsin(150 град. )
87Найти точное значениеsin((2pi)/3)
88Найти точное значениеtan((2pi)/3)
89Преобразовать из радианов в градусыpi/4
90Найти точное значениеsin(pi/2)
91Найти точное значениеsec(45)
92Найти точное значениеcos((5pi)/4)
93Найти точное значениеcos((7pi)/6)
94		Найти точное значениеarcsin(0)
95Найти точное значениеsin(120 град. )
96Найти точное значениеtan((7pi)/6)
97Найти точное значениеcos(270)
98Найти точное значениеsin((7pi)/6)
99Найти точное значениеarcsin(-( квадратный корень из 2)/2)
100
Преобразовать из градусов в радианы		88 град.

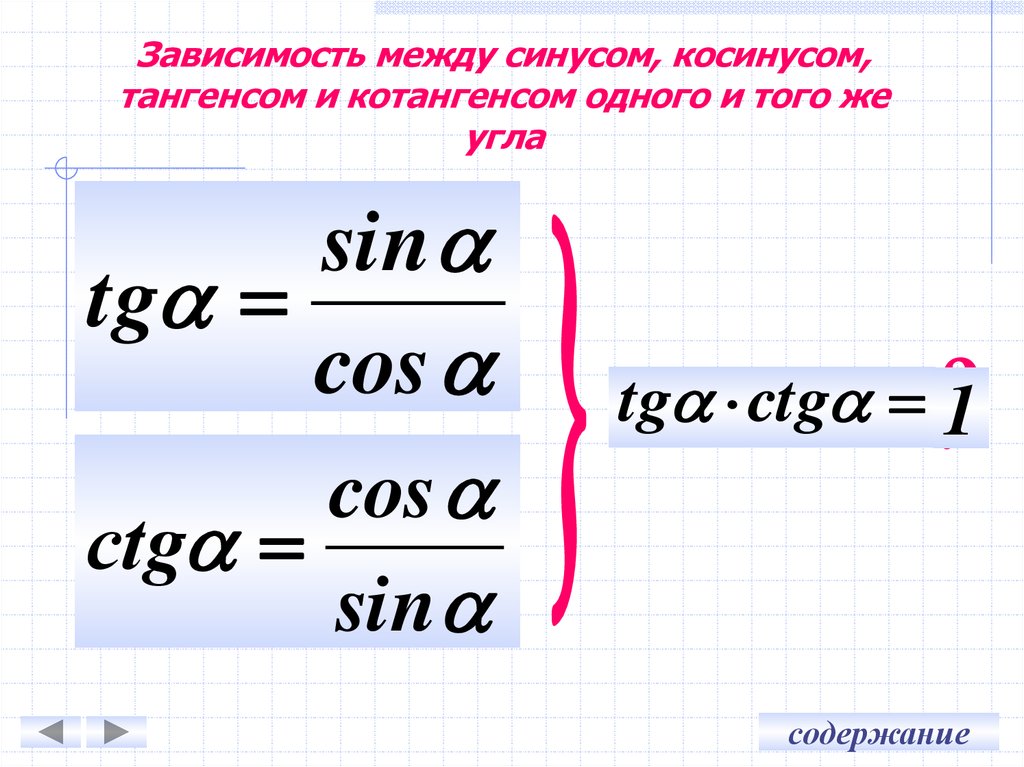
Его Можно Найти, Если Синус Поделить На Косинус

Решение этого кроссворда состоит из 7 букв длиной и начинается с буквы Т

Ниже вы найдете правильный ответ на Его можно найти, если синус поделить на косинус, если вам нужна дополнительная помощь в завершении кроссворда, продолжайте навигацию и воспользуйтесь нашей функцией поиска.

ответ на кроссворд и сканворд

Воскресенье, 23 Мая 2021 Г.

CodyCross На курорте Rруппа 547

ТАНГЕНС

предыдущий следующий

ты знаешь ответ ?

ответ:

CODYCROSS На курорте Группа 547 ГОЛОВОЛОМКА 1

  1. Главный аэропорт санкт петербурга
  2. Лекарство в желатиновой оболочке
  3. Шаурма по питерски
  4. Японское искусство составления букетов
  5. Оборудованный летний лагерь с местами для палаток
  6. Приготовленная еда, кушанье
  7. Автор «алисы в стране чудес»
  8. Мультсериал о животном, гибриде собаки и кошки
  9. Часть здания, выступающая за главную линию фасада
  10. Столица государства словения
  11. Детский лагерь на черном море, назван как птенец
  12. Видна из под пятницы
  13. Сердце римско католической церкви
  14. Вид пауков кругопрядов
  15. Фильм лунгина владелец капитала, магнат
  16. Взрывчатое вещество
  17. Маленькая гавайская гитара
  18. Комната работника умственного труда
  19. Крупный одноядерный лейкоцит

связанные кроссворды

  1. Тангенс
    1. Эта функция связана с катетами
  2. Тангенс
    1. Тригонометрическая функция
    2. Единица, деленная на котангенс

CSC X — Google Suce

AllebildervideoSnewsmapsshoppingBücher

Sucoptionen

Sekans und Kosekans — Wikipedia

De. wikipedia.organs. Der Sekans wird mit sec ⁡ ( Икс ) {\ displaystyle \ sec (x)} \ sec (x) bezeichnet, der Kosekans mit csc …

Eigenschaften · Extremstellen · Wichtige Funktionswerte · Reihenentwicklung

Ähnliche Fragen

Был ли CSC в Мате?

Была ли это Косек?

Была ли это функция SEC?

Был ли SEC Tangens?

Sekans und Kosekans

Sekans und Kosekans sind trigonometrische Funktionen. Der Sekans wird mit \sec bezeichnet, der Kosekans mit \csc oder \operatorname{cosec}. Die Funktionen haben ihren Namen durch die Definition im Einheitskreis. Die Funktionswerte entsprechen der… Wikipedia

Darstellung des Graphen

Grafikrechner

Trigomometrische Funktion — Wikipedia

de.wikipedia.org ›Wiki› Trigonometrische_funktion

. von sec(x) и csc(x).0003

Косеканс кск. Der Kosekans ist im rechtwinkeligen Dreieck das Verhältnis von Hypotenuse zu Gegenkathete und somit der Kehrwert der Sinusfunktion.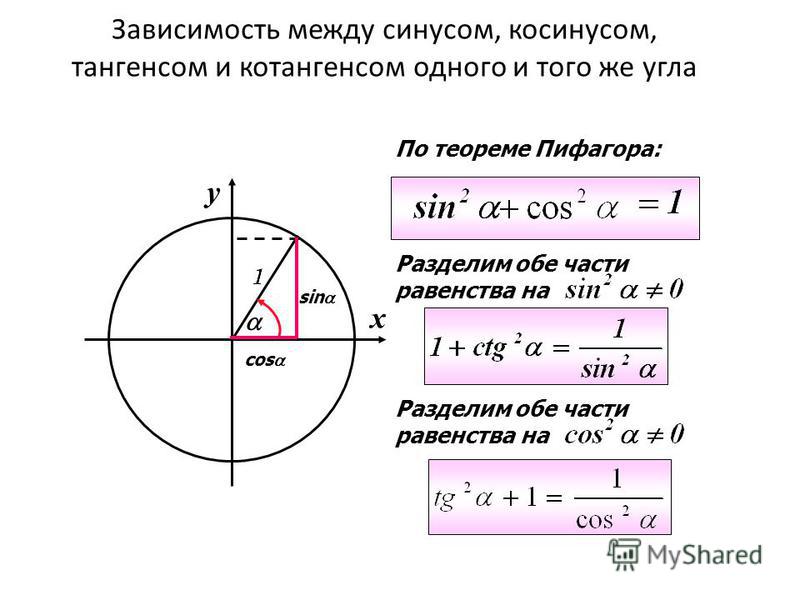

Sekans und Kosekans — Mathepedia

mathepedia.de › Sekans_und_Kosekans

Sekans: f ( x ) = sec ⁡ ( x ) f (x) = \ sec (x) \, f (x) = sec (x) ). Косеканы: f ( x ) = csc ⁡ ( x ) f(x) = \csc (x) \, f(x)=csc(x) …

Sekans und Kosekans

www.biancahoegel.de › геометрия › винкель › sekans_cosekans

Sekans und Kosekans sind trigonometrische Funktionen. Der Sekans wird mit \sec (x) bezeichnet, der Kosekans mit \csc (x) oder \operatorname{cosec} (x) .

Beweis für die Ableitung von csc(x) — MatheGuru Ableitung des Cosekans ist. Herleitung унд Beweis.

Найти асимптоты csc(x) — Mathway

www.mathway.com › Popular-задачи › Тригонометрия

Für jedes y=csc(x) y = csc (x) вертикальная асимптотика существования x=nπ x = n π , wobei n n eine Ganzzahlist. Verwende die Grundperiode für y=csc(x) y …

Ermittle die Stammfunktion csc(x) — Mathway

www.mathway.com csc ( x ) также Funktion. ж · csc ; Шаг 2. Die Funktion F(x) F ( x ) kann bestimmt werden, indem das unbestimmte Integral der Ableitung f(x) …

csc(x) — Wolfram|Alpha 92 mathe

Kosekans Taschenrechner

csc(0)

Тета-формула Cos — Объяснение, прямоугольный треугольник и часто задаваемые вопросы

В математике существует шесть различных типов тригонометрических функций: синус (sin), косинус (cos), секанс (sec), косеканс (cosec), тангенс (tan) и котангенс (cot). Все эти шесть различных типов тригонометрических функций символизируют отношения между отношениями разных сторон прямоугольного треугольника. Эти тригонометрические функции важны для изучения треугольников, высоты и расстояния, света, звука, волны и т. д. Тета-формула для разных тригонометрических функций различна, тета представлена ​​θ.

в правом треугольнике

  • SINE (θ) = противоположность/гипотенуза

  • COS (θ) = соседний/Гипотен. θ) = Смежный/Противоположный

  • Коссек (θ) = Гипотенуза/Противоположный

  • Сек (θ) = Гипотенуза/Смежный

углы.

Формула угла косоглазия

В прямоугольном треугольнике. Cos theta или cos θ — это отношение прилежащей стороны к гипотенузе.

(Изображение будет загружено в ближайшее время)

В данном прямоугольном треугольнике A — смежная сторона, O — перпендикуляр, а H — гипотенуза.

Cos θ = Смежный/Гипотенуза

Здесь θ представляет собой угол треугольника. Углы, которыми могут быть представлены тригонометрические функции, называются углами тригонометрии. Важными углами тригонометрии являются 0°, 30°, 45°, 60°, 9°.0°. Все это стандартные углы тригонометрических отношений, такие как sin, cos, tan, sec, cosec и cot. Каждый из этих углов имеет разные значения с разными тригонометрическими функциями.

θ

0°

30°

45°

60°

90°

sinθ

0

1/2

1/√2

√3/2

1

cos θ

1

√3 /2

1/√2

1/2

0

tan θ

0

1/√3

1

√3

Undefined

cosec θ

Undefined

2

√2

2/√3

1

sec θ

1

2/√3

√2

2

Undefined

cot θ

Undefined

√3

1

1/√3

0

Note: 1 cos theta = 1.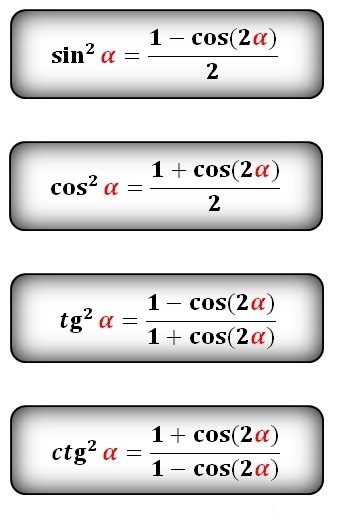 Cos θ; Например: 1 cos 30° = 1. Cos 30° = 1 x √3/2 = √3/2

И cos θ = \[\frac{1}{sec\theta }\]

Или, sec θ = \[\frac{1}{cos\theta }\]

Кроме того, sin (90 —  θ) = cos θ и Cos (90 —  θ) = sin θ.

Также помните, что sin 45 = cos 45 = 1/√2. Значение sin θ и cos θ никогда не может быть больше 1,9.0003

Определение Cos Theta

Формула Cos Theta — это математическая формула, используемая для вычисления косинуса угла. Его можно сократить как Cos(θ) и он выглядит следующим образом: Cos(θ) = смежный/гипотенуза. Другими словами, он берет длину прилежащей стороны (стороны рядом с углом) и делит ее на длину гипотенузы (самая длинная сторона прямоугольного треугольника). Это даст вам приблизительное значение косинуса этого конкретного угла.

Является ли прямоугольный треугольник ключом?

Формула Cos Theta особенно полезна при работе с прямоугольными треугольниками. В прямоугольном треугольнике косинусом угла всегда будет длина прилежащей стороны, деленная на длину гипотенузы. Это делает его отличным инструментом для решения задач, связанных с косинусом.

Важность изучения cos Theta важна, потому что ее можно использовать для решения задач косинуса. Кроме того, косинус является частью формулы SOHCATOA, которая поможет вам найти все шесть тригонометрических функций (синус, косинус, тангенс, вертикальный угол/косеканс, косой угол/секанс и котангенс) из одного угла. Это делает Cos Theta ценным инструментом при работе с другими формулами тригонометрии.

Косинус Тета применяется во многих различных областях

Косинус используется в различных областях, включая инженерию, физику и строительство. Это может быть полезно при работе с прямоугольными треугольниками или при поиске углов в сложных задачах.

Вот несколько советов по изучению Cos Theta

  1. Понимание основ Косинус — это математический термин, используемый для нахождения значения косинуса угла в прямоугольных треугольниках. Это полезно при работе с другими формулами тригонометрии и может быть применено к задачам, связанным с прямыми углами в геометрии, физике, строительстве, астрологии/астрономии и т. д. Чтобы помочь вам лучше понять Cos Theta, попробуйте применить ее к некоторым примерам из реальной жизни или потренируйтесь находить Cos (x) для различных значений x, не равных 90 градусов. Таким образом, вы сможете более комфортно использовать Cos Theta, прежде чем переходить к решению более сложных тригонометрических задач.

  2. Практика на Cos Theta Вопросы. Косинус проверяется на экзаменах ACT, SAT и GRE. Это потому, что у него много приложений в геометрии, физике, астрологии/астрономии и т. д. Если вы готовитесь к одному из этих тестов, попробуйте изучить некоторые практические задачи Cos Theta, чтобы освоиться с косинусом перед сдачей экзамена.

  3. Пробные тесты. Потому что Тета — важная концепция для понимания, а вопросы косинуса можно найти в тестах. Чтобы подготовиться к тесту, попробуйте пройти несколько практических тестов по косинусу или пробных экзаменов по косинусу. Таким образом, вы получите представление о том, как будет выглядеть ваш экзамен, какие темы он охватывает и насколько хорошо вы справляетесь с типами вопросов косинуса.

  4. Управление временем. Косинус может быть сложной темой для изучения. Важно, чтобы у вас было достаточно времени, чтобы понять все концепции и практические вопросы. Косинус обычно проверяется в математическом разделе различных экзаменов, поэтому важно, чтобы вы соответствующим образом сосредоточили свои исследования на этой теме.

  5. Избегайте зубрежки в последнюю минуту. Тета — важная тема, на которой основаны косинусные вопросы. Однако лучше не зубрить экзамен Cosinethe в последнюю минуту.

    No related posts.

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *