Мерзляк 5 класс — § 14. Треугольник и его виды
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
Вопросы к параграфу
1. Какие бывают виды треугольников в зависимости от вида их углов?
- остроугольные — все из углы острые;
- прямоугольные — один из углов треугольника прямой — равен 90°;
- тупоугольные — один из углов треугольника тупой.
2. Какой треугольник называют остроугольным? Прямоугольным? Тупоугольным?
- Остроугольные прямоугольники — это треугольники, у которых все углы острые (< 90°).
- Прямоугольные треугольники — это прямоугольники, у которых один из углов прямой (= 90°).
- Тупоугольные треугольники — это треугольники, у которых один из углов тупой (> 90°).
3. Какие бывают виды треугольников в зависимости от количества равных сторон?
- равнобедренные треугольники — 2 стороны равны;
- равносторонние треугольники — 3 стороны равны.
4. Какой треугольник называют равнобедренным? Равносторонним? Разносторонним?
- Равнобедренный треугольник — это треугольник, у которого две стороны равны.
- Равносторонний треугольник — это треугольник, у которого три стороны равны.
- Разносторонний треугольник — это треугольник, у которого все стороны имеют различную длину.
5. Как называют стороны равнобедренного треугольника?
- равные стороны равнобедренного треугольника называют боковыми сторонами;
- отличающуюся по длине сторону равнобедренного треугольника называют основанием.
6. По какой формуле вычисляют периметр равностороннего треугольника? — Периметр равностороннего треугольника равен произведению числа 3 и длины его стороны : P = 3a.
Решаем устно
1. Чему равен периметр восьмиугольника, каждая сторона которого равна 4 см?
8 • 4 = 32 (см) — периметр восьмиугольника.
Ответ: 32 см.
2. Вычислите сумму 27 + 16 + 33 + 24.
27 + 16 + 33 + 24 = (27 + 33) = (16 + 24) = 60 + 40 = 100
Ответ: 100.
3. Каких чисел не хватает в цепочке вычислений?
4. На трёх кустах расцвело 15 роз. Когда на одном из этих кустов распустились ещё 3 розы, то на всех кустах роз стало поровну. Сколько роз было на каждом кусте вначале?
1) Мы знаем, что вначале на всех кустах было 15 роз, но потом на одной розе распустилось ещё 3 цветка:
15 + 3 = 18 (цветов) — стало на всех кустах в конце.
2) Мы знаем, что в конце на каждом из трёх кустов роз было поровну:
18 : 3 = 6 (цветов) — было на каждом кусте в конце.
3) Мы знаем, что на одном из кустов роз вначале было на 3 меньше:
6 — 3 = 3 (цветка) — было на одном из кустов вначале.
4) Мы знаем, что количество роз на остальных кустах не изменилось, то есть было и осталось по 6 цветков.
Ответ: 6, 6 и 3 розы.
Упражнения
338. Определите вид треугольника, изображённого на рисунке 121, в зависимости от вида его углов и количества равных сторон.
- а) треугольник ABC — это разносторонний остроугольный треугольник;
- б) треугольник MNK — это разносторонний прямоугольный треугольник;
- в) треугольник PEF — это равнобедренный остроугольный треугольник;
- г) треугольник QSR — это равнобедренный тупоугольный треугольник;
- д) треугольник OTR — это разносторонний тупоугольный треугольник;
- е) треугольник DAB — это равнобедренный прямоугольный треугольник.
339. Начертите:
- RTQ — разносторонний остроугольный треугольник;
- JLD — равнобедренный прямоугольный треугольник;
- POS — равнобедренный тупоугольный треугольник.
340. Начертите:
- ABC — разносторонний прямоугольный треугольник;
- MNK — разносторонний тупоугольный треугольник;
- EFH — равнобедренный остроугольный треугольник.
341. Найдите периметр треугольника со сторонами 16 см, 22 см и 28 см.
Периметр треугольника равен сумме длин все его сторон.
P = 16 + 22 + 28 = 66 (см)
Ответ: P = 66 см.
342. Найдите периметр треугольника со сторонами 14 см, 17 см и 17 см.
Периметр треугольника равен сумме длин все его сторон.
P = 14 + 17 + 17 = 48 (см)
Ответ: P = 48 см.
343. Начертите произвольный треугольник, измерьте его стороны и углы, найдите периметр и сумму углов этого треугольника.
Начертим произвольный треугольник ABC.
При помощи линейки измерим длины его сторон:
- AB = 4,2 см
- BC = 3,2 см
- AC = 4,6 см
При помощи транспортира измерим его углы:
- ∠A = 42º
- ∠B = 74º
- ∠C = 64º
Найдём периметр треугольника ABC:
P = AB + BC + AC =4,2 + 3,2 + 4,6 = 12 (см)
∠A + ∠B + ∠C = 42º + 74º + 64º = 180º
Ответ: в треугольнике ABC: AB = 4,2 см, BC = 3,2 см, AC = 4,6 см, ∠A = 42º, ∠B = 74º, ∠C = 64º, периметр P = 12 см, сумма углов равна 180º.
344. Одна сторона треугольника равна 24 см, вторая сторона — на 18 см больше первой, а третья сторона — в 2 раза меньше второй. Найдите периметр треугольника.
1) 24 + 18 = 42 (см) — длина второй стороны треугольника.
2) 42 : 2 = 21 (см) — длина третьей стороны треугольника.
3) 24 + 42 + 21 = 87 (см) — периметр треугольника.
Ответ: P = 87 см.
345. Одна сторона треугольника равна 12 см, вторая сторона в 3 раза больше первой, а третья — на 8 см меньше второй. Найдите периметр треугольника.
1) 12 • 3 = 36 (см) — длина второй стороны треугольника.
2) 36 — 8 = 28 (см) — длина третьей стороны треугольника.
3) 12 + 36 + 28 = 78 (см) — периметр треугольника.
Ответ: P = 78 см.
346. 1) Найдите периметр равнобедренного треугольника, основание которого равно 13 см, а боковая сторона — 8 см.
У равнобедренного треугольника боковые стороны равны. Значит у данного треугольника дву стороны по 8 см и одна сторона (основание) — 13 см.
Найдём периметр:
8 + 8 + 13 = 29 (см) — периметр треугольника.
Ответ: 29 см.
2) Периметр равнобедренного треугольника равен 39 см, а основание — 15 см. Найдите боковые стороны треугольника.
Мы знаем, тто периметр треугольника — это сумма длин всех его сторон. Также мы знаем, что боковые стороны равнобедренного треугольника равны. Найдем длину боковой стороны:
(39 — 15) : 2 = 24 : 2 = 12 (см) — длина боковой стороны.
Ответ: Каждая из двух боковых сторон этого равнобедренного треугольника равна 12 см.
347. Периметр равнобедренного треугольника равен 28 см, а боковая сторона — 10 см. Найдите основание треугольника.
Мы знаем, тто периметр треугольника — это сумма длин всех его сторон. Также мы знаем, что боковые стороны равнобедренного треугольника равны. Найдем длину основания:
28 — 10 • 2 = 28 — 20 = 8 (см) — длина основания.
Ответ: 8 см.
348. Периметр треугольника равен p см, одна сторона — 22 см, вторая сторона — b см.
Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если р = 72, b = 26.
Пусть третья сторона равна с см. Составим выражения для нахождения длины третьей стороны треугольника:
с = p — 22 — b (см)
При р = 72, b = 26:
с = 72 — 22 — 26 = 50 — 26 = 24 (см).
Ответ: с = p — 22 — b, с = 24 см.
349. Периметр треугольника равен 97 см, одна сторона — а см, вторая — b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если а = 32, b = 26.
Пусть третья сторона равна с см. Составим выражения для нахождения длины третьей стороны треугольника:
с = 97 — а — b (см)
При а = 32, b = 26:
с = 97 — 32 — 26 = 65 — 26 = 39 (см).
Ответ: с = 97 — а — b, с = 39 см.
350. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:
1) две стороны равны 3 см и 6 см, а угол между ними — 40° — разносторонний тупоугольный треугольник (тупым является угол B).
2) две стороны равны 2 см 5 мм и 5 см, а угол между ними — 130° — разносторонний тупоугольный треугольник (тупым является угол А).
3) две стороны равны по 3 см 5 мм, а угол между ними — 54° — равнобедренный остроугольный треугольник
4) сторона АВ равна 4 см, а углы САВ и СВА соответственно равны 30° и 70° — разносторонний остроугольный треугольник.
5) сторона АВ равна 2 см 5 мм, а углы САВ и СВА соответственно равны 100° и 20° — разносторонний тупоугольный треугольник.
6) сторона ВС равна 5 см, а углы ABC и ВСА соответственно равны 30° и 60° — разносторонний прямоугольный треугольник.
7) сторона ВС равна 5 см 5 мм, а углы ABC и ВСА равны по 45° — равнобедренный прямоугольный треугольник.
8) сторона АС равна 5 см 5 мм, а углы ВАС и ВСА равны по 60°
351. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:
2) две стороны равны по 4 см 5 мм, а угол между ними — 60° — равносторонний остроугольный треугольник.
3) сторона АС равна 6 см, а углы ВАС и ВСА соответственно равны 90° и 45° — равнобедренный прямоугольный треугольник.
4) сторона АВ равна 4 см 5 мм, а углы САВ и СВА соответственно равны 35° — равнобедренный тупоугольный треугольник.
352. Постройте треугольник, стороны которого содержат четыре точки, изображённые на рисунке 122.
353. Сколько треугольников изображено на рисунке 123?
- а) Изображено 7 треугольников (4 маленьких и 3 больших).
- б) Изображено 20 треугольников(12 маленьких, 6 средних и 2 больших).
Упражнения для повторения
354. Запишите все углы, изображённые на рисунке 124, и укажите вид каждого угла.
- ∠ABC — развёрнутый угол
- ∠ABM — острый угол
- ∠ABK — тупой угол
- ∠MBK — прямой угол
- ∠MBC — тупой угол
- ∠KBC — острый угол
355.
Миша делал домашнее задание по математике с 16 ч 48 мин до 17 ч 16 мин, а Дима — с 17 ч 53 мин до 18 ч 20 мин. Кто из мальчиков дольше делал задание и на сколько минут?
1) 17 ч 16 мин — 16 ч 48 мин = 16 ч 76 мин — 16 ч 48 мин = 28 мин — делал задание Миша.
2) 18 ч 20 мин — 17 ч 53 мин = 17 ч 80 мин — 17 ч 53 мин = 27 мин — делал задание Дима.
3) 28 мин — 27 мин = 1 мин — делал дольше Миша, чем Дима.
Ответ: Миа делал домашнее задание на 1 минуту дольше, чем Дима.
356. Решите уравнение:
357. Вместо звёздочек поставьте цифры так, чтобы действие было выполнено правильно:
Задача от мудрой совы
358. Каждый учащийся гимназии изучает по крайней мере один из двух иностранных языков. Английский язык изучают 328 учеников, французский язык — 246 учеников, а английский и французский одновременно — 109 учеников. Сколько всего учеников учится в гимназии?
1) 328 — 109 = 219 (учеников) — изучает только английский язык.
2) 246 — 109 = 137 (учеников) — изучает только французский язык.
3) 219 + 109 + 137 = 465 (учеников) — всего в гимназии.
Ответ: 465 учеников.
- Ответы к учебнику для 5 класса. А. Г. Мерзляк
- Переход на главную страницу сайта
ГДЗ По Математике 5 Класс. Треугольник и его виды
Перейти к контенту
ГДЗ по Математике 5 класс Мерзляк А.Г. § 14. Треугольник и его виды
Вопросы к параграфу
1. Какие бывают виды треугольников в зависимости от вида их углов?
2. Какой треугольник называют остроугольным? Прямоугольным? Тупоугольным?
3. Какие бывают виды треугольников в зависимости от количества равных сторон?
4. Какой треугольник называют равнобедренным? Равносторонним? Разносторонним?
5. Как называют стороны равнобедренного треугольника?
6.
По какой формуле вычисляют периметр равностороннего треугольника?
Решаем устно
1. Чему равен периметр восьмиугольника, каждая сторона которого равна 4 см?
2. Вычислите сумму 27 + 16 + 33 + 24.
3. Каких чисел не хватает в цепочке вычислений?
4. На трёх кустах расцвело 15 роз. Когда на одном из этих кустов распустились ещё 3 розы, то на всех кустах роз стало поровну. Сколько роз было на каждом кусте вначале?
Упражнения
338. Определите вид треугольника, изображённого на рисунке 121, в зависимости от вида его углов и количества равных сторон.
339. Начертите: RTQ
340. Начертите: ABC
341. Найдите периметр треугольника со сторонами 16 см, 22 см и 28 см.
342. Найдите периметр треугольника со сторонами 14 см, 17 см и 17 см.
343. Начертите произвольный треугольник, измерьте его стороны и углы, найдите периметр и сумму углов этого треугольника.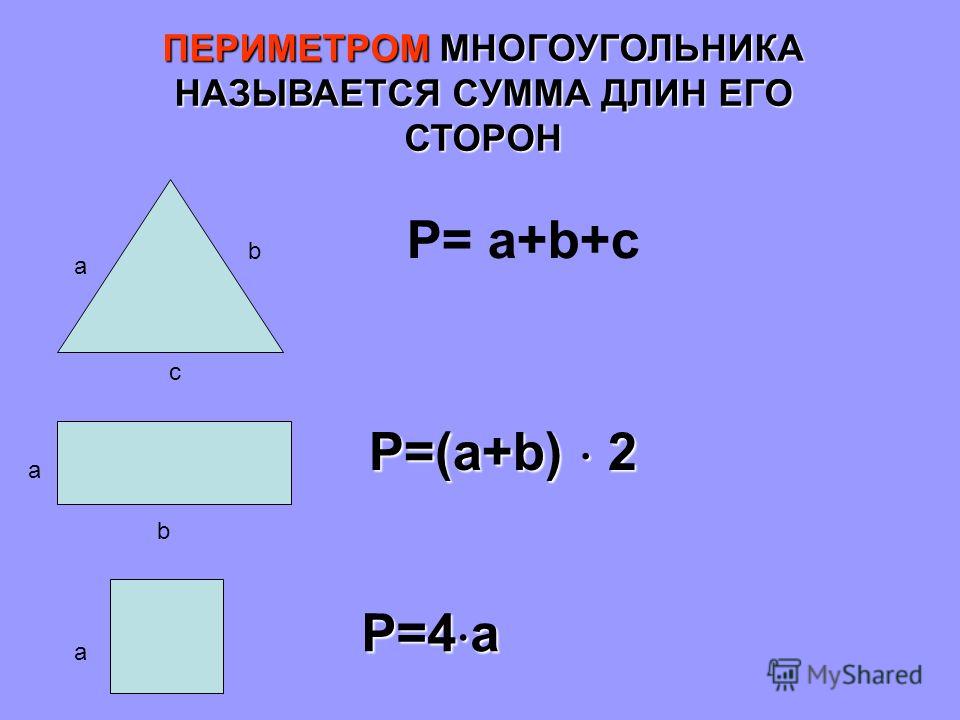
344. Одна сторона треугольника равна 24 см, вторая сторона — на 18 см больше первой, а третья сторона — в 2 раза меньше второй. Найдите периметр треугольника.
345. Одна сторона треугольника равна 12 см, вторая сторона в 3 раза больше первой, а третья — на 8 см меньше второй. Найдите периметр треугольника.
346. 1) Найдите периметр равнобедренного треугольника, основание которого равно 13 см, а боковая сторона — 8 см.
347. Периметр равнобедренного треугольника равен 28 см, а боковая сторона — 10 см. Найдите основание треугольника.
348. Периметр треугольника равен p см, одна сторона — 22 см, вторая сторона — b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если р = 72, b = 26.
349. Периметр треугольника равен 97 см, одна сторона — а см, вторая — b см. Составьте выражение для нахождения третьей стороны. Вычислите длину третьей стороны, если а = 32, b = 26.
350. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:
351. С помощью линейки и транспортира постройте треугольник ABC и укажите его вид, если:
352. Постройте треугольник, стороны которого содержат четыре точки, изображённые на рисунке 122.
353. Сколько треугольников изображено на рисунке 123?
Упражнения для повторения
354. Запишите все углы, изображённые на рисунке 124, и укажите вид каждого угла.
355. Миша делал домашнее задание по математике с 16 ч 48 мин до 17 ч 16 мин, а Дима — с 17 ч 53 мин до 18 ч 20 мин. Кто из мальчиков дольше делал задание и на сколько минут?
356. Решите уравнение:
357. Вместо звёздочек поставьте цифры так, чтобы действие было выполнено правильно:
Задача от мудрой совы
358. Каждый учащийся гимназии изучает по крайней мере один из двух иностранных языков.
Английский язык изучают 328 учеников, французский язык — 246 учеников, а английский и французский одновременно — 109 учеников. Сколько всего учеников учится в гимназии?
Этот сайт использует cookie для хранения данных.
Вопрос Видео: Нахождение периметра треугольника по координатам его вершин с использованием формулы расстояния
Учитывая 𝐴(4, 5), 𝐵(5, 5) и 𝐶(−4, −7), каков периметр △𝐴𝐵𝐶?
Стенограмма видео
Учитывая, что 𝐴 имеет координаты четыре, пять, 𝐵 имеет координаты пять, пять, а 𝐶 имеет координаты минус четыре, минус семь, каков периметр треугольника 𝐴𝐵𝐶?
Начнем с того, что вспомним, что мы можем вычислить расстояние между любыми двумя точками с координатами 𝑥 меньше единицы, 𝑦 меньше единицы и 𝑥 меньше двух, 𝑦 меньше двух, используя наше знание теоремы Пифагора. Горизонтальное расстояние нашего прямоугольного треугольника равно 𝑥 меньше двух минус 𝑥 меньше единицы, а вертикальное расстояние равно 𝑦 меньше двух минус 𝑦 меньше единицы.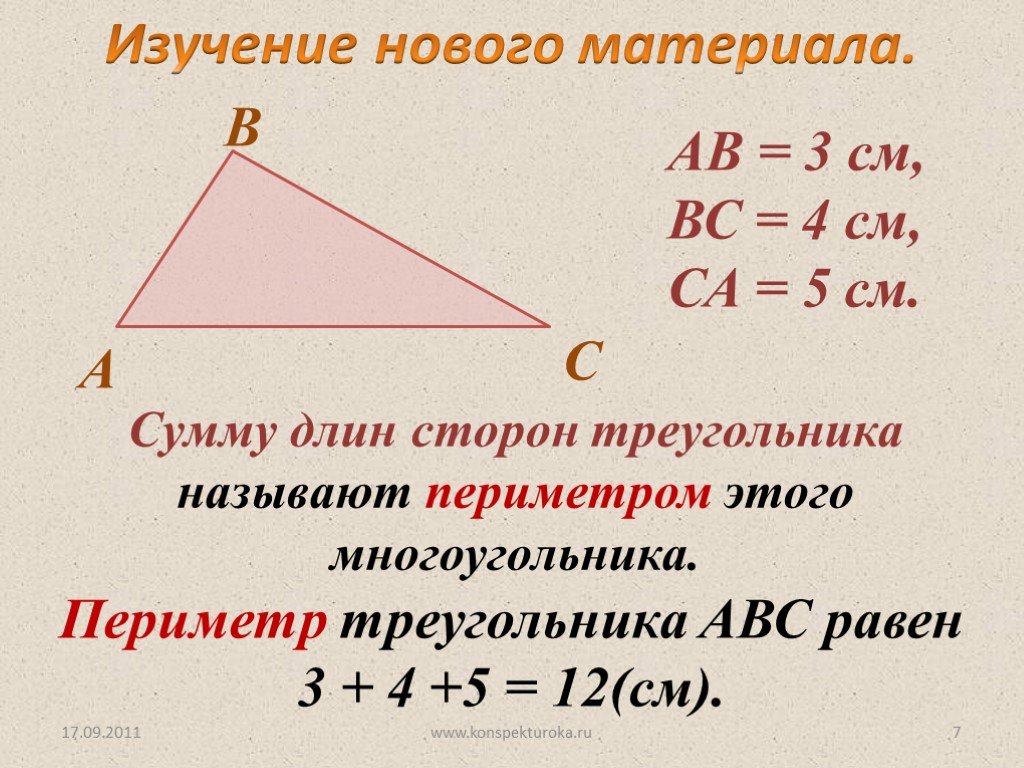
Отрезок 𝐴𝐵 является гипотенузой нашего треугольника. Если мы допустим, что это имеет длину 𝑑 единиц, то, применяя теорему Пифагора, мы имеем 𝑑 в квадрате равно 𝑥 меньше двух минус 𝑥 меньше единицы все в квадрате плюс 𝑦 меньше двух минус 𝑦 меньше единицы все в квадрате. Извлекая квадратный корень из обеих частей этого уравнения и используя тот факт, что 𝑑 должно быть положительным, мы получаем формулу длины линии между двумя точками на двумерной координатной плоскости. В этом вопросе мы будем использовать эту формулу, чтобы вычислить периметр треугольника 𝐴𝐵𝐶.
Нам даны координаты трех точек. А поскольку периметр — это расстояние вокруг внешней стороны нашего треугольника, нам нужно рассчитать длину отрезков 𝐴𝐵, 𝐵𝐶 и 𝐶𝐴. Здесь стоит отметить, что 𝐴 и 𝐵 имеют одну и ту же 𝑦-координату. Это означает, что они лежат на горизонтальной линии. И нам на самом деле не нужна формула расстояния для вычисления длины отрезка 𝐴𝐵. Это будет просто разница между 𝑥-координатами. Пять минус четыре равно единице, и это будет длина стороны 𝐴𝐵 в нашем треугольнике.
Чтобы вычислить длину стороны 𝐵𝐶, сначала пусть точка 𝐵 имеет координаты 𝑥 меньше единицы, 𝑦 меньше единицы, а точка 𝐶 имеет координаты 𝑥 меньше двух, 𝑦 меньше двух. Подставляя наши координаты в формулу расстояния, мы получаем, что 𝐵𝐶 равно квадратному корню из отрицательных четырех минус пять в квадрате плюс минус семь минус пять в квадрате. Отрицательное четыре минус пять равно отрицательному числу девять, и возведение этого числа в квадрат дает нам 81. Отрицательное семь минус пять дает отрицательное число 12, и возведение этого числа в квадрат дает нам 144. Таким образом, 𝐵𝐶 равно квадратному корню из 225. 225 является квадратным числом, поскольку оно равно до 15 кв. Это означает, что квадратный корень из 225 равен 15. Длина стороны 𝐵𝐶 равна 15 единицам длины.
Теперь мы повторим этот процесс для длины стороны 𝐶𝐴, где на этот раз мы позволим точке 𝐴 иметь координаты 𝑥 под единицу, 𝑦 под единицу. Таким образом, 𝐶𝐴 равно квадратному корню из отрицательных четырех минус четыре в квадрате плюс отрицательные семь минус пять в квадрате.
Это равно квадратному корню из 64 плюс 144, что упрощается до квадратного корня из 208. Мы можем упростить это, используя наши знания о законах радикалов. Поскольку 16, умноженное на 13, равно 208, квадратный корень из 208 можно записать как квадратный корень из 16, умноженный на квадратный корень из 13. Мы знаем, что квадратный корень из 16 равен четырем. 𝐶𝐴 равно четырем корням из 13.
Теперь у нас есть длины всех трех сторон нашего треугольника. Периметр — это их сумма. Это равно единице плюс 15 плюс четыре корня из 13. Это можно упростить до 16 плюс четыре корня из 13. Это периметр треугольника 𝐴𝐵𝐶 в единицах длины.
модуль 5 тест отношений в треугольниках ключ ответа Джина Уилсон
AlleBilderVideosNewsMapsShoppingBücher
suchoptionen
Отвечено: Модуль 5: отношения в треугольниках… | бартлби
www.bartleby.com › … › Библиотека вопросов и ответов по геометрии
Решение для модуля 5: Отношения в треугольниках Джордан Райт Имя: Пер: +th Домашнее задание 6: Неравенства треугольников Дата: /13/22 ** Это 2-страничный документ!
Отношения в треугольниках (Учебная программа по геометрии — Раздел 5) | Все .
.. — TPT
www.teacherspayteachers.com › Продукт › Отношения…
17,95 $
Этот комплект «Отношения в треугольниках» содержит инструкции, домашние задания, три теста, учебное пособие и модульный тест, который охватывает …
Unit-5-Review-Guide-Relationships-in-Triangles-4.docx — Имя
www.coursehero.com › файл › Unit-5-Review-Guide-…
View Unit-5 -Review-Guide-Relationships-in-Triangles-4.docx из MATH S4980520 в средней школе Уилсона. Название: _ Период: _ Дата: _ ОТНОШЕНИЯ ВНУТРИ …
Раздел 5: Отношения внутри треугольников — Водопад Чиппева — Математика
tiluslm.weebly.com › блок-5-отношения-внутри-триа…
Я могу использовать отношения между сторонами и углами в треугольниках, чтобы найти неизвестные меры. 7. Я могу использовать неравенства для сравнения двух треугольников. Единица …
Блок 5 Отношения в треугольниках Рабочие листы — Learny Kids
Learnykids.
com › рабочие листы › unit-5-relationships-i…
Отображаются 8 лучших рабочих листов по запросу — Блок 5 Отношения в треугольниках. Некоторые рабочие листы для этой концепции: Джина Уилсон, все, алгебра, 2014 …
Глава 5, отношения в треугольниках, ключ ответа
federicafiumarapsicologa.it › глава-5-отношения…
Результаты 1–24 · 5 точечные графики; Texas Go Math, 3 класс, раздел 5, оценочный ответ. … в этой геометрии Джина Уилсон Глава 5 Отношения в треугольниках …
Джина Уилсон все вещи алгебра 2014 треугольник конгруэнтность аза и аас Джина УилсонВсе вещи алгебра ООО. … Сохранить сохранить ключ к ответу на оценку блока конгруэнтных треугольников.
Geometry 5.3 Notes — YouTube
www.youtube.com › смотреть
26.10.2020 · Адаптировано из All Things Algebra, Джина Уилсон. Обложки перпендикулярной биссектрисы и угла …
Dauer: 30:32
Прислан: 26.10.2020
Geometry 5.1 Notes — YouTube
www.