Сколько штук бруса в одном кубе – как правильно рассчитать?
Приступая к строительству дома, необходимо правильно рассчитать количество материалов. Конечно, можно доверить этот вопрос застройщику. Но нередко хочется самому точно знать требуемое количество. Еще одна ситуация: будущий хозяин дома решил возводить коттедж самостоятельно. В таком случае следует самостоятельно разобраться в особенностях расчета.
Как правило, в магазинах цена за брус рассчитывается за метр кубический. Поэтому перед покупкой, чтобы узнать точную стоимость, следует перевести погонные метры в кубические.
Что такое кубический метр?
Кубометр – это мера, обозначающая объем. Он равен объему куба, у которого все ребра имеют длину один метр. Согласно ГОСТу материалы из дерева должны идентифицироваться по длине и сечению. Эта информация позволит легко рассчитать количество, входящее в кубический метр.
Как определить размер сечения? Для этого следует отступить от торца в пределах 10 сантиметров и замерить высоту и ширину балки.
Далее эти значения перемножаются, и на выходе мы узнаем площадь сечения балки. После того как умножим ее на длину, определим объем одного бруса.
Что нам дает количество брусьев в кубе? Эта цифра позволит понять разницу между ценой одного бруса и целого куба.
Самый частый вопрос наших покупателей – сколько штук бруса в одном кубометре? При этом, их интересует количество бруса 150х150, 150х200 и так далее.
Приведем примерную таблицу расчета, по которой легко ориентироваться перед покупкой:
При таком расчете подразумевается брус длиной 6 или 12 метров. Точно зная, сколько брусьев размером 150х150х6000 содержится в кубе, вы сведете к нулю риск переплаты.
Сколько бруса размером 100х100 находится в кубе?
Чтобы узнать эту цифру, следует оперировать такими данными, как ширина, длина и высота бруса. Сперва узнаем объем одной штуки. Для этого перемножим длину на ширину и на высоту. Порядок цифр здесь не имеет значения.
Формула расчета объема бруса:
Пример: 100мм х 100мм х 6000 мм = 0,1м х 0,1м х 6м = 0,06 м3
Теперь можно высчитать количество единиц в одном кубометре.
Для этого один кубометр делимся на получившийся объем.
Пример: 1м3 / 0,06м3 = 16 шт./м3
где 1 м3 – один куб
0,06м3 – объем одной штуки.
Сколько бруса размером 100х150 вмещается в один куб?
В строительных и интернет-магазинах содержится следующая информация о брусе: высота и ширина. Длина в большинстве случаев неизменна – 6000 мм.
Как рассчитать объем одного бруса размеров 100х150х6000? Как в предыдущем случае, необходимо просто перемножить эти показатели, разделив сначала каждое число на 1000.
Пример: 0,1 м х 0,15 м х 6 м = 0,09 м³.
Ну а теперь осталось посчитать, сколько единиц бруса помещается в один куб. Для этого мы воспользуемся все той же формулой, как и в случае с брусом 100х100:
1 м3 / объем 0,09 м3.
Сложно? Достаточно легко произвести эти расчеты даже людям с нематематическим складом ума.
Иногда требуется сравнить брус 100х100 с 200х200. При равной длине можно полученный результат при расчете бруса 100х100 разделить на 4.
Так, если в один куб вмещается 33 штуки бруса длиной 3 метра размером 100х100, то при той же длине, но размерах 200х200 вместится 8 единиц.
Если длина остается 100, а высота 200, то делим 33 на 2 и получаем 16.
Разобравшись с формулой и таблицей, можно легко высчитать количество штук бруса 100х100, 150х200, 200х200. Главное, не ошибиться при расчете, подставляя данные.
Делая заказ в компании «Время строить», вы получите квалифицированную консультацию, а также помощь в расчете нужного объема бруса и количества в одном кубометре. Звоните прямо сейчас!
Многомерный куб
Рассмотрим графическое представление функции в виде многомерного куба. Каждой вершине n-мерного куба можно поставить в соответствие конституенту единицы.
Подмножество отмеченных вершин является отображением на n-мерном кубе булевой функции от n переменных в СДНФ.
Для отображения
функции от n переменных, представленной в любой
ДНФ, необходимо установить соответствие
между ее минитермами и элементами n-мерного
куба.
Минитерм (n-1)-го ранга можно рассматривать как результат склеивания двух минитермовn-го ранга, т.е.
=
На n-мерном кубе это соответствует замене двух вершин, которые отличаются только значениями координат хi, соединяющих эти вершины ребром (говорят, что ребро покрывает инцидентные ему вершины).
Аналогично устанавливается соответствие минитермов (n-2)-го порядка граням n-мерного куба, каждая из которых покрывает четыре вершины (и четыре ребра).
Элементы n-мерного куба, характеризующиеся S измерениями, называются S-кубами.
Так вершины являются 0-кубами, ребра 1-кубами, грани 2-кубами и т.д.
Обобщая, можно
сказать, что минитерм (n-S)
ранга в ДНФ для функции n переменных отображается S-кубом,
причем каждый S-куб
покрывает все те кубы низшей размерности,
которые связаны только с его вершинами.
Пример. На рис. дано отображение
Здесь минитермы исоответствуют 1-кубам (S=3-2=1), а минитерм х3 отображается 2-кубам (S=3-1=2).
Итак, любая ДНФ отображается на n-мерном кубе совокупностью S-кубов, которые покрывают все вершины, соответствующие конституентам единицам (0-куба).
Конституенты. Для переменных х1, х2,… хn выражение называют конституентой единицы, а— конституентой нуля (означает либо, либо).
Данная конституента единицы (нуля) обращается в единицу (нуль) только при одном соответствующем ей наборе значений переменных, который получается, если все переменные принять равными единице (нулю), а их отрицания — нулю (единице).
Например: конституенте единице соответствует набор (1011), а конституенте нуля— набор (1001).
Так как СД(К)НФ
является дизъюнкцией (конъюнкцией)
конституент единицы (нуля), то можно
утверждать, что представляемая ею
булева функция 
На остальных наборах эта функция
обращается в 0 (единицу).
Справедливо и обратное утверждение, на котором основан способ представления в виде формулы любой булевой функции, заданной таблицей.
Для этого необходимо записать дизъюнкции (конъюнкции) конституент единицы (нуля), соответствующих наборам значений переменных, на которых функция принимает значение, равное единице (нулю).
Например, функции, заданной таблицей
соответствуют
Полученные выражения можно преобразовать к другому виду на основании свойств алгебры логики.
Справедливо и
обратное утверждение: если некоторая
совокупность S-кубов
покрывает множество всех вершин,
соответствующих единичным значениям
функции, то дизъюнкция соответствующих
этим S-кубам
минитермов является выражением данной
функции в ДНФ.
Говорят, что такая совокупность S-кубов (или соответствующих им минитермов) образует покрытие функции. Стремление к минимальной форме интуитивно понимается как поиск такого покрытия, число S-кубов которого было бы поменьше, а их размерность S — побольше. Покрытие, соответствующее минимальной форме, называют минимальным покрытием.
Например, для функции
рис a) у=,
а покрытия на рис б) у=, рис в) у=минимальные.
Рис. Покрытие функции у=:
а) неминимальное; б), в) минимальное.
Отображение функции на n-мерном наглядно и просто при n3. Четырехмерный куб можно изобразить, как показано на рис., где отображены функции четырех переменных и ее минимальное покрытие, соответствующее выражению у=
Использование
этого метода при n>4
требует настолько сложных построений,
что теряет все его преимущества.
Как кубировать биномы | Наука
Обновлено 29 октября 2018 г.
Автор Lisa Maloney
Алгебра полна повторяющихся закономерностей, которые каждый раз можно вычислять с помощью арифметики. Но поскольку эти шаблоны настолько распространены, обычно существует какая-то формула, которая упрощает вычисления. Куб бинома — отличный пример: если бы вам приходилось решать его каждый раз, вы бы потратили много времени на работу с карандашом и бумагой. Но как только вы узнаете формулу для решения этого куба (и несколько удобных приемов для ее запоминания), найти ответ будет так же просто, как вставить правильные термины в нужные слоты переменных.
TL;DR (слишком длинный; не читал)
Формула куба двучлена ( a + b ):
( a + b 2 6 9092 ) 39092 a 3 + 3_A_ 2 B + 3_AB_ 2 + B 3
CALLAGLING OF ARIIL AN BINOM 9099. + б)
3 перед вами.
Как только вы разобьете его на знакомые компоненты, он начнет выглядеть как более знакомые математические задачи, которые вы решали раньше.В этом случае полезно помнить, что
(a + b) 3
совпадает с
(a + b)(a + b)(a + b) , что должно выглядеть намного более знакомым.
Но вместо того, чтобы каждый раз вычислять математику с нуля, вы можете использовать «ярлык» формулы, представляющей ответ, который вы получите. Вот формула куба двучлена:
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
Чтобы использовать формулу, определите, какие числа (или переменные) занимают слоты для «a» и «b» в левой части уравнения, затем подставьте те же самые числа (или переменные ) в слоты «a» и «b» в правой части формулы.
Пример 1: Решите (x + 5) 3
Как видите, x занимает слот «a» в левой части формулы, а 5 занимает слот «b» .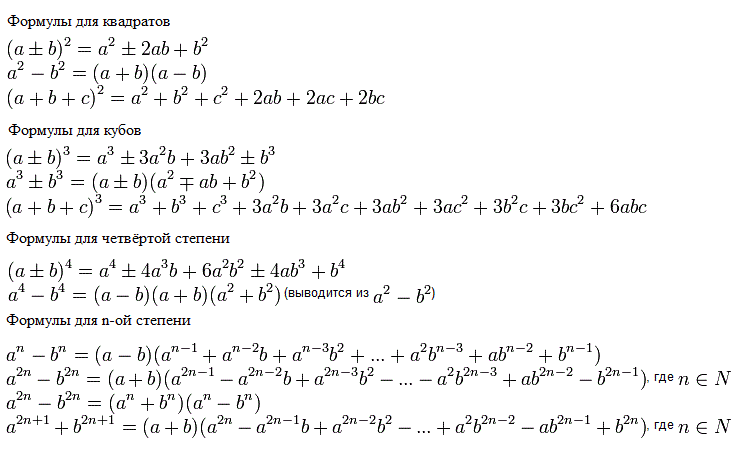
Замена x и 5 в правой части формулы дают вам:
x 3 + 3x 2 5 + 3×5 2 + 5 3
7 Немного упрощая ответ :
x 3 + 3(5)x 2 + 3(25)x + 125
И наконец, как только вы максимально упростили:
x 3 3 15x 2 + 75x + 125
Как насчет вычитания?
Вам не нужна другая формула, чтобы решить такую задачу, как (y — 3) 3 . Если вы помните, что y — 3 равно y + (-3) , вы можете просто переписать задачу в виде [y + (-3)] 3 и решить ее по знакомой вам формуле.
Пример 2: Решите (y — 3) 3
Как уже обсуждалось, ваш первый шаг — переписать задачу в виде [y + (-3)] 3 .
Next, remember your formula for the cube of a binomial:
(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3
In ваша проблема, y занимает слот «a» в левой части уравнения, а -3 занимает слот «b». Подставьте их в соответствующие слоты в правой части уравнения, обращая особое внимание на скобки, чтобы сохранить отрицательный знак перед -3. Это дает вам:
г 3 + 3г 2 (-3) + 3г(-3) 2 + (-3) 3
Теперь пришло время упростить. Опять же, обратите особое внимание на этот отрицательный знак при применении показателей:
y 3 + 3(-3)y 2 + 3(9)y + (-27)
Еще один раунд упрощения дает вам ответ:
y 3 — 9y 2 + 27y — 27
Следите за суммой и разностью кубов
Всегда внимательно следите за тем, где в задаче находятся показатели степени.