Интегральные функции:
- Si(x)
- Интегральный синус от x
- Ci(x)
- Интегральный косинус от x
- Shi(x)
- Интегральный гиперболический синус от x
- Chi(x)
- Интегральный гиперболический косинус от x
В выражениях можно применять следующие операции:
- Действительные числа
- вводить в виде 7.
3- — возведение в степень
- x + 7
- — сложение
- x — 6
- — вычитание
- 15/7
- — дробь
3Другие функции:
- asec(x)
- Функция — арксеканс от x
- acsc(x)
- Функция — арккосеканс от x
- sec(x)
- Функция — секанс от x
- csc(x)
- Функция — косеканс от x
- floor(x)
- Функция — округление x в меньшую сторону (пример floor(4.5)==4.0)
- ceiling(x)
- Функция — округление x в большую сторону (пример ceiling(4.5)==5.0)
- sign(x)
- Функция — Знак x
- erf(x)
- Функция ошибок (или интеграл вероятности)
- laplace(x)
- Функция Лапласа
- asech(x)
- Функция — гиперболический арксеканс от x
- csch(x)
- Функция — гиперболический косеканс от x
- sech(x)
- Функция — гиперболический секанс от x
- acsch(x)
- Функция — гиперболический арккосеканс от x
Постоянные:
- Число «Пи», которое примерно равно ~3. 14159..
- e
- Число e — основание натурального логарифма, примерно равно ~2,7183..
- i
- Комплексная единица
- oo
- Символ бесконечности — знак для бесконечности
14159..
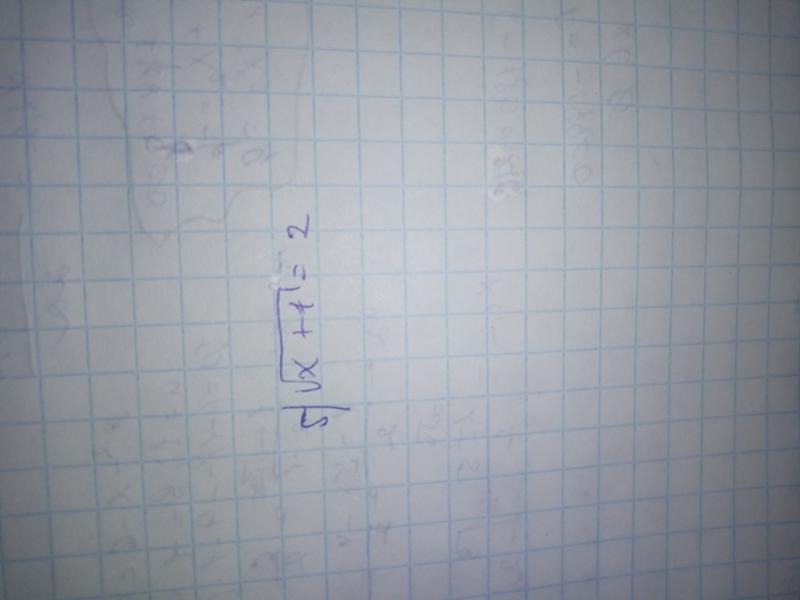
Если f(x)=((3x+1)(2sqrt(x)-1))/(sqrt(x)), то f'(1) равно
Вопрос
Вопрос
ICSE-ОГРАНИЧЕНИЯ И ПРОИЗВОДНЫЕ — Вопросы с несколькими вариантами ответов
20 видеоРЕКЛАМА
Ab Padhai karo bina ads ke
Khareedo DN Pro и dekho sari videos bina kisi ad ki rukaavat ke!
Обновлено: 27-06-2022
Текстовое решение
Ответ
Правильный ответ A
Ответ
Пошаговое решение, разработанное экспертами, чтобы помочь вам избавиться от сомнений и получить отличные оценки на экзаменах.
Стенограмма
привет всем нравится следующий вопрос вопрос в том, что если f x равно 3 X + 1 в x минус 1 на корень x, то слева, как единица равна ok вот человек дан, так что давайте посмотрим, как мы можем решить эту проблему, прежде всего, мы должны написать, что у нас есть f x равно 3 X + 1 в 2 квадратный корень из X — 1 из квадратного корня из X хорошо, так что давайте посмотрим, что мы можем записать это, поскольку F из X равно от 3 до 6 6 х в степени 3 на 2 минус 3 х, а затем + 2 х в степени 1 на 2 минус один 92 — 3 X при x в степени 1 на 2 + 2 x в степени 1 на 2 при 3 части 1 на 2 минус один при x в степени 1 на 2 ок, так что здесь мы решаем этот f из X равен что это будет 6 х минус 3 х квадрат на 2 + 2 — 3 степени минус 1 на 2 хорошо снова дифференцировать это X равно тому, что 6 минус 1 на 2 в 3 степени ки минус 1 на 2 ок + 1 на 2
в степени x ki минус 3 на 2, потому что мы знаем, что формула, используемая в этом, поскольку они обдумывают степень x x n, равна n для и -1 ok против всего этого, мы получаем, что f адреса X равно 6 минус 3 на 2 x степень ki минус 1 на 2 k + 1 на 2 x минус 3 на 2 теперь поместите значение одного из X хорошо, поэтому мы помещаем значение x равно 1 случае мы получаем f тире 1 равно 6 минус 3 на 2 в степени 1 минус 1 на 2 + 1 на 2 в степени 1 минус 3 на 2, так что мы получаем
f тире 1 равно 6 минус 3 на 2 + 1 на 2 ок против всего этого получаем адрес 1 равно 6 минус здесь будет здесь будет единица потому что — 3 + 1 равно минус 2 минус 2.
2 равно минус 1 минус 1 равно тому, что 5 хорошо так что давайте посмотрим, какой вариант здесь правильный, мы видели, что номер варианта заставляет исправить хорошо извините отметьте наш первый, так что здесь необязательный самый быстрый правильный 5 хорошо спасибо
Связанные Видео
Если t=2√2−(1+√3)√3−1 и f(x)=2×1−x2 g(x)=3x−x31−3×2, то ddt{f(g(t))} =
Пусть f(x)=√x−2√x−1√x−1−1.x, тогда
Если f(x)=(1)/(sqrt(x+2sqrt(2x-4))) +(1)/(sqrt(x-2sqrt(2x-4))) для x<2, тогда f(11)=
354572
Если f(x) =x−42√x, то f′(1 ) равно
26871411
. f(x)=√x−1+2√3−x равно
118622024
)=1√x+2√2x−4+1√x−2√2x−4 для x>2, тогда f(11)=
200893808
Если f(x)=2sin−1√1−x+sin−1(2√x(1−x)) где x∈(0,12), то f'(x) имеет значение, равное до
203514983
Текстовое решение
মনে করো, F (x) = √x — 2√x — 1√x — 1 — 1x হয়, তবে —
333025887
if ∫2 –1xin –Iin –Iin — 233025887
IF ∫ 233025887
IF ∫Iin — 233025887
IF ∫2
333025887
IF ∫Iin — 233025887
.