Калькулятор матриц метод гаусса онлайн: Онлайн калькулятор. Решение систем линейных уравнений. Метод Гаусса

Метод Гаусса онлайн

Назначение сервиса. Онлайн-калькулятор предназначен для решения системы линейных уравнений методом Гаусса, а также методом Гаусса-Жордано (чем они отличаются). Результат решения сохраняется в формате Word и Excel.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word
• Также решают

Инструкция. Для получения онлайн решения необходимо выбрать количество переменных: 2345678 и количество строк 23456

Вместе с этим калькулятором также используют следующие:
По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы

По координатам вершин пирамиды найти

Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных

Вычисление пределов

Смысл метода: последовательно исключаем переменную за переменной, пока в одной из строк не будет однозначно определена переменная x_i. Идею можно проиллюстрировать на простом примере:
 x1 - x2 = 3
-x1 + 2x2 = 1
=========== (складываем строки)
      -x2 + 2x2= 3 + 1 = 4 или x2 = 4
Откуда, x1 = 7

Суть метода можно понять, проанализировав пример решения.

Пример.
2x₁-x₂=0
-x₁+x₂+4x₃=13
x₁+2x₂+3x₃=14

Решение.
Запишем систему в виде расширенной матрицы:

2 -1 0 -1 1 4 1 2 3

Далее умножаем 2-ую строку на (2) и добавляем к первой:

0 1 8 -1 1 4 1 2 3

26 13 14

Добавим 3-ую строку к 2-ой:

0 1 8 0 3 7 1 2 3

26 27 14

Умножим первую строчку на (3), 2-ую строку умножаем на (-1). Следующее действие: складываем первую и вторую строки:

0 0 17 0 3 7 1 2 3

51 27 14

Теперь исходную систему можно записать как:
x3 = 51/17
x2 = [27 - 7x3]/3
x1 = [14 - (2x2 + 3x3)]
Из 1-ой строки выражаем x₃: 51/17 = 3
Из 2-ой строки выражаем

x₂: (27 - 7*3)/3 = 2
Из 3-ой строки выражаем x₁: (14 - 2*2 - 3*3) = 1

Вывод: метод Гаусса является достаточно простым методом при небольшом количестве переменных и позволяет найти точное значение переменных. Процесс отыскания переменных можно упростить, если каждый раз сортировать столбцы по возрастанию.

Метод Гаусса

Определение метода Гаусса

Пусть дана система ,  ∆≠0.           (1)
Метод Гаусса – это метод последовательного исключения неизвестных.

Суть метода Гаусса состоит в преобразовании (1) к системе с треугольной матрицей, из которой затем последовательно (обратным ходом) получаются значения всех неизвестных.

Вычислительные схемы

1. Схема единственного деления.
2. Схема последовательного алгоритма. На первом шаге метода среди элементов a _ij определяют максимальный по модулю элемент. Первое уравнение системы и уравнение с номером i₁ меняют местами. Далее стандартным образом производят исключение неизвестного x_i1 из всех уравнений, кроме первого.

Схема единственного деления

Пусть a₁₁≠0 (ведущий элемент) разделим на a₁₁ первое уравнение. Получим
x₁+a⁽¹⁾₁₂·x₂+…+a⁽¹⁾_1n·x_n=b⁽¹⁾₁              (2)
Пользуясь уравнением (2), легко исключить неизвестные x₁ из остальных уравнений системы (для этого достаточно из каждого уравнения вычесть уравнение (2) предварительно умноженное на соответствующий коэффициент при x₁), то есть на первом шаге получим
.
Иными словами, на 1 шаге каждый элемент последующих строк, начиная со второй, равен разности между исходным элементом и произведением его «проекции» на первый столбец и первую (преобразованную) строку.
Вслед за этим оставив первое уравнение в покое, над остальными уравнениями системы, полученной на первом шаге, совершим аналогичное преобразование: выберем из их числа уравнение с ведущим элементом и исключим с его помощью из остальных уравнений x₂ (шаг 2).
После n шагов вместо (1) получим равносильную систему
              (3)
Таким образом, на первом этапе мы получим треугольную систему (3). Этот этап называется прямым ходом.
На втором этапе (обратный ход) мы находим последовательно из (3) значения x_n , x_n-1, …, x₁.
Обозначим полученное решение за x₀. Тогда разность ε=b-A·x0 называется невязкой.
Если ε=0, то найденное решение x₀ является верным.

Вычисления по методу Гаусса выполняются в два этапа:

1. Первый этап называется прямым ходом метода. На первом этапе исходную систему преобразуют к треугольному виду.
2. Второй этап называется обратным ходом. На втором этапе решают треугольную систему, эквивалентную исходной.

Коэффициенты а₁₁, а₂₂, …, называют ведущими элементами.
На каждом шаге предполагалось, что ведущий элемент отличен от нуля. Если это не так, то в качестве ведущего можно использовать любой другой элемент, как бы переставив уравнения системы.

Назначение метода Гаусса

Метод Гаусса предназначен для решения систем линейных уравнений. Относится к прямым методам решения.

Виды метода Гаусса

1. Классический метод Гаусса;
2. Модификации метода Гаусса. Одной из модификаций метода Гаусса является схема с выбором главного элемента. Особенностью метода Гаусса с выбором главного элемента является такая перестановка уравнений, чтобы на k-ом шаге ведущим элементом оказывался наибольший по модулю элемент k-го столбца.
3. Метод Жордано-Гаусса;

Отличие метода Жордано-Гаусса от классического метода Гаусса состоит в применении правила прямоугольника, когда направление поиска решения происходит по главной диагонали (преобразование к единичной матрице). В методе Гаусса направление поиска решения происходит по столбцам (преобразование к системе с треугольной матрицей).
Проиллюстрируем отличие метода Жордано-Гаусса от метода Гаусса на примерах.

Пример решения методом Гаусса
Решим систему:

Для удобства вычислений поменяем строки местами:

Умножим 2-ую строку на (2). Добавим 3-ую строку к 2-ой

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой

Из 1-ой строки выражаем x₃:
Из 2-ой строки выражаем x₂:
Из 3-ой строки выражаем x₁:

Пример решения методом Жордано-Гаусса
Эту же СЛАУ решим методом Жордано-Гаусса.

Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен (1).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.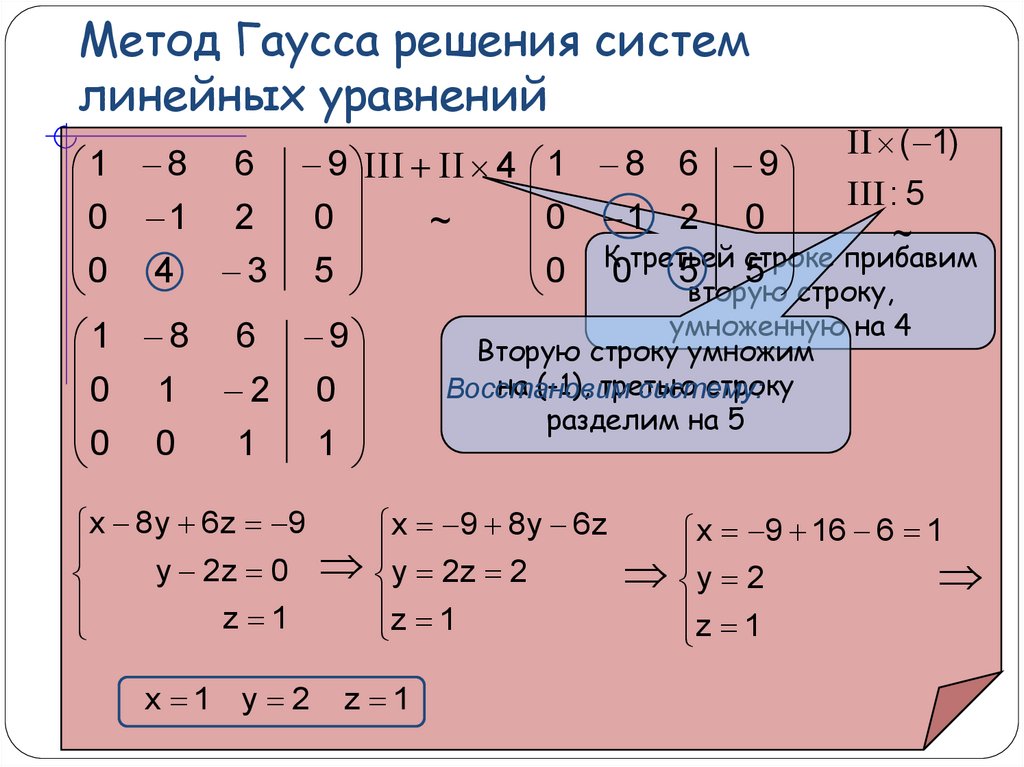

НЭ = СЭ — (А*В)/РЭ
РЭ — разрешающий элемент (1), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:

x1	x2	x3	B
1 / 1 = 1	2 / 1 = 2	-2 / 1 = -2	1 / 1 = 1

Разрешающий элемент равен (3).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:

x1	x2	x3	B
0 / 3 = 0	3 / 3 = 1	1 / 3 = 0.33	4 / 3 = 1.33

Разрешающий элемент равен (-4).
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:

x1	x2	x3	B
0 / -4 = 0	0 / -4 = 0	-4 / -4 = 1	-4 / -4 = 1

Ответ: x₁ = 1, x₂ = 1, x₃ = 1

Показатель	Метод Гаусса	Метод Жордано-Гаусса
Вид матрицы	Треугольная матрица	Единичная матрица
Время решения	0. 031	0.022
Объем используемой памяти, байт	5647	3277

Реализация метода Гаусса

Метод Гаусса реализован на многих языках программирования, в частности: Pascal, C++, php, Delphi, а также имеется реализация метода Гаусса в онлайн режиме.

Использование метода Гаусса

Применение метода Гаусса в теории игр

В теории игр при отыскании максиминной оптимальной стратегии игрока составляется система уравнений, которая решается методом Гаусса.

Применение метода Гаусса при решении дифференциальных уравнений

Для поиска частного решения дифференциального уравнения сначала находят производные соответствующей степени для записанного частного решения (y=f(A,B,C,D)), которые подставляют в исходное уравнение. Далее, чтобы найти переменные A,B,C,D составляется система уравнений, которая решается методом Гаусса.

Применение метода Жордано-Гаусса в линейном программировании

В линейном программировании, в частности в симплекс-методе для преобразования симплексной таблицы на каждой итерации используется правило прямоугольника, в котором используется метод Жордано-Гаусса.

Примеры

Пример №1. Решить систему методом Гаусса:
x₁ +2x₂ — 3x₃ + x₄ = -2
x₁ +2x₂ — x₃ + 2x₄ = 1
3x₁ -x₂ + 2x₃ + x₄ = 3
3x₁ +x₂ + x₃ + 3x₄ = 2

• Решение
• Видео решение

Решение находим с помощью калькулятора.
Запишем систему в виде:

Для удобства вычислений поменяем строки местами:

Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой

Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой

Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой

Для удобства вычислений поменяем строки местами:

Умножим 1-ую строку на (0). Добавим 2-ую строку к 1-ой

Умножим 2-ую строку на (7). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой

Умножим 1-ую строку на (15). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой

Из 1-ой строки выражаем x₄

Из 2-ой строки выражаем x₃

Из 3-ой строки выражаем x₂

Из 4-ой строки выражаем x₁

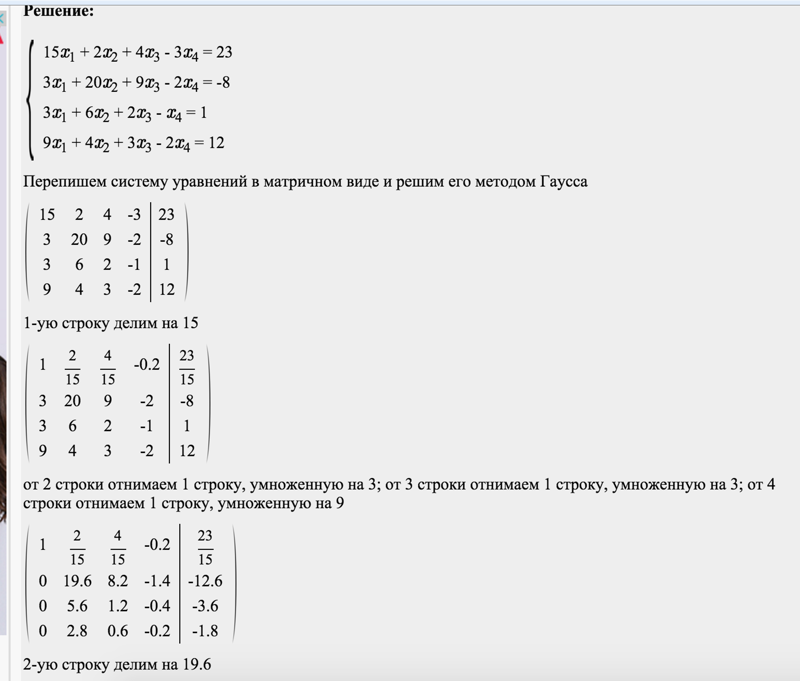
Пример №3.

1. Решить СЛАУ методом Жордано-Гаусса. Запишем систему в виде:

   5	-1	-1	3
   1	2	3	6
   4	3	2	9

   Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
   Разрешающий элемент равен (5). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
   НЭ = СЭ — (А*В)/РЭ
   РЭ — разрешающий элемент (5), А и В — элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.

   1	-0.2	-0.2	0.6
   0	2.2	3.2	5.4
   0	3.8	2.8	6.6

   Разрешающий элемент равен (2.2). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

   1	0	0.0909	1.09
   0	1	1.45	2.45
   0	0	-2.73	-2.73

   Разрешающий элемент равен (-2.73). На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.

   1	0	0	1
   0	1	0	1
   0	0	1	1

   x₁ = 1. 00, x₂ = 1.00, x₃ = 1.00

   Перейти к решению своей задачи

   
   Example1

2. Систему линейных уравнений решить методом Гаусса
   Пример

   Посмотрите, как быстро можно определить, является ли система совместной

3. Применяя метод Гаусса исключения неизвестных, решить систему линейных уравнений. Сделать проверку найденного решения: Решение
4. Example 4
5. Решить систему уравнений методом Гаусса. Рекомендуется преобразования, связанные с последовательным исключением неизвестных, применять к расширенной матрице данной системы. Сделать проверку полученного решения.
   Решение:xls
6. Решить систему линейных уравнений тремя способами: а) методом Гаусса последовательных исключений неизвестных; б) по формуле x = A^-1b с вычислением обратной матрицы A^-1; в) по формулам Крамера.
   Решение:xls
7. Решить методом Гаусса следующую вырожденную систему уравнений.
   Скачать решение doc
8. Решите методом Гаусса систему линейных уравнений записанную в матричной форме:
   7 8 -3 x 92
   2 2 2 y = 30
   -9 -10 5 z -114

Перейти к онлайн решению своего примера

Решение системы уравнений методом сложения

Решите 6x+5y=3, 3x+3y=4 систему уравнений методом сложения.
Решение.
6x+5y=3
3x+3y=4
Умножим второе уравнение на (-2).
6x+5y=3
-6x-6y=-8
============ (складываем)
-y=-5
Откуда y = 5
Находим x:
6x+5*5=3 или 6x=-22
Откуда x = -22/6 = -11/3

Пример №2. Решение СЛАУ в матричной форме означает, что исходную запись системы необходимо привести к матричной (так называемая расширенная матрица). Покажем это на примере.
Запишем систему в виде расширенной матрицы:

2 4 3 -2 5 4 3 0 1

Добавим 2-ую строку к 1-ой:

0 9 7 -2 5 4 3 0 1

Умножим 2-ую строку на (3). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой:

0 9 7 0 15 14 3 0 1

Умножим 1-ую строку на (15). Умножим 2-ую строку на (-9). Добавим 2-ую строку к 1-ой:

0 0 -21 0 15 14 3 0 1

-21 29 4

Теперь исходную систему можно записать как:
x₃ = -21/(-21) = 1
x₂ = [29 — (14x₃)]/15
x₁ = [4 — (x₃)]/3
Из 2-ой строки выражаем x₂:
Из 3-ой строки выражаем x₁:

Пример №3. Решить систему методом Гаусса: x₁ +2x₂ — 3x₃ + x₄ = -2
x₁ +2x₂ — x₃ + 2x₄ = 1
3x₁ -x₂ + 2x₃ + x₄ = 3
3x₁ +x₂ + x₃ + 3x₄ = 2

Решение:
Запишем систему в виде:
Для удобства вычислений поменяем строки местами:

 Умножим 2-ую строку на (-1). Добавим 2-ую строку к 1-ой

 Умножим 2-ую строку на (3). Умножим 3-ую строку на (-1). Добавим 3-ую строку к 2-ой

 Умножим 4-ую строку на (-1). Добавим 4-ую строку к 3-ой

 Для удобства вычислений поменяем строки местами:

 Умножим 1-ую строку на (0). Добавим 2-ую строку к 1-ой

 Умножим 2-ую строку на (7). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой

 Умножим 1-ую строку на (15). Умножим 2-ую строку на (2). Добавим 2-ую строку к 1-ой

 Из 1-ой строки выражаем x₄

 Из 2-ой строки выражаем x₃

 Из 3-ой строки выражаем x₂

 Из 4-ой строки выражаем x₁

Калькулятор исключения Гаусса

с шагами

Установите матрицу линейного уравнения и запишите ее элементы, чтобы найти решение, применяя метод исключения Гаусса с помощью этого калькулятора.

РЕКЛАМА

Размер матрицы:

2345678910

x

2345678910

Матрица

РЕКЛАМА

РЕКЛАМА

Содержание

1	Что такое класс PriceEight?
2	Таблица классов priceeight:
3	Как рассчитать плотность priceeight (шаг за шагом):
4	Факторы, определяющие цену8 Классификация:
5	Для чего предназначен класс priceeight?
6	Упомянутая цена8 классов проверена официальными лицами?
7	Являются ли классы цен для UPS и FedEx одинаковыми?

Получите виджет!

Добавьте этот калькулятор на свой сайт, чтобы пользователи могли выполнять простые расчеты.

Получить код

Обратная связь

Насколько легко было пользоваться нашим калькулятором? Сталкивались ли вы с какой-либо проблемой, сообщите нам!

ОБРАТНАЯ СВЯЗЬ

Этот бесплатный калькулятор исключения Гаусса специально разработан, чтобы помочь вам решать системы уравнений. Да, теперь получить максимально точное решение уравнений можно всего за пару кликов.

Что такое алгоритм исключения Гаусса?

В свете математического анализа:

«Особый метод, который используется для решения линейных уравнений путем составления расширенной матрицы чисел их коэффициентов, известен как алгоритм Гаусса»

Как подать заявку Алгоритм исключения Гаусса?

Здесь мы собираемся применить эту теорему к примеру ниже. Поэтому для лучшего понимания просто оставайтесь сосредоточенными!

Пример № 01:

Найдите решение следующей системы уравнений, как показано ниже:

$$ 3x_{1} + 6x_{2} = 23 $$

$$ 6x_{1} + 2x_{2 } = 34 $$

Решение:

Без сомнения, наш широко используемый калькулятор исключения Гаусса с шагами покажет подробные вычисления для упрощения этих уравнений, но нам нужно проанализировать сценарий вручную.

Эквивалентная расширенная матричная форма приведенных выше уравнений выглядит следующим образом:

$$ \begin{bmatrix} 3&6&23 \\ 6&2&34 \\\end{bmatrix} $$

Шаги исключения по Гауссу:

Шаг № 01:

Разделить нулевую строку $2 \ на 3.

left[\begin{array}{cc|c}1&2& \frac{23}{3} \\6&2&34 \\\end{array}\right] $$

Шаг № 02:

Умножить первую строку на 6, а затем вычесть его из нулевой строки.

$$ \left[\begin{array}{cc|c}1&2&\frac{23}{3} \\0&-10&-12 \\\end{array}\right] $$

Шаг № 03:

Перейти к делению первой строки на -10.

$$ \left[\begin{array}{cc|c}1&2&\frac{23}{3} \\0&1&\frac{6}{5}\\\end{array}\right] $$

Шаг № 04:

Приступаем к нахождению произведения нулевой строки и 2. После этого вычитаем результат из первой строки.

$$ \left[\begin{array}{cc|c}1&0&\frac{26333333334}{5000000000}\\0&1& \frac{6}{5}\\\end{array}\right] $$

Как вы видите в левой части матрицы, мы получаем единичную матрицу. Таким образом, ответом в правой части уравнения будут значения переменных в уравнениях.

Таким образом, окончательные результаты следующие:

$$ b_{1} = 5,266 $$

$$ b_{2} = 1,2 $$

Те же результаты можно также проверить с помощью внешнего калькулятора исключения Гаусса. .

Как работает калькулятор метода исключения Гаусса?

Получите представление о том, как этот бесплатный алгоритм уменьшения строки матрицы решения с методом исключения Гаусса упрощает системы уравнений.

Ввод:

• Сначала настройте порядок матрицы из выпадающих списков
• После этого нажмите кнопку «Установить матрицы», чтобы получить нужный формат матрицы
• Теперь извлеките числа из их полей
• После того, как вы закончите с материалом, нажмите кнопку расчета

Вывод:

Лучший калькулятор исключения Гаусса Джордана с шагами выполняет следующие вычисления:

• Показывает коэффициенты переменных
• Отображает шаги исключения Гаусса

Ссылки:

Из источника Википедии: Исключение Гаусса, Операции со строками, Эшелонная форма, Вычисление определителей, обратная матрица, Ранги

Калькулятор Гаусса — это бесплатный онлайн-инструмент, используемый для преобразования матрицы в уменьшенную ступенчатую форму.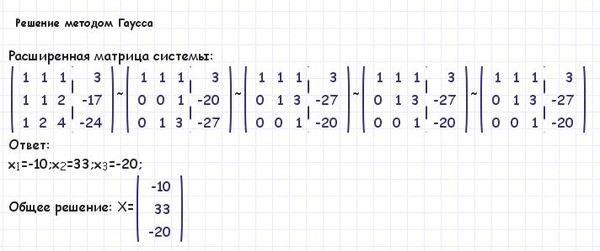 Он применяет операции со строками к матрице, чтобы найти обратную матрицу. Он может решить любую систему линейных уравнений методом исключения.

В математике всегда нужно решить систему линейных уравнений. Существует более двух методов решения системы линейных уравнений. Одним из таких методов является метод исключения Гаусса-Жордана.

Использование онлайн-инструмента — эффективный способ решить любую проблему. Итак, здесь мы представляем онлайн-инструмент, который является наиболее эффективным инструментом для поиска обратной матрицы.

Формула, используемая калькулятором метода исключения Гаусса

Исключение Гаусса Жордана — это алгоритм решения системы линейных уравнений путем представления ее в виде расширенной матрицы, сокращения ее с использованием операций со строками и представления системы в сокращенной строке- форма эшелона, чтобы найти решение.

Калькулятор Гаусса Жордана преобразует заданную матрицу в редуцированную ступенчатую форму для решения системы линейных уравнений и находит ее обратную. Сокращенную форму эшелона можно получить с помощью калькулятора исключения Гаусса, выполнив следующие шаги:

1. Преобразуйте все диагональные записи в 1, применяя операции со строками и столбцами.
2. Преобразование всех элементов, кроме диагоналей, в 0.

Сокращенная ступенчатая форма матрицы получается путем преобразования матрицы в единичную матрицу с помощью калькулятора исключения Жордана.

Как пользоваться калькулятором метода Гаусса-Жордана?

С помощью калькулятора Гаусса легко найти решение любой задачи, потому что он прост в использовании. Чтобы использовать этот инструмент, выполните следующие шаги:

1. На первом этапе вам необходимо ввести количество строк и столбцов матрицы.
2. Теперь введите значения всех элементов матрицы.
3. Вы можете использовать случайную кнопку, чтобы выбрать случайный вариант.
4. Нажмите кнопку расчета.

Вы получите пошаговое решение через несколько секунд после нажатия на кнопку расчета.

Зачем использовать калькулятор исключения Гаусса?

Концепция исключения в матрицах важна, потому что обычно она нам нужна для формирования эшелонированной и редуцированной эшелонированной формы. Эти две формы являются ключом к решению системы линейных уравнений.

Но ручные расчеты иногда становятся сложными. Эффективный и простой способ решить эту проблему — использовать онлайн-инструмент. Вы можете использовать калькулятор метода исключения Гаусса, потому что он прост в использовании.

Преимущества использования Калькулятора метода исключения Гаусса Джордана

В Интернете доступно множество математических инструментов, которые помогают решать многие задачи. Точно так же инструмент Gaussian преобразует матрицу в уменьшенную ступенчатую форму. Он имеет много полезных применений для улучшения ваших математических навыков. Вот некоторые из этих преимуществ:

1. Калькулятор исключения Гаусса с шагами может исключить любую матрицу за короткий промежуток времени.
2. Калькулятор исключения Гаусса может работать с матрицей до 4-го порядка.
3. Он предоставляет вам пошаговое решение, чтобы вы могли легко его понять.
Калькулятор исключения Джордана
4. надежен, потому что он экономит ваше время и дает точный ответ.
5. Gauss jordan калькулятор с шагами — это бесплатный онлайн-инструмент, поэтому вам не нужно подписываться на какой-либо платный план.

Другие связанные калькуляторы

Помимо этого калькулятора Гаусса, на этом веб-сайте есть много других связанных инструментов, которые вы можете использовать. Некоторые из бесплатных инструментов:

• Добавление калькулятора матриц
• Калькулятор вычитания матриц
• Калькулятор матриц умножения
• Определитель матричного калькулятора
• Калькулятор транспонирования матрицы
• Калькулятор обратной матрицы
• Ранг матричного калькулятора
• Матрица для калькулятора мощности
• Калькулятор собственных векторов
• Калькулятор собственных значений
• Недействительность матричного калькулятора
• Калькулятор матрицы трасс
• Калькулятор разложения Matrix Lu
• Калькулятор формы эшелона с уменьшенным рядом
• Калькулятор сопряженных матриц

Часто задаваемые вопросы

Что такое пошаговый калькулятор исключения Гаусса-Жордана и как он работает?

Калькулятор метода Гаусса-Жордана с шагами — это инструмент, используемый для решения систем линейных уравнений с использованием метода исключения Гаусса, также известного как исключение Гаусса-Жордана. Он использует серию операций со строками для преобразования матрицы в форму эшелона строк, а затем в сокращенную форму эшелона строк, чтобы найти решение системы уравнений.

Каковы преимущества использования калькулятора исключения Гаусса с шагами по сравнению с другими методами решения систем линейных уравнений?

Калькулятор метода Гаусса Джордана с шагами особенно полезен для решения систем уравнений с большим количеством переменных, поскольку он эффективен с точки зрения времени и пространства. Кроме того, его легко понять и реализовать, что делает его популярным среди студентов и профессионалов.

Могу ли я использовать калькулятор декомпозиции Гаусса Джордана для решения нелинейных уравнений?

Нет, матричный калькулятор исключения Гаусса предназначен только для решения систем линейных уравнений. Он не будет работать для нелинейных уравнений, потому что метод исключения Гаусса применяется только к матрицам, которые имеют форму эшелона строк или форму редуцированного эшелона строк, что невозможно для нелинейных уравнений.