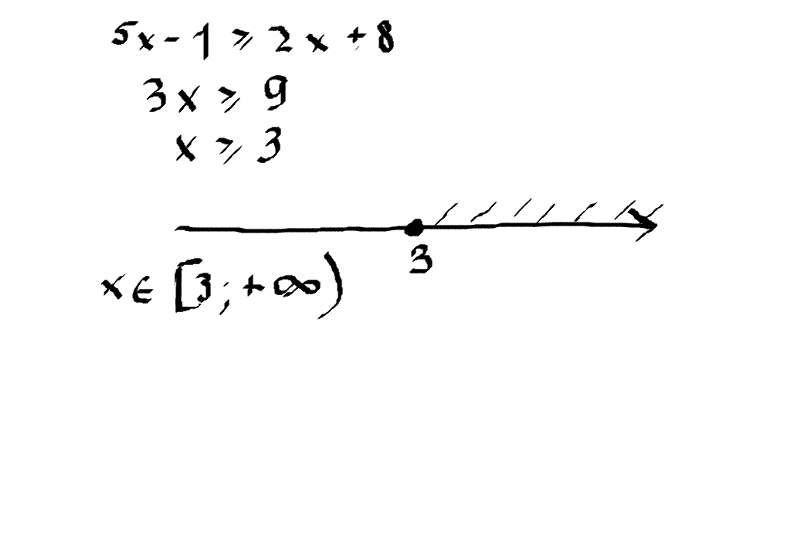1 меньше х меньше 3: ‘(«) } ym(1313667, ‘reachGoal’, ‘adBlockDetectedWarningMessage’) } if(typeof fuckAdBlock === ‘undefined’) { adBlockDetected() } else { fuckAdBlock.onDetected(adBlockDetected) } $(document).on(‘krapi.checker.run.complete’, () => { if(typeof fuckAdBlock === ‘undefined’) { adBlockDetectedWarningMessage() } else { fuckAdBlock.check() fuckAdBlock.onDetected(adBlockDetectedWarningMessage) } }) })

Открытое элективное занятие по теме «Решение уравнений и неравенств с использованием области определения функций и области значения функций»

Цели занятия:

1. Научить решать уравнения с использованием следующих понятий и свойств:
   а) при a = b = 0,
   б) выделения полного квадрата,
   в) области значений выражений:   и .
2. Научить решать неравенства с использованием области определения функций у = tgx, y = ctgx

I. Актуализация ключевых компетенций учащихся по данной теме.

На доске:

Ключевые компетенции:

1)  при a = b = 0.

2) D(tgx): x≠, D(ctgx): x≠

3) Области значений выражений:

0≤ ≤ 1, -1≤ -≤ 0, 0≤ ≤ 1, -1≤ -≤ 0, и  ≥ 0.

4)  -разность квадратов.

 — квадрат суммы (разности).

5) Решение квадратных неравенств методом интервалов.

1. Найдите область определения функции (можно при этом пользоваться опорным конспектом по данному элективному курсу)

а) у = tg x.

Запись в тетради: Решив уравнение, найдем значения х, не входящие в область определения данной функции

x = , │∙3, х =.
D(y): x ≠.

б) y = ctg 5x.

5x =, │∙, x = .
D(y): x ≠.

в) у = tg x,

 x = , │∙
х = 2 + .
D(y): x ≠ 2 + , (т. е. x ≠…-2; -1;.0, 1; 2; …)

г) у = сtg x,

 x = , │∙
х = 2·.
D(y): x ≠ 2·. (т. е. x ≠…-4; -2; 0, 2; 4; …).

2. Решите неравенство

а) 5х+3>0.

Учитывая, что х≥ 0 при всех x(), получим, что 5х+3>0 при всех x().

б) 1+ tg x > 0

Решениями неравенства являются все значения х, при которых определен tg x.

Ответ: x ≠ 2 + .

в) 1 + сtg x > 0

Решениями неравенства являются все значения х, при которых определен сtg x .

Ответ: x ≠ 2·.

3. Решите уравнение (- 4) = -(х + 2) .

Запись в тетради:

Используя свойство  при a = b = 0, получим  х = -2.

Ответ: -2.

4. Какова область значений функции

а) у = ?

Учитывая, что Е (cost) =  и свойство , получим Е() =

б) у = ?

Учитывая, что Е (sint) =  и свойство -, получим Е() =

Ответ: а) , б) .

II. Решение заданий из ЕГЭ (у всех учащихся распечатки заданий В и В)

Устная работа:

Выделить полный квадрат из квадратного трехчлена:

а) х-2 х – 1, б) х-6 х + 11, в) 4х- 4 х +1, г) 9х- 12 х +7.

1) Решить уравнение х- 2 х = (1- sin)(1+ sin) – 2.

Учитель с помощью учащихся решает и оформляет задание на доске.

Это комбинированное уравнение.

О.Д.З. x()

х- 2x = 1 — 2, х- 2x +1 = , (x — 1)  = ,

Используя свойство  при a = b = 0, получим   

x =1.

Первое уравнение системы имеет единственный корень x =1, следовательно, если система имеет решение, то решением системы может быть только x =1, мы проверяем это, подставив х = 1 во второе уравнение системы.

Ответ: 1

2) Решить уравнение 9х- 12 х +7 = ()().

Решение этого уравнения оформляет ученик на доске.

О.Д.З. xR

9х- 12 х + 7 = 3 — , 9х- 12 х + 4 = — , (3x — 2) = -,

   . Ответ: .

3).

Решение оформляет учитель.

Это комбинированное уравнение.

Учитывая, что Е() = , а E() = , получим, что данное уравнение равносильно системе

Корни первого уравнения: х = 2 и х = 3. Если система имеет решения, то ее решениями могут быть только числа 2 или 3, подставив эти числа во второе уравнение системы, получим

 (верно),  (верно), следовательно 2 и 3 решения системы.

Ответ: 2 и 3.

4) Сколько целочисленных решений имеет неравенство ?

Решение оформляет учитель.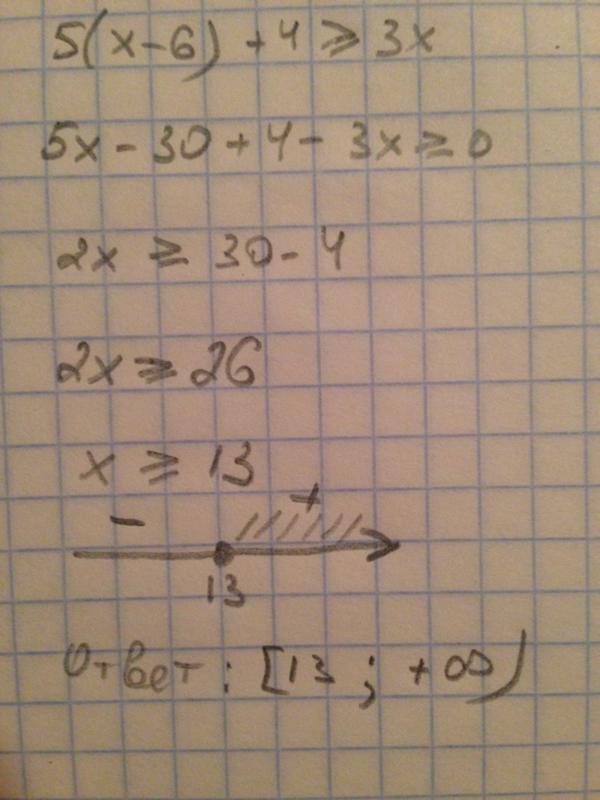

Найдем область определения сtg x.

 x = , │∙
х = 3·.
О.Д.З. x ≠ 3·. (т. е. x ≠…-6; -3; 0, 3; 6; …).

Заметим, что при всех х из О.Д.З., знаменатель дроби принимает положительные значения, поэтому неравенство равносильно системе

-х+ 4х -3 ≥ 0, │∙(-1)
х- 4х + 3 ≤ 0, ( х- 4х + 3 =0 при х = 1 или х =3)
(х — 1)(х – 3) ≤ 0,

Методом интервалов, определим, что x, с учетом, что x ≠ 3·, решениями системы являются x, в данный интервал входит всего два целых числа – это 1 и 2.

Ответ: 2

III. Проверочная самостоятельная работа 

1 вариант	2 вариант
1. Найти область определения функции а) у = tg 2x; б) у = ctg . 2. Решите неравенство а); б) 4+ ctg  >0 3. Решить уравнение: 4. Сколько целочисленных решений имеет неравенство . 5. Решить уравнение:	1. Найти область определения функции а) у = ctg ; б) у = tg. 2. Решите неравенство а)1+; б) 4+ tg >0. 3. Решить уравнение: 4. Сколько целочисленных решений имеет неравенство . 5. Решить уравнение:

IV. На дом предлагается решить задания из В и В на выбор, но не менее чем по 2 задания из В и из В.

ЕГЭ 2009 г. Задание В

1. Найдите количество целочисленных решений неравенства х+7 х – 8 ≤ 0, удовлетворяющих условию ctg+ > 0.
2. Найдите количество целочисленных решений неравенства 16 — х≥ 0, удовлетворяющих условию 3tg+ > 0.
3. Найдите количество целочисленных решений неравенства х+4 х – 21< 0, удовлетворяющих условию ctg+ 13 >0.
4. Найдите количество целочисленных решений неравенства 8 – 7x — х≥ 0, удовлетворяющих условию ctg + t g > 0.
5. Сколько целочисленных решений неравенства 15 – 2x — х≥ 0, удовлетворяющих условию  + 1 > 0.
6. Сколько целочисленных решений имеет неравенство  ?
7. Сколько целочисленных решений имеет неравенство  ?
8. Сколько целочисленных решений неравенства x — х + 6 > 0, удовлетворяющих условию ?
9. Сколько целочисленных решений имеет неравенство  ?
10. Сколько целочисленных решений имеет неравенство  ?

ЕГЭ -2009 г. Задание В

1. Решите уравнение х- 4 х = (2 — соs)(2 + соs) – 8.
2. Решите уравнение 3 — ( — sin)( + sin) = 1 — 3х
3. Решите уравнение -25х+ 40 х -23 = (соs)(соs)..
4. Решите уравнение 16х- 24x + 12 = ( — sin)( + sin).
5. Решите уравнение х+2x = (1- sin)(1+ sin) – 2.
6. Решите уравнение 25х+ 60 х + 39 = ( — соs)( + соs).
7. Решите уравнение 25х- 40 х +21 = ()().
8. Решите уравнение 25х+ 80 х +69 = ()().
9. Решите уравнение  Если корень не единственный, то укажите сумму корней.
10. Решите уравнение

Опорный конспект.

Вариант 1. С-5. № 3. ГДЗ Алгебра 7 класс Звавич. Запишите каждое предложение с помощью знаков неравенства. – Рамблер/класс

Вариант 1. С-5. № 3. ГДЗ Алгебра 7 класс Звавич. Запишите каждое предложение с помощью знаков неравенства. – Рамблер/класс

Интересные вопросы

Школа

Подскажите, как бороться с грубым отношением одноклассников к моему ребенку?

Новости

Поделитесь, сколько вы потратили на подготовку ребенка к учебному году?

Школа

Объясните, это правда, что родители теперь будут информироваться о снижении успеваемости в школе?

Школа

Когда в 2018 году намечено проведение основного периода ЕГЭ?

Новости

Будет ли как-то улучшаться система проверки и организации итоговых сочинений?

Вузы

Подскажите, почему закрыли прием в Московский институт телевидения и радиовещания «Останкино»?

Как это решить?
Запишите каждое предложение с помощью знаков неравенства.

Подберите три значения переменной, при которых данное неравенство верно, и три, при которых неверно:
1)       a) t меньше 5;
б) р больше или равно -11,3;
в) m — неотрицательное число;
 
2)       а) х меньше 5 и больше или равно 4;
б)   а больше 0,01 и меньше 0,02;
в)   с больше или равно -0,7 и отрицательно.
 

ответы

1.   a) t > 5;
б)   р ≥ -11,3;
в)   m ≥ 0;
 
2.    а) 4 ≤ х < 5;
б)  0,01 < а < 0,02;
в)  -0,7 ≤ с < 0.
 

ваш ответ

Можно ввести 4000 cимволов

отправить

дежурный

Нажимая кнопку «отправить», вы принимаете условия  пользовательского соглашения

похожие темы

ЕГЭ

10 класс

9 класс

11 класс

похожие вопросы 5

Найдем тангенс угла. ГДЗ 10 класс алгебра Алимов Упражнения для повторения № 1500

Вот уж не думала, что не справлюсь( Но что то никак не сходиться, спасайте! Вот условие:
Найти тангенс угла, который касательная к (Подробнее. ..)

ГДЗ11 классАлимов Ш.А.Алгебра

Задание 272 Буквы о и а на конце наречий. Русский язык. 7 класс. Т.А. Ладыженская ГДЗ

Ребята, как сделать задание?
Назовите слова, с помощью которых в этом маленьком рассказе вы-
ражается отношение к персонажам (Подробнее…)

ГДЗРусский языкЛадыженская Т.А.7 класс

Lesson 6. № 19. ГДЗ Английский язык 5 класс Верещагина. Кто выполнил упражнение? Поделитесь!

a) Read the text “Continents and Countries” to get some new information about the world around us. Say what the smallest country in the (Подробнее…)

ГДЗАнглийский язык5 классВерещагина И.Н.

Внесите предложения 2B № 9 ГДЗ Spotlight Английский 11 класс Афанасьева О.В.

Think of ten new words/ expressions you have learnt during this lesson. Make sentences using them.

ГДЗSpotlightАнглийский язык11 классАфанасьева О. В.

Lesson 7. № 20. ГДЗ Английский язык 5 класс Верещагина. Скажите, что вы любите обе вещи. Поможете?

Say you are fond of both things.
 
Example: I am fond of both fruit and vegetables. (Подробнее…)

ГДЗАнглийский язык5 классВерещагина И.Н.

Символ «больше или равно»

Знак «больше или равно» — это математический символ, обозначающий неравенство между двумя значениями или числами. Это форма, в которой два штриха одинаковой длины соединяются под острым углом справа. Эти знаки классифицируются как:

• Символ больше, чем (>). Например, если 6>3, мы прочитаем это как «6 больше, чем 3».
• Символ «меньше» (<). Например, если 6<3, мы прочитаем это как «6 меньше 3».
• больше или равно (≥). Например, если 6≥3, мы прочитаем это как «6 больше или равно 3».
• меньше или равно (≤). Например, если 6≤3, мы прочитаем это как «6 меньше или равно 3′.

Все эти символы уменьшают временную сложность и облегчают понимание.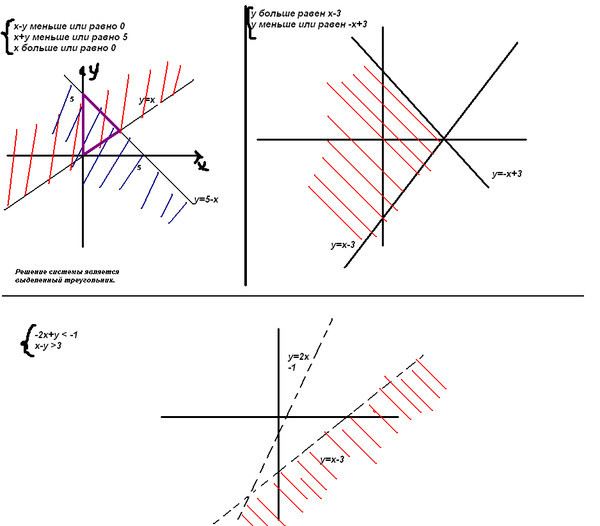 Типичное использование символа «больше» — сравнение двух значений. Первое число больше второго или одно значение больше другого. Применение этого символа осуществляется в порядке убывания, где с его помощью выполняется расположение от наибольшего числа к наименьшему. Это приближение закрывающей угловой скобки.

Символы с примерами

Знаем ли мы, что означает знак больше или равно? В следующей таблице подробно показаны символы с их определением и примерами.

Символ	Описание	Пример
=	равно	3+4 = 7
≠	Не равно	4 + 3 ≠ 5
>	Больше	6 > 3
≥	Больше или равно	Студенты ≥ 6
<	Менее	3 < 9
≤	Меньше или равно	Учащиеся до 60 лет

Как использовать эти символы?

Символы могут сбивать с толку, когда дело доходит до их применения. Есть несколько методов, чтобы понять это лучше. Эти методы следующие:

• Понимание символов с помощью точек
• Аллигаторный метод
• L метод

Сейчас мы кратко обсудим эти методы.

1. Знакомство с символами, использующими точки

• Символ больше (>)

Понимать символ слева направо. С левой стороны у него две точки, а с правой стороны одна точка. Поэтому напишите символ (>).

• Символ меньше (<) 

Понимать символ слева направо. С левой стороны он имеет одну точку, а с правой стороны — две точки. Поэтому напишите символ (<).

2. Метод аллигатора

• Метод крокодила или аллигатора прост для понимания, и это известный метод.
• Предположим, что крокодил (<) и числа с обеих сторон являются его пищей.
• Крокодил всегда голоден и хочет съесть много еды, поэтому его пасть будет открываться там, где еда находится в большем количестве.
• Мы предполагаем, что значения с обеих сторон представляют собой количество рыбы. Например, 9>2 Здесь пасть аллигатора открывается в сторону числа девять, что означает, что девять больше, чем 2.

3. L-метод

• Буква «L» напоминает символ «<»
• Уловка, позволяющая запомнить, как выглядит знак меньше, очень проста. Поскольку «меньше чем» начинается с l, символ < больше похож на букву L.

Несколько примеров, чтобы лучше понять символы:

• 4>2, что означает, что 4 больше 2.
• 2<6, что означает, что 2 меньше 6.
• 2 ⁴ >2, что означает, что 2×2×2×2 = 16 больше 2.
• (10/2)>(4/2), что означает 5>2.
• -1<-2, -1 меньше -2.
• 0,1>0,00001, здесь значение 0,1 больше 0,00001

Символ «больше или равно» обозначает неравенство в математике. Он сообщает, что данное значение больше или равно определенному значению. Этот символ предназначен для линейных неравенств, когда мы не знаем, больше или равно значение переменной определенному значению. Этот символ представляет собой символ «больше чем» (>) с чертой под ним. Строка под большим знаком означает «равно». Например, x ≥ 6 означает, что x больше или равно 6. Он определяет диапазон значений, которые может принимать x, начиная с 6 и заканчивая бесконечностью.

• Слово «больше чем» означает, что одна величина больше другой величины.
• «равно» означает, что две величины равны.
• При объединении этих терминов получается новый термин Больше или равно.
• Этот термин показывает, что предел количества или суммы может быть равен или превышать указанный предел.

Некоторые примеры больше или равно:

Q.Express x ≥ 17 уравнение в словесной форме.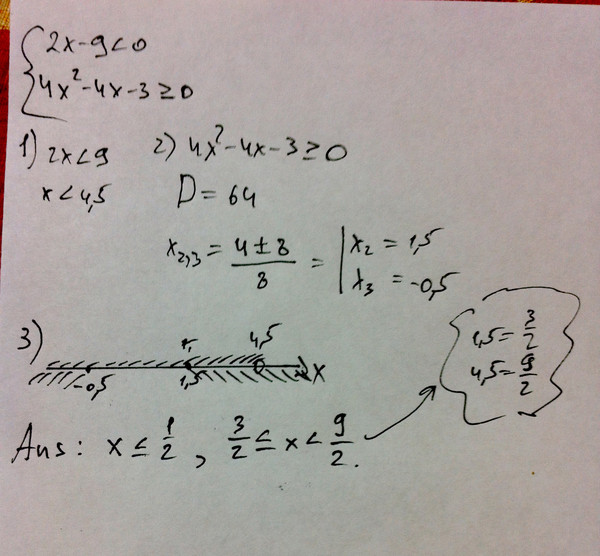

A. Здесь x больше или равно 17.

Q.Raj должен набрать не менее 50% баллов, чтобы сдать экзамен. Выразите это, используя неравенство.

A.x ≥ 50%

Как решать задачи на неравенство в Word

Начните решать задачу с:

• Внимательно прочитайте
• Выделите детали
• Распознать переменные
• Запишите уравнение на бумаге
• Решите данную постановку задачи 
• Запишите решение полными предложениями

Решено Примеры:

Пример 1: В начале лета на счету Дева было 500 рупий. Он снимает 25 фунтов стерлингов каждую неделю и хочет, чтобы к концу лета на банковском счету было не менее 200 фунтов стерлингов — ситуация Express Dev с использованием символа неравенства.

Решение: Пусть x будет количеством недель

Следовательно, выражение неравенства будет

500 – 25x ≥ 200

Здесь подходит символ (≥), так как Дев хочет, чтобы к концу лета было больше 200 денег.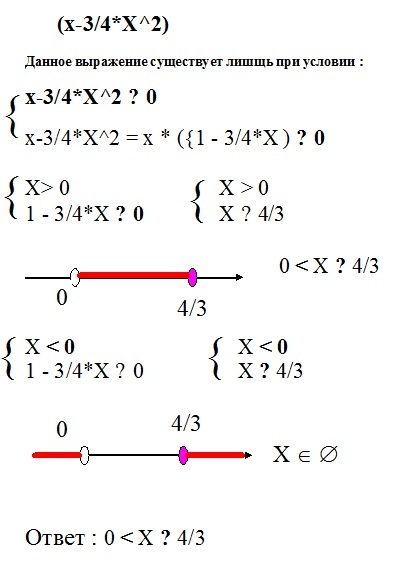

Пример 2: Владелец фруктового магазина продает стакан сока за 50 ₹. Он стремится зарабатывать деньги, превышающие или равные ₹ 5000 в день. Запишите неравенство, представляющее эту ситуацию.

Решение: Стоимость каждого стакана сока = 50 ₹

Пусть x равно количеству стаканов сока, которые он продает за день 

Следовательно, общая стоимость x стаканов сока, которые он продает за день, = ₹ 50x

Общий заработок должен быть больше или равен ₹5000 в день.

Таким образом, неравенство, представляющее это, равно 50x ≥ 5000.

Пример 3: Минимальные оценки, которые Джон должен набрать, составляют 50 из 100, чтобы сдать экзамен по математике. Представьте это утверждение, используя знак больше или равно неравенству.

Решение: Пусть x будет отметками Джона.

Мы знаем, что проходной балл 50 или больше.

Неравенство, x ≥ 50, представляет описанную выше ситуацию.

Здесь x — количество баллов, набранных Джоном.

Пример 4: Найдите числа, принадлежащие следующему множеству {x ∈ N / x ≥ 6}.

Решение: Здесь N — множество натуральных чисел.

Задано множество: {x ∈ N / x ≥ 6 }

Это означает, что мы должны найти все натуральные числа, большие или равные 6.

Поскольку множество натуральных чисел до бесконечности, числа которые принадлежат данному набору, равны 6,7,8,9,……до бесконечности.

Пример 5: Сурав набрал 30 баллов на экзамене по математике. Рия набрала 24 балла на том же экзамене. Кто набрал меньше очков?

Решение: Даны данные:

Баллы, выставленные Суравом = 30 баллов,

Баллы, выставленные Рией = 24 балла

Неравенство будет 24<30. Поэтому Рия забил меньше, чем Сурав.

Базовая алгебра — Алгебраические выражения

Предыдущий Следующий

Алгебраические выражения

Давайте приступим к делу. Выражение состоит из терминов. Термины — это отдельные значения в выражении. Каждый термин может быть переменной, числом и переменной или числом и многими переменными с показателями степени или без них, если все умножается вместе в единый самородок математического совершенства. Вот некоторые из наших любимых терминов:

7
7 x
7 x ² y
x ⁶ y ¹¹ z ²

Все они считаются одним термином.

Число рядом с переменной означает, что число и переменная перемножаются. То же самое верно для двух переменных рядом друг с другом: это означает, что они перемножаются. Поскольку символ ×, который мы использовали для умножения в прошлом, очень похож на переменную x , мы вообще перестанем использовать символ для умножения. Некоторые называют это ленью; мы называем это эффективным.

Некоторые термины являются только числами. Они называются константами или числами, которые не изменяются. Другие имеют переменных (буквы, которые представляют неизвестное или изменяющееся число), а некоторые имеют смешанные вместе переменные и числа, и в этом случае числа называются коэффициентами .

Иногда термины, такие как последний выше, не имеют коэффициента. Вот в чем дело: коэффициент 1 у них действительно есть. Просто лень появляться. Поскольку 1 умножить на что угодно — это просто что угодно, мы обычно не пишем 1 в качестве коэффициента, но оно всегда есть.

Пример: x — то же самое, что 1 x и x ³ y ² M — то же самое, что и 1 4. M . м .

Переменная : неизвестное или изменяющееся число. Часто представлен x .
Константа : число, которое не меняется.
Коэффициент : число, умноженное на переменную.

Нам нравятся термины, и особенно нам нравятся термины , как и термины . Подобные термины — это термины, которые имеют одни и те же переменные, включая показатели степени, соответствующие этим переменным. Переменные могут быть разного порядка и иметь разные коэффициенты, но все они должны быть.

Примеры:
3 xy и -5 xy являются подобными терминами (одинаковые переменные).
3 xy и -5 xym не похожие термины (у второго термина есть переменная, которой нет у первого).

-2 m ² xh и 4 m ² hx — это подобных членов (те же переменные и показатели степени, только в другом порядке).
-2 m ³ xh и 4 m ² xh не являются подобными членами (переменная m имеет разные члены).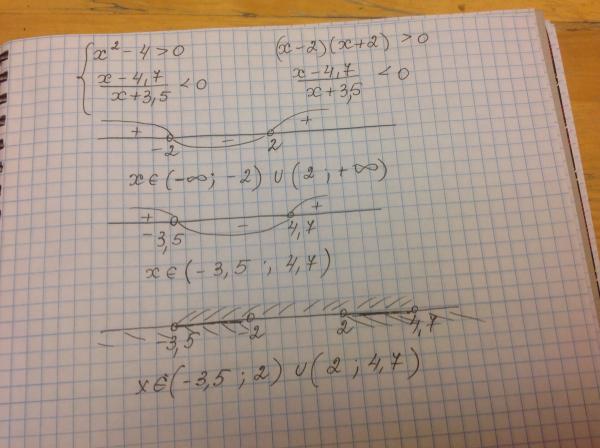

Если имеется более одного термина, разделенного знаками плюс или минус, то у нас есть выражение . For example:

5 x ² y – 3 xy + y + 5

This expression has four terms: 5 x ² y , -3 xy , y (or 1 y ), and 5.

Names for algebraic expressions

monomial	1 Term	xy
binomial	2 Terms	xy – 2 x
trinomial	3 Terms	xy – 2 x + 3 y
quadnomial	4 Terms	xy – 2 x + 3 y – 1

Вот таблица общих фраз.

Общие слова и фразы для:
Добавить	Вычесть	Умножить	Разделить	Равно
плюс добавить сумма более в дополнение к больше всего и	разница вычесть менее забрать	товар из раз дважды (×2) коэффициент	разделить на частное сплит поделиться распределить	равно

В этих переводах мы будем использовать букву x для представления переменной, хотя подойдет любая буква, символ или смайлик. Смайлики и сердечки, кто-нибудь?

7799999994 .0028

Экспрессия в словах	Экспрессия в символах
Число увеличилось на двенадцать	x + 12
2 x + 6
eighty less than a number	x – 80
twenty-eight split in half	28 ÷ 2
the product of a number and seven	7 x
the quotient of a number and four	x ÷ 4
five greater than three times a number	3 x + 5
a number distributed evenly among six	x ÷ 6
в сумме сорок и число	40 + x
в три раза больше числа и пяти	3( x + 28)

Уравнение словами	Уравнение символами
Число отрицательное десять. No related posts. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт