1 ответ(ов)
Алгебра
Вгараже находилось 340 автомашин трех видов. автомашины «москвич» составляли 45% от числа машин «жигули»,а число автомашин «запорожец» составляло 5/9 от числа автомашин «москвич»….
2 ответ(ов)
Алгебра
Решите систему неравенств: 0.5-0.2х> 1.7 0.6 — x< 1.6 — 3x…
2 ответ(ов)
Алгебра
Одно из чисел втрое больше второго , а разность этих чисел равна 62 . найдите большее из этих чисел….
3 ответ(ов)
Алгебра
Высота прямоугольного параллелепипеда равна 20см., что на 4 см. меньше его длины и в 5 раз больше его ширины . вычислите обьем данного параллелепипеда…
1 ответ(ов)
Знаешь правильный ответ?
Найдите значение выражения: (корень из 32 минус корень из 2) всё это в квадрате минус корень из 6,4…
Вопросы по предметам
Математика
Товарный поезд км за 3 часа проходя за каждый час одинаковые расстояние с какой средней скоростью двигался поезд? можно еще краткое действие ?. ..
..
3 ответ(ов)
Алгебра
Подскажите как решить. постройте график функции y=x в квадрате минус 2х минус 3. с графика найдите: а)промежутки возрастания и убывания функции б)наименьшее и наибольшее значения ф…
1 ответ(ов)
Обществознание
Какие силы приводят катушку в движение?…
2 ответ(ов)
Алгебра
Tg(альфа)= -2,4 найти синус, косинус, катангенс…
3 ответ(ов)
Геометрия
Углы треугольника пропорциональны числам 3,8,5.докажите, что этот треугольник прямоугольный….
1 ответ(ов)
Литература
К. д ушинский первое знакомство с родиной поезка из столицы в деревню составь план поездки по проселочной дороге . что видели дети…
1 ответ(ов)
История
Дайте характеристику александра1 предварительный сосав план доклада…
3 ответ(ов)
Русский язык
Речевая ситуация в которой можно употребить одну из пословиц : правда светлее солнца, дороже золота или маленькое дело лучше большого безделья или утро вечера мудренее.
1 ответ(ов)
Литература
Составьте сказку о животных. какие события будут происходить в сказке, составьте рабочий план: 1) присказка, 3) концовка…
3 ответ(ов)
Алгебра
Верно ли утверждение число, оканчивающееся на три нуля делится на 8…
2 ответ(ов)
Больше вопросов по предмету: Алгебра Случайные вопросы
Задать вопрос
Популярные вопросы
Найдите объем и число молекул 132 кг оксида углеро…
3 ответ(ов)
Present simple 158 1)когда вы встаю без четвер-сем…
3 ответ(ов)
Составьте по уравнению! а) (y + 6) — 2 = 15 б) 2(а…
2 ответ(ов)
Из чисел 3,2; 27,10; 39,4; 177,20; 801,100 выделит…
2 ответ(ов)
На каком и в какой части материка находится вулкан…
3 ответ(ов)
Пары веществ: а) оксид металла и водорода простое…
1 ответ(ов)
Найти площадь круга если его радиус равен 5,4 дм (…
3 ответ(ов)
Скажите , верно ли я решил? «какую массу соляной к.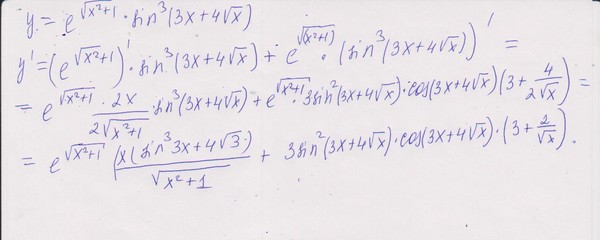 ..
..
1 ответ(ов)
Фотон электромагнитного излучения имеет энергию 6,…
1 ответ(ов)
Сочинение на тему что взять с собой в дорогу…
2 ответ(ов)
упростите выражение корень18 минус корень 2
2x+12•|x+11|+3 при x =-9
Школьники посадили в парке саженцы березок , тополей и лип . Тополей они посадили в 4 раза больше чем остальных деревьев вместе взятых. Сколько всего саженцев посадили ребята, если лип было посаже…
Школьники посадили в парке саженцы березок , тополей и лип . Тополей они посадили в 4 раза больше чем остальных деревьев вместе взятых. Сколько всего саженцев посадили ребята, если лип было посаже…
Школьники посадили в парке саженцы березок , тополей и лип . Тополей они посадили в 4 раза больше чем остальных деревьев вместе взятых. Сколько всего саженцев посадили ребята, если лип было посаже…
Школьники посадили в парке саженцы березок , тополей и лип . Тополей они посадили в 4 раза больше чем остальных деревьев вместе взятых. Сколько всего саженцев посадили ребята, если лип было посаже…
Школьники посадили в парке саженцы березок , тополей и лип . Тополей они посадили в 4 раза больше чем остальных деревьев вместе взятых. Сколько всего саженцев посадили ребята, если лип было посаже…
Школьники посадили в парке саженцы березок , тополей и лип .
Тополей они посадили в 4 раза больше чем остальных деревьев вместе взятых. Сколько всего саженцев посадили ребята, если лип было посаже…
Школьники посадили в парке саженцы березок , тополей и лип . Тополей они посадили в 4 раза больше чем остальных деревьев вместе взятых. Сколько всего саженцев посадили ребята, если лип было посаже…
Школьники посадили в парке саженцы березок , тополей и лип . Тополей они посадили в 4 раза больше чем остальных деревьев вместе взятых. Сколько всего саженцев посадили ребята, если лип было посаже…
Школьники посадили в парке саженцы березок , тополей и лип . Тополей они посадили в 4 раза больше чем остальных деревьев вместе взятых. Сколько всего саженцев посадили ребята, если лип было посаже…
Школьники посадили в парке саженцы березок , тополей и лип . Тополей они посадили в 4 раза больше чем остальных деревьев вместе взятых. Сколько всего саженцев посадили ребята, если лип было посаже…
Школьники посадили в парке саженцы березок , тополей и лип .

| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| Найти точное значение | cos(pi/4) | ||
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт.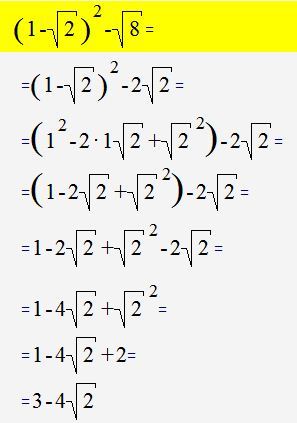 )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
math — Как вычислить квадратный корень в Python?
Вариант 1:
math. sqrt()
sqrt() Модуль math из стандартной библиотеки имеет функцию sqrt для вычисления квадратного корня числа. Он принимает любой тип, который может быть преобразован в с плавающей запятой (включая int ) в качестве аргумента, и возвращает с плавающей запятой .
>>> импорт математики >>> math.sqrt(9) 3.0
Вариант 2: дробная экспонента
Степенной оператор ( ** ) или встроенный 9Функция 0907 pow() также может быть использована для вычисления квадратного корня. С математической точки зрения, квадратный корень из из равен из в степени 1/2 .
Степенной оператор требует числовых типов и соответствует правилам преобразования для двоичных арифметических операторов, поэтому в этом случае он вернет либо число с плавающей запятой , либо комплексное число .
>>> 9 ** (1/2) 3.0 >>> 9 ** .5 # То же самое 3.0 >>> 2** .5 1.4142135623730951
(Примечание: в Python 2 1/2 усекается до 0 , поэтому вам нужно принудительно использовать арифметику с плавающей запятой с помощью 1.0/2 или аналогичного. См. Почему Python дает «неправильный» ответ для квадрата. root?)
Этот метод можно обобщить до корня n-й степени, хотя дроби, которые не могут быть точно представлены в виде числа с плавающей запятой (например, 1/3 или любой другой знаменатель, не являющийся степенью двойки), могут привести к некоторой неточности:
>>> 8** (1/3) 2.0 >>> 125** (1/3) 4.999999999999999
Пограничные случаи
Отрицательные и комплексные
Возведение в степень работает с отрицательными и комплексными числами, хотя результаты имеют небольшую неточность:
>>> (-25) ** .5 # Должно быть 5j (3,061616997868383e-16+5j) >>> 8j ** .5 # Должно быть 2+2j (2.0000000000000004+2j)
Обратите внимание на круглые скобки -25 ! В противном случае он анализируется как -(25**., потому что возведение в степень является более строго обязательным, чем унарное отрицание. 5)
5)
Между тем, math создан только для чисел с плавающей запятой, поэтому для x<0 math.sqrt(x) вызовет ValueError: math domain error , а для комплексного x - TypeError: невозможно преобразовать комплекс в число с плавающей запятой . Вместо этого вы можете использовать cmath.sqrt(x) , что более точно, чем возведение в степень (и, вероятно, будет быстрее):
>>> import cmath >>> cmath.sqrt(-25) 5j >>> cmath.sqrt(8j) (2+2к)
Precision
Оба варианта включают неявное преобразование в float , поэтому важным фактором является точность с плавающей запятой. Например:
>>> n = 10**30 >>> х = п**2 >>> корень = х**.5 >>> п == корень ЛОЖЬ >>> n - root # насколько они удалены? 0,0 >>> int(root) - n # насколько далеко float от int? 19884624838656
Очень большие числа могут даже не поместиться в число с плавающей запятой, и вы получите Между тем, . 5 В зависимости от вашей цели может быть хорошей идеей отложить вычисление квадратных корней как можно дольше. SymPy может помочь. SymPy — это библиотека Python для символьной математики. Сначала это кажется не очень полезным. Но sympy может дать больше информации, чем числа с плавающей запятой или десятичные дроби: Точность не теряется. (√2)² по-прежнему целое число: Для сравнения, числа с плавающей запятой и десятичные числа вернут число, очень близкое к 2, но не равное 2: Sympy также понимает более сложные примеры, такие как интеграл Гаусса: Наконец, если требуется десятичное представление, можно запросить больше цифр, чем когда-либо потребуется: docs Для отрицательных реалов возвращается Еще один вариант, конечно, сначала преобразовать в комплекс: 0 Наиболее простым и точным способом вычисления квадратного корня является метод Ньютона. У вас есть число, из которого вы хотите вычислить квадратный корень ( Эта строка вычисляет более точную оценку с этими двумя параметрами. Вы можете пройти Например, нам нужно найти квадратный корень из 30-х. Мы знаем, что результат находится между 5 и 6. число равно 30, а оценка равна 5. Последний результат — наиболее точное вычисление квадратного корня из числа. Это то же значение, что и у встроенной функции Этот ответ был первоначально опубликован gunesevitan, но теперь удален. 6 Модуль Python Следующий метод принимает положительное число Подробнее о реализации этой операции см. в ссылке ниже. Там же показано, как реализовать другие операции с верхними и нижними границами (хотя там видимо как минимум одна ошибка с операцией В качестве альтернативы, используя Python В предыдущем 1 Отказ от ответственности: это для более специализированного варианта использования. Этот метод не может быть практичным во всех обстоятельствах. Преимущества: Я лично реализовал это для крипто CTF-вызова (атака кубического корня RSA), где мне нужно было точное целочисленное значение. Общая идея может быть распространена на любой другой корень. Как также указал @wjandrea, ** этот код примера НЕ может вычислять **. Это побочный эффект того факта, что он ничего не конвертирует в числа с плавающей запятой, поэтому точность не теряется. Для меньших чисел вы можете просто использовать все остальные методы из других ответов. Обычно они используют числа с плавающей запятой, что может означать потерю точности, но для небольших целых чисел это вообще не должно означать проблем. Все те методы, которые используют числа с плавающей запятой, имеют одинаковый (или почти одинаковый) лимит. Если вы все еще хотите использовать этот метод и получать результаты с плавающей запятой, должно быть тривиально преобразовать его для использования с плавающей запятой. Для больших чисел, когда в игру вступает потеря точности с числами с плавающей запятой, этот метод может дать результаты, более близкие к фактическому ответу (в зависимости от того, насколько велик ввод). Если вы хотите работать с нецелыми числами в этом диапазоне, вы также можете использовать другие типы, например числа с фиксированной точностью в этом методе. В настоящее время, и на самом деле, единственный другой ответ, который имеет аналогичную или лучшую точность для больших чисел, чем эта реализация, - это тот, который предлагает SymPy от Эрика Думинила. Эта версия также проще в использовании и работает с любым числом, единственным недостатком является то, что для нее требуется SymPy. 9 Этот вариант использует операции со строками для преобразования строки, представляющей десятичное число с плавающей запятой, в Входная строка, Аргумент Для небольшого количества цифр быстрее использовать Вот действующая версия, работающая на сервере SageMathCell. OverflowError: int слишком большой для преобразования в число с плавающей запятой . См. предел Python sqrt для очень больших чисел? Пример
Traceback (последний последний вызов):
Файл "
См. предел Python sqrt для очень больших чисел? Пример
Traceback (последний последний вызов):
Файл " math и cmath будут молча преобразовывать свои аргументы в float и complex соответственно, что может означать потерю точности. десятичный также имеет свой собственный .sqrt() . См. также вычисление n-го корня с использованием десятичного модуля Python 3 SymPy
импорт Симпи
sympy.
 sqrt(2)
# => квадрат(2)
sqrt(2)
# => квадрат(2)
sympy.sqrt(8) / sympy.sqrt(27)
# => 2*кв.(6)/9
s = sympy.sqrt(2)
секс 2
# => 2
тип(s**2)
#=> <класс 'sympy.core.numbers.Integer'>
(2**0,5)**2
# => 2.00000000000000004
из десятичного импорта Decimal
(Десятичный ('2') ** Десятичный ('0,5')) ** Десятичный ('2')
# => Десятичный('1.999999999999999999999999999')
from sympy import Symbol, Integrated, pi, sqrt, exp, oo
х = Символ ('х')
интегрировать (exp (-x ** 2), (x, -oo, oo))
# => квт(пи)
интегрировать (exp (-x ** 2), (x, -oo, oo)) == sqrt (pi)
# => Верно
sympy.
 N(sympy.sqrt(2), 1_000_000)
# => 1.4142135623730950488016.........20441930161204
N(sympy.sqrt(2), 1_000_000)
# => 1.4142135623730950488016.........20441930161204
NumPy
>>> импортировать numpy как np
>>> np.sqrt(25)
5,0
>>> np.sqrt([2, 3, 4])
массив([1.41421356, 1.73205081, 2. ])
Отрицательный
нан , поэтому для этого случая доступно np.emath.sqrt() . >>> a = np.array([4, -1, np.inf])
>>> np.sqrt(а)
>>> a = a.astype(complex)
>>> np.sqrt(а)
массив([ 2.+0.j, 0.+1.j, inf+0.j])
Метод Ньютона
число ), и у вас есть предположение о его квадратном корне ( оценка ).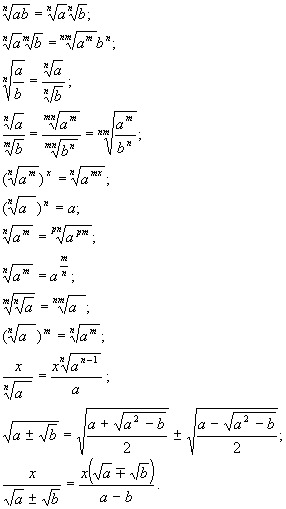 Оценка может быть любым числом больше 0, но число, имеющее смысл, значительно сокращает глубину рекурсивного вызова.
Оценка может быть любым числом больше 0, но число, имеющее смысл, значительно сокращает глубину рекурсивного вызова. new_estimate = (оценка + число/оценка) / 2
new_estimate значение функции и вычислить другое new_estimate , которое является более точным, чем предыдущее, или вы можете сделать определение рекурсивной функции, подобное этому. def newtons_method(число, оценка):
# Вычисление new_estimate
new_estimate = (оценка + число/оценка) / 2
печать (новая_оценка)
# Базовый вариант: сравнение нашей оценки со значением встроенных функций
если new_estimate == math.sqrt(число):
вернуть Истина
еще:
вернуть newtons_method (число, новая_оценка)
newtons_method(30,5)
 Результат каждого рекурсивного вызова:
Результат каждого рекурсивного вызова: 5.5
5.477272727272727
5.4772255752546215
5.477225575051661
math.sqrt() . Fraction и его класс Fraction реализуют арифметику с рациональными числами. Класс Fraction не реализует операцию извлечения квадратного корня, поскольку большинство квадратных корней являются иррациональными числами. Однако его можно использовать для аппроксимации квадратного корня с произвольной точностью, поскольку числитель и знаменатель дроби дроби являются целыми числами произвольной точности. x и количество итераций и возвращает верхнюю и нижнюю границы квадратного корня из x .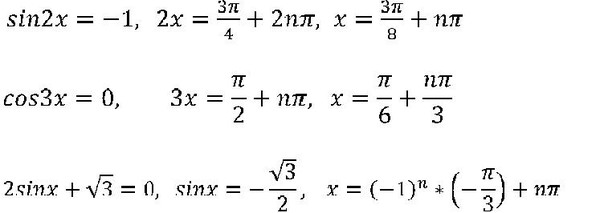
из фракций импорт Фракция
защита sqrt(x, n):
x = x, если isinstance (x, дробь), иначе дробь (x)
верхний = х + 1
для i в диапазоне (0, n):
верхний = (верхний + x/верхний) / 2
нижний = х / верхний
если нижний > верхний:
поднять ValueError("Проверка работоспособности не удалась")
возврат (нижний, верхний)
log ). math.isqrt , мы можем вычислить квадратный корень с произвольной точностью: i в пределах 1/2 n от правильного значения, где i — целое число: Fraction(math. . isqrt(i * 2**(n*2)), 2**н)
isqrt(i * 2**(n*2)), 2**н) i с точностью до 1/10 n правильного значения, где i — целое число: Fraction(math.isqrt(i * 10**(n*2)), 10* *н) . x в пределах 1/2 n от правильного значения, где x кратно 1/2 n : Fraction(math.isqrt(x * 2**(n)), 2**n) . x в пределах 1/10 n правильного значения, где x кратно 1/10 n : (н)), 10**н) . i или x должно быть 0 или больше.
def int_squareroot(d: int) -> tuple[int, bool]:
"""Попробуйте вычислить целочисленный квадратный корень и вернуться, если он точен"""
влево, вправо = 1, (d+1)//2
пока слева<справа-1:
х = (левый+правый)//2
если х**2 > д:
влево, вправо = влево, х
еще:
влево, вправо = х, вправо
вернуться влево, влево**2==d
РЕДАКТИРОВАТЬ:
 Если корень является целым числом, вы получите его обратно. Если это не так, вы получите наибольшее число, квадрат которого меньше вашего числа. Я обновил код, чтобы он также возвращал логическое значение, указывающее, правильное значение или нет, а также исправил проблему, вызывающую бесконечный цикл (на что также указал @wjandrea). Эта реализация общего метода по-прежнему работает немного странно для меньших чисел, но больше 10 у меня не было проблем.
Если корень является целым числом, вы получите его обратно. Если это не так, вы получите наибольшее число, квадрат которого меньше вашего числа. Я обновил код, чтобы он также возвращал логическое значение, указывающее, правильное значение или нет, а также исправил проблему, вызывающую бесконечный цикл (на что также указал @wjandrea). Эта реализация общего метода по-прежнему работает немного странно для меньших чисел, но больше 10 у меня не было проблем. Преодоление проблем и ограничений этого метода/реализации:
 Обратите внимание, что это снова приведет к потере точности, уникальному преимуществу этого метода по сравнению с другими, и в этом случае вы также можете просто использовать любой из других ответов. Я думаю, что версия метода Ньютона сходится немного быстрее, но я не уверен.
Обратите внимание, что это снова приведет к потере точности, уникальному преимуществу этого метода по сравнению с другими, и в этом случае вы также можете просто использовать любой из других ответов. Я думаю, что версия метода Ньютона сходится немного быстрее, но я не уверен. Редактировать 2, по другим ответам:
 Моя реализация свободна от каких-либо огромных зависимостей, если это то, что вы ищете.
Моя реализация свободна от каких-либо огромных зависимостей, если это то, что вы ищете. Квадратный корень произвольной точности
int , вызывает math.isqrt для фактического извлечения квадратного корня, а затем форматирует результат как десятичная строка. math.isqrt округляет в меньшую сторону, поэтому все полученные цифры правильные. num , должна использовать простой формат с плавающей запятой: нотация 'e' не поддерживается. num строка может быть простым целым числом, а ведущие нули игнорируются. цифр задает количество знаков после запятой в строке результата, т. е. количество знаков после запятой. из математического импорта isqrt
def str_sqrt (число, цифры):
""" Квадратный корень произвольной точности
num arg должен быть строкой
Возвращает строку с `цифрами` после
десятичная точка
Написал PM 2Ring 2022. 01.26
"""
int_part , _, frac_part = num.partition('.')
число = целая_часть + дробная_часть
# Определяем требуемую точность
ширина = 2 * цифры - len(frac_part)
# Обрезать или дополнить нулями
num = num[:width], если ширина <0, иначе num + '0' * ширина
s = ул (isqrt (целое (число)))
если цифры:
# Накладка, если необходимо
s = '0' * (1 + цифры - длина (ы)) + s
s = f"{s[:-цифры]}.{s[-цифры:]}"
вернуть с
01.26
"""
int_part , _, frac_part = num.partition('.')
число = целая_часть + дробная_часть
# Определяем требуемую точность
ширина = 2 * цифры - len(frac_part)
# Обрезать или дополнить нулями
num = num[:width], если ширина <0, иначе num + '0' * ширина
s = ул (isqrt (целое (число)))
если цифры:
# Накладка, если необходимо
s = '0' * (1 + цифры - длина (ы)) + s
s = f"{s[:-цифры]}.{s[-цифры:]}"
вернуть с
Тест
print(str_sqrt("2.0", 30))
Выход
1.414213562373095048801688724209
decimal.Decimal.sqrt . Около 32 цифр или около того, str_sqrt примерно с той же скоростью, что и Decimal.sqrt . Но при 128 цифрах str_sqrt в 2,2 раза быстрее, чем Decimal.sqrt , при 512 цифрах это в 4,3 раза быстрее, при 8192 цифрах это в 7,4 раза быстрее.

 sqrt()
sqrt()  0
>>> 9 ** .5 # То же самое
3.0
>>> 2** .5
1.4142135623730951
0
>>> 9 ** .5 # То же самое
3.0
>>> 2** .5
1.4142135623730951