§ 3. Метод подстановок
Заменяя некоторые переменные функционального уравнения либо конкретными значениями, либо какими-либо другими выражениями пытаемся либо упростить это уравнение, либо привести его к такому виду, что дальнейшее решение станет очевидным. Особенность применяемого метода как раз и состоит в том, что в ряде случаев он позволяет отыскать решения в классе всевозможных функций. Поясним метод на следующих примерах.
Пример 8. Найти все решения функционального уравнения
f(xy) = yk f(x), k N.
Решение. Положим в уравнении x = 0: f(0) = yk f(0). Так как y — произвольно, то f(0) = 0.
Пусть теперь x ≠ 0. Подставим в уравнение , получим:
или (a=f(1))
Функция f(x) = axk

Пример 9. Пусть — некоторое действительное число. Найти функциюf(x), определённую для всех x ≠ 1 и удовлетворяющую уравнению
,
где g – заданная функция, определённая при x ≠ 1.
Решение. При замене
получаем систему
.
решением которой при a2 ≠ 1 является функция
Пример 10. Найти все функции f(x), заданные на промежутке , для которых выполнено равенство
Решение. Выполнив последовательно две замены
приходим к системе функциональных уравнений:
Последнее
уравнение есть сумма первых двух,
умноженных на -1, т. е. из данной системы
функция f(x) однозначно не определяется. Из первых
двух уравнений находим
е. из данной системы
функция f(x) однозначно не определяется. Из первых
двух уравнений находим
Мы можем определить f(x) произвольным образом на одном из интервалов и эти формулы дадут нам расширениеf(x) на вcё множество I.
Пример 11. Найти решение системы функциональных уравнений относительно неизвестных функций f(x) и g(x):
Решение. В первом уравнении сделаем подстановку 2x = 1/z.
При этом
и первое уравнение принимает вид:
или
В результате получаем систему уравнений:
решение которой g(x) = 1/x, f(x) = x+1.
В
уравнении
под знаком неизвестной функцииf(x) стоят функции g1 = х и g2 = а – х. В результате замены х на а
– х получено еще одно уравнение, содержащее
те же функции f
(х) и f (а – х).
Функции g1 и g2 образуют группу относительно композиции
функций. Понятие группы позволяет в
ряде случаев выбрать целесообразные
подстановки для решения функциональных
уравнений.
В результате замены х на а
– х получено еще одно уравнение, содержащее
те же функции f
(х) и f (а – х).
Функции g1 и g2 образуют группу относительно композиции
функций. Понятие группы позволяет в
ряде случаев выбрать целесообразные
подстановки для решения функциональных
уравнений.
Пусть в функциональном уравнении
(4.1)
выражения f0 (x)
= x, f1(x),
…, fn-1(x), стоящие под знаком неизвестной функции g
(x),
являются элементами конечной группы
порядка n
относительно композиции функций.
Коэффицненты уравнения (4.1) а0,
а1 …, аn-1,
b в общем случае зависят от x.
Некоторые из них могут равняться 0. Предположим, что уравнение (4.1) имеет
решение. Заменим х на f1(x).
Эта замена равносильна умножению справа
всех элементов группы f1.
В результате последовательность функций f0, f1,
…, fn-1перейдет
в последовательность
,
состоящую из всех элементов группы.
Предположим, что уравнение (4.1) имеет
решение. Заменим х на f1(x).
Эта замена равносильна умножению справа
всех элементов группы f1.
В результате последовательность функций f0, f1,
…, fn-1перейдет
в последовательность
,
состоящую из всех элементов группы.
Произведенная
замена перевела уравнение (4.1) —линейное
относительно неизвестных g(f0), g(f1),
…,g( fn-1)
— в новое линейное уравнение относительно
тех же неизвестных. Заменяя далее x → f2(x), x → f3(x),…, x → fn(x) получим систему n
линейных уравнений с n
неизвестными.
Решая эту систему, находим неизвестную функцию g(f0) = g(x), если, конечно, система имеет решение. Непосредственной проверкой следует убедиться, что полученная функция удовлетворяет исходному уравнению. Рассмотренный метод ограничивает область определения функции, так как приходится отбрасывать те значения аргумента, при которых элементы группы не имеют смысла.
Пример 12. Найти функцию f (х), определенную на множестве действительных чисел, отличных от 0, 1, –1, и удовлетворяющую уравнению
(4.2)
Решение. Выражения , стоящие под знаком неизвестной функцииf, являются элементами группы, заданной таблицей:
Заменяя последовательно х на,,, получим систему
Последовательно исключая неизвестные ,,, имеем
Рассуждения
вытекали из предположения, что решение
уравнения
(4. 2) существует. Подставляя в (4.2) полученную
функцию, убедимся,
что она удовлетворяет уравнению.
2) существует. Подставляя в (4.2) полученную
функцию, убедимся,
что она удовлетворяет уравнению.
где а — постоянная, отличная от 0.
Решение. Нетрудно проверить, что выражения х,, вместе с составляют группу с таблицей:
Здесь xR\{0, а}.
Рассуждая аналогично решению примера 12, получим систему
из нее находим . Проверка показывает, что эта функция удовлетворяет уравнению.
Иногда
в функциональном уравнении выражения,
стоящие под знаком неизвестной функции,
являются значениями элементов некоторой
группы от одной и той же функции g. После
замены g(x) на x получаем
уравнение, которое решается изложенным
выше методом.
Рассмотрим функциональные уравнения, в которых под знаков неизвестной функции стоят, кроме выражений, зависящих от х, и константы.
Пример 14. Решить уравнение
(4.3)
Решение. На множестве {х, 1, –х, 1, 0} определена операция композиции, если рассматривать числа 1 и 0 как функции, тождественно равные константе. Таблица умножения здесь имеет вид:
Из таблицы видно, что для элементов 1 и 0 не существует обратных, т. е. данное множество функций не является группой. В алгебре множества с ассоциативной операцией называют полугруппами. Полугруппы в отдельных случаях можно применить к решению функциональных уравнений.
Делая в (4.3) последовательно замены х → 1 – х, x → 1, x → 1 получим систему
Из двух последних уравнений имеем .
Теперь
из первых двух уравнений найдем:
. Проверка показывает, что найденная
функция удовлетворяет уравнению (4.3).
Проверка показывает, что найденная
функция удовлетворяет уравнению (4.3).
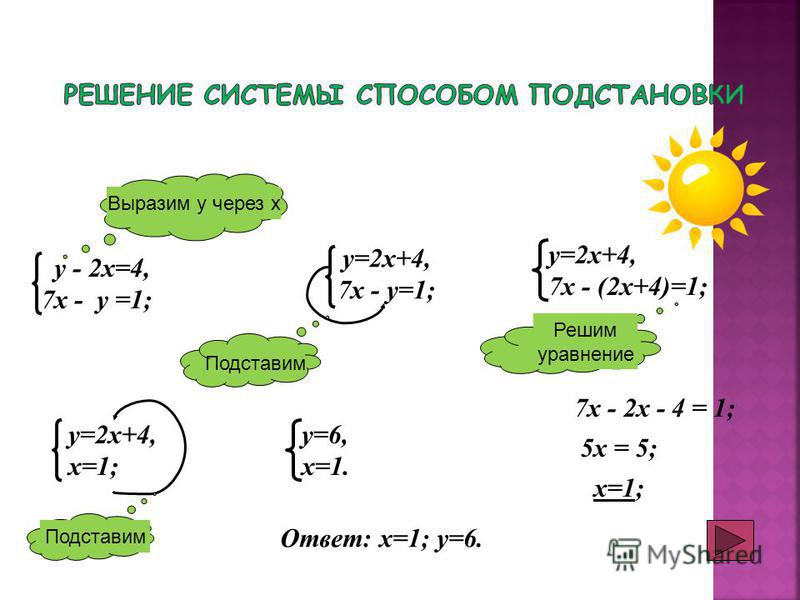
Конспект урока математики «Метод подстановки»
МОУСОШ №2 с.Александровское Ставропольского края
Учитель математики Ерёмина Л.А.
Конспекты уроков с аспектным анализом.
Конспект урока алгебры в 7 классе по теме
« Метод подстановки»
Цель урока: познакомить учащихся с алгоритмом решения систем двух уравнений с двумя переменными методом подстановки; сформировать умение решать системы данным методом.
Задачи урока: формировать умение формулировать проблему и находить пути её решения; развивать навыки самоанализа своей деятельности;
воспитывать интерес к математике как части мировой культуры, стремление к расширению своего кругозора и самосовершенствованию.
Ход урока.
Вступление. Мотивация познавательной деятельности.

Ребята, сегодняшний урок я хочу начать словами замечательного русского поэта Афанасия Фета:
Пора узнать, что в мирозданье,
Куда ни обратись, — вопрос, а не ответ.
Думаю, что вы согласны со мной в том, что жизнь ставит перед нами множество вопросов, ответы на которые мы стремимся найти. А на уроках математики вопросы и поиск ответов на них неизбежны. И бывает на уроке главный вопрос, проблема, которую обязательно нужно решить. Сегодня на уроке мы с вами вместе попытаемся сформулировать такой вопрос и найти на него ответ.
Актуализация знаний.
На предыдущих уроках вы многое узнали о системах линейных уравнений с двумя переменными. Давайте вспомним некоторые сведения.
— Что значит решить систему уравнений?
— Что называется решением системы уравнений?
— Сколько решений может иметь система линейных уравнений?
— Какие методы решения систем уравнений вы знаете?
Устная работа (задания проецируются на экран)
Решим систему уравнений методом угадывания:
a) б) в)
Ответ: (7;5) Ответ: (1;1)
— В чём суть графического метода решения систем линейных уравнений?
Ответ: преобразуем оба уравнения системы к виду линейной функции. Построим в одной системе координат графики линейных функций. Определим координаты точки пересечения графиков. Они являются единственным решением заданной системы. Если прямые параллельны, то система не имеет решений. Если прямые совпадают, то система имеет бесконечно много решений.
Построим в одной системе координат графики линейных функций. Определим координаты точки пересечения графиков. Они являются единственным решением заданной системы. Если прямые параллельны, то система не имеет решений. Если прямые совпадают, то система имеет бесконечно много решений.
Подготовка к восприятию нового материала.
Найдём графическое решение системы
с помощью компьютера.
Выполняется работа с использованием диска « Математика».
Получаем ответ : x=1, y=1.
— Установим, имеет ли решение следующая система:
с помощью компьютера
Ответ: прямые параллельны. Решений нет.
И система сколько имеет решений?
Ответ: прямые совпадают. Система имеет бесконечно много решений.
— Сможем ли мы найти известными вам методами решение системы
Точка пересечения прямых находится за пределами чертежа.
Итак, метод угадывания ненадёжен, графический метод также выручает не всегда.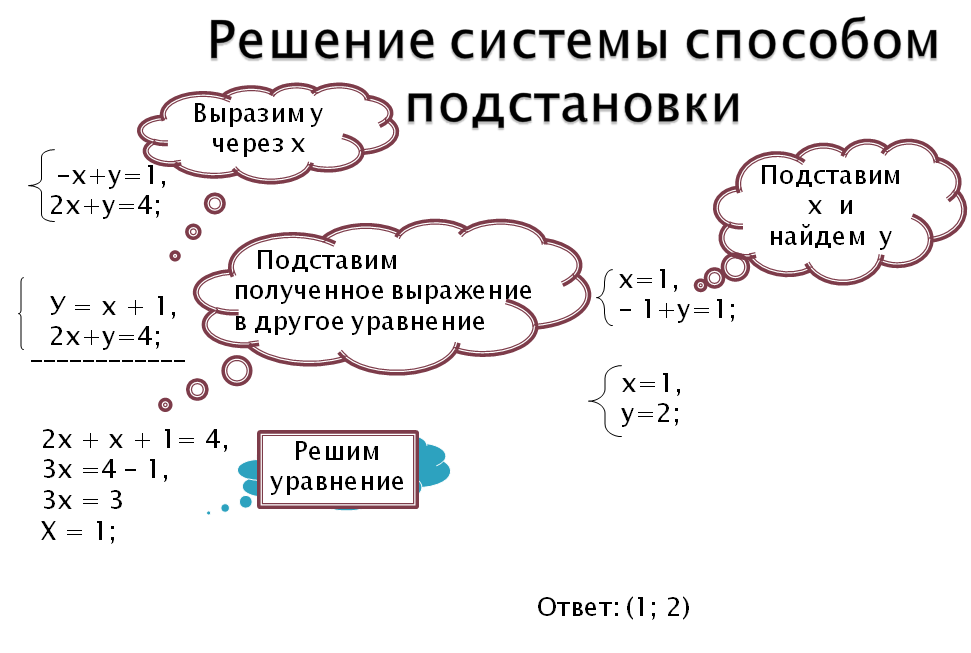 Значит, нам нужно располагать надёжными алгебраическими методами решения системы двух уравнений с двумя переменными.
Значит, нам нужно располагать надёжными алгебраическими методами решения системы двух уравнений с двумя переменными.
Новый материал.
Мы столкнулись с проблемой. Сформулируем эту проблему, которая представляет собой главный вопрос сегодняшнего урока.
( Дети предлагают варианты формулировки возникшей проблемы)
—Как решить систему линейных уравнений с двумя переменными алгебраическим методом?
— Такой метод есть. Он называется метод подстановки. Этот метод универсальный, он выручит всегда, даже в старших классах, когда вы будете решать более сложные системы уравнений.
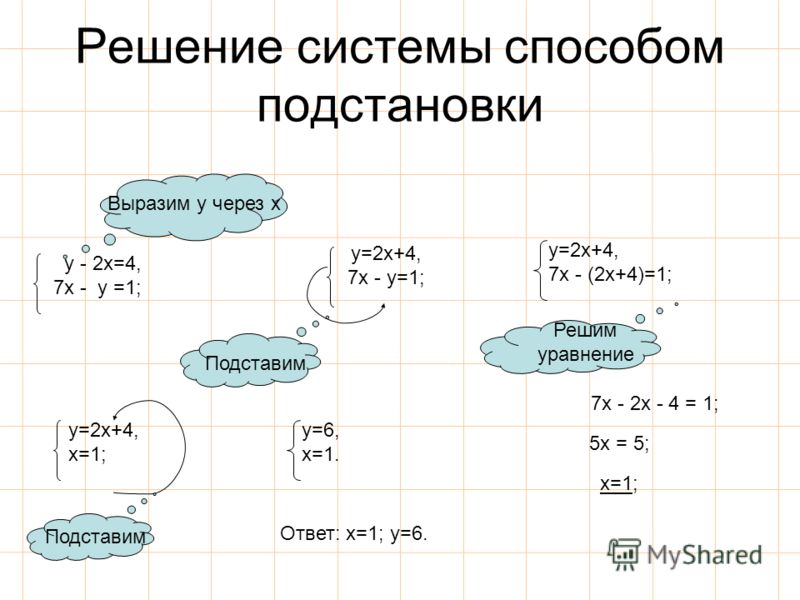
В тетрадях записываем тему урока «Метод подстановки».
Запишем систему :
Выразим y через x в обоих уравнениях:
Нас интересует такое значение x, при котором
Ответ: (-27;-32)
Графиков строить не пришлось. Обязательно ли было выражать у и из второго уравнения?
— Можно было подставить во второе уравнение.
Алгоритм решения системы двух уравнений с двумя переменными методом подстановки.
1. Выразить у через х из первого уравнения системы.
У=
2 Подставить полученное на первом шаге выражение вместо y во второе уравнение системы
3. Решить полученное уравнение относительно x.
4. Подставить найденное значение x в выражение y через x, полученное на первом шаге
5. Записать ответ в виде пары значений (x;y), которые были найдены на третьем и четвертом шагах.
Ответ: (-27;-32)
Вопрос. Не легче ли было бы вычислять значение у, если бы мы выразили его из второго уравнения?
Оказывается, можно выражать любую переменную из любого уравнения системы. Ищем наиболее простой вариант.
Решим систему уравнений из учебника: № 1085(б) (у доски решает сильный ученик с объяснением)
Промежуточная рефлексия
— Какой вопрос стоял перед нами?
— Какой ответ мы получили на этот вопрос?
— Кому понятен алгоритм метода подстановки? Поднимите руки.
5. Закрепление.
№ 1082(а), 1085(а,в,г), 1086(а,б).
6. Подведение итогов урока.
Закончить урок я хочу словами древнегреческого мыслителя Платона:
«Математикой нужно заниматься не ради её приложения, а во имя той духовной прибыли, которая связана с ней».
Мы с вами получили такую прибыль, обогатившись новыми знаниями, умениями, получив удовольствие от общения друг с другом. Мы убедились, что наш мозг может очень многое, в частности, мы сумели сформулировать вопрос урока и найти ответ на него. Открыли для себя новый способ решения систем уравнений.
Итоговая рефлексия.
— На уроке мне удалось…
— Мне не удалось…
— Я научился…
— Я понял …
— На уроке я чувствовал себя…
7. Домашнее задание.
п. 36, выучить алгоритм, №1079(а,б), 1081(б), 1082(б),1087(б)
Понимать, что рациональные выражения образуют систему, аналогичную рациональным числам, замкнутую относительно сложения, вычитания, умножения и деления на ненулевое рациональное выражение; складывать, вычитать, умножать и делить рациональные выражения.
 | СС | ЧСА | HSA-APR | HSA-APR.D
| СС | ЧСА | HSA-APR | HSA-APR.DPopular Tutorials
in Понимать, что рациональные выражения образуют систему, аналогичную рациональным числам, замкнутую относительно сложения, вычитания, умножения и деления на ненулевое рациональное выражение; складывать, вычитать, умножать и делить рациональные выражения.Как умножать частные мономы на сокращающие множители?
Умножать одночленные дроби проще, чем вы думаете! Вы можете отменить общие множители в числителе и знаменателе, чтобы упростить работу. Затем просто умножьте, чтобы получить окончательный ответ! Этот урок покажет вам, как это сделать.
Как делить мономы на частные?
Деление дробей, состоящих из одночленов, проще, чем вы думаете! Во-первых, превратите это в задачу умножения, умножая на обратную величину делителя. Затем вы можете отменить общие множители в числителе и знаменателе, чтобы упростить работу.
Наконец, умножьте, чтобы получить окончательный ответ! Этот урок покажет вам, как это сделать.
Как умножить рациональное выражение на многочлен?
Чтобы умножить рациональное выражение на многочлен, просто превратите этот многочлен в дробь, умножьте и упростите, чтобы получить ответ! Этот урок покажет вам этот процесс шаг за шагом!
Как разделить рациональное выражение на многочлен?
Разделить рациональное выражение на многочлен проще, чем вы думаете! Следуйте инструкциям, поскольку это руководство шаг за шагом проведет вас через этот процесс!
Как уменьшить количество общих факторов в рациональном выражении?
Умножение рациональных выражений? Хотите исключить общие факторы, чтобы упростить работу? В этом руководстве вы увидите, как исключить общие множители, чтобы найти упрощенное произведение двух рациональных выражений. Проверьте это!
Как сложить два рациональных выражения с разными знаменателями?
Сложение рациональных выражений вместе? У вас нет общих знаменателей? Без проблем! Найдите наименьший общий знаменатель (LCD) и замените каждое рациональное выражение эквивалентным выражением с этим LCD.

Как вычесть два рациональных выражения с разными знаменателями?
Вычитание рациональных выражений? У вас нет общих знаменателей? Без проблем! Найдите наименьший общий знаменатель (LCD) и замените каждое рациональное выражение эквивалентным выражением с этим LCD. Когда у вас есть общие знаменатели, вы готовы вычитать и упрощать! Смотрите все это в этом уроке!
Как умножить два рациональных выражения?
Умножение двух рациональных выражений не так сложно, особенно если вы знаете правильные шаги! Этот учебник проведет вас через все шаги, необходимые для умножения двух рациональных выражений, а затем упростит произведение, чтобы получить ответ. Проверьте это!
Как разделить два рациональных выражения?
Деление двух рациональных выражений? Превратите это в задачу на умножение, умножив на обратную величину второго рационального выражения (делителя)! Этот урок покажет вам, как это сделать! Затем вы увидите, как выполнить умножение и упростить, чтобы получить ответ!
Как умножать мономы в частном?
Умножить два одночлена не так уж сложно, особенно если вы знаете правильные шаги! Этот учебник проведет вас через все шаги, необходимые для умножения двух мономов.
 Затем вы увидите, как разделить числитель и знаменатель на наибольший общий делитель (НОД), чтобы упростить и получить ответ!
Затем вы увидите, как разделить числитель и знаменатель на наибольший общий делитель (НОД), чтобы упростить и получить ответ!Как сложить два рациональных выражения с одинаковым знаменателем?
Сложение рациональных выражений вместе? Если у них есть общий знаменатель, просто сложите числители и упростите. Так же, как и с любыми другими фракциями! Смотрите процесс в этом уроке.
Как вычесть два рациональных выражения с одинаковым знаменателем?
Вычитание рациональных выражений? Если у них есть общий знаменатель, просто вычтите числители и упростите. Так же, как и с любыми другими фракциями! Смотрите процесс в этом уроке.
Что такое рациональное выражение?
Получилась дробь с полиномом в числителе и знаменателе? У тебя рациональное выражение! Узнайте о рациональных выражениях в этом уроке.
Решение систем уравнений с помощью подстановки — задача 1
Если два уравнения представлены в форме пересечения наклона и пересечения, вы можете легко решить систему с помощью подстановки, приравняв одно значение y к другому значению y (поскольку в оба уравнения, y равно чему-то). Оттуда используйте обратные операции, чтобы найти x. Получив значение x, подставьте его в любое из двух исходных уравнений системы, чтобы найти значение y. Значения x и y составляют координатную точку решения системы. Проверьте свой ответ, подставив значения x и y в оба уравнения, чтобы убедиться, что они оба верны.
Оттуда используйте обратные операции, чтобы найти x. Получив значение x, подставьте его в любое из двух исходных уравнений системы, чтобы найти значение y. Значения x и y составляют координатную точку решения системы. Проверьте свой ответ, подставив значения x и y в оба уравнения, чтобы убедиться, что они оба верны.
система уравнений решение замена y=mx+b
Эта задача с использованием подстановки не будет слишком сложной, потому что у меня есть 2 уравнения, оба из которых уже решены для y. Поскольку я знаю, что y равно выражению 3x плюс 1, а y также равно выражению 2x минус 3, математически имеет смысл написать 3x плюс 1 равно 2x минус 3. Этот парень равен y, и этот парень также равно y, поэтому я просто заменяю эти два уравнения, чтобы они выглядели как одно уравнение с одной переменной.
Теперь это простая задача для решения. Я собираюсь найти x, а затем вернуться и найти свое значение y. Итак, если я хочу найти x, я вычту 2 X с обеих сторон, так что теперь у меня x плюс 1 равно -3. Теперь мне нужно получить x сам по себе, вычитая 1 с обеих сторон, x равно -4. Имейте в виду, что это будет только половина моего ответа. Я собираюсь обвести это рамкой, как и весь ответ, помня, что мне все еще нужно найти, что это за значение y.
Я собираюсь найти x, а затем вернуться и найти свое значение y. Итак, если я хочу найти x, я вычту 2 X с обеих сторон, так что теперь у меня x плюс 1 равно -3. Теперь мне нужно получить x сам по себе, вычитая 1 с обеих сторон, x равно -4. Имейте в виду, что это будет только половина моего ответа. Я собираюсь обвести это рамкой, как и весь ответ, помня, что мне все еще нужно найти, что это за значение y.
Чтобы найти y, я возьму x равным -4 и подставлю его в любое из исходных уравнений, таким образом я получу свое значение y, а через секунду вернусь и проверю. Я просто выберу первое уравнение. Я мог бы также использовать второй вариант, и я все равно получу тот же ответ для y. Y равно 3, умноженному на мое количество x плюс 1, поэтому y равно -11, упс, это +1 прямо здесь, плюс 1 хорошо. Y равно -11. Я почти уверен, что это мой ответ, я почти уверен, что это точка пересечения этих линий, хотя я не рисовал их на графике.
Чтобы проверить свою работу, я вернусь назад и подставлю -4 для x и -11 для y в оба исходных уравнения и удостоверюсь, что я получаю равенства.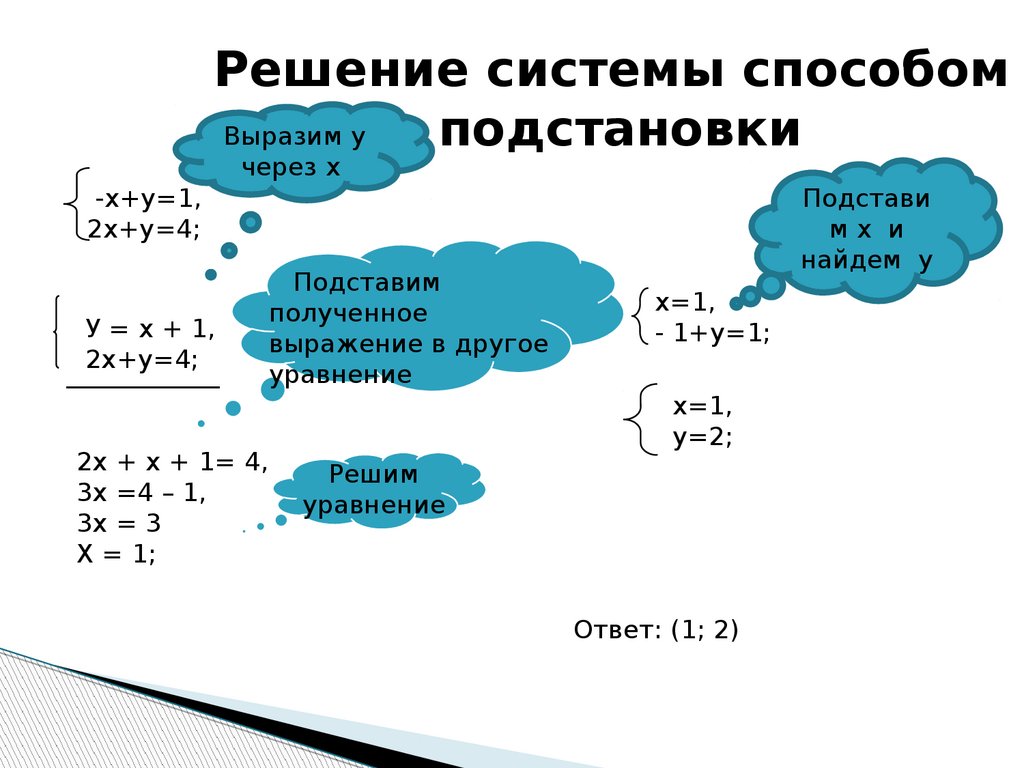



 Затем вы увидите, как разделить числитель и знаменатель на наибольший общий делитель (НОД), чтобы упростить и получить ответ!
Затем вы увидите, как разделить числитель и знаменатель на наибольший общий делитель (НОД), чтобы упростить и получить ответ!