ln(n) 1 : Анализ-I
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| |||
12/01/11 |
| ||
|
| |||
| nnosipov |
| |||
20/12/10 |
| |||
| ||||
| Whitaker |
| ||
12/01/11 Москва |
| ||
| |||
| Klad33 |
| |||
11/09/11 |
| |||
| ||||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| Klad33 |
| |||
11/09/11 |
| |||
| ||||
| gris |
| |||
13/08/08 |
| |||
| ||||
| Whitaker |
| ||
12/01/11 |
| ||
| |||
| Legioner93 |
| |||
28/07/09 |
| |||
| ||||
| PAV |
| |||
29/07/05 |
| |||
| ||||
| bot |
| |||
21/12/05 |
| |||
| ||||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 11 ] |
Модераторы: Модераторы Математики, Супермодераторы
\infty $$ и на самом деле интеграл расходится.
Это часть семейства примеров, которые стоит запомнить. Обратите внимание, что
$$
d/dx \log(\log(\log x)) = d/dx \log(\log x) \cdot \frac{1}{\log (\log x)} = \frac{1}{x \ журнал х \ журнал (\ журнал х)}
$$
и $\log (\log (\log x)) \to \infty$ при $x \to \infty$, следовательно, $\sum \frac{1}{n \log n \log (\log n)}$ расходится также. 2x}$ сходится, и на самом деле (опять же по индукции), если вы возведете в квадрат любой из повторяющихся журналов в $\sum \frac{1} {n \log n \log(\log n) \ldots \log (\ldots (\log n) \ldots )}$ сумма будет сходиться. 9\infty \frac{1}{n\log(n)}$ расходится. С этой целью мы сейчас приступим.
2x}$ сходится, и на самом деле (опять же по индукции), если вы возведете в квадрат любой из повторяющихся журналов в $\sum \frac{1} {n \log n \log(\log n) \ldots \log (\ldots (\log n) \ldots )}$ сумма будет сходиться. 9\infty \frac{1}{n\log(n)}$ расходится. С этой целью мы сейчас приступим.
Воспользуемся известными неравенствами для логарифмирования (СМ. ЭТОТ ОТВЕТ)
$$\frac{x-1}{x} \le \log(x)\le x-1 \tag1$$
Используя правое неравенство в $(1)$, мы видим, что
$$\log\left(\frac{n+1}{n}\right)\le \frac1n \tag 2$$
и
$$\log\left(\frac{\log(n+1)}{\log(n)}\right)\le \frac{\log(n+1)}{\log( п)}-1 \tag3$$
9N \left(\log(\log(n+1)) -\log(\log(n)) \right)\\\\ &=\log(\log(N+1))-\log(\log(3)) \end{align}$$Поскольку $\lim_{N\to \infty}\log(\log(N+1))=\infty$, интересующий ряд расходится при сравнении.
Готово!
ИСПОЛЬЗУЕМЫЕ ИНСТРУМЕНТЫ: Правое неравенство в $(1)$ и суммирование телескопического ряда.

$\endgroup$
2
9xI(t)dt=C+O\left(\frac{1}{x\log x}\right)$ (первый интеграл не связан с $x$ и ограничен $1/2\log 2$, так что это константа).Следовательно, имеем $$\sum_{1< n\leqslant x}\frac{1}{n\log n}=\log\log x+B+O\left(\frac{1}{x\log x}\right) $$
Это говорит нам о том, что при $x\to\infty$ сумма также стремится к бесконечности.
Я понимаю, что эта асимптотическая формула не нужна для доказательства расхождения, но она может предоставить вам другой способ доказательства сходимости или расхождения. 9{\infty} \zeta_{2}(x) dx$ также расходится.
Отсюда следует, что $\sum_{n≥2} \frac{1}{n(\log n)}$ расходится.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.

 09.2011, 13:53
09.2011, 13:53 
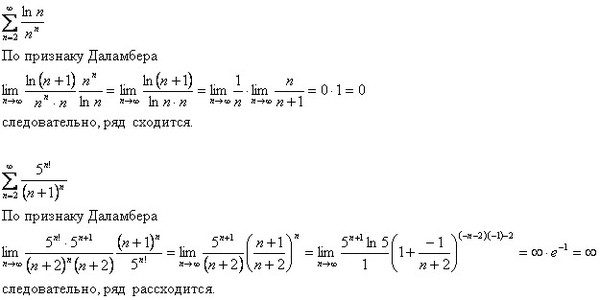
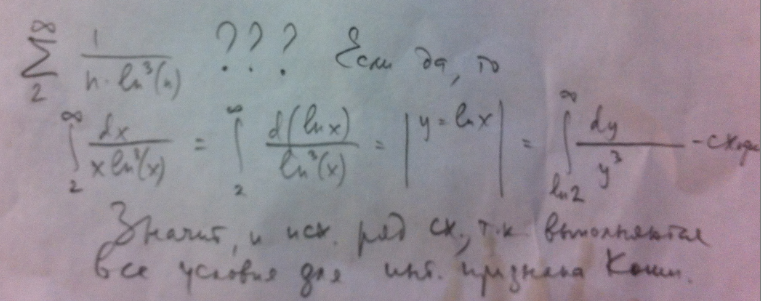




 Лагранжа (формула конечных приращений). Экспонента достаточно гладкая, поэтому записываем
Лагранжа (формула конечных приращений). Экспонента достаточно гладкая, поэтому записываем …
…
