Определитель системы: Онлайн калькулятор. Определитель матрицы. Детерминант матрицы

Определители и системы линейных уравнений

1.1. Системы двух линейных уравнений и определители второго порядка

Рассмотрим систему двух линейных уравнений с двумя неизвестными:

Коэффициенты при неизвестных и имеют два индекса: первый указывает номер уравнения, второй – номер переменной.

Главным определителем системы называется таблица, составленная из коэффициентов при неизвестных и заключенная в прямые скобки:

Вспомогательным определителем называют определитель, полученный из главного определителя заменой одного из столбцов на столбец свободных членов:

Главнаядиагональ определителя – это диагональ, направленная из левого верхнего угла в правый нижний угол. Вторая диагональ называетсяпобочной.

Определитель второго порядка равен разности между произведением элементов главной диагонали и произведением элементов побочной диагонали:

Правило Крамера: Решение системы находят путем деления вспомогательных определителей на главный определитель системы

,

Замечание 1.Использование правила Крамера возможно, если определитель системы не равен нулю.

Замечание 2.Формулы Крамера обобщаются и на системы большего порядка.

Пример 1. Решить систему: .

Решение.

; ;

;

Проверка:

Вывод: Система решена верно: .

Рассмотрим систему трех линейных уравнений с тремя неизвестными:

Определитель, составленный из коэффициентов при неизвестных, называется определителем системы или главным определителем:

.

Если то система имеет единственное решение, которое определяется по формулам Крамера:

где

где определители – называются вспомогательными и получаются из определителя путем замены его первого, второго или третьего столбца столбцом свободных членов системы.

Пример 2.Решить систему .

Сформируем главный и вспомогательные определители:

Осталось рассмотреть правила вычисления определителей третьего порядка. Их три: правило дописывания столбцов, правило Саррюса, правило разложения.

а) Правило дописывания первых двух столбцов к основному определителю:

.

Вычисление проводятся следующим образом: со своим знаком идут произведения элементов главной диагонали и по параллелям к ней, с обратным знаком берут произведения элементов побочной диагонали и по параллелям к ней.

б) Правило Саррюса:

Со своим знаком берут произведения элементов главной диагонали и по параллелям к ней, причем недостающий третий элемент берут из противоположного угла. С обратным знаком берут произведения элементов побочной диагонали и по параллелям к ней, третий элемент берут из противоположного угла.

в) Правило разложения по элементам строки или столбца:

Определитель равен сумме произведений элементов какой-нибудь строки (столбца) на их соответствующие алгебраические дополнения.

Если , тогда .

Алгебраическое дополнение– это определитель более низкого порядка, получаемый путем вычеркивания соответствующей строки и столбца и учитывающий знак , где– номер строки,– номер столбца.

Например,

, , и т.д.

Вычислим по этому правилу вспомогательные определители и , раскрывая их по элементам первой строки.

Вычислив все определители, по правилу Крамера найдем переменные:

Проверка:

Вывод: система решена верно: .

3. Основные свойства определителей

Необходимо помнить, что определитель – это число, найденное по некоторым правилам. Его вычисление может быть упрощено, если пользоваться основными свойствами, справедливыми для определителей любого порядка.

Свойство 1.Значение определителя не изменится от замены всех его строк соответствующими по номеру столбцами и наоборот.

Операция замены строк столбцами называется транспонированием. Из этого свойства вытекает, что всякое утверждение, справедливое для строк определителя, будет справедливым и для его столбцов.

Свойство 2.Если в определителе поменять местами две строки (столбца), то знак определителя поменяется на противоположный.

Свойство 3.Если все элементы какой-нибудь строки определителя равны 0, то определитель равен 0.

Свойство 4.Если элементы строки определителя умножить (разделить) на какое-нибудь число , то и значение определителя увеличится (уменьшится) в раз.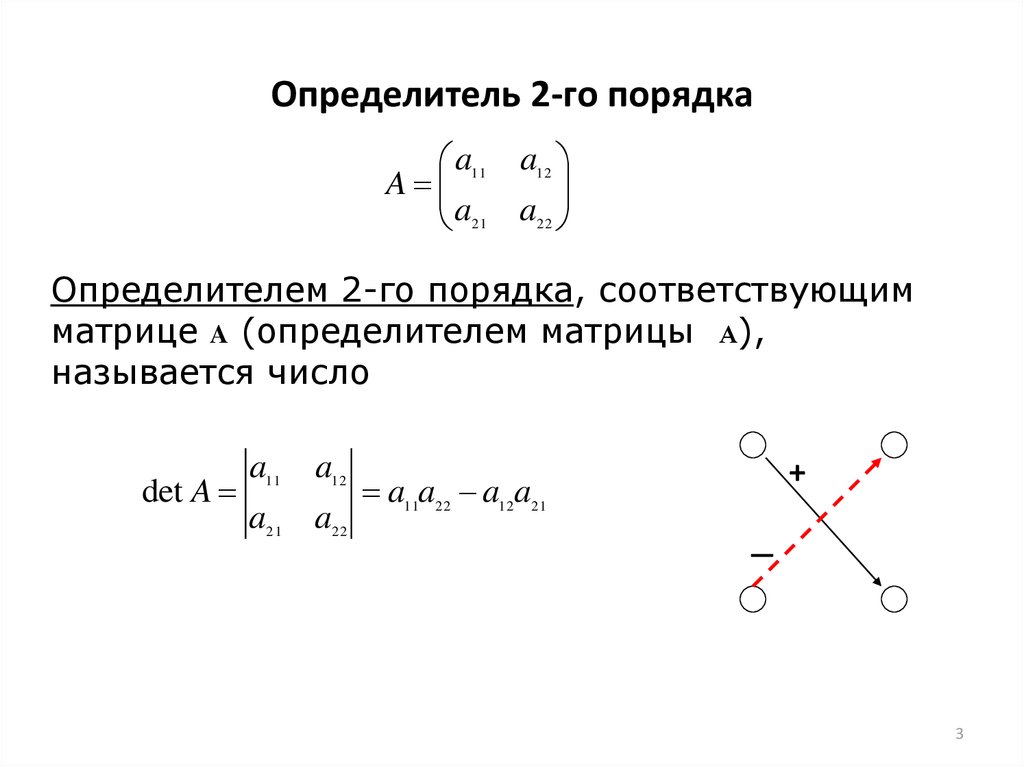

Если элементы какой-нибудь строки, имеют общий множитель, то его можно вынести за знак определителя.

Свойство 5. Если определитель имеет две одинаковые или пропорциональные строки, то такой определитель равен 0.

Свойство 6. Если элементы какой-нибудь строки определителя представляют собой сумму двух слагаемых, то определитель равен сумме двух определителей.

Свойство 7. Значение определителя не изменится, если к элементам какой-нибудь строки добавить элементы другой строки, умноженной на одно и то же число.

В этом определителе вначале ко второй строке прибавили третью, умноженную на 2, затем из третьего столбца вычли второй, после чего вторую строку прибавили к первой и третьей, в результате получили много нулей и упростили подсчет.

Элементарными преобразованиями определителя называются упрощения его благодаря использованию указанных свойств.

Пример 1.Вычислить определитель

Непосредственный подсчет по одному из рассмотренных выше правил приводит к громоздким вычислениям. Поэтому целесообразно воспользоваться свойствами:

а) из І строки вычтем вторую, умноженную на 2;

б) из ІІ строки вычтем третью, умноженную на 3.

В результате получаем:

Разложим этот определитель по элементам первого столбца, содержащего лишь один ненулевой элемент.

.

3. Системы и определители высших порядков

Систему линейных уравнений с неизвестными можно записать в таком виде:

Для этого случая также можно составить главный и вспомогательные определители, а неизвестные определять по правилу Крамера. Проблема состоит в том, что определители более высокого порядка могут быть вычислены только путем понижения порядка и сведения их к определителям третьего порядка. Это может быть осуществлено способом прямого разложения по элементам строк или столбцов, а также с помощью предварительных элементарных преобразований и дальнейшего разложения.

Пример 4. Вычислить определитель четвертого порядка

Решение найдем двумя способами:

а) путем прямого разложения по элементам первой строки:

б) путем предварительных преобразований и дальнейшего разложения

	а) из І строки вычтем ІІІ
	б) ІІ строку прибавим к ІV

а) из IV строки вынесем 2
б) сложим III и IV столбцы
в) умножим на 2 III столбец и прибавим ко II

Пример 5.

Вычислить определитель пятого порядка, получая нули в третьей строке с помощью четвертого столбца

из первой строки вычтем вторую, из третьей вычтем вторую, из четвертой вычтем вторую, умноженную на 2.

из второго столбца вычтем третий:

из второй строки вычтем третью:

Пример 6.Решить систему:

Решение.Составим определитель системы и, применив свойства определителей, вычислим его:

(из первой строки вычтем третью, а затем в полученном определителе третьего порядка из третьего столбца вычитаем первый, умноженный на 2). Определитель , следовательно, формулы Крамера применимы.

Вычислим остальные определители:

Четвертый столбец умножили на 2 и вычли из остальных

Четвертый столбец вычли из первого, а затем, умножив на 2, вычли из второго и третьего столбцов.

.

Здесь выполнили те же преобразования, что и для .

.

При нахождении первый столбец умножили на 2 и вычли из остальных.

По правилу Крамера имеем:

.

После подстановки в уравнения найденных значений убеждаемся в правильности решения системы.

2. МАТРИЦЫ и ИХ ИСПОЛЬЗОВАНИЕ

В РЕШЕНИИ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ

Определитель матрицы

Рассмотрим систему двух линейных уравнений с двумя неизвестными:

(1)

Умножим обе части первого уравнения на a₂₂ а второе на —a₁₂ и сложим. Получим следующее уравнение

Далее, первое уравнение умножим на —a₂₁ а второе на a₁₁ и сложим:

Пусть Тогда решение системы (1) примет следующий вид:

Выражение называется определителем матрицы

и обозначается:

Нетрудно заметить, что

Таким образом, решение системы линейных уравнений можно представить в виде:

Рассмотрим случай из трех неизвестных и трех уравнений. Пусть дана система линейных уравнений

(2)

Исключим неизвестные x₂ и x₃. Для этого умножим первое уравнение на a₂₂a₃₃—a₃₂a₂₃, второе на —(a₁₂a₃₃—a₁₃a₃₂), третье на a₁₂a₂₃—a₂₂a₁₃, и сложим:

Сделаем следующие обозначения:

Учитывая, что выражения перед элементами x₂ и x₃ равны нулю, имеем:

Выражение называется определителем матрицы

(3)

и обозначается:

(3a)

Элементы M_ij называются минорами элементов a_ij, и являются определителями матрицы (3), полученные вычеркиванием i-ой строки и j-го столбца.

Заметим, что выражение

является определителем матрицы

Если определитель (3a) неравен нулю, то x₁ вычисляется из следующего выражения:

Аналогично вычисляются x₂ и x₃, умножая уравнения системы (2) на соответствующие выражения и суммируя:

Распространяя вышеизложенное на системы линейных уравнений с n неизвестными и n уравнениями можно сформулировать понятие определителя для квадратной матрицы порядка n.

Пусть задана матрица

(4)

Определителем порядка n, соответствующим матрице (4), называется число равное

(5)

Сделаем следующее обозначение:

Тогда выражение (5) можно переписать в следующем виде:

(6)

A_ij называется алгебраическим дополнением элемента a_ij.

В вышеизложенном выражении определитель вычисляется суммируя произведения всех элементов первого столбца на соответствующие им алгебраические дополнения. Аналогично можно показать, что определитель равна сумме произведений всех элементов какой либо строки (или столбца) на соответствующие алгебраические дополнения:

(7)

Однако, для вычисления определителя матрицы большой размерности, такой подход требует больших усилий. Ниже мы представим более оптимальный метод вычисления определителя. Для этого сначала изложим некоторые важные свойства определителей.

Свойства определителей

1. Перестановка строк меняет знак определителя на обратное.
2. Общий для всех элементов множитель какой либо строки, можно выносить за знак определителя.
3. При сложении двух определителей, различающихся только одной строкой, соответствующие элементы этой строки складываются.
4. Прибавление одной строки к другой строке, умноженной на число, не изменяет значение определителя.
5. При замене местами строк и столбцов (при транспонировании) определитель не изменит своего значения.

Вычисление определителя матрицы с помощью исключения Гаусса

Для вычисления определителя приведем матрицу к верхнему треугольному виду с помощью исключения Гаусса. Тогда выражение (7) примет следующий вид:

(8)

где Z— общее количество перестановок. При каждой перестановке строк, изменяется знак определителя на обратное (свойство 1). Если общее число перестановок нечетное, то нужно поменять знак произведения элементов главной диагонали на обратное.

Онлайн нахождение определителя матрицы

Для нахождения определителя матрицы вы можете использовать матричный онлайн калькулятор. Для подробного решения используйте онлайн калькулятор для вычисления определителя матрицы.

Компоненты NIMS — руководство и инструменты

Национальная квалификационная система

Типирование ресурсов

Инвентаризация

Взаимная помощь

Система управления инцидентами

Центры управления чрезвычайными ситуациями, различные события, угрозы и сообщества в стране

9000 . Размер, частота, сложность и масштабы этих происшествий различаются, но все они связаны с участием целого ряда сотрудников и организаций для координации усилий по спасению жизней, стабилизации ситуации и защите имущества и окружающей среды.

Каждый день юрисдикции и организации работают вместе, чтобы делиться ресурсами, интегрировать тактики и действовать сообща. Независимо от того, находятся ли эти организации поблизости или поддерживают друг друга со всей страны, их успех зависит от общего, совместимого подхода к совместному использованию ресурсов, координации и управлению инцидентами, а также к обмену информацией.

Национальная система управления инцидентами (NIMS) определяет этот комплексный подход.

Загрузите доктрину Национальной системы управления инцидентами.

Национальная система квалификаций

Национальная система квалификаций (NQS) представляет собой основополагающее руководство по типизации кадровых ресурсов в рамках NIMS, а также вспомогательные инструменты.

Дополнительные руководства и инструменты

Общие рекомендации NIMS для Национальной системы квалификаций, а также два дополнительных руководства для комиссий по проверке квалификаций и тренеров/оценщиков.

Просмотреть все руководства

Должности и квалификации NQS

Минимальные квалификационные критерии для персонала, занимающего определенные должности управления инцидентами и поддержки. Эти документы также можно найти в инструменте библиотеки типизации ресурсов.

Просмотреть все критерии

Книги задач по должности NQS

Компетенции, поведение и задачи, которые должен продемонстрировать персонал, чтобы получить квалификацию для определенной должности управления инцидентами и поддержки.

Просмотреть все рабочие тетради

OneResponder

OneResponder — это веб-приложение для управления ресурсами, размещенное в облачной среде, бесплатное и доступное для всех членов всего сообщества.

Узнайте больше об OneResponder

Типизация ресурсов

Типизация ресурсов определяет и классифицирует по возможностям ресурсы, запрошенные, развернутые и используемые в инцидентах. Определения типов ресурсов устанавливают общий язык и определяют минимальные возможности ресурса (для оборудования, команд и подразделений). Определения типов ресурсов NIMS служат общим языком для мобилизации ресурсов.

Инструмент библиотеки типизации ресурсов

Инвентаризация

Владельцы и поставщики ресурсов должны проводить инвентаризацию и поддерживать текущую информацию о своих общих ресурсах. Запасы ресурсов должны быть адаптируемыми и масштабируемыми. Хотя инвентаризация ресурсов может быть такой же простой, как бумажная или электронная таблица, многие поставщики ресурсов используют системы инвентаризации на основе информационных технологий (ИТ).

Система инвентаризации ресурсов при инцидентах (IRIS) — это распределенный программный инструмент, бесплатно предоставляемый FEMA. IRIS позволяет пользователям определять и инвентаризировать свои ресурсы для операций взаимопомощи и обмениваться информацией с другими агентствами.

Система инвентаризации ресурсов на случай чрезвычайных ситуаций

Взаимная помощь

Соглашения о взаимной помощи уже существуют в различных формах между всеми уровнями правительства. Эти соглашения разрешают взаимную помощь между двумя или более соседними сообществами, между всеми юрисдикциями в штате и между штатами. Соглашения также могут заключаться с организациями частного сектора, НПО и другими партнерами в масштабах всего сообщества и между ними. Сообщество по управлению чрезвычайными ситуациями должно рассмотреть ресурсы и возможности всего сообщества и разработать письменные соглашения, облегчающие доступ к потенциально необходимым ресурсам.

Руководство NIMS по взаимопомощи

Ресурсы системы управления инцидентами

Система управления инцидентами (ICS) представляет собой систему управления, предназначенную для обеспечения эффективного и действенного управления внутренними инцидентами путем интеграции средств, оборудования, персонала, процедур и средств связи. работают в рамках единой организационной структуры. Это позволяет менеджерам по инцидентам определять ключевые проблемы, связанные с инцидентом, часто в срочных условиях, не жертвуя вниманием к какому-либо компоненту системы управления.

ICS, как правило, структурировано для облегчения деятельности в шести основных функциональных областях:

• Команда
• Операции
• Планирование

• Логистика
• СИСТЕМСТВА
СИСТЕМАРИЧЕСКИЕ НА СИСТЕМАРИЧЕСКИЙ И СЕМЕРБА

70002. СИСТЕМСТВА. Интеллектуальные и следственные функции Руководство

Центры операций в чрезвычайных ситуациях

В юрисдикциях создаются центры операций в чрезвычайных ситуациях (EOC) для удовлетворения их уникальных требований и потребностей, поэтому нет двух абсолютно одинаковых центров EOC. В этом разделе FEMA предоставило инструменты и ресурсы для создания или обслуживания EOC в соответствии с NIMS.

Наборы навыков Центра аварийных операций

Измененные подходы к должностным задачам для квалификации персонала EOC, сохраняя при этом гибкость для адаптации к различным организационным структурам EOC.

Просмотреть все наборы навыков

Инструментарий Центра аварийных операций

Инструментарий EOC охватывает такие темы, как оценка уязвимости к угрозам, выбор физической площадки, соображения по смягчению последствий, возможности и требования, системы управления информацией, а также обучение и учения.

Загрузить Инструментарий EOC

Справочник и ресурсы

Загрузить Процесс планирования действий в случае инцидента инциденты.

Загрузить Инструментарий для руководителей высшего звена

Краткое справочное руководство Центра операций в чрезвычайных ситуациях

Краткое справочное руководство по EOC представляет собой сборник рекомендаций и передового опыта, который поможет разработать EOC, способный успешно удовлетворить потребности юрисдикции. Обновления включают рекомендации для виртуальных и гибридных рабочих сред.

Загрузить Краткое справочное руководство EOC

Квалификационный сертификат инженера по эксплуатации холодильных систем (Q-01)

верхний

• О
• Подать заявление
• После того, как вы подадите заявку
• Эксплуатация и обновление

Новые сборы за подачу заявки: 285 долларов США КАК ПРИМЕНИТЬ

Заявка рассмотрена в течение: 1 день ПОСЛЕ ПОДАЧИ ЗАЯВКИ

Плата за продление: 15 долларов ЭКСПЛУАТАЦИЯ И ОБНОВЛЕНИЕ

Цикл обновления: 3 года ЭКСПЛУАТАЦИЯ И ОБНОВЛЕНИЕ

Любая холодильная система, требующая разрешения FDNY, должна находиться под наблюдением держателя квалификационного сертификата (инженер по эксплуатации холодильной системы Q-01) во время работы системы. Настоящий квалификационный сертификат относится к помещениям.

Может потребоваться персональный или общий надзор за холодильной системой, как указано в таблице FC 606.1.1

• Если требуется личный надзор:

1. Держатель Q-01 должен ПРИСУТСТВОВАТЬ В ЗДАНИИ все время, пока работает холодильная система, и чтобы работа такой системы находилась под его или ее личным руководством и контролем. С другой стороны, если холодильная система отключена, в здании не требуется держателя Q-01.
2. Владелец Q-01 не может осуществлять личный надзор одновременно за холодильными установками, которые эксплуатируются более чем в одном здании. С другой стороны, владелец Q-01 может обеспечить личный контроль за работой более чем одной системы одновременно, при условии, что все системы установлены В ОДНОМ ЗДАНИИ.

• Если требуется общий надзор:
  • Присутствие держателя Q-01 в здании во время работы холодильной системы не требуется. Тем не менее, владелец Q-01 по-прежнему несет ответственность за обеспечение безопасной работы системы и за то, чтобы такая система работала под его/ее общим руководством и контролем.
  • Дополнительные рабочие места:
    • Любой обладатель квалификационного сертификата, желающий зарегистрировать более одного места работы, должен предоставить дополнительные документы, перечисленные в Уведомлении об экзамене, от всех работодателей для каждого места работы. Плата за подачу заявки в размере 60 долларов США будет взиматься за дополнительную карту сертификата квалификации.
  
  

  Далее: Подать заявку
  9 Центр МетроТех, 1 этаж
  Бруклин, Нью-Йорк 11201
  Телефон: (718) 999-1988
  [email protected]

  Открыто с понедельника по пятницу с 8:00 до 14:30. Закрыт в праздничные дни.

  Для получения дополнительной помощи позвоните по номеру 311 и запросите: Свидетельство о пригодности
  Веб-сайт: http://www.

  No related posts.