§ Как избавиться от иррациональности
Квадратный корень Квадратный корень из произведения Квадратный корень из дроби Как избавиться от иррациональности Как вынести из-под корня Как внести под знак корня
Важно!
Иррациональностью в знаменателе (нижней части дроби) называют наличие корней в знаменателе.
Что такое иррациональность в знаменателе дроби
Рассмотрим на примерах ниже, в каких дробях в знаменателе есть иррациональность, а в каких её нет.
- в знаменателе нет корней, значит иррациональности нет;
-
в знаменателе есть
корень «√6» — иррациональность в знаменателе есть.
в знаменателе есть корни «√7» и «√3» — иррациональность есть.4 √7 − √3
в знаменателе естьa + b √c − 3 
Запомните!
Избавиться от иррациональности в знаменателе означает убрать все корни из знаменателя.
Возникает логичный вопрос, как это можно сделать?
Чаще всего встречаются два вида примеров. Рассмотрим решение обоих видов.
Как избавиться от иррациональности, когда в знаменателе только один корень
На помощь приходит основное свойство дроби. Вспомним, что оно позволяет умножить и разделить дробь на одно и то же число, чтобы в конечном итоге дробь не изменилась.
Запомните!
Чтобы избавиться от иррациональности в знаменателе с одним корнем, нужно умножить и числитель, и знаменатель на корень из знаменателя.
По традиции разберемся на практике.
Разбор примера
Исключить иррациональность из знаменателя:
Зададим себе вопрос, на что нужно умножить «√5» в знаменателе, чтобы избавиться от корня.
Ответ: на «√5». В самом деле, если квадратный корень умножить сам на себя получится число под корнем. Проверим.
В самом деле, если квадратный корень умножить сам на себя получится число под корнем. Проверим.
√5 · √5 = √5 · 5 = √52 = 5
Используем основное свойство дроби, умножим и числитель, и знаменатель на «√5», чтобы избавиться от корня в знаменателе.
=
| 3 · √5 |
| √5 · √5 |
=
| 3 · √5 |
| √5 · 5 |
=
| 3 · √5 |
| √52 |
=
=
| 3 · √5 |
| 5 |
Как избавиться от иррациональности, когда в знаменателе несколько корней
Чтобы избавиться от иррациональности в знаменателе c несколькими корнями, нужно использовать
формулы сокращённого умножения.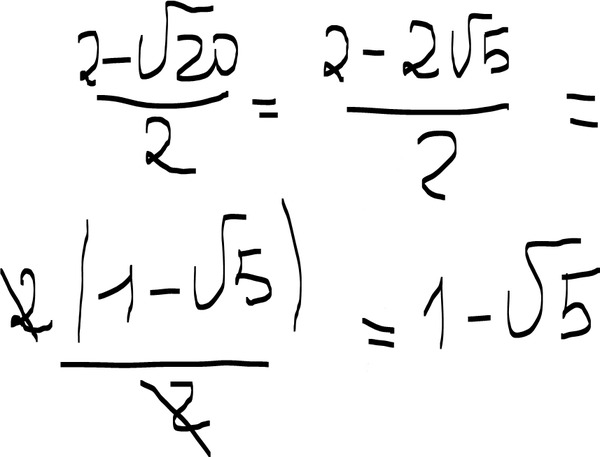
Разберемся по традиции на примере.
Разбор примера
Исключить иррациональность из знаменателя:
| 1 |
| 2 − √3 |
На что нужно умножить знаменатель «2 − √3», чтобы убрать из него корень?
Теперь недостаточно умножить знаменатель на «√3», ведь в таком случае все равно остается квадратный корень.
(2 − √3) · √3 = 2√3 − √3 · √3 =
= 2√3 − 3
Мы видим, что корень никуда не исчез. Нужно искать другие варианты решения.
Вспомним формулу сокращенного умножения «Разность квадратов».
a2 − b2 = (a + b)(a − b)
Формула разности квадратов также работает в обратную сторону.
(a + b)(a − b) = a2 − b2
Представим, что «2 − √3» — это часть формулы.
(a + b)(a − b) = a2 − b2
(? + ?)(2 − √3) = ?2 − ?2
Логично предположить, что в формуле «a» — это
«2», «b» —
«√3». Подставим вместо знаков «?» числа.
Подставим вместо знаков «?» числа.
(a + b)(a − b) = a2 − b2
(2 + √3)(2 − √3) = 22 − √32 = 4 − 3 = 1
То есть, чтобы избавиться от иррациональности в дроби
требуется умножить знаменатель
«2 − √3»
на
«2 + √3»
и через формулу «Разность квадратов» убрать квадратные корни.
Не забываем, что по основному свойству дроби мы обязаны также умножить числитель на «2 + √3».
| 1 |
| 2 − √3 |
| 1 · (2 + √3) |
| (2 − √3) · (2 + √3) |
=
| 2 + √3 |
| 22 − √32 |
| 2 + √3 |
| 4 − 3 |
| 2 + √3 |
| 1 |
Примеры
освобождения от иррациональности в знаменателеРазбор примера
Исключить иррациональность из знаменателя:
2)
=
| 2 · √6 |
| √6 · √6 |
=
| 2 · √6 |
| √6 · 6 |
=
| 2· √6 |
| √62 |
=
=
| 2 · √6 |
| 6 |
Рассмотрим пример, когда в знаменателе несколько корней.
7)
| √5 − √7 |
| √5 + √7 |
=
Используем формулу сокращенного умножения «Разность квадратов».
a2 − b2 = (a + b)(a − b)
(a + b)(a − b) = a2 − b2
Умножим и числитель, и знаменатель на «(√5 − √7)», чтобы использовать формулу сокращённого умножения в знаменателе и избавиться от корней.
| √5 − √7 |
| √5 + √7 |
=
| (√5 − √7)(√5 − √7) |
| (√5 + √7)(√5 − √7) |
=
=
| (√5 − √7)2 |
| √52 − √72 |
= …
Используем в числителе (наверху в дроби) формулу «Квадрат разности».
(a − b)2 = a2 − 2ab + b2
| √5 − √7 |
| √5 + √7 |
=
| (√5 − √7)(√5 − √7) |
| (√5 + √7)(√5 − √7) |
=
=
| (√5 − √7)2 |
| √52 − √72 |
=
=
| (√5)2 − 2 · √5 · √7 + (√7)2 |
| √52 − √72 |
=
=
| 5 − 2√5 · 7 + 7 |
| 5 − 7 |
=
| 12 − 2√35 |
| − 2 |
=
=
−
| 12 − 2√35 |
| 2 |
= …
Вынесем общий множитель в числителе и
сократим дробь.
| √5 − √7 |
| √5 + √7 |
=
| (√5 − √7)(√5 − √7) |
| (√5 + √7)(√5 − √7) |
=
=
| (√5 − √7)2 |
| √52 − √72 |
=
=
| (√5)2 − 2 · √5 · √7 + (√7)2 |
| √52 − √72 |
=
=
| 5 − 2√5 · 7 + 7 |
| 5 − 7 |
=
| 12 − 2√35 |
| − 2 |
=
= −
| 12 − 2√35 |
| 2 |
= −
| 2 · (6 − √35) |
| 2 |
=
=
−
| 2 (6 − √35) |
| 2 |
=
=
−
(6 − √35)
= −6 + √35
Разбор примера
Освободитесь от иррациональности в знаменателе дроби:
5)
| 1 |
| √a − √b |
Используем формулу сокращенного умножения «Разность квадратов».
a2
− b2 = (a + b)(a − b)(a + b)(a − b) = a2 − b2
Умножим и числитель, и знаменатель на «(√a + √b)», чтобы использовать формулу «Разность квадратов» в знаменателе и освободиться от корней.
5)
| 1 |
| √a − √b |
=
| 1 · (√a + √b) |
| (√a − √b) · (√a + √b) |
=
=
| √a + √b |
| (√a)2 − (√b)2 |
=
| √a + √b |
| a − b |
Квадратный корень Квадратный корень из произведения Квадратный корень из дроби Как избавиться от иррациональности Как вынести из-под корня Как внести под знак корня
Вопрос гуманитария. Почему на ноль делить нельзя, а извлекать квадратный корень из отрицательного числа можно? В чем принципиальная разница?
ПопулярноеСообщества
Стать экспертом Кью
МатематикаНаукаМатематические действия
Vladimir Domashko
405Z»>13 декабря 2016 ·
166,1 K
ОтветитьУточнитьКонстантин Щербаков
Математика
125
Интересуюсь математикой, физикой, техникой · 4 авг 2020
Ноль это по определению такое число, что при умножении его на что угодно, получается ноль. То есть, если вы сможете поделить 1 / 0 и получится x, то 0 * x = 1, то есть нарушается определение нуля. У отрицательных чисел такого нет. Можно построить систему с корнями из отрицательных чисел, в которой не нарушаются никакие определения и аксиомы. Вот и вся разница. Конечно, надо упомянуть, что можно работать с пределами и делить на бесконечно малые, но не на ноль.
P.S. Существует т.н. «колесо», в котором можно делить на ноль, но там приходится убирать такие тождества, как 0x=0, x — x = 0, x/x = 1. И вообще там обычное деление заменяется на унарный оператор /x, значит это уже другое «деление»
Комментировать ответ…Комментировать…
Dmitriy Razorenov
11,1 K
Старший научный сотрудник ИНЭОС РАН, химик, музыкант и радиолюбитель · 15 дек 2016
На ноль делить нельзя, но можно делить на очень маленькие числа близкие к нулю и получать очень большие числа. Технически, если речь идет о каких-то измеряемых параметрах, мы никогда не имеем дело с настоящим нулем и поэтому мы можем рассуждать с помощью пределов, и предел 1/x при x→0 будет ∞.
А насчет мнимых чисел, если вы гуманитарий, то вы наверно знаете английский… Читать далее
Технически, если речь идет о каких-то измеряемых параметрах, мы никогда не имеем дело с настоящим нулем и поэтому мы можем рассуждать с помощью пределов, и предел 1/x при x→0 будет ∞.
А насчет мнимых чисел, если вы гуманитарий, то вы наверно знаете английский… Читать далее
Комментировать ответ…Комментировать…
Алексей Васин
-2
Программист, Python3, С/C++, Datasence · 6 нояб 2020
В школьной программе ноль объясняется, как пустота, а что-то разделить на пустоту мы не можем. При более глубоком изучении математики. Ноль это неопределенное поведение, так же как и бесконечность. Именно бесконечность на ноль мы можем разделить. ∞/0=∞*1/0= ∞*∞ = ∞. Теперь про корень из отрицательного числа. Например квадратный корень это интерпретация квадрата. √4… Читать далее
Комментировать ответ…Комментировать…
Maxim Vyalkov
Математика
1,1 K
Интересующие темы: история математики, история христианства, библеистика. 2 = -1 . Эта запись корректна, через квадратный корень — нет, в том случае, если нотация радикала передаёт арифметический корень (для алгебраического корня запись допустима)… Читать далее
2 = -1 . Эта запись корректна, через квадратный корень — нет, в том случае, если нотация радикала передаёт арифметический корень (для алгебраического корня запись допустима)… Читать далее
Комментировать ответ…Комментировать…
konstantin kazartsev
Программирование
102
программист · 19 мая 2021
Есть примитивный ответ (и я его дам ниже). Но к каждому ответу можно задать вопрос «почему на самом деле» это так. И этого никто не знает. Во-первых: если мы пробуем построить хорошую математическую структуру, в которой делить на 0 можно и получим «число», то придём к противоречию: пусть (1) 1 / 0 = Inf (1) если Inf это число, то обратное к (1) уравнение даёт нам Inf *… Читать далее
Комментировать ответ…Комментировать…
Первый
Ксандер Кейдж
27 окт 2020
Не то что бы это нельзя\запрещено, просто бессмысленно. Вот смотрите, делим 1\1=1, 1\0.5=2, 1\0,00001=100000. Тенденция думаю ясна, чем меньше число в знаменателе, то есть чем ближе оно к нулю, тем больше результат деления. Если учесть что знаменатель может быть бесконечно маленьким числом и если быть последовательным то, никогда не сможет быть 0, ведь мы всегда может… Читать далее
Вот смотрите, делим 1\1=1, 1\0.5=2, 1\0,00001=100000. Тенденция думаю ясна, чем меньше число в знаменателе, то есть чем ближе оно к нулю, тем больше результат деления. Если учесть что знаменатель может быть бесконечно маленьким числом и если быть последовательным то, никогда не сможет быть 0, ведь мы всегда может… Читать далее
Комментировать ответ…Комментировать…
Первый
Карина Болычева
-6
Меня зовут Карина.Я задаю вопросы и хотелось бы сразу получать ответы · 12 окт 2020
когда перед корнем стоит знак минус то это число имеет смысл.но когда минус стоит внутри корня то не имеет смысла .например если 24 под корнем то это выражение имеет смысл а если минус 24 под корнем то нет
Алексей Васин
6 ноября 2020
Для минус 24 под корнем были придуманы комплексные числа
Комментировать ответ…Комментировать…
Достоверно
Pavel Vilenkin
224
Программирование, машинное обучение, анализ данных, статистика, теория вероятностей · 15 дек 2016
Обе эти операции сводятся к решению определенных уравнений. Деление на ноль — суть решение уравнения x*0=1. Извлечение корня — уравнение x*x=-1
Так вот, из внутренних свойств нуля (как нейтрального элемента относительно сложения) можно вывести, что любое число при умножении на ноль равно нулю. Эта теорема делает первое уравнение принципиально неразрешимым. Уточню, что… Читать далее
Деление на ноль — суть решение уравнения x*0=1. Извлечение корня — уравнение x*x=-1
Так вот, из внутренних свойств нуля (как нейтрального элемента относительно сложения) можно вывести, что любое число при умножении на ноль равно нулю. Эта теорема делает первое уравнение принципиально неразрешимым. Уточню, что… Читать далее
2 эксперта согласны
23,6 K
Антон Коцюбинский
22 февраля 2021
Вы из школы наверное знаете что есть аксиомы. Аксиома — это правило для какой-то системы, которое определяется и… Читать дальше
Комментировать ответ…Комментировать…
Виктор Брыксин
92
пенсионер · 27 мар 2021
Вам уже ответили а этот вопрос, правда, без особых подробностей. Что касается деления на ноль, то это сводится к не возможным попыткам решать уравнение x*0=1 (формально x=1/0). Правильно было замечено, что левая часть уравнения по свойствам нуля всегда ноль, а правая всегда единица, и верного равенства ни при каком x быть не может. Правило простое: на ноль делить… Читать далее
Правило простое: на ноль делить… Читать далее
Комментировать ответ…Комментировать…
. · 20 нояб 2020
Потому что деление вводится в рамках арифметики, где присутствуют только конечные рациональные числа, результат деления на 0 выходит за рамки понятий, которыми оперирует эта дисциплина. Квадратный корень вводится в рамках более сложной дисциплины: алгебры. Результат извлечения корня из минус единицы, т.е. мнимая единица, как и комплексное число уже попадает под понятия… Читать далее
Комментировать ответ…Комментировать…
Как упростить квадратный корень. Разложение квадратного корня на множители: внесение и вынесение
Для вычисления квадратного корня без калькулятора существует несколько методов.
Как найти корень из числа – 1 способ
- Один из методов заключается в разложении на множители того числа, которое находится под корнем. Эти составляющие в результате умножения образуют подкоренное значение.
 Точность полученного результата зависит от числа под корнем.
Точность полученного результата зависит от числа под корнем. - Например, если взять число 1 600 и начать раскладывать его на множители, то рассуждение построится таким образом: данное число кратно 100, значит, его можно разделить на 25; так как корень из числа 25 извлекается, то число является квадратным и подходит для дальнейших вычислений; при делении получаем еще одно число – 64. Это число тоже квадратное, поэтому корень извлекается хорошо; после этих расчетов под корнем можно записать число 1600 в виде произведения 25 и 64.
- Одно из правил извлечения корня гласит, что корень из произведения множителей равен числу, которое получается при умножении корней из каждого множителя. Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
- Но бывает так, что число, находящееся под корнем, не раскладывается на два множителя, из которых извлекается целый корень.
 Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается. - В таком случае можно высчитать только приблизительное значение. Поэтому нужно извлечь корень из множителя, который является квадратным числом. Это значение затем умножить на корень из второго числа, которое не является квадратным членом уравнения.
- Выглядит это таким образом, например, возьмем число 320. Его можно разложить на 64 и 5. Из 64 целый корень извлечь можно, а из 5 – нет. Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
- Если есть необходимость, то можно найти приблизительное значение этого результата, вычислив
√5 ≈ 2,236, следовательно, √320 = 8 * 2,236 = 17,88 ≈ 18. - Также число под корнем можно разложить на несколько простых множителей, а одинаковые можно вынести из-под него. Пример: √75 = √(5*5*3) = 5√3 ≈ 8,66 ≈ 9.
Как найти корень из числа – 2 способ
- Другой способ заключается в делении в столбик.
 Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень. - В этом случае квадратное число пишем сверху и отнимаем его в левой части, а извлеченный корень снизу.
- Теперь второе значение нужно удвоить и записать снизу справа в виде: число_х_=. Пропуски необходимо заполнить числом, которое будет меньше или равно необходимому значению слева – все как в обычном делении.
- При необходимости этот результат снова вычитается слева. Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.
На первый взгляд может показаться, что процедура разложения квадратного корня на множители сложная и неприступная. Но это не так. В этой статье мы расскажем вам, как подступиться к квадратному корню и множителям, а также легко и просто разложить квадратный корень, воспользовавшись двумя проверенными методами.
Yandex.RTB R-A-339285-1
Разложение корня на множители
Для начала определим цель процедуры разложения квадратного корня на множители. Цель — упростить квадратный корень и записать его в удобном для вычислений виде.
Цель — упростить квадратный корень и записать его в удобном для вычислений виде.
Определение 1
Разложение квадратного корня на множители — нахождение двух или нескольких чисел, которые, при условии перемножения их друг на друга, дадут число равное исходному. Например: 4×4 = 16.
Если вы найдете множители, то сможете легко упростить выражение с квадратным корнем или вовсе его упразднить:
Пример 1
Разделите подкоренное число на 2, если оно четное.
Подкоренное число всегда следует делить на простые числа, поскольку любое значение простого числа можно разложить на простые множители. Если у вас нечетное число, то попробуйте разделить его на 3. Не делится на 3? Делите дальше на 5, 7, 9 и т.д.
Запишите выражение в виде корня произведения двух чисел.
Например, можно упростить таким способом 98: = 98 ÷ 2 = 49 . Из этого следует, что 2 × 49 = 98 , поэтому можно переписать задачу следующим образом: 98 = (2 × 49) .
Продолжите раскладывать числа, пока под корнем не останется произведение двух одинаковых чисел и других чисел.
Возьмем наш пример (2 × 49) :
Поскольку 2 уже и так максимально упрощено, необходимо упростить 49 . Ищем простое число, на которое можно разделить 49 . Очевидно, что ни 3 , ни 5 не подходят. Остается 7: 49 ÷ 7 = 7 , поэтому 7 × 7 = 49 .
Записываем пример в следующем виде: (2 × 49) = (2 × 7 × 7) .
Упростите выражение с квадратным корнем.
Поскольку в скобках у нас произведение 2 и двух одинаковых чисел (7) , то мы можем вынести за знак корня число 7 .
Пример 2
(2 × 7 × 7) = (2) × (7 × 7) = (2) × 7 = 7 (2) .
В тот момент, когда под корнем оказалось два одинаковых числа, останавливайтесь с разложением чисел на множители. Конечно, если вы использовали все возможности по максимуму.
Запомните: существуют корни, которые можно упрощать многократно.
В таком случае, числа, которые мы выносим из-под корня, и числа, которые стоят перед ним, перемножаются.
Пример 3
180 = (2 × 90) 180 = (2 × 2 × 45) 180 = 2 45
но 45 можно разложить на множители и еще раз упростить корень.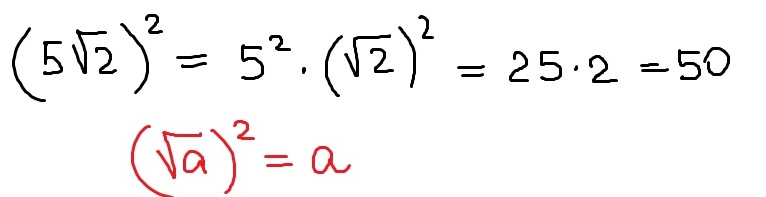
180 = 2 (3 × 15) 180 = 2 (3 × 3 × 5) 180 = 2 × 3 5 180 = 6 5
Когда невозможно получить два одинаковых числа под знаком корня, это значит, что упростить такой корень нельзя.
Если после разложения подкоренного выражения на произведение простых чисел, у вас не получилось получить два одинаковых числа, то такой корень упростить нельзя.
Пример 4
70 = 35 × 2 , поэтому 70 = (35 × 2)
35 = 7 × 5 , поэтому (35 × 2) = (7 × 5 × 2)
Как видим, все три множителя — простые числа, которые нельзя разложить на множители. Среди них нет одинаковых чисел, поэтому не представляется возможным вынести целое число из-под корня. Упростить 70 нельзя.
Полный квадрат
Запомните несколько квадратов простых чисел.
Квадрат числа получается, если умножить его на самого себя, т.е. при возведении в квадрат. Если вы запомните десяток квадратов простых чисел, то это очень упростить вам жизнь в дальнейшем упрощении корней.
Пример 5
1 2 = 1 2 2 = 4 3 2 = 9 4 2 = 16 5 2 = 25 6 2 = 36 7 2 = 49 8 2 = 64 9 2 = 81 10 2 = 100
В случае если под знаком корня квадратного корня находится полный квадрат, то стоит убрать знак корня и записать квадратный корень данного полного квадрата.
Сложно? Нет:
Пример 6
1 = 1 4 = 2 9 = 3 16 = 4 25 = 5 36 = 6 49 = 7 64 = 8 81 = 9 100 = 10
Попробуйте разложить число под знаком корня на произведения полного квадрата и другого числа.
Если вы видите, что подкоренное выражение раскладывается на произведение полного квадрата и какого-либо числа, то, запомнив несколько примеров, вы существенно сэкономите время и нервы:
Пример 7
50 = (25 × 2) = 5 2 . Если подкоренное число оканчивается на 25, 50 или 75, вы всегда можете разложить его на произведение 25 и какого-то числа.
1700 = (100 × 17) = 10 17 . Если подкоренное число оканчивается на 00, вы всегда можете разложить его на произведение 100 и какого-то числа.
72 = (9 × 8) = 3 8 . Если сумма цифр подкоренного числа равна 9, вы всегда можете разложить его на произведение 9 и какого-то числа.
Попробуйте разложить подкоренное число на произведение нескольких полных квадратов: вынесите их из-под знака корня и перемножьте.
Пример 8
72 = (9 × 8) 72 = (9 × 4 × 2) 72 = 9 × 4 × 2 72 = 3 × 2 × 2 72 = 6 2
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Формулы корней.
 Свойства квадратных корней.
Свойства квадратных корней.Внимание!
К этой теме имеются дополнительные
материалы в Особом разделе 555.
Для тех, кто сильно «не очень…»
И для тех, кто «очень даже…»)
В предыдущем уроке мы разобрались, что такое квадратный корень . Пришла пора разобраться, какие существуют формулы для корней , каковы свойства корней , и что со всем этим можно делать.
Формулы корней, свойства корней и правила действий с корнями — это, по сути, одно и то же. Формул для квадратных корней на удивление немного. Что, безусловно, радует! Вернее, понаписать всяких формул можно много, но для практической и уверенной работы с корнями достаточно всего трёх. Все остальное из этих трёх проистекает. Хотя и в трех формулах корней многие плутают, да…
Начнём с самой простой. Вот она:
Если Вам нравится этот сайт…Кстати, у меня есть ещё парочка интересных сайтов для Вас.)
Можно потренироваться в решении примеров и узнать свой уровень. Тестирование с мгновенной проверкой. Учимся — с интересом!)
Тестирование с мгновенной проверкой. Учимся — с интересом!)
можно познакомиться с функциями и производными.
Пришло время разобрать способы извлечения корней . Они базируются на свойствах корней , в частности, на равенстве , которое справедливо для любого неотрицательного числа b.
Ниже мы по очереди рассмотрим основные способы извлечения корней.
Начнем с самого простого случая – с извлечения корней из натуральных чисел с использованием таблицы квадратов, таблицы кубов и т.п.
Если же таблицы квадратов, кубов и т.п. нет под руками, то логично воспользоваться способом извлечения корня, который подразумевает разложение подкоренного числа на простые множители.
Отдельно стоит остановиться на , что возможно для корней с нечетными показателями.
Наконец, рассмотрим способ, позволяющий последовательно находить разряды значения корня.
Приступим.
Использование таблицы квадратов, таблицы кубов и т.д.
В самых простых случаях извлекать корни позволяют таблицы квадратов, кубов и т. д. Что же представляют собой эти таблицы?
д. Что же представляют собой эти таблицы?
Таблица квадратов целых чисел от 0 до 99 включительно (она показана ниже) состоит из двух зон. Первая зона таблицы располагается на сером фоне, она с помощью выбора определенной строки и определенного столбца позволяет составить число от 0 до 99 . Для примера выберем строку 8 десятков и столбец 3 единицы, этим мы зафиксировали число 83 . Вторая зона занимает оставшуюся часть таблицы. Каждая ее ячейка находится на пересечении определенной строки и определенного столбца, и содержит квадрат соответствующего числа от 0 до 99 . На пересечении выбранной нами строки 8 десятков и столбца 3 единицы находится ячейка с числом 6 889 , которое является квадратом числа 83 .
Таблицы кубов, таблицы четвертых степеней чисел от 0 до 99 и так далее аналогичны таблице квадратов, только они во второй зоне содержат кубы, четвертые степени и т.д. соответствующих чисел.
Таблицы квадратов, кубов, четвертых степеней и т.д. позволяют извлекать квадратные корни, кубические корни, корни четвертой степени и т. д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
д. соответственно из чисел, находящихся в этих таблицах. Объясним принцип их применения при извлечении корней.
Допустим, нам нужно извлечь корень n -ой степени из числа a , при этом число a содержится в таблице n -ых степеней. По этой таблице находим число b такое, что a=b n . Тогда , следовательно, число b будет искомым корнем n -ой степени.
В качестве примера покажем, как с помощью таблицы кубов извлекается кубический корень из 19 683 . Находим число 19 683 в таблице кубов, из нее находим, что это число является кубом числа 27 , следовательно, .
Понятно, что таблицы n -ых степеней очень удобны при извлечении корней. Однако их частенько не оказывается под руками, а их составление требует определенного времени. Более того, часто приходится извлекать корни из чисел, которые не содержатся в соответствующих таблицах. В этих случаях приходится прибегать к другим методам извлечения корней.
Разложение подкоренного числа на простые множители
Достаточно удобным способом, позволяющим провести извлечение корня из натурального числа (если конечно корень извлекается), является разложение подкоренного числа на простые множители.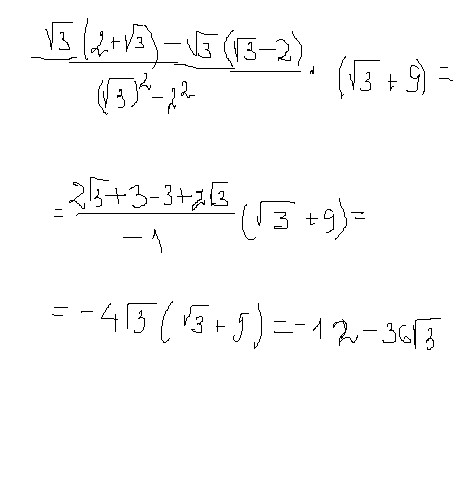 Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Его суть заключается в следующем : после его достаточно легко представить в виде степени с нужным показателем, что позволяет получить значение корня. Поясним этот момент.
Пусть из натурального числа a извлекается корень n -ой степени, и его значение равно b . В этом случае верно равенство a=b n . Число b как любое натуральное число можно представить в виде произведения всех своих простых множителей p 1 , p 2 , …, p m в виде p 1 ·p 2 ·…·p m , а подкоренное число a в этом случае представляется как (p 1 ·p 2 ·…·p m) n . Так как разложение числа на простые множители единственно, то разложение подкоренного числа a на простые множители будет иметь вид (p 1 ·p 2 ·…·p m) n , что дает возможность вычислить значение корня как .
Заметим, что если разложение на простые множители подкоренного числа a не может быть представлено в виде (p 1 ·p 2 ·…·p m) n , то корень n -ой степени из такого числа a нацело не извлекается.
Разберемся с этим при решении примеров.
Пример.
Извлеките квадратный корень из 144 .
Решение.
Если обратиться к таблице квадратов, данной в предыдущем пункте, то хорошо видно, что 144=12 2 , откуда понятно, что квадратный корень из 144 равен 12 .
Но в свете данного пункта нас интересует, как извлекается корень с помощью разложения подкоренного числа 144 на простые множители. Разберем этот способ решения.
Разложим 144
на простые множители:
То есть, 144=2·2·2·2·3·3 . На основании с полученным разложением можно провести такие преобразования: 144=2·2·2·2·3·3=(2·2) 2 ·3 2 =(2·2·3) 2 =12 2 . Следовательно, .
Используя свойства степени и свойства корней , решение можно было оформить и немного иначе: .
Ответ:
Для закрепления материала рассмотрим решения еще двух примеров.
Пример.
Вычислите значение корня .
Решение.
Разложение на простые множители подкоренного числа 243 имеет вид 243=3 5 . Таким образом, .
Ответ:
Пример.
Является ли значение корня целым числом?
Решение.
Чтобы ответить на этот вопрос, разложим подкоренное число на простые множители и посмотрим, представимо ли оно в виде куба целого числа.
Имеем 285 768=2 3 ·3 6 ·7 2 . Полученное разложение не представляется в виде куба целого числа, так как степень простого множителя 7 не кратна трем. Следовательно, кубический корень из числа 285 768 не извлекается нацело.
Ответ:
Нет.
Извлечение корней из дробных чисел
Пришло время разобраться, как извлекается корень из дробного числа. Пусть дробное подкоренное число записано в виде как p/q . Согласно свойству корня из частного справедливо следующее равенство . Из этого равенства следует правило извлечения корня из дроби : корень из дроби равен частному от деления корня из числителя на корень из знаменателя.
Разберем пример извлечения корня из дроби.
Пример.
Чему равен квадратный корень из обыкновенной дроби 25/169 .
Решение.
По таблице квадратов находим, что квадратный корень из числителя исходной дроби равен 5
, а квадратный корень из знаменателя равен 13
. Тогда . На этом извлечение корня из обыкновенной дроби 25/169
завершено.
Тогда . На этом извлечение корня из обыкновенной дроби 25/169
завершено.
Ответ:
Корень из десятичной дроби или смешанного числа извлекается после замены подкоренных чисел обыкновенными дробями.
Пример.
Извлеките кубический корень из десятичной дроби 474,552 .
Решение.
Представим исходную десятичную дробь в виде обыкновенной дроби: 474,552=474552/1000 . Тогда . Осталось извлечь кубические корни, находящиеся в числителе и знаменателе полученной дроби. Так как 474 552=2·2·2·3·3·3·13·13·13= (2·3·13) 3 =78 3 и 1 000=10 3 , то и . Осталось лишь завершить вычисления .
Ответ:
.
Извлечение корня из отрицательного числа
Отдельно стоит остановиться на извлечении корней из отрицательных чисел. При изучении корней мы сказали, что когда показатель корня является нечетным числом, то под знаком корня может находиться отрицательное число. Таким записям мы придали следующий смысл: для отрицательного числа −a
и нечетного показателя корня 2·n−1
справедливо . Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Это равенство дает правило извлечения корней нечетной степени из отрицательных чисел : чтобы извлечь корень из отрицательного числа нужно извлечь корень из противоположного ему положительного числа, и перед полученным результатом поставить знак минус.
Рассмотрим решение примера.
Пример.
Найдите значение корня .
Решение.
Преобразуем исходное выражение, чтобы под знаком корня оказалось положительное число: . Теперь смешанное число заменим обыкновенной дробью: . Применяем правило извлечения корня из обыкновенной дроби: . Осталось вычислить корни в числителе и знаменателе полученной дроби: .
Приведем краткую запись решения: .
Ответ:
.
Порязрядное нахождение значения корня
В общем случае под корнем находится число, которое при помощи разобранных выше приемов не удается представить в виде n
-ой степени какого-либо числа. Но при этом бывает необходимость знать значение данного корня, хотя бы с точностью до некоторого знака. В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
В этом случае для извлечения корня можно воспользоваться алгоритмом, который позволяет последовательно получить достаточное количество значений разрядов искомого числа.
На первом шаге данного алгоритма нужно выяснить, каков старший разряд значения корня. Для этого последовательно возводятся в степень n числа 0, 10, 100, … до того момента, когда будет получено число, превосходящее подкоренное число. Тогда число, которое мы возводили в степень n на предыдущем этапе, укажет соответствующий старший разряд.
Для примера рассмотрим этот шаг алгоритма при извлечении квадратного корня из пяти. Берем числа 0, 10, 100, … и возводим их в квадрат, пока не получим число, превосходящее 5 . Имеем 0 2 =05 , значит, старшим разрядом будет разряд единиц. Значение этого разряда, а также более младших, будет найдено на следующих шагах алгоритма извлечения корня.
Все следующие шаги алгоритма имеют целью последовательное уточнение значения корня за счет того, что находятся значения следующих разрядов искомого значения корня, начиная со старшего и продвигаясь к младшим. К примеру, значение корня на первом шаге получается 2
, на втором – 2,2
, на третьем – 2,23
, и так далее 2,236067977…
. Опишем, как происходит нахождение значений разрядов.
К примеру, значение корня на первом шаге получается 2
, на втором – 2,2
, на третьем – 2,23
, и так далее 2,236067977…
. Опишем, как происходит нахождение значений разрядов.
Нахождение разрядов проводится за счет перебора их возможных значений 0, 1, 2, …, 9 . При этом параллельно вычисляются n -ые степени соответствующих чисел, и они сравниваются с подкоренным числом. Если на каком-то этапе значение степени превзойдет подкоренное число, то значение разряда, соответствующее предыдущему значению, считается найденным, и производится переход к следующему шагу алгоритма извлечения корня, если же этого не происходит, то значение этого разряда равно 9 .
Поясним эти моменты все на том же примере извлечения квадратного корня из пяти.
Сначала находим значение разряда единиц. Будем перебирать значения 0, 1, 2, …, 9
, вычисляя соответственно 0 2 , 1 2 , …, 9 2
до того момента, пока не получим значение, большее подкоренного числа 5
. Все эти вычисления удобно представлять в виде таблицы:
Так значение разряда единиц равно 2
(так как 2 2 5
). Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Переходим к нахождению значения разряда десятых. При этом будем возводить в квадрат числа 2,0, 2,1, 2,2, …, 2,9
, сравнивая полученные значения с подкоренным числом 5
:
Так как 2,2 2 5
, то значение разряда десятых равно 2
. Можно переходить к нахождению значения разряда сотых:
Так найдено следующее значение корня из пяти, оно равно 2,23 . И так можно продолжать дальше находить значения : 2,236, 2,2360, 2,23606, 2,236067, … .
Для закрепления материала разберем извлечение корня с точностью до сотых при помощи рассмотренного алгоритма.
Сначала определяем старший разряд. Для этого возводим в куб числа 0, 10, 100 и т.д. пока не получим число, превосходящее 2 151,186 . Имеем 0 3 =02 151,186 , таким образом, старшим разрядом является разряд десятков.
Определим его значение.
Так как 10 3 2 151,186
, то значение разряда десятков равно 1
. Переходим к единицам.
Таким образом, значение разряда единиц равно 2
. Переходим к десятым.
Так как даже 12,9 3
меньше подкоренного числа 2 151,186
, то значение разряда десятых равно 9
.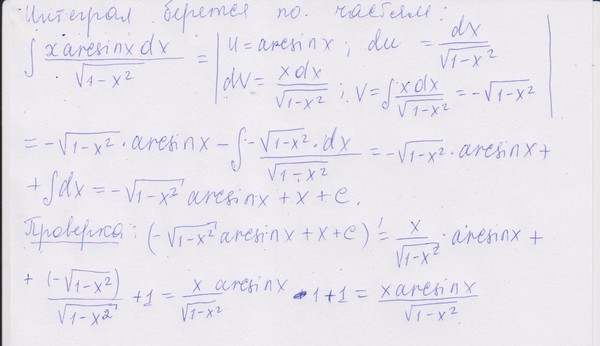 Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
Осталось выполнить последний шаг алгоритма, он нам даст значение корня с требуемой точностью.
На этом этапе найдено значение корня с точностью до сотых: .
В заключение этой статьи хочется сказать, что существует масса других способов извлечения корней. Но для большинства задач достаточно тех, которые мы изучили выше.
Список литературы.
- Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Алгебра: учебник для 8 кл. общеобразовательных учреждений.
- Колмогоров А.Н., Абрамов А.М., Дудницын Ю.П. и др. Алгебра и начала анализа: Учебник для 10 — 11 классов общеобразовательных учреждений.
- Гусев В.А., Мордкович А.Г. Математика (пособие для поступающих в техникумы).
Как извлечь корень из 7. Как высчитать квадратный корень из числа без помощи калькулятора
Для вычисления квадратного корня без калькулятора существует несколько методов.
Как найти корень из числа – 1 способ
- Один из методов заключается в разложении на множители того числа, которое находится под корнем.
 Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем.
Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем. - Например, если взять число 1 600 и начать раскладывать его на множители, то рассуждение построится таким образом: данное число кратно 100, значит, его можно разделить на 25; так как корень из числа 25 извлекается, то число является квадратным и подходит для дальнейших вычислений; при делении получаем еще одно число – 64. Это число тоже квадратное, поэтому корень извлекается хорошо; после этих расчетов под корнем можно записать число 1600 в виде произведения 25 и 64.
- Одно из правил извлечения корня гласит, что корень из произведения множителей равен числу, которое получается при умножении корней из каждого множителя. Это значит, что: √(25*64) = √25 * √64. Если из 25 и 64 извлечь корни, то получим такое выражение: 5 * 8 = 40. То есть, квадратный корень из числа 1600 равен 40.
- Но бывает так, что число, находящееся под корнем, не раскладывается на два множителя, из которых извлекается целый корень.
 Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается. - В таком случае можно высчитать только приблизительное значение. Поэтому нужно извлечь корень из множителя, который является квадратным числом. Это значение затем умножить на корень из второго числа, которое не является квадратным членом уравнения.
- Выглядит это таким образом, например, возьмем число 320. Его можно разложить на 64 и 5. Из 64 целый корень извлечь можно, а из 5 – нет. Поэтому, выражение будет выглядеть так: √320 = √(64*5) = √64*√5 = 8√5.
- Если есть необходимость, то можно найти приблизительное значение этого результата, вычислив
√5 ≈ 2,236, следовательно, √320 = 8 * 2,236 = 17,88 ≈ 18. - Также число под корнем можно разложить на несколько простых множителей, а одинаковые можно вынести из-под него. Пример: √75 = √(5*5*3) = 5√3 ≈ 8,66 ≈ 9.
Как найти корень из числа – 2 способ
- Другой способ заключается в делении в столбик.
 Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень. - В этом случае квадратное число пишем сверху и отнимаем его в левой части, а извлеченный корень снизу.
- Теперь второе значение нужно удвоить и записать снизу справа в виде: число_х_=. Пропуски необходимо заполнить числом, которое будет меньше или равно необходимому значению слева – все как в обычном делении.
- При необходимости этот результат снова вычитается слева. Такие вычисления продолжаются до тех пор, пока результат не будет достигнут. Нули также можно добавлять, пока не получите нужное количество знаков после запятой.
Рассмотрим этот алгоритм на примере. Найдем
1-й шаг. Число под корнем разбиваем на грани по две цифры (справа налево):
2-й шаг. Извлекаем квадратный корень из первой грани, т. е. из числа 65, получаем число 8. Под первой гранью пишем квадрат числа 8 и вычитаем. К остатку приписываем вторую грань (59):
(число 159 — первый остаток).
3-й шаг. Удваиваем найденный корень и пишем результат слева:
4-й шаг. Отделяем в остатке (159) одну цифру справа, слева получаем число десятков (оно равно 15). Затем делим 15 на удвоенную первую цифру корня, т. е. на 16, так как 15 на 16 не делится, то в частном получается нуль, который записываем как вторую цифру корня. Итак, в частном получили число 80, которое опять удваиваем, и сносим следующую грань
(число 15 901 — второй остаток).
5-й шаг. Отделяем во втором остатке одну цифру справа и полученное число 1590 делим на 160. Результат (цифру 9) записываем как третью цифру корня и приписываем к числу 160. Полученное число 1609 умножаем на 9 и находим следующий остаток (1420):
В дальнейшем действия выполняются в той последовательности, которая указана в алгоритме (корень можно извлекать с нужной степенью точности).
Замечание. Если подкоренное выражение — десятичная — дробь, то ее целую часть разбивают на грани по две цифры справа налево, дробную часть — по две цифры слева направо и извлекают корень по указанному алгоритму.
ДИДАКТИЧЕСКИЙ МАТЕРИАЛ
1. Извлеките квадратный корень из числа: а) 32; б) 32,45; в) 249,5; г) 0,9511.
Извлечение корня – обратная операция возведению степени. То есть Извлекая корень из числа Х, получим число, которое в квадрате даст то самое число Х.
Извлечение корня довольно-таки несложная операция. Таблица квадратов сможет облегчить работу по извлечению. Потому что, наизусть помнить все квадраты и корни невозможно, а числа могут встретиться большие.
Извлечение корня из числа
Извлечение квадратного корня из числа – просто. Тем более что это можно делать не сразу, а постепенно. Например, возьмем выражение √256. Изначально, незнающему человеку сложно дать ответ сразу. Тогда будем делать по шагам. Сначала разделим на просто число 4, из которого вынесем за корень выделенный квадрат.
Изобразим: √(644), тогда это будет равносильно 2√64. А как известно, по таблице умножения 64=8 8. Ответ будет 2*8=16.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная арифметика», чтобы научиться быстро и правильно складывать, вычитать, умножать, делить, возводить числа в квадрат и даже извлекать корни.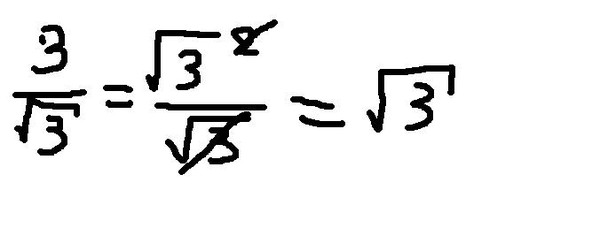 За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
За 30 дней вы научитесь использовать легкие приемы для упрощения арифметических операций. В каждом уроке новые приемы, понятные примеры и полезные задания.
Извлечение комплексного корня
Корень квадратный не может вычисляться из отрицательных чисел, потому что любое число в квадрате – положительное число!
Комплексное число – число i, которое в квадрате равно -1. То есть i2=-1.
В математике существует число, которое получается при извлечении корня из числа -1.
То есть есть возможность вычислить корень из отрицательного числа, но это уже относится к высшей математике, не школьной.
Рассмотрим пример такого извлечения корня: √(-49)=7*√(-1)=7i.
Калькулятор корня онлайн
С помощью нашего калькулятора, Вы сможете посчитать извлечение числа из квадратного корня:
Преобразование выражений, содержащих операцию извлечения корня
Суть преобразования подкоренных выражений в разложении подкоренного числа на более простые, из которых можно извлечь корень. Такие как 4, 9, 25 и так далее.
Такие как 4, 9, 25 и так далее.
Приведем пример, √625. Поделим подкоренное выражение на число 5. Получим √(1255), повторим операцию √(25 25), но мы знаем, что 25 это 52. А значит ответом будет 5*5=25.
Но бывают числа, у которых корень таким методом не вычислить и просто нужно знать ответ или иметь таблицу квадратов под рукой.
√289=√(17*17)=17
Итог
Мы рассмотрели лишь верхушку айсберга, чтобы понять математику лучше — записывайтесь на наш курс: Ускоряем устный счет — НЕ ментальная арифметика.
Из курса вы не просто узнаете десятки приемов для упрощенного и быстрого умножения, сложения, умножения, деления, высчитывания процентов, но и отработаете их в специальных заданиях и развивающих играх! Устный счет тоже требует много внимания и концентрации, которые активно тренируются при решении интересных задач.
Столбиком наджней, а когда нужно больше пятнадцати знаков, то компьютеры и телефоны с калькуляторами чаще всего отдыхают. Осталось проверить, займт ли описание методики 4-5 тыс. знаков.
Берм любое число, от запятой отсчитываем пары цифр вправо и влево
Например, 1234567890,098765432100
Пара цифр — это как бы двузначное число. Корень из двузначного — однозначное. Подбираем однозначное, квадрат которого меньше первой пары цифр.
 В нашем случае это 3.
В нашем случае это 3.Как при делении столбиком, под первой парой выписываем этот квадрат и из первой пары вычитаем. Результат сносим под подчерк. 12 — 9 = 3. Добавляем к этой разнице вторую пару цифр (будет 334). Слева от числа берм удвоенное значение той части результата, которую уже нашли о дополняем цифрой (у нас 2*6=6), такой, чтобы при умножении на не полученное число не превосходило число со второй парой цифр. Получаем, что найденная цифра — пятрка. Снова находим разность (9), сносим следующую пару цифр получая 956, снова выписываем удвоенную часть результата (70), снова е дополняем нужной цифрой и так далее до упора. Или до нужной точности вычислений.
Во-первых для того что бы вычислить квадратный корень надо хорошо знать таблицу умножения. Самые простые примеры — это 25 (5 на 5 = 25) и так далее. Если же брать числа посложнее, то можно использовать данную таблицу, где по горизонтали единицы, а по вертикале десятки.
Есть хороший способ как найти корень из числа без помощи калькуляторов.
 Для этого вам понадобится линейка и циркуль. Суть в том, что вы находите на линейке значение, которое у вас под корнем. Например, ставите отметку возле 9. Ваша задача — поделить это число на равное количество отрезков, то есть на два линии по 4,5 см, а на ровный отрезок. Несложно догадаться, что в итоге получится 3 отрезка по 3 сантиметра.
Для этого вам понадобится линейка и циркуль. Суть в том, что вы находите на линейке значение, которое у вас под корнем. Например, ставите отметку возле 9. Ваша задача — поделить это число на равное количество отрезков, то есть на два линии по 4,5 см, а на ровный отрезок. Несложно догадаться, что в итоге получится 3 отрезка по 3 сантиметра.Способ нелегкий и для больших чисел не подойдет, но зато считается без калькулятора.
без помощи калькулятора способу извлечения корня квадратного учили в советские времена в школе в 8-м классе.
Для этого надо разбить многозначное число справа налево на грани по 2 цифры :
Первая цифра корня это целый корень из левой грани, в данном случае, 5.
Вычитаем 5 в квадрате из 31, 31-25=6 и к шестерке приписываем следующую грань, имеем 678.
Следующая цифра х подбирается к удвоенной пятерке так, чтобы
10х*х было максимально большим, но меньшим чем 678.
х=6, поскольку 106*6 = 636,
теперь вычисляем 678 — 636 = 42 и добавляем следующую грань 92, имеем 4292.

Снова ищем максимальный х, такой что 112х*х lt; 4292.
Ответ: корень равен 563
Так можно продолжать сколько требуется.
В некоторых случаях можно попытаться разложить подкоренное число на два или несколько квадратных множителей.
Также полезно запомнить таблицу (или хотя бы какую-то ее часть) — квадраты натуральных чисел от 10 до 99.
Предлагаю изобретенный мною вариант извлечения квадратного корня в столбик. Он отличается от общеизвестного, исключением подбора чисел. Но как выяснил позже, данный метод уже существовал за много лет до моего рождения. Описал его в своей книге Всеобщая арифметика или книга об арифметических синтезе и анализе великий Исаак Ньютон. Так что здесь излагаю свое видение и обоснование алгоритма метода по Ньютону. Запоминать алгоритм не стоит. Можно просто при необходимости пользоваться схемой на рисунке в качестве наглядного пособия.
С помощью таблиц можно не вычислить, а найти, корни квадратные толь из чисел которые есть в таблицах.
 Проще всего вычислять корни не только квадратные, но и других степеней, методом последовательных приближений. Например вычислим корень квадратный из 10739, заменяем три последние цифры нулями и извлечем корень из 10000 получим 100 с недостатком, поэтому берем число 102 возводим его в квадрат, получаем 10404, что тоже меньше заданного, берем 103*103=10609 опять с недостатком, берем 103,5*103,5=10712,25, берем ещ больше 103,6*103,6=10732, берем 103,7*103,7=10753,69, что уже с избытком. Можно принять корень из 10739 примерно равны 103,6. Более точно 10739=103,629… . . Аналогично вычисляем корень кубический сначала из 10000 получаем примерно 25*25*25=15625, что с избытком, берем 22*22*22=10,648, берем чуть больше 22,06*22,06*22,06=10735, что очень близко к заданному.
Проще всего вычислять корни не только квадратные, но и других степеней, методом последовательных приближений. Например вычислим корень квадратный из 10739, заменяем три последние цифры нулями и извлечем корень из 10000 получим 100 с недостатком, поэтому берем число 102 возводим его в квадрат, получаем 10404, что тоже меньше заданного, берем 103*103=10609 опять с недостатком, берем 103,5*103,5=10712,25, берем ещ больше 103,6*103,6=10732, берем 103,7*103,7=10753,69, что уже с избытком. Можно принять корень из 10739 примерно равны 103,6. Более точно 10739=103,629… . . Аналогично вычисляем корень кубический сначала из 10000 получаем примерно 25*25*25=15625, что с избытком, берем 22*22*22=10,648, берем чуть больше 22,06*22,06*22,06=10735, что очень близко к заданному.
Вычисление (или извлечение) квадратного корня можно производить несколькими способами, но все они не сказать что уж очень просты. Проще, конечно, прибегнуть к помощи калькулятора. Но если такой возможности нет (или вы хотите понять суть квадратного корня), могу посоветовать пойти следующим путем, его алгоритм таков:
Проще, конечно, прибегнуть к помощи калькулятора. Но если такой возможности нет (или вы хотите понять суть квадратного корня), могу посоветовать пойти следующим путем, его алгоритм таков:
Если на такие длительные вычисления у вас нет сил, желания или терпения, можно прибегнуть к помощи грубого подбора, его плюс в том, что он невероятно быстрый и при должной смекалке точный. Пример:
Когда я учился в школе (в начале 60-х годов), нас учили извлекать квадратный корень из любого числа. Методика несложная, внешне похожа на quot;деление столбикомquot;, но излагать е здесь, это потребуется полчаса времени и 4-5 тысяч знаков текста. Но зачем это Вам? У вас есть телефон или иной гаджет, в нм есть калькулятор. Калькулятор есть и в любом компьютере. Лично я предпочитаю производить такого рода вычисления в Excel.
Зачастую в школе требуется находить квадратные корни разных чисел. Но если вот мы привыкли пользоваться постоянно для этого калькулятором, то на экзаменах такой возможности не будет, поэтому нужно учиться искать корень без помощи калькулятора.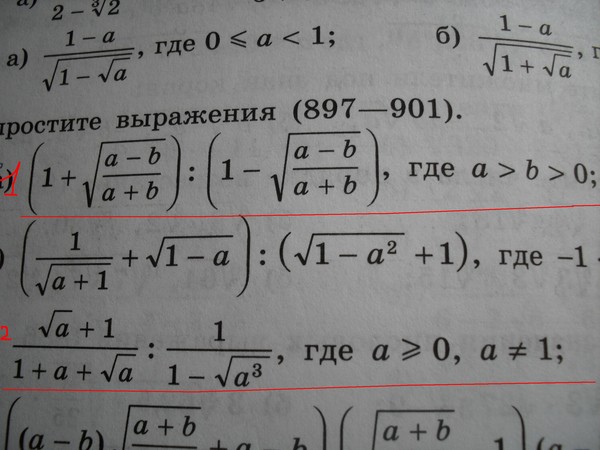 А сделать-то это в принципе возможно.
А сделать-то это в принципе возможно.
Алгоритм таков:
Смотрите сначала на последнюю цифру вашего числа:
Например,
Теперь требуется определить примерно значение для корня из самой левой группы
В случае когда число имеет больше двух групп, то находить корень надо так:
А вот следующая циферка должна быть именно наибольшей, подобрать е надо так:
Теперь надо образовать новое число А посредством добавления к остатку, который был получен выше, следующую группу.
В наших примерах:
Деление на 0,5. Деление натурального числа на дробь.
- org/ListItem»>Альфашкола
- Статьи
- Как легко разделить на 0,5
Как быстрее разделить число на \(0,5\)? Для этого тебе даже не понадобится калькулятор, ведь есть специальное правило. \(0,5-\) это десятичная дробь приведём её к виду обыкновенной дроби:
То есть деление на \(0,5\) можно заменить делению на \(\frac{1}{2}\), а при делении на \(\frac{1}{2}\) , дробь меняет местами числитель и знаменатель . Число обратное \(\frac{1}{2}-\) это \(2.\) То есть для того чтобы разделить на \(0,5\) надо умножить на \(2.\) Легко не так ли?
Пример 1. Разделите \(9\) на \(0,5\).
Решение: \(9:0,5=9:\frac{1}{2}=9*2=18\)
Ответ: \(18\).
Пример 2. Разделите \(25\) на \(0,5\).
Решение: \(25:0,5=25:\frac{1}{2}=25*2=50\)
Ответ: \(50\).
Пример 3. Разделите \(125\) на \(0,5\).
Решение: \(125:0,5=125:\frac{1}{2}=125*2=250\)
Ответ: \(250\).
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Гуля Исмоиловна Ибадулаева
Репетитор по математике
Стаж (лет)
Образование:
Таджикский государственный педагогический университет имени С. Айни
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-8 классов. Моя профессия – это радость общения с детьми. Это моменты счастья, когда я вижу удивление детей от того, что у них получается выполнить задание.
Считаю, что нужно подбирать индивидуальную методику для каждого ученика (обратить внимание на характер, настроение).
Мне очень хочется научить детей грамотно писать и говорить. Уверена, что после наших уроков у детей останутся только хорошие впечатления.
Не ленитесь, уделяйте больше времени образованию, упорно совершенствуйте свои способности!
Моя профессия – это радость общения с детьми. Это моменты счастья, когда я вижу удивление детей от того, что у них получается выполнить задание.
Считаю, что нужно подбирать индивидуальную методику для каждого ученика (обратить внимание на характер, настроение).
Мне очень хочется научить детей грамотно писать и говорить. Уверена, что после наших уроков у детей останутся только хорошие впечатления.
Не ленитесь, уделяйте больше времени образованию, упорно совершенствуйте свои способности!
Анжела Валентиновна Самсонова
Репетитор по математике
Стаж (лет)
Образование:
Костанайской педагогический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Информатика: 5-11 класс (объяснение материала, корректировка знаний по темам, решение логических задач), подготовка к контрольным работам, ОГЭ, ЕГЭ. Математика: 3-6 класс (объяснение материала, корректировка знаний по темам, решение логических задач), подготовка к контрольным работам, ВПР.
Математика: 3-6 класс (объяснение материала, корректировка знаний по темам, решение логических задач), подготовка к контрольным работам, ВПР.
Татьяна Николаевна Бычкова
Репетитор по математике
Стаж (лет)
Образование:
Таганрогский государственный педагогический институт
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Преподаватель математики в 5-9 классах, подготовка к ОГЭ и ВПР. Очень люблю свой предмет и делаю всё возможное для того, чтобы мои ученики без проблем решали математические задания любой сложности. Имею большой опыт подготовки к ОГЭ обучающихся с разным уровнем знаний. Объясняю просто и понятно. Вместе с ребятами мы рассуждаем, мыслим, анализируем и достигаем поставленной цели.
Имею большой опыт подготовки к ОГЭ обучающихся с разным уровнем знаний. Объясняю просто и понятно. Вместе с ребятами мы рассуждаем, мыслим, анализируем и достигаем поставленной цели.
Похожие статьи
- Признаки делимости (Часть 1)
- Признак делимости на 14
- Задачи с показательными уравнениями и неравенствами
- Решаем олимпиадные задачи для 4 класса
- Престижные премии по математике
- Гигиена зрения: как сохранить здоровье глаз школьника
- Закаливание детей: мифы и реальность или почему нельзя сходу с головой в прорубь?
- Умные по-разному: 8 видов интеллекта, о которых должен знать каждый родитель
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
3-8Квадратный корень из 1.
 Метод расчета и примеры решений
Метод расчета и примеры решенийКвадратный корень из числа — это значение, полученное путем возведения числа в степень ½. Число, полученное путем умножения числа само на себя, называется квадратным числом. Квадрат и квадратный корень являются обратными математическими операциями. Квадраты и квадратные корни обычно используются при решении квадратных уравнений и многих других математических расчетах. Квадратный корень обозначается символом «√». Квадратный корень из числа «x» записывается как √x или x½. Квадратный корень из любого числа имеет два значения: положительное и отрицательное. Однако величина обоих значений остается неизменной.
(Изображение будет загружено в ближайшее время)
Значение корня 1 = +1 или -1
Важные факты о «1»
1 — самый важный элемент математики. Единица или единица в математике используется для представления одного объекта в числе, измерении или расчете. Число «1» имеет несколько специфических свойств, которые очень важны в математических расчетах. Вот они:
Вот они:
«1» – это число, используемое для обозначения одного идентификатора.
«1» добавляется к любому целому числу, чтобы получить следующее за ним целое число.
При вычитании «1» из любого целого числа получается непосредственно предшествующее ему целое число.
1 — мультипликативная единица любого числа. т. е. при умножении любого числа само на себя само число получается как произведение.
Мультипликативная инверсия любого числа — это значение, полученное при делении «1» на это число.
Когда любое число делится на «1», ответом является само число.
 {2}\]. 9{2} — 4x \times 1 \times -1}}{2 \times 1} = \pm \frac{\sqrt{4}}{2} =\pm \frac{2}{2} \rightarrow (2 )\]
{2}\]. 9{2} — 4x \times 1 \times -1}}{2 \times 1} = \pm \frac{\sqrt{4}}{2} =\pm \frac{2}{2} \rightarrow (2 )\] Сравнивая уравнения (1) и (2), мы можем заключить, что значение под корнем 1 равно либо положительной, либо отрицательной единице.
Значение корня 1 = \[\pm\] 1
Чаще всего значение корня 1 принимается как положительная единица или + 1.
Значение квадратного корня из -1
Значение корня ‘- 1’ теоретически не существует. Это мнимое число, представленное как «i». Корень из -1 обычно используется для представления комплексных чисел, которые включают как действительную, так и мнимую части. Зная квадратный корень из отрицательной единицы, можно найти значение корня любого отрицательного числа. Квадратный корень из -1 — это положительная или отрицательная мнимая единица «i». Однако в большинстве случаев значение корня из -1 принимается за положительную мнимую единицу «i».
Square Root of First 30 Integers:
(Graph will be Uploaded soon)
Number
Square
Number
Square
±1
1
±16
256
±2
4
±17
289
±3
9
±18
324
±4
16
±19
361
±5
25
±20
400
±6
36
±21
441
±7
49
±22
484
±8
64
±23
529
±9
81
±24
576
±10
100
±25
625
±11
121
±26
676
±12
144
±27
729
±13
169
±28
784
±14
196
±29
841
±15
225
± 30
900
Square root 1 to 10:
Values of Square Root 1 to 10 is Listed in the Table Below:
Number
Square Root
Number
Square Root
1
1
6
2.
 4495
44952
1,4142
7
2,6458
3
3
90001.7321
8
2.8284
4
2
9
3
5
2.2361
10
3,1623
Эти значения квадратного корня от 1 до 10 изображены на числовой прямой в виде спирали квадратного корня. 9{2} = — 5 \]
\[p = \sqrt{-5} = \sqrt{-1} . \sqrt{5} \]
\[p = \sqrt{5i}\]
2. Найдите значение \[7\sqrt{1} — 5\sqrt{1} + 2\sqrt{1} \] используя значение root 1.

Решение:
Значение \[\sqrt{1} = 1\]
\[7\sqrt{1} — 5\sqrt{1} + 2\sqrt {1}\]
= 7 (1) — 5 (1) + 2 (1)
= 7 — 5 + 2 = 4.
Интересные факты:
Значение квадратных корней
В прикладной области В математике понятие квадратных корней считается очень важным. Эта концепция закладывает основу алгебры. Учащиеся, которые планируют получить исключительные баллы по предмету, должны подробно изучить эту главу.
Веданту пытается объяснить сложные понятия простыми словами. Это позволяет учащимся глубже погрузиться в логическое обоснование числовых значений. Есть много преимуществ для изучения квадратных корней-
Квадратные корни от простого к сложному имеют значительный вес на экзаменах.
Хитрости, связанные с вычислением квадратных корней, помогают составить ментальную карту для освоения математики.

Это еще больше помогает поднять ваши математические навыки на уровень абстракции.
С помощью квадратных корней учащиеся смогут разумно отточить свои вычислительные навыки.
Квадратные корни не только важны для концепции алгебры, но и играют важную роль в совершенствовании теоретических и статистических методов вашего ребенка.
Помимо математики, квадратные корни помогут вам лучше понять некоторые важные законы физики.
Изучайте квадратные корни легко
Квадратные корни иногда могут показаться сложными. С Веданту студенты могут развеять все свои сомнения, связанные с этим.
Чтобы упростить концепцию, мы предлагаем примеры задач через определенные промежутки времени.
 Вы можете легко овладеть темами, которые считаются наиболее важными при решении алгебры.
Вы можете легко овладеть темами, которые считаются наиболее важными при решении алгебры.Для начала учащиеся должны понять определение понятия, данное экспертами Веданту. Определение сформулировано экспертами и останется с вами в долгосрочной перспективе.
Прежде чем перейти к другим номерам, важно, чтобы вы делали по одному шагу за раз. Начиная с номера 1, Vedantu охватывает все детали, связанные с его значением, методом и примерами задач, чтобы помочь вам получить хорошие оценки по теме.
Vedantu предоставляет подробное табличное представление квадратного корня из первых 30 целых чисел. Он также предоставляет таблицу, состоящую из значений от 1 до 10.
Эксперты Vedantu позаботятся о том, чтобы включить все понятия для конкретной темы, которую вы ищете.
 Наряду с квадратным корнем из +1 он также охватывает квадратный корень из -1. Вопросы, связанные с ним, чаще всего задают на экзаменах. Это поможет вам набрать хорошие баллы по навыкам мышления высокого порядка (HOTS).
Наряду с квадратным корнем из +1 он также охватывает квадратный корень из -1. Вопросы, связанные с ним, чаще всего задают на экзаменах. Это поможет вам набрать хорошие баллы по навыкам мышления высокого порядка (HOTS).Чтобы учащиеся получали удовольствие от процесса обучения, Vedantu содержит «забавные факты»
, относящиеся к теме. Студенты всех классов находят это интригующим и достаточно любопытным, чтобы узнать больше об этой концепции.
Чтобы получить высокие баллы по математике, очень важно постоянно практиковаться в примерах задач. Вместе с решениями эксперты Vedantu сформулировали несколько важных примеров. Это поможет вам понять, какие вопросы ожидаются вне темы.
Воображаемые числа
Мнимое число при возведении в квадрат дает отрицательный результат . 
Попробуйте
Давайте попробуем возвести некоторые числа в квадрат, чтобы посмотреть, сможем ли мы получить отрицательный результат:
- 2 × 2 = 4
- (−2) × (−2) = 4 (поскольку отрицательное число, умноженное на отрицательное, дает положительное) 909:20
- 0 × 0 = 0
- 0,1 × 0,1 = 0,01
Не повезло! Всегда положительный или ноль.
Кажется, мы не можем умножить число само на себя, чтобы получить отрицательный ответ…
… но представьте себе , что есть такое число (назовем его i для воображаемого), которое могло бы сделать это:
я × я = −1
Было бы это полезно, и что мы могли бы сделать с ним?
Итак, извлекая квадратный корень из обеих частей, мы получаем:
Это означает, что i является ответом на квадратный корень из −1. 
Что на самом деле очень полезно потому что…
… просто принимая , что i существует, мы можем решать задачи
, для которых нужен квадратный корень из отрицательного числа.Попробуем:
Пример: Чему равен квадратный корень из −9?
√(−9)= √(9 × −1)
= √(9) × √(−1)
= 3 × √(−1)
= 3 i
(см. как 91 для упрощения квадратных корней)Эй! это было интересно! Квадратный корень из −9 — это просто квадратный корень из +9, умноженный на i .
Всего:
√(−x) = i √x
До тех пор, пока мы сохраняем эту маленькую букву «i», чтобы напомнить нам, что нам все еще нужно
умножить на √−1, мы можем безопасно продолжить наше решение!Использование
iПример: Что такое (5
i ) 2 ?(5 i ) 2 = 5 i × 5 i
= 5× 5× i × i
= 25 × i 2
= 25 × −1
= −25
Интересно! Мы использовали мнимое число (5 i ) и получили действительное решение (-25).

Мнимые числа могут помочь нам решить некоторые уравнения:
Пример: Решите x
2 + 1 = 0Используя действительные числа, решения нет, но теперь мы можем решить его !
Вычесть 1 из обеих сторон:
x 2 = −1
Извлечь квадратный корень из обеих сторон:
x = ± √(−1)
x = ± i
Ответ: x = −i или +i
Проверить:
- (−i) 2 + 1 = ( (−i) + 1 = +i 2 + 1 = −1 + 1 = 0
- (+i) 2 +1 = (+i)(+i) +1 = +i 2 +1 = −1 + 1 = 0
Воображаемый номер блока
Квадратный корень из минус одного √(−1) — это «единица» мнимого числа, эквивалентная 1 для реальных чисел.
В математике символ √(−1) равен i для мнимого.
Можете ли вы извлечь квадратный корень из −1?
А вот в электронике используют j (потому что «i» уже означает ток, а следующая за i буква — j).
Ну и можно!
Примеры мнимых чисел
и 12.38i −i 3i/4 0.01i πi Мнимые числа не являются
«Мнимыми»Воображаемые числа когда-то считались невозможными , поэтому их называли «воображаемыми» (чтобы высмеять их).
Но затем люди исследовали их глубже и обнаружили, что они на самом деле были полезными и важными , потому что они заполнили пробел в математике… но «воображаемое» название прижилось.
Так же и появилось название «Реальные числа» (реальные не мнимые).
Воображаемые числа полезны
Комплексные числа
Мнимые числа становятся наиболее полезными в сочетании с действительными числами для получения комплексных чисел, таких как 3+5i или 6−4i
.Анализатор спектра
Те классные дисплеи, которые вы видите, когда играет музыка? Да, комплексные числа используются для их вычисления! Использование чего-то под названием «Преобразование Фурье».

На самом деле, используя комплексные числа, со звуком можно делать много умных вещей, например, фильтровать звуки, слышать шепот в толпе и так далее.
Это часть предмета «Обработка сигналов».
Электричество
AC (переменный ток) Электричество меняется между положительным и отрицательным синусоидальным сигналом.
Когда мы объединяем два переменного тока, они могут не совпадать должным образом, и это может быть очень тяжело разобраться в новом токе.
Но использование комплексных чисел значительно упрощает вычисления.
И результат может иметь «мнимый» ток, но он все равно может причинить вам боль!
Набор Мандельброта
Красивое множество Мандельброта (часть его изображена здесь) основано на комплексных числах.
Квадратное уравнение
Квадратное уравнение, которое имеет множество применений,
.
может давать результаты, включающие мнимые числа
Также в науке, квантовой механике и теории относительности используются комплексные числа.
Интересное имущество
Единичное мнимое число i обладает интересным свойством. Он «циклически» проходит через 4 разных значения каждый раз, когда мы умножаем:
1 × i = i я × я = −1 −1 × i = − i − i × i = 1 Вернуться к 1 снова! Итак, у нас есть это:
i = √−1 i 2 = −1 i 3 = −√−1 i 4 = +1 i 5 = √−1 i 6 = −1 .  ..и т. д.
..и т. д.Пример Что такое i
10 ?i 10 = i 4 × i 4 × i 2
= 1 × 1 × −1
= −1
И это приводит нас к другой теме, сложной плоскости:
Заключение
Единичное мнимое число i равно квадратному корню из минус 1
Воображаемые числа не являются «воображаемыми», они действительно существуют и имеют множество применений.
SHORT-ROOT 1 имеет решающее значение для деления клеток и развития трахейных элементов в корнях риса
. 2021 март; 105(5):1179-1191.
doi: 10.1111/tpj.15095. Epub 2020 18 декабря.
Яди Син 1 2 , Нань Ван 1 , Тяньцюань Чжан 1 г.
 , Цюли Чжан г.
1 , Дэн Ду 1 , Синьлун Чен 1 , Синь Лу 1 , Инъин Чжан 1 , Маоди Чжу 1 , Минминг Лю 1 , Сяньчунь Сан 1 , Юньфэн Ли 1 , Инхуа Лин 1 , Гуанхуа Хэ 1
, Цюли Чжан г.
1 , Дэн Ду 1 , Синьлун Чен 1 , Синь Лу 1 , Инъин Чжан 1 , Маоди Чжу 1 , Минминг Лю 1 , Сяньчунь Сан 1 , Юньфэн Ли 1 , Инхуа Лин 1 , Гуанхуа Хэ 1 Принадлежности
- 1 Научно-исследовательский институт риса, Ключевая лаборатория применения и контроля безопасности генетически модифицированных культур, Академия сельскохозяйственных наук, Юго-Западный университет, Чунцин, 400715, Китай.
- 2 Сельскохозяйственный колледж, Университет Чжэнчжоу, Чжэнчжоу, 450001, Китай.

- PMID: 33231904
- DOI: 10.1111/tpj.15095
Бесплатная статья
Яди Син и др. Плант Дж. 2021 9 марта0907
Бесплатная статья
. 2021 март; 105(5):1179-1191.
doi: 10.1111/tpj.15095. Epub 2020 18 декабря.
Авторы
Яди Син 1 2 , Нань Ван 1 , Тяньцюань Чжан 1 г.
 , Цюли Чжан г.
1 , Дэн Ду 1 , Синьлун Чен 1 , Синь Лу 1 , Инъин Чжан 1 , Маоди Чжу 1 , Минминг Лю 1 , Сяньчунь Сан 1 , Юньфэн Ли 1 , Инхуа Лин 1 , Гуанхуа Хэ 1
, Цюли Чжан г.
1 , Дэн Ду 1 , Синьлун Чен 1 , Синь Лу 1 , Инъин Чжан 1 , Маоди Чжу 1 , Минминг Лю 1 , Сяньчунь Сан 1 , Юньфэн Ли 1 , Инхуа Лин 1 , Гуанхуа Хэ 1 Принадлежности
- 1 Научно-исследовательский институт риса, Ключевая лаборатория применения и контроля безопасности генетически модифицированных культур, Академия сельскохозяйственных наук, Юго-Западный университет, Чунцин, 400715, Китай.
- 2 Сельскохозяйственный колледж, Университет Чжэнчжоу, Чжэнчжоу, 450001, Китай.
 909:20
909:20
- PMID: 33231904
- DOI: 10.1111/tpj.15095
Абстрактный
Экзоциста является ключевым фактором транспорта везикул и участвует в клеточной секреции, росте клеток, делении клеток и других цитологических процессах у эукариот. EXO70 является ключевой субъединицей экзоцисты. Мы получили ген SHORT-ROOT 1 (SR1) путем клонирования на основе карты и генетической комплементации. SR1 представляет собой консервативный белок с доменом EXO70 в растениях. Мутация SR1 повлияла на весь процесс развития корней: образование более коротких корешков, придаточных корней и боковых корней, а также демонстрация аномального развития ксилемы, что привело к карликовости и снижению водного потенциала и содержания влаги.
 SR1 был в значительной степени экспрессирован в корнях, но только в развивающихся корневых меристемах и трахеарных элементах. Короткие корни мутанта sr1 были вызваны наличием меньшего количества клеток меристемы. Паттерны экспрессии гистона h5 in situ подтвердили нарушение пролиферации клеток во время развития корня. Дисплазия элементов трахеи была обусловлена выраженным уменьшением внутренних диаметров и расстояний между перфорациями соседних элементов трахеи. Мембранный транспорт мутантов sr1 был блокирован, влияя на деление клеток в апикальной области корня и развитие элементов трахеи корня. Изучение SR1 углубит наше понимание функции генов EXO70 в Oryza sativa (рис) и направит будущие исследования молекулярных механизмов, участвующих в развитии корней растений.
SR1 был в значительной степени экспрессирован в корнях, но только в развивающихся корневых меристемах и трахеарных элементах. Короткие корни мутанта sr1 были вызваны наличием меньшего количества клеток меристемы. Паттерны экспрессии гистона h5 in situ подтвердили нарушение пролиферации клеток во время развития корня. Дисплазия элементов трахеи была обусловлена выраженным уменьшением внутренних диаметров и расстояний между перфорациями соседних элементов трахеи. Мембранный транспорт мутантов sr1 был блокирован, влияя на деление клеток в апикальной области корня и развитие элементов трахеи корня. Изучение SR1 углубит наше понимание функции генов EXO70 в Oryza sativa (рис) и направит будущие исследования молекулярных механизмов, участвующих в развитии корней растений.Ключевые слова: Ориза сатива; СР1; ЕХО70; экзоциста; мембранный транспорт; развитие корня.
© 2020 Общество экспериментальной биологии и John Wiley & Sons Ltd.

Похожие статьи
Гомеодоменовый белок риса WOX11 рекрутирует комплекс гистон-ацетилтрансферазы для установления программ клеточной пролиферации меристемы корня короны.
Чжоу С., Цзян В., Лун Ф., Ченг С., Ян В., Чжао И., Чжоу Д.С. Чжоу С. и др. Растительная клетка. 2017 май; 29(5):1088-1104. doi: 10.1105/tpc.16.00908. Эпаб 2017 9 мая. Растительная клетка. 2017. PMID: 28487409 Бесплатная статья ЧВК.
OsSPL3, белок SBP-домена, регулирует развитие корня короны у риса.
Шао И, Чжоу ХЗ, У И, Чжан Х, Линь Дж, Цзян Х, Хэ Ц, Чжу Дж, Ли И, Ю Х, Мао С. Шао Ю и др. Растительная клетка. 201931 июня (6): 1257-1275. doi: 10.1105/tpc.19.00038. Epub 2019 2 апр. Растительная клетка. 2019. PMID: 30940685 Бесплатная статья ЧВК.

Rice ROOT ARCHITECTURE ASSOCIATED1 связывает субъединицу протеасомы RPT4 и расщепляется D-боксом и зависимым от протеасом образом.
Хань И, Цао Х, Цзян Дж, Сюй И, Ду Дж, Ван Х, Юань М, Ван З, Сюй Зи, Чонг К. Хан Ю и др. Завод Физиол. 2008 г., октябрь; 148 (2): 843–55. дои: 10.1104/стр.108.125294. Epub 2008, 13 августа. Завод Физиол. 2008. PMID: 18701670 Бесплатная статья ЧВК.
Молекулярный механизм инициации корончатого корня и различные механизмы между корончатым корнем и корешком риса.
Китоми Ю., Китано Х., Инукай Ю. Китоми Ю. и др. Поведение сигналов растений. 2011 Сентябрь;6(9):1270-8. doi: 10.4161/psb.6.9.16787. Поведение сигналов растений. 2011. PMID: 21847023 Бесплатная статья ЧВК.

Аль-индуцируемый ген экспансина, OsEXPA10, участвует в удлинении клеток корня риса.
Че Дж., Ямаджи Н., Шен Р.Ф., Ма Дж.Ф. Че Дж. и др. Плант Дж. Октябрь 2016 г.; 88 (1): 132–142. doi: 10.1111/tpj.13237. Epub 2016 22 сентября. Завод Дж. 2016. PMID: 27302336
Посмотреть все похожие статьи
Цитируется
Локус основного количественного признака общей длины корней пшеницы связан с распределением осадков.
Чен Х., Вэй Дж., Тянь Р., Цзэн З., Тан Х., Лю И., Сюй Ц., Дэн М., Цзян Ц., Чен Г., Лю И., Ли В., Ци П., Цзян И., Цзян И., Тан Л., Вэй И, Чжэн И, Лань С, Ма Дж. Чен Х и др. Фронт завод науч. 2022 24 августа; 13:995183. doi: 10.3389/fpls.2022.995183. Электронная коллекция 2022.
 Фронт завод науч. 2022.
PMID: 360
Фронт завод науч. 2022.
PMID: 360Бесплатная статья ЧВК.
GhMYC2 активирует ген цитохрома P450 CYP71BE79, чтобы регулировать биосинтез госсипола в хлопке.
Хань X, Син Ю, Чжу Ю, Луо Л, Лю Л, Чжай Ю, Ван В, Шао Р, Рен М, Ли Ф, Ян Ц. Хан Х и др. Планта. 2022 23 августа; 256 (3): 63. doi: 10.1007/s00425-022-03974-4. Планта. 2022. PMID: 35995890
Необходимость устойчивости риса к цикадкам для OsEXO70h4, регулирующего экскрецию SAMSL и отложение лигнина в клеточных стенках.
У Д., Го Дж., Чжан Ц., Ши С., Гуань В., Чжоу С., Чен Р., Ду Б., Чжу Л., Хе Г. Ву Д и др. Новый Фитол. 2022 май; 234(3):1031-1046. doi: 10.1111/nph.18012. Epub 2022 26 февраля. Новый Фитол. 2022. PMID: 35119102 Бесплатная статья ЧВК.

Идентификация и всесторонний структурно-функциональный анализ семейства генов EXO70 в хлопке.
Zhu YQ, Qiu L, Liu LL, Luo L, Han XP, Zhai YH, Wang WJ, Ren MZ, Xing YD. Чжу Ю.К. и др. Гены (Базель). 2021 9 окт;12(10):1594. doi: 10.3390/genes12101594. Гены (Базель). 2021. PMID: 34680988 Бесплатная статья ЧВК.
использованная литература
- Бимстер, Г.Т., Фиорани, Ф. и Инзе, Д. (2003) Клеточный цикл: ключ к контролю роста растений? Тенденции Растениевод. 8, 154-158.
- Бин, В. и Вей, Г. (2015) Взгляд на экзоцисту. Дж. Клеточные науки. 128, 2957-2964.
- Бонифачино, Дж.
 С. и Глик, Б.С. (2004) Механизмы почкования и слияния пузырьков. Ячейка, 116, 153-166.
С. и Глик, Б.С. (2004) Механизмы почкования и слияния пузырьков. Ячейка, 116, 153-166.
- Бонифачино, Дж.
- Boyd, C., Hughes, T., Pypaert, M. and Novick, P. (2004) Везикулы переносят большинство экзоцистных субъединиц в экзоцитарные сайты, отмеченные оставшимися двумя субъединицами, Sec3p и Exo70p. Дж. Клеточная биология. 167, 889-901.
- Чен С., Тао Л., Зенг Л., Вега-Санчес М.Е., Умемура К. и Ван Г.Л. (2006) Высокоэффективная переходная система протопластов для анализа экспрессии защитных генов и белок-белковых взаимодействий в рисе. . Молекулярный растительный патол. 7, 417-427.
Типы публикаций
термины MeSH
вещества
Функция SQRT и другие способы
В учебнике показано, как извлечь квадратный корень в Excel, а также как вычислить корень N из любого значения.

Возведение числа в квадрат и извлечение квадратного корня — очень распространенные операции в математике. Но как сделать квадратный корень в Excel? Либо с помощью функции SQRT, либо путем возведения числа в степень 1/2. Следующие примеры показывают полную информацию.
- Поиск квадратного корня с помощью функции Excel SQRT
- Получение квадратного корня с помощью формулы экспоненты
- Найдите квадратный корень с помощью функции POWER
- Как вычислить корень N в Excel
Как извлечь квадратный корень в Excel с помощью функции SQRT
Самый простой способ извлечь квадратный корень в Excel — использовать специально разработанную для этого функцию: ячейка, содержащая число, для которого вы хотите найти квадратный корень.
Например, чтобы получить квадратный корень из 225, используйте следующую формулу:
=КОРЕНЬ(225)Чтобы вычислить квадратный корень из числа в A2, используйте эту формулу:
=КОРЕНЬ(A2)Если число отрицательное, как в строках 7 и 8 на снимке экрана выше, функция Excel SQRT возвращает #ЧИСЛО! ошибка.
 ), который находится над цифрой 6 на большинстве клавиатур. 9(1/2), «»)
), который находится над цифрой 6 на большинстве клавиатур. 9(1/2), «») Почему показатель степени 1/2 равен квадратному корню?
Для начала, что мы называем квадратным корнем? Это не что иное, как число, которое при умножении само на себя дает исходное число. Например, квадратный корень из 25 равен 5, потому что 5×5=25. Это кристально ясно, не так ли?
Ну, умножение 25 1/2 само по себе также дает 25:
25 ½ x 25 ½ = 25 (½+½) = 25 (1) (1) 1653 = 25
сказал другой способ:
√25 x √25 = 25
и:
25 ½ x 25 ½ = 25
. SO, 25 . ½ 9153.
Как найти квадратный корень с помощью функции СТЕПЕНЬ
Функция СТЕПЕНЬ — это просто еще один способ выполнить приведенное выше вычисление, т. е. возвести число в степень 1/2.
Синтаксис функции СТЕПЕНЬ Excel следующий:
СТЕПЕНЬ(число, мощность)
=Как вы можете легко догадаться, чтобы получить квадратный корень, вы добавляете 1/2 к аргументу в степени .
 Например:
Например:=СТЕПЕНЬ(A2, 1/2)Как показано на снимке экрана ниже, все три формулы квадратного корня дают одинаковый результат, какую из них использовать, зависит от ваших личных предпочтений:
Как для вычисления корня N в Excel
Формула экспоненты, обсуждавшаяся несколькими абзацами выше, не ограничивается нахождением только квадратного корня. Те же методы можно использовать для получения любого n 90,25.
Обратите внимание, что дробных показателей степени всегда должны быть заключены в скобки , чтобы обеспечить правильный порядок операций в вашей формуле квадратного корня — сначала деление (косая черта (/) является оператором деления в Excel), а затем повышение к власти.
Те же результаты могут быть получены при использовании функции СТЕПЕНЬ:
- Кубический корень из 64: =СТЕПЕНЬ(64, 1/3)
- 4 -й корень из 16: =POWER(16, 1/4) 9(1/B$2)
На снимке экрана ниже показаны результаты, округленные до 2 знаков после запятой:
Совет.
 Чтобы выполнить несколько вычислений с помощью одной формулы, как в приведенном выше примере, исправьте ссылку на столбец и/или строку, где это необходимо, используя знак доллара ($). Дополнительные сведения см. в разделе Зачем использовать знак доллара в формулах Excel.
Чтобы выполнить несколько вычислений с помощью одной формулы, как в приведенном выше примере, исправьте ссылку на столбец и/или строку, где это необходимо, используя знак доллара ($). Дополнительные сведения см. в разделе Зачем использовать знак доллара в формулах Excel.Вот как вы можете извлечь квадратный корень в Excel. Я благодарю вас за чтение и надеюсь увидеть вас в нашем блоге на следующей неделе!
Вас также может заинтересовать
Война в Украине!
Чтобы поддержать Украину и спасти жизни
, пожалуйста, посетите эту страницу. Mathwords: правила извлечения квадратного корня
Mathwords: правила извлечения квадратного корняиндекс: нажмите на букву индекс: предметные области Правила извлечения квадратного корня
Правила алгебры для квадрата перечислены корни ниже.
 Правила квадратного корня являются подмножеством н й
корневые правила и экспонента
правила.
Правила квадратного корня являются подмножеством н й
корневые правила и экспонента
правила.Определения
1. если оба b ≥ 0 и b 2 = a .
2.
Примеры
, потому что 3 2 = 9.
3. Если a ≥ 0, то .
Распределение ( a ≥ 0 и b ≥ 0)
1.
2. ( b ≠ 0)
3.
Примеры
4.

Рационализация знаменателя
( a > 0, b > 0, c > 0)Примеры Осторожно!!
1.
2.
3.
Примеры
См.


 Точность полученного результата зависит от числа под корнем.
Точность полученного результата зависит от числа под корнем.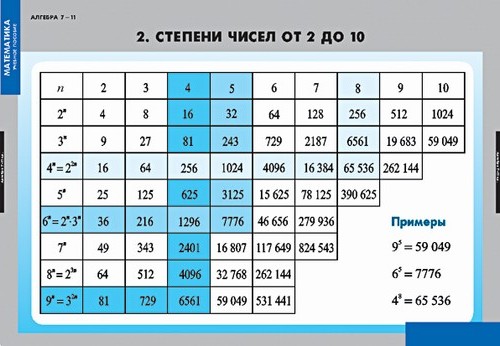 Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается. Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень. Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем.
Эти составляющие в результате умножения образуют подкоренное значение. Точность полученного результата зависит от числа под корнем. Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается.
Обычно такое можно осуществить только для одного из множителей. Поэтому чаще всего найти абсолютно точный ответ в таком уравнении не получается. Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень.
Деление происходит аналогично, но только искать нужно квадратные числа, из которых потом извлекать корень. В нашем случае это 3.
В нашем случае это 3. Для этого вам понадобится линейка и циркуль. Суть в том, что вы находите на линейке значение, которое у вас под корнем. Например, ставите отметку возле 9. Ваша задача — поделить это число на равное количество отрезков, то есть на два линии по 4,5 см, а на ровный отрезок. Несложно догадаться, что в итоге получится 3 отрезка по 3 сантиметра.
Для этого вам понадобится линейка и циркуль. Суть в том, что вы находите на линейке значение, которое у вас под корнем. Например, ставите отметку возле 9. Ваша задача — поделить это число на равное количество отрезков, то есть на два линии по 4,5 см, а на ровный отрезок. Несложно догадаться, что в итоге получится 3 отрезка по 3 сантиметра.
 Проще всего вычислять корни не только квадратные, но и других степеней, методом последовательных приближений. Например вычислим корень квадратный из 10739, заменяем три последние цифры нулями и извлечем корень из 10000 получим 100 с недостатком, поэтому берем число 102 возводим его в квадрат, получаем 10404, что тоже меньше заданного, берем 103*103=10609 опять с недостатком, берем 103,5*103,5=10712,25, берем ещ больше 103,6*103,6=10732, берем 103,7*103,7=10753,69, что уже с избытком. Можно принять корень из 10739 примерно равны 103,6. Более точно 10739=103,629… . . Аналогично вычисляем корень кубический сначала из 10000 получаем примерно 25*25*25=15625, что с избытком, берем 22*22*22=10,648, берем чуть больше 22,06*22,06*22,06=10735, что очень близко к заданному.
Проще всего вычислять корни не только квадратные, но и других степеней, методом последовательных приближений. Например вычислим корень квадратный из 10739, заменяем три последние цифры нулями и извлечем корень из 10000 получим 100 с недостатком, поэтому берем число 102 возводим его в квадрат, получаем 10404, что тоже меньше заданного, берем 103*103=10609 опять с недостатком, берем 103,5*103,5=10712,25, берем ещ больше 103,6*103,6=10732, берем 103,7*103,7=10753,69, что уже с избытком. Можно принять корень из 10739 примерно равны 103,6. Более точно 10739=103,629… . . Аналогично вычисляем корень кубический сначала из 10000 получаем примерно 25*25*25=15625, что с избытком, берем 22*22*22=10,648, берем чуть больше 22,06*22,06*22,06=10735, что очень близко к заданному.