1 в степени 1 равно: Число в первой и нулевой степени

Содержание

§ Отрицательная степень

Прежде чем перейти к изучению определения «отрицательная степень» рекомендуем повторно прочитать урок «Степень» и «Свойства степеней».

Необходимо уверенно понимать, что такое положительная степень числа и уверенно использовать её свойства в решении примеров.

Как возвести число в отрицательную степень

Запомните!

Чтобы возвести число в отрицательную степень нужно:

«перевернуть» число. Записать его в виде дроби с единицой наверху (в числителе) и с исходным числом в степени внизу;
заменить отрицательную степень на положительную;
возвести число в положительную степень.

Общая формула возведения в отрицательную степень выглядит следующим образом.

a⁻ⁿ = ,где a ≠ 0, n ∈ z (n принадлежит целым числам).

Примеры возведения в отрицательную степень.

6⁻² = =
(−3)⁻³ =
1
(−3)³
= = −
0,2⁻² = =

Запомните!

Любое число в нулевой степени — единица.

a⁰ = 1 ,где a ≠ 0

Примеры возведения в нулевую степень.

()⁰ = 1
(−5)⁰ = 1
d⁰ = 1

Как найти

10 в минус 1 степени

В уроке 8 класса «Стандартный вид числа» мы уже сталкивались с записью:

10⁻¹ = 0,1

Теперь, зная определение отрицательной степени, давайте разберемся, почему «10» в минус первой степени равно «0,1».

Возведем «10⁻¹» по правилам отрицательной степени. Перевернем «10» и запишем её в виде дроби «

» и заменим отрицательную степень «−1» на
положительную степень «1».

10⁻¹ =

Возведем «10» в «1» степень. Помним, что любое число в первой степени равно самому числу.

10⁻¹ = =

Теперь по определению десятичной дроби запишем обыкновенную дробь в виде десятичной.

10⁻¹ = = = 0,1

По такому же принципу можно найти «10» в минус второй, третьей и т.д.

10⁻² = 0,01

10⁻³ = 0,001

10⁻⁴ = 0,0001

Запомните!

Для упрощения перевода «10» в минус первую, вторую и т.д степени, нужно запомнить правило:
«Количество нулей после запятой равно положительному значению степени минус один».

Проверим правило выше для «10⁻²».

Т.к. у нас степень «−2», значит, будет всего один ноль (положительное значение степени «2 − 1 = 1». Сразу после запятой ставим один ноль и за ним «1».

10⁻² = 0,01

Рассмотрим «10⁻¹».

Т.к. у нас степень «−1», значит, нулей после запятой не будет (положительное значение степени «1 − 1 = 0». Сразу после запятой ставим «1».

10⁻¹ = 0,1

То же самое правило работает и для «10⁻¹²». При переводе в десятичную дробь будет «12 − 1 = 11 » нулей и «1» в конце.

10⁻¹² = 0,000 000 000 001

Как возвести в отрицательную степень дробь

Запомните!

Чтобы возвести дробь в отрицательную степень нужно:

«перевернуть» дробь;
заменить отрицательную степень на положительную;
возвести дробь в положительную степень.

Пример. Требуется возвести в отрицательную степень дробь.

()⁻³ =

Перевернем дробь «

» и заменим отрицательную степень «−3» на положительную «3».

()⁻³ = ()³

Возведем дробь в положительную степень по правилу возведения дроби в положительную степень. Т.е. возведем и числитель «3», и знаменатель «10» в третью степень.

(

)⁻³ = (

)³ =

1000

Для более грамотного ответа запишем полученный результат в виде десятичной дроби.

(

)⁻³ = (

)³

1000

= 0,027

Как возвести отрицательное число в отрицательную степень

Как и при возведении отрицательного числа в положительную степень, в первую очередь необходимо определить конечный знак результата возведения в степень. Вспомним основные правила еще раз.

Запомните!

Отрицательное число, возведённое в чётную степень, — число положительное.

Отрицательное число, возведённое в нечётную степень, — число отрицательное.

Пример.

(−5) ⁻² =

Перевернем число «−5» и заменим отрицательную степень «−2»
на положительную «2».

(−5) ⁻² = (− ) ² =

Так как степень «2» — четная, значит, результат возведения в степень будет положительный. Поэтому убираем знак минуса при раскрытии скобок.

Далее откроем скобки и возведем во вторую степень и числитель «1»,
и знаменатель «5».

(−5) ⁻² = (− ) ² = =

Как возвести отрицательную дробь в отрицательную степень

Конечный знак результата возведения в степень отрицательной дроби определяется по тем же правилам, что и для целого отрицательного числа.

Запомните!

Отрицательная дробь, возведённая в чётную степень, — дробь положительная.

Отрицательная дробь, возведённая в нечётную степень, — дробь отрицательная.

Разберемся на примере. Задание: возвести отрицательную дробь «(−

)» в «−3» степень.

По правилу возведения дроби в отрицательную степень перевернем дробь и заменим отрицательную степень «−3» на положительную «3».

(− ) ⁻³ = (− ) ³ =

Теперь определим конечный знак результата возведения в «3» степень.

Степень «3» — нечетная, значит, по правилу возведения отрицательного числа в степень дробь останется отрицательной.

Нам остается только раскрыть скобки и возвести в степень и числитель «3», и знаменатель «2» в третью степень.

(− ) ⁻³ = (− ) ³ = − = −

Для окончательного ответа выделим целую часть из дроби.

(− ) ⁻³ = (− ) ³ = − = − = − 3

Рассмотрим другой пример возведения отрицательной дроби в отрицательную степень.

Правило возведения отрицательного числа в степень гласит: если степень четная, значит, результат возведения будет положительным.

(− ) ⁻² = (− ) ² = = = 1

Свойства отрицательной степени

Все свойства степени, которые используются для положительной степени, точно также применяются и для отрицательной степени.

В этом уроке мы не будем повторно подробно разбирать каждое свойство степени, но еще раз приведем основные формулы свойств степени и покажем примеры их использования.

Запомните!

a^m · aⁿ = a^{m + n}

= a^{m − n}

(aⁿ)^m = a^{n · m}

(a · b)ⁿ = aⁿ · bⁿ

Примеры решений заданий с отрицательной

степенью

Разбор примера

Представить в виде степени.

2) a⁶ · b⁶ = (ab)⁶

4) (c⁵)² = c¹⁰

Разбор примера

Записать в виде степени с отрицательным числом.

1) = 4⁻⁵
2) = a⁻⁹

Разбор примера

Вычислить.

3) () ⁻¹² : () ² = () ¹² · () ² = () ¹² · () ² =

13¹²

2¹²

· =

13¹² · 2²

2¹² · 13²

=
=

13¹² · 2²

13² · 2¹²

13¹²

13²

· = 13^{12 − 2} · 2^{2 − 12} = 13¹⁰ · 2⁻¹⁰ = 13¹⁰ · =

13¹⁰ · 1

2¹⁰

=
=

13¹⁰

2¹⁰

= () ¹⁰

Разбор примера

Выполнить действия.

3) (

2x⁶

3y⁻⁴

) ² =

2²x^{6 · 2}

3²y^{−4 · 2}

4x¹²

9y⁻⁸

Почему 0 в степени 0 равно 1? — Обсуждай

М(

Михаил (Москва)

Почему 0 в степени 0 равно 1? степень

1 год

838

Ответы

Elchin Tehmezov

Ноль в степени ноль равно нулю. Я знаком с методами как доказывают обратное. Все они не приемлемы. Вот внизу ролик поставили. Человек вычитывает степень числа которое приближается к нулю. Итог приближается к единице. Но во первых это не ноль, на самом деле это бесконечность. Ибо число приближается к нулю бесконечно. Значит тот число в его степени бесконечно приближается к единице. Но то число никогда не станет нулем, и степень ни когда не станет единицей. По этому такой подход не верный. Если использовать логарифму, получается то же самое. Ничего если возвести на степень ни чего, то ничего не будет происходить. Ибо нет какого либо числа, над чем можно работать. Ноль- на самом деле не число а дополнение, без которого математика просто не работает. А само по себе, это ни что. То есть нуля нет.

1 год

Elchin Tehmezov

А в калькуляторах и т.п. вычисляется один по простой причине. Компьютер не понимает всего этого. 0=0/0. А 0/0 не обязательно единица, это неопределенность, ведь на 0 делить нельзя))) это работает для выражения «а в степени b, где a и b стремятся к 0».

1 год

АВ

Александра Воронцова

Из всего, что нагуглила в интернете, самое доступное для нематематиков обьяснение нашла вот это: «отображение пустого множества в пустое, а оно единственно». Такое литературное выражение хоть как-то (с трудом), но можно переварить.

1 год

ЗБ

Зинаида Бадяева

Глубоко ошибаетесь — в математике -это неопределенность такого типа и доказывается эта единица с помощью известных теорем из теории пределов высшей математики совсем не просто не для математиков !

1 год

АР

Алексей Райтман

Математический парадокс,любое число в степени ноль,равно единице,в случае с нолем,ответ считается неочевидным. Просто математический закидон.

1 год

Михаил Киранов

Значит так решили принять.
А вообще-то это одна из неопределённостей. Но всё зависит от того, что является этим нулём.

1 год

Дмитрий Кузнецов

Известно, что абсолютно любое число в нулевой степени равно единице.Если правильно помню,класс 2-3….

1 год

Rion West

Это чисто символически. В нуле эта функция разрывается и не имеет значения

1 год

Ла

Лариса

Математики всего мира ещё не пришли к единому мнению по этому вопросу.

1 год

ЛЗ

Любовь Золотарева

Любое число или выражение в нулевой степени равно 1(правило).

1 год

Timur Sa

Потому что это не так. значение 0 в степени 0 – не определено

1 год

Александр Патрушев

Ноль — число, а любое число в нулевой степени равно единице.

1 год

Ех

Ехидна

Хороший вопрос…. Ответ думаю только один — «Потому что»))))

1 год

ВМ

В М

Все просто. Это и есть великая тайна сотворения мира. = 0!

1 год

ЛС

Лиана Сафарли

Любое число в нулевой степени равно единице.

1 год

~ Eva Lansca ~

Насколько я помню , число в степени ноль = 1

1 год

ИЕ

Ина Ева

Поавило тако, любое число в нулевой — один

1 год

Ан

Андрей

Потому, что сахар сладкий, но всегда один

1 год

ДА

Дмитрий Арбузов

В мире абсурда всё стремится к единице. 2=9*4=36;$$

Полезные ссылки на теорию

Метод координат. Задача 14 ЕГЭ

Подробный разбор метода координат в стереометрии. Формулы расстояния и угла между скрещивающимися прямыми. Уравнение плоскости. Координаты вектора. Расстояние от точки до плоскости. Угол между плоскостями. Выбор системы координат.

Как решать показательные уравнения. Методы и способы решения

Как решать уравнения со степенями. Разбираем основные методы и способы решения простейших показательных уравнений.

Логарифм и его свойства. Как решать логарифмы

Урок по теме логарифмы и их свойства. Разбираемся, что такое логарифм и какие у него свойства. Научимся считать выражения, содержащие логарифмы. И рассмотри несколько возможных заданий №4 из ЕГЭ по профильной математике.

Степень с рациональным показателем. Как считать и ограничения

Разбираем, как вычислить степень с рациональным (дробным) показателем. Свойства степени с рациональным показателем. Примеры решения задания №9 из ЕГЭ по математике профильного уровня.

Корень степени n и его свойства

Что такое корень n-й степени. Познакомимся со свойствами коня n-й степени и методами оценки значения корня. Разберем какая у него областью определения.

Квадратный корень и его свойства

В данном уроке разбираем, что такое квадратный корень и знакомимся с основными его свойствами.

Степени и логарифмы

Цикл уроков про степени и логарифмы и их свойства. Учимся решать показательные и логарифмические уравнения и неравенства. Задания №9 и №15 ЕГЭ по профильной математике.

Финансовая математика в ЕГЭ. Экономическая задача в задании 15

Теория для решения заданий 15 по финансовой математике. Аннуитетные и дифференцированные платежи, понятие сложного процента. Основные методы решения задач на проценты.

Уравнения и неравенства с параметром. Задание 18 (С6)

Как решать номер 18 (С6) из ЕГЭ по математике профильного уровня. Разбор основных методов и типов решения задач с параметром. Графический и аналитические методы.

Репетитор по математике и физике в Видном

Индивидуальные занятия с репетитором для учеников 6-11 классов. Для каждого ученика я составляю индивидуальную программу обучения. Стараюсь заинтересовать ребенка предметом, чтобы он с удовольствием занимался математикой и физикой.

Курсы подготовки к ЕГЭ и ОГЭ Видное

Курсы эффективной подготовки к ЕГЭ и ОГЭ по математике и физике. Занятия индивидуально и в группах по 2-4 человека. Преподаватели высшей категории. Прирост от обучения на 42 балла.

Таблица степеней

Определение Калькулятор — возведения числа в степень Таблица степеней

Скачать таблицу степеней

Определение. Возведение в степень — операция, происходящая из сокращения для множественного умножения числа на самого себя.

aⁿ =	a · a · . .. · a

	n

Калькулятор для вычисления степени числа

^= 9

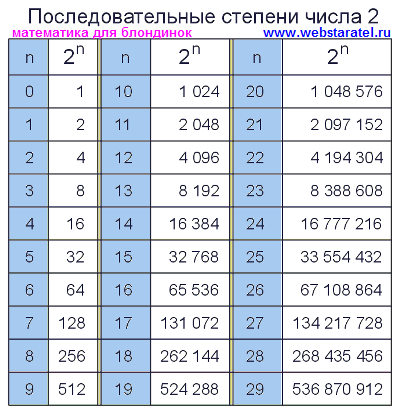
Таблица степеней чисел от 1 до 10

1¹ = 1

1² = 1

1³ = 1

1⁴ = 1

1⁵ = 1

1⁶ = 1

1⁷ = 1

1⁸ = 1

1⁹ = 1

1¹⁰ = 1

2¹ = 2

2² = 4

2³ = 8

2⁴ = 16

2⁵ = 32

2⁶ = 64

2⁷ = 128

2⁸ = 256

2⁹ = 512

2¹⁰ = 1024

3¹ = 3

3² = 9

3³ = 27

3⁴ = 81

3⁵ = 243

3⁶ = 729

3⁷ = 2187

3⁸ = 6561

3⁹ = 19683

3¹⁰ = 59049

4¹ = 4

4² = 16

4³ = 64

4⁴ = 256

4⁵ = 1024

4⁶ = 4096

4⁷ = 16384

4⁸ = 65536

4⁹ = 262144

4¹⁰ = 1048576

5¹ = 5

5² = 25

5³ = 125

5⁴ = 625

5⁵ = 3125

5⁶ = 15625

5⁷ = 78125

5⁸ = 390625

5⁹ = 1953125

5¹⁰ = 9765625

6¹ = 6

6² = 36

6³ = 216

6⁴ = 1296

6⁵ = 7776

6⁶ = 46656

6⁷ = 279936

6⁸ = 1679616

6⁹ = 10077696

6¹⁰ = 60466176

7¹ = 7

7² = 49

7³ = 343

7⁴ = 2401

7⁵ = 16807

7⁶ = 117649

7⁷ = 823543

7⁸ = 5764801

7⁹ = 40353607

7¹⁰ = 282475249

8¹ = 8

8² = 64

8³ = 512

8⁴ = 4096

8⁵ = 32768

8⁶ = 262144

8⁷ = 2097152

8⁸ = 16777216

8⁹ = 134217728

8¹⁰ = 1073741824

9¹ = 9

9² = 81

9³ = 729

9⁴ = 6561

9⁵ = 59049

9⁶ = 531441

9⁷ = 4782969

9⁸ = 43046721

9⁹ = 387420489

9¹⁰ = 3486784401

10¹ = 10

10² = 100

10³ = 1000

10⁴ = 10000

10⁵ = 100000

10⁶ = 1000000

10⁷ = 10000000

10⁸ = 100000000

10⁹ = 1000000000

10¹⁰ = 10000000000

 Распечатать таблицу степеней

Таблица степеней

n	1	2	3	4	5	6	7	8	9	10
1ⁿ	1	1	1	1	1	1	1	1	1	1
2ⁿ	2	4	8	16	32	64	128	256	512	1024
3ⁿ	3	9	27	81	243	729	2187	6561	19683	59049
4ⁿ	4	16	64	256	1024	4096	16384	65536	262144	1048576
5ⁿ	5	25	125	625	3125	15625	78125	390625	1953125	9765625
6ⁿ	6	36	216	1296	7776	46656	279936	1679616	10077696	60466176
7ⁿ	7	49	343	2401	16807	117649	823543	5764801	40353607	282475249
8ⁿ	8	64	512	4096	32768	262144	2097152	16777216	134217728	1073741824
9ⁿ	9	81	729	6561	59049	531441	4782969	43046721	387420489	3486784401
10ⁿ	10	100	1000	10000	100000	1000000	10000000	100000000	1000000000	10000000000

 Распечатать таблицу степеней

Скачать таблицу степеней в высоком качестве

Скачать таблицу степеней

Скачать картинкой

Таблица умножения a × b Таблица квадратов a² Таблица кубов a³ Таблица степеней aⁿ Таблица факториалов a!

 Все таблицы и формулы

Объяснение «правила нулевой мощности».

Показатели кажутся довольно простыми… | Бретт Берри | Math Hacks

Экспоненты кажутся довольно простыми, не так ли? Возведение числа в степень 1 означает, что у вас есть одно из этого числа, возведение в степень 2 означает, что у вас есть два числа, умноженные вместе, степень 3 означает, что число равно трем, и так далее.

А как же нулевая мощность? Почему любое ненулевое число, возведенное в нулевую степень, равно 1? А что произойдет, если мы возведем ноль в нулевую степень? Это все еще 1?

Посмотрите видео или прочитайте ниже, чтобы узнать!

Нажмите здесь, чтобы подписаться на Math Hacks

Давайте начнем с изучения деления значений с показателями степени.

Вызов степени представляют собой повторное умножение . Таким образом, мы можем переписать приведенное выше выражение как:

Поскольку 2/2 = 1, сокращаем три набора 2/2. Это оставляет 2 • 2, или 2 в квадрате.

Конечно, мы можем пойти по упрощенному пути и вычесть количество двоек внизу из числа двоек сверху. Поскольку эти величины представлены их соответствующими показателями степени, все, что нам нужно сделать, это записать общее основание с разницей в значениях степени в качестве степени.

Если мы обобщим это правило, то получим следующее, где n представляет собой ненулевое действительное число, а x и y также являются действительными числами.

Правило деления чисел с общим основанием

Отсюда легко вывести объяснение, почему любое ненулевое число, возведенное в нулевую степень, равно 1. Опять же, давайте рассмотрим конкретный пример.

Мы знаем, что любое ненулевое число, деленное само на себя, равно 1 . Итак, я могу написать следующее:

Это то же самое, что написать:

Теперь я воспользуюсь приведенным выше правилом экспоненты, чтобы переписать левую часть этого уравнения.

Конечно, это эквивалентно:

Мы можем использовать тот же процесс, что и в этом примере, вместе с приведенным выше обобщенным правилом, чтобы показать, что любое ненулевое действительное число, возведенное в нулевую степень, должно дать 1.

Здесь все становится сложнее. Приведенный выше метод не работает, потому что, конечно, делить на ноль нельзя. Давайте рассмотрим, почему.

Начнем с обычного деления на ноль ОШИБКА .

Как насчет 2÷0? Давайте посмотрим, почему мы не можем сделать это.

Деление на самом деле просто форма умножения, так что же произойдет, если я перепишу приведенное выше уравнение как:

Какое значение может удовлетворять этому уравнению для x?

Нет значения! Любое число, умноженное на ноль, дает ноль, оно никогда не может равняться 2. Поэтому мы говорим 9.0007 деление на ноль не определено . Возможного решения нет.

Теперь давайте посмотрим на 0÷0.

Опять же, перепишите это как задачу на умножение.

Здесь мы сталкиваемся с совершенно другой ситуацией. Решением для x может быть ЛЮБОЕ действительное число! Невозможно определить, что такое x. Следовательно, 0/0 считается неопределенным*, а не неопределенным.

Если мы попытаемся использовать описанный выше метод с нулем в качестве основы, чтобы определить, какой будет ноль в нулевой степени, мы немедленно остановимся и не сможем продолжить, потому что знаем, что 0÷0 ≠ 1, но это неопределенно.

Так чему же равен ноль в нулевой степени?

Это очень обсуждается. Некоторые считают, что это должно быть определено как 1, в то время как другие считают, что это 0, а некоторые считают, что это не определено. Для каждого есть хорошие математические аргументы, и, пожалуй, правильнее всего считать неопределенным .

Несмотря на это, математическое сообщество выступает за то, чтобы определял ноль в нулевой степени как 1, по крайней мере, для большинства целей.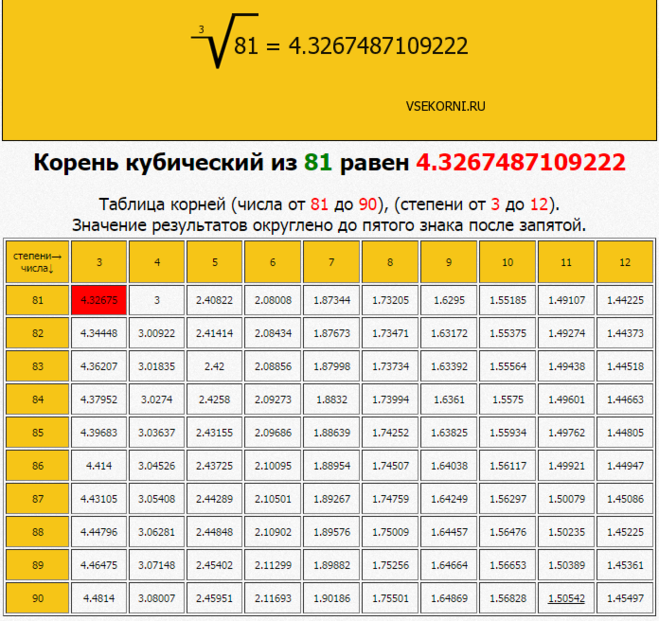

Возможно, полезное определение показателей для математика-любителя выглядит следующим образом:

Включив «1» в определение, мы можем заключить, что любое число (включая ноль) , повторенное ноль умноженное на , дает 1. Простой пример того, почему 0/0 является неопределенным, можно найти, изучив некоторые основные ограничения.

Подписывайтесь на Math Hacks в Instagram

Эти ограничения нельзя оценить напрямую, поскольку они являются неопределенными формами. Вместо этого мы должны использовать правило 9 Лопиталя .0010 , взяв производную от числителя и знаменателя отдельно, найти решения равные 2 и 3 соответственно.

При работе с уравнением, результатом которого является неопределенная форма нуля в степени нуль, во время занятий исчислением обязательно применяйте методы для неопределенных величин, такие как правило Лопиталя, чтобы правильно оценить предел.

❤ ОСТАВАЙТЕСЬ НА СВЯЗИ ❤

Будьте в курсе всех новостей Math Hacks!

Инстаграм | Фейсбук | Твиттер

Следующий урок: Распространенное заблуждение о вероятности

Подпишитесь сейчас! Math Hacks уже на YouTube!

Присоединяйтесь ко мне, пока мы вместе решаем математические задачи.

Распространение любви к математике + расширение прав и возможностей. Подпишитесь на новые…
www.youtube.com
10 главных секретов треугольника Паскаля
Биномиальная теорема, последовательность Фибоначчи, треугольник Серпинского и многое другое
medium.com
0117
и проблемы с запоминанием
medium.com
Использование деревьев факторов для нахождения НОК и НОК
Мы обсуждали алгоритм Евклида и способы нахождения наибольшего общего делителя двух чисел. Алгоритм…
medium.com
Руководство по дробям в 10 простых фактах
урок двадцать второй
medium.com
Калькулятор экспоненты — CalcuNation
Калькулятор степени используется для решения экспоненциальных форм выражений. Он также известен как калькулятор повышения мощности или калькулятор мощности.
Силу какого числа вы хотите найти?
К какой мощности?
Заполнить в значениях, чтобы определить ответ.
Например, если вы хотите узнать, сколько будет 4 в 3-й степени, введите 4
в первый пробел и 3 во второй.
Ответ = 4 x 4 x 4
Ответ: 64
92.
3 ² = 3×3 =9.
Онлайн-калькулятор экспоненты от calcination.com.
Этот калькулятор может упростить задачи с отрицательными показателями, положительными показателями и дробными показателями в виде десятичной дроби. Этот калькулятор находит мощность данного основного числа. Например, 4 в степени 3 или 3 в степени 4.
Что такое положительный показатель?
Положительный показатель степени показывает, сколько раз нужно умножить число само на себя. Используйте этот калькулятор степени, чтобы решить ваши проблемы. Примером может быть 8 ³ =8×8×8=512.
Как вычислить отрицательные показатели?
Для основания с отрицательной степенью его обратная величина положительна, и после нахождения обратной величины отрицательного показателя степени можно выполнить ее решение.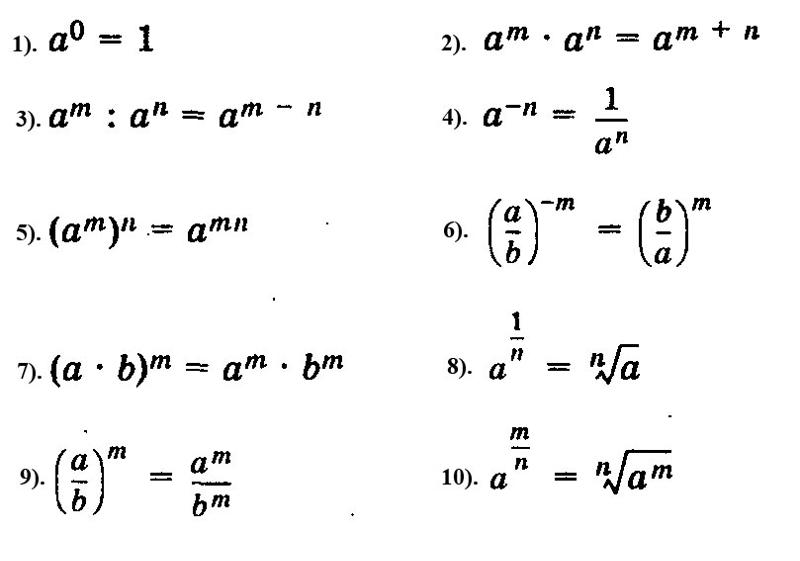 В этом калькуляторе вы можете узнать результат для отрицательного показателя степени. Просто поставьте знак минус перед числом в поле открытого поля, и результат будет рассчитан. ^(-n) =1/a ⁿ
3 ^(-2) =1/3 ² =1/9= 0,111.
Что такое показатель степени дроби?
Если вы хотите вычислять дроби в этом калькуляторе, просто измените его на десятичный и получите результат для дробного выражения. Например 5 в степени ½ можно вычислить, поставив 0,5 в поле экспоненты. Как рассчитать 0 или 1 показатель степени? Если показатель степени равен 1, результатом является само число. 6 ¹ =6 Если показатель степени равен нулю, то результат равен 1 ⁰ =1.
6 ⁰ =1
Как решить 0
⁰ ?
Это может быть либо 1, либо 0, поэтому он называется «Неопределенный». Следующая группа выражает упомянутые выше правила экспоненциальных выражений. 5 ² = 25
5 ¹ = 5
5 ⁰ = 1
5 ^(-1) = 1/5
5 ^{(-2) 5} = 0 0 0 0 0 9
Как вычислить мощность экспоненциального выражения?
Когда выражение экспоненты имеет степень, то сначала вам нужно умножить степени, а затем решить выражение с помощью этого калькулятора. 〖(a ⁿ ) 〗 ^m = a ^(n.m) Пример: Решите 〖(a ² ) 〗 ³
〖(a ² ) 〗 ³ = a ⁶
Теперь это ^{6 9020 можно легко вычислить с помощью калькулятора.
Пример:
〖(3 ² ) 〗 ⁴ = 3 ^2×4 =3 ⁸ =6561}
Как умножать показательные уравнения?
Если разные базы обладают одинаковой силой, то базы будут обладать силой по отдельности.
Пример: Упростить 〖(4×5)〗 ²
4 ² ×5 ² = 16×25 = 400
Если одни и те же базы обладают разной силой, силы будут добавлены.
4 ² ×4 ³ = 4 ⁽²⁺³⁾ = 4 ⁵
=4×4×4×4×4
=1024
В этом калькуляторе вы можете легко вычислить 4 ⁵ после ручного упрощения. A ^N x A ^M = A ^(N+M)
2 ² x 2 ³ = 2 ⁽²⁺³⁾
3 ² X 2 ² = (3x 3x 〖3x 〖3x 〖3x 〖3x 〖3x 〖3x 〖3x 〖3x 〖3x 〖3x 〖3x 〖3x 〖3x 〖3x 〖3x = (3x 3 ² x 2 ^{2). 2)〗 ² =6 ²}
Деление показательных дробей или частное свойство показателей степени.
Когда два одинаковых основания имеют разные показатели степени, которые необходимо разделить, их степени разделяются.
Пример: Упростить 5 ⁷ /5 ³ =5 ⁷ /5 ³ =5 ^(7-3) =5 ⁽⁴⁾
=5×5×5×5
=625
В этом калькуляторе 5 ⁽⁴⁾ может быть легко вычисляется после ручного вычитания показателей степени.
A ^N /A ^M = A ^(N-M)
2 ³ /2 ² = 2 ^(3-2)
4 ² /2 ² = 〖40204 = 〖40185 40203 2 /2
/2)〗 ² =2 ² =4
Экспоненциальный рост
Экспоненциальный рост относится к процессу, который увеличивает количество с течением времени. Это происходит из-за того, что мгновенная скорость изменения величины во времени пропорциональна самой величине. Если бы вы построили экспоненту известного основания, она показала бы линию, которая изгибается вверх и достигает почти идеального вертикального роста. Эта концепция используется в калькуляторе сложного роста.
Эта концепция используется в Калькулятор сложного роста.
Примеры экспоненты.
2 в степени 3 равно 2x2x2, или 4×2, или 8.
3 в степени 2 равно 3×3 или 9.
3 в степени 4 равно 3x3x3x3, или 9x3x3, или 27×3, или 81.
3 в степени 8 равно 3x3x3x3x3x3x3x3, или 6561.
4 в степени 3 равно 4x4x4, или 16×4, или 64.
7 в степени 3 равно 7x7x7, или 49×7, или 343.
8 в степени 3 равно 8x8x8, или 64×8, или 512.
In слова 8 ³ можно назвать «8 в степени 3»
90. Как повторить ноль ноль раз и получить 1?
Нельзя, пока показатели степени повторяются. Сегодня наша ментальная модель нуждается в обновлении.
Рассмотрение арифметики как преобразований
Вернемся назад — как мы изучаем арифметику? Нас учат, что числа — это счет чего-то (пальцы), сложение — это сумма счетов (3 + 4 = 7), а умножение — это многократное сложение (2 раза по 3 = 2 + 2 + 2 = 6).
Повторное сложение работает при умножении на красивые круглые числа, такие как 2 и 10, но не при использовании таких чисел, как -1 и $\sqrt{2}$. Почему?
Наша модель была неполной. Числа — это не просто счет; лучшая точка зрения — позиция на линии . Эта позиция может быть отрицательной (-1), между другими числами ($\sqrt{2}$) или в другом измерении (i).
Арифметика стала способом преобразования числа: сложение было скользящим (+3 означает смещение на 3 единицы вправо), а умножение было масштабным (умножение на 3 означает увеличение в 3 раза).
Так что же такое экспоненты?
Войдите в Expand-o-tron(TM)
Позвольте представить Expand-o-tron 3000.
Да, это устройство выглядит как дрянная микроволновка — но вместо того, чтобы разогревать пищу, оно увеличивает цифры. Введите номер, и появится новый. Вот как:
Начните с 1.0
Установите рост на желаемое изменение через одну секунду (2x, 3x, 10,3x)
Установите время на количество секунд
Нажмите кнопку
И шазам! Звенит звонок, и мы вытаскиваем наш блестящий новый номер. Предположим, мы хотим изменить 1.0 на 9:
Поместите 1.0 в Expand-o-Tron
Установите изменение для роста «3x» и время на 2 секунды
Нажмите кнопку
Число начинает преобразовываться, как только мы начинаем: мы видим 1,0, 1,1, 1,2… и как только заканчиваем первую секунду, мы на 3,0. Но это продолжается: 3.1, 3.5, 4.0, 6.0, 7.5. Как только мы заканчиваем 2-ю секунду, мы на 9,0. Встречайте наш новый блестящий номер!
Математически Expand-o-tron (функция экспоненты) делает это: 93), мы начинаем с 1.0.
Понимание экспоненциального коэффициента масштабирования
При умножении мы можем просто указать окончательный коэффициент масштабирования. Хотите в 8 раз больше? Умножьте на 8. Готово.
Экспоненты немного… привередливы:

Вы: Я бы хотел увеличить это число.
Expand-o-tron: Хорошо, вставляй.
Вы: Насколько большим он станет?
Expand-o-tron: Ну и дела, не знаю. Давайте узнаем… 910 значит для тебя? Как это заставляет вас чувствовать? Вместо красивого аккуратного коэффициента масштабирования экспоненты хотят, чтобы мы чувствовали, заново переживали и даже ощущали запах процесса роста. Чем бы вы ни закончили, это ваш коэффициент масштабирования.
Звучит окольно и раздражающе. Ты знаешь почему? Большинство вещей в природе не знают, где они окажутся!
Как вы думаете, бактерии планируют удваиваться каждые 14 часов? Нет, он просто съедает заплесневелый хлеб, о котором вы забыли в холодильнике, так быстро, как только может, и по мере того, как его становится больше, он начинает расти еще быстрее. Чтобы предсказать поведение, мы используем, как быстро они растут (текущая скорость) и как долго они будут меняться (время), чтобы определить их окончательное значение. 91,5 означает 1,5 секунды в машине, то есть где-то между 2-кратным и 4-кратным ростом (подробнее позже). Идея «повторяющегося подсчета» заставила нас застрять на использовании целых чисел, но доли секунды вполне допустимы.
Умножение показателей степени
Что, если мы хотим два цикла роста подряд? Допустим, мы используем машину в течение 2 секунд, а затем используем ее в течение 3 секунд при той же мощности:
Подумайте о своей обычной микроволновой печи — разве это не то же самое, что один непрерывный цикл в 5 секунд? Это точно. Пока настройка мощности (базовая) остается неизменной, мы можем просто добавить время:
Опять же, expand-o-tron дает нам масштабный коэффициент для изменения нашего числа. Чтобы получить общий эффект от двух последовательных применений, мы просто перемножаем коэффициенты масштабирования.
Квадратные корни
Продолжаем. Допустим, мы находимся на уровне мощности a и растем в течение 3 секунд:
Не так уж плохо. Как будет выглядеть рост в течение половины этого времени? Это будет 1,5 секунды:
Что произойдет, если мы сделаем это дважды?
Глядя на это уравнение, мы видим, что «частичный рост» — это квадратный корень из полного роста! Если мы разделим на пополам, мы получим квадратный корень из коэффициента масштабирования. А если разделить время на трети?
И получаем кубический корень! Для меня это интуитивная причина, по которой деление показателей дает корни: мы делим время на равные части, поэтому каждый период «частичного роста» должен иметь одинаковый эффект. Если три одинаковых эффекта перемножаются вместе, это означает, что каждый из них является кубическим корнем. 90 зависит от сценария (непрерывного или дискретного) и обсуждается. Аналогия с микроволновкой не связана со строгостью — она помогает мне понять, почему может быть равным 1, в отличие от «повторяющегося подсчета».)
Вот что происходит, когда мы пытаемся подставить реальные числа:
Дополнительно : Повторяющиеся показатели (от a до b и c)
Повторяющиеся показатели сложны. Что означает
? Это «повторяющееся умножение, повторяющееся» — еще один способ сказать «сделайте эту экспоненту один раз и сделайте это снова». Разберём: 94) просто знает, как взять предыдущую сумму (8) и увеличить ее в 4 раза. Каждая единица времени в «Фазе II» аналогична повторению всей фазы I:
Именно здесь повторная интерпретация подсчета помогает нам сориентироваться. Но затем мы запускаем расширение-о-трон: мы растем на 3 секунды в фазе I и повторяем это еще на 4 секунды. Это работает для дробных степеней — например,
означает «Увеличение в течение 3,1 секунды и использование этой новой скорости роста в течение 4,2 секунды». Мы можем смешать время (3,1 × 4,2) следующим образом: 92 = 7$)».
Мы как дети усваиваем, что 3 умножить на 7 = 7 умножить на 3. (Или что % от b = b% от а — это правда!).
Продвинутый уровень: переписывание экспонентов для гровера
Расширить-о-трон немного странно: числа начинают расти в тот момент, когда они находятся внутри, но мы указываем желаемый рост на -й конец -й секунды.
Мы говорим, что нам нужен двукратный рост в конце первой секунды. Но как узнать, с какой ставки начинать? Как быстро мы должны расти на 0,5 секунды? Это не может быть полная сумма, иначе мы превзойдем нашу цель, так как наши проценты увеличиваются. 9x с точки зрения наблюдателя, а не производителя.
Значение «2» измеряется на конце интервала, и мы работаем в обратном направлении, чтобы создать показатель степени. Нам это удобно, но не растущее количество — бактерии, радиоактивные элементы и деньги не заботятся о том, чтобы выровняться с нашими конечными интервалами!
Нет, эти твари знают свою текущую, мгновенную скорость роста , и не пытаются выровнять ее с нашими границами. Это все равно, что сравнивать радианы и градусы — радианы «естественны», потому что они измеряются с точки зрения движущегося объекта. 90 = 1?)
Использование логарифмов в реальном мире
Как думать с помощью показателей и логарифмов
Сравнение дискретного и непрерывного роста
Что на самом деле означает показатель степени?
В: Почему e особенный? (2,718…, а не 2, 3,7 или другое число?)
Экспоненциальные правила | Законы показателей
Правила показателей, законы показателей и примеры.
Что такое показатель степени
Экспоненты правил
Калькулятор экспонент
Что такое показатель степени
Основание а в степени n равно произведению а, n раз:
а ⁿ = × × … ×
n раз
а — основание, а n — показатель степени.
Примеры
3 ¹ = 3
3 ² = 3 × 3 = 9
3 ³ = 3 × 3 × 3 = 25
03 4 = 3 × 3 × 3 × 3 = 81
3 ⁵ = 3 × 3 × 3 × 3 × 3 = 243 Правило Пример Правила продукта а ^н ⋅ а ^м = а ^н+м 2 ³ ⋅ 2 ⁴ = 2 ³⁺⁴ = 128 а ^н ⋅ б ^н = ( а ⋅ б ) ^н 3 ² ⋅ 4 ² = (3⋅4) ² = 144 Частные правила а ^н / а ^м = а ^н ^{— м} 2 ⁵ / 2 ³ = 2 ^5-3 = 4 а ^н / б ^н = ( а / б ) ^н 4 ³ / 2 ³ = (4/2) ³ = 8 Силовые правила ( б ^н ) ^м = б ^н⋅м (2 ³ ) ² = 2 ^3⋅2 = 64 _б н ^м _{= б} ( н ^м ) ₂ 3 ² _{= 2} (3 ² ) _{= 512} ^м √( б ^н ) = б ^{н / м} ² √(2 ⁶ ) = 2 ^6/2 = 8 б ^{1/ н} = ^н √ б 8 ^1/3 = ³ √8 = 2 Отрицательные показатели степени б ^-н = 1 / б ^н 2 ^-3 = 1/2 ³ = 0,125 Нулевые правила б ⁰ = 1 5 ⁰ = 1 0 ⁿ = 0 , для n >0 0 ⁵ = 0 Единые правила б ¹ = б 5 ¹ = 5 1 ^п = 1 1 ⁵ = 1 Минус одно правило (-1) ⁵ = -1 Производное правило ( x ⁿ ) ‘ = n ⋅ x ⁿ ^-1 ( х ³ ) ‘ = 3⋅ х ^3-1 Интегральное правило ∫ x ⁿ dx = x ⁿ ⁺¹ /( n +1)+ C ∫ x ² dx = x ²⁺¹ /(2+1)+ C
Правила произведения экспонентов
Правило произведения с одинаковым основанием
A ^N ⋅ A ^M = A ^N+M
Пример:
2 ³ ⋅ 2 ⁴ = 2 ^{3+40204 = 2 ^{3+40204 = 2 ^{3+40204 = 2 ^{3+40204 = 2 ^{3+40204 = 2 ^{3+40204 = 2 ^{3 ³. 2=2=2 ОТДОВОГО РАБОТА.}}}}}}}
Пример:
3 ² ⋅ 4 ² = (3⋅4) ² = 12 ² = 12om12 = 144
См.: Правила коэффициента с коэффициентом в Multplying
.
^{— M}
Пример:
2 ⁵ /2 ³ = 2 ^5-3 = 2 ² = 2–2 = 4
котировочное правило с той же эксплуатацией
959595959595 гг. ^п / B ^N = ( A / B ) ^N
Пример:
4 ³ /2 ³ = (40009
4 ³ /2 ^{3 9000 = (40005}
4 ³
2 ³ = 2 % 2 = 8
См.: Разделительные экспоненты
Правила мощности
Правило мощности I
( A ^N ) ^M = ) ^M = ).
Пример:
(2 ³ ) ² = 2 ^3⋅2 = 2 ⁶ = 2⋅2⋅2⋅2⋅2⋅2 = 64
Power rule II
_a ⁿ ^m ₌ _a ( n ^m )
Example:
₂ 3 ² _{= 2} (3 ² ) _{= 2} (3⋅3) _{= 2} 9 _{= 2⋅2⋅2⋅2⋅2⋅2⋅2⋅2⋅2 = 512}
Степенное правило с радикалами
^M √ ( A ^N ) = A ^N ^{/ M}
Пример:
²
= 2 ³ = 2 % 2 = 8
Отрицательные экспоненты Правило
B ^-N = 1 / B ^N
Пример:
2 ^{04 = 1 /10005}
. 2 ³ = 1/(2⋅2⋅2) = 1/8 = 0,125
См. Отрицательные показатели степени

Калькулятор степени ►

Добавление степени
Показатель степени деления
Дробные показатели
Умножение показателей
Отрицательные показатели
Упрощение показателей
Нулевой показатель
Калькулятор экспоненты
Калькулятор логарифмов
Калькулятор экспоненциального роста
Антилогарифмический калькулятор
лог(х) правила
п(х) правила
e константа
Калькулятор экспоненты (мощности) — капитанский калькулятор
ПОСЛЕДНЕЕ ОБНОВЛЕНИЕ: 24 сентября 2020 г.
Калькулятор показателей степени
Обратите внимание: для работы этого калькулятора требуется JavaScript
Определение – Что такое показатель степени?
Показатель степени — это количество раз, которое нужно умножить число само на себя.
Запишите показатель степени в виде приподнятого числа. В числе 2 ⁴ (2 в степени 4 или 2 в степени 4) «4» является показателем степени. «2» — это число, которое нужно умножить само на себя 4 раза. В этом случае 2 х 2 х 2 х 2 = 16,
Формула – Как найти показатель степени
Найдите показатель степени числа, умножив это число само на число показателей степени.
номер ² = номер x номер
номер ³ = номер x номер x номер
номер ⁴ = номер x номер x номер x номер
9
9 ⁵ = 9 x 9 x 9 x 9 x 9 = 59 049
5 ¹⁰ = 5 x 5 x 5 x 5 x 5 x 5 x 5 x 5 x 5 x 5 = 9,765,625
Правила экспоненты (Законы экспоненты)
Произведение с одинаковым основанием
Чтобы умножить одинаковые основания, оставьте основание одинаковым и добавьте показатели степени.
x ^A • x ^B = x ^{(A + B)}
Пример: 7 ³ • 7 ⁵ = 7 ^{(3 + 5)} = 7 ⁸ = 5764,80195014 = 7 ⁸ = 5 764,80195555 = 7 ⁸ = 5764,801 = 7 ⁸ = 5764,801 .
Степень экспоненты (или степень в степени)
Чтобы вычислить экспоненту экспоненты, перемножьте экспоненты.
(x ^A) ^B = x ^{(A • B)} = x ^AB
Пример: (4 ³) ² = 4 ^{(3 • 2)} = 4 ^{. 6} = 4,096
Деление чисел с показателями степени (частное с одинаковым основанием)
Чтобы разделить два основания с одинаковым показателем степени, вычтите показатель степени знаменателя из показателя степени числителя.
x ^a ÷ x ^b = x ^{(a – b )}
Пример: 5 ⁷ ÷ 5 ³ = 5 ^{(7 – 3)} = 5 ⁴ = 625
Умножение чисел в степени
Умножение чисел в степени может быть возведено в эту степень.
(xy) ^z = x ^Z • Y ^Z
Пример: (9x) ⁵ =
Чтобы разделить дробь, возведенную в степень, приведите степень к числителю и знаменателю.
(x ÷ y) ^z = x ^z ÷ y ^z
Example: (7 ÷ 5) ⁴ = 7 ⁴ ÷ 5 ⁴ = 2,401 ÷ 625 = 3.8416
Показатель степени 0
Любое число в степени 0 равно 1.
x ⁰ = 1
Пример: 450 ⁰ = 1
Отрицательные степени
^{показатель степени}
x ^-a = 1 ÷ 1 ^a
Пример: 6 ^-4 = 1 ÷ 6 ⁴ = 1 ÷ 1,296 = 0,0007716
Деление с отрицательным показателем степени
сделал положительным.
1 ÷ x ^-a = x ^a
Пример: 1 ÷ 3 ^-4 = 3 ⁴ = 81
-щелкните и выберите «Шрифт», чтобы открыть меню шрифтов. Выберите «Верхний индекс». 9символ перед показателем степени. Если в показателе степени более одного символа, заключите символы в (квадратные скобки).
Таблица показателей степени
Обратите внимание: для работы этой таблицы требуется JavaScript
Часто задаваемые вопросы
Что такое показатель степени (в математике)?
Показатель степени — это количество раз, которое нужно умножить число само на себя. Например, от 3 до 4-го (пишется 3) означает 3 х 3 х 3 х 3 = 81. Это не то же самое, что 3 х 4 (12).
В чем разница между «Power Of» и «Exponent»?
Это одно и то же. Большинство людей используют термины «в степени» и «в степени» как синонимы.
Мы находим, что при описании вещи «показатель» является более естественным термином. («Какова степень числа в этом уравнении?» звучит лучше, чем «Какова степень числа в этом уравнении?»).
При описании действия термин «степень числа» является более естественным («Вычислить пять в степени три» звучит лучше, чем «Вычислить пять в степени три»).
Что такое отрицательный показатель?
Отрицательный показатель степени означает, сколько раз нужно разделить число. 3 ⁴ (положительный показатель степени) означает умножить 3 раза на себя 4 раза (3 х 3 х 3 х 3 = 81). 3 ^-4 (отрицательный показатель степени) означает разделить 3 на себя 4 раза (3 ÷ 3 ÷ 3 ÷ 3 = 0,012346).
Источники и другие ресурсы
Простое введение в степени и показатели из Math Planet, Purple Math, Math is Fun и Школы общественного здравоохранения Университета Миннесоты.
Экспонентные правила и законы экспонентов от команды математиков Ольстерского муниципального колледжа, Wolfram MathWorld и Math is Fun.
Статьи Википедии о возведении в степень и экспоненциальной функции, описывающие показатели степени и их использование.
Видео-знакомство с представителями Академии Хана и Math Concepts.
Видео с объяснением законов экспонент от Брайана Маклогана, Math Antics, The Organic Chemistry Tutor и Mario’s Math Tutoring.
Power-1 — Радиальное машиностроение
Подавитель перенапряжения и стабилизатор напряжения
Radial Engineering Power-1 — это чистый блок кондиционирования питания в прочном корпусе для монтажа в стойку, обеспечивающий всех, у кого есть ценное электронное и аудиооборудование, превосходной фильтрацией от помех, а также надежной защитой от перенапряжений.
РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ
РУКОВОДСТВО ПОЛЬЗОВАТЕЛЯ
Фотографии
Сделано в США MOV (металлооксидный варистор)
Фильтр высокочастотных помех с высоким уровнем подавления
USB-порт для зарядки на передней панели
Несколько передних и задних розеток с расстоянием между стенками
Создан «радиально прочный», чтобы выдерживать годы использования в турах
Бескомпромиссная разработка Radial
Ограничители перенапряжений Radial Power Clean обеспечивают музыкантам, инженерам, продюсерам, владельцам студий, коммерческих объектов и всем, кто работает с ценным электронным оборудованием, защиту от скачков напряжения, которые могут мгновенно повредить или разрушить музыкальное оборудование. Предусмотрено восемь розеток на задней панели (четыре с расстоянием между стенами для размещения блока питания любого размера), а также три розетки на передней панели и USB-порт для зарядки для удобного питания персональных устройств. Надежный выключатель питания, прочные разъемы для розеток и стальная конструкция гарантируют бесперебойную работу Power-1 ночь за ночью.
Низкий уровень шума, высокий уровень надежности
В отличие от продуктов конкурентов, в которых для защиты от перенапряжения используются низкокачественные металлооксидные варисторы (MOV), оба блока Radial Power построены с использованием MOV американского производства. Было доказано, что этот критический компонент обеспечивает превосходную тепловую защиту и имеет гораздо более длительный срок службы, чем альтернативы. В обоих устройствах используется технология шунтового режима, и они не загрязняют землю, что снижает системный шум. Фильтр высокочастотных помех с высоким уровнем подавления используется для защиты высокочастотных и AM-радиосигналов от линии электропередач, предотвращая загрязнение аудиосигналов.
Видео
«Все мое оборудование питается от больших изолирующих трансформаторов и использует распределитель с защитой от перенапряжения, но удобство этих передних розеток и USB-порта заставляет меня хотеть получить еще несколько в критических точках, чтобы улучшить рабочий процесс в студии. отличное дополнение к линейке продуктов Radial Engineering».
Майк Макнайт
Мэрайя Кэри, Мадонна, American Idol
«Мне не терпится заменить все мои старые стабилизаторы напряжения на Radial! единица, которой я владею на сегодняшний день!»
Профиль исполнителя
Пит Торн
Гитаристы — Дон Хенли, Крис Корнелл, Мелисса Этеридж, Джуэл, Пинк, Алисия Киз. Соло-исполнитель. Youtuber
«Radial Power-1 очень удобен, у него больше разъемов питания на передней панели, чем у других моих стабилизаторов напряжения, а USB позволяет мне легко заряжать телефон. Radial — хорошая штука!»
Профиль исполнителя
Joey Landreth
The Bros Landreth
«Мне нравится, что Power-1 имеет три выхода на передней панели, а USB-порт — это приятное прикосновение! по дороге!»
Профиль исполнителя
Дэн Ричардс
Гитарист — One Direction, Дэвид Миллиган, Джейми Эбботт
«Сила-1 отлично работает для меня, делая именно так, как я себе представлял, сохраняя чистоту и предотвращая неприятности. треск, который я раньше слышал при включении некоторых устройств. Мне также нравится его цвет, определенно более привлекательный, чем у других на рынке».
Профиль исполнителя
Сопутствующие товары
Из блога
Образование
Готовимся к возвращению живой музыки
Вещи могут не обязательно выглядеть так же, когда музыкальные площадки вновь откроются, а гастролирующие группы начнут заказывать новые концерты (см., например, концерт-пузырь The Flaming Lips), но играть и наслаждаться… Подробнее
Дизайнерские идеи
Что нужно для разработки экологически чистой и безопасной энергии
Билл Уитлок, бывший президент и главный инженер Jensen Transformers Inc., имеет многолетний опыт в обеспечении чистоты сигналов для аудиотрансформаторов и стабилизаторов напряжения. Он написал… Подробнее
Образование
Скачки напряжения: как защитить свой Gear
Выпуск Power-1 — это первый шаг Radial в мир стоечных источников питания и ограничителей перенапряжений.
No related posts.