Подготовка к колоноскопии 8 или 7 или 6 баллов что значит 2-1-3? Бостонская шкала качества подготовки
Просмотренные публикации
QR-код этой страницы
Для продолжения изучения на мобильном устройстве ПРОСКАНИРУЙТЕ QR-код с помощью спец. программы или фотокамеры мобильного устройства
Случайный выбор
данная функция, случайным образом выбирает информацию для Вашего изучения,
запустите выбор нажав кнопку ниже
Обратная связь
Напишите нам
Имя: *
Фамилия: *
Телефон: *
E-mail: *
Тема: *
Сообщение: *
Прикрепить файл или скриншот удалить
Я даю согласие на обработку персональных данных *
Я принимаю условия пользовательского соглашения *
Закрытая часть портала предназначена для только для работников здравоохранения. Оставив свой e-mail и специалищацию, Вы подтверждаете, что являетесь работником здравоохранения и что Вы ознакомились с текстом и поняли его.
Оставив свой e-mail и специалищацию, Вы подтверждаете, что являетесь работником здравоохранения и что Вы ознакомились с текстом и поняли его.
Сообщение об ошибке
Что улучшить?
Фамилия: *
Телефон: *
E-mail: *
Тема: *
Сообщение: *
Прикрепить файл или скриншот удалить
Я даю согласие на обработку персональных данных *
Я принимаю условия пользовательского соглашения *
Закрытая часть портала предназначена для только для работников здравоохранения. Оставив свой e-mail и специалищацию, Вы подтверждаете, что являетесь работником здравоохранения и что Вы ознакомились с текстом и поняли его.
Анонс:
Подготовка к колоноскопии 8 (2-3-3) баллов что значит?
Полный текст статьи:
Это Шкала Бостон. Количественная 4-балльная система оценки подготовки к колоноскопии, которая проводится по трем сегментам толстой кишки:
- правые отделы (слепая и восходящая ободочная кишка)
- средние отделы (поперечно-ободочная кишка, включая печеночный и селезеночный изгибы)
- левые отделы (нисходящая и сигмовидная ободочная кишка, прямая кишка).
Каждому из трех отделов выставляется оценка от 0 до 3 баллов:
- Отличная (3) — отличная визуализация слизистой оболочки без наличия остаточной жидкости в кишке.
- Хорошая (2) — небольшое количество мутной жидкости с примесью жидкого кала. Хорошая визуализация слизистой оболочки.
- Плохая (1) — в кишке жидкие и твердые каловые массы.

- Неадекватная (0) — в кишке твердый стул, слизистая оболочка не визуализируется.
Общее количество баллов суммируется, и максимальное их количество, соответствующее идеальному качеству подготовки, в сумме составляет 9.
Адекватной считается подготовка с общей суммой баллов 6 и/или при условии, что общая сумма баллов по каждому сегменту >2.
Пример описания в протоколе исследования:
Качество подготовки: отличное, 9 баллов (3-3-3) по Бостонской шкале.
Качество подготовки: хорошее, почти отличное, 8 баллов (2-3-3) по Бостонской шкале.
Качество подготовки: хорошее, 7 баллов (2-2-3) по Бостонской шкале.
Качество подготовки: адекватное, 6 баллов (2-2-2) по Бостонской шкале.
Качество подготовки: не адекватное, 5 баллов и ниже (1-2-2) по Бостонской шкале.
Читайте по теме:
- Статьи: Стандарты качественной колоноскопии (пособие для врачей)
- Пациентам: Двухэтапная подготовка к колоноскопии препаратом «МОВИПРЕП» и симетиконом
Создайте вашу публикацию
Работаем и учимся при поддержке
Партнеры
ОПТИМИЗАЦИЯ СПОСОБА ПОЛУЧЕНИЯ НАНОКАПСУЛ, РАЗРАБОТКА МЕТОДИКИ ОПРЕДЕЛЕНИЯ СТЕПЕНИ ВКЛЮЧЕНИЯ ЦИННАРИЗИНА В ПРОЛОНГИРОВАННУЮ ЛЕКАРСТВЕННУЮ ФОРМУНА ОСНОВЕ ПОЛИ-D,L-ЛАКТИД-КО-ГЛИКОЛИДА И ЕЕ ВАЛИДАЦИЯ | Сорокоумова
1. Щукин И.А., Лебедева А.В., Бурд С.Г., Фидлер М.С., Шихкеримов Р.К., Исмаилов А.М., Болотов А.В., Бельгушева М.Х. Хронические цереброваскулярные заболевания: вопросы диагностики и лечения // Consilium Medicum. – 2016. – №2. – С. 85–94.
Щукин И.А., Лебедева А.В., Бурд С.Г., Фидлер М.С., Шихкеримов Р.К., Исмаилов А.М., Болотов А.В., Бельгушева М.Х. Хронические цереброваскулярные заболевания: вопросы диагностики и лечения // Consilium Medicum. – 2016. – №2. – С. 85–94.
2. Smith E.E., Saposnik G., Biessels G.J., Doubal F.N., Fornage M., Gorelick P.B., Greenberg S.M., Higashida R.T., Kasner S.E., Seshadri S. American Heart Association Stroke Council; Council on Cardiovascular Radiology and Intervention; Council on Functional Genomics and Translational Biology; and Council on Hypertension. Prevention of Stroke in Patients With Silent Cerebrovascular Disease: A Scientific Statement for Healthcare Professionals From the American Heart Association/American Stroke Association // Stroke. – 2017. – Vol. 48, №2. – P. e44–e71. DOI: 10.1161/STR.0000000000000116.
3. Thrift A.G., Howard G., Cadilhac D.A., Howard V., Rothwell P.M., Thayabaranathan T., Feigin V.L., Norrving B., Donnan G.A. Global stroke statistics: An update of mortality data from countries using a broad code of «cerebrovascular diseases» // International Journal of Stroke. – 2017. – Vol. 12, №8. – P. 796– 801. DOI: 10.1177/1747493017730782.
– 2017. – Vol. 12, №8. – P. 796– 801. DOI: 10.1177/1747493017730782.
4. Patel R.A.G., McMullen P.W. Neuroprotection in the Treatment of Acute Ischemic Stroke // Prog Cardiovasc Dis. – 2017. – Vol. 59, №6. – P. 542–548. DOI:10.1016/j.pcad.2017.04.005.
5. Ashrafi M.R., Salehi S., Malamiri R.A., Heidari M., Hosseini S.A., Samiei M., Tavasoli A.R., Togha M. Efficacy and safety of cinnarizine in the prophylaxis of migraine in children: a double-blind placebo-controlled randomized trial // Pediatr Neurol. – 2014. – Vol. 51, №4. – P. 503–8. DOI:10.1016/j.pediatrneurol.2014.05.031.
6. Сорокоумова М.В., Компанцев В.А., Щербакова Л.И., Мирошниченко К.А., Платонова А.Ю. Общая характеристика, применение в медицине, методы качественного и количественного анализа циннаризина // Вестник ВГУ, серия: Химия. Биология. Фармация. – 2017. – №4. – С. 135–140.
7. Raghuvanshi S., Pathak K. Recent Advances in Delivery Systems and Therapeutics of Cinnarizine: A Poorly Water Soluble Drug with AbsorptionWindow in Stomach // Journal of Drug Delivery. – 2014., 2014:479246 DOI:10.1155/2014/479246.
– 2014., 2014:479246 DOI:10.1155/2014/479246.
8. Shahba A.A., Mohsin K., Alanazi F.K. Novel self-nanoemulsifying drug delivery systems (SNEDDS) for oral delivery of cinnarizine: design, optimization, and in-vitro assessment.//AAPS PharmSciTech. – 2012. – Vol. 13. – P. 967–977. DOI:10.1208/s12249-012-9821
9. Nguyen T.H., Hanley T., Porter C.J., Boyd B.J. Nanostructured liquid crystalline particles provide long duration sustained-release effect for a poorly water soluble drug after oral administration // Journal Control Release. – 2011. – Vol. 153, №2. – P. 180– 186. DOI: 10.1016/j.jconrel.2011.03.033.
10. Сорокоумова М.В., Компанцев В.А., Мирошниченко К.А. Разработка и исследование пролонгированного лекарственного средства циннаризина на основе поли-D,L-лактид-когликолида // Евразийский союз ученых. – 2017. – № 10–1(43). – С. 75–79.
11. Verma S., Nagpal K., Singh S.K., Mishra D.N. Unfolding type gastroretentive film of Cinnarizine based on ethyl cellulose and hydroxypropylmethyl cellulose // International journal of biological macromolecules. – 2014, Vol. 64. – P. 347–352. DOI: 10.1016/j.ijbiomac.2013.12.030
– 2014, Vol. 64. – P. 347–352. DOI: 10.1016/j.ijbiomac.2013.12.030
12. Shahba A.A., Ahmed A.R., Alanazi F.K., Mohsin K., Abdel-Rahman S.I. Multi-Layer Self-Nanoemulsifying Pellets Delivery System for the Poorly Water-Soluble Drug Cinnarizine // AAPS PharmSciTech. – 2018. – Vol. 19, №5 – P. 2087–2102. DOI: 10.1208/s12249-018-0990-7
13. Sassene P.J., Mosgaard M.D., Löbmann K., Mu H., Larsen F.H., Rades T., Müllertz A.. Elucidating the Molecular Interactions Occurring during Drug Precipitation of Weak Bases from Lipid-Based Formulations: A Case Study with Cinnarizine and a Long Chain Self-Nanoemulsifying Drug Delivery System // Molecular Pharmaceutics – 2015. – Vol. 12, №11. – P. 4067–4076. DOI: 10.1021/acs.molpharmaceut.5b00498.
14. Morrison J.S., Nophsker M.J., Haskell R.J. A combination turbidity and supernatant microplate assay to rank-order the supersaturation limits of early drug candidates // Journal of pharmaceutical sciences. – 2014. – Vol. 103, №10 – P. 3022–3032.
15. Ammar H.O., Ghorab M., Kamel R., Salama A.H. Design and optimization of gastro-retentive microballoons for enhanced bioavailability of cinnarizine // Drug Delivery and Translational Research. – 2016. – Vol. 6, №3. – P. 210–224. DOI:1007/s13346-016-0280-4.
16. Haress N.G. Cinnarizine: Comprehensive Profile // Profiles Drug Subst Excip Relat Methodol. – 2015. – Vol. 40. – P. 1–41. DOI: 10.1016/bs.podrm.2015.01.001
17. Ciftci Z., Deniz M., Yilmaz I., Ciftci H.G., Sirin D.Y., Gultekin E. In vitro analysis of a novel controlled release system designed for intratympanic administration of N-acetylcysteine: a preliminary report // Am J Otolaryngol. – 2015. – Vol. 36, № 6. – P. 786–793. DOI: 10.1016/j.amjoto.2015.08.004.
18. Портнова С.В., Мцариашвили М.Р. Валидация методики количественного определения циннаризина в смывах // Вестник казанского технологического университета. – 2016. – Т. 19. – №12. – С. 75–78.
19. Morrison J., Nophsker M. , Elzinga P., Donoso M., Park H., Haskell R. A polychromatic turbidity microplate assay to distinguish discovery stage drug molecules with beneficial precipitation properties // Int J Pharm. – 2017. – Vol. 531, №1. – P. 24–34. DOI: 10.1016/j.ijpharm.2017.07.086.
, Elzinga P., Donoso M., Park H., Haskell R. A polychromatic turbidity microplate assay to distinguish discovery stage drug molecules with beneficial precipitation properties // Int J Pharm. – 2017. – Vol. 531, №1. – P. 24–34. DOI: 10.1016/j.ijpharm.2017.07.086.
20. Abdelrahman M.M. Simultaneous determination of Cinnarizine and Domperidone by area under curve and dual wavelength spectrophotometric methods // Spectrochim Acta A Mol Biomol Spectrosc. – 2013. – Vol. 113. – P. 291–296. DOI: 10.1016/j.saa.2013.04.120.
21. Choudhari V.P., Ingale S., Gite S.R., Tajane D.D., Modak V.G., Ambekar A. Spectrophotometric simultaneous determination of Tenofovir disoproxil fumarate and Emtricitabine in combined tablet dosage form by ratio derivative, first order derivative and absorbance corrected methods and its application to dissolution study// Pharm Methods. – 2011; Vol. 2, №1 – P. 47–52. DOI:10.4103/2229-4708.81096
22. Lamie N.T. Comparative study of spectrophotometric methods manipulating ratio spectra: an application on pharmaceutical binary mixture of cinnarizine and dimenhydrinate. Spectrochim Acta A Mol Biomol Spectrosc. – 2015 – Vol. 141. – P. 193–201. DOI: 10.1016/j.saa.2015.01.033.
Spectrochim Acta A Mol Biomol Spectrosc. – 2015 – Vol. 141. – P. 193–201. DOI: 10.1016/j.saa.2015.01.033.
23. Благоразумная Е.Ю., Дуккардт Л.Н., Благоразумная Н.В. Качественный и количественный анализ триметилоктадецил аммония бромида в лекарственном средстве бактерицид // Известия вузов. Северо-Кавказский регион. Серия: Естественные науки. – 2006. – № S23. – C. 60–61.
24. Береговых В.В., Пятигорская Н.В., Беляев В.В., Аладышева Ж.И., Мешковский А.П. Валидация в производстве лекарственных средств/ Учебное пособие. – М.: Издательский дом Русский Врач, 2010. – 286 с. https://www.twirpx.com/file/1570313/
25. Mishra B., Sahoo J., Prasanna K.D. Enhanced bioavailability of cinnarizine nanosuspensions by particle size engineering: Optimization and physicochemical investigations // Materials Science and Engineering: – 2016. – Vol. 63. – P. 62–69. DOI: 10.1016/j.msec.2016.02.046.
26. Чмелевская Н.В., Илларионова Е.А. Аналитический контроль однородности дозирования таблеток циннаризина // Сибирский медицинский журнал. – 2009. – №3. – С. 50–52.
– 2009. – №3. – С. 50–52.
27. Илларионова Е.А., Чмелевская Н.В., Муравьева Г.М. Разработка методик обнаружения пикамилона и циннаризина в комбинированных сочетаниях с психотропными лекарственными средствами. // Сибирский медицинский журнал. – 2015. – №4. – С. 68–71.
28. Общая фармакопейная статья ОФС 1.1.0013.15 «Статистическая обработка результатов химического эксперимента». – ГФ XIV. – М., 2018.
3-8Полномочия (основания и показатели) | Происхождение, законы, заблуждения, примеры
Что такое экспонента? Показатель степени указывает, сколько раз число должно быть умножено само на себя. Показатели также называются степенями или индексами. Обычно показатель степени записывается в виде надстрочного индекса справа от основания.
Показатели также называются степенями или индексами. Обычно показатель степени записывается в виде надстрочного индекса справа от основания.
Рассмотрим число 5 3 .
В этом примере 5 — основание, а 3 — показатель степени. А основание — это число, которое мы многократно будем умножать на себя, а показатель степени скажет нам, сколько раз основание будет умножено на себя. Таким образом, 5 3 означает то же самое, что и 5 x 5 x 5.
Для нас, чтобы прочитать 5 3 , мы можем прочитать как:
- пять в степени три,
- пять в степени три , и
- пять в степени три.
Возведение в степень — математическая операция, записанная в виде x n , где x обозначает основание, а n представляет показатель степени.
Каково происхождение показателей? Слово мощность произошло от латинского слова potentia, potestas, dignitas , которое является неправильным переводом древнегреческого термина δύναμις ( dúnamis) , который Евклид использовал для обозначения квадрата линии, следуя Гиппократу. Хиоса.
Хиоса.
Тем временем Архимед открыл и доказал законы экспонент в своем труде «Счетчик песка». В своей работе он смог доказать 10 а х 10 б = 10 а + б . В 19 -м -м веке Мухаммад ибн Муса аль-Хорезми ввел термин مَال (мал, «имущество», «имущество») для квадрата.
Йост Бюрги использовал экспоненты для римских цифр в конце 16 века. В 15 веке Николя Шюке создал тип экспоненциальной записи, который позже был использован Хенрикусом Грамматеусом и Майклом Стифелем в 16 веке. Майкл Штифель ввел термин «экспонент» в 1544 г. В 169 г.6 Сэмюэл Джик ввел термин «индексы».
Рене Декарт установил первую форму современной нам экспоненциальной записи в своем трактате под названием «Геометрия» в начале 17 века; обозначения вводятся в Книге I текста.
Леонард Эйлер предложил переменные показатели степени и, неявно, нецелые показатели степени в 1748 году, когда он написал:
«рассмотрите экспоненты или степени, в которых показатель степени является переменной. Ясно, что величины такого рода не являются алгебраическими функциями, так как в них показатели степени должны быть постоянными».
Ясно, что величины такого рода не являются алгебраическими функциями, так как в них показатели степени должны быть постоянными».
Чтобы ответить и решить задачи, связанные с показателями, законы показателей являются фундаментальными. Эти правила необходимо соблюдать, чтобы иметь возможность упростить формулы с показателями степени. Давайте взглянем на следующие правила, которые у нас есть для показателей!
Правило произведения
Правило произведения показателей степени используется для умножения выражений, имеющих одинаковые основания. Это правило гласит, что для любого ненулевого члена есть , где m and n are real numbers,
a m x a n = a m + n
Это означает, что для получения произведения показателей степени, имеющих одинаковое основание, мы просто складываем их показатели степени и основания.
Пример #1
Каково произведение 5 2 и 5 3 ?
Solution
| Process | Explanation |
| 5 2 x 5 3 | Set-up the multiplication process. |
| 5 2 x 5 3 = 5 2 + 3 | Используя правило произведения, мы просто скопируем основание и добавим показатели степени. |
| 5 2 + 3 = 5 5 | Сложите показатели степени. Следовательно, 2 + 3 = 5 |
| 5 5 = 3125 | Следовательно, 5 х 5 х 5 х 5 х 5 = 3125 |
Следовательно, произведение 5 2 и 5 3 равно 5 5 или 3125 . |
Пример #2
Найдите произведение a и a 6 .
Solution
| Process | Explanation |
| a 1 x a 6 | Настройте процесс умножения. |
| A 1 X A 6 = A 1 + 6 = A 1 + 6 = A . Показатель степени a равен 1. Следовательно, мы будем иметь a 1 + 6 | |
| a 1 + 6 = a 7 | Сложите показатели степени. Следовательно, Следовательно, 1 + 6 = 7 |
| Следовательно, произведение на и на 6 равно на 7 . |
Example #3
Find the product of x 3 y and x 3 y 2 .
Решение
| Process | Explanation |
| (x 3 y)(x 3 y 2 ) | Настройка процесса умножения. |
| (х 3 у)(х 3 y 2 ) = x 3 + 3 y 1 + 2 | Using product rule, we will simply copy основание и добавить показатели. Поскольку у нас есть две переменные, мы по-прежнему будем копировать оба основания, но обратите внимание на показатели степени каждой переменной. Следовательно, мы будем иметь x 3 + 3 y 1 + 2 |
| x 3 + 3 y 1 + 2 = x 6 y 3 | Добавьте показатели степени. Следовательно, показатель степени x будет равен x 3 + 3 = x 6 , а показатель степени будет равен y 1 + 2 = y 3 |
Therefore, the product of x 3 y and x 3 y 2 is x 6 г 3 .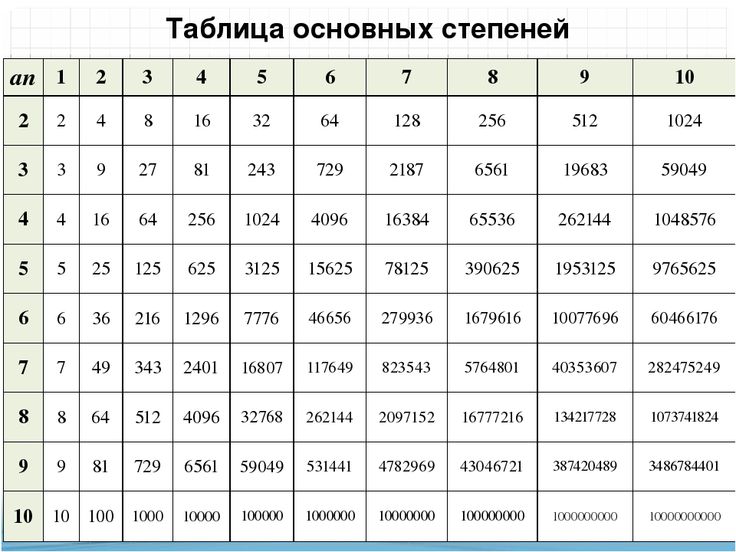 |
Правило частных
Правило частных показателей используется для упрощения алгебраических терминов или выражений, имеющих одинаковые основания. Это правило гласит, что для любого ненулевого члена 9{m – n}$
Это означает, что для того, чтобы получить частное экспоненты с тем же основанием, мы просто скопируем основание и вычтем показатель степени числителя на показатель степени знаменателя.
Пример #1
Чему равно частное, если 9 7 разделить на 9 3 ?
Решение
| Процесс | Объяснение | |
| $\frac{9{7 – 3}$ | Используя правило отношения, просто скопируйте основание и вычтите показатели степени. | |
| 9 7 – 3 = 9 4 | Вычтите показатели степени. Следовательно, 7 – 3 = 4 | |
| 9 4 = 6561 | Вычислить 5 515 . Следовательно, 9 x 9 x 9 x 9 = 6561 Следовательно, 9 x 9 x 9 x 9 = 6561 | |
| Следовательно, частное 9 7 и 9 3 равно 9{10 – 7}$ | Используя правило отношения, просто скопируйте основание и вычтите показатели степени. | |
| a 10 – 7 = a 3 | Вычтите показатели степени. Следовательно, 10 – 7 = 3 | |
| Следовательно, частное a 10 и a 7 равно a 3 9. |
Пример №3
93y$while the exponent of will be y 3 – 2 = y 1 .
Поскольку показатель степени y равен 1, мы можем просто записать его как y вместо y 1 .

Правило нулевой степени
Правило нулевой степени используется для упрощения алгебраических терминов или выражений, имеющих нулевой показатель степени. Это правило просто гласит, что если показатель степени любого ненулевого основания a равен нулю, то он всегда равен 1.
a 0 = 1
3 0 ?
Solution
| Process | Explanation |
| 3 0 = 1 | By zero exponent rule, 3 0 is simply equal на 1. |
Следовательно, 3 0 равно 1 . |
Пример #2
Определите значение а 0 .
Solution
| Process | Explanation |
| a 0 = 1 | By zero exponent rule, a 0 is simply equal на 1. |
| Следовательно, 0 равно 1 . |
Пример №3
Найдите эквивалент x 0 y 0 .
Solution
| Process | Explanation |
| x 0 y 0 = (1)(1) | По правилу нулевого порядка, x 0 = 1, y 0 = 1.  |
| (1)(1) = 1 | Получите продукт 1 и 1. Таким образом, 1 x 1 = 1 |
| Следовательно, x 0 Y 0 равен 1 . |
Правило отрицательного показателя степени
Правило отрицательного показателя степени используется для упрощения алгебраических терминов или выражений, имеющих отрицательный показатель степени. Это правило гласит, что если показатель степени любого ненулевого основания a отрицателен, нам нужно преобразовать его в положительный показатель, получив его обратную величину. 93}$ .
Сила степенного правила
Сила степенного правила используется для упрощения алгебраических терминов, когда показатель степени основания возводится в другую степень, мы получим произведение двух степеней. This rule states that if a non-zero term a and m and n are integers,
(a m ) n = a mn
Example #1
Simplify (4 3 ) 2 .
Solution
| Process | Explanation |
| (4 3 ) 2 = 4 3 x 2 | Чтобы упростить (4 3 ) 2 , мы будем использовать силу правила степени. Следовательно, (4 3 ) 2 = 4 3 x 2 |
| 4 3 x 2 = 4 6 | 8 Таким образом, 3 x 2 = 6|
| 4 6 = 4096 | Оценить 1 615 615 Таким образом, 4 x 4 x 4 x 4 x 4 x 4 = 4096 |
Следовательно, (4 3 ) 2 равно 4 6 или 4096. |
Пример #2
Упростить (a 3 ) 7 .
Solution
| Process | Explanation |
| (a 3 ) 7 = a 3 x 7 | Для упрощения (a 3 ) 7 , мы будем использовать силу правила мощности. Hence, (a 3 ) 7 = a 3 x 7 |
| a 3 x 7 = a 21 | Multiply the exponents. Таким образом, 3 x 7 = 21 |
Следовательно, (a 3 ) 7 равно a 21 . |
Сила правила продукта
Сила правила произведения используется для упрощения алгебраических терминов с более чем одной переменной, которые перемножаются вместе и возводятся в степень. Это правило гласит, что если ненулевой член a и b и m является целым числом,
(ab) m = a m b m
(аб) 8 .
Решение
| Процесс | Explanation | ||||||||
| (ab) 8 = a 8 y 8 | To simplify (ab) 8 , we will использовать силу правила продукта. Следовательно, (AB) 8 = A 8 Y 8 | ||||||||
Следовательно, (x 4 Y 5 ) 3 — это равное на x ) . 0915 15 . Пример №2 0915 15 . Пример №2Solution
Степень правила отношенияСтепень правила отношения используется для упрощения отношения частного алгебраического члена с более чем одной переменной путем простого распределения показателя степени на числитель и знаменатель. Это правило гласит, что если ненулевой член 9{30}}$ . |
Когда дело доходит до упрощения показателей, учащиеся допускают ошибки, которые приводят к неправильному ответу. Некоторые из этих ошибок перечислены ниже:
- Умножение основания и показателя степени .
 Обычно ученики просто умножают основание на число, написанное на показателе степени.
Обычно ученики просто умножают основание на число, написанное на показателе степени.
Неверно: 3 4 ≠3 x 4
Правильно: 3 3 = 3 x 3 x 3 x 3
- Неверное применение силы правила произведения . Некоторые учащиеся распределяют показатель степени, даже если он не является произведением двух или более переменных.
Неправильно: (4 + 5) 2 ♠ 4 2 + 5 2
Правильно: (4 + 5) 2 = (9) 2 = 81915 2 = (9) 2 = 81915
03. значение показателей?Экспоненты обычно используются как сокращение для представления числа, которое многократно умножается само на себя. Большую часть времени мы не видим и не используем показатели в нашей повседневной жизни, но они очень важны, особенно в науке.
Экспоненты используются в , показывая квадратные или кубические измерения , такие как квадратные футы (футы 2 ), квадратные метры (м 2 ), квадратные дюймы (в 2 ), квадратные мили (ми 2 ) , кубические футы (футы 3 ), кубические метры (м 3 ). С помощью показателей нам легче различать квадратные и кубические измерения. Проведение измерений и вычисление многомерных величин — одно из наиболее распространенных приложений экспоненты в реальном мире. Поскольку площадь является двумерной мерой пространства (длина х ширина), она всегда измеряется в квадратных единицах, таких как квадратные футы или квадратные метры.
С помощью показателей нам легче различать квадратные и кубические измерения. Проведение измерений и вычисление многомерных величин — одно из наиболее распространенных приложений экспоненты в реальном мире. Поскольку площадь является двумерной мерой пространства (длина х ширина), она всегда измеряется в квадратных единицах, таких как квадратные футы или квадратные метры.
Ученые используют показатель степени для отображения чрезвычайно больших или малых чисел . С помощью показателей степени стало возможным записывать числа в научной записи. В научной записи 150 000 можно записать как 1,5 x 10 5 , что означает 1,5 x 10 x 10 x 10 x 10 x 10.
Показатель степени имеет большое значение в любом научном измерении, в котором используется такая шкала, как pH. шкала и шкала Рихтера. Шкала pH и шкала Рихтера являются логарифмическими шкалами, где каждое целое число означает десятикратное увеличение по сравнению с предыдущим значением.
Скажем, например, ученый знает, что вещество с pH 4 обозначает 10 4 , а вещество с pH 8 представляет 10 5 .


 Таким образом,
Таким образом, 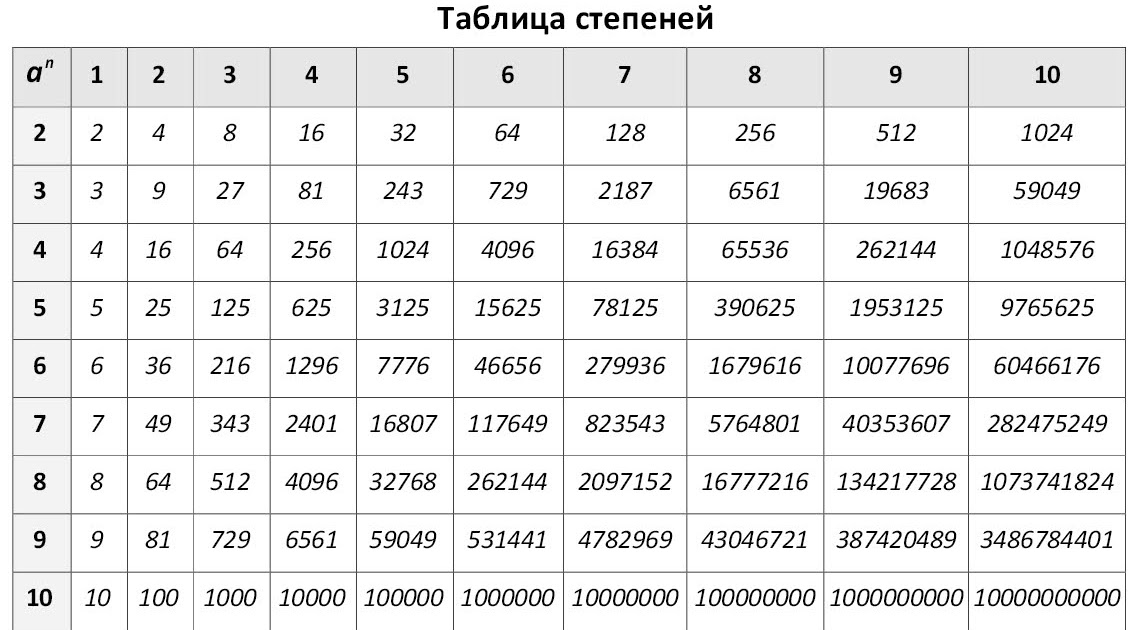 Обычно ученики просто умножают основание на число, написанное на показателе степени.
Обычно ученики просто умножают основание на число, написанное на показателе степени.