1. Первообразная и неопределенный интеграл.
Первообразная. Функция F(x) называется первообразной от функции f(x) на отрезке [a,b], если во всех точках выполняется равенство F(x) = f(x).
Так как С-произвольная постоянная, у любой функции бесчисленное множество первообразных.
Теорема. Если F1(x) и F2(x) – 2 первообразные от функции f(x) на отрезке [a,b], то разность между ними равна постоянному числу.
Доказательство. Пусть F1(x) = f(x) и F2(x) = f(x). Таким образом F1(x) = F2(x). Рассмотрим производную разности
(F1(x) – F2(x)) = F1(x) — F2(x) = 0.
Производная
разности двух функций равна нулю,
следовательно, эти функции отличаются
друг от друга на константу, ч. т. д.
Неопределенный интеграл. Если функция F(x) является первообразной для f(x), то выражение F(x)+C называется неопределенным интегралом от функции f(x).
Таким образом,
f(x) – подынтегральная функция, f(x) dx – подынтегральное выражение.
Из определения неопределенного интеграла следует:
1. Производная от неопределенного интеграла равна подынтегральной функции, т.е. если F(x) = f(x), то и
2.Дифференциал неопределенного интеграла равен подынтегральному выражению
3. Неопределенный интеграл от дифференциала некоторой функции равен этой функции плюс произвольная постоянная
с точностью до
постоянного слагаемого.
Свойства неопределенного интеграла.
Теорема1. Неопределенный интеграл от алгебраической суммы двух или нескольких функций равен алгебраической сумме их интегралов.
Доказательство. Найдем производные от левой и правой части равенства. Так как они равны, по теореме о том, что любая функция, стоящая в левой части, отличается от любой функции, стоящей в правой части, на постоянное слагаемое.
Теорема2. Постоянный множитель можно выносить за знак интеграла, т.е. если а=const, тогда
Доказательство. Найдем производные от левой и правой частей —
Они равны. Как и в теореме1, разность двух функций – есть постоянная.
___
При вычислении неопределенных интегралов полезно знать следующие правила:
1.
2.
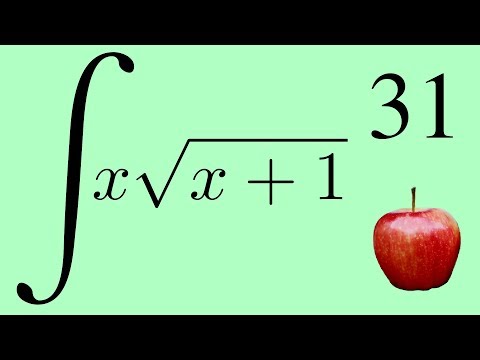
3.
Интегрирование методом замены переменного или способом подстановки.
Требуется найти f(x)dx. Делаем замену x = (t). Получаем f(x)dx = f((t))(t)dt.
Для того, чтобы подтвердить, что эти выражения равны, можно взять производные от левой и правой частей. Они равны.
Интегрирование по частям. Пусть u и v – непрерывно дифференцируемые функции от x. Тогда d(uv) = udv + vdu. Отсюда получаем Или
Полученная формула называется формулой интегрирования по частям
.Определенный интеграл. Если при любых разбиениях отрезка [a,b] таких, что и при любом выборе точекна отрезках [хi-1, xi] интегральная сумма стремится к одному и тому же пределуS, то этот предел называют определенным интегралом от функции f(x) на отрезке [a,b]и обозначают
Число
а – нижний предел, число b
– верхний предел.
Отрезок [a,b]
– отрезок интегрирования, х – переменная
интегрирования.
Функция называется интегрируемой на отрезке [a,b], если для функции f(x) существует предел
Если построить график подынтегральной функции y=f(x), то в случае интеграл будет численно равен площади криволинейной трапеции, ограниченной прямыми х=а, х=b и осью Ох. В этом и заключается геометрический смысл
Примечание автора. Обязательна графическая иллюстрация.
Физические задачи, решаемые с помощью определенного интеграла.
С помощью определенных интегралов решаются задачи на нахождение работы, скорости, пути, моментов инерции. Это осуществляется путем нахождения площадей, длин дуг, объемов и пр.
3.
Теорема существования определенного
интеграла. Если функция кусочно-непрерывна на
отрезке [a,b],
то она интегрируема на этом отрезке.
Примечание автора. В методическом пособии теорема приведена без доказательства.
Свойства определенного интеграла.
Свойство1. Постоянный множитель можно выносить за знак определенного интеграла: если А= const, то
Доказательство.
Свойство2. Определенный интеграл от алгебраической суммы нескольких функций равен алгебраической сумме интегралов от слагаемых.
Доказательство.
Свойство3. Если на отрезке [a,b], где а<b, функции f(x) и (х) удовлетворяют условию то
Доказательство. Рассмотрим разность
Каждая разность
Сл-но, неотрицательно
каждое слагаемое, неотрицательны вся
сумма и весь предел.
Свойство4. Если m и М – наименьшее и наибольшее значения функции f(x) на отрезке [a,b] и то
Доказательство. По условию
Подставляя 2 последние выражения в неравенство получаем исходное неравенство.
Свойство5 (теорема о среднем). Если функция f(x) непрерывна на отрезке [a,b], то на этом отрезке найдется такая точка что справедливо равенство:
Доказательство. Пусть a<b, m – наименьшее значение функции, М – наибольшее значение f(x) на отрезке [a,b]. Тогда получаем
Отсюда где
Так как функция непрерывна на отрезке, то она принимает все промежуточные значения, заключенные между m и М. Следовательно, при некотором значении будетто есть
Примечание
автора. Доказательство приведено и в
одном из следующих вопросов.
Свойство6. Для любых трех чисел a,b,c справедливо равенство если все эти три интеграла существуют.
Доказательство. Допустим сначала, что и составим интегральную сумму для функцииf(x) на отрезке [a,b].
Так как предел интегральной суммы не зависит от способа разбиения отрезка, будем разбивать отрезок так, чтобы точка с была точкой деления. Тогда
Переходя к пределу при получим исходное соотношение.
Если на основании доказанногоили
Поэтому имеем
Аналогично доказывается это свойство при любом взаимном расположении трех точек.
Определенный интеграл — презентация онлайн
Похожие презентации:
Элементы комбинаторики ( 9-11 классы)
Применение производной в науке и в жизни
Проект по математике «Математика вокруг нас. Узоры и орнаменты на посуде»
Знакомство детей с математическими знаками и монетами
Тренажёр по математике «Собираем урожай».
Счет в пределах 10
Методы обработки экспериментальных данных
Лекция 6. Корреляционный и регрессионный анализ
Решение задач обязательной части ОГЭ по геометрии
Дифференциальные уравнения
Подготовка к ЕГЭ по математике. Базовый уровень Сложные задачи
Определенный
интеграл
Правила интегрирования
cf ( x)dx c f ( x)dx, c const
( f ( x) g ( x))dx f ( x)dx g ( x)dx
1
f (ax b)dx a F (ax b) C , a 0
Определенный интеграл
В декартовой прямоугольной
системе координат XOY фигура,
ограниченная осью OX, прямыми
x=a, x=b (a<b) и графиком
непрерывной неотрицательной
на отрезке [a;b] функции y=f(x),
называется криволинейной
трапецией
Определенный интеграл
отрезок [a;b] на n равных частей. Проведем через
полученные точки прямые, параллельные оси OY.
Заданная криволинейная трапеция разобьется на n
частей. Площадь всей трапеции приближенно равна
сумме площадей столбиков.
S n f ( x0 ) x0 f ( x1 ) x1 … f ( xn 1 ) xn 1
S Sn
по определению S lim S n , его называют
n
определенным интегралом от функции
y=f(x) по отрезку [a;b] и обозначают так:
b
f ( x)dx
a
Связь между определенным
интегралом и первообразной
(Формула Ньютона — Лейбница)
Для непрерывной функции
b
f
(
x
)
dx
F
(
x
)
|
F
(
b
)
F
(
a
)
b
a
a
где F(x) – первообразная функции f(x).
Основные свойства определенного
интеграла
a
f
(
x
)
dx
0
b
dx
b
a
a
b
a
a
b
f
(
x
)
dx
f
(
x
)
dx
Основные свойства определенного
интеграла
b
c
b
a
a
c
f
(
x
)
dx
f
(
x
)
dx
f
(
x
)
dx
b
b
a
a
cf
(
x
)
dx
c
f
(
x
)
dx
,
c
const
b
b
b
a
a
a
(
f
(
x
)
g
(
x
))
dx
f
(
x
)
dx
g
(
x
)
dx
Геометрический смысл
определенного интеграла
Площадь криволинейной трапеции,
ограниченной графиком непрерывной
положительной на промежутке [a;b] функции
f(x), осью x и прямыми x=a и x=b:
b
S f ( x)dx
a
Геометрический смысл
определенного интеграла
Площадь криволинейной трапеции,
ограниченной графиком непрерывной
отрицательной на промежутке [a;b] функции f(x),
осью x и прямыми x=a и x=b:
b
S f ( x)dx
a
Геометрический смысл
определенного интеграла
Замечание: Если функция изменяет знак на
промежутке [a;b] , то
b
S1 S 2 f ( x)dx
a
Физический смысл
определенного интеграла
При прямолинейном движении перемещение s
численно равно площади криволинейной
трапеции под графиком зависимости скорости v
от времени t:
t2
S v(t )dt
t1
Вычисление площадей и объемов
с помощью определенного интеграла
Площадь фигуры,
Ограниченной графиками непрерывных
функций y=f(x) и y=g(x) таких, что f ( x) g ( x)
для любого x из [a;b], где a и b – абсциссы точек
пересечения графиков функций:
b
S ( f ( x) g ( x))dx
a
Объем тела,
полученного в результате вращения вокруг оси
x криволинейной трапеции, ограниченной
графиком непрерывной и неотрицательной
функции y=f(x) на отрезке [a;b]:
b
V f ( x)dx
2
a
English Русский Правила
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Почему интеграл от 1/x равен натуральному логарифму от x?
В заголовке этого поста содержится вопрос, который многих студентов-математиков сбивает с толку.
Здесь я дам немного геометрической интуиции, стоящей за этим. Я оставляю небольшие логические пробелы, чтобы не лишать читателя удовольствия от их открытия.
Одной из существенных особенностей логарифмов является то, что они делают задачу на умножение эквивалентной задаче на сложение, под которой я подразумеваю
Между тем, обычно считается геометрически как площадь под кривой. Таким образом, проблема состоит в том, чтобы попытаться визуально увидеть, какое отношение площадь под кривой имеет к превращению умножения в сложение.
Вот график , и мы находим, например, площадь под ним от 1 до 2. область от 2 до 4. Вот как это выглядит.
: Эти две части на самом деле очень похожи друг на друга по своей общей форме. Оранжевый в два раза шире зеленого, но и вполовину выше. Здесь они накладываются.
Если вы возьмете зеленую фигуру и сначала сожмете ее по вертикали в два раза, а затем растянете по горизонтали в два раза, вы получите точно оранжевую форму.
(Если вы не верите в это, убедитесь, что это работает!) Это означает, что площади этих фигур абсолютно одинаковы, даже если мы не знаем, что это за площадь.
Покажите сами, что этот результат является общим. Область от до такая же, как и от до .
Чему же тогда равна площадь от 1 до 6? Мы можем разбить его на две части — площадь от 1 до 2 и площадь от 2 до 6. Но площадь от 2 до 6 — это то же самое, что и площадь от 1 до 3, по рассуждениям выше.
Таким образом, площадь от 1 до 6 равна сумме площадей от 1 до 2 и от 1 до 3. Обратите внимание, что 6 = 3*2. Опять же, это общее. Площадь под от до равна сумме площадей от до и от до .
Это довольно хорошая мотивация для определения
Обратите внимание, что это рассматривается как определение натурального логарифма, а не доказательство связи. Наше рассуждение об интеграле от now преобразуется в утверждение
Теперь шаг за шагом мы покажем, что все остальные свойства, которые вы ожидаете от натурального логарифма, следуют из этого определения.
Очевидно, что
Наше определение подразумевает, что логарифм неограниченно растет, потому что, если мы постоянно умножаем аргумент логарифма на два, мы постоянно прибавляем к значению. (т.е. ). Поскольку мы можем умножать любое число на два снова и снова, мы можем прибавлять к логарифму столько раз, сколько захотим. Это означает, что мы можем сделать логарифм сколь угодно большим.
Это также означает, что начинать интеграл не с нуля, а с нуля было хорошей идеей. Если мы начнем с нуля, интеграл будет бесконечен. Мы можем видеть это, потому что он симметричен относительно линии .
Это означает, что площадь слева от кривой такая же, как площадь под кривой, как здесь.
Мы только что показали, что площадь под кривой расходится, когда мы смещаем правую часть интеграла в бесконечность, поэтому площадь слева от кривой также расходится. Если бы мы начали интеграл с нуля, он был бы бесконечен.
Как насчет логарифмирования чисел меньше единицы? Хорошей проверкой того, все ли имеет смысл до сих пор, является работа над этим.
Так как площадь под начинается с нуля, когда и увеличивается до бесконечности, ясно, что должно быть некоторое число такое, что . Давайте позвоним по этому номеру. Мы еще не знаем, что это такое, но оно определенно существует. Итак,
Опять же, это определение, а не доказательство.
Сразу видно, что, например, . Получается довольно удобное число. Он показывает нам, что логарифм числа — это то, сколько раз нужно умножить на себя, чтобы получить .
Как насчет? То есть . Итак, чтобы понять логарифмы рациональных чисел, нам нужно понять корни .
Впрочем, это не так сложно.
.
С другой стороны,
Из этого мы выводим . Возвращаясь к незаконченному примеру, . Не будет большим скачком сказать, что для любого рационального числа мы имеем
. Это важный результат; вероятно, это то определение, к которому вы привыкли. Детали встают на свои места. Главное оставшееся препятствие состоит в том, чтобы найти значение и показать, что оно сводится к тому, что мы ожидаем.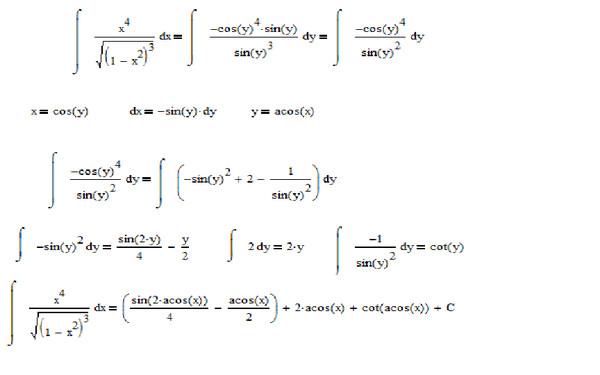
Перед этим следует упомянуть, как это соотношение работает для иррациональных чисел. Иррациональные числа втиснуты между рациональными, а поскольку определение логарифма как площади под кривой, очевидно, является гладким, тесно втиснут и логарифм иррационального числа. В конечном счете, указанное выше соотношение выполняется для всех положительных чисел. Однако мелкие детали действительных чисел более сложны, чем я хотел бы здесь затронуть. (Логарифм отрицательного числа или нуля не определен, по крайней мере, в действительных числах. Какая трудность в этом?)
Наконец, нам нужен способ определить, что есть. Вот один из способов сделать это. Для малых значений , мы можем видеть, что
Это следует из чрезвычайно простой аппроксимации ниже.
Красная рамка представляет собой аппроксимацию площади зеленого интеграла. Красный квадрат явно имеет площадь, а зеленый интеграл равен . Таким образом,
Это грубо, но работает все лучше и лучше по мере того, как становится крошечным.