| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
Math 116 Practice Final Printable Key
Решите каждую из данных задач.
Кредит будет основан
на шагах, которые вы показываете на пути к окончательному ответу. Покажи свою работу
Задача 1 Найдите производную следующих функций
А. f(x) = ln(ln(1 — x))
Раствор
Мы используем цепное правило. У нас есть
ты = 1 — x u’ = -1
v = ln(u) v’ = 1/u
f(v) = ln(v) f ‘(v) = 1/v
Отсюда
ф ‘(х) = (-1)(1/и)(1/в)
-1
=
(1 — х)(ln(1 — х))
Б.
Раствор
У нас есть
Пусть
u = х 2 ln х u’ = 2x ln x + x 2 (1/x) = 2x ln х + х
f(u) = e u f ‘(и) = е и
Отсюда
f ‘(x) = e u (2x ln x + x)
С.
е x
f(x) =
грех
Икс
Раствор
Мы использовать правило отношения. У нас есть
(sin x)e x — e x (cos
Икс)
e x (sin x — cos x)
ф'(х)
знак равно
=
грех 2 Икс
грех 2 x
Проблема 2 Вычислите следующие интегралы
А.
Раствор
Используем интегрирование по частям
u = x dv = e 2x дх ж = 2x dw = 2dx 1/2 дв = дх
du = dx v = 1/2 e 2x
Мы получить
Б.
Мы используйте частичные дроби здесь
3x +
1
А
Б
знак равно
+
х 2 — х —
6 х —
3 х + 2
или
3x + 1 = A(x + 2) + B(x — 3)
Пусть х = 3: 10 = 5A A = 2
Пусть х = -2: -5 = -5B B = 1
Это дает нам
С.
Мы используйте u-замену
u = 2x + 1 du = 2dx
x = 1/2 u — 1/2 dx = 1/2 du
Мы есть
Д.
Раствор
Это является несобственным интегралом, мы используем u-подстановку с
u = x 3 du = 3x 2 dx 1/3u = x 2 dx
Мы есть
Э.
Раствор
Мы пусть
ты = потому что x du = -sin x dx
Мы получить
Проблема 3
Найдите объем тела, образованного вращением области, ограниченной кривые
у = х 2 + 4 и г = 5 x 90 909
о ось х.
Раствор
Сначала мы изобразим два уравнения и построим поперечное сечение вокруг ось х.
Чтобы найти точки пересечения, мы задаем уравнения, равные каждому
Другой.
У нас есть
x 2 + 4 = 5x
x 2 — 5x + 4 = 0
(х — 4)(х — 1) = 0
х = 4 или х = 1
Обратите внимание, что верхняя кривая y = 5x а нижняя кривая y = x 2 + 4. Площадь шайбы
А = pr 2 — pr 2
Р = 5x r = x 2 + 4
Если все это объединить, получится
.Проблема 4
В 1980 было 200 зарегистрированы случаи заражения вирусом ВИЧ. Это было предсказал, что число случаев ВИЧ в конечном итоге стабилизируется на уровне около 80 000 000 человек. Определите год, когда число инфицированных достигнет 50 000 000, решив дифференциальное уравнение
. ДП
= .01P(80 000 000 — P) 90 939
дт
Раствор
Интегрируем
Интеграл правой руки равен 0,3t + C.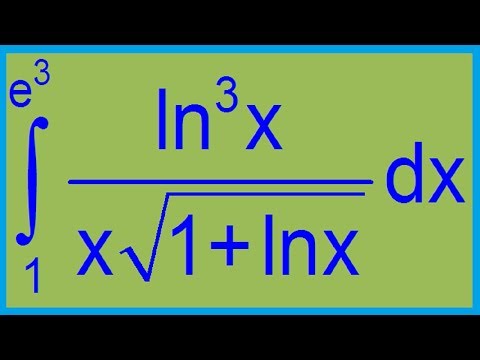
Для левого
ручной интеграл мы используем частичные дроби. У нас есть
1
А
Б
знак равно
+
Р(80 000 000 —
П)
п
80 000 000 — П
Так что
1 = A(80 000 000 — P) + 90 909 BP
Пусть P = 80 000 000: 1 = 80 000 000B B = 1/80 000 000
Пусть Р = 0: 1 = 80 000 000 А А = 1/80 000 000
Сейчас интегрировать, чтобы получить
1 1лнП — ln(80 000 000 — P) = .01t + C
80 000 000 80 000 000
Умножение на 80 000 000 дает
lnP — ln(80 000 000 — P) = 24 000 000 т + M M = 80 000 000C
Затыкание в P = 200, когда т = 0 дает
M = ln 200 — ln(80 000 000 — 200) = -12,9 90 909
Мы нужен год, когда P = 50 000 000. У нас есть
50 000 000 ln — 30 000 000 ln = 0,3t — 12,9
0,51 = 0,3 т — 12,9 т = 44,7
Можно сделать вывод, что в 2025 году вирус ВИЧ
заразили 50 000 000 человек.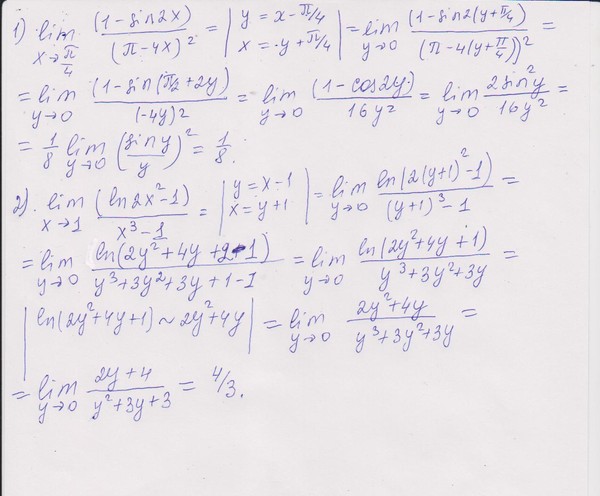
Проблема 5
Рост ВНП с 1980 г. можно смоделировать с помощью уравнение
y = 3 cos(0,8t) + 2
А. Найдите период этой функции и объясните, что это говорит о росте.
Раствор
Мы есть
Период = 2p/0,8 = 7,85
Это означает, что существует цикл роста, который повторяется каждые 7,85 годы.
Б. Каков максимальный рост и когда он происходит? (Используйте исчисление, чтобы показать это).
Раствор
Находим производную по цепному правилу.
ты = .8t u’ = .8
f(u) = 3cos u + 2 f ‘(u) = -3sin u
г’ = (0,8)(-3sin(0,8t)) = -2,4sin(0,8t) 90 909
Это ноль, когда
.8т = кп t = kp/0,8 = 3,9k
Вторая производная равна
.г» = (.8)(-cos(.8t))
, что отрицательно для четного k. Следовательно
максимум происходит каждые 7,85 лет, начиная с
конец 1980.