10 класс иррациональные числа: Иррациональные числа — урок. Алгебра, 10 класс.

Содержание

Иррациональные числа — Математика — Презентации

Иррациональные числа

5 ед. отр.

ОА 2 ед.отр.

ОА 2,34 ед.отр.

ОА 2,3 ед.отр.

ОА 2,345… ед.отр.

1. Либо на каком-то шаге не получится остатка и тогда результатом измере-

ния длины отрезка будет натуральное число или десятичная дробь .

2. Либо остатки будут получаться в каждом шаге и тогда результатом изме-

рения длины отрезка будет бесконечная десятичная дробь .

Среди рациональных чисел нет

такого числа, квадрат которого равен 2.

– чётное

Бесконечные десятичные периодические дроби представляют

рациональные числа .

Каждое такое число можно записать в виде отношения , где – целое

число, а – натуральное.

называют

иррациональными .

Бесконечные десятичные непериодические дроби

Примеры иррациональных чисел:

Множество иррациональных чисел обозначают латинской заглавной буквой .

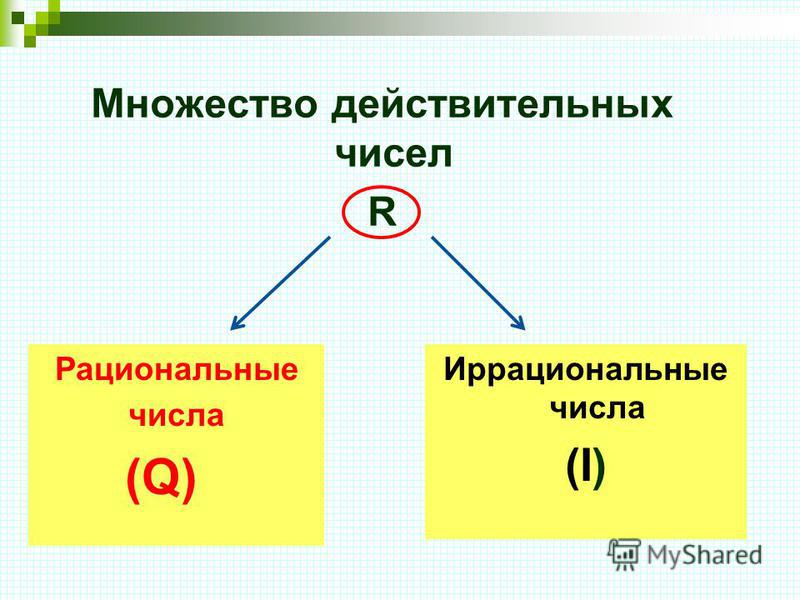
Рациональные

числа

Иррациональные

числа

Действительные числа

Множество действительных чисел –

От первой буквы латинского слова realis – реальный,

существующий в действительности.

Действительные числа, записанные с помощью бесконечных десятичных дробей, сравнивают по тем же правилам, что и конечные десятичные дроби.

Пример 1: сравнить числа

Пример 2: сравнить числа

Действительные числа также можно складывать , вычитать , умножать и делить (при условии, что делитель не равен нулю).

Пример 3: найти приближенное значение выражения , где

, округлив предварительно и до сотых.

Решение:

Пример 4: найти приближенное значение площади круга, радиус которого

равен 5 м (число округлите до сотых).

Решение:

Ответ: .

Повторим главное:

Бесконечные десятичные непериодические дроби называют иррациональными числами .

Множество действительных чисел состоит из множества рациональных

чисел и множества иррациональных чисел.

Действительные числа, записанные с помощью бесконечных десятичных

дробей, сравнивают по тем же правилам, что и конечные десятичные дроби.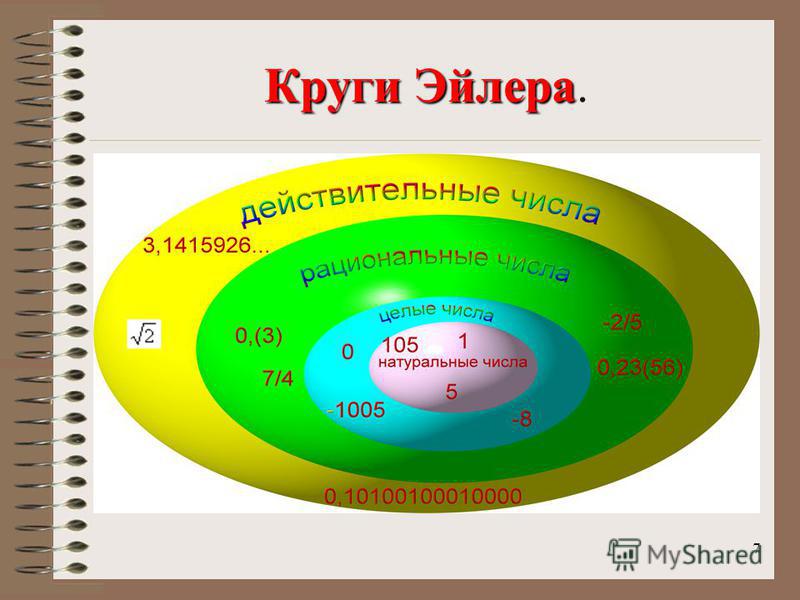

Действительные числа также можно складывать , вычитать , умножать и делить (при условии, что делитель не равен нулю).

Действия над действительными числами обладают теми же свойствами, что и действия над рациональными числами.

Презентация к уроку алгебры в 10 классе по теме «Действительные числа» | Презентация к уроку по алгебре (10 класс) по теме:

Слайд 1

Действительные числа 02.09.13

Слайд 2

Текст Числовые множества Обозначение Название множества N Множество натуральных чисел Z Множество целых чисел Q=m/n Множество рациональных чисел I=R/Q Множество иррациональных чисел R Множество вещественных чисел

Слайд 3

Множество натуральных чисел Натуральные числа — это числа счета. N={1,2,…n,…}. Заметим, что множество натуральных чисел замкнуто относительно сложения и умножения, т.е. сложение и умножение выполняются всегда, а вычитание и деление в общем случае не выполняются

Слайд 4

Множество целых чисел. Введем в рассмотрение новые числа: 1) число 0 (ноль), 2) число (- n ), противоположное натуральному n. При этом полагаем: n+(-n)=(-n)+n=0, -(-n)=n. Тогда множество целых чисел можно записать так: Z ={…,-n,…-2,-1,0,1,2,…,n,…}. Заметим также, что: Это множество замкнуто относительно сложения, вычитания и умножения, т.е. Из множества целых чисел выделим два подмножества: 1) множество четных чисел 2) множество нечетных чисел

Слайд 5

Множество рациональных чисел. Множество рациональных чисел можно представить в виде: В частности, Таким образом, Множество рациональных чисел замкнуто относительно сложения, вычитания, умножения и деления (кроме случая деления на 0).

Слайд 6

Но в множестве рациональных чисел нельзя, например, измерить гипотенузу прямоугольного треугольника с катетам . По теореме Пифагора гипотенуза будет равна .Но число не будет рациональным, так как ни для каких m и n . Нельзя решить уравнение . Нельзя измерить длину окружности и т.д. Заметим, что всякое рациональное число можно представить в виде конечной или бесконечной периодической десятичной дроби.

Слайд 7

Множество иррациональных чисел. Числа, которые представляются бесконечной непериодической дробью, будем называть иррациональными. Множество иррациональных чисел обозначим I . Для иррациональных чисел нет единой формы обозначения. Отметим два иррациональных числа, которые обозначаются буквами – это числа и е .

Слайд 8

Число «пи» Отношение длины окружности к диаметру есть величина постоянная, равная числу d

Слайд 9

Число е. Если рассмотреть числовую последовательность: с общим членом последовательности то с ростом п значения будут возрастать, но никогда не будет больше 3. Это означает, что последовательность ограничена. Такая последовательность имеет предел, который равен числу е.

Слайд 10

Известно, что мощность иррациональных чисел больше мощности рациональных, т.е. Иррациональных чисел «больше», чем рациональных. Кроме того, как бы ни были близки два рациональных числа, между ними всегда есть иррациональное, т.е.

Слайд 11

Множество вещественных (действительных) чисел. Множество вещественных чисел – это объединение множества рациональных чисел. Вывод:

Слайд 12

Определение модуля вещественного числа Пусть на числовой оси точка А имеет координату а . Расстояние от точки начала отсчета О до точки А называется модулем вещественного числа а и обозначается | a | . | a | = | OA | R’ a a A A O 2) Раскрытие модуля происходит по правилу:

Слайд 13

Например: Замечание. Определение модуля можно расширить: Пример. Раскрыть знак модуля. где f ( x )  функция аргумента x

Слайд 14

Основные свойства модуля 1) 2) 3) 4) 5) 6)

Слайд 15

Решение примеров с использованием свойств модуля Пример 1. Вычислить Пример 2. Раскрыть знак модуля Пример 3. Вычислить 1) 2) 3)

Иррациональные числа

Математика — это магия чисел. Мы уже знаем, что существуют разные типы чисел. Натуральные числа, целые числа, комплексные числа, действительные числа и целые числа — все это примеры различных типов чисел, с которыми мы знакомы. Вещественные числа также можно разделить на рациональные и иррациональные категории.

Иррациональные числа нельзя представить как отношение двух целых чисел. Они могут быть выражены на числовой прямой и являются подмножеством действительных чисел. Кроме того, десятичное расширение иррационального числа не заканчивается и не повторяется.

Что такое иррациональное число?

В математике действительные числа, которые не могут быть выражены в виде $\dfrac{p}{q}$, где p и q — целые числа, а q не равно нулю, называются иррациональными числами.

Эти номера представлены с помощью символа «Q».

Как определить иррациональные числа?

Мы знаем, что существуют иррациональные числа, которые нельзя выразить с помощью формулы $\dfrac{p}{q}$, где p и q — целые числа, а $q \neq 0$. К иррациональным числам относятся такие, как $\sqrt{5}$, $\sqrt{3}$ и т. д. Напротив, числа, которые можно представить в виде $\dfrac{p}{q}$, где p и q – целые числа и $q \neq 0$ — рациональные числа. Например: $\dfrac{3}{10}$, $\dfrac{1}{4}$ и т. д.

Некоторые известные примеры иррациональных чисел

Существует факт, что Пи является иррациональным числом, поскольку оно вычисляется с точностью более чем до квадриллиона знаков после запятой без какой-либо закономерности. $\pi=3,1415926535\ldots $.
Число Эйлера (e) не может быть записано в виде дроби и не заканчивается и не повторяется при записи в виде десятичной дроби, что делает его иррациональным числом. $e=2,7182818284 \ldots$
Одним из распространенных примеров иррационального числа является $\sqrt{2}=1,41421356237309.540488\ldots $
Во многих дисциплинах, включая информатику, дизайн, искусство и архитектуру, используется золотое сечение — иррациональное число. Первое число в золотом сечении, представленное символом $\Phi=1,61803398874989484820 \ldots$

Свойства иррациональных чисел

Десятичные числа с непрерывающимися и неповторяющимися образцами составляют иррациональные числа. Например, $\pi=3.141592653…5\ldots $ имеет не повторяющийся и не завершающийся шаблон.
Сложение, вычитание, умножение и деление двух иррациональных чисел может дать рациональное число, а может и не дать. Предположим, что если ab=c истинно, то $a = \dfrac{x}{b}$ истинно, что противоречит предположению об иррациональности x. Произведение a*b должно быть иррациональным.
Любое иррациональное число, умноженное на любое ненулевое рациональное число, дает иррациональное число.
Не обязательно, чтобы результат умножения двух иррациональных чисел всегда был иррациональным числом. Например, $\sqrt{2}+\sqrt{2}=2$, что рационально.

Интересные факты

Гиппас, бывший ученик Пифагора, как сообщается, открыл иррациональные числа, пытаясь выразить квадратный корень из 2 в виде дроби (используя геометрию). К сожалению, его теория была осмеяна и брошена в воду.

Решенные задачи на иррациональные числа

Пример 1. Определите, какие из следующих чисел являются рациональными и иррациональными.

$\sqrt{12}, \sqrt{16}, \sqrt{5}, 1.23123123412…$.

Решение: 92 $

$\Стрелка вправо (\sqrt{5}+\sqrt{2})(\sqrt{5}+\sqrt{2})$

$\Стрелка вправо \sqrt{5}(\sqrt{5} +\sqrt{2})+\sqrt{2}(\sqrt{5}+\sqrt{2})$

$\Стрелка вправо \sqrt{5} \times \sqrt{5}+\sqrt{5} \times \sqrt{2}+\sqrt{2} \times \sqrt{5}+\sqrt{2} \times \sqrt{2}$

$\Rightarrow 5+\sqrt{10}+\sqrt{ 10}+2$

$\Rightarrow 7+2 \sqrt{10}$

Самостоятельная практика

Вопрос 1. Что из перечисленного ниже является иррациональным?

0,14$
$ 0,14 \ Overline {16} $
$ 0. \ Overline {1416} $
$ 0,4014001400014 \ LDOTS

ANS: (D)

at.

$\sqrt{10} \times \sqrt{15}$ равно

$6 \sqrt{5}$
$5 \sqrt{6}$
$3 \sqrt $
$10 \sqrt{5}$

Ответ: (B)

Заключение

В этой статье резюмируется, что иррациональные числа определяются как разновидность действительных чисел, которые нельзя представить в виде $\dfrac{a}{b}$, где a и b — целые числа, а b не равно нулю.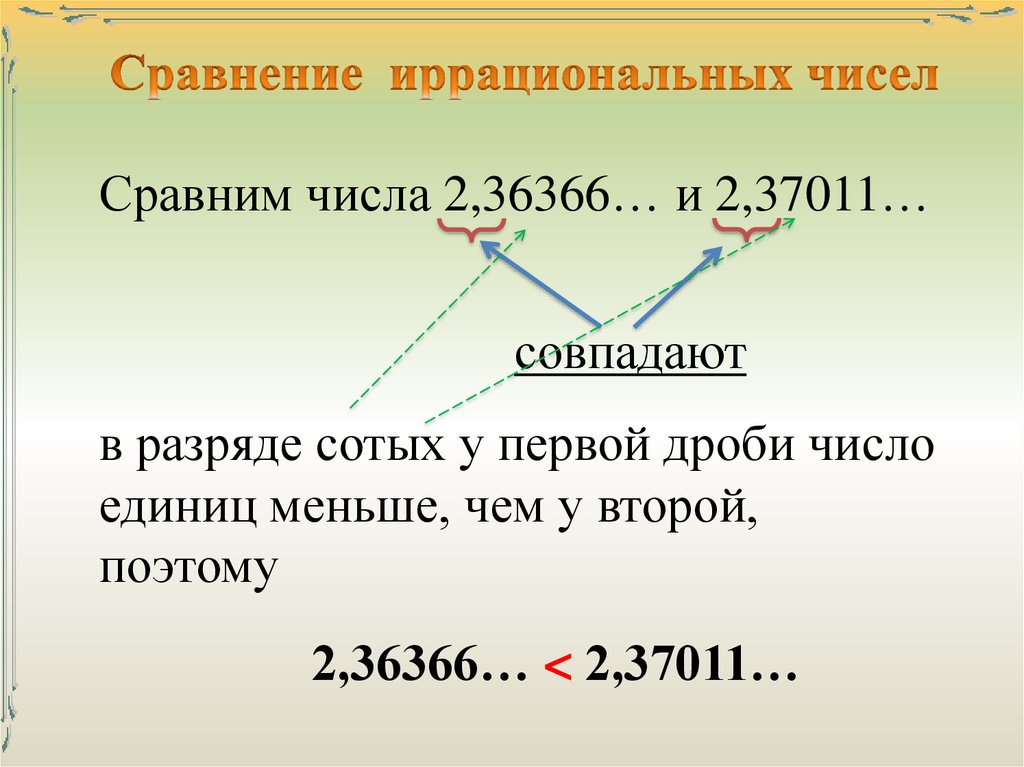 Они не могут быть выражены, потому что они являются неповторяющимися и неконечными десятичными знаками. Пи, $\sqrt{2}$, $\sqrt{5}$, золотое сечение, число Эйлера и другие являются хорошо известными примерами этого типа чисел.

Вещественные числа 10 класса — основы, задачи и примеры решения

Что такое действительные числа? Почему числа здесь называются реальными ? Прежде чем начать, попробуйте ответить на этот вопрос. Мы все изучали числа из класса 1 или даже раньше, и поэтому все мы знаем такое огромное разнообразие чисел, которые могут быть в миллионах, триллионах или любом другом числе. Но здесь позвольте мне спросить вас, как мы их классифицируем и в основном на каком основании они были классифицированы. Итак, давайте найдем несколько интересных ответов на эти интересные вопросы.

Любое число, которое может быть представлено на числовой прямой, называется действительным числом. Здесь числа называются реальными, потому что мы используем и применяем эти числа в нашем реальном мире, и они в равной степени связаны с сущностями реального мира.

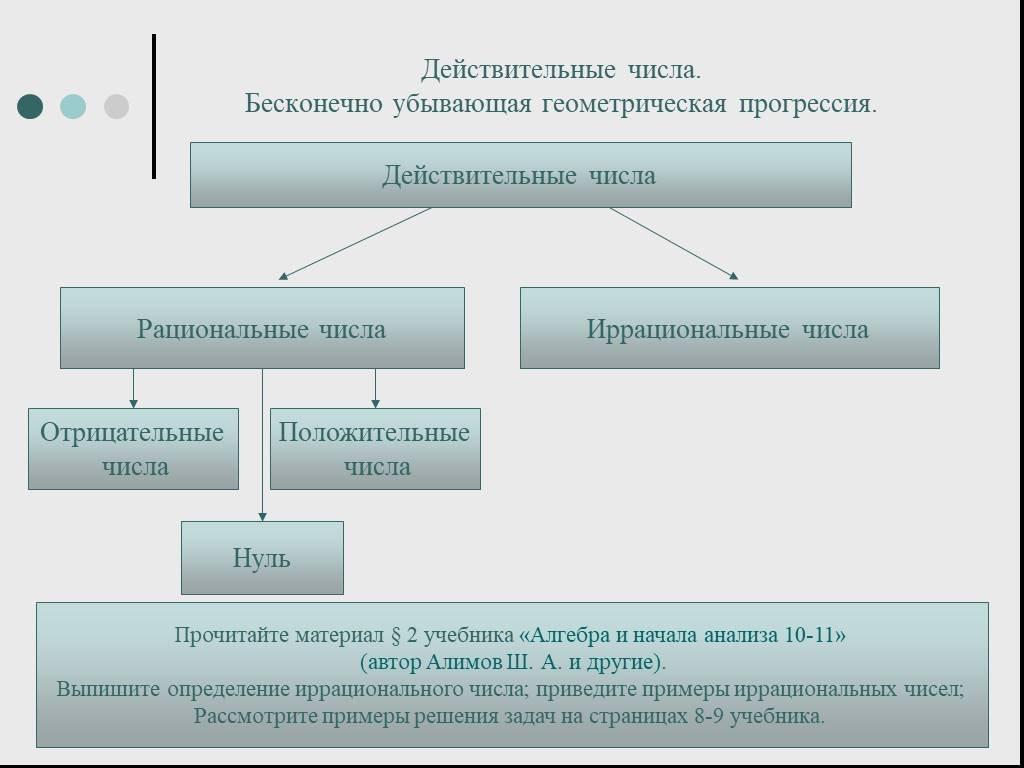
Если мы рассматриваем Действительные числа как множество, то рациональные числа и иррациональные числа являются его подмножествами, а целые числа, целые числа и натуральные числа являются далее подмножествами рациональных чисел.

Вещественные числа подразделяются на две основные категории, а эти две категории подразделяются на подкатегории. Давайте рассмотрим блок-схему, описанную ниже:

Рациональные числа

Числа, которые могут быть представлены в виде p/q, где p и q — целые числа, а q≠0 называется рациональным числом.

Пример 1: 2/3, 4/9, 8/7, 11/10 и т. д.

Здесь важно помнить, что p и q должны быть взаимно простыми числами.

Рациональные числа подразделяются на две категории:

Целые числа: Целое число — это любое число, которое может быть записано без дробной части. Например, 3,-2,56 являются целыми числами, потому что у них нет дробной части.

Целые числа далее классифицируются как:
Целые числа: Целые числа, начинающиеся с 0, называются целыми числами.
Натуральные числа: Целые числа, начинающиеся с 1, называются натуральными числами.

Нецелые числа : Те числа, которые не являются целыми числами, то есть фактически являются дробями, называются нецелыми числами. Например, 2/7, 3/5 и т. д. являются дробями.

Нецелые числа могут быть положительными, например 7/4, 8/9 и т. д., а также могут быть отрицательными, например -7/4 или -8/9.и т. д.

Иррациональные числа

Числа, которые нельзя записать в виде p/q, называются иррациональными числами. Пример √2, √3 и т.д.

Здесь возникает вопрос √2 можно представить как √2/1 даже тогда, когда это иррационально. Почему?

У него очень простой ответ, который скрывается в определении рациональных чисел. Там было упомянуто, что в p/q, p и q оба должны быть целыми числами, и здесь √2 строго не является целым числом.

Свойства

Рациональные и иррациональные числа обладают определенными тождествами, а также определенными свойствами:

Пусть R1 и R2 — два рациональных числа, а S1 и S2 — два иррациональных числа:

Пример 2: Пусть 2/7 и 4 будут двумя рациональными числами. Покажите, что их произведение и деление также рациональны.

Решение: Произведение = 2/7 x 4/1 = 8/7. (рациональное число)

Деление = 2/7 ÷ 4/1 = 2/7 x 1/4 = 1/14. (рациональное число)

R1±R2 всегда будет рациональным числом.

Пример 3: Пусть 7/2 и 5/2 — два рациональных числа. Покажите, что их сложение и вычитание дают рациональное число.

Решение: Сложение = 7/2 + 5/2 = 12/2 = 6 (рациональное число).

Вычитание = 7/2 – 5/2 = 2/2 = 1 (рациональное число).

R ± S всегда будет иррациональным.

Пример 4: Пусть 4 и √4 — рациональные и иррациональные числа. Покажите, что их сложение и вычитание дает иррациональное число.

Решение: Сложение = 4+√4 (иррациональное число).

Вычитание = 4-√4 (иррациональное число).

R x S или R÷S всегда будет иррациональным.

Пример 5: Пусть 2 и √2 — рациональное и иррациональное числа. Покажите, что их произведение и деление дают иррациональное число.

Решение: Произведение = 2 x √2 = 2√2 (иррациональное число).

Деление = 2/√2 и после рационализации получаем √2

(Иррациональное число).

S1±S2 всегда будет иррациональным.

Пример 6: Пусть √3 и √5 два иррациональных числа. Покажите, что их сложение и вычитание дает иррациональное число.

Решение: Сложение = √3+√5 (иррациональное число).

Вычитание = √3-√5 (иррациональное число).

S1 x S2 или S1÷S2 могут быть рациональными или иррациональными.

Пример 7: Пусть √3 и 4√3 — два иррациональных числа. Найдите их произведение и деление.

Решение: Произведение = √3 x 4√3 = 4 x 3 = 12. (Рациональное число)

Деление = 4√3 ÷ √3 = 4 (рациональное число)

Пример 8: Пусть √ 5 и √3 — два иррациональных числа. Найдите их произведение и деление.

Решение: Произведение = √5 x √3 = √15 (иррациональное число)

Деление = √5 ÷ √3 = √(5/3) (иррациональное число).

Свойства действительных чисел

Практические вопросы

Q1) в чем разница между рациональными и иррациональными числами.

Q2) Укажите True или False:

Все целые числа являются натуральными числами.
No related posts.