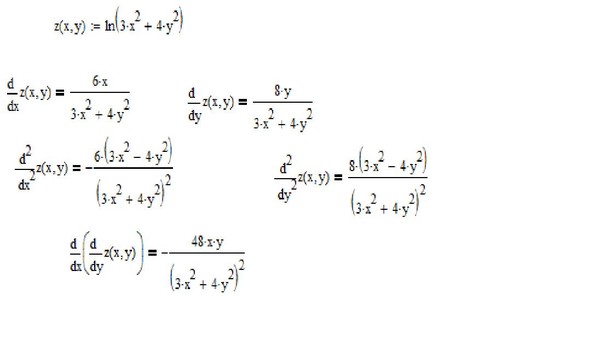2+n-72)=1/(n+9)3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92Производная от ln2x – формула, доказательство, примеры
Производная от ln2x равна 1/x.
Чтобы вычислить эту производную, мы можем использовать цепное правило дифференцирования или мы можем вычислить производную от ln2x, используя логарифмические свойства. Дифференцирование — это процесс вычисления производной функции, который дает скорость изменения функции по отношению к небольшому изменению переменной. Производная от ln2x математически записывается как d[ln(2x)] / dx = 1/x. 92x и выведите его формулу вместе с несколькими решенными примерами, включающими производные логарифмической функции, для лучшего понимания концепции.
| 1. | Какая производная от ln2x? |
| 2. | Производная формулы ln2x |
| 3. | Производная от ln2x Доказательство |
| 4. | Производная от ln2x с использованием логарифмических свойств 92x (лин 2 х) |
| 6. | Часто задаваемые вопросы о производной от ln2x |
Какая производная от ln2x?
Производная от ln2x определяется выражением d[ln(2x)] / dx = 1/x.
В общем случае можно сказать, что производная от ln(kx), где k — действительное число, равна 1/x, что можно доказать с помощью метода дифференцирования по цепному правилу. Мы также можем вычислить производную от ln(2x), используя логарифмическое свойство, определяемое формулой log(ab) = log a + log b. Давайте рассмотрим формулу для производной от ln2x в следующем разделе.
Производная формулы ln2x
Формула для производной ln2x имеет вид d[ln(2x)] / dx = 1/x, где дифференцирование ln2x дано по переменной x. Мы можем вывести эту формулу, используя метод цепного правила. На изображении ниже показана формула для производной ln2x:
Производная от ln2x Доказательство
Теперь, когда мы знаем, что производная от ln2x равна 1/x, мы докажем это, используя метод дифференцирования по цепному правилу. Этот метод используется для нахождения производной композиции функций. Формула цепного правила: d[f(g(x))] / dx = d[f(x)]/d[g(x)] × d[g(x)]/dx.
Здесь предположим, что f(x) = ln x и g(x) = 2x, тогда f(g(x)) = ln2x. Кроме того, мы будем использовать следующие формулы для получения производной от ln2x:
- Производная от lnx: d(ln x)/dx = 1/x
- Производная от 2x: d(2x)/dx = 2
Используя приведенные выше формулы, мы имеем
d[ln(2x)] / dx = d[ln(2x)] / d(2x) × d(2x) / x — [Используя формулу производных сложных функций ]
= 1/(2x) × 2 — [Поскольку производная от lnx равна 1/x, а производная от ax равна a.]
= 2/2x
= 1/x
Отсюда , мы доказали, что производная от ln2x равна 1/x, используя формулу цепного правила.
Производная от ln2x с использованием логарифмических свойств
Мы используем логарифмические свойства, чтобы упростить математические задачи и найти решение. У нас есть различные логарифмические свойства. Мы будем использовать свойство ln произведения ab, т. е. ln(ab) = ln a + ln b. Здесь рассмотрим a = 2 и b = x, тогда имеем ln(2x) = ln2 + lnx.
Теперь мы знаем, что ln2 — постоянный член и, следовательно, его производная равна нулю, а производная от ln x равна 1/x. Следовательно, у нас есть 92x равно (2 ln x) / x.
Важные замечания по производной от ln2x
- Производная от ln2x равна 1/x.
- Мы можем определить производную от ln2x, используя формулу цепного правила и логарифмические свойства.
- Производная от ln 2 x равна (2 ln x) / x.
☛ Похожие темы:
- Журнал
- Интеграция logx
- Производное от 2lnx 9(ln2x).
Решение: Производная от e ln2x вычисляется с использованием метода цепного правила. Мы знаем, что производная экспоненциальной функции e x определяется выражением d(e x )/dx = e x . Кроме того, мы будем использовать формулу для производной ln2x, определяемую как d[ln(2x)] / dx = 1/x. Итак, мы имеем
d[e ln2x ] / dx = d(e ln2x ) / d(ln2x) × d(ln2x)/dx
= e ln2x × (1/x)
.
= е ln2x /x
Ответ: Производная от e ln2x равна e ln2x /x.
Пример 3: Вычислите производную от ln (2x + 1). Равно ли оно производной от ln2x?
Решение: Производная от ln (2x + 1) определяется выражением
d[ln (2x + 1)] / dx = d[ln (2x + 1)] / d(2x + 1) × d(2x+1) / x — [По цепному правилу]
= 1/(2x + 1) × 2 — [Поскольку производная от ln x равна 1/x, а производная от ax + b равна равно а]
= 2 / (2x + 1)
Теперь производная ln(2x) равна 1/x. Следовательно, производная от ln (2x + 1) не равна производной от ln2x.
Ответ: Производная от ln (2x + 1) равна 2 / (2x + 1). Он не равен производной от ln2x.
перейти к слайдуперейти к слайдуперейти к слайду
Отличное обучение в старшей школе с использованием простых подсказок
Увлекаясь зубрежкой, вы, скорее всего, забудете понятия.