Формула расчета длины окружности: Длина окружности. Площадь круга — урок. Математика, 6 класс.

Расчет сечения кабеля | Таблицы, формулы и примеры

Самое уязвимое место в сфере обеспечения квартиры или дома электрической энергией – это электропроводка. Во многих домах продолжают использовать старую проводку, не рассчитанную на современные электроприборы. Нередко подрядчики и вовсе стремятся сэкономить на материалах и укладывают провода, не соответствующие проекту. В любом из этих случаев необходимо сначала сделать расчет сечения кабеля, иначе можно столкнуться с серьезными и даже трагичными последствиями.

Для чего необходим расчет кабеля

В вопросе выбора сечения проводов нельзя следовать принципу «на глаз». Протекая по проводам, ток нагревает их. Чем выше сила тока, тем сильнее происходит нагрев. Эту взаимосвязь легко доказать парой формул. Первая из них определяет активную силу тока:

где I – сила тока, U – напряжение, R – сопротивление.

Из формулы видно: чем больше сопротивление, тем больше будет выделяться тепла, т. е. тем сильнее проводник будет нагреваться. Сопротивление определяют по формуле:

R = ρ · L/S (2),

где ρ – удельное сопротивление, L – длина проводника, S – площадь его поперечного сечения.

Чем меньше площадь поперечного сечения проводника, тем выше его сопротивление, а значит выше и активная мощность, которая говорит о более сильном нагреве. Исходя из этого, расчет сечения необходим для обеспечения безопасности и надежности проводки, а также грамотного распределения финансов.

Что будет, если неправильно рассчитать сечение

Без расчета сечения проводника можно столкнуться с одной из двух ситуаций:

• Слишком сильный перегрев проводки. Возникает при недостаточном диаметре проводника. Создает благоприятные условия для самовозгорания и коротких замыканий.
• Неоправданные затраты на проводку. Такое происходит в ситуациях, когда были выбраны проводники избыточного диаметра. Конечно, опасности здесь нет, но кабель большего сечения стоит дороже и не столь удобен в работе.

Что еще влияет на нагрев проводов

Из формулы (2) видно, что сопротивление проводника зависит не только от площади поперечного сечения. В связи с этим на его нагрев будут влиять:

• Материал. Пример – у алюминия удельное сопротивление больше, чем у меди, поэтому при одинаковом сечении проводов медь будет нагреваться меньше.
• Длина. Слишком длинный проводник приводит к большим потерям напряжения, что вызывает дополнительный нагрев. При превышении потерь уровня 5% приходится увеличивать сечение.

Пример расчета сечения кабеля на примере BBГнг 3×1,5 и ABБбШв 4×16

Трехжильный кабель BBГнг 3×1,5 изготавливается из меди и предназначен для передачи и распределения электричества в жилых домах или обычных квартирах. Токопроводящие жилы в нем изолированы ПВХ (В), из него же состоит оболочка. Еще BBГнг 3×1,5 не распространяет горение нг(А), поэтому полностью безопасен при эксплуатации.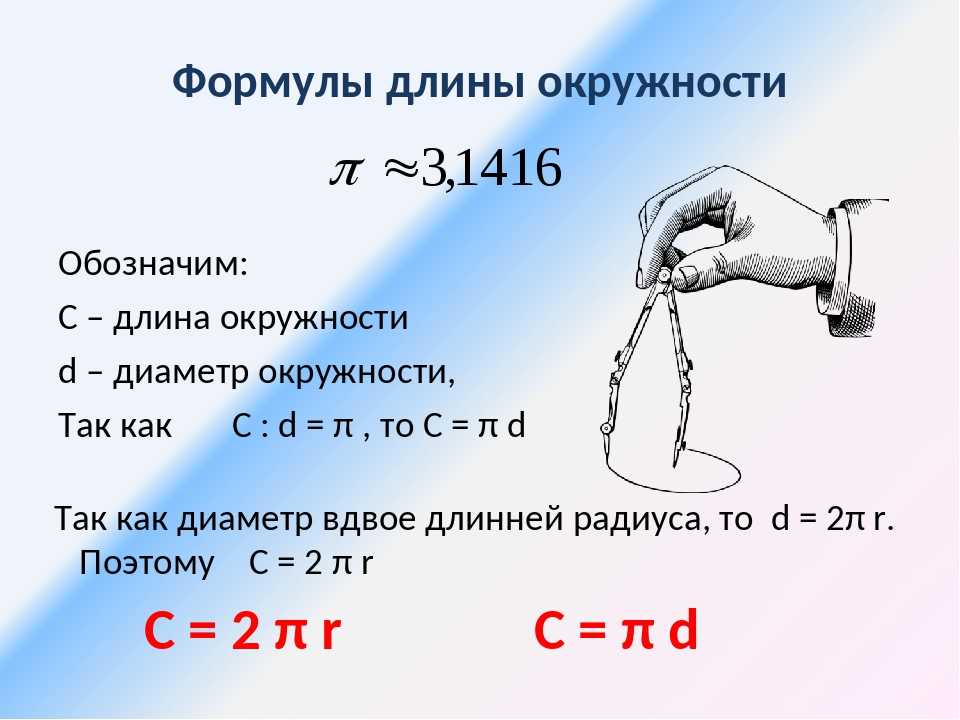

Кабель ABБбШв 4×16 четырехжильный, включает токопроводящие жилы из алюминия. Предназначен для прокладки в земле. Защита с помощью оцинкованных стальных лент обеспечивает кабелю срок службы до 30 лет. В компании «Бонком» вы можете приобрести кабельные изделия оптом и в розницу по приемлемой цене. На большом складе всегда есть в наличии вся продукция, что позволяет комплектовать заказы любого ассортимента.

Порядок расчета сечения по мощности

В общем виде расчет сечения кабеля по мощности происходит в 2 этапа. Для этого потребуются следующие данные:

• Суммарная мощность всех приборов.
• Тип напряжения сети: 220 В – однофазная, 380 В – трехфазная.
• ПУЭ 7. Правила устройства электроустановок. Издание 7.
• Материал проводника: медь или алюминий.
• Тип проводки: открытая или закрытая.

Шаг 1. Потребляемую мощность электроприборов можно найти в их инструкции или же взять средние характеристики. Формула для расчета общей мощности:

ΣP = (P₁ + Р₂ + … + Рₙ) · Кс · Кз,

где P₁, P

2 и т. д. – мощность подключаемых приборов, К_с – коэффициент спроса, который учитывает вероятность включения всех приборов одновременно, К_з – коэффициент запаса на случай добавления новых приборов в доме. К_с определяется так:

• для двух одновременно включенных приборов – 1;
• для 3-4 – 0,8;
• для 5-6 – 0,75;
• для большего количества – 0,7.

К_з в расчете кабеля по нагрузке имеет смысл принять как 1,15-1,2. Для примера можно взять общую мощность в 5 кВт.

Шаг 2. На втором этапе остается по суммарной мощности определить сечение проводника. Для этого используется таблица расчета сечения кабеля из ПУЭ. В ней дана информация и для медных, и для алюминиевых проводников. При мощности 5 кВт и закрытой однофазной электросети подойдет медный кабель сечением 4 мм

2.

Правила расчета по длине

Расчет сечения кабеля по длине предполагает, что владелец заранее определил, какое количество метров проводника потребуется для электропроводки. Таким методом пользуются, как правило, в бытовых условиях. Для расчета потребуются такие данные:

• L – длина проводника, м. Для примера взято значение 40 м.
• ρ – удельное сопротивление материала (медь или алюминий), Ом/мм²·м: 0,0175 для меди и 0,0281 для алюминия.
• I – номинальная сила тока, А.

Шаг 1. Определить номинальную силу тока по формуле:

I = (P · К_с) / (U · cos ϕ) = 8000/220 = 36 А,

где P – мощность в ваттах (суммарная всех приборов в доме, для примера взято значение 8 кВт), U – 220 В, К_с – коэффициент одновременного включения (0,75), cos φ – 1 для бытовых приборов.

В примере получилось значение 36 А.

Шаг 2. Определить сечение проводника. Для этого нужно воспользоваться формулой (2):

R = ρ · L/S.

Потеря напряжения по длине проводника должна быть не более 5%:

dU = 0,05 · 220 В = 11 В.

Потери напряжения dU = I · R, отсюда R = dU/I = 11/36 = 0,31 Ом. Тогда сечение проводника должно быть не меньше:

S = ρ · L/R = 0,0175 · 40/0,31 = 2,25 мм².

В случае с трехжильным кабелем площадь поперечного сечения одной жилы должна составить 0,75 мм². Отсюда диаметр одной жилы должен быть не менее (√S/ π) · 2 = 0,98 мм. Кабель BBГнг 3×1,5 удовлетворяет этому условию.

Как рассчитать сечение по току

Расчет сечения кабеля по току осуществляется также на основании ПУЭ, в частности, с использованием таблиц 1. 3.6. и 1.3.7. Зная суммарную мощность электроприборов, можно по формуле определить номинальную силу тока:

I = (P · К_с) / (U · cos ϕ).

Для трехфазной сети используется другая формула:

I=P/(U√3cos φ),

где U будет равно уже 380 В.

Если к трехфазному кабелю подключают и однофазных, и трехфазных потребителей, то расчет ведется по наиболее нагруженной жиле. Для примера с общей мощностью приборов, равной 5 кВт, и однофазной закрытой сети получается:

I = (P · К_с) / (U · cos ϕ) = (5000 · 0,75) / (220 · 1) = 17,05 А, при округлении 18 А.

BBГнг 3×1,5 – медный трехжильный кабель. По таблице 1.3.6. для силы тока 18 А ближайшее в значение – 19 А (при прокладке в воздухе). При номинальной силе тока 19 А сечение его токопроводящей жилы должно составлять не менее 1,5 мм². У кабеля BBГнг 3×1,5 одна жила имеет сечение S = π · r² = 3,14 · (1,5/2)² = 1,8 мм², что полностью соответствует указанному требованию.

Если рассматривать кабель ABБбШв 4×16, необходимо брать данные из таблицы 1.3.7. ПУЭ, где указаны значения для алюминиевых проводов. Согласно ей, для четырехжильных кабелей значение тока должно определяться с коэффициентом 0,92. В рассматриваемом примере к 18 А ближайшее значение по таблице 1.3.7. составляет 19 А.

С учетом коэффициента 0,92 оно составит 17,48 А, что меньше 18 А. Поэтому необходимо брать следующее значение – 27 А. В таком случае сечение токопроводящей жилы кабеля должно составлять 4 мм². У кабеля ABБбШв 4×16 сечение одной жилы равно:

S = π · r² = 3,14 · (4,5/2)² = 15,89 мм².

Согласно таблице 1.3.7. этот кабель рациональнее использовать при номинальном токе 60 А (при прокладке по воздуху) и до 90 А (при прокладке в земле).

назад

Калькулятор формулы окружности

— MathCracker.com

Инструкции: Используйте этот калькулятор формулы окружности, чтобы вычислить значение длины окружности для круга с заданным радиусом r при условии, что в поле ниже.

Подробнее об окружности круга

Этот калькулятор позволит вам вычислить длину окружности для заданного радиуса. Итак, вам необходимо предоставить правильное выражение для радиуса. Это может быть любое допустимое числовое выражение, например «2» или «1/3». Единственным ограничением является то, что он должен быть положительным.

После того, как вы укажете допустимый радиус, будет использована формула длины окружности со всеми показанными шагами.

Окружность — это мера длины, полученная, если бы мы получили круг и могли бы его «выпрямить», почти как если бы круг состоял из тонкого узла, и мы могли бы разрежьте его и измерьте длину лапши.

Как рассчитать длину окружности?

Идея окружности круга как длины геометрически ясна, но ее не так просто перевести в реальное измерение. Потребовалось математики веками на самом деле придумали формулу длины окружности:

\[\displaystyle C = 2 \pi г \]

Действительно просто, но очень концептуально. Математики искали что-то простое, но искали что-то более «квадратное». Эта загадочная константа \(\pi\) был необходимым концептуальным шагом, чтобы фундаментально различать квадраты и круги.

Как вычислить длину окружности с радиусом

• Шаг 1: Определите радиус предоставленной окружности. Если он отрицательный, то вы не можете продолжить
• Шаг 2: Составьте уравнение \( C = 2 \pi r \) и подставьте известное значение r
• Шаг 3: Если фактическая длина окружности зависит от \(\pi\), вы можете оставить ее в единицах \(\pi\) или использовать калькулятор для расчета ее числового значения
• Шаг 4: Если r указано в единицах длины, используйте те же единицы длины для конечного результата длины окружности

Процесс нахождения длины окружности и вычисления длины окружности тривиален, если использовать формулу, подставив в нее значение r.

Вопрос: Что такое окружность?

Хотя вычисления тривиальны, вы все еще можете думать о том, что такое настоящая окружность и что она представляет. И это логично, ведь для этого понадобились математики у древних греков много мыслей, чтобы придумать на него ответ.

Окружность — это длина окружности, по крайней мере, так она определяется. Теперь, хотя идея существования четко определенной длины окружности легко принять, это концептуальная проблема, чтобы прийти к соглашению о том, как определяется «длина».

Калькулятор отношения диаметра к окружности

• Шаг 1: Если вместо радиуса вам предоставлен диаметр d, определите его и его возможную единицу длины. Он должен быть положительным, иначе вы не сможете продолжить
• Шаг 2: Поскольку мы знаем, что d = 2r, мы просто вычисляем радиус r, разделив диаметр на 2
• Шаг 3: Затем мы используем обычное уравнение \( C = 2 \pi r \) и подставляем значение, которое мы вычислили для r

Другой способ увидеть это — вычислить длину окружности непосредственно из диаметра по формуле \(C = \pi d\).

Зачем мне формула длины окружности, если я могу пользоваться калькулятором

Справедливая точка. Хотя в данном конкретном случае очень важно понять, откуда берется формула длины окружности. Это очень простая формула, но она также имеет глубокий смысл. Вы наверняка можете использовать калькулятор окружности, особенно если он показывает вам шаги, подобные этому.

Длина окружности имеет множество применений, и, что более важно, она порождает множество других понятий.

Пример: вычисление длины окружности

Используйте формулу длины окружности, чтобы найти длину окружности с радиусом \(r =\frac{3}{4}\).

Решение: Нам нужно найти длину окружности \(C\) круга, и из предоставленной информации мы знаем, что радиус круг равен \(r = \frac{3}{4}\).

Теперь формула для длины окружности имеет вид \(C = 2\pi r\), и поэтому все, что нам нужно сделать, это подставить в эту формулу известное значение известного радиуса \(r = \frac{3}{4}\).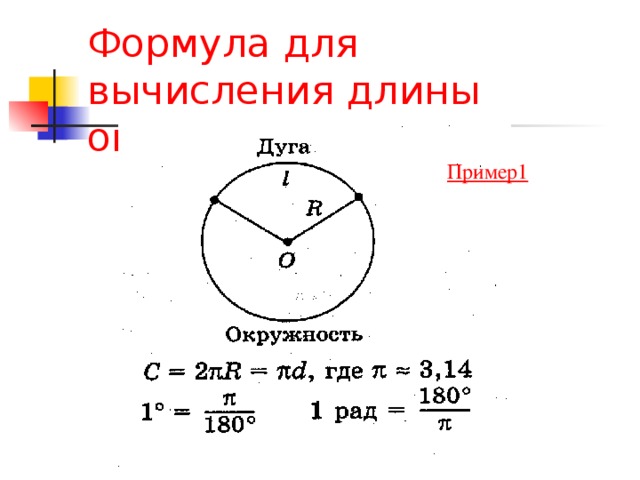 Получается следующее:

\[ \begin{array}{ccl} C & = & \displaystyle 2 \pi r \\\\ \\\\ & = & \displaystyle 2 \pi \cdot \frac{3}{4} \\\\ \\\\ & = & \displaystyle \frac{3}{2}\pi{} \end{массив} \]

На этом расчет завершен. Таким образом, мы обнаружили, что длина окружности равна \(\displaystyle C = \frac{3}{2}\pi{}\).

Пример: Еще одно вычисление длины окружности

Теперь предположим, что диаметр окружности равен d = 2. Вычислите ее длину окружности.

Решение: Нам нужно найти длину окружности \(C\) окружности, а диаметр известен как d = 2. Так как диаметр должен быть равен в два раза больше его радиуса, мы заключаем, что радиус окружность \(r = 1\).

Отсюда, используя формулу длины окружности:

\[ C = \displaystyle 2 \pi r = 2 \pi \cdot 1 = 2\pi \]

тогда длина окружности равна \(\displaystyle C = 2\pi{}\).

Пример: Другой пример

Можно ли найти длину окружности для радиуса r = -3?

Решение: Нет.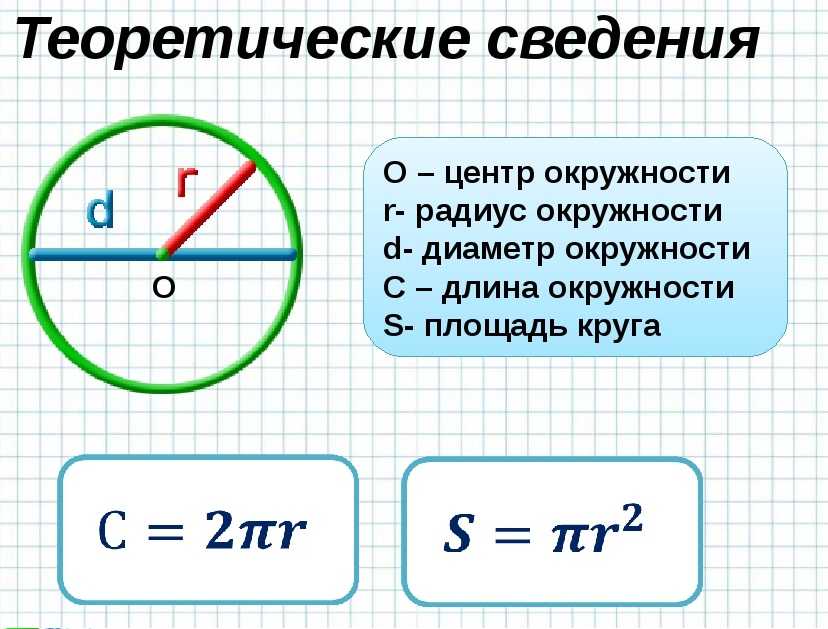 Чтобы найти правильную длину окружности, радиус должен быть положительным.

Другие полезные калькуляторы

Есть много других вещей, которые вы хотели бы сделать с кругами. Например, вам может понадобиться вычислить площадь круга или найти уравнение окружности. Обратите внимание, что для вычисления периметра требуется только радиус, а не все уравнение окружности.

Иногда у вас будет уравнение окружности в общем виде, что может потребовать некоторых манипуляций с формула окружности, чтобы найти радиус и вычислить его длина окружности.

Как рассчитать длину окружности – ноу-хаувадда

Круг представляет собой простую замкнутую форму. Математическое определение круга — это набор всех точек на плоскости, которые находятся на постоянном заданном расстоянии (радиусе) от данной точки (центра). Объясняемый с помощью конических сечений, круг — это коническое сечение, полученное пересечением конуса с плоскостью, перпендикулярной оси симметрии конусов.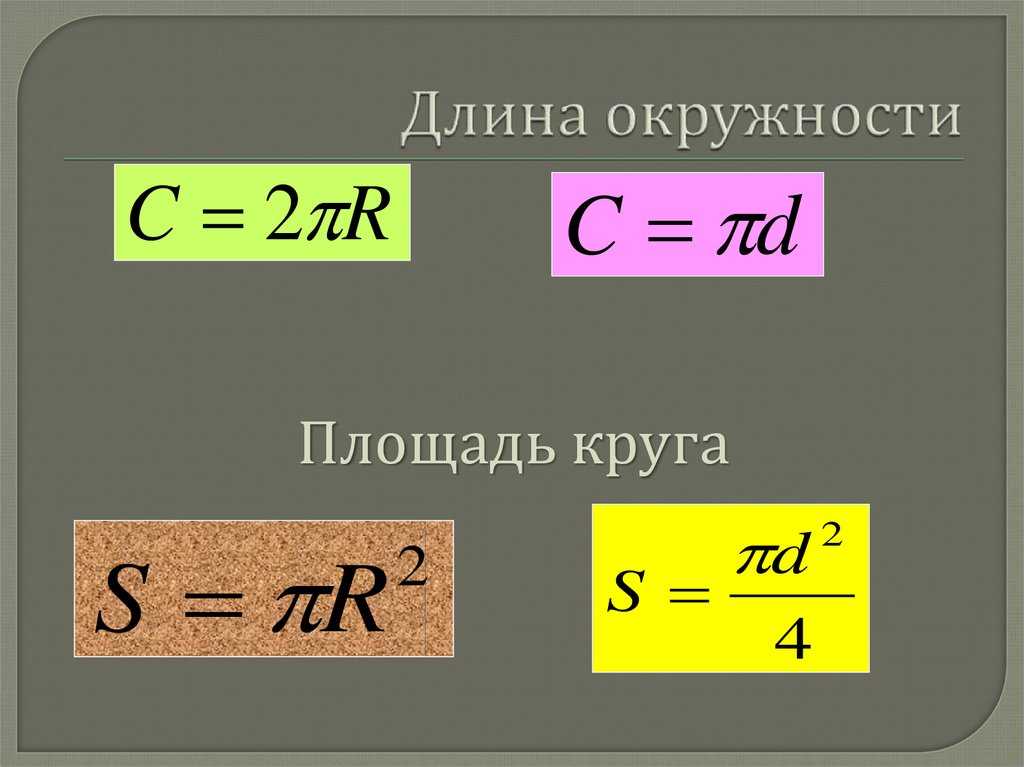 Окружность — это двумерная фигура, не имеющая ни ребра, ни вершины. Итак, как любая правильная двумерная замкнутая фигура, она обладает двумя основными свойствами: периметром и площадью.

Здесь мы рассмотрим, как вычислить периметр или длину окружности. Давайте сначала рассмотрим основную терминологию.

• Периметр или окружность — непрерывная линия, образующая границу замкнутой геометрической фигуры
• Площадь – это величина, выражающая размер двумерной фигуры или формы на плоскости.
• Центр круга — это точка, равноудаленная от точек на краю круга.
• Радиус окружности — это расстояние от центральной точки до точки на окружности. Поскольку круг имеет радиальную симметрию, расстояние равно кругу.
• Прямая линия, проходящая от одной стороны к другой через центр окружности, называется диаметром.
• Число пи или ? математическая константа, используемая для вычисления длины окружности и площади круга. Будучи иррациональным числом, ? не может быть выражено в виде точной числовой формы, но обычно обобщается как 3,14 или 22/7 для целей расчета.

До создания формулы существовали другие способы вычисления длины окружности.

Например, по непрерывной границе круга проходила нить, которую распрямляли для проверки охватываемого ею периметра.

Здесь мы поговорим о трех формулах вычисления длины окружности

 

 

Когда задан радиус-

Формула, используемая, когда дан радиус окружности:

• С=2?р

Здесь C — это длина окружности, а r — заданный радиус.

Давайте изучим это на примере-

• Вычислите длину окружности радиусом 14см

Решение – здесь указан радиус, r = 14 см

• C=2?r
• С= 2?14
• С= 2(22/7)(14) или 2(3,14)(14)
• С= 88 см

Следовательно, длина окружности равна 88 см.

Когда указан диаметр-

Формула, используемая для диаметра круга:

• C=?d

Здесь C — длина окружности, а d — заданный диаметр окружности.