10 в степенях: Таблица степеней

Сила степеней числа 10 « Папа Карп

Чтобы спокойно и качественно изучать физику и химию, надо владеть действиями со степенями числа 10 – уверенно и во всех вариациях.

При решении задачек по физике (даже самых начальных и самых простых) любое число удобно представлять в стандартном виде. То есть в виде “число от 1 до 10 умножить на 10 в какой-то степени”. Причем степень числа 10 может быть и положительной, и отрицательной.

Необходимо уметь действовать с числами, записанными таким образом.

Поэтому к началу изучения физики в 7 классе очень желательно, чтобы ученик полностью освоил все навыки, касающиеся степеней числа 10.

Однако базовая школьная программа по математике не полностью это обеспечивает, к сожалению.

Мой опыт преподавания физики показывает, что весьма целесообразно некоторые недостающие моменты (например, отрицательные степени числа 10 и действия с ними) изучить пораньше. Да и все прочие нюансы данной темы хорошо бы повторить и доработать, если они слегка подзабылись.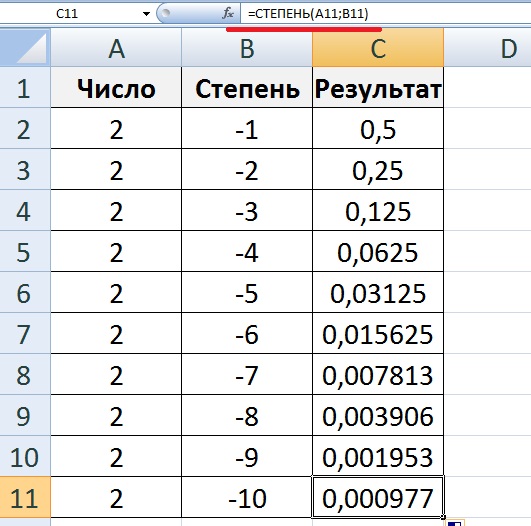

Важно видеть цель: мы должны дать ученику в руки надежный математический инструмент для расчетов по сложным физическим и химическим формулам. Это именно математический аппарат. Но нужен он в основном как раз в физике и в химии.

В данной статье я кратко перечислю то, что хорошо бы знать про степени числа 10 к самому началу изучения физики.

Разумеется, моя цель – лишь показать общую схему. Если вам понадобится более подробная информация, то ее легко найти в любых школьных учебниках.

Попадая в стихию физики (а затем и химии), школьники вынуждены оперировать с числами в огромном диапазоне величин: от крошечных размеров атомов до межзвездных расстояний, от массы электрона до массы Юпитера или Солнца… Это очень отличается от привычных масштабов, на которых обычно в основном строится изучение математики.

И вот тут-то и пригождаются положительные и отрицательные степени числа 10. В науке о природе без них просто никак.

Запись чисел в стандартном виде – великолепное изобретение человечества! Но оно, разумеется, используется преимущественно в науке и в технике, а не в обычной нашей жизни. Поэтому надо специально приучить школьника к такому стилю математических вычислений. К нему необходимо привыкнуть.

Для начала как следует разберитесь с положительными степенями числа 10. Это проще и понятнее. Это уже знакомо с начальных классов. Какова положительная степень числа 10 – столько ноликов и приписываем к единичке. Умножение и деление таких чисел не вызывает труда.

Существуют простые правила действий со степенями. Я их нарисовал здесь на картинке конкретно для случая, когда основание степени – число 10. Разумеется, для любого другого основания степени правила будут точно те же самые. Но в физике нас интересует обычно именно 10.

Когда мы сталкиваемся с физическими расчетами, где числа записаны с использованием степеней числа 10, то можно использовать все правила действий со степенями и правило сокращения дробей.

Фактически, обычно удобнее отдельно разбираться со степенями числа 10, а отдельно – со всеми другими числами в выражении. И лишь в конце соединить это в один ответ.

Вот я захотел вычислить плотность объекта. Исходно мне известны его масса и объем. Посмотрите, как просто получилось посчитать по формуле!

Теперь добавим и отрицательные степени числа 10.

Надо хорошо понять определение: что такое отрицательная степень.

Посмотрите на картинку ниже.

Я проиллюстрировал там общий принцип: число в отрицательной степени – это единица делить на то же самое число в такой же степени, но только показатель степени уже без знака “минус”.

Так просто договорились – что такое отрицательная степень. И это потрясающе удобно!

Конечно, само понятие отрицательной степени поначалу может вызвать некоторое недоумение… Возможно, потребуется поразмышлять и посмотреть, как такая штука работает – на самых простых примерах…

Возвращаемся к формулам по физике.

Теперь будем использовать и отрицательные степени числа 10.

Все правила действий со степенями остались те же самые. Мы так же складываем или вычитаем показатели степени при умножении или делении. И все остальные правила сохраняются.

Требуется некоторая практика, конечно. Но если понимать принцип, то сложностей особых нет.

Складывая положительные и отрицательные показатели степени, мы действуем точно так же, как и при сложении положительных и отрицательных чисел.

Поглядите, как легко вычисляется масса объекта, если известны его плотность и объем.

Особенная практическая фишка: “перебрасывать” 10 в какой-то степени через дробную черту – снизу вверх или сверху вниз.

Посмотрите на картинке, как 10 в отрицательной степени “перебирается” из-под дробной черты вверх. И после этого считать делается уже совсем просто.

Важно уловить принцип: при таком “перебросе” через дробную черту знак показателя степени у числа 10 меняется на противоположный. Для практических расчетов по формулам очень удобный прием!

Кстати об удобстве расчетов… Не всегда имеет смысл переводить числа именно в стандартный вид. Иногда проще использовать более свободное сочетание степеней числа 10 и обычных чисел.

Важно приучиться действовать именно так, как наиболее индивидуально удобно, как меньше шансов запутаться и ошибиться.

В физике и в химии вообще главное – получить правильный ответ. А как конкретно мы вычисляли – это наше дело.

Здесь еще надо уверенно владеть навыком переноса десятичной запятой.

Казалось бы, такая простая штука…

Скажем, расстояние в 6300 метров мы хотим записать в километрах почему-то. Ясно, что это будет 6,3 км. А наоборот? Снова получим 6300 м.

Или, к примеру, напряжение 0,00065 В – это сколько будет в милливольтах? Надо перенести запятую на три знака вправо. Получится 0,65 мВ.

Такие переходы используются в физике на каждом шагу. И у школьника не должно быть ну абсолютно никаких проблем с тем, чтобы перемещать запятую вправо или влево на нужное количество знаков.

Само собой, когда мы встречаем числа типа 0,0001 или 10000000, то их сразу же удобнее представить в виде степеней числа 10.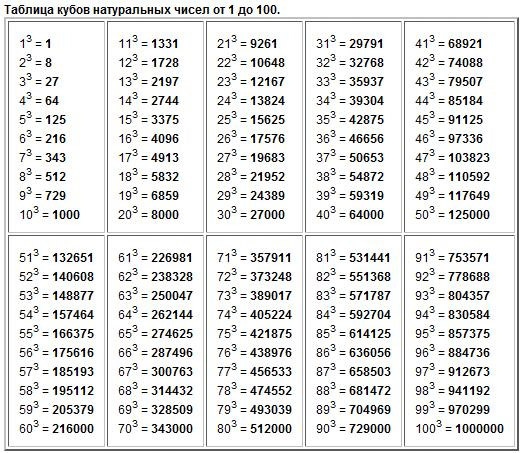 И далее во всех расчетах действовать по стандартной процедуре со степенями.

Все эти мучительные размышления, куда и на сколько знаков надо перенести запятую при умножении или делении на 0,0000001… Они нам теперь не нужны! Мы умеем представлять все степени числа 10 именно в виде степеней, а не десятичных дробей. Почти всегда это значительно удобнее!

Отдельный вопрос состоит в том, когда надо вообще начинать говорить с детьми о степенях числа 10…

Мне кажется, что уже в начальной школе сие вполне уместно.

Ведь, по сути, это просто еще один способ записи чисел. Особенно легко его понять для положительных степеней числа 10. Скажем, умножить миллиметр на миллион! Сколько это будет?

С другой стороны, можно попробовать разделить километр на миллион равных частей… Почему бы не представить такую процедуру? Так что и отрицательные степени числа 10 тоже легко вводить на самом элементарном уровне.

Мой личный опыт преподавания показывает, что маленькие дети с удовольствием разбираются с большими числами.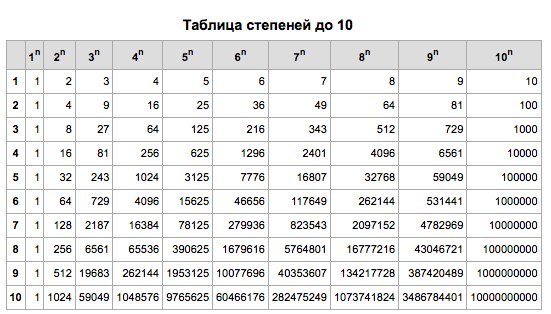

Это даже интереснее, чем возиться со сложением и вычитанием в пределах 100. Представляете: целый миллиард разделить пополам! И узнать, сколько это будет!

Но самое главное – к началу изучения физики в 7 классе разобраться со всеми нюансами данной темы!

Тогда изучение физики и химии будет значительно более удобным.

Хотя бы вот даже взять перевод единиц измерения физических величин друг в друга… Насколько проще это делать, используя степени числа 10!

Немного практики – и ученик получает ключ ко всему диапазону масштабов: от ангстремов и нанометров до световых лет и парсеков, от постоянной Планка до числа Авогадро…

Посмотрите, например, как изящно происходит для льда переход от одних единиц плотности к другим.

Итак, овладение почти магической математической силой степеней числа 10 – это надежное подспорье для изучения физики и химии. Данный навык пригодится с 7 класса и до 11 класса включительно.

Удобно, что вся эта тема – проста по сути.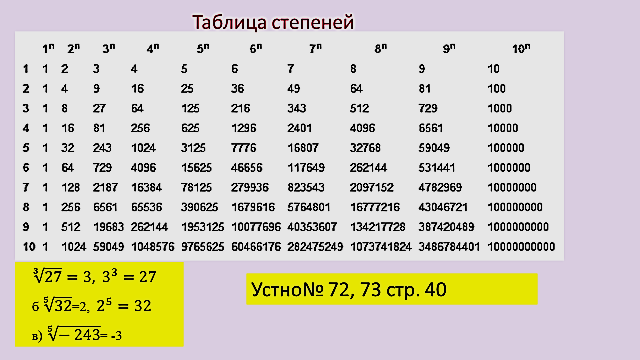 Ее легко понимать и осваивать. Важно лишь довести знания до устойчивого системного уровня. Чтобы применять при необходимости, не задумываясь особо и не путаясь по мелочам. Как таблицу умножения и действия столбиком.

И просто по жизни весьма полезно ориентироваться в данном вопросе. Сила степеней числа 10 – один из краеугольных камней нашей интеллектуальной культуры.

Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней.

	Навигация по справочнику TehTab.ru:  главная страница  / / Техническая информация / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса  / / Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней. Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица квадратов Таблица кубов Таблица логарифмов Таблица синусов/косинусов Таблица тангенсов/котангенсов и другие таблицы численных значений 67=279 936 В степени: Число 2 3 4 5 6 7 8 9 10 2 4 8 16 32 64 128 256 512 1 024 3 9 27 81 243 729 2 187 6 561 19 683 59 049 4 16 64 256 1 024 4 096 16 384 65 536 262 144 1 048 576 5 25 125 625 3 125 15 625 78 125 390 625 1 953 125 9 765 625 6 36 216 1 296 7 776 46 656 279 936(пример) 1 679 616 10 077 696 60 466 176 7 49 343 2 401 16 807 117 649 823 543 5 764 801 40 353 607 282 475 249 8 64 512 4 096 32 768 262 144 2 097 152 16 777 216 134 217 728 1 073 741 824 9 81 729 6 561 59 049 531 441 4 782 969 43 046 721 387 420 489 3 486 784 401 10 100 1 000 10 000 100 000 1 000 000 10 000 000 100 000 000 1 000 000 000 10 000 000 000 11 121 1 331 14 641 161 051 1 771 561 19 487 171 214 358 881 2 357 947 691 25 937 424 601 12 144 1 728 20 736 248 832 2 985 984 35 831 808 429 981 696 5 159 780 352 61 917 364 224 13 169 2 197 28 561 371 293 4 826 809 62 748 517 815 730 721 10 604 499 373 137 858 491 849 14 196 2 744 38 416 537 824 7 529 536 105 413 504 1 475 789 056 20 661 046 784 289 254 654 976 15 225 3 375 50 625 759 375 11 390 625 170 859 375 2 562 890 625 38 443 359 375 576 650 390 625 16 256 4 096 65 536 1 048 576 16 777 216 268 435 456 4 294 967 296 68 719 476 736 1 099 511 627 776 17 289 4 913 83 521 1 419 857 24 137 569 410 338 673 6 975 757 441 118 587 876 497 2 015 993 900 449 18 324 5 832 104 976 1 889 568 34 012 224 612 220 032 11 019 960 576 198 359 290 368 3 570 467 226 624 19 361 6 859 130 321 2 476 099 47 045 881 893 871 739 16 983 563 041 322 687 697 779 6 131 066 257 801 20 400 8 000 160 000 3 200 000 64 000 000 1 280 000 000 25 600 000 000 512 000 000 000 10 240 000 000 000 21 441 9 261 194 481 4 084 101 85 766 121 1 801 088 541 37 822 859 361 794 280 046 581 16 679 880 978 201 22 484 10 648 234 256 5 153 632 113 379 904 2 494 357 888 54 875 873 536 1 207 269 217 792 26 559 922 791 424 23 529 12 167 279 841 6 436 343 148 035 889 3 404 825 447 78 310 985 281 1 801 152 661 463 41 426 511 213 649 24 576 13 824 331 776 7 962 624 191 102 976 4 586 471 424 110 075 314 176 2 641 807 540 224 63 403 380 965 376 25 625 15 625 390 625 9 765 625 244 140 625 6 103 515 625 152 587 890 625 3 814 697 265 625 95 367 431 640 625 Раздел: Таблицы численных значений + Таблицы Брадиса: Таблица умножения — традиционная 10×10, 12х12 и 20х20 Таблица деления — традиционная 10×10 и 12х12 Таблицы квадратов. Натуральных чисел от 1 до 30 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99. Таблица квадратов натуральных чисел от 1 до 99 (от 1 до 9, от 10 до 99 ). Таблицы кубов. Натуральных чисел от 1 до 20 и от 1 до 100. Удобная расчетная таблица 1,00 — 9,99. Степени — квадрат и куб, корни — квадратный и кубический и обратные величины чисел от 1 до 100. Таблица степеней. Таблица степеней натуральных чисел от 2 до 25 (включая от «2 до 10» и от «2 до 20»). Степени от 2 до 10. Таблица степеней. Таблица 4-ой и 5-ой степени чисел от 1 до 100. Точная и приблизительная таблицы факториалов (1-255) Таблицы логарифмов и основные формулы Таблица. Длина окружности диаметра D. Таблица соотношений между длинами дуг, стрелками, длинами хорд, площадями сегментов при радиусе, равном единице. Длина хорды, центральный угол в ° (угловых градусах) и радианах при делении окружности единичного диаметра на равные сегменты. Таблица и формулы соотношений между стороной, радиусами вписанной и описанной окружности и площадью для правильных многоугольников Определение и численные соотношения между единицами измерения углов в РФ. Тысячные, угловые градусы, минуты, секунды, радианы, обороты. Таблица соответствия угловых градусов, радиан, оборотов, тысячных (артиллерийских РФ). 0-360 градусов, 0-2π радиан. Таблица синусов, она-же косинусов (см.примечание внутри). Углы в угловых градусах. Таблица значений синусов. Таблица синусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов. Таблица косинусов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений косинусов. Таблица тангенсов, она же котангенсов (см.примечание внутри). Углы в угловых градусах. Таблица тангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений тангенса, tg Таблица котангенсов углов углов от 0° — 360°. Углы с шагом в 1°. Таблица значений котангенса, ctg Углы 0°,30°,45°,60°,90°,180°,270°,360°,(π/6,π/4,π/3,π/2,π,3π/2,2π). Синусы, косинусы, тангенсы и котангенсы. Таблица значений тригонометрических функций. Знаки тригонометрических функций синус, косинус, тангенс и котангенс по четвертям в тригонометрическом круге. Таблицы Брадиса. Значения тригонометрических, логарифмических функций. Прочее Чиcло пи. π, 2π, 1/π, π/2, π/3, π/4, π/180, (π/180)2, π2, π3, π4 и др. Численные значения числа e, 1/e, e2, log10 e и др. Постоянная Эйлера γ, золотое сечение (золотая пропорция) φ, ln γ, eγ, 1/φ и др. Таблица простых чисел от 1 до 10000. Таблица простых чисел от 1 до 1000 Таблица случайных чисел. Таблицы : 100 случайных двузначных чисел и генератор случайных последовательностей.
Нашли ошибку? Есть дополнения? Напишите нам об этом, указав ссылку на страницу.
TehTab.ru Реклама, сотрудничество: [email protected]	Обращаем ваше внимание на то, что данный интернет-сайт носит исключительно информационный характер. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Все риски за использование информаци с сайта посетители берут на себя. Проект TehTab.ru является некоммерческим, не поддерживается никакими политическими партиями и иностранными организациями.

Степень с натуральным показателем

Предварительные навыки

Что такое степень?

Степенью называют произведение из нескольких одинаковых множителей. Например:

2 × 2 × 2

Значение данного выражения равно 8

2 × 2 × 2 = 8

Левую часть этого равенства можно сделать короче – сначала записать повторяющийся множитель и указать над ним сколько раз он повторяется. Повторяющийся множитель в данном случае это 2. Повторяется он три раза. Поэтому над двойкой записываем тройку:

2³ = 8

Это выражение читается так: «два в третьей степени равно восемь» или «третья степень числа 2 равна 8».

Короткую форму записи перемножения одинаковых множителей используют чаще. Поэтому надо помнить, что если над каким-то числом надписано другое число, то это есть перемножение нескольких одинаковых множителей.

Например, если дано выражение 5³, то следует иметь ввиду, что это выражение равносильно записи 5 × 5 × 5.

Число, которое повторяется называют основанием степени. В выражении 5³ основанием степени является число 5.

А число, которое надписано над числом 5 называют показателем степени. В выражении 5³ показателем степени является число 3. Показатель степени показывает сколько раз повторяется основание степени. В нашем случае основание 5 повторяется три раза

Саму операцию перемножения одинаковых множителей называют возведением в степень.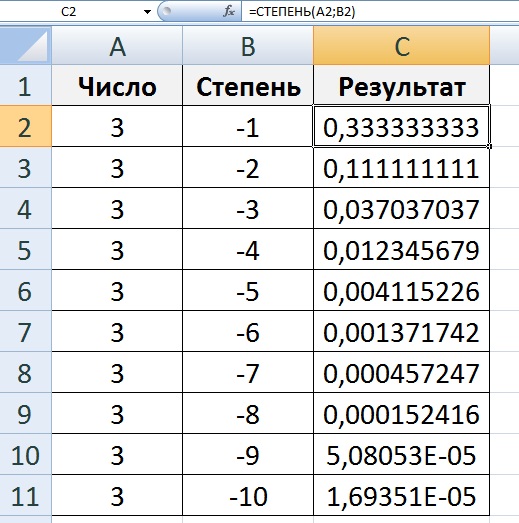

Например, если нужно найти произведение из четырёх одинаковых множителей, каждый из которых равен 2, то говорят, что число 2 возводится в четвёртую степень:

Видим, что число 2 в четвёртой степени есть число 16.

Отметим, что в данном уроке мы рассматриваем степени с натуральным показателем. Это вид степени, показателем которой является натуральное число. Напомним, что натуральными называют целые числа, которые больше нуля. Например, 1, 2, 3 и так далее.

Вообще, определение степени с натуральным показателем выглядит следующим образом:

Степень числа a с натуральным показателем n — это выражение вида aⁿ, которое равно произведению n множителей, каждый из которых равен a

Примеры:

Следует быть внимательным при возведении числа в степень. Часто по невнимательности человек умножает основание степени на показатель.

Например, число 5 во второй степени есть произведение двух множителей каждый из которых равен 5. Это произведение равно 25

Теперь представим, что мы по невнимательности умножили основание 5 на показатель 2

Получилась ошибка, поскольку число 5 во второй степени не равно 10.

Дополнительно следует упомянуть, что степень числа с показателем 1, есть само это число:

Например, число 5 в первой степени есть само число 5

Соответственно, если у числа отсутствует показатель, то надо считать, что показатель равен единице.

Например, числа 1, 2, 3 даны без показателя, поэтому их показатели будут равны единице. Каждое из этих чисел можно записать с показателем 1

А если возвести 0 в какую-нибудь степень, то получится 0. Действительно, сколько бы раз ничего не умножалось на само себя получится ничего. Примеры:

А выражение 0⁰  не имеет смысла. Но в некоторых разделах математики, в частности анализе и теории множеств, выражение 0⁰ может иметь смысл.

Для тренировки решим несколько примеров на возведение чисел в степени.

Пример 1. Возвести число 3 во вторую степень.

Число 3 во второй степени это произведение двух множителей, каждый из которых равен 3

3² = 3 × 3 = 9

---

Пример 2. Возвести число 2 в четвертую степень.

Число 2 в четвертой степени это произведение четырёх множителей, каждый из которых равен 2

2⁴ =2 × 2 × 2 × 2 = 16

---

Пример 3. Возвести число 2 в третью степень.

Число 2 в третьей степени это произведение трёх множителей, каждый из которых равен 2

2³ =2 × 2 × 2 = 8

---

Возведение в степень числа 10

Чтобы возвести в степень число 10, достаточно дописать после единицы количество нулей, равное показателю степени.

Например, возведем число 10 во вторую степень. Сначала запишем само число 10 и в качестве показателя укажем число 2

10²

Теперь ставим знак равенства, записываем единицу и после этой единицы записываем два нуля, поскольку количество нулей должно быть равно показателю степени

10² = 100

Значит, число 10 во второй степени это число 100. Связано это с тем, что число 10 во второй степени это произведение двух множителей, каждый из которых равен 10

10² = 10 × 10 = 100

---

Пример 2. Возведём число 10 в третью степень.

В данном случае после единицы будут стоять три нуля:

10³ = 1000

---

Пример 3. Возведем число 10 в четвёртую степень.

В данном случае после единицы будут стоять четыре нуля:

10⁴ = 10000

---

Пример 4. Возведем число 10 в первую степень.

В данном случае после единицы будет стоять один нуль:

10¹ = 10

---

Представление чисел 10, 100, 1000 в виде степени с основанием 10

Чтобы представить числа 10, 100, 1000 и 10000 в виде степени с основанием 10, нужно записать основание 10, и в качестве показателя указать число, равное количеству нулей исходного числа.

Представим число 10 в виде степени с основанием 10. Видим, что в нём один нуль. Значит, число 10 в виде степени с основанием 10 будет представлено как 10¹

10 = 10¹

---

Пример 2. Представим число 100 в виде степени основанием 10. Видим, что число 100 содержит два нуля. Значит, число 100 в виде степени с основанием 10 будет представлено как 10²

100 = 10²

---

Пример 3. Представим число 1 000 в виде степени с основанием 10.

1 000 = 10³

---

Пример 4. Представим число 10 000 в виде степени с основанием 10.

10 000 = 10⁴

---

Возведение в степень отрицательного числа

При возведении в степень отрицательного числа, его обязательно нужно заключить в скобки.

Например, возведём отрицательное число −2 во вторую степень. Число −2 во второй степени это произведение двух множителей, каждый из которых равен (−2)

(−2)² = (−2) × (−2) = 4

Если бы мы не заключили в скобки число −2, то получилось бы что мы вычисляем выражение −2², которое не равно 4.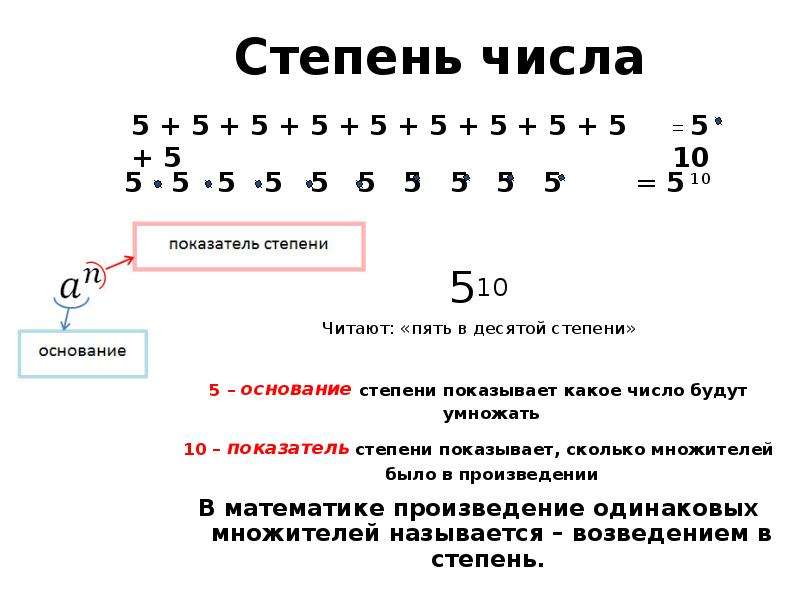 Выражение −2² будет равно −4. Чтобы понять почему, коснёмся некоторых моментов.

Когда мы ставим перед положительным числом минус, мы тем самым выполняем операцию взятия противоположного значения.

Допустим, дано число 2, и нужно найти его противоположное число. Мы знаем, что противоположное числу 2 это число −2. Иными словами, чтобы найти противоположное число для 2, достаточно поставить минус перед этим числом. Вставка минуса перед числом уже считается в математике полноценной операцией. Эту операцию, как было указано выше, называют операцией взятия противоположного значения.

В случае с выражением −2² происходит две операции: операция взятия противоположного значения и возведение в степень. Возведение в степень является более приоритетной операцией, чем взятие противоположного значения.

Поэтому выражение −2² вычисляется в два этапа. Сначала выполняется операция возведения в степень. В данном случае во вторую степень было возведено положительное число 2

Затем выполнилось взятие противоположного значения. Это противоположное значение было найдено для значения 4. А противоположное значение для 4 это −4

−2²  = −4

Скобки же имеют самый высокий приоритет выполнения. Поэтому в случае вычисления выражения (−2)² сначала выполняется взятие противоположного значения, а затем во вторую степень возводится отрицательное число −2. В результате получается положительный ответ 4, поскольку произведение отрицательных чисел есть положительное число.

Пример 2. Возвести число −2 в третью степень.

Число −2 в третьей степени это произведение трёх множителей, каждый из которых равен (−2)

(−2)³ = (−2) × (−2) × (−2) = −8

---

Пример 3. Возвести число −2 в четвёртую степень.

Число −2 в четвёртой степени это произведение четырёх множителей, каждый из которых равен (−2)

(−2)⁴ = (−2) × (−2) × (−2) × (−2) = 16

Легко заметить, что при возведении в степень отрицательного числа может получиться либо положительный ответ либо отрицательный. Знак ответа зависит от показателя исходной степени.

Если показатель степени чётный, то ответ будет положительным. Если показатель степени нечётный, ответ будет отрицательным. Покажем это на примере числа −3

В первом и в третьем случае показатель был нечётным числом, поэтому ответ стал отрицательным.

Во втором и в четвёртом случае показатель был чётным числом, поэтому ответ стал положительным.

---

Пример 7. Возвести число −5 в третью степень.

Число −5 в третьей степени это произведение трёх множителей каждый из которых равен −5. Показатель 3 является нечётным числом, поэтому мы заранее можем сказать, что ответ будет отрицательным:

(−5)³ = (−5) × (−5) × (−5) = −125

---

Пример 8. Возвести число −4 в четвёртую степень.

Число −4 в четвёртой степени это произведение четырёх множителей, каждый из которых равен −4. При этом показатель 4 является чётным, поэтому мы заранее можем сказать, что ответ будет положительным:

(−4)⁴ = (−4) × (−4) × (−4) × (−4) = 256

---

Нахождение значений выражений

При нахождении значений выражений, не содержащих скобки, возведение в степень будет выполняться в первую очередь, далее умножение и деление в порядке их следования, а затем сложение и вычитание в порядке их следования.

Пример 1. Найти значение выражения 2 + 5²

Сначала выполняется возведение в степень. В данном случае во вторую степень возводится число 5 — получается 25. Затем этот результат складывается с числом 2

2 + 5² = 2 + 25 = 27

---

Пример 10. Найти значение выражения −6² × (−12)

Сначала выполняется возведение в степень. Заметим, что число −6 не взято в скобки, поэтому во вторую степень будет возведено число 6, затем перед результатом будет поставлен минус:

−6² × (−12) = −36 × (−12)

Завершаем пример, умножив −36 на (−12)

−6² × (−12) = −36 × (−12) = 432

---

Пример 11. Найти значение выражения −3 × 2²

Сначала выполняется возведение в степень. Затем полученный результат перемножается с числом −3

−3 × 2² = −3 × 4 = −12

Если выражение содержит скобки, то сначала нужно выполнить действия в этих скобках, далее возведение в степень, затем умножение и деление, а затем сложение и вычитание.

---

Пример 12. Найти значение выражения (3² + 1 × 3) − 15 + 5

Сначала выполняем действия в скобках. Внутри скобок применяем ранее изученные правила, а именно сначала возводим во вторую степень число 3, затем выполняем умножение 1 × 3, затем складываем результаты возведения в степень числа 3 и умножения 1 × 3. Далее выполняется вычитание и сложение в порядке их следования. Расставим такой порядок выполнения действия над исходным выражением:

(3² + 1 × 3) − 15 + 5 = 12 − 15 + 5 = 2

---

Пример 13. Найти значение выражения 2 × 5³ + 5 × 2³

Сначала возведем числа в степени, затем выполним умножение и сложим полученные результаты:

2 × 5³ + 5 × 2³ = 2 × 125 + 5 × 8 = 250 + 40 = 290

---

Тождественные преобразования степеней

Над степенями можно выполнять различные тождественные преобразования, тем самым упрощая их.

Допустим, потребовалось вычислить выражение (2³)². В данном примере два в третьей степени возводится во вторую степень. Иными словами, степень возводится в другую степень.

(2³)²это произведение двух степеней, каждая из которых равна 2³

При этом каждая из этих степеней является произведением трёх множителей, каждый из которых равен 2

Получили произведение 2 × 2 × 2 × 2 × 2 × 2, которое равно 64. Значит значение выражения (2³)² или равно 64

Этот пример можно значительно упростить. Для этого показатели выражения (2³)² можно перемножить и записать это произведение над основанием 2

Получили 2⁶. Два в шестой степени это произведение шести множителей, каждый из которых равен 2. Это произведение равно 64

Данное свойство работает по причине того, что 2³ это произведение 2 × 2 × 2, которое в свою очередь повторяется два раза. Тогда получается, что основание 2 повторяется шесть раз. Отсюда можно записать, что 2 × 2 × 2 × 2 × 2 × 2 это 2⁶

Вообще, для любого основания a с показателями m и n, выполняется следующее равенство:

(aⁿ)^m = a^n × m

Это тождественное преобразование называют возведением степени в степень. Его можно прочитать так: «При возведении степени в степень основание оставляют без изменений, а показатели перемножают».

После перемножения показателей, получится другая степень, значение которой можно найти.

Пример 2. Найти значение выражения (3²)²

В данном примере основанием является 3, а числа 2 и 2 являются показателями. Воспользуемся правилом возведения степени в степень. Основание оставим без изменений, а показатели перемножим:

Получили 3⁴. А число 3 в четвёртой степени есть 81

Рассмотрим остальные преобразования.

Умножение степеней

Чтобы перемножить степени, нужно по отдельности вычислить каждую степень, и полученные результаты перемножить.

Например, умножим 2² на 3³.

2² это число 4, а 3³ это число 27. Перемножаем числа 4 и 27, получаем 108

2² × 3³ = 4 × 27 = 108

В этом примере основания степеней были разными. В случае, если основания будут одинаковыми, то можно записать одно основание, а в качестве показателя записать сумму показателей исходных степеней.

Например, умножим 2² на 2³

В данном примере основания у степеней одинаковые. В этом случае можно записать одно основание 2 и в качестве показателя записать сумму показателей степеней 2² и 2³. Иными словами, основание оставить без изменений, а показатели исходных степеней сложить. Выглядеть это будет так:

Получили 2⁵. Число 2 в пятой степени есть 32

Данное свойство работает по причине того, что 2² это произведение 2 × 2, а 2³ это произведение 2 × 2 × 2. Тогда получается произведение из пяти одинаковых множителей, каждый из которых равен 2. Это произведение представимо в виде 2⁵

Вообще, для любого a и показателей m и n выполняется следующее равенство:

Это тождественное преобразование носит название основного свойства степени. Его можно прочитать так: «При перемножении степеней с одинаковыми основаниями, основание оставляют без изменений, а показатели складывают».

Отметим, что данное преобразование можно применять при любом количестве степеней. Главное, чтобы основание было одинаковым.

Например, найдем значение выражения 2¹ × 2² × 2³. Основание 2 оставим без изменений, а показатели сложим:

В некоторых задачах достаточным бывает выполнить соответствующее преобразование, не вычисляя итоговую степень. Это конечно же очень удобно, поскольку вычислять большие степени не так-то просто.

Пример 1. Представить в виде степени выражение 5⁸ × 25

В данной задаче нужно сделать так, чтобы вместо выражения 5⁸ × 25 получилась одна степень.

Число 25 можно представить в виде 5². Тогда получим следующее выражение:

В этом выражении можно применить основное свойство степени — основание 5 оставить без изменений, а показатели 8 и 2 сложить:

Задачу можно считать решённой, поскольку мы представили выражение 5⁸ × 25 в виде одной степени, а именно в виде степени 5¹⁰.

Запишем решение покороче:

---

Пример 2. Представить в виде степени выражение 2⁹ × 32

Число 32 можно представить в виде 2⁵. Тогда получим выражение 2⁹ × 2⁵. Далее можно применить основание свойство степени — основание 2 оставить без изменений, а показатели 9 и 5 сложить. В результате получится следующее решение:

---

Пример 3. Вычислите произведение 3 × 3, используя основное свойство степени.

Все хорошо знают, что три умножить на три равно девять, но задача требует в ходе решения воспользоваться основным свойством степени. Как это сделать?

Вспоминаем, что если число дано без показателя, то показатель нужно считать равным единице. Стало быть сомножители 3 и 3 можно записать в виде 3¹ и 3¹

3¹ × 3¹

Теперь воспользуемся основным свойством степени. Основание 3 оставляем без изменений, а показатели 1 и 1 складываем:

3¹ × 3¹ = 3²

Далее вычисляем значение выражения. Число 3 во второй степени равно числу 9

3¹ × 3¹ = 3² = 9

---

Пример 4. Вычислите произведение 2 × 2 × 3² × 3³, используя основное свойство степени.

Произведение 2 × 2 заменим на 2¹ × 2¹, затем на 2^1 + 1, а затем на 2². Произведение 3² × 3³ заменим на 3^2 + 3, а затем на 3⁵

Далее вычисляем значение каждой степени и находим произведение:

---

Пример 5. Выполнить умножение x × x

Это два одинаковых буквенных сомножителя с показателями 1. Для наглядности запишем эти показатели. Далее основание x оставим без изменений, а показатели сложим:

Находясь у доски, не следует записывать перемножение степеней с одинаковыми основаниями так подробно, как это сделано здесь. Такие вычисления нужно выполнять в уме. Подробная запись скорее всего будет раздражать учителя и он снизит за это оценку. Здесь же подробная запись дана, чтобы материал был максимально доступным для понимания.

Решение данного примера желательно записать так:

---

Пример 6. Выполнить умножение x² × x

Показатель второго сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:

---

Пример 7. Выполнить умножение y³y²y

Показатель третьего сомножителя равен единице.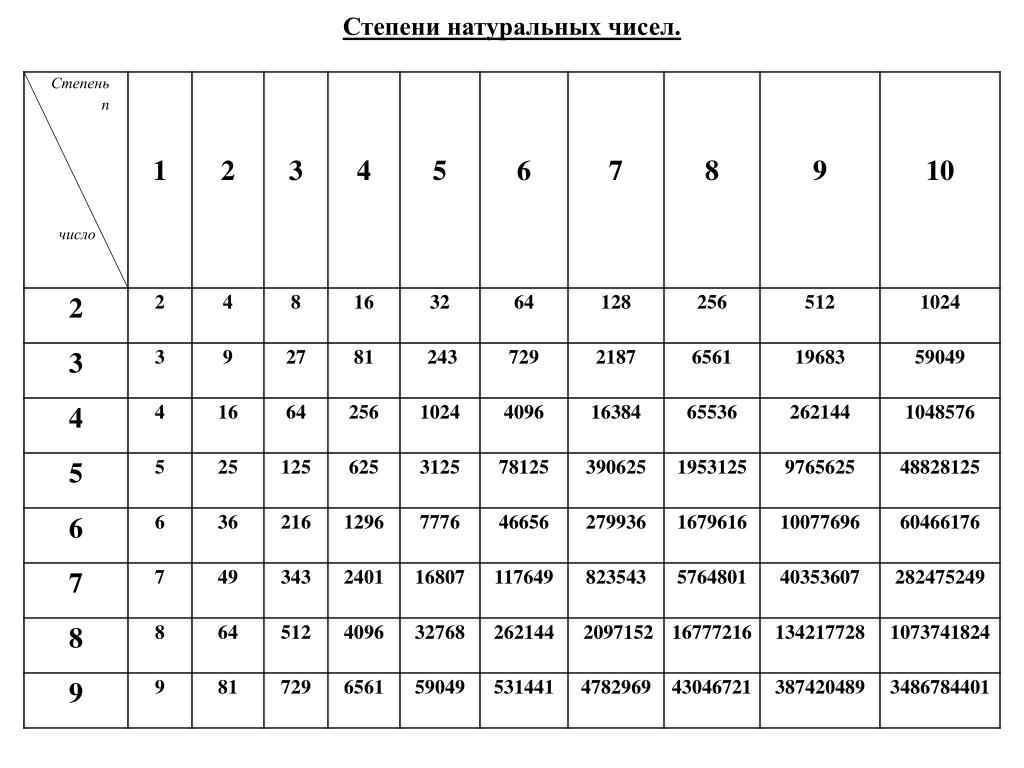 Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:

---

Пример 8. Выполнить умножение aa³a²a⁵

Показатель первого сомножителя равен единице. Для наглядности запишем его. Далее основание оставим без изменений, а показатели сложим:

---

Пример 9. Представить степень 3⁸ в виде произведения степеней с одинаковыми основаниями.

В данной задаче нужно составить произведение степеней, основания которых будут равны 3, и сумма показателей которых будет равна 8. Можно использовать любые показатели. Представим степень 3⁸ в виде произведения степеней 3⁵ и 3³

В данном примере мы опять же опирались на основное свойство степени. Ведь выражение 3⁵ × 3³ можно записать как 3^5 + 3, откуда 3⁸.

Конечно можно было представить степень 3⁸ в виде произведения других степеней. Например, в виде 3⁷ × 3¹, поскольку это произведение тоже равно 3⁸

Представление степени в виде произведения степеней с одинаковыми основаниями это по большей части творческая работа. Поэтому не нужно бояться экспериментировать.

---

Пример 10. Представить степень x¹² в виде различных произведений степеней с основаниями x.

Воспользуемся основным свойство степени. Представим x¹² в виде произведений с основаниями x, и сумма показателей которых равна 12

Конструкции с суммами показателей были записаны для наглядности. Чаще всего их можно пропустить. Тогда получится компактное решение:

---

Возведение в степень произведения

Чтобы возвести в степень произведение, нужно возвести в указанную степень каждый множитель этого произведения и перемножить полученные результаты.

Например, возведём во вторую степень произведение 2 × 3. Возьмём в скобки данное произведение и в качестве показателя укажем 2

Теперь возведём во вторую степень каждый множитель произведения 2 × 3 и перемножим полученные результаты:

Принцип работы данного правила основан на определении степени, которое было дано в самом начале.

Возвести произведение 2 × 3 во вторую степень означает повторить данное произведение два раза. А если повторить его два раза, то можно получить следующее:

2 × 3 × 2 × 3

От перестановки мест сомножителей произведение не меняется. Это позволяет сгруппировать одинаковые множители:

2 × 2 × 3 × 3

Повторяющиеся множители можно заменить на короткие записи — основания с показателями. Произведение 2 × 2 можно заменить на 2², а произведение 3 × 3 можно заменить на 3². Тогда выражение 2 × 2 × 3 × 3 обращается в выражение 2² × 3².

Пусть ab исходное произведение. Чтобы возвести данное произведение в степень n, нужно по отдельности возвести множители a и b в указанную степень n

Данное свойство справедливо для любого количества множителей. Следующие выражения также справедливы:

---

Пример 2. Найти значение выражения (2 × 3 × 4)²

В данном примере нужно возвести во вторую степень произведение 2 × 3 × 4. Чтобы сделать это, нужно возвести во вторую степень каждый множитель этого произведения и перемножить полученные результаты:

---

Пример 3. Возвести в третью степень произведение a × b × c

Заключим в скобки данное произведение, и в качестве показателя укажем число 3

Далее возводим в третью степень каждый множитель данного произведения:

---

Пример 4. Возвести в третью степень произведение 3xyz

Заключим в скобки данное произведение, и в качестве показателя укажем 3

(3xyz)³

Возведём в третью степень каждый множитель данного произведения:

(3xyz)³ = 3³x³y³z³

Число 3 в третьей степени равно числу 27. Остальное оставим без изменений:

(3xyz)³ = 3³x³y³z³ = 27x³y³z³

В некоторых примерах умножение степеней с одинаковыми показателями можно заменять на произведение оснований с одним показателем.

Например, вычислим значение выражения 5² × 3². Возведем каждое число во вторую степень и перемножим полученные результаты:

5² × 3² = 25 × 9 = 225

Но можно не вычислять по отдельности каждую степень. Вместо этого, данное произведение степеней можно заменить на произведение с одним показателем (5 × 3)². Далее вычислить значение в скобках и возвести полученный результат во вторую степень:

5² × 3² = (5 × 3)² = (15)² = 225

В данном случае опять же было использовано правило возведения в степень произведения. Ведь, если (a × b)ⁿ = aⁿ × bⁿ, то aⁿ × bⁿ = (a × b)ⁿ. То есть левая и правая часть равенства поменялись местами.

---

Возведение степени в степень

Это преобразование мы рассматривали в качестве примера, когда пытались понять суть тождественных преобразований степеней.

При возведении степени в степень основание оставляют без изменений, а показатели перемножают:

(aⁿ)^m = a^n × m

К примеру, выражение (2³)² является возведением степени в степень — два в третьей степени возводится во вторую степень. Чтобы найти значение этого выражения, основание можно оставить без изменений, а показатели перемножить:

(2³)² = 2^3 × 2 = 2⁶

Далее вычислить степень 2⁶, которая равна 64

(2³)² = 2^3 × 2 = 2⁶ = 64

Данное правило основано на предыдущих правилах: возведении в степень произведения и основного свойства степени.

Вернёмся к выражению (2³)². Выражение в скобках 2³ представляет собой произведение из трёх одинаковых множителей, каждый из которых равен 2. Тогда в выражении (2³)² степень, находящуюся внутри скобок можно заменить на произведение 2 × 2 × 2.

(2 × 2 × 2)²

А это есть возведение в степень произведения, которое мы изучили ранее. Напомним, что для возведения в степень произведения, нужно возвести в указанную степень каждый множитель данного произведения и полученные результаты перемножить:

(2 × 2 × 2)² = 2² × 2² × 2²

Теперь имеем дело с основным свойством степени. Основание оставляем без изменений, а показатели складываем:

(2 × 2 × 2)² = 2² × 2² × 2² = 2^{2 + 2 + 2} = 2⁶

Как и раньше получили 2⁶. Значение этой степени равно 64

(2 × 2 × 2)² = 2² × 2² × 2² = 2^{2 + 2 + 2} = 2⁶ = 64

В степень также может возводиться произведение, сомножители которого тоже являются степенями.

Например, найдём значение выражения (2² × 3²)³. Здесь показатели каждого множителя нужно умножить на общий показатель 3. Далее найти значение каждой степени и вычислить произведение:

(2² × 3²)³ = 2^2×3  × 3^2×3 = 2⁶ × 3⁶ = 64 × 729 = 46656

Примерно тоже самое происходит при возведении в степени произведения. Мы говорили, что при возведении в степень произведения, в указанную степень возводится каждый множитель этого произведения.

Например, чтобы возвести произведение 2 × 4 в третью степень, нужно записать следующее выражение:

Но ранее было сказано, что если число дано без показателя, то показатель надо считать равным единице. Получается, что множители произведения 2 × 4 изначально имеют показатели равные 1. Значит в третью степень возводилось выражение 2¹ × 4¹. А это есть возведение степени в степень.

Перепишем решение с помощью правила возведения степени в степень. У нас должен получиться тот же результат:

---

Пример 2. Найти значение выражения (3³)²

Основание оставляем без изменений, а показатели перемножаем:

Получили 3⁶. Число 3 в шестой степени есть число 729

---

Пример 3. Выполнить возведение в степень в выражении (xy)³

Возведём в третью степень каждый множитель произведения:

---

Пример 4. Выполнить возведение в степень в выражении (abc)⁵

Возведём в пятую степень каждый множитель произведения:

---

Пример 5. Выполнить возведение в степень в выражении (−2ax)³

Возведём в третью степень каждый множитель произведения:

Поскольку в третью степень возводилось отрицательное число −2, оно было взято в скобки.

Далее нужно вычислить то, что вычисляется. В данном случае можно вычислить (−2)³ — получится −8. Буквенная часть останется без изменений:

---

Пример 6. Выполнить возведение в степень в выражении (10xy)²

---

Пример 7. Выполнить возведение в степень в выражении (−5x)³

---

Пример 8. Выполнить возведение в степень в выражении (−3y)⁴

---

Пример 9. Выполнить возведение в степень в выражении (−2abx)⁴

---

Пример 10. Упростите выражение x⁵ × (x²)³ 

Степень x⁵ пока оставим без изменений, а в выражении (x²)³ выполним возведение степени в степени:

x⁵ × (x²)³ = x⁵ × x^2 × 3 = x⁵ × x⁶

Теперь выполним умножение x⁵× x⁶. Для этого воспользуемся основным свойством степени — основание x оставим без изменений, а показатели сложим:

x⁵ × (x²)³ = x⁵ × x^2× 3 = x⁵ × x⁶ = x^5 + 6 = x¹¹

---

Пример 9. Найти значение выражения 4³ × 2², используя основное свойство степени.

Основное свойство степени можно использовать в случае, если основания  исходных степеней одинаковы. В данном примере основания разные, поэтому для начала исходное выражение нужно немного видоизменить, а именно сделать так, чтобы основания степеней стали одинаковыми.

Посмотрим внимательно на степень 4³. Основание у этой степени есть число 4, которое можно представить в виде 2². Тогда исходное выражение примет вид (2²)³ × 2². Выполнив возведение степени в степень в выражении (2²)³, мы получим 2⁶. Тогда исходное выражение примет вид 2⁶ × 2², вычислить которое можно, используя основное свойство степени.

Запишем решение данного примера:

---

Деление степеней

Чтобы выполнить деление степеней, нужно найти значение каждой степени, затем выполнить деление обыкновенных чисел.

Например, разделим 4³ на 2².

Вычислим 4³, получим 64. Вычислим 2², получим 4. Теперь разделим 64 на 4, получим 16

Если при делении степеней основания окажутся одинаковыми, то основание можно оставить без изменений, а из показателя степени делимого вычесть показатель степени делителя.

Например, найдем значение выражения 2³ : 2²

Основание 2 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Значит, значение выражения 2³ : 2² равно 2.

Данное свойство основано на умножении степеней с одинаковыми основаниями, или как мы привыкли говорить на основном свойстве степени.

Вернемся к предыдущему примеру 2³ : 2². Здесь делимое это 2³, а делитель 2².

Разделить одно число на другое означает найти такое число, которое при умножении на делитель даст в результате делимое.

В нашем случае, разделить 2³ на 2² означает найти такую степень, которая при умножении на делитель 2² даст в результате 2³. А какую степень можно умножить на 2², чтобы получить 2³ ? Очевидно, что только степень 2¹. Из основного свойства степени имеем:

Убедиться, что значение выражения 2³ : 2² равно 2¹ можно непосредственно вычислив само выражение 2³ : 2². Для этого сначала найдём значение степени 2³, получим 8. Затем найдём значение степени 2², получим 4. Разделим 8 на 4, получим 2 или 2¹, поскольку 2 = 2¹.

2³ : 2² = 8 : 4 = 2

Таким образом, при делении степеней с одинаковыми основаниями выполняется следующее равенство:

Может случиться и так, что одинаковыми могут оказаться не только основания, но и показатели. В этом случае в ответе получится единица.

Например, найдём значение выражения 2² : 2². Вычислим значение каждой степени и выполним деление получившихся чисел:

При решении примера 2² : 2² также можно применить правило деления степеней с одинаковыми основаниями. В результате получается число в нулевой степени, поскольку разность показателей степеней 2² и 2² равна нулю:

В математике принято считать, что любое число в нулевой степени есть единица:

Почему число 2 в нулевой степени равно единице мы выяснили выше. Если вычислить 2² : 2² обычным методом, не используя правило деления степеней, получится единица.

---

Пример 2. Найти значение выражения 4¹² : 4¹⁰

Воспользуемся правилом деления степеней. Основание 4 оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

4¹² : 4¹⁰ = 4^{12 − 10} = 4² = 16

---

Пример 3. Представить частное x³ : x в виде степени с основанием x

Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя. Показатель делителя равен единице. Для наглядности запишем его:

---

Пример 4. Представить частное x³ : x² в виде степени с основанием x

Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Деление степеней можно записывать в виде дроби. Так, предыдущий пример можно записать следующим образом:

Числитель и знаменатель дроби  разрешается записывать в развёрнутом виде, а именно в виде произведений одинаковых множителей. Степень x³ можно записать как x × x × x, а степень x² как x × x. Тогда конструкцию x^3 − 2 можно будет пропустить и воспользоваться сокращением дроби. В числителе и в знаменателе можно будет сократить по два множителя x. В результате останется один множитель x

Или ещё короче:

Также, полезно уметь быстро сокращать дроби, состоящие из степеней. Например, дробь  можно сократить на x². Чтобы сократить дробь  на x² нужно числитель и знаменатель дроби  разделить на x²

Деление степеней подробно можно не расписывать. Приведённое сокращение можно выполнить короче:

Или ещё короче:

---

Пример 5. Выполнить деление x¹² : x³

Воспользуемся правилом деления степеней. Основание x оставим без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Запишем решение при помощи сокращения дроби. Деление степеней x¹² : x³ запишем в виде  . Далее сократим данную дробь на x³.

---

Пример 6. Найти значение выражения 

В числителе выполним умножение степеней с одинаковыми основаниями:

Теперь применяем правило деления степеней с одинаковыми основаниями. Основание 7 оставляем без изменений, а из показателя степени делимого вычтем показатель степени делителя:

Завершаем пример, вычислив степень 7²

---

Пример 7. Найти значение выражения 

Выполним в числителе возведение степени в степень. Сделать это нужно с выражением (2³)⁴

Теперь выполним в числителе умножение степеней с одинаковыми основаниями:

Теперь применяем правило деления степеней с одинаковыми основаниями:

Значит, значение выражения  равно 16

В некоторых примерах можно сокращать одинаковые множители в ходе решения. Это позволяет упростить выражение и само вычисление в целом.

Например, найдём значение выражения . Степень 4³ запишем в виде возведения степени в степень (2²)³. Тогда получим следующее выражение:

В числителе выполним возведение степени в степень. Сделать это нужно с выражением (2²)³

В числителе и в знаменателе получившегося выражения содержится степень 2⁶, которую можно сократить на 2⁶

Видим, что в результате осталась единственная степень 3², значение которой равно 9.

---

Пример 8. Найти значение выражения 

В знаменателе содержится произведение степеней с одинаковыми показателями. Согласно правилу возведения в степень произведения, конструкцию 7⁵ × 4⁵ можно представить в виде степени с одним показателем (7 × 4)⁵. Далее перемножим выражение в скобках, получим 28⁵. В результате исходное выражение примет следующий вид:

Теперь можно применить правило деления степеней:

Значит, значение выражения  равно 28. Запишем решение полностью:

---

Возведение в степень обыкновенных дробей

Чтобы возвести в степень обыкновенную дробь, нужно возвести в указанную степень числитель и знаменатель этой дроби.

Например, возведём обыкновенную дробь  во вторую степень. Возьмём в скобки данную дробь и в качестве показателя укажем 2

Если не брать в скобки всю дробь, то это равносильно возведению в степень только числителя данной дроби. Иными словами, если мы хотим возвести во вторую степень дробь , мы не должны записывать это как .

Итак, чтобы вычислить значение выражения , нужно возвести во вторую степень числитель и знаменатель данной дроби:

Получили дробь в числителе и в знаменателе которой содержатся степени. Вычислим каждую степень по отдельности

Значит обыкновенная дробь  во второй степени равна дроби .

Приведённое правило работает следующим образом. Дробь  во второй степень это произведение двух дробей, каждая из которых равна 

Мы помним, что для перемножения дробей необходимо перемножить их числители и знаменатели:

А поскольку в числителе и в знаменателе происходит перемножение одинаковых множителей, то выражения 2 × 2 и 3 × 3 можно заменить на 2² и 3² соответственно:

Откуда и получится ответ .

Вообще, для любого a и b ≠ 0 выполняется следующее равенство:

Это тождественное преобразование называют возведением в степень обыкновенной дроби.

---

Пример 2. Возвести дробь  в третью степень

Заключим данную дробь в скобки и в качестве показателя укажем число 3. Далее возведём числитель и знаменатель данной дроби в третью степень и вычислим получившуюся дробь:

Отрицательная дробь возводится в степень таким же образом, но перед вычислениями надо определиться какой знак будет иметь ответ. Если показатель четный, то ответ будет положительным. Если показатель нечетный, то ответ будет отрицательным.

Например, возведём дробь  во вторую степень:

Показатель является чётным числом. Значит ответ будет положительным. Далее применяем правило возведения в степень дроби и вычисляем получившуюся дробь:

Ответ положителен по причине того, что выражение  представляет собой произведение двух сомножителей, каждый из которых равен дроби 

А произведение отрицательных чисел (в том числе и рациональных) есть положительное число:

Если возводить дробь  в третью степень, то ответ будет отрицательным, поскольку в данном случае показатель будет нечётным числом. Правило возведения в степень остаётся тем же, но перед выполнением этого возведения, нужно будет поставить минус:

Здесь ответ отрицателем по причине того, что выражение  представляет собой произведение трёх множителей, каждый из которых равен дроби 

Сначала перемножили  и , получили , но затем умножив  на  мы получим отрицательный ответ 

---

Пример 3. Найти значение выражения 

Выполним возведение в степень обыкновенной дроби:

Далее вычислим значение получившегося выражения:

---

Возведение в степень десятичных дробей

При возведении в степень десятичной дроби её необходимо заключить в скобки. Например, возведём во вторую степень десятичную дробь 1,5

Допускается переводить десятичную дробь в обыкновенную и возводить в степень эту обыкновенную дробь. Решим предыдущий пример, переведя десятичную дробь в обыкновенную:

---

Пример 2. Найти значение степени (−1,5)³

Показатель степени является нечётным числом. Значит ответ будет отрицательным

---

Пример 3. Найти значение степени (−2,4)²

Показатель степени является чётным числом. Значит ответ будет положительным:

---

Задания для самостоятельного решения

Задание 1. Найдите значение выражения:

Решение:

Задание 2. Найдите значение выражения:

Решение:

Задание 3. Найдите значение выражения:

Решение:

Задание 4. Найдите значение выражения:

Решение:

Задание 5. Найдите значение выражения:

Решение:

Задание 6. Найдите значение выражения:

Решение:

Задание 7. Представьте в виде степени произведение:

Решение:

Задание 8. Представьте в виде степени произведение:

Решение:

Задание 9. Представьте в виде степени произведение:

Решение:

Задание 10. Представьте в виде степени произведение:

Решение:

Задание 11. Представьте в виде степени произведение:

Решение:

Задание 12. Представьте в виде степени произведение:

Решение:

Задание 13. Представьте в виде степени частное:

Решение:

Задание 14. Представьте в виде степени частное:

Решение:

Задание 15. Представьте в виде степени частное:

Решение:

Задание 16. Представьте в виде степени частное:

Решение:

Задание 17. Представьте в виде степени частное:

Решение:

Задание 18. Представьте в виде степени частное и найдите значение получившейся степени при x = 3 и n = 2

Решение:

Задание 19. Представьте в виде степени частное:

Решение:

Задание 20. Сократите дробь на c¹

Решение:

Задание 21. Представьте в виде степени следующее произведение:

Решение:

Задание 22. Представьте в виде степени следующее произведение:

Решение:

Задание 23. Представьте в виде степени следующее произведение:

Решение:

Задание 24. Представьте в виде степени следующее произведение:

Решение:

Задание 25. Представьте в виде степени следующее произведение:

Решение:

Задание 26. Представьте следующую степень в виде произведения степеней:

Решение:

Задание 27. Представьте следующую степень в виде произведения степеней:

Решение:

Задание 28. Представьте следующую степень в виде произведения степеней:

Решение:

Задание 29. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:

Решение:

Задание 30. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:

Решение:

Задание 31. Пользуясь тождественными преобразованиями степеней, найдите значение следующего выражения:

Решение:

Задание 32. Представьте в виде степени следующее выражение:

Решение:

Задание 33. Представьте в виде степени следующее выражение:

Решение:

Задание 34. Представьте в виде степени следующее выражение:

Решение:

Задание 35. Представьте в виде степени следующее выражение:

Решение:

Задание 36. Представьте в виде степени следующее выражение:

Решение:

Задание 37. Представьте в виде степени следующее выражение:

Решение:

Задание 38. Найдите значение следующего выражения:

Решение:

Задание 39. Найдите значение следующего выражения:

Решение:

Задание 40. Найдите значение следующего выражения:

Решение:

Задание 41. Найдите значение следующего выражения:

Решение:

Задание 42. Найдите значение следующего выражения:

Решение:

Задание 43. Найдите значение следующего выражения:

Решение:

Задание 44. Найдите значение следующего выражения:

Решение:

---

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Действия со степенями и корнями

1. При умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним:

.

Например, .

2. При делении степеней с одинаковыми основаниями показатели степеней вычитаются, а основание остаётся прежним:

.

Например, .

3. При возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним:

.

Например, .

4. Степень произведения равна произведению степеней множителей:

.

Например, .

5. Степень частного равна частному степеней делимого и делителя:

.

Например, .

Пример 1. Найти значение выражения

.

Решение. В данном случае в явной форме ни одно из свойств степени с натуральным показателем применить нельзя, так как все степени имеют разные основания. Запишем некоторые степени в другом виде:

(степень произведения равна произведению степеней множителей),

(при умножении степеней с одинаковыми основаниями показатели складываются, а основание остаётся прежним, при возведении степени в степень показатели степеней перемножаются, а основание остаётся прежним).

Теперь получим:

В данном примере были использованы первые четыре свойства степени с натуральным показателем.

Свойства степеней и корней интенсивно используются при упрощении выражений в задачах математического анализа, например, для нахождения производной параметрически заданной функции и производной функции, заданной неявно.

Имеют место следующие тождества:

1) ;

2) ;

3) .

Выполнить действия со степенями самостоятельно, а затем посмотреть решения

Пример 2. Найти значение выражения

.

Пример 3. Найти значение выражения

.

1. Корень k-й степени из произведения неотрицательных чисел равен произведению корней той же степени из сомножителей: , где (правило извлечения корня из произведения).

2. Если , то (правило извлечения корня из дроби).

3. Если , то (правило извлечения корня из корня).

4. Если , то (правило возведения корня в степень).

5. Если , то , где , т. е. показатель корня и показатель подкоренного выражения можно умножить на одно и то же число.

6. Если , то , т. е. большему положительному подкоренному выражению соответствует и большее значение корня.

7. Все указанные выше формулы часто применяются в обратном порядке (т. е. справа налево). Например:

(правило умножения корней),

(правило деления корней),

.

8. Правило вынесения множителя из-под знака корня. При .

9. Обратная задача — внесение множителя под знак корня. Например,

10. Уничтожение иррациональности в знаменателе дроби. Рассмотрим некоторые типичные случаи.

а) , так как .

Например, .

б)

Например,

в)

и т. д.

Другие темы в блоке «Школьная математика»

Функция СТЕПЕНЬ — Служба поддержки Office

Предположим, что вам нужно вычислить очень маленький допуск для детали механизма или огромное расстояние между двумя галактиками. Для возведения числа в степень используйте функцию СТЕПЕНЬ.

Описание

Возвращает результат возведения числа в степень.

Синтаксис

СТЕПЕНЬ(число;степень)

Аргументы функции СТЕПЕНЬ описаны ниже.2.

Пример

Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД. При необходимости измените ширину столбцов, чтобы видеть все данные.

Формула	Описание	Результат
=СТЕПЕНЬ(5;2)	Число 5 в квадрате.	25
=СТЕПЕНЬ(98,6;3,2)	Число 98,6, возведенное в степень 3,2.	2401077,222
=СТЕПЕНЬ(4;5/4)	Число 4, возведенное в степень 5/4.	5,656854249

Степени сравнения имён прилагательных — teorija. Krievu valoda, 10. klase.

Прилагательные имеют две степени сравнения: сравнительную  и превосходную.

Красивый – красивее (сравнительная степень).

Красивый – красивейший (превос­ходная степень).

  

Сравнительная степень прилагательных

  

Сравнительная степень прилагательного обозначает, что какой-то признак проявляется в одном предмете в большей или меньшей степени, чем в другом.
Он лучше меня. Он красивее меня. Твой портфель тяжелее, чем мой.

 

Сравнительная степень бывает простая и сложная.

Простая сравнительная степень образуется с помощью суффиксов:

• -ее(-ей): красивый – красивее, смелый – смелее, холодный – холоднее;
   

• -е (с чередованием последнего согласного основы или без чередования):
   
  

  Согласные чередуются	Примеры
  	дорогой — дороже узкий — уже молодой — моложе короткий — короче богатый — богаче простой — проще тонкий — тоньше сладкий — слаще молодой – моложе богатый – богаче чистый – чище низкий – ниже узкий – уже высокий – выше близкий – ближе далёкий – дальше долгий – дольше тонкий – тоньше

     

• -ше: старый – старше, молодой – младше, большой — больше.

Иногда при образовании сравнительной степени прилагательного используется другой корень:

хороший – лучше, плохой – хуже, маленький – меньше.

 

Сложная сравнительная степень образуется от полной формы положительной степени прилагательного с помощью частиц более и менее:

большой – более/менее большой, красивый – более/менее красивый.

 

Сложная форма сравнительной степени, как и полная форма положительной степени прилагательных, изменяется по родам, числам и падежам.

    

Превосходная степень прилагательных

  

Превосходная степень обозначает, что какой-то признак проявляется в одном предмете в наибольшей или наименьшей степени.

Он мой лучший друг. Она самая красивая девочка в нашем классе.

 

Превосходная степень бывает простая и сложная.

Простая превосходная степень образуется с помощью суффиксов -ейш-, -айш-.

Svarīgi!

Прилагательные большой, высокий, низкий, хороший, плохой образуют следующие формы превосходной степени: больший, высший, низший, лучший, худший.

 

Не все  прилагательные образуют простую форму превосходной степени.

Svarīgi!

К ним относятся:

• прилагательные с суффиксом —ск-, —еск-:
  братский, дружеский, вражеский, бесовский, адский, уродский;

• некоторые прилагательные с суффиксом -н-:
  родной, дельный, кровный, склочный, избыточный;

• прилагательные с суффиксом —ов-(-ев-):
  передовой, деловой, дармовой, боевой, ключевой, лобовой, круговой, легковой;

• отглагольные прилагательные с суффиксом -л-:
  горелый, бывалый, плесневелый, задубелый, усталый;

• некоторые прилагательные с суффиксом -к-:
  броский, жидкий, веский, падкий, липкий, терпкий, сыпкий, зоркий, цепкий, юркий, терпкий;

• прилагательные с суффиксами -аст-, -ист-:
  глазастый, бровастый, клыкастый, слоистый, изгибистый, рукастый, языкастый;

• некоторые непроизводные прилагательные:
  частый, гордый, молодой.

Иногда при образовании превосходной степени прилагательного используется другой корень:

хороший – лучший, плохой – худший.

   

Сложная превосходная степень образуется:

1. от частиц самый, наиболее и наименее + полное прилагательное:
   большой – самый/наиболее/наименее большой,
   красивый – самый/наиболее/наименее красивый;

2. простая форма сравнительной степени + слово всех:
   сильнее всех, лучше всех и т. д.

Прилагательные в превосходной степени, как и полные формы положительной степени прилагательных, изменяются по родам, числам и падежам.

  

Полное прилагательное	Простая сравнительная степень (-ее(-ей),   -е,   -ше)	Сложная   сравнительная  степень  (более  или менее)	Простая   превосходная  степень (-ейш-, -айш-)	Сложная превосходная степень (самый,   наиболее, наименее)
дорогой узкий молодой короткий богатый простой тонкий сладкий богатый чистый низкий высокий близкий далёкий долгий тонкий красивый добрый	дороже уже моложе короче богаче проще  тоньше слаще богаче чище ниже выше ближе дальше дольше тоньше красивее добрее	более дорогой более узкий более молодой более короткий более богатый более простой более тонкий более сладкий более богатый более чистый более низкий более высокий более близкий более далёкий более долгий более тонкий более красивый более добрый	дражайший — — кратчайший богатейший простейший тончайший сладчайший богатейший чистейший нижайший высочайший ближайший – – тончайший красивейший  добрейший	самый дорогой самый узкий самый молодой самый короткий самый богатый самый простой самый тонкий самый сладкий самый богатый самый чистый самый низкий самый высокий самый близкий самый далёкий самый долгий самый тонкий самый красивый   самый добрый

 

 

При образовании сравнительной и превосходной степеней нельзя одновременно использовать простую и сложную форму степеней сравнения.

Svarīgi!

Неправильно: более красивее, более тяжелее, наиболее спокойнейший.

 

 

 

Степени и возведение в степень, вторая, третья, четвёртая степени

Когда число умножается само на себя, произведение называется степенью.

Так      2.2 = 4, квадрат или вторая степень 2-х
     2.2.2 = 8, куб или третья степень.
     2.2.2.2 = 16, четвёртая степень.

Также,      10.10 = 100, вторая степень 10.
     10.10.10 = 1000, третья степень.
    10.10.10.10 = 10000 четвёртая степень.

И      a.a = aa, вторая степень a
     a.a.a = aaa, третья степень a
     a.a.a.a = aaaa, четвёртая степень a

Первоначальное число называется корнем степени этого числа, потому что это число, из которого были созданы степени.

Однако не совсем удобно, особенно в случае высоких степеней, записывать все множители, из которых состоят степени. Поэтому используется сокращенный метод обозначения. Корень степени записывается только один раз, а справа и немного выше возле него, но чуть меньшим шрифтом записывается сколько раз выступает корень как множитель. Это число или буква называется показателем степени или степенью числа. Так, а² равно a.a или aa, потому что корень a дважды должен быть умножен сам на себя, чтобы получилось степень aa. Также, a³ означает aaa, то есть здесь a повторяется три раза как множитель.

Показатель первой степени есть 1, но он обычно не записывается. Так, a¹ записывается как a.

Вы не должны путать степени с коэффициентами. Коэффициент показывает, как часто величина берётся как часть целого. Степень показывает, как часто величина берётся как множитель в произведении.
Так, 4a = a + a + a + a.      Но a⁴ = a.a.a.a

Схема обозначения со степенями имеет своеобразное преимущество, позволяя нам выражать неизвестную степень. Для этой цели в показатель степени вместо числа записывается буква. В процессе решения задачи, мы можем получить величину, которая, как мы можем знать, есть некоторой степенью другой величины. Но пока что мы не знаем, это квадрат, куб или другая, более высокая степень. Так, в выражении a^x, показатель степени означает, что это выражение имеет некоторую степень, хотя не определено какую степень. Так, b^m и dⁿ возводятся в степени m и n. Когда показатель степени найден, число подставляется вместо буквы. Так, если m=3, тогда b^m = b³; но если m = 5, тогда b^m=b⁵.

Метод записи значений с помощью степеней является также большим преимуществом в случае использования выражений . Tак, (a + b + d)³ есть (a + b + d).(a + b + d).(a + b + d), то есть куб трёхчлена (a + b + d). Но если записать это выражение после возведения в куб, оно будет иметь вид
a³ + 3a²b + 3a²d + 3ab² + 6abd + 3ad² + b³ + d³.

Если мы возьмем ряд степеней, чьи показатели увеличиваются или уменьшаются на 1, мы обнаружим, что произведение увеличивается на общий множитель или уменьшается на общий делитель, и этот множитель или делитель есть первоначальным числом, которое возводится в степень.

Так, в ряде      aaaaa, aaaa, aaa, aa, a;
или        a⁵, a⁴, a³, a², a¹;
показатели , если считать справа налево, равны 1, 2, 3, 4, 5; и разница между их значениями равна 1. Если мы начнем справа умножатьна a, мы успешно получим несколько значений.

Tак a.a = a², второй член. И a³.a = a⁴
     a².a = a³, третий член. a⁴.a = a⁵.

Если мы начнем слева делить на a,
мы получим a⁵:a = a⁴      и a³:a = a².
a⁴:a = a³       a²:a = a¹

Но такой процесс деления может быть продолжен и далее, и мы получаем новый набор значений.

Так, a:a = a/a = 1. (1/a):a = 1/aa
     1:a = 1/a      (1/aa):a = 1/aaa.

Полный ряд будет: aaaaa, aaaa, aaa, aa, a, 1, 1/a, 1/aa, 1/aaa.

Или a⁵, a⁴, a³, a², a, 1, 1/a, 1/a², 1/a³.

Здесь значения справа от единицы есть обратными значениям слева от единицы. Поэтому эти степени могут быть названы обратными степенями a. Можно также сказать, что степени слева есть обратными к степеням справа.

Так, 1:(1/a) = 1.(a/1) = a. И 1:(1/a³) = a³.

Тот же самый план записи может применяться к многочленам. Так, для a + b, мы получим множество,
(a + b)³, (a + b)², (a + b), 1, 1/(a + b), 1/(a + b)², 1/(a + b)³.

Для удобства используется еще одна форма записи обратных степеней.

Согласно этой форме, 1/a или 1/a¹ = a^-1. И 1/aaa или 1/a³ = a^-3.
1/aa или 1/a² = a^-2. 1/aaaa или 1/a⁴ = a^-4.

А чтобы сделать с показателями законченный ряд с 1 как общая разница, a/a или 1, рассматривается как такое, что не имеет степени и записывается как a⁰.

Тогда, учитывая прямые и обратные степени
вместо aaaa, aaa, aa, a, a/a, 1/a, 1/aa, 1/aaa, 1/aaaa
можно записать      a⁴, a³, a², a¹, a⁰, a^-1, a^-2, a^-3, a^-4.
Или      a⁺⁴, a⁺³, a⁺², a⁺¹, a⁰, a^-1, a^-2, a^-3, a^-4.

А ряд только отдельно взятых степеней будет иметь вид:
     +4,+3,+2,+1,0,-1,-2,-3,-4.

Корень степени может выражен более чем одной буквой.

Так, aa.aa или (aa)² есть второй степенью aa.
И aa.aa.aa или (aa)³ есть третьей степенью aa.

Все степени цифры 1 одинаковы: 1.1 или 1.1.1. будет равно 1.

Возведение в степень есть нахождение значения любого числа путем умножения этого числа само на себя. Правило возведения в степень:

Умножайте величину саму на себя столько раз, сколько указано в степени числа.

Это правило является общим для всех примеров, которые могут возникнуть в процессе возведения в степень. Но будет правильно дать объяснение, каким образом оно применяется к частным случаям.

Если в степень возводится только один член, то он умножается сам на себя столько раз, сколько указывает показатель степени.

Четвертая степень a есть a⁴ или aaaa. (Art. 195.)
Шестая степень y есть y⁶ или yyyyyy.
N-ая степень x есть xⁿ или xxx….. n раз повторенное.

Если необходимо возвести в степень выражение из нескольких членов, применяется принцип, согласно которому степень произведения нескольких множителей равна произведению этих множителей, возведенных в степень.

Tак (ay)² =a²y²; (ay)² = ay.ay.
Но ay.ay = ayay = aayy = a²y².
Так, (bmx)³ = bmx.bmx.bmx = bbbmmmxxx = b³m³x³.

Поэтому, в нахождении степени произведения мы можем или оперировать со всем произведением сразу, или мы можем оперировать с каждым множителем отдельно, а потом умножить их значения со степенями.

Пример 1. Четвертая степень dhy есть (dhy)⁴, или d⁴h⁴y⁴.

Пример 2. Третья степень 4b, есть (4b)³, или 4³b³, или 64b³.

Пример 3. N-ая степень 6ad есть (6ad)ⁿ или 6ⁿaⁿdⁿ.

Пример 4. Третья степень 3m.2y есть (3m.2y)³, или 27m³.8y³.

Степень двочлена, состоящего из членов, соединенных знаком + и -, вычисляется умножением его членов. Tак,

(a + b)¹ = a + b, первая степень.
(a + b)¹ = a² + 2ab + b², вторая степень (a + b).
(a + b)³ = a³ + 3a²b + 3ab² + b³, третья степень.
(a + b)⁴ = a⁴ + 4a³b + 6a²b² + 4ab³ + b⁴, четвертая степень.

Квадрат a — b, есть a² — 2ab + b².

3 + 3a² + 3a + 1.

Квадрат a + b + h есть a² + 2ab + 2ah + b² + 2bh + h²

Упражнение 1. Найдите куб a + 2d + 3

Упражнение 2. Найдите четвертую степень b + 2.

Упражнение 3. Найдите пятую степень x + 1.

Упражнение 4. Найдите шестую степень 1 — b.

Квадраты суммы суммы и разницы двочленов встречаются так часто в алгебре, что необходимо их знать очень хорошо.

Если мы умножаем a + h само на себя или a — h само на себя,
мы получаем: (a + h)(a + h) = a² + 2ah + h²      также, (a — h)(a — h) = a² — 2ah + h².

Отсюда видно, что в каждом случае, первый и последний члены есть квадраты a и h, а средний член есть удвоеннное произведение a на h. Отсюда, квадрат суммы и разницы двочленов может быть найден, используя следующее правило.

Квадрат двочлена, оба члена которых положительны, равен квадрату первого члена + удвоенное произведение обоих членов, + квадрат последнего члена.

Квадрат разницы двочленов равен квадрату первого члена минус удвоенное произведение обоих членов плюс квадрат второго члена.

Пример 1. Квадрат 2a + b, есть 4a² + 4ab + b².

Пример 2. Квадрат ab + cd, есть a²b² + 2abcd + c²d².

Пример 3. Квадрат 3d — h, есть 9d₂ + 6dh + h².

Пример 4. Квадрат a — 1 есть a² — 2a + 1.

Чтобы узнать метод нахождения более высоких степеней двочленов, смотрите следующие разделы.

Во многих случаях является эффективным записывать степени без умножения.

Так, квадрат a + b, есть (a + b)².
N-ая степень bc + 8 + x есть (bc + 8 + x)ⁿ

В таких случаях, скобки охватывают все члены под степенью.

Но если корень степени состоит из нескольких множителей, скобки могут охватывать всё выражение, или могут применяться отдельно к множителям в зависимости от удобства.

Так, квадрат (a + b)(c + d) есть или [(a + b).(c + d)]² или (a + b)².(c + d)².

Для первого из этих выражений результатом есть квадрат произведения двух множителей, а для второго — произведением их квадратов. Но они равны друг другу.

Куб a.(b + d), есть [a.(b + d)]³, или a³.(b + d)³.

Необходимо также учитывать и знак перед вовлеченными членами. Очень важно помнить, что когда корень степени положительный, все его положительные степени также положительны. Но когда корень отрицательный, значения с нечетными степенями отрицательны, в то время как значения чётных степеней есть положительными.

Вторая степень (- a) есть +a²
Третья степень (-a) есть -a³
Четвёртая степень (-a) есть +a⁴
Пятая степень (-a) есть -a⁵

Отсюда любая нечётная степень имеет тот же самый знак, что и число. Но чётная степень есть положительна вне зависимости от того, имеет число отрицательный или положительный знак.
Так, +a.+a = +a²
И -a.-a = +a²

Величина, уже возвёденная в степень, еще раз возводится в степень путем умножения показателей степеней.

Третья степень a² есть a^2.3 = a⁶.

Для a² = aa; куб aa есть aa.aa.aa = aaaaaa = a⁶; что есть шестой степенью a, но третьей степенью a².

Четвертая степень a³b² есть a^3.4b^2.4 = a¹²b⁸

Третья степень 4a²x есть 64a⁶x³.

Пятая степень (a + b)² есть (a + b)¹⁰.

N-ая степень a³ есть a³ⁿ

N-ая степень (x — y)^m есть (x — y)^mn

(a³.b³)² = a⁶.b⁶

(a³b²h⁴)³ = a⁹b⁶h¹²

Правило одинаково применяется к отрицательным степеням.

Пример 1. Третья степень a^-2 есть a^-3.3=a^-6.

Для a^-2 = 1/aa, и третья степень этого
(1/aa).(1/aa).(1/aa) = 1/aaaaaa = 1/a⁶ = a^-6

Четвертая степень a²b^-3 есть a⁸b^-12 или a⁸/b¹².

Квадрат b³x^-1, есть b⁶x^-2.

N-ая cтепень ax^-m есть x^-mn или 1/x.

Однако, здесь надо помнить, что если знак, предшествующий степени есть «-«, то он должен быть изменен на «+» всегда, когда степень есть четным числом.

Пример 1. Квадрат -a³ есть +a⁶. Квадрат -a³ есть -a³.-a³, которое, согласно правилам знаков при умножении, есть +a⁶.

2. Но куб -a³ есть -a⁹. Для -a³.-a³.-a³ = -a⁹.

3. N-ая степень -a³ есть a³ⁿ.

Здесь результат может быть положительным или отрицательным в зависимости от того, какое есть n — чётное или нечётное.

Если дробь возводится в степень, то возводятся в степень числитель и знаменатель.

Квадрат a/b есть a²/b². Согласно правилу умножению дробей,
     (a/b)(a/b) = aa/bb = a²b²

Вторая, третья и n-ая степени 1/a есть 1/a², 1/a³ и 1/aⁿ.

Примеры двочленов, в которых один из членов является дробью.

1. Найдите квадрат x + 1/2 и x — 1/2.
(x + 1/2)² = x² + 2.x.(1/2) + 1/2² = x² + x + 1/4
(x — 1/2)² = x² — 2.x.(1/2) + 1/2² = x² — x + 1/4

2. Квадрат a + 2/3 есть a² + 4a/3 + 4/9.

3. Квадрат x + b/2 = x² + bx + b²/4.

4 Квадрат x — b/m есть x² — 2bx/m + b²/m².

Ранее было показано, что дробный коэффициент может быть перемещен из числителя в знаменатель или из знаментеля в числитель. Используя схему записи обратных степеней, видно, что любой множитель также может быть перемещен, если будет изменен знак степени.

Так, в дроби ax^-2/y, мы можем переместить x из числителя в знаменатель.
Тогда ax_-2/y = (a/y).x^-2 = (a/y).(1/x² = a/yx².

В дроби a/by³ мы можем переместить у из знаменателя в числитель.
Тогда a/by₂ = (a/b).(1/y³) = (a/b).y^-3 = ay^-3/b.

Таким же образом мы можем переместить множитель, который имеет положительный показатель степени в числитель или множитель с отрицательной степенью в знаменатель.

Так, ax³/b = a/bx^-3. Для x³ обратным есть x_-3, что есть x³ = 1/x^-3.

Следовательно, знаменатель любой дроби может быть полностью удален, или числитель может быть сокращен до единицы, что не изменит значение выражения.

Так, a/b = 1/ba^-1, or ab^-1.

отзывов — 10 градусов

Наша фантастическая служба поддержки клиентов будет сопровождать нас в нашем новом месте в Джорджтауне! Ниже приведены несколько прекрасных слов о нашем месте на Капитолийском холме.

Ознакомьтесь с нашими онлайн-обзорами по адресу: Yelp, Wedding Wire, The Knot и Facebook! Ниже несколько драгоценных камней.

«ПРЕКРАСНОЕ пространство для мероприятий. Здесь можно сделать так много, и то, как персонал преображает пространство, потрясающе! Мне посчастливилось встретиться с владельцами, и я могу поручиться за них, когда я скажу, что они одни из самых приятных людей, которых я знаю когда-либо встречал!» -Lauren

«Я отпраздновала здесь первый день рождения моего сына, и я бы выбрала их снова для следующего мероприятия в мгновение ока.Я планировал эту вечеринку из другого штата по электронной почте с Брит, и с ней было так здорово работать — от помощи мне в планировании общей картины вечеринки до проработки мельчайших деталей. . »–Мэри Джейн

« Мы не могли бы быть более довольны персоналом и пространством здесь. Бритт была фантастической точкой нашего контакта и взяла на себя огромный объем планирования. Наш день координатора, Тара, был таким же исключительный, и позаботился о том, чтобы все прошло без проблем.Росио, менеджер по производству, был невероятно любезен, а персонал бара не мог быть лучше.”–Shane

“ Это МЕСТО для небольшой вечеринки или мероприятия! А у владельцев винокурни OOLA есть возможность сдать в аренду свою бочку, чтобы добавить еще больше места. Это было прекрасным дополнением к праздничной вечеринке нашей компании, потому что мы могли пить вкусные коктейли в атмосфере винокурни и переходить на 10 градусов к обеду ». -Meredith

«5 звезд! У нас там был детский душ для нашей дочери. Перед мероприятием Бритт, менеджер места проведения мероприятия, была очень внимательной и отзывчивой, ответила на все наши вопросы четко и подробно, иногда на наши повторяющиеся вопросы, лол.В день мероприятия экипаж 10d был чрезвычайно любезным и вежливым, постоянно следя за чистотой стола. Они позаботились о том, чтобы о гостях всегда заботились. Они также были отличными барными тендерами 🙂 Обязательно вернусь на другое мероприятие! ​​»-Jack

Warm Winter Running Gear для 30, 20 и 10 градусов F — The Runner’s Plate

Как одеваться для зимних пробежек?

Одежда для зимних пробежек — дело непростое. Не только температура имеет значение, но и скорость ветра, время дня, реальная температура и влажность могут изменить то, что вам нужно носить, чтобы оставаться комфортным во время бега.

Проведя всю свою беговую карьеру (25 лет) в штатах, где зимы холодные, ветер кусает и солнце редко, я чувствую, что могу поделиться некоторыми советами и приемами, которые я усвоил за эти годы. Ха!

Прежде всего, я настоятельно рекомендую покупать 1 или 2 качественных предмета одежды, которые прослужат несколько зим и обеспечат вам комфорт, а не 5-6 предметов посредственного качества. Я знаю, что может быть трудно потратить 100-200 долларов на зимнюю куртку и более 100 долларов на пару колготок, но я действительно думаю, что оно того стоит.Я, как правило, покупаю у брендов, специализирующихся на беге: Oiselle, lululemon и New Balance — мои покупатели, а также некоторые другие бренды, такие как Rabbit, Craft, Skida и Brooks.

Вам определенно стоит отказаться от хлопка и выбрать синтетические волокна. Синтетические волокна будут отводить влагу от вашей кожи, заставляя вас чувствовать себя намного комфортнее и сводя к минимуму риск обморожения или переохлаждения.

Я разделил этот пост на три температурные категории: 30 * F, 20 * F, 10 * F и перечислил количество и тип снаряжения, подходящего для каждой температуры.Конечно, некоторым из вас становится жарче или холоднее, поэтому используйте эти предложения в качестве ориентира, а затем ограничьте свои потребности вокруг них.

Я также дал ссылки на качественное снаряжение, которое я бы порекомендовал для каждого предмета. Я искренне верю, что в 90% случаев вы получаете то, за что платите, поэтому я часто предпочитаю потратить немного больше на качественное снаряжение, которое, как я знаю, будет работать. И хотя 10 градусов не кажутся слишком разными, я считаю, что температура в верхней части 20 и нижней 20 может ощущаться немного по-другому, а это значит, что мне придется одеваться по-другому, поэтому примите эти предложения во внимание. а затем выясните, что работает для вас.

Тридцать градусов по Фаренгейту — это когда длинные колготки выходят наружу, мне нужно два слоя сверху, а мои конечности должны быть прикрыты — по крайней мере, на протяжении первых миль или двух. Мне не нужно полностью закрывать голову, и я могу бегать с голыми лодыжками, но мне нравится, когда уши закрыты, и обычно меня устраивают повязка на голову, тонкий базовый слой, легкая ветрозащитная / непродуваемая куртка, полностью плотно (или не менее 7/8 длины) и перчатки.

Я связал несколько разных вариантов для каждого изделия — некоторые из них мои любимые, другие были бы одинаково прекрасны.

Повязки на голову / грелка для ушей
Skida Nordic Headband
Oiselle Firecracker Reflective Earband
Oiselle Lux Earband
Rabbit Headband
Brooks Greenlight Headband

Базовые слои
Amazon Long Sleeve
lululemon Swiftly Long Sleeve
Oiselle Flyte Long Sleeve

Легкая куртка
Oislle Reflective Vim Jacket (на фото выше)
Nike Essential Running Jacket
lululemon Mist Over Windbreaker Jacket
Brooks Canopy Jacket

Колготки
New Balance Impact Run Tight
lululemon High Rise Fast & Free Brushed Tights
Oiselle Triple Threat Tights
Brooks Greenlight Tight
Nike Luxe Tights

Перчатки
Перчатки Oiselle Lux
New Balance Heat Grid Fleece Glove
Перчатки lululemon Run for It All

* Еще один отличный вариант при такой температуре — надеть более толстый базовый слой + жилет вместо куртки, особенно если вы склонны бегать по более горячей стороне.Я думаю, что этот жилет lululemon действительно симпатичный, и вы можете найти список более толстых и теплых базовых слоев ниже в разделе 20 * F.

---

Двадцать градусов по Фаренгейту могут действительно различаться для меня — если ветер спокойный, он может казаться немного приятным, но как только он опускается до подросткового возраста с ветром, я замечаю, что мое лицо становится намного холоднее, а руки не согреваются. так быстро. При температуре около 20 * F мне нравится использовать грелку для ушей с флисовой подкладкой или тонкую шляпу, влагоотводящий базовый слой (более тонкий для температуры до 20 градусов, более толстый, если температура немного ниже 20 градусов), более толстая куртка, обладающая ветрозащитными или, по крайней мере, ветрозащитными свойствами, колготки с начесом или слегка флисовой подкладкой, а также трансформируемая рукавица / перчатка или более тонкая рукавица.

Я связал несколько разных вариантов для каждого изделия — некоторые из них мои любимые, другие были бы одинаково прекрасны.

Повязки / головные уборы
Повязки Skida Alpine (на фото выше)
lululemon Down for It All Earwarmer
Повязка из флиса с кроликом
Повязка из флиса New Balance Heat Grid
Флисовая шляпа New Balance Heat Grid

Базовые слои
* Все эти слои толще, теплее или сделаны из шерсти. Если вам нужен более легкий базовый слой, посмотрите варианты, перечисленные для 10 и 30 градусов.
lululemon Chase the Chill с длинным рукавом
lululmeon Runderful с длинным рукавом
New Balance Heat Grid Hoodie
New Balance Heat Gird с длинным рукавом
Rabbit Ribbit (шерсть)
Oiselle Flyout Wool Wool Long Sleeve
Oiselle Wazzie Wool Long Sleeve

Более толстая куртка
New Balance Impact Run Winter Jacket (на фото выше)
New Balance Reflective Impact Run Winter Jacket
lululemon Cross Chill Jacket
Oiselle Insulated Vim Jacket

Колготки
New Balance Impact Heat Tight
lululemon Brushed Fast & Free Tight
Oiselle Flyout Tights
Mizuno Breath Thermo Tight

Перчатки / рукавицы
Oiselle Bad Weather Gloves
lululemon Run for it All Перчатки с капюшоном
New Balance Performance Insulate Gloves
Craft Hybrid Weather Glove

---

При 10 градусах по Фаренгейту мне становится очень холодно.Я все еще выдерживаю холод, потому что это лучше, чем беговая дорожка, но еще труднее получить мотивацию выйти на улицу. Однако хорошее снаряжение делает его более терпимым, и я наконец нашла пару колготок, которые действительно согревают мои ноги, что шокирует, потому что мои ноги иногда краснеют в 30-градусную погоду.

Вот некоторые вещи, которые я рекомендую при температуре около 10 градусов F.

Шапки
Rabbit Performance Beanie
Lululemon Run for It All Beanie
Oiselle Lux Beanie
Skida Alpine Hat
New Balance Heavy Fleece Hat

Утеплители для шеи
Утеплители для шеи Skida Apline и Tour (на фото выше)
New Balance Heavyweight Fleece Neckwarmers

Рукавицы
Рукавицы lululemon Down For It All
Рукавицы Oiselle Super Puff
Рукавицы lululemon Pinnacle Warmth (если вы можете найти их на Poshmark / Ebay)

Базовый слой
(Мне нужен только тонкий базовый слой с курткой Down for It All, потому что он такой теплый.Однако, если вам действительно нужен более толстый и теплый базовый слой, есть хороший список в разделе 20 * F.)
Amazon Long Sleeve
lululemon Swiftly Long Sleeve
Oiselle Flyte Long Sleeve

Пуховая / очень теплая куртка
Куртка lululemon Down For It All (на фото выше — у меня их 4)
Куртка lululemon Another Mile (даже теплее для «Down for It All» — может быть, слишком теплая для большинства трассы)
Arc’Teryx Atom Jacket

Колготки
Athleta Altitude Polartec Tights (Самые теплые колготки, которые я когда-либо пробовала.
Колготки Craft Subzero Wind Tights

---

Все мы знаем, что погода по-разному ощущается в разных местах, и такие вещи, как ветер, влажность, облачность, солнце и время суток, имеют значение в том, что вы носите. Я приложил все усилия, чтобы обобщить эти предложения и найти золотую середину, потому что я знаю, что есть много людей, которым понадобятся дополнительные слои, а есть и те из вас, кто в некоторых из этих нарядов пропотел бы до смерти. Если вы склонны перегреваться, вы, вероятно, перейдете в категорию более холодных и наоборот, но я надеюсь, что это, по крайней мере, поможет вам получить отправную точку.

Нравится:

Нравится Загрузка …

10 градусов | Minor, Сиэтл, Вашингтон, США

10 градусов | Минор, Сиэтл, Вашингтон, США — Отчет о месте проведения Нажмите, чтобы отправить сообщение + посмотреть расценки ×

Успешно отправлено!

Пожалуйста, введите текст вашего сообщения.

Лимит мест

Достигнуто

Пожалуйста, приходите завтра
, чтобы связаться с другими местами.

Этот пользователь поместил вашу учетную запись в черный список.

Расположенный в самом сердце Сиэтла, городская среда 10 Degrees предлагает гостям уединение и уединение для любого мероприятия.

10 градусов и винокурня OOLA — единственные помещения для проведения мероприятий, спроектированные архитектурной фирмой Graham Baba Architects из Сиэтла. Мы делим внутреннюю дверь с нашим соседом, заводом OOLA Distillery. Если вы бронируете с 10 градусами, у вас есть возможность использовать оба места.

Inside Scoop

Красиво освещенная палуба — лучшее место, чтобы провести летний вечер, потягивая крафтовые коктейли.Вам наверняка позавидуют обычные люди. Рядом с площадкой нашего отеля припаркованы фургоны с едой или уличная тележка, предлагая вкусные угощения всех видов.

Удобства

• Аудио / видео оборудование
• Парковка на улице
• Wi-Fi
• Стулья для обедов
• Обеденные столы
• Туалеты на территории
• Другое

Характеристики места

Место действия:

Район Хилл в Сиэтле, наше заведение кажется уединенным и уединенным.Пройдя через нашу двухуровневую палубу, вы открываете 12-футовую металлическую дверь в 10-градусное пространство. Редкая древесина покрывает большие двери, шкафы и полы с подогревом и пружинами. Пространство кажется интимным и теплым. Через другую дверь вы попадаете в более промышленную бочку винокурни OOLA. Слева от вас поднимается стена из бочек с виски, и вы видите 15-футовый металл все еще перед собой. И в бочковой, и в 10-градусном пространстве есть рулонные двери с оконными панелями, которые открываются на улицу.Дегустационный и торговый зал OOLA может быть добавлен к частным мероприятиям вместе с сотрудником, который будет разливать образцы продуктов, сделанных на месте. Палуба, 10 градусов и бочка — это уникальные пространства, где гости могут создать незабываемые впечатления от близких на специальных мероприятиях.

Отличительные особенности заведения:

10 градусов имеет высококлассный штат барных торговцев, которые предлагают ремесленные коктейли с использованием спиртных напитков OOLA. Клиенты могут пригласить свою собственную кейтеринговую компанию для управления баром или привлечь для этого наш штатный персонал.Винокурня OOLA имеет частный дегустационный зал, где спиртные напитки сидят на готовой 10-футовой столешнице из досок, а бочки в деревенском стиле служат в качестве коктейльных столов. Клиент может купить спиртные напитки, чтобы забрать домой и узнать о том, как создавался и создавался каждый продукт.

Дополнительные льготы:

(1) Менеджер объекта
(8) 6-дюймовые банкетные столы
(50) черные обеденные стулья
(8) столы для бистро и (24) табуреты
(3) столики для кафе и (6) стулья для кафе
Роликовый бар в стиле середины века
Стереосистема Mackie
Диспенсер для воды и чашки
Вотивы и чайные свечи
Подключение к Wi-Fi

Награды и знаменитости

Все наши онлайн-обзоры 5-звездочные

Места проведения праздников

10 градусов:

Уютное пространство для мероприятий в самом сердце Капитолийского холма, Сиэтл

— Вид: городской пейзаж с разнообразными персонажами, прогуливающимися мимо

— Максимальная вместимость: 50

— Цена: Присоединяйтесь к вечеринке и войдите в систему, чтобы посмотреть цены

10 градусов и винокурня OOLA:

Уютное пространство для мероприятий в самом сердце Капитолийского холма, Сиэтл

— Вид: городской пейзаж с разнообразными персонажами, прогуливающимися мимо

— Максимальная вместимость: 85

— Цена: Присоединяйтесь к вечеринке и войдите в систему, чтобы просмотреть цены

НА ЭТОМ МЕСТЕ НЕТ ОТЧЕТОВ В ЭТО ВРЕМЯ.

Загляните снова скоро!

Видео не найдено

Видео не найдено.

{{roomType.description}}

Этого не существует, мы должны указать здесь политику невозврата и курения.

Доступны эксклюзивные удобства.

Специальная цена в Интернете при бронировании онлайн.

Для некурящих

{{averageBeforeTax}} usdAvg. цена / ночь

Осталось переговорных комнат: {{roomType.numberOfUnits}}

забронируйте сейчас

{{{hotelDescription.Генеральная}}}

{{/если}} {{#if Удобства}}

Удобства

{{#each Удобства}}
• {{.}}
{{/каждый}}

{{/если}}

Характеристики

{{#if hotelDescription.airportShuttle}} {{/если}} {{#if hotelDescription.breakfastIsComplimentary}} {{/если}} {{#if hotelDescription.parking}} {{/если}} {{#if hotelDescription.miscFees}} {{/если}}

Информация об аэропорте и маршрутном такси	{{{hotelDescription.airportShuttle}}}
информация о завтраке	{{hotelDescription.BreakfastIsComplimentary}}
информация о парковке	{{hotelDescription.parking}}
прочие сборы / правила	{{{hotelDescription.miscFees}}}

Похоже, вы немного пораньше. Информация об отеле скоро будет здесь. Посетите вкладку места проведения выше, чтобы получить дополнительную информацию об этом объекте.

Вы должны быть опубликовать подсказку.

Просто отправьте текстовое сообщение, отправьте электронное письмо и поделитесь своей ссылкой Coco со своими гостями, чтобы передать эксклюзивные предложения отелей и получить скидку 5 долларов на каждое бронирование до 4 августа.

ПРИВЕТ ЗДЕСЬ,

СТОРОННИКИ

Мы — The Venue Report, и мы ЕЖЕНЕДЕЛЬНО ОБСЛУЖИВАЕМ
последних критических отчетов на ваш электронный почтовый ящик.

Узнайте, где проводить званые обеды, дни рождения,
свадеб, светские мероприятия; вы называете это.

Мы сообщаем о самых крутых заведениях по всей стране,
внутренних подсказках, эксклюзивных предложениях в вашем городе и создаем
новых заведений, чтобы вы могли первыми устроить там вечеринку.

Где отпразднуете?

СПАСИБО!

Пожалуйста, проверьте свою электронную почту

* мы никому не передадим вашу информацию

10 градусов — это не вдвое теплее, чем 5 градусов, но полезно предположить, что это

. Постоянные читатели заметят, что в h3Open мы иногда немного привередливы в выборе слов.Нам не нравится называть пловцов в гидрокостюмах, прыгающих в воду с температурой 20 градусов, как «храбрых» или «выносливых», и мы не любим использовать слово «замерзание» для воды, температура которой далеко от нуля градусов Цельсия.
Еще одна вещь, которая нас раздражает, — это то, что 10 градусов по Цельсию описываются как вдвое теплее, чем 5, или 30 — как вдвое теплее, чем 15. Это не так. Это просто результат используемой нами шкалы. Мы увидим, что это бессмысленно, если перейдем на шкалу Фаренгейта.

• 5 градусов Цельсия = 41 градус Фаренгейта
• 10 градусов Цельсия = 50 градусов Фаренгейта

И 50 определенно не дважды 41, даже если кажется, что это так, когда вы приближаетесь к своему пятидесятилетию, но это уже другая тема.
Причина в том, что ноль градусов Цельсия — это не нижняя граница шкалы. Самая низкая возможная температура или абсолютный ноль составляет -273,15 градусов по Цельсию или 0 градусов по Кельвину.
Итак, 10 градусов по Цельсию (и это не следует понимать слишком буквально) на самом деле только примерно на 1,8 процента теплее, чем 5 градусов, а 30 градусов — лишь примерно на 5,2 процента теплее, чем 15 градусов. Половина 10 градусов будет очень холодным -131,5 градуса по Цельсию.
Однако, несмотря на эту небольшую разницу в абсолютном выражении, для пловцов разница очень значительна.С практической точки зрения, мы можем рассматривать 10 градусов по Цельсию как два раза по 5 градусов, как видно из ожидаемого времени выживания в холодной воде без защитной одежды. При 5 градусах ожидаемое время выживания составляет от 30 до 90 минут (это для тех, кто находится на плаву с чистыми дыхательными путями — потеря ловкости может занять менее трех минут, а потеря сознания может произойти в течение 15 минут). При 10 градусах ожидаемое время выживания составляет от одного до шести часов (с потерей ловкости через 10-15 минут и потерей сознания через один-два часа), а при 20 градусах — от трех часов до неопределенного срока.
Теперь, хотя мы знаем, что существует много индивидуальных особенностей и что обученные, опытные и тщательно контролируемые пловцы могут значительно превосходить эти цифры, они подчеркивают опасность холодной воды.
Итак, хотя 10 градусов не вдвое теплее, чем 5 градусов, при планировании плавания разумным практическим правилом может быть предположение, что это так. Как мы видели на прошлой неделе с Давиной МакКолл, к холодной воде нужно относиться с уважением.
Фото: Колин Хилл готовится к плаванию в холодной воде

Присоединяйтесь к счастливому часу в 10 Degrees Bar в Нью-Йорке, Нью-Йорк 10009

Присоединяйтесь к счастливому часу в 10 Degrees Bar в Нью-Йорке, NY 10009

** Цены и специальные предложения могут быть изменены в любое время

Счастливые часы

Ежедневно с 15:00 до 20:00

Рекомендованный специальный выпуск

U-образный бар и черные кожаные кресла делают Ten Degrees Bar отличным баром в восточной деревне.Гуляйте с соседями по комнате или собирайтесь с друзьями, Ten Degrees устраивает счастливый час. 2 напитка по цене 1 и фирменные блюда дня, приходите в любой день недели, и вы знаете, что уйдете счастливыми. Приходите к понедельнику, купите вина за половину цены и добавьте к ним отличные сыры.

Больше «счастливых часов»

Ежедневно с 15:00 до 20:00

Сообщить неточно

Информация о местонахождении

Панель 10 градусов

Бары на Таймс-сквер

121 Санкт-ПетербургМарки Пл

Нью-Йорк, Нью-Йорк 10009

США

212-358-8600

Часы работы

Понедельник и среда, пятница и воскресенье, 12:00 — 4a
Вторник и четверг, 15:00 — 4:00

Прочие

БарыБезалкогольные ЛаунжиРестораныГей-бары

около 10 градусов бар

Напитки для напитков по $ 4, с понедельника по пятницу с 15:00 до 20:00.

Мы предлагаем ежедневный «счастливый час» с 16:00 до 20:00 со специальными предложениями на напитки и еду!

Скидка 1/2 на все напитки с понедельника по пятницу с 15:00 до 20:00.

загружен в 46.7993 мс | 01.06.2021 6:17:43

10 — Шариковый инклинометр, +/- 10 градусов

Высококачественный шариковый инклинометр для индикации угла в диапазоне ± 10 °. Прочный алюминиевый корпус с механической обработкой придает устройству исключительную прочность и долговечность. Стеклянный флакон изготавливается и заполняется в нашей чистой комнате, а индикаторный шар представляет собой черный керамический шар с точной шлифовкой. Чистота флакона и прецизионный керамический шарик гарантируют, что угол отображается точно, а шарик не застревает и не дает ложных показаний.

Характеристики

• Прецизионный флакон с черным керамическим шариком
• Диапазон ± 10 °
• Широкий температурный диапазон от -20 до 70 ° C
• Водонепроницаемый, с механически обработанным алюминиевым корпусом

Применения

• Контроль наклона внедорожника
• Техника для стрижки травы
• Экскаваторы и погрузчики
• Измерение угла стрелы крана

Спецификация продукта

Параметр	Значение	Блок
Длина	90	мм
Диапазон	± 10 °	–
Разрешение	1 °	–
Точность	10%	–
Высота	9	мм
Ширина	35	мм
Тип измерения	Мяч	–
Материал корпуса	Черный анодированный алюминий	–
Материал флакона	Стекло	–
Способ монтажа	Винтовое крепление или лента VHB	–
Диаметр шарика	3.2	мм
Камера расширения	№	–
Легкая	Нет	–

Размер	Значение	Блок
Длина	90	мм
Ширина	35	мм
Высота	9	мм
Масса	38	граммов

Параметр	Значение	Блок
Диапазон рабочих температур	от -20 до 60 ° C	° С
Диапазон температур хранения	от -40 до 60 ° C	° С

Прогнозирование центрального поля зрения 10 градусов при глаукоме путем применения алгоритма глубокого обучения к изображениям оптической когерентной томографии

1.

Куигли, Х. А. и Броман, А. Т. Число людей с глаукомой во всем мире в 2010 и 2020 годах. Br. J. Ophthalmol. 90 , 262–267 (2006).

CAS PubMed PubMed Central Статья Google Scholar

2.

Алтангерел, У., Спет, Г. Л. и Ри, Д. Дж. Зрительные функции, инвалидность и психологическое влияние глаукомы. Curr. Opin. Офтальмол. 14 , 100–105 (2003).

PubMed Статья PubMed Central Google Scholar

3.

Керриган-Баумринд, Л. А., Куигли, Х. А., Пиз, М. Э., Керриган, Д. Ф. и Митчелл, Р. С. Число ганглиозных клеток в глаукомных глазах по сравнению с пороговыми тестами поля зрения у тех же людей. Инвест офтальмол. Vis. Sci 41 , 741–748 (2000).

CAS PubMed PubMed Central Google Scholar

4.

Harwerth, R. S. et al. Нервные потери коррелировали с потерей зрения в клинической периметрии. Инвест. Офтальмол. Vis. Sci. 45 , 3152–3160 (2004).

PubMed Статья PubMed Central Google Scholar

5.

Куигли, Х. А., Дункельбергер, Г. Р. и Грин, У. Р. Атрофия ганглиозных клеток сетчатки коррелировала с автоматической периметрией в глазах человека с глаукомой. Am. J. Ophthalmol. 107 , 453–464 (1989).

CAS PubMed Статья PubMed Central Google Scholar

6.

Харверт, Р. С., Картер-Доусон, Л., Шен, Ф., Смит, Э. Л. и Кроуфорд, М. Потери ганглиозных клеток, лежащие в основе дефектов поля зрения при экспериментальной глаукоме. Инвест. Офтальмол. Vis. Sci. 40 , 2242–2250 (1999).

CAS PubMed PubMed Central Google Scholar

7.

Tan, O. et al. Обнаружение потери ганглиозных клеток желтого пятна при глаукоме с помощью оптической когерентной томографии в области Фурье. Офтальмология 116 , 2305–2314 (2009).

PubMed PubMed Central Статья Google Scholar

8.

Гарас, А., Варга, П. и Холло, Г. Точность диагностики слоя нервных волокон, толщины макулы и измерений диска зрительного нерва с помощью оптического когерентного томографа RTVue-100 для обнаружения глаукомы. Глаз 25 , 57–65 (2011).

CAS PubMed Статья PubMed Central Google Scholar

9.

Moreno, P. A. et al. Спектральная оптическая когерентная томография для ранней оценки глаукомы: анализ комплекса макулярных ганглиозных клеток по сравнению со слоем перипапиллярных нервных волокон сетчатки. банка. J. Ophthalmol. 46 , 543–547 (2011).

PubMed Статья PubMed Central Google Scholar

10.

Rao, H. L. et al. Влияние смещения спектра на диагностическую точность спектральной оптической когерентной томографии при глаукоме. Инвест. Офтальмол. Vis. Sci. 53 , 1058–1065 (2012).

PubMed Статья PubMed Central Google Scholar

11.

Tan, A. M. et al. Микроимпульсная транссклеральная диодная лазерная циклофотокоагуляция в лечении рефрактерной глаукомы. Clin. Exp. Офтальмол. 38 , 266–272 (2010).

PubMed Статья PubMed Central Google Scholar

12.

Schulze, A. et al. Диагностическая способность комплекса ганглиозных клеток сетчатки, слоя нервных волокон сетчатки и измерений головки зрительного нерва с помощью оптической когерентной томографии в области Фурье. Graefes Arch. Clin. Exp. Офтальмол. 249 , 1039–1045 (2011).

PubMed Статья PubMed Central Google Scholar

13.

Kim, N. R. et al. Взаимосвязь между структурой и функцией и диагностическая ценность измерения комплекса ганглиозных клеток желтого пятна с использованием ОКТ в Фурье-области при глаукоме. Инвест. Офтальмол. Vis. Sci. 51 , 4646–4651 (2010).

PubMed Статья PubMed Central Google Scholar

14.

Rao, H., Babu, J., Addepalli, U., Senthil, S. & Garudadri, C. Измерения слоя нервных волокон сетчатки и внутренней сетчатки желтого пятна с помощью оптического когерентного томографа спектральной области в глазах в Индии с ранней глаукома. Глаз 26 , 133–139 (2012).

CAS PubMed Статья PubMed Central Google Scholar

15.

Худ, Д. К. Улучшение нашего понимания и обнаружения глаукомного повреждения: подход, основанный на оптической когерентной томографии (ОКТ). Prog. Ретин. Eye Res. 57 , 46–75 (2017).

PubMed Статья PubMed Central Google Scholar

16.

Худ, Д. К. и Кардон, Р. Х. Основы для сравнения структурных и функциональных показателей глаукомного повреждения. Prog. Retin Eye Res. 26 , 688–710 (2007).

PubMed PubMed Central Статья Google Scholar

17.

Ю, Ю. К., Ли, К. М. и Парк, Дж. Х. Изменения в распределении перипапиллярного слоя нервных волокон сетчатки по осевой длине. Optom. Vis. Sci. 89 , 4–11 (2012).

PubMed Статья PubMed Central Google Scholar

18.

Хонг, С. В., Ан, М. Д., Кан, С. Х. и Им, С. К. Анализ распределения перипапиллярных нервных волокон сетчатки у здоровых молодых людей. Инвест. Офтальмол. Vis. Sci. 51 , 3515–3523 (2010).

PubMed Статья PubMed Central Google Scholar

19.

Шилдс, М.B. Учебник глаукомы (Уильям и Уилкинс, Мэриленд, 1997).

Google Scholar

20.

Циммерман Т. Дж. И Кунер К. С. Клинические пути при глаукоме (Тим, Нью-Йорк, 2001).

Забронировать Google Scholar

21.

Mwanza, J.-C., Warren, J. L. & Budenz, D. L. Сочетание структурных параметров оптической когерентной томографии в спектральной области для диагностики глаукомы с ранней потерей поля зрения. Инвест. Офтальмол. Vis. Sci. 54 , 8393–8400 (2013).

PubMed PubMed Central Статья Google Scholar

22.

Бурганский-Элиаш, З. и др. Классификаторы машинного обучения для оптической когерентной томографии для обнаружения глаукомы: предварительное исследование. Инвест. Офтальмол. Vis. Sci. 46 , 4147–4152 (2005).

PubMed PubMed Central Статья Google Scholar

23.

Баскаран, М. и др. Алгоритмы классификации позволяют отличить глаукому от нормального глаза с помощью оптической когерентной томографии высокого разрешения. Инвест. Офтальмол. Vis. Sci. 53 , 2314–2320 (2012).

PubMed Статья PubMed Central Google Scholar

24.

Asaoka, R. et al. Подтверждение полезности классификатора «Случайные леса» для диагностики ранней глаукомы с помощью оптической когерентной томографии. Am. J. Ophthalmol. 174 , 95–103 (2017).

PubMed Статья PubMed Central Google Scholar

25.

Zhu, H. et al. Прогнозирование зрительной функции на основе измерений структуры слоя нервных волокон сетчатки. Инвест. Офтальмол. Vis. Sci. 51 , 5657–5666 (2010).

PubMed Статья PubMed Central Google Scholar

26.

Hinton, G.E., Osindero, S. & Teh, Y.-W. Алгоритм быстрого обучения для сетей глубоких убеждений. Neural Comput. 18 , 1527–1554 (2006).

MathSciNet PubMed МАТЕМАТИКА Статья PubMed Central Google Scholar

27.

Чавла, Н. В., Бойер, К. В., Холл, Л. О. и Кегельмейер, В. П. SMOTE: синтетический метод избыточной выборки меньшинств. J. Artif. Intell. Res. 16 , 321–357 (2002).

MATH Статья Google Scholar

28.

Ting, D. S. W. et al. Разработка и валидация системы глубокого обучения для диабетической ретинопатии и связанных с ней глазных заболеваний с использованием изображений сетчатки глаза многоэтнических популяций с диабетом. JAMA 318 , 2211–2223 (2017).

PubMed PubMed Central Статья Google Scholar

29.

Li, Z. et al. Эффективность системы глубокого обучения для обнаружения глаукомной оптической невропатии на основе цветных фотографий глазного дна. Офтальмология 125 , 1199–1206 (2018).

PubMed Статья PubMed Central Google Scholar

30.

Liu, S. et al. Алгоритм на основе глубокого обучения определяет глаукомные диски с помощью моноскопических фотографий глазного дна. Офтальмол.Глаукома 1 , 15–22 (2018).

PubMed Статья PubMed Central Google Scholar

31.

Shibata N , et al. Разработка алгоритма глубокого остаточного обучения для выявления глаукомы по фотографии глазного дна. Sci Rep ( в печати ).

32.

Asaoka, R. et al. Использование глубокого обучения и трансферного обучения для точной диагностики глаукомы с ранним началом по изображениям оптической когерентной томографии желтого пятна. Am. J. Ophthalmol. 198 , 136–145 (2019).

PubMed Статья PubMed Central Google Scholar

33.

Crabb, D.P. и др. из Частота тестирования поля зрения при наблюдении за пациентами с впервые диагностированной глаукомой: смешанные методы и моделирование (Саутгемптон (Великобритания), 2014).

34.

Малик Р., Бейкер Х., Рассел Р. А. и Крэбб Д. П. Обзор отношения узких специалистов по глаукоме в Англии и Уэльсе к интервалам тестирования поля зрения в соответствии с рекомендациями NICE. BMJ Open 3 , e002067 (2013).

PubMed PubMed Central Статья Google Scholar

35.

Grillo, L. M. et al. Тест поля зрения 24–2 пропускает центральное повреждение желтого пятна, подтвержденное тестом поля зрения 10–2 и оптической когерентной томографией. Пер. Vis. Sci. Technol. 5 , 15 (2016).

PubMed PubMed Central Статья Google Scholar

36.

Murata, H. et al. Определение областей поля зрения, важных для качества жизни пациентов с глаукомой. PLoS ONE 8 , e58695 (2013).

ADS CAS PubMed PubMed Central Статья Google Scholar

37.

Суми, И., Ширато, С., Мацумото, С. и Арайе, М. Взаимосвязь между нарушением зрения и полем зрения у пациентов с глаукомой. Офтальмология 110 , 332–339 (2003).

PubMed Статья PubMed Central Google Scholar

38.

Asaoka, R. Взаимосвязь между остротой зрения и чувствительностью центрального поля зрения при запущенной глаукоме. Br. J. Ophthalmol. 97 , 1355–1356 (2013).

PubMed Статья Google Scholar

39.

Андерсон Д., Пателла В. А. и Периметри, С. St 152–153 (Мосби, Луис, 1999).

Google Scholar

40.

Matsuura, M. et al. Улучшение взаимосвязи структура-функция в глаукомных и нормальных глазах за счет включения толщины слоя фоторецепторов. Sci. Отчет 8 , 10450 (2018).

ADS PubMed PubMed Central Статья CAS Google Scholar

41.

Asaoka, R. et al. Связь между толщиной слоя фоторецепторов, измеренной с помощью оптической когерентной томографии, и зрительной чувствительностью глаукомных глаз. PLoS ONE 12 , e0184064 (2017).

PubMed PubMed Central Статья CAS Google Scholar

42.

Чу, Т., Рэнсон, В. и Саттон, М.А. Применение методов корреляции цифровых изображений в экспериментальной механике. Exp. Мех. 25 , 232–244 (1985).

Артикул Google Scholar

43.

He, K., Чжан, X., Рен, С. и Сан, Дж. Глубокое остаточное обучение для распознавания изображений. in Материалы конференции IEEE по компьютерному зрению и распознаванию образов 770–778 (2016).

44.

Симонян К. и Зиссерман А. Очень глубокие сверточные сети для распознавания крупномасштабных изображений. препринт arXiv arXiv: 1409.1556 (2014).

45.

Крижевский А., Суцкевер И. и Хинтон Г. Классификация Imagenet с глубокими сверточными нейронными сетями.в Достижения в области нейронных систем обработки информации 1097–1105 (2012).

46.

Хе К., Чжан Х, Рен С. и Сун Дж. Глубокое остаточное обучение для распознавания изображений. arXiv: 1512.03385 (2015).

47.

Йосински, Дж., Клун, Дж., Бенжио, Й. и Липсон, Х. Насколько переносимы функции в глубоких нейронных сетях ?. Adv. Neural Inf. Процесс. Syst. 27 , 3320–3328 (2014).

Google Scholar

48.

Пан, С. Дж. И Янг, К. Обзор трансфертного обучения. IEEE Trans. Знай. Data Eng. 22 , 1345–1359 (2009).

Артикул Google Scholar

49.

Christopher, M. et al. Подходы глубокого обучения позволяют прогнозировать глаукомное повреждение поля зрения на основе изображений головного мозга зрительного нерва с помощью ОКТ и карт толщины слоя нервных волокон сетчатки. Офтальмология 127 , 346–356 (2020).

PubMed Статья PubMed Central Google Scholar

50.

Artes, P.H., Iwase, A., Ohno, Y., Kitazawa, Y. & Chauhan, B.C. Свойства оценок периметрического порога из стратегий Full Threshold, SITA Standard и SITA Fast. Инвест. Офтальмол. Vis. Sci. 43 , 2654–2659 (2002).

PubMed PubMed Central Google Scholar

51.

Sugisaki, K. , et al. Предсказание поля зрения Хамфри 10–2 из поля зрения 24–2 в глазах с развитой глаукомой. Br J Ophthalmol , bjophthalmol-2019–314170 (2019).

52.

Вебер Дж., Шульце Т. и Ульрих Х. Поле зрения при развитой глаукоме. Внутр. Офтальмол. 13 , 47–50 (1989).

CAS PubMed Статья PubMed Central Google Scholar

53.

Худ, Д. К., Раза, А. С., де Мораес, К. Г., Либманн, Дж. М. и Ритч, Р. Глаукомное повреждение макулы. Prog. Retin Eye Res. 32 , 1–21 (2013).

PubMed Статья PubMed Central Google Scholar

54.

Swanson, W. H., Felius, J. & Pan, F. Периметрические дефекты и повреждение ганглиозных клеток: интерпретация линейных отношений с использованием двухэтапной нейронной модели. Инвест. Офтальмол. Vis.Sci. 45 , 466–472 (2004).

PubMed Статья PubMed Central Google Scholar

55.

Asaoka, R. Измерение прогрессии поля зрения в центральных 10 градусах с использованием дополнительной информации из центральных 24-градусных полей зрения и «регрессии лассо».

No related posts.