100 поделить на 3: 100 делить на 3 с остатком

Содержание

100 Поделить на 3

Онлайн-калькулятор «Деление чисел столбиком«. Наш калькулятор позволяет делить любые натуральные числа столбиком. Введите два числа (делимое и делитель) и нажмите кнопку «Вычислить». Подробное решение, которое выдает калькулятор, поможет вам разобраться, как правильно делить числа столбиком.

Деление столбиком (или деление в столбик) – метод предназначенный для деления чисел, посредством разложения процедуры деления на ряд простых действий. Число, которое делится, называется делимое. Число, на которое производится деление, называется делитель. Полученный результат от деления называется частным.

Процедура деления столбиком представляется следующим образом:

Как правильно решить пример 100 делить на 3 и какой правильный ответ?

100/3=33.333333333333

При делении чисел 100 и 3 мы получаем ответ: 33.333333333333.

сто делить на

три равно 33. 333333333333

Это понял метеоролог Лоренц, незадачливый предсказатель погоды: сегодня бабочка трепещет своими крыльями в Пекине, а через месяц это вызовет ураган в Нью-Йорке. Эффект бабочки.

Ну что ж. Осталось провести эксперемент и выяснить – действительно ли трепет крыльев бабочки привел к урагану. 😉

Методика проведения эксперемента:
1. Воссоздать мир на момент «до начала трепета крыльев».
2. Учпокоить бабочку, чтоб не трепетала.
3. Смотреть, что будет дальше в Нью-Йорке.
4. Сравнить результаты «с» и «без» трепета крыльев.

Недоказуемо это всё.
Красивая гипотеза – не более. С тем, что всё взаимосвязано никто спорить не будет. А вот доказать, в т.ч. и эксперементально, причинно-следственную связь двух такого рода событий, ИМХО не возможно. Делаем вывод: следовательно, это не наука. И уж тем более не физика. 🙂

Gerald, это начало Эффекта бабочки))

А про калькулятор, чего этот автор так разнервничался, это итак понятно, это ж в курсе вычмата первая тема – погрешности и ошибки. Есть числа точные, их используют реже всего.. Намного чаще – приближенные, это точноые +- погрешность..

А чего он хотел?? Точности?? Ха-ха.. очень смешно! Нету в мире абсолюта НИ В ЧЕМ. Вообще ни в чем.

да тут, собственно, без разницы: что воссоздать картину мира и перенестись в прошлое, что создать адекватную модель мира для исселдования Эффекта бабочки. 😉

Другое дело, что сам факт заключается в другом

нету факта.
Что, интересно, Вы называете фактом?

Пара ссылок о том, что такое эффект бабочки. Во второй описаны прямо исследования Лоренца.

P.S.Слушай, а ты не овен случайно=)?Или козерог.

. а в исторической перспективе смерть бабочки может вызвать изменения в общественном строе и грамматике:) это уже Бредбери

In fact, history already depends on your treading on any ants that you happen to step on. Any ants you tread on, you’ve already trodden on, so if you do it again it’ll be for the first time, because you’re doing it now because you did it then. Which is also now.

Это уже Терри Пратчетт.. (извините, что вмешиваюс..)

Never Mind
Лоренц обнаружил, что казалось бы небольшие погрешности могут привести к принципиально иному развитию системы. Отсюда, и калькулятор как простейшая иллюстрация этого факта.

BlueSky,
нет, не овен и не козерог.
Я – зануда. :lol2:

Если интересно, я бы советовал прочитать более обстоятельные статьи, а не иллюстрации к своим мыслям спецов по НЛП:
Джеймс Глейк, «Хаос: создание новой науки» или
С.П.Капица, С.П.Курдюмов, Г.Г.Малинецкий, «Синергетика и прогнозы будущего»

Это факт из физики. Обоснованный на реальном примере.
это действительно факт, который изучают очень многие известные физики. Другое дело, что сам факт заключается в другом, а этот конкретный его случай дал ему название.

Американское издание фейнмановских лекций вышло в 1963 г. В том же году в «Journal of the Atmospheric Sciences» появилась статья американского метеоролога Эдварда Лоренца, положившая начало новому направлению в естествознании – исследованию хаоса в детерминированных системах.

Тем не менее, можно только удивляться научной смелости Э. Лоренца, выбравшего простейшую модель – систему всего лишь трех обыкновенных дифференциальных уравнений, просчитавшего ее на компьютере и сумевшего понять, что он имеет дело не с ошибками вычислений, а с открытием.

Так что же Вы называете фактом? 😉

Факта, что взмах крыла бабочки вызвал бурю – не существует.
Мы не умеем моделировать столь сложные системы, чтобы ответить на вопрос причинно-следственной связи между этими двумя КОНРЕТНЫМИ событиями. Мы не умеем измерить столь малое влияние и заложить его в модель, в том числе и в силу «эффекта бабочки».

Я говорил исключительно об этом, ничуть не отрицая существование самого эффекта.

В любом случае, спасибо, что напомнили об этом удивительном феномене. :white:

BlueSky, эээ. мммм. как бы это объяснить-то.. ненавязчиво так. Английский писатель, автор книг про Плоский мир. Этакая юмористическая фентези (хотя юмористическая – это слишком мягко сказано). Всякие там гномы, тролли, боги, герои-варвары, ведьмы, волшебники. эльфы. только отнють не добренькие толкиеновские. Ну и прочая, и прочая, и прочая.
Игра слов, гротеск, изменение общеизвестных фактов и прочего до невероятнейшей степени.. И вместе с тем довольно таки умная вещь.
К тому же множество ассоциаций с другими авторами: по крайней мере, у него в двух книгах обыграны пьесы Шекспира, есть сноски к Эшеру, Борхесу, и многим другим.. В одной книге даже три сестры Чехова. Есть история инквизиции и Голивуд, сказки братьев Гримм и Фауст, «Полицейская академия» и «Призрак Оперы», а «Пирамиды» и «Роковая музыка» вообще в объяснениях не нуждаются. Отдельно от Плоского Мира есть еще книга про Апокалипсис (Good Omens) и пара других циклов.

Вобщем, сами напросились. Советую. Найти можно наверняка в любом книжном магазине, на любом развале. Если что, вот здесь есть и переводы, и оригиналы.

—-
Свою книгу я отдала читать, так что про бабочку бурь оставлю опять же в оригинале.
«The Quantum Weather Butterfly (Papilio tempestae) is an undistinguished yellow colour, although the mandelbrot patterns on the wings are of considerable interest. Its outstanding feature is its ability to create weather.
This presumably began as a survival trait, since even an extremely hungry bird would find itself incon-venienced by a nasty localized tornado*.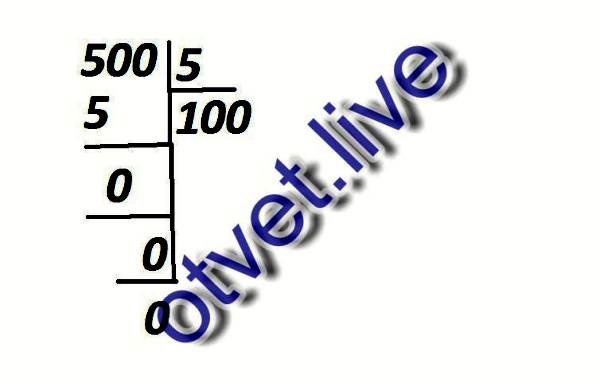 From there it possibly became a secondary sexual characteristic, like the plumage of birds or the throat sacs of certain frogs. Look at me, the male says, flapping his wings lazily in the canopy of the rain forest. I may be an undistinguished yellow colour but in a fortnight’s tone, a thousand miles away, Freak Gales Cause Road Chaos.

*Usually about six inches across.»

Он же. «Интересные времена»

BlueSky, гхм.. знаешь, человек, собравший 18 книг в переводе и читавший около десятка в оригинале (с компа до нервного тика), врядли скажет о своем любимом авторе (по крайней мере, одном из) «типа чувак такой». и к тому ж, я привыкла.. много говорить про него. Уж полгруппы подсадила, да к тому ж учителей в школе. Просто лень набивать все было. И так раз десять исправляла..

Ага, я больной человек, я знаю! *зверски лыбится* счаз вон перевожу одну.. да-да, делать мне больше нефига! ага! *счастливое выражение лица идиота* (опять же ненавязчиво так: если хошь, ссылку на дайри дам)

Почему нельзя делить на ноль?

«Делить на ноль нельзя!» — большинство школьников заучивает это правило наизусть, не задаваясь вопросами.

Все дети знают, что такое «нельзя» и что будет, если в ответ на него спросить: «Почему?» А ведь на самом деле очень интересно и важно знать, почему же нельзя.

Всё дело в том, что четыре действия арифметики — сложение, вычитание, умножение и деление — на самом деле неравноправны. Математики признают полноценными только два из них — сложение и умножение. Эти операции и их свойства включаются в само определение понятия числа. Все остальные действия строятся тем или иным образом из этих двух.

Рассмотрим, например, вычитание. Что значит 5 – 3? Школьник ответит на это просто: надо взять пять предметов, отнять (убрать) три из них и посмотреть, сколько останется. Но вот математики смотрят на эту задачу совсем по-другому. Нет никакого вычитания, есть только сложение. Поэтому запись

5 – 3 означает такое число, которое при сложении с числом 3 даст число 5. То есть 5 – 3 — это просто сокращенная запись уравнения: x + 3 = 5. В этом уравнении нет никакого вычитания.

Есть только задача — найти подходящее число.

Точно так же обстоит дело с умножением и делением. Запись 8 : 4 можно понимать как результат разделения восьми предметов по четырем равным кучкам. Но в действительности это просто сокращенная форма записи уравнения 4 · x = 8.

Вот тут-то и становится ясно, почему нельзя (а точнее невозможно) делить на ноль. Запись 5 : 0 — это сокращение от 0 · x = 5. То есть это задание найти такое число, которое при умножении на 0 даст 5. Но мы знаем, что при умножении на 0 всегда получается 0. Это неотъемлемое свойство нуля, строго говоря, часть его определения.

Такого числа, которое при умножении на 0 даст что-то кроме нуля, просто не существует. То есть наша задача не имеет решения. (Да, такое бывает, не у всякой задачи есть решение.) А значит, записи 5 : 0 не соответствует никакого конкретного числа, и она просто ничего не обозначает и потому не имеет смысла. Бессмысленность этой записи кратко выражают, говоря, что на ноль делить нельзя.

Самые внимательные читатели в этом месте непременно спросят: а можно ли ноль делить на ноль? В самом деле, ведь уравнение 0 · x = 0 благополучно решается. Например, можно взять x = 0, и тогда получаем 0 · 0 = 0. Выходит, 0 : 0=0? Но не будем спешить. Попробуем взять x = 1. Получим 0 · 1 = 0. Правильно? Значит, 0 : 0 = 1? Но ведь так можно взять любое число и получить 0 : 0 = 5, 0 : 0 = 317 и т. д.

Но если подходит любое число, то у нас нет никаких оснований остановить свой выбор на каком-то одном из них. То есть мы не можем сказать, какому числу соответствует запись 0 : 0. А раз так, то мы вынуждены признать, что эта запись тоже не имеет смысла. Выходит, что на ноль нельзя делить даже ноль. (В математическом анализе бывают случаи, когда благодаря дополнительным условиям задачи можно отдать предпочтение одному из возможных вариантов решения уравнения 0 · x = 0; в таких случаях математики говорят о «раскрытии неопределенности», но в арифметике таких случаев не встречается. )

Вот такая особенность есть у операции деления. А точнее — у операции умножения и связанного с ней числа ноль.

Ну, а самые дотошные, дочитав до этого места, могут спросить: почему так получается, что делить на ноль нельзя, а вычитать ноль можно? В некотором смысле, именно с этого вопроса и начинается настоящая математика. Ответить на него можно только познакомившись с формальными математическими определениями числовых множеств и операций над ними. Это не так уж сложно, но почему-то не изучается в школе. Зато на лекциях по математике в университете вас в первую очередь будут учить именно этому.

Ответил: Александр Сергеев

Деление десятичных дробей: правила, примеры

Основы деления десятичных дробей

Десятичные дроби — это дроби, у которых в знаменателе стоят числа, кратные 10. То есть 10, 100, 1000 и так далее.

Как делить десятичные дроби друг на друга — процесс представляет собой деление обыкновенных дробей. То есть для выполнения действий деления мы переписываем десятичную дробь в стандартный вид.

Рассмотрим пример: разделите 1,2 на 0,6

Как решаем

Запишем десятичные дроби в виде обыкновенных. У нас получится:

Таким образом, нам надо разделить

Ответ: 1,2÷0,6 = 2

Если для деления нам попадается периодические и непериодические дроби, то действуем следующим образом.

Периодические переводим в обыкновенную:

Если же встречается непериодическая десятичная дробь, то мы ее округляем до сотых и дальше делим, как обычно:

Как разделить целое число на десятичную дробь и наоборот

Здесь всё просто: приводим десятичную дробь к стандартному виду и натуральное число тоже представляем в виде дроби — само число нужно поделить на единицу.

Пример: 3,5 поделить на 55

Как решаем

Ответ: 3,5÷55 = 0,063 (63)

Как разделить десятичную дробь на натуральное число столбиком

Делить столбиком можно не только натуральные числа, но и дроби. Алгоритм мы подробно опишем здесь. Итак, как делить десятичные дроби на натуральные числа в столбик:

1. Добавить к десятичной дроби справа несколько нулей (для деления мы можем добавлять любое их количество, которое нам необходимо).

2. Выполнить деление по стандартной схеме. Когда деление целой части дроби подойдет к концу, мы ставим запятую в получившемся частном и считаем дальше.

Результатом такого деления может стать как конечная, так и бесконечная периодическая десятичная дробь. Это зависит от остатка: если он нулевой, то результат окажется конечным, а если остатки начнут повторяться — получится периодическая дробь.

Пример: Разделить столбиком 49,14÷3

Как решаем

1. Делим столбиком, предварительно дописав два нуля к десятичной дроби.

2. После того, как мы поделили целую часть дроби и получили 16, отделяем ответ запятой (16) и продолжаем деление уже для дробной части

В конце у нас нулевой остаток, значит деление завершено.

Ответ: 49,14÷3 = 16,38

Как разделить столбиком одну десятичную дробь на другую

Все просто: умножаем делимое и делитель на 10, 100 и так далее — так, чтобы делитель превратился в натуральное число. А потом решаем также, как в примере выше:

1. Переносим запятую в делимом и делителе вправо на то количество знаков, которое необходимо для превращения делителя в натуральное число. Если в делимом не хватит знаков, дописываем в него нули с правой стороны.

2. После этого делим дробь столбиком на получившееся натуральное число.

Пример: поделить столбиком 63,42 на 2,1

Как решаем

Переносим запятую на один знак вправо, чтобы делитель (2,1) стало натуральным числом. Запятую переносим в обоих числах — у нас получается 634,2÷21.

Затем производим деление

Ответ: 63,42÷2,1 = 30,2

Как разделить десятичные дроби на 1000, 100, 10 и другие

Как вы уже заметили, есть основное правило деления десятичных дробей: по нему деление дроби на десятки, сотни, тысячи аналогично ее умножению на 1/1000, 1/100, 1/10 и другие.

Чтобы выполнить действие, нужно просто перенести запятую влево на нужное количество цифр (равное нулям). Если значений в числе не хватит для переноса — дописываем нужное количество нулей:

Как разделить десятичные дроби на 0,001, 0,01, 0,1 и другие

Правило из предыдущего пункта поможет нам без труда разделить дроби на указанные значения. Переводим эти числа в стандартные дроби и затем при делении действие будет аналогично умножению на 1000, 100, 10 (так как дробь, на которую делим переворачивается).

Чтобы найти ответ в подобных задачах, мы переносим запятую на одну, две, три цифры вправо (в зависимости от числа, на которое делим) и дописываем нули, если цифр в числе окажется недостаточно.

Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот

Это действие мы также сводим к операциям с обыкновенными дробями. Вот как поступим со смешанным числом: записываем его в виде неправильной дроби, десятичную — в виде обычной дроби и делим по уже стандартной схеме.

В детской онлайн-школе Skysmart ученики решают такие задачки на интерактивной платформе. Внутри: автоматическая проверка, тысячи интересных задач и головоломок, онлайн-доска, на которой можно чертить и рисовать и поддержка чутких учителей. Запишите вашего ребенка на бесплатный вводный урок — мы покажем, как все проходит и вдохновим ребенка на дружбу с математикой.

Калькулятор онлайн — Калькулятор процентов. Найти сколько процентов составляет одно число от другого

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

Понятие о проценте

Проценты — одно из понятий прикладной математики, которые часто встречаются в повседневной жизни. Так, часто можно прочитать или услышать, что, например, в выборах приняли участие 56,3% избирателей, рейтинг победителя конкурса равен 74%, промышленное производство увеличилось на 3,2%, банк начисляет 8% годовых, молоко содержит 1,5% жира, ткань содержит 100% хлопка и т. д. Ясно, что понимание такой информации необходимо в современном обществе.

Одним процентом от любой величины — денежной суммы, числа учащихся школы и т.д. — называется одна сотая ее часть. Обозначается процент знаком %, Таким образом,
1% — это 0,01, или $ \frac{1}{100} $ часть величины

Приведем примеры:
— 1% от минимальной заработной платы 2300 р. (сентябрь 2007 г.) — это 2300/100 = 23 рубля;
— 1% от населения России, равного примерно 145 млн. человек (2007 г.), — это 1,45 млн. человек;
— 3%-я концентрация раствора соли — это 3 г соли в 100 г раствора (напомним, что концентрация раствора — это часть, которую составляет масса растворенного вещества от массы всего раствора).

Понятно, что вся рассматриваемая величина составляет 100 сотых, или 100% от самой себя. Поэтому, например, надпись на этикетке «хлопок 100%» означает, что ткань состоит из чистого хлопка, а стопроцентная успеваемость означает, что в классе нет неуспевающих учеников.

Слово «процент» происходит от латинского pro centum, означающего «от сотни» или «на 100». Это словосочетание можно встретить и в современной речи. Например, говорят: «Из каждых 100 участников лотереи 7 участников получили призы». Если понимать это выражение буквально, то это утверждение, разумеется, неверно: ясно, что можно выбрать 100 человек, участвующих в лотерее и не получивших призы. В действительности точный смысл этого выражения состоит в том, что призы получили 7% участников лотереи, и именно такое понимание соответствует происхождению слова «процент»: 7% — это 7 из 100, 7 человек из 100 человек.

Знак «%» получил распространение в конце XVII века. В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «с/о» за дробь и напечатал «%». Так из-за опечатки этот знак вошел в обиход.

Любое число процентов можно записать в виде десятичной дроби, выражающей часть величины.

Чтобы выразить проценты числом, нужно количество процентов разделить на 100. Например:

$ 58\% = \frac{58}{100} = 0,58; \;\;\; 4,5\% = \frac{4,5}{100} = 0,045; \;\;\; 200\% = \frac{200}{100} = 2 $

Для обратного перехода выполняется обратное действие. Таким образом, чтобы выразить число в процентах, надо его умножить на 100:

$ 0,58 = (0,58 \cdot 100)\% = 58\% $ $ 0,045 = (0,045 \cdot 100)\% = 4,5\% $

В практической жизни полезно понимать связь между простейшими значениями процентов и соответствующими дробями: половина — 50%, четверть — 25%, три четверти — 75%, пятая часть — 20%, три пятых — 60% и т.д.

Полезно также понимать разные формы выражения одного и того же изменения величины, сформулированные без процентов и с помощью процентов. Например, в сообщениях «Минимальная заработная плата повышена с февраля на 50%» и «Минимальная заработная плата повышена с февраля в 1,5 раз» говорится об одном и том же. Точно так же увеличить в 2 раза — это значит увеличить на 100%, увеличить в 3 раза — это значит увеличить на 200%, уменьшить в 2 раза — это значит уменьшить на 50%.

Аналогично
— увеличить на 300% — это значит увеличить в 4 раза,
— уменьшить на 80% — это значит уменьшить в 5 раз.

Задачи на проценты

Поскольку проценты можно выразить дробями, то задачи на проценты являются, по существу, теми же задачами на дроби. В простейших задачах на проценты некоторая величина а принимается за 100% («целое»), а ее часть b выражается числом p%.

В зависимости от того, что неизвестно — а, b или р, выделяются три типа задач на проценты. Эти задачи решаются так же, как и соответствующие задачи на дроби, но перед их решением число р% выражается дробью.

1. Нахождение процента от числа.
Чтобы найти $ \frac{p}{100} $ от a, надо a умножить на $ \frac{p}{100} $:

$ b = a \cdot \frac{p}{100} $

Итак, чтобы найти р% от числа, надо это число умножить на дробь $ \frac{p}{100} $. Например, 20% от 45 кг равны 45 • 0,2 = 9 кг, а 118% от х равны 1,18x

2. Нахождение числа по его проценту.
Чтобы найти число по его части b, выраженной дробью $ \frac{p}{100} , \; (p \neq 0) $, надо b разделить на $ \frac{p}{100} $:
$ a = b : \frac{p}{100} $

Таким образом, чтобы найти число по его части, составляющей р% этого числа, надо эту часть разделить на $ \frac{p}{100} $. Например, если 8% длины отрезка составляют 2,4 см, то длина всего отрезка равна 2,4:0,08 = 240:8 = 30 см.

3. Нахождение процентного отношения двух чисел.
Чтобы найти, сколько процентов число b составляет от а $ (a \neq 0) $, надо сначала узнать, какую часть b составляет от а, а затем эту часть выразить в процентах:

$ p = \frac{b}{a} \cdot 100\% $ Значит, чтобы узнать, сколько процентов первое число составляет от второго, надо первое число разделить на второе и результат умножить на 100.
Например, 9 г соли в растворе массой 180 г составляют $ \frac{9 \cdot 100}{180} = 5\% $ раствора.

Частное двух чисел, выраженное в процентах, называется процентным отношением этих чисел. Поэтому последнее правило называют правилом нахождения процентного отношения двух чисел.

Нетрудно заметить, что формулы

$ b = a \cdot \frac{p}{100}, \;\; a = b : \frac{p}{100}, \;\; p = \frac{b}{a} \cdot 100\% \;\; (a,b,p \neq 0 ) $ взаимосвязаны, а именно, две последние формулы получаются из первой, если выразить из нее значения a и p. Поэтому первую формулу считают основной и называют формулой процентов. Формула процентов объединяет все три типа задач на дроби, и, при желании, можно ею пользоваться, чтобы найти любую из неизвестных величин a, b и p.

Составные задачи на проценты решаются аналогично задачам на дроби.

Простой процентный рост

Когда человек не вносит своевременную плату за квартиру, на него налагается штраф, который называется «пеня» (от латинского роеnа — наказание). Так, если пеня составляет 0,1% от суммы квартплаты за каждый день просрочки, то, например, за 19 дней просрочки сумма составит 1,9% от суммы квартплаты. Поэтому вместе, скажем, с 1000 р. квартплаты человек должен будет внести пеню 1000 • 0,019 = 19 р., а всего 1019 р.

Ясно, что в разных городах и у разных людей квартплата, размер пени и время просрочки разные. Поэтому имеет смысл составить общую формулу квартплаты для неаккуратных плательщиков, применимую при любых обстоятельствах.

Пусть S — ежемесячная квартплата, пеня составляет р% квартплаты за каждый день просрочки, а n — число просроченных дней. Сумму, которую должен заплатить человек после n дней просрочки, обозначим S_n.
Тогда за n дней просрочки пеня составит рn% от S, или $ \frac{pn}{100}S $, а всего придется заплатить $ S + \frac{pn}{100}S = \left( 1+ \frac{pn}{100} \right) S $
Таким образом:
$ S_n = \left( 1+ \frac{pn}{100} \right) S $

Эта формула описывает многие конкретные ситуации и имеет специальное название: формула простого процентного роста.

Аналогичная формула получится, если некоторая величина уменьшается за данный период времени на определенное число процентов. Как и выше, нетрудно убедиться, что в этом случае
$ S_n = \left( 1- \frac{pn}{100} \right) S $

Эта формула также называется формулой простого процентного роста, хотя заданная величина в действительности убывает. Рост в этом случае «отрицательный».

Сложный процентный рост

В банках России для некоторых видов вкладов (так называемых срочных вкладов, которые нельзя взять раньше, чем через определенный договором срок, например, через год) принята следующая система выплаты доходов: за первый год нахождения внесенной суммы на счете доход составляет, например, 10% от нее. В конце года вкладчик может забрать из банка вложенные деньги и заработанный доход - «проценты», как его обычно называют.

Если же вкладчик этого не сделал, то проценты присоединяются к начальному вкладу (капитализируются), и поэтому в конце следующего года 10% начисляются банком уже на новую, увеличенную сумму. Иначе говоря, при такой системе начисляются «проценты на проценты», или, как их обычно называют, сложные проценты.

Подсчитаем, сколько денег получит вкладчик через 3 года, если он положил на срочный счет в банк 1000 р. и ни разу в течение трех лет не будет брать деньги со счета.

10% от 1000 р. составляют 0,1 • 1000 = 100 р., следовательно, через год на его счете будет
1000 + 100 = 1100 (р.)

10% от новой суммы 1100 р. составляют 0,1 • 1100 = 110 р., следовательно, через 2 года на его счете будет
1100 + 110 = 1210 (р.)

10% от новой суммы 1210 р. составляют 0,1 • 1210 = 121 р., следовательно, через 3 года на его счете будет
1210 + 121 = 1331 (р.)

Нетрудно представить себе, сколько при таком непосредственном, «лобовом» подсчете понадобилось бы времени для нахождения суммы вклада через 20 лет. Между тем подсчет можно вести значительно проще.

А именно, через год начальная сумма увеличится на 10%, то есть составит 110% от начальной, или, другими словами, увеличится в 1,1 раза. В следующем году новая, уже увеличенная сумма тоже увеличится на те же 10%. Следовательно, через 2 года начальная сумма увеличится в 1,1 • 1,1 = 1,1² раз.

Еще через один год и эта сумма увеличится в 1,1 раза, так что начальная сумма увеличится в 1,1 • 1,1² = 1,1³ раз. При таком способе рассуждений получаем решение нашей задачи значительно более простое: 1,1³ • 1000 = 1,331 • 1000 — 1331 (р.)

Решим теперь эту задачу в общем виде. Пусть банк начисляет доход в размере р% годовых, внесенная сумма равна S р., а сумма, которая будет на счете через n лет, равна S_n р.

Величина p% от S составляет $ \frac{p}{100}S $ р., и через год на счете окажется сумма
$ S_1 = S+ \frac{p}{100}S = \left( 1+ \frac{p}{100} \right)S $
то есть начальная сумма увеличится в $ 1+ \frac{p}{100} $ раз.

За следующий год сумма S₁ увеличится во столько же раз, и поэтому через два года на счете будет сумма
$ S_2 = \left( 1+ \frac{p}{100} \right)S_1 = \left( 1+ \frac{p}{100} \right) \left( 1+ \frac{p}{100} \right)S = \left( 1+ \frac{p}{100} \right)^2 S $

Аналогично $ S_3 = \left( 1+ \frac{p}{100} \right)^3 S $ и т. n S \)

Эту формулу называют формулой сложного процентного роста, или просто формулой сложных процентов.

Деление

В данном уроке мы изýчим деление чисел. Деление чисел довольно непростая операция как в освоении, так и в использовании. Рекомендуем набраться терпения, чтобы осилить этот урок до конца.

Что такое деление?

Деление это действие, позволяющее что-либо разделить.

Деление состоит из трёх параметров: делимого, делителя и частного. Делимое это то, что делят. Делитель это число, показывающее на сколько частей нужно разделить делимое. Частное это собственно результат.

Пусть у нас имеются 4 яблока:

Разделим их поровну на двоих друзей. Тогда деление покажет сколько яблок достанется каждому. Нетрудно увидеть, что каждому достанется по два яблока:

Процесс деления четырех яблок на двоих друзей можно описáть следующим выражением:

В этом примере роль делимого играют яблоки. Роль делителя играют двое друзей, показывающих на сколько частей нужно разделить 4 яблока. Роль частного играют два яблока, показывающие сколько досталось каждому.

Говоря о делении, можно рассуждать и по-другому. Вернёмся к предыдущему выражению 4 : 2 = 2. Можно посмотреть на делитель 2 и задать вопрос «сколько двоек в четвёрке?» и ответить: «две двойки». Действительно, если сложить две двойки, то получится число 4

В ситуации с четырьмя яблоками можно задать вопрос «сколько раз два яблока содержатся в четырёх яблоках» и ответить: «два раза».

Чтобы научиться делить, нужно хорошо знать таблицу умножения. Почему же умножения? Ведь мы говорим о делении. Дело в том, что деление это действие, обратное умножению. Данную фразу можно понимать в прямом смысле. Например, если 2 × 5 = 10, то 10 : 5 = 2.

Видно, что второе выражение записано в обратном порядке. Если у нас имеются два яблока и мы захотим увеличить их в пять раз, то запишем 2 × 5 = 10. Получится десять яблок. Затем, если мы захотим обратно уменьшить эти десять яблок до двух, то запишем 10 : 5 = 2

Знак деления выглядит в виде двоеточия : но также можно встретить знак двоеточия и тире ÷

На письме разумнее использовать двоеточие, поскольку оно выглядит аккуратнее.

Деление с остатком

Остаток — это то, что осталось от действия деления неразделённым.

Например, пять разделить на два будет два и один в остатке:

5 : 2 = 2 (1 в остатке)

Можно проверить это умножением:

(2 × 2) + 1 = 5

Допустим, у нас имеются пять яблок

Разделим их поровну на двоих друзей. Но разделить поровну пять целых яблок не получится. Тогда данное деление покажет, что каждому достанется два яблока, а одно яблоко будет в остатке:

Деление уголком

Когда требуется разделить большое число, то прибегают к такому методу как деление уголком.

Прежде чем делить уголком, человек должен понимать:

обычное деление маленьких чисел;
деление с остатком;
умножение в столбик;
вычитание в столбик.

Рассмотрим деление уголком на простом примере. Пусть требуется найти значение выражения 9 : 3. Уголком это выражение записывается следующим образом:

Это простой пример. Все знают, что девять разделить на три будет три. Ответ (частное) записывается под правым углом:

Чтобы проверить есть ли остаток от деления, нужно частное умножить на делитель и полученный ответ записать под делимым. Частное в данном случае это 3, делитель тоже 3. Перемножаем эти два числа: 3 × 3 = 9. Получили 9. Записываем эту девятку под делимым:

Теперь от делимого вычитаем девятку, которую мы под ним написали: 9 − 9 = 0. Остаток равен нулю. Проще говоря, остатка нет. На этом деление успешно завершено:

Пример 2. Найти значение выражения 8 : 3

Восемь на три просто-так не разделится. Таблица умножения тоже не поможет. В данном случае будет присутствовать остаток от деления.

Сначала запишем данное выражение уголком:

Теперь надо задать вопрос: «сколько троек в восьмёрке?» В восьмёрке содержится две тройки. Это можно увидеть даже воочию, если мы представим восьмёрку как восемь палочек:

В школе частное подбирается методом подбора. Все мы слышали такие фразы как «берём по одному» , «берём по два» или «берём по три». У нас сейчас как раз такой случай. Мы взяли по два, ответив что в восьмёрке две тройки. Записываем двойку в правом уголке:

Теперь вынимаем остаток. Для этого умножаем частное на делитель (2 на 3) и записываем полученное число под делимым:

Далее из 8 вычитаем 6. Полученное число и будет остатком:

8 : 3 = 2 (2 в остатке)

Проверка: (2 × 3) + 2 = 6 + 2 = 8

Деление многозначного числа на однозначное

Данная тема с первого раза может показаться непонятной. Не спешите отчаиваться и забрасывать обучение. Понимание придёт в любом случае. Если не сразу, то немного позже. Главное не сдаваться и продолжать упорно изучать.

В предыдущих примерах мы делили однозначное число на однозначное, и это не доставляло нам лишних проблем. Сейчас мы займёмся тем, что будем делить многозначное число на однозначное.

Если непонятно, что такое однозначные и многозначные числа, советуем изучить предыдущий урок, который называется умножение.

Чтобы разделить многозначное число на однозначное, нужно сначала посмотреть на первую цифру этого многозначного числа, и проверить больше ли она делителя. Если больше, то разделить, а если нет, то проверить больше ли делителя первые две цифры многозначного числа. Если первые две цифры больше делителя, то разделить, а если нет, то проверить больше ли первые три цифры многозначного числа. И так до тех пор, пока не будет выполнено первое деление.

Сложно? Ни чуть, если мы разберём несколько примеров.

Пример 1. Найти значение выражения 25 : 3

25 это многозначное число, а 3 — однозначное. Применяем правило. Смóтрим на первую цифру многозначного числа. Первая цифра это 2. Два больше, чем три? Нет. Поэтому смóтрим первые две цифры многозначного числа. Первые две цифры образуют число 25. Двадцать пять больше, чем три? Да, больше. Поэтому выполняем деление числа 25 на 3. Записываем уголком данное выражение и начинаем делить:

Сколько троек в числе 25? Если с первого раза ответить сложно, можно заглянуть в таблицу умножения на три. Там необходимо отыскать произведение, которое меньше 25, но очень близко к нему или равно ему. Если найдём такое произведение, то необходимо забрать оттуда множитель, который дал такое произведение:

Это таблица умножения на три. В ней необходимо найти произведение, которое меньше 25, но очень близко к нему или равно ему. Очевидно, что это произведение 24, которое выделено синим. Из этого выражения необходимо забрать множитель, который дал такое произведение. Это множитель 8, который закрашен красным.

Данная восьмёрка и отвечает на вопрос сколько троек в числе 25. Записываем её в правом уголке нашего примера:

Теперь вынимаем остаток. Для этого умножаем частное на делитель (8 на 3) и полученное число записываем под делимым:

Теперь из делимого вычитаем число 24, получим 1. Это и будет остатком:

25 : 3 = 8 (1 в остатке)

(8 × 3) + 1 = 24 + 1 = 25

Последний остаток всегда меньше делителя. Если последний остаток больше делителя это означает, что деление не завершено.

В приведённом примере последним остатком было число 1, а делителем число 3. Единица меньше, чем три, поэтому деление завершено. Последний остаток, меньший делителя, говорит о том, что он не содержит чисел, равных делителю.

В нашем примере, если задать вопрос «сколько троек в единице?», то ответом будет «нисколько», потому что единица не содержит троек, поскольку она меньше тройки.

Пример 2. Разделить 326 на 4.

Смотрим на первую цифру числа 326. Первая цифра это 3. Она больше делителя 4? Нет. Тогда проверяем две цифры делимого. Две цифры делимого образуют число 32. Больше ли оно делителя 4? Да, больше. Поэтому делим. Записываем уголком данное выражение:

Теперь задаём вопрос: «сколько четвёрок в числе 32?». В числе 32 восемь четвёрок. Это можно увидеть в таблице умножения на четыре:

Данная восьмёрка, которая выделена красным отвечает на вопрос сколько четвёрок в числе 32. Записываем её в правом уголке нашего примера:

Теперь умножаем 8 на 4, получаем 32 и записываем это число под делимым. Далее вычитаем это число из 32. Получим 0. Поскольку решение ещё не завершено, ноль не записываем:

Первое число 32 разделили. Осталось разделить оставшуюся 6. Для этого сносим эту шестёрку:

Теперь делим 6 на 4. Для этого задаём вопрос: «сколько четвёрок в шестёрке?» В шестёрке одна четвёрка, это можно увидеть воочию, если представить шестёрку как шесть палочек:

Записываем единицу в правом уголке нашего ответа:

Теперь умножаем нашу единицу на делитель (1 на 4) и записываем полученное число под шестёркой:

Затем из 6 вычитаем 4, получаем число 2, которое является остатком:

Получили 326 : 4 = 81 (2 в остатке)

Проверка: (81 × 4) + 2 = 324 + 2 = 326

Процедура, в которой мы ищем первое число для деления, сравнивая больше ли оно делителя или меньше, называется нахождением первого неполного делимого.

Вернёмся к предыдущему примеру 326 : 4. Первое неполное делимое в данном выражении было число 32, поскольку его мы разделили в первую очередь.

А в примере 25 : 3 первое неполное делимое было 25.

Пример 3. Найти значение выражения 384 : 5

Записываем данное выражение в уголком:

Сначала находим первое неполное делимое. Первая цифра меньше делителя, поэтому проверяем две цифры. Две цифры вместе образуют число 38, которое больше делителя. Это число будет первым неполным делимым. Его и будем в первую очередь делить на делитель:

Сколько пятёрок в числе 38? Если сразу ответить сложно, то можно посмотреть в таблицу умножения на пять и найти произведение, которое меньше 38, но очень близко к нему или равно ему. Найдя такое произведение, нужно забрать оттуда множитель, который будет отвечать на наш вопрос:

Это таблица умножения на пять. Находим произведение, которое меньше 38, но очень близко к нему или равно ему. Очевидно, что это произведение 35, которое выделено синим. Из этого выражения забираем множитель, который дал такое произведение. Это множитель 7, который выделен красным.

Данная семёрка отвечает на вопрос сколько пятёрок в числе 38. Записываем эту семёрку в правом уголке нашего примера:

Умножаем 7 на 5, получаем 35 и записываем его под 38:

Теперь из 38 вычитаем 35, получим 3:

Эта тройка является остатком, которая осталась неразделённой в результате деления 38 на 5. Но видно, что ещё надо разделить и 4. Эту 4 мы снесём и разделим вместе с тройкой:

Видно, что после того, как мы снесли четвёрку, она вместе с тройкой образовала число 34. Это число 34 мы будем делить на 5. Для этого опять задаем вопрос: «сколько пятёрок в числе 34?». Можно снова глянуть в таблицу умножения на пять и найти произведение, которое меньше 34, но очень близко к нему или равно ему:

Видно, что в таблице умножения на пять число 30 меньше нашего 34, но близко к нему. Из этого выражения забираем множитель 6, который отвечает на наш вопрос. Записываем эту шестёрку в правом уголке нашего примера:

Теперь умножаем 6 на 5, получаем 30 и записываем это число под 34:

Теперь из 34 вычитаем 30, получаем 4. Эта четвёрка будет остатком от деления 384 на 5

384 : 5 = 76 (и 4 в остатке)

Проверка: (76 × 5) + 4 = 380 + 4 = 384

Пример 4. Найти значение выражения 8642 : 4

Этот пример немного посложнее. Записываем уголком данное выражение:

Первая цифра 8 больше делителя. Эта восьмёрка будет первым неполным делимым. Делим 8 на 4, получаем 2

Теперь умножаем 2 на 4, получаем 8. Записываем эту восьмёрку под первым неполным делимым:

Вытаскиваем остаток: 8 − 8 = 0. Остаток от деления 8 на 4 это ноль. Ноль не записываем, поскольку решение примера не завершено.

Далее сносим цифру 6 и делим её на делитель, получаем 1

Умножаем 1 на 4, получаем 4. Записываем эту четвёрку под снесённой шестёркой. Затем вынимаем остаток, отняв от шести четыре:

Получили остаток 2. Это остаток, который остался от деления 6 на 4.

Теперь сносим следующую цифру из делимого. Это цифра 4. Эта четвёрка вместе с предыдущим остатком 2 образует число 24. Его делим на делитель. Получим 6

Умножаем 6 на 4, получаем 24. Записываем это число под 24

Вытаскиваем остаток: 24 − 24 = 0. Ноль это остаток от деления 24 на 4. Ноль, как мы уже договорились, не записываем. Далее сносим последнюю цифру 2

Здесь начинается самое интересное. Двойка это последняя цифра, которую мы снесли и которую надо разделить на делитель 4. Но дело в том, что двойка меньше четвёрки, а ведь делимое должно быть больше делителя. Если мы зададим вопрос «сколько четвёрок в двойке?«, то ответом будет ноль, поскольку двойка меньше четвёрки и не может содержать в себе число, бóльшее себя самогó.

Поэтому два разделить на четыре это ноль:

Умножаем 0 на 4, получаем 0. Пишем этот 0 под двойкой:

Теперь находим остаток: 2 − 0 = 2. Двойка это остаток от деления 8642 на 4. Таким образом, пример завершён:

8642 : 4 = 2160 (2 в остатке)

Проверка: (2160 × 4) + 2 = 8640 + 2 = 8642

Деление чисел, у которых на конце 0

Чтобы разделить число, у которого на конце ноль, нужно временно отбросить этот ноль, выполнить обычное деление, и дописать этот ноль в ответе.

Например, разделим 120 : 3

Сколько троек в числе 120? Чтобы ответить на этот вопрос, временно отбрасываем ноль на конце у 120 и делим 12 на 3, получаем 4. И дописываем этот ноль в частном. В итоге получаем 40:

Теперь умножаем частное на делитель (40 на 3), получаем 120. Далее находим остаток: 120 − 120 = 0. Остаток равен нулю. Пример завершён.

120 : 3 = 40

Проверка 40 × 3 = 120.

Такие простые примеры не нуждаются в том, чтобы их решали уголком. Достаточно знать таблицу умножения. Далее просто дописывать нули на конце. Например:

12 : 3 = 4 (делимое без нулей на конце)

120 : 3 = 40 (здесь у делимого один ноль)

1200 : 3 = 400 (здесь у делимого два нуля)

12000 : 3 = 4000 (здесь у делимого три нуля)

В этом способе есть небольшой подвох. Если вы заметили, деля такие числа, мы ссылаемся на таблицу умножения. А представьте, что надо разделить 400 на 5.

Можно рассуждать по старому — отбросить временно все нули и разделить обычные числа. А что будет если отбросить все нули в числе 400? Мы обнаружим, что делим 4 на 5, что недопустимо. В этом случае, надо отбрасывать только один ноль, и делить 40 на 5, а не 4 на 5

Завершаем этот пример, как обычно умножая частное на делитель, и выводя остаток:

Этот способ работает только в том случае, если удаётся гладко применить таблицу умножения. В остальных случаях, придётся искать обходные пути, вычисляя уголком или собирая частное подобно детскому конструктору.

Например, найдём значение выражения 1400 : 5. Здесь отбрасывание нулей нам ничего не даст. Этот пример надо решать уголком или собрать ответ, подобно конструктору. Давайте рассмотрим второй способ.

Что такое 1400? Вспоминаем разряды чисел. 1400 это одна тысяча и четыре сотни:

1000 + 400 = 1400

Можно по-отдельности разделить 1000 на 5 и 400 на 5:

1000 : 5 = 200

400 : 5 = 80

и сложить полученные результаты:

200 + 80 = 280

Итого: 1400 : 5 = 280

Решим этот же пример уголком:

Деление многозначного числа на многозначное

Здесь придётся хорошенько напрячь свой мозговой аппарат и выжать из него по максимуму, потому что разделить многозначное число на многозначное не так то просто.

Принцип деления остаётся тем же что и раньше. Здесь так же надо находить первое неполное делимое. Здесь так же могут присутствовать остатки от деления.

Для начала введём новое понятие — круглое число. Круглым будем называть число, которое оканчивается нулём. Например, следующие числа являются круглыми:

10, 20, 30, 500, 600, 1000, 13000

Любое число можно превратить в круглое. Для этого первые цифры, образующие старший разряд, оставляют без изменений, а остальные цифры заменяют нулями.

Например, превратим число 19 в круглое число. Первая цифра этого числа 1 образует старший разряд (разряд десятков) — эту цифру оставляем как есть, а оставшуюся 9 заменяем на ноль. В итоге получаем 10

Ещё пример. Превратим число 125 в круглое число. Первая цифра 1 образует старший разряд (разряд сотен) — эту цифру оставляем без изменений, а оставшиеся цифры 25 заменяем нулями. В итоге получаем 100.

Ещё пример. Превратим число 2431 в круглое число. Первая цифра 2 образует старший разряд (разряд тысяч) — эту цифру оставляем без изменений, а остальные цифры 431 заменяем нулями. В итоге получаем 2000.

Ещё пример. Превратим число 13 735 в круглое число. Первые две цифры 13 образуют старший разряд (разряд десятков тысяч) — эти две цифры оставляем без изменений, а остальные цифры 735 заменяем нулями. В итоге получаем 13 000.

Внимание! В дальнейшем понятия круглого числа и перевод любого числа в круглое будут обобщены.

Возвращаемся к делению многозначных чисел на многозначные. Сложность деления таких чисел заключается в том, что частное надо находить методом подбора. Для этого прибегают к различным техникам, например, превращают делимое и делитель в круглые числа.

Пример 1. Найти значение выражения 88 : 12

Записываем данное выражение уголком:

Задаём вопрос сколько чисел 12 в числе 88? С первого раза ответить сложно. Придётся рассуждать.

Со школы мы помним, что частное подбиралось методом угадывания, говоря «берем по два» или «берем по три».

Давайте попробуем угадать частное. К сожалению, его просто так с неба взять нельзя. Это частное должно быть таким, чтобы при его умножении на делитель, получалось число, которое меньше делимого, но очень близко к нему или равно ему.

Давайте предположим, что частное равно 2. Умножаем это частное на делитель 12

Что это нам дало? Полученное число меньше делимого, но близко к нему? Нет. Оно конечно же меньше делимого 88, но очень далеко от него. Значит двойка как частное не подходит.

Пробуем следующее число. Допустим частное равно 5

Полученное число конечно меньше, но оно не близко к делимому 88. Значит пятёрка как частное тоже не подходит.

Попробуем сразу взять по 8

На этот раз полученное число превзошло делимое. А оно должно быть меньше делимого, но очень близким к нему или равным ему. Значит восьмёрка как частное тоже не подходит Попробуем тогда взять по 7

Наконец-то нашли подходящее частное! Умножив частное 7 на делитель 12, мы получили 84, которое меньше делимого, но близко к нему. Теперь находим остаток от деления. Для этого из 88 вычитаем 84, получаем 4.

88 : 12 = 7 (4 в остатке)

Проверка: (12 × 7) + 4 = 84 + 4 = 88

Как видно из примера, на подбор частного уходит драгоценное время. Если мы будем сидеть на контрольной или на экзамене, где каждая минута очень дорогá, этот метод нам явно не поможет.

Чтобы сэкономить время, можно делимое и делитель превратить в круглые числа, а затем осуществить деление этих круглых чисел. Делить круглые числа намного проще и удобнее.

Например, чтобы разделить 90 на 10, достаточно отбросить нули у обоих чисел и разделить 9 на 1. В итоге получим 90 : 10 = 9.

Количество отбрасываемых нулей должно быть строго одинаковым. К примеру, если мы делим 900 на 90, то отбрасываем по нулю от каждого числа, поскольку у числа 900 два нуля, а у 90 только один. Отбросив по нулю от каждого числа, мы получим выражение 90 : 9 = 10. В итоге получаем 900 : 90 = 10.

В делении круглых чисел также нет ничего сложного. Постарайтесь понять это. Если непонятно, изучите этот момент несколько раз. Это очень важно.

Ниже приведено несколько примеров, где делятся круглые числа. Отбрасываемые нули закрашены серым цветом:

800 : 10 = 80 (отбросили по нулю и разделили 80 на 1, получили 80)

800 : 80 = 10 (отбросили по нулю и разделил 80 на 8, получили 10)

900 : 10 = 90 (отбросили по нулю и разделили 90 на 1, получили 90)

400 : 50 = 8 (отбросили по нулю и разделили 40 на 5, получили 8)

320 : 80 = 4 (отбросили по нулю и разделили 32 на 8, получили 4)

Заметно, что всё в конечном итоге свóдится к таблице умножения. Именно поэтому в школе требуют знать её наизусть. Мы тоже этого требуем, хоть и не принуждаем.

Теперь давайте решим предыдущий пример 88 : 12 где мы бились, находя частное методом угадывания.

Для начала превращаем делимое и делитель в круглые числа.

Круглым числом для 88 будет число 80.

А круглым числом для 12 будет число 10.

Теперь делим полученные круглые числа:

80 разделить 10 будет 8. Эту восьмёрку мы пишем в частном:

Теперь проверяем, верно ли подобралось частное. Для этого умножаем частное на делитель (8 на 12). Восьмёрку как частное мы уже проверяли, когда решали этот пример методом угадывания. Она нам не подошла, поскольку после её умножения на делитель, получилось число 96, которое больше делимого. Зато подошло частное 7, которое меньше восьмёрки всего-лишь на единицу.

Отсюда можно сделать вывод, что в выражении 88 : 12 частное, полученное путём превращения делимого и делителя в круглые числа, больше лишь на единицу. Наша с вами задача уменьшить это частное на единицу.

Так и сделаем — уменьшим 8 на единицу: 8 − 1 = 7. Семёрка это частное. Записываем её в правом уголке нашего примера:

Как видно, этим способом мы решили этот пример намного быстрее.

Пример 2. Найти значение выражения 1296 : 144

Записываем уголком данное выражение. Сразу же находим первое неполное делимое. Его образуют все четыре цифры делимого:

Это деление многозначного числа на многозначное. Давайте применим только что изученный метод. Превратим делимое и делитель в круглые числа, а затем разделим их.

Для делимого 1296 круглым числом будет 1000. А для делителя 144 круглым числом будет 100.

Делим 1000 на 100, получим 10. Проверим полученную десятку, умножив её на делитель 144

Десятка не подходит, поскольку при умножении получается число, которое больше делимого.

Попробуем взять по 9, уменьшив десятку на единицу.

Проверяем девятку. Для этого умножаем её на делитель:

Красота! Полученное число оказалось не только ближе к делимому, но и равным ему. Это значит, что деление выполнилось без остатка. Завершаем данный пример, вычитая из 1296 полученное число 1296

1296 : 144 = 9

Проверка: 144 × 9 = 1296

Пример 3. Попробуем решить большой и сложный пример 227 492 : 331

Записываем уголком данное выражение. Сразу же определяем первое неполное делимое. Его образуют первые четыре цифры делимого 2274. Значит сначала будем делить 2274 на 331. Их же превратим в круглые числа.

Для числа 2274 круглым числом будет 2000. А для 331 круглым числом будет 300

Получили 6. Проверим верно ли подобралась эта шестёрка. Для этого, умножим её на делитель 331:

Шестёрка подошла, потому что она отвечает на вопрос сколько чисел 331 в числе 2274. Если бы мы взяли по семь, то получилось бы следующее:

Если бы мы взяли по 7 и проверили эту семёрку, то получили бы 2317, которое больше делимого, а это недопустимо.

Продолжаем решать наш пример. Вычитаем из 2274 число 1986, получаем 288:

288 это остаток от деления 2274 на 331. Далее, чтобы продолжить деление, нужно снести девятку:

Теперь надо разделить 2889 на 331. Превращаем их в круглые числа и делим их. Сразу же проверяем полученное таким способом частное:

Умножив 6 на 331, мы снова получили 1986. Это число должно быть меньше делимого 2889, но близким к нему или равным ему. Но 1986 очень далеко от него. Значит шестёрка, как частное не подходит. Проверим тогда семёрку. Это первый случай, когда нам не помог второй способ, который экономил нам время. Дальнейшее решение придётся проводить методом угадывания частного:

Проверили семёрку. Снова получили число, которое далеко от делимого 2889. Значит семёрка тоже не подходит. Проверим восьмёрку:

Восьмёрка подошла. Она отвечает на вопрос сколько чисел 331 в числе 2889. Если бы мы взяли по девять, то при умножении на делитель, получили бы число 2979, а это уже больше делимого 2889.

Теперь вынимаем остаток от деления 2889 на 331. Для этого от 2889 вычитаем 2648 и получаем 241

241 это остаток от деления 2889 на 331. Чтобы продолжить деление, нужно снести 2 из главного делимого:

Теперь делим 2412 на 331. Возьмём по 7

Теперь находим последний остаток. Для этого из 2412 вычитаем 2317, получаем 95. На этом пример завершается:

227 492 : 331 = 687 (95 в остатке)

Проверка: (331 × 687) + 95= 227 397 + 95 = 227 492

На этом данный урок можно завершить. Не расстраивайтесь, если сразу не научитесь делить числа уголком. Этот навык нарабатывается со временем в сочетании с интенсивными тренировками. Ошибки дело не страшное. Самое главное — понимать.

Отметим, что в данном уроке рассмотрено только деление с остатком. Деление без остатка мы рассмотрим в следующих уроках. Сделано это с целью не усложнять обучение. Как говорится, всему своё время.

Задания для самостоятельного решения

Задание 1. Выполните деление:

Решение:

Задание 2. Выполните деление:

Решение:

Задание 3. Выполните деление:

Решение:

Задание 4. Выполните деление:

Решение:

Задание 5. Выполните деление:

Решение:

Задание 6. Выполните деление:

Решение:

Задание 7. Выполните деление:

Решение:

Задание 8. Выполните деление:

Решение:

Задание 9. Выполните деление:

Решение:

Задание 10. Выполните деление:

Решение:

Задание 11. Выполните деление:

Решение:

Задание 12. Выполните деление:

Решение:

Задание 13. Выполните деление:

Решение:

Задание 14. Выполните деление:

Решение:

Задание 15. Выполните деление:

Решение:

Задание 16. Выполните деление:

Решение:

Задание 17. Выполните деление:

Решение:

Задание 18. Выполните деление:

Решение:

Задание 19. Выполните деление:

Решение:

Задание 20. Выполните деление:

Решение:

Задание 21. Выполните деление:

Решение:

Задание 22. Выполните деление:

Решение:

Задание 23. Выполните деление:

Решение:

Задание 24. Выполните деление:

Решение:

Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках

Возникло желание поддержать проект?
Используй кнопку ниже

Навигация по записям

Урок 42. деление числа на произведение. деление с остатком на 10, на 100, на 1 000 — Математика — 4 класс

Математика, 4 класс

Урок № 42. Деление числа на произведение. Деление с остатком на 10, на 100, на 1 000

Перечень вопросов, рассматриваемых в теме:

— как разделить число на произведение чисел?

— какие есть способы деления числа на произведение чисел?

Глоссарий по теме:

Деление – действие, обратное умножению. Деление заменяет неоднократное повторённое вычитание. Число, которое делят, называют делимым, число, на которое делят, называют делителем, результат деления называют частным.

Произведение – результат операции умножения.

Основная и дополнительная литература по теме урока:

1. Моро М. И., Бантова М. А. и др. Математика 4 класс. Учебник для общеобразовательных организаций. Ч.2 — М.; Просвещение, 2017. – с.25-26

2. Моро М. И., Волкова С. И. Математика. Рабочая тетрадь 4 класс. Часть 2. М.; Просвещение, 2016. – с.26

3. Волкова С. И. Математика. Проверочные работы.4 класс. М.: Просвещение, 2017. – с.60-61

Теоретический материал для самостоятельного изучения

Сегодня Миша отмечает свой день рождения. Он пригласил к себе 5 своих друзей. Перед приходом друзей они с мамой готовят угощения, пиццу и именинный пирог. Поскольку у мамы только одна форма для выпечки, пицца и пирог получились одинаковой прямоугольной формы. Всё уже на столе. Но вот проблема, как разделить пиццу и пирог на 6 равных частей, чтобы не обидеть никого из гостей?

Миша попросил маму помочь ему. Мама сказала, что разделить на 6 совсем не трудно, если вспомнить, что 6 – произведение чисел 2 и 3.

6 = 2 • 3

Разделим нашу пиццу на 2 половины. Затем каждую из полученных частей делим ещё на 3 равные части. Получилось 6 одинаковых по размеру кусков пиццы.

Тут к праздничному столу подошёл папа и предложил свой способ деления на 6. Он разделили пирог сначала на 3 части, а затем каждую из полученных частей ещё пополам, т.е. на 2. У папы тоже получилось 6 равных по размеру пирога. И Миша и его друзья были очень довольны. Итак, для деления на 6, мы использовали правило деления на произведение чисел.

Посмотри, как выглядит это правило в случае деления числа 12 на произведение чисел 2 и 3. Разделить число на произведение можно тремя способами:

— вычислить произведение и разделить на него число:

12 : (2 • 3) = 12 : 6 = 2

— разделить число на первый множитель и результат разделить на второй множитель:

12 : (2 • 3) = (12 : 2) : 3 = 6 : 3 = 2

— разделить число на второй множитель и результат разделить на первый множитель:

12 : (2 • 3) = (12 : 3) : 2 = 4 : 2 = 2

Ты можешь выполнять деление любым из этих способов. Но лучше выбирать тот, который будет наиболее удобным.

Посмотри, как правило деления числа на произведение упрощает нахождение частного чисел 560 и 14. Представим 14 в виде произведения чисел 7 и 2. Затем разделим число 560 на первый множитель 7, а полученный результат разделим на второй множитель 2. 560 разделить на 7 будет 80. 80 разделить на 2 получится 40.

560 : 14 = 560 : (7 • 2) = 560 : 7 : 2 = 80 : 2 = 40

А вот как выполняется деление на числа, оканчивающиеся нолями. Чтобы разделить 4800 на 800, представим 800 в виде произведения чисел 100 и 8. Разделим сначала 4800 на 100, получим 48. Теперь этот результат делим на 8, получаем 6. Обрати внимание, что деление числа 4800 на 800 можно заменить делением числа 48 на 8. Эти числа, полученные из делимого и делителя отбрасыванием двух нолей, находящихся справа в их записях.

4800 : 800 = 4800 : (100 • 8) = 4800 : 100 : 8 = 48 : 8 = 6

Задания тренировочного модуля:

1. К каждой записи первого столбца выбери соответствующую запись из второго столбца.

48 : (2 · 4)	96 : 4 : 8
63 : (3 · 7)	48 : 2 : 4
96 : (4 · 8)	63 : 3 : 7

Правильный ответ:

48 : (2 · 4)	48 : 2 : 4
63 : (3 · 7)	63 : 3 : 7
96 : (4 · 8)	96 : 4 : 8

2. Зачеркни неверные решения.

44 : (4 • 11) = 44 : 11 = 4

54 : (6 • 3) = 54 : 6 : 3 = 3

72 : (9 • 2) = 72 : 9 • 2 = 16

Правильный вариант:

Нужно зачеркнуть: 44 : (4 • 11) = 44 : 11 = 4 и 72 : (9 • 2) = 72 : 9 • 2 = 16.

3. Впиши пропущенные числа.

3600 : (4 • 100 ) =___

750 : (25 • 10) = ___

210 : (7 • 6) = ___

Правильный вариант: 9; 3; 5.

Умножение и деление чисел в Excel

Умножение и деление в Excel не представляют никаких сложностей: достаточно создать простую формулу. Не забывайте, что все формулы в Excel начинаются со знака равенства (=), а для их создания можно использовать строку формул.

Умножение чисел

Предположим, требуется определить количество бутылок воды, необходимое для конференции заказчиков (общее число участников × 4 дня × 3 бутылки в день) или сумму возмещения транспортных расходов по командировке (общее расстояние × 0,46). Существует несколько способов умножения чисел.

Умножение чисел в ячейке

Для выполнения этой задачи используйте арифметический оператор * (звездочка).

Например, при вводе в ячейку формулы =5*10 в ячейке будет отображен результат 50.

Умножение столбца чисел на константу

Предположим, необходимо умножить число в каждой из семи ячеек в столбце на число, которое содержится в другой ячейке. В данном примере множитель — число 3, расположенное в ячейке C2.

Введите =A2*$B$2 в новом столбце таблицы (в примере выше используется столбец D). Не забудьте ввести символ $ в формуле перед символами B и 2, а затем нажмите ввод.

Примечание: Использование символов $ указывает Excel, что ссылка на ячейку B2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку B2. Если вы не использовали символы $ в формуле и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3*C3, которая не будет работать, так как в ячейке B3 нет значения.
Перетащите формулу вниз в другие ячейки столбца.

Примечание: В Excel 2016 для Windows ячейки заполняются автоматически.

Перемножение чисел в разных ячейках с использованием формулы

Функцию PRODUCT можно использовать для умножения чисел, ячеек и диапазонов.

Функция ПРОИЗВЕД может содержать до 255 чисел или ссылок на ячейки в любых сочетаниях. Например, формула =ПРОИЗВЕДЕНИЕ(A2;A4:A15;12;E3:E5;150;G4;h5:J6) перемножает две отдельные ячейки (A2 и G4), два числа (12 и 150) и три диапазона (A4:A15, E3:E5 и h5:J6).

Деление чисел

Предположим, что вы хотите узнать, сколько человеко-часов потребовалось для завершения проекта (общее время проекта ÷ всего людей в проекте) или фактический километр на лилон для вашего последнего меж страны(общее количество километров ÷ лилонов). Деление чисел можно разделить несколькими способами.

Деление чисел в ячейке

Для этого воспользуйтесь арифметическим оператором / (косая черта).

Например, если ввести =10/5 в ячейке, в ячейке отобразится 2.

Важно: Не забудьте ввести в ячейку знак равно(=)перед цифрами и оператором /. в противном случае Excel интерпретирует то, что вы введите, как дату. Например, если ввести 30.07.2010, Excel может отобразить в ячейке 30-июл. Если ввести 36.12.36, Excel сначала преобразует это значение в 01.12.1936 и отобразит в ячейке значение «1-дек».

Примечание: В Excel нет функции DIVIDE.

Деление чисел с помощью ссылок на ячейки

Вместо того чтобы вводить числа непосредственно в формулу, можно использовать ссылки на ячейки, такие как A2 и A3, для обозначения чисел, на которые нужно разделить или разделить числа.

Пример:

Чтобы этот пример проще было понять, скопируйте его на пустой лист.

Копирование примера

Создайте пустую книгу или лист.
Выделите пример в разделе справки.

Примечание: Не выделяйте заголовки строк или столбцов.

Выделение примера в справке
Нажмите клавиши CTRL+C.
Выделите на листе ячейку A1 и нажмите клавиши CTRL+V.
Чтобы переключиться между просмотром результатов и просмотром формул, которые возвращают эти результаты, нажмите клавиши CTRL+’ (ударение) или на вкладке «Формулы» нажмите кнопку «Показать формулы».

	A	B	C
1	Данные	Формула	Описание (результат)
2	15000	=A2/A3	Деление 15000 на 12 (1250).
3	12

Деление столбца чисел на константу

Предположим, вам нужно разделить каждую ячейку в столбце из семи чисел на число, которое содержится в другой ячейке. В этом примере число, на которые нужно разделить, составляет 3, содержалось в ячейке C2.

	A	B	C
1	Данные	Формула	Константа
2	15000	=A2/$C$2	3
3	12	=A3/$C$2
4	48	=A4/$C$2
5	729	=A5/$C$2
6	1534	=A6/$C$2
7	288	=A7/$C$2
8	4306	=A8/$C$2

В ячейке B2 введите =A2/$C$2. Не забудьте в формуле включить символ $ перед символами C и 2.
Перетащите формулу в ячейке B2 вниз в другие ячейки в столбце B.

Примечание: Символ $ указывает Excel, что ссылка на ячейку C2 является абсолютной, то есть при копировании формулы в другую ячейку ссылка всегда будет на ячейку C2. Если вы не использовали в формуле символы $ и перетащили формулу вниз на ячейку B3, Excel изменит формулу на =A3/C3, которая не будет работать, так как в ячейке C3 нет значения.

Дополнительные сведения

Вы всегда можете задать вопрос специалисту Excel Tech Community или попросить помощи в сообществе Answers community.

См. также

Умножение столбца чисел на одно и то же число

Умножение на процентное значение

Создание таблицы умножения

Операторы вычислений и порядок операций

элементарная теория чисел — 100% деление на 3 без остатка

В вашем вопросе есть ряд концептуальных ошибок.

В математике, насколько мне известно, нельзя разделить 100% на 3, не имея 0,1 …%.

В математике «100%» означает не больше и не меньше, чем «100 на 100», а именно «100/100 = 1 $. Таким образом, в математике можно разделить 100 \% $ на 3 $, не имея 0,1 \% $. слева. $ 100 \% / 3 = 1/3 = \ frac13 $.

Представьте себе яблоко, которое было клонировано два раза, поэтому два других полностью равны по «качеству». Сумма 3 яблок составляет 100%. Теперь вы можете разделить эти 3 яблока на 3 человека, и вы получите 100%, разделенные на 3, и ничего не останется.

Здесь вы правильно заметили, что если вы рассматриваете группу из 3 одинаковых яблок и считаете эти яблоки за 100%, то вы можете разделить эту группу на 3 (равные) части, и не останется ни одной. Как объяснялось выше, это не противоречит «делению 100% на 3».

Это потому, что 1: математика нереальна 2: нет 1 или 2, и на самом деле это просто изобретение для измерений? Итак, деление 100% на 3 БЕЗ каких-либо остатков — это НЕ точно?

№

Математика, относящаяся к целым числам, рациональным числам и действительным числам, — это очень реальная , в том смысле, что, используя чисто логические рассуждения , мы можем с помощью математических аксиом строго и недвусмысленно доказать многие утверждения о целых, рациональных и действительных числах, которые можно интерпретировать как утверждения о явлениях реального мира, и таким образом, чтобы эти утверждения могли быть эмпирически проверены . В частности, эта часть математики имеет объяснительную силу , и способность предсказания , о реальном мире, что означает, что она дает краткое объяснение наблюдаемых нами явлений и позволяет нам предсказывать будущие явления, которые мы еще не наблюдали. .

Например, прямо сейчас веб-страницы, которые вы читаете с https://math.stackexchange.com, были зашифрованы с использованием шифрования RSA, а процесс дешифрования полагается на истинность маленькой теоремы Ферма, если ее интерпретировать как утверждение о закодированных больших положительных целых числах. на вашем компьютере в двоичном формате (с операциями сложения и умножения, определенными в соответствии с тем, как ваш компьютер их выполняет)!

Другими словами: если маленькая теорема Ферма (интерпретируемая как прогнозирующее утверждение о вашем компьютере) не верна, вы просто не сможете прочитать эти веб-страницы!

Оказывается, малая теорема Ферма может быть доказана в подходящей форме в математической теории под названием PA (Арифметика Пеано первого порядка). И до сих пор ни одна известная теорема PA не была признана ложной при стандартной интерпретации как утверждение реального мира. Так что у нас определенно есть веские основания полагать, что «математика , генерируемая PA, является реальной ».

Что касается изобретений 1 и 2 долларов, то абстрактная концепция натуральных чисел как модели ПА (т.е. они удовлетворяют всем аксиомам ПА) действительно является человеческим изобретением, но это не обязательно означает, что эта абстрактная Концепция не имеет реального значения, как объяснялось выше.

Чтобы прояснить, 100% можно разделить точно на 3, как в математике, так и в подходящей интерпретации понятий «100%» и «3» в реальном мире.

~ ~

Возвращаясь к вашему упоминанию «$ 0.1 \% $», это на самом деле концептуальная ошибка. Это (математический) факт, что $ 100 $ не является целым числом , кратным $ 3 $. То есть не существует целого числа $ k $ такого, что $ 100 = 3 × k $. Однако существует рациональное значение $ r $ , такое что $ 100 = 3 × r $.Когда мы пишем «$ 100 \% / 3 $» в математике, мы имеем в виду точное деление на , которое в данном случае дает рациональное число $ \ frac13 $ в качестве ответа.

Если вы нажмете на базовом калькуляторе (который предназначен для отображения только некоторых чисел с основанием десять) и попросите 100% / 3 , то вы можете получить что-то вроде 0,333333333 . Почему? Это не потому, что ответ — 0,333333333 $. Скорее, калькулятор не может показать ответ в десятичной системе координат .Более того, если вы настроите свой калькулятор на округление ответа до 3 знаков после запятой, то вместо этого вы получите 0,333 , только потому, что вы запросили ответ, округленный до 3 знаков после запятой! Таким образом, (математический) факт, что $ 100 \% = 0,333 × 3 + 0,1 \% $ означает, что , а не , на самом деле имеет какое-либо отношение к делению 1 доллара на 3 доллара.

Между прочим, это явление, связанное с калькуляторами, является артефактом нашего выбора базовой системы для повседневной жизни, которая влияет на дизайн таких калькуляторов.Это не имеет ничего общего с математической концепцией деления. Если бы у людей было только по 3 пальца на каждой руке, мы могли бы использовать основание шесть в повседневной жизни.

Фактически мы можем точно показать, что произошло бы, если бы мы использовали базовые 6 долларов. Мы (используя основание десять) пишем $ 21_6 $ для обозначения числа, представленного строкой символов «21» в базе $ 6 $, что означает $ 2 × 6 + 1 = 13 $. Точно так же в базе $ 6 $ у нас будет $ 1/3 = 0,2_6 $, потому что $ \ frac13 = \ frac26 $. Обратите внимание, что у нас также есть $ \ frac13 = 0.333 \ overline {3} $, где «$ 3 $» с надписями означает, что «$ 3 $» повторяется бесконечно. Здесь нет противоречия. Всякий раз, когда мы не пишем нижний индекс числа, это , по соглашению понимается как десятичное число. Чтобы прояснить, $ \ frac13 = 0,333 \ overline {3} _ {10} = 0,2_6 $.

Сколько 1/3 делится на 100 (Вычислите 1/3 ÷ 100?)

Значит, вы хотите разделить дробь 1/3 на целое число 100, верно? Вы попали в нужное место. В этом простом пошаговом руководстве мы точно покажем вам, что вам нужно сделать, чтобы разделить любую дробь на целое число (это очень просто).Продолжайте читать, чтобы узнать!

Если вы уже подготовили какое-либо из наших пошаговых руководств по фракциям, вы знаете, что мы всегда начинаем шоу с краткого обзора для детей. Число над разделительной линией — это числитель, а число под линией — знаменатель. Простые вещи, но иногда мы все можем немного забыть!

Чтобы визуализировать вопрос, который мы пытаемся решить, поместим 1/3 и 100 рядом, чтобы было легче увидеть:

1 / 3 ÷ 100

Итак, вот невероятно простой способ вычислить, что такое 1/3, разделенная на 100.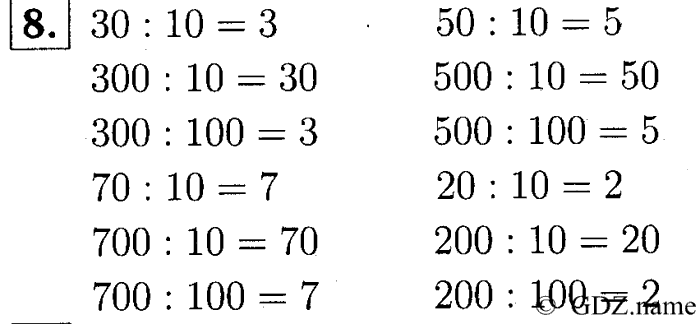 Все, что нам нужно здесь сделать, это оставить числитель в точности таким же (1) и умножить знаменатель на целое число:

1 / 3 х 100 знак равно 1 / 300

Неужели так просто разделить дробь на целое число? Ага.Ненавижу разочаровывать вас, но это, возможно, самая простая проблема, которую вам приходилось решать за весь день!

В некоторых случаях новая дробь, которую мы получаем после выполнения вычисления, может быть упрощена до более низких членов, но в этом случае дробь уже находится в самой низкой форме.

Готово! Теперь вы точно знаете, как рассчитать 1/3, деленную на 100. Надеюсь, вы поняли процесс и можете использовать те же методы для деления других дробей на целые числа.

Преобразовать 1/3, деленную на 100, в десятичную дробь

Вот небольшой бонусный расчет, который поможет вам легко определить десятичный формат вычисленной дроби. Когда у вас будет окончательная дробь, просто разделите числитель на знаменатель, чтобы получить ответ в десятичной форме:

1 / 300 знак равно 0.0033

Цитируйте, ссылайтесь или ссылайтесь на эту страницу

Если вы нашли этот контент полезным в своем исследовании, пожалуйста, сделайте нам большое одолжение и используйте инструмент ниже, чтобы убедиться, что вы правильно ссылаетесь на нас, где бы вы его ни использовали. Мы очень ценим вашу поддержку!

Что 1/3 делится на 100
«Что 1/3 делится на 100». VisualFractions.com . По состоянию на 2 июня 2021 г. https://visualfractions.com/calculator/fraction-divided-by-whole/what-is-1-3-divided-by-100/.
«Что 1/3 делится на 100». VisualFractions.com , https://visualfractions.com/calculator/fraction-divided-by-whole/what-is-1-3-divided-by-100/. По состоянию на 2 июня 2021 г.
Что 1/3 делится на 100. VisualFractions.com. Получено с https://visualfractions.com/calculator/fraction-divided-by-whole/what-is-1-3-divided-by-100/.

Калькулятор дроби на целое число

Введите числитель, знаменатель и целое число

3 разделить на 100 | 3 разделить на 100 с остатком

Ответ на математические задачи Этапы решения

Математические ответы на деление дроби 3/100

3100 = 0. 03

0,03 = 0,3 с точностью до десятых

0,03 = 0,03 с точностью до сотых

0,03 = 0,03 с точностью до тысячных

= 0 с точностью до десятых

= 0 с точностью до сотых

= 0 с точностью до тысячных

Другие разделы Домашнее задание по математике —

3 разделить пополам плюс 20

Домашнее задание: (3/2) + 20 = 21,5

3 разделить пополам плюс 40

Домашнее задание: (3/2) + 40 = 41.5

3/100 разделить на 2

Ответ: (3/100) ÷ 2 = 0,015

С помощью этого бесплатного инструмента можно легко решить домашнее задание по математике

Division. Чтобы решить домашнее задание или задание, все, что вам нужно сделать, это ввести значение в соответствующее поле и нажать «вычислить», чтобы получить математические ответы.

Что такое числитель / знаменатель

Числитель: мы называем верхнее число числителем, это число в верхней части имеющейся у вас дроби.

Знаменатель: мы называем нижнее число знаменателем, это целое число внизу, это число, на которое делится.

Шаги преобразования дробной части в десятичную

Шаг 1: Найдите число, которое можно умножить на нижнюю часть дроби, чтобы получилось 10, 100, 1000 или любая единица с последующими нулями.

Шаг 2: Умножьте верхнюю и нижнюю часть на выбранное вами число.

Шаг 3. Затем запишите только верхнее число, поместив десятичную запятую в правильное место, то есть на один пробел с правой стороны для каждого нуля в нижнем числе.

a / b = c В приведенных выше выражениях a называется делимым, b называется делителем, а c называется частным; в выражении a / b, a также называется числителем, а b также называется знаменателем.

Этот калькулятор дроби также можно использовать для вычисления доли в процентах, скидок на покупки, купонов, жировых отложений, валовой прибыли, потери веса, любви, налогов, увеличения и уменьшения населения, прибыли от продаж. Как только вы знаете значения, определить% легко.

Если вы обнаружите ошибку на этом сайте, мы будем благодарны, если вы сообщите нам об этом, используя предоставленный контактный адрес электронной почты.отправьте электронное письмо в контакт на нашем сайте.

Далее Назад

Калькулятор деления больших чисел — деление больших десятичных чисел онлайн

Поиск инструмента

Отдел

Инструмент для вычисления деления, инструмент, совместимый с большими числами, произвольной точностью или арифметическими формулами с переменными.

Результаты

Дивизия — dCode

Тэги: Арифметика

dCode и другие

dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокешинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !

Дивизион 2-х номеров

Расчет с делениями

Сделайте евклидово деление

Вычислить дроби

Поиск повторяющихся десятичных знаков

Ответы на вопросы (FAQ)

Как рассчитать деление?

Операция деление должна рассматриваться как разделение числа на меньшие количества на равные части.

Деление может быть точным (разделение 10 элементов на стопки по 2) или иметь остаток (разделение 10 элементов на стопки по 3, остается 1 элемент), последнее также называется евклидовым делением .

dCode имеет инструмент для реализации евклидова деления (с подробностями расчетов).

Пример: 10 делить на 5 обозначается 10/5 или 10 ÷ 5 или $ \ frac {10} {5} $ равно 2, так как можно разделить 10 на 2 равные части размера 5.

Пример: 10 делить на 4 отмечается 10/4 или 10 ÷ 4 или $ \ frac {10} {4} $ равно 2,5 (2 с половиной), потому что можно сделать 2 сваи. из 4 и стопка из 2 (половина стопки из 4)

В случае неточного деления , можно округлить значение с помощью определенного количества цифр после десятичной точки.

Как сделать деление без калькулятора?

В школе преподается Евклидово деление, которое состоит из размещения деления вручную, без калькулятора, с остатком или без него. В dCode есть инструмент для этого: Евклидово деление.

Как рассчитать деление с большими числами?

DCode использует алгоритмы вычисления произвольной точности для получения точных значений при делении больших чисел без экспоненциальной записи (миллиарды, триллионы и более), до 1 миллиона цифр.

Как рассчитать целочисленное деление?

Целое деление похоже на евклидово деление, принцип заключается не в вычислении после десятичной точки и определении остатка.

Пример: 14/3 доллара = 4 доллара остаток 2 доллара

Задайте новый вопрос

Исходный код

dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Подразделение».За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / бесплатно), любого алгоритма, апплета или фрагмента «Разделение» (преобразователь, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любой функции «Разделение» (вычислить, преобразовать, решить, расшифровать / зашифровать, расшифровать / зашифровать, декодировать / закодировать, перевести), написанные на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т.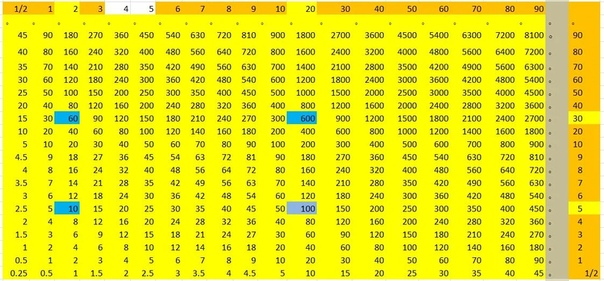 д.), без загрузки данных, скрипт, копирование -паста или доступ к API для «Дивизиона» будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.

Нужна помощь?

Пожалуйста, посетите наше сообщество dCode Discord для запросов о помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!

Вопросы / комментарии

Сводка

Похожие страницы

Поддержка

Форум / Справка

Ключевые слова

деление, деление, алгоритм, большое, число, целое

Ссылки

Источник: https://www.dcode.fr/big-numbers-division

100 разделить на 120 — в столбик | 100/120 в простейшей форме

Используйте форму ниже, чтобы выполнить преобразование, разделяя числа запятыми.

2 дек. Места 2 дек. Места 3 дек. Места 4 дек. Места 5 дек. Мест 6 дек. Мест 7 дек. Мест 8 дек. Мест 9 дек. Мест 11 дек. Места 12 дек. Мест 1 дек.

100 делится на 120 равно 100 ÷ 120

100 разделить на 120 в виде дроби

100/120 ÷ 2
50/60 ÷ 2
25/30 ÷ 2
5/6

100/120 в простейшей форме = 5/6

100 / 120 = 0.833333333333 в десятичной форме

100/120 = 0,83 с точностью до 2 десятичных знаков

100/120 = 0,8 с точностью до десятых

100/120 = 0,83 с точностью до сотых

100/120 = 0,833 с точностью до тысячных

Калькулятор упрощения дробей или Калькулятор сокращения дробей — это онлайн-математический инструмент, который преобразует заданную дробь в ее простейшую или сокращенную форму. Он легко упрощает дроби и показывает этап преобразования в простейшую форму

Пример упрощения 50/100

Допустим, мы хотим упростить 50/100 до его сокращенной формы.Мы начинаем тестировать все целые числа, чтобы увидеть, делят ли они 50 и 100, чтобы получить последующее результирующее значение. Полученное значение будет упрощенной дробью. Итак, мы начинаем с 2 и продолжаем проверять до числа 19.

50/100 ÷ 2 = 25/50; который делит, мы начинаем снова с 2
25/50 ÷ 2 = 12,5 / 25, не целых значений, поэтому попробуйте следующее наибольшее число, 3
25/50 ÷ 3 = 8,333 / 16,67, не целое, поэтому попробуйте следующее наибольшее число, 4
25 / 50 ÷ 4 = 6,25 / 12,5, не целое число, поэтому попробуйте следующее по величине число, 5
25/50 ÷ 5 = 5; который делится, мы снова начинаем с 2
5/10 ÷ 2 = 2.5/5, не целое число, поэтому попробуйте следующее наибольшее число, 3
5/10 ÷ 3 = 1,67 / 3,33, не целое, поэтому попробуйте следующее наибольшее число, 4
5/10 ÷ 4 = 1,25 / 2,5, не целое число, поэтому попробуйте следующее наибольшее число, 5
5/10 ÷ 5 = 1/2
Таким образом, упрощенное 50/100 то же самое, что и 1/2

  Инструкции: 
 Введите число, которое вы хотите преобразовать. 
 Выберите, сколько десятичных знаков вы хотите. 
 Щелкните, чтобы преобразовать в простейшую форму.

Другие числовые преобразования, которые следует учитывать

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 101

23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 101

100 (разделено на 2) причин любить новые уроки празднования 100-летнего юбилея ФРС

100 (разделено на 2) причин любить уроки празднования нового столетия ФРС

Посмотрим правде в глаза, экономисты любят математику! Итак, как только вы закончите с проблемой разделения в заголовке, продолжайте читать, чтобы найти интересные способы узнать о некоторых характеристиках новых Уроков празднования столетия Федеральной резервной системы.(Уроки называются «Определяющие моменты в истории Федеральной резервной системы», «Перетасовка Федеральной резервной системы» и «Современная Федеральная резервная система».)

Может и не быть «бесплатного обеда», но есть уроки, которые бесплатны для учителей!
Студентам нравится новая 100-долларовая купюра. Расскажите им о том, кто его выпустил!
Последние 100 лет были полны экономических волнений. Узнайте, как ФРС успокаивает нас.
Вы можете сказать слово «Knickerbocker», и люди будут воспринимать вас всерьез.
Слова «Конгресс» и «компромисс» встречаются в одном предложении.
Великие вещи попадают в тройку!
Мы уже сделали слайды PowerPoint.
Сыграйте (каламбур!) На драматическое чутье ваших учеников в Reader’s Theater.
Оживите исторические моменты из ФРС с помощью трекера Time Travel Trekker.
Станьте свидетелями зарождения операций на открытом рынке.
Экон Эд — первоклассный журналист, путешествующий во времени.
Кому бы не понравился исчерпывающий глоссарий ФРС !?
Из концептуальных карточек получается отличная стена слов Федерального правительства.
Воспоминания о Глассе-Стигалле.
Узнайте, почему выпуск эластичной валюты — это несложно.
Узнайте, что Бреттон-Вудс — это место и соглашение, а не личность.
Наконец, возможность рассказать о Международном валютном фонде и Всемирном банке!
Поймите разницу между платежными и кредитными картами.
Узнайте, почему Америка навсегда изменилась в 1966 году.
Раскройте правду о Постановлении Z.
Представьте себе мир без банкоматов.
Объясните своим студентам, что кредиторам запрещено дискриминировать заявителей.
Узнайте, как Конгресс пытался стереть «красные линии» (и нет, мы не имеем в виду красные отметки, которые учителя оставляют на школьных документах).
Великая инфляция так же важна, как и Великая депрессия.
У целей ФРС два яблочка вместо одного!
J показывает преимущества наличия одного свода правил для всех.
Если вы думаете, что REI имеет какое-то отношение только к кемпингу, подумайте еще раз!
Обратите внимание на значение 72 000 в час.
Доступны ли ваши чековые депозиты быстро? Узнай почему!
Хронология — это хабр!
Ссылки. Множество ссылок.
Урок 3 в моде!
Дайте старшеклассникам академическую причину играть за лидером.
Действуйте как залог. Казначейская облигация.
Содержит отличные неформальные стратегии оценки.
Прозрачная пленка, для которой не требуется проектор или маркер.
Beige — это новый черный цвет. Узнайте, как Бежевая книга описывает стратегии бизнеса, направленные на то, чтобы оставаться «в черном».
Откройте для себя еще одну версию «трех рупий»: реформа, восстановление и регулирование, о боже!
Узнайте, почему вы не можете купить окно со скидкой на местном складе для ремонта дома.
У вас есть тайное желание узнать Базель III.
Учителя знают все о «стресс-тестах» — хорошо знать, что финансовые учреждения тоже их проходят!
Ваши любимые знаменитости Econ Ed из Майами, Бирмингема и Нэшвилла написали некоторые уроки.
Вау, они согласованы с Общим Ядром!
Узнайте, что имеет в виду Додд-Франк.
Узнайте, кто «только что проходит» через Автоматизированную клиринговую палату.
Вы тоже можете свободно говорить на «Федезе».
Расскажите своему классу о рынке студенческих ссуд.
Всегда интересно думать о прямых депозитах!
Студенты узнают, что коммерческие банки — это не просто банки, рекламируемые по телевидению.
ФРС ставит «супер» в надзор и регулирование.

Плюс еще несколько …

Теперь, когда у вас есть много причин использовать уроки, вот несколько ссылок на другие сайты, посвященные столетнему юбилею Федеральной резервной системы.

От первой бумажной валюты до последнего финансового кризиса вы и ваши ученики узнаете о финансовой истории Соединенных Штатов и хронологии истории Федерального резерва.

Любите мультики? Серия видеороликов «Разъяснения ФРС» предлагает увлекательный взгляд на создание и структуру Федеральной резервной системы под заголовками «ФРС объясняет Центральный банк» и «ФРС объясняет региональные банки».

Вы любите ФРС и первоисточники? Если да, ознакомьтесь с Проектом инвентаризации коллекций ФРС и найдите в изобилии документы по истории ФРС!

Шерилин Наркер, специалист по экономическому и финансовому образованию Федерального резервного банка Атланты

6 ноября 2013 г.

Калькулятор деления в столбик

с десятичными знаками и остатками

Добро пожаловать в калькулятор деления в столбик, инструмент, который поможет вам понять, как выполнять деление в столбик с десятичными знаками .Читайте дальше, чтобы узнать, как решать задачи длинного деления, и , как работать с длинным делением с остатками . Вы также можете найти пример деления в столбик с подробным объяснением шагов деления в столбик.

Деление в столбик с остатками

Поскольку мы хотим научиться делать столбики, давайте начнем с основ — определений.

Обычно мы хотим найти результат, который представляет собой отношение двух чисел. Эти два числа: — дивиденд (не путать с дивидендом в финансах) и — делитель .Мы также можем записать это как:

результат = дивиденд / делитель .

Мы можем записать результат в различных формах: как дробь, десятичная дробь (преобразованная из дроби) или как комбинация двух чисел: как частное и как остаток . Последнее составляет суть проблем с делением в столбик.

Как сделать длинное деление с десятичными знаками?

Весь процесс относительно прост, так как вам нужно повторить шаги длинного деления :

Поскольку мы собираемся разделить каждую часть дивиденда отдельно, нам необходимо разделить ее.Начните с того, что посмотрите, сколько цифр у вашего делителя. Это то количество цифр, которое мы берем из левой части дивиденда для работы с статистикой. Например, если мы разделим 378 на 14, мы посмотрим на 37 часть 378. Мы будем называть числа, которые мы берем n₁ .
Если n₁ меньше делителя, возьмите и следующую цифру из делимого.
Разделите это значение на делитель и округлите результат до ближайшего целого числа.Это первая цифра частного.
Умножьте эту цифру на делитель. Назовем это n₂ .
Вычтем n₁ и n₂ . Обычно мы получаем остаток.
С этим новым числом запишите следующую цифру справа от делимого (шаг 1) справа от этого значения, которое является нашим новым n₁ .
Продолжайте эти шаги долгого деления, пока у вас не закончатся цифры в делимом.
Когда вы используете последнюю цифру из делимого и разность n₁ - n₂ дает ненулевое значение, это , последний остаток
Вы можете продолжить, записав следующие нули в конце, чтобы получить большую точность и иметь более значащие цифры. Но будьте осторожны, иногда это никогда не заканчивается, например, с повторяющимися десятичными знаками!

Между прочим, если вас интересует только остаток, вы можете использовать оператор по модулю, потому что равенство делимое по модулю деления = остаток всегда истинно.

Пример длинного деления с шагом

Поскольку мы уже изучили теорию, давайте попробуем решить конкретный пример деления в столбик и посмотрим, как работает наш калькулятор деления в столбик. В этом случае давайте посмотрим, как сделать длинное деление 65321 и 31 :

Возьмите первые две цифры делимого: 65 . Разделите это значение на 31 и округлите его до целого числа, что даст нам 2 . Запишите это выше как первую цифру частного.
Умножьте 2 на 31 , что равно 62 . Запишите это сразу под 65 от дивиденда. Вычтите эти два числа: 65-62 = 3 . Это первая цифра нового значения.
Запишите следующую цифру делимого: 3 . Вместе они составили 33 .
31 подходит только один раз в 33 , поэтому следующая цифра частного — 1 .
Затем разница 33-31 = 2 и следующая цифра из делимого ( 2 ) образуют новое число, 22 .
Прежде чем продолжить деление, мы видим, что 22 меньше, чем 31 , поэтому мы можем записать 0 как следующую цифру в частном и записать еще одну цифру из делимого, что дает нам 221 .
Разделив 221 на 31 и округлив его до целого числа, мы получим 7 — последнюю цифру частного.
Тогда последний стандартный шаг равен 7 * 31 = 217 и 221-217 = 4 .
No related posts.

100 Поделить на 3

Похожие примеры с 100 и 3

Комментарии

Почему нельзя делить на ноль?

Деление десятичных дробей: правила, примеры

Основы деления десятичных дробей

Как разделить целое число на десятичную дробь и наоборот

Как разделить десятичную дробь на натуральное число столбиком

Как разделить столбиком одну десятичную дробь на другую

Как разделить десятичные дроби на 1000, 100, 10 и другие

Как разделить десятичные дроби на 0,001, 0,01, 0,1 и другие

Как разделить смешанное число или обыкновенную дробь на десятичную и наоборот

Калькулятор онлайн — Калькулятор процентов. Найти сколько процентов составляет одно число от другого

Понятие о проценте

Задачи на проценты

Простой процентный рост

Сложный процентный рост

Деление

Что такое деление?

Деление с остатком

Деление уголком

Деление многозначного числа на однозначное

Деление чисел, у которых на конце 0

Деление многозначного числа на многозначное

Задания для самостоятельного решения

Навигация по записям

Урок 42. деление числа на произведение. деление с остатком на 10, на 100, на 1 000 — Математика — 4 класс

Умножение и деление чисел в Excel

Умножение чисел

Умножение чисел в ячейке

Умножение столбца чисел на константу

Перемножение чисел в разных ячейках с использованием формулы

Деление чисел

Деление чисел в ячейке

Деление чисел с помощью ссылок на ячейки

Деление столбца чисел на константу

Дополнительные сведения

См. также

элементарная теория чисел — 100% деление на 3 без остатка

Сколько 1/3 делится на 100 (Вычислите 1/3 ÷ 100?)

Преобразовать 1/3, деленную на 100, в десятичную дробь

Цитируйте, ссылайтесь или ссылайтесь на эту страницу

Калькулятор дроби на целое число

3 разделить на 100 | 3 разделить на 100 с остатком

Ответ на математические задачи Этапы решения

Калькулятор деления больших чисел — деление больших десятичных чисел онлайн

Дивизион 2-х номеров

Расчет с делениями

Сделайте евклидово деление

Вычислить дроби

Поиск повторяющихся десятичных знаков

Ответы на вопросы (FAQ)

Как рассчитать деление?

Как сделать деление без калькулятора?

Как рассчитать деление с большими числами?

Как рассчитать целочисленное деление?

Исходный код

Нужна помощь?

Вопросы / комментарии

100 разделить на 120 — в столбик | 100/120 в простейшей форме

100 (разделено на 2) причин любить новые уроки празднования 100-летнего юбилея ФРС

с десятичными знаками и остатками

Деление в столбик с остатками

Как сделать длинное деление с десятичными знаками?

Пример длинного деления с шагом

Добавить комментарий Отменить ответ