План-конспект урока по информатике и икт на тему: Решение логических задач
Тема: «Решение логических задач»
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет.
Запрос | Найдено страниц (в тысячах) |
ШОКОЛАД⎮ЗЕФИР | 15000 |
ШОКОЛАД & ЗЕФИР | 8000 |
ЗЕФИР | 12000 |
Какое количество страниц (в тысячах) будет найдено по запросу ШОКОЛАД? Решите задачу, используя круги Эйлера.
2)
Запрос | Найдено страниц (в тысячах) |
ЗУБР & ТУР | 5000 |
ЗУБР | 18000 |
ТУР | 12000 |
Какое количество страниц (в тысячах) будет найдено по запросу ЗУБР ⎮ ТУР? Решите задачу, используя круги Эйлера.
3)
Запрос | Найдено страниц (в тысячах) |
ФУТБОЛ⎮ХОККЕЙ | 20000 |
ФУТБОЛ | 14000 |
ХОККЕЙ | 16000 |
Какое количество страниц (в тысячах) будет найдено по запросу ФУТБОЛ & ХОККЕЙ? Решите задачу, используя круги Эйлера.
4) Некоторый сегмент сети Интернет состоит из 1000 сайтов. В таблице приведены запросы и количество найденных по ним страниц:
Запрос | Найдено страниц |
ЧЕРНИКА | 350 |
МАЛИНА | 200 |
БРУСНИКА | 500 |
ЧЕРНИКА & БРУСНИКА | 50 |
ЧЕРНИКА & МАЛИНА | 20 |
МАЛИНА & БРУСНИКА | 10 |
МАЛИНА & БРУСНИКА & ЧЕРНИКА | 5 |
Сколько сайтов будет найдено по запросу ЧЕРНИКА⎮МАЛИНА⎮БРУСНИКА?
Решите задачу, используя круги Эйлера.
nsportal.ru
Задача 17 — разбор задания ЕГЭ по предмету Информатика
Решение №1
Для решения данной задачи полезно воспользоваться визуализацией в виде кругов Эйлера. Разберём эту визуализацию подробнее.
У нас имеются три разных слова в запросах:
- Гомер
- Илиада
- Одиссея
Обозначим страницы, в которых встречаются эти слова, за круги. При этом сделаем так, чтобы эти круги пересекались.
Что нам известно по условию согласно таблице?
- Гомер & Илиада = 200. Что это означает?
- Что количество страниц, где встречаются одновременно слова и Гомер, и Илиада («и», так как используется &), равно 200.
- Что на рисунке соответствует таким страницам?
- Им соответствует область, которая лежит и в Гомере, и в Илиаде (см. светло-зелёную область).
- Теперь по аналогии отметим красным область Гомер & Одиссея:
- Теперь давайте разберём строку Гомер & (Одиссея | Илиада). Это пересечение двух областей, одна из которых понятна (Гомер). Давайте разберёмся со второй: Одиссея | Илиада.
- Одиссея | Илиада — это Одиссея или Илиада. То есть, это страницы, на которых есть или Одиссея, или Илиада, или обе. То есть, это — объединение Одиссеи и Илиады.
- Это объединение пересекается с Гомером в общих областях (см. картинку, розовый цвет).
- Что нам надо сосчитать? — Гомер & Одиссея & Илиада. То есть, пересечение всех трёх областей (маленький «псевдотреугольник» в центре).
- Давайте посмотрим внимательно, как мы его можем посчитать.
- Если мы в уме сложим области «Гомер & Одиссея» (бордовый) и «Гомер & Илиада» (зелёный), то получится, что мы охватили все пересечения (розовый), но при этом маленький треугольник мы посчитали два раза.
- То есть, если из суммы бордового и зелёного отнять розовый, получится как раз один маленький треугольничек (так как все области кроме него сократятся).
- Значит, Гомер & Одиссея & Илиада = 355 + 200 — 470 = 85
Ответ: 65 тысяч страниц.
Евгений Смирнов
Эксперт в IT, учитель информатики
newtonew.com
Решение задач с помощью кругов Эйлера

Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Изобретены Леонардом Эйлером. Используется в математике, логике, менеджменте и других прикладных направлениях.
Задача №1
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| Запрос | Найдено страниц (в тысячах) |
| Торты | Пироги | 12000 |
| Торты & Пироги | 6500 |
| Пироги | 7700 |
Какое количество страниц (в тысячах) будет найдено по запросу Торты?Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
Решение задачи №1
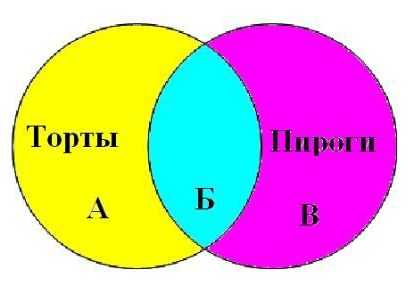
Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Торты │Пироги = А+Б+В = 12000
Торты & Пироги = Б = 6500
Пироги = Б+В = 7700
Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.
Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300
Сектор А равен 4300, следовательно
Торты = А+Б = 4300+6500 = 10800
Задача №2
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросу Выпечка
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.Решение задачи №2
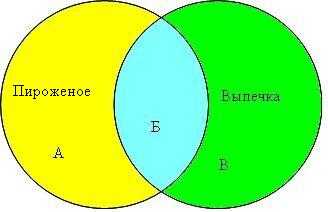
Для решения задачи отобразим множества Пироженых и Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Пироженое & Выпечка = Б = 5100
Пироженое = А+Б = 9700
Пироженое │ Выпечка = А+Б+В = 14200
Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти сектор В, для этого из общего множества (Пироженое │ Выпечка ) отнимем множество Пироженое.
Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500Сектор В равен 4500, следовательно Выпечка = Б + В = 4300+5100 = 9400
Задача №3
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | спаниели | (терьеры & овчарки) |
| 2 | спаниели | овчарки |
| 3 | спаниели | терьеры | овчарки |
| 4 | терьеры | овчарки |
Решение задачи №3
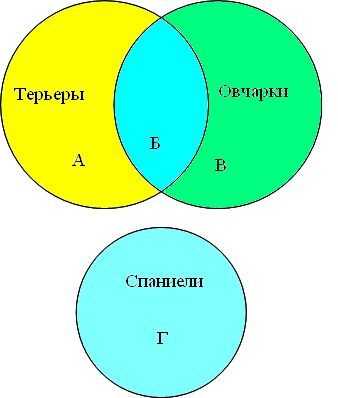
Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
спаниели │(терьеры & овчарки) = Г + Б
спаниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4
Задача №4
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | барокко | классицизм | ампир |
| 2 | барокко | классицизм & ампир |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Решение задачи №4
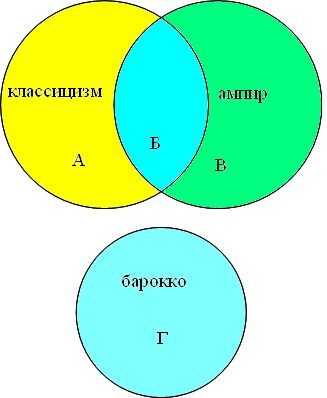 Представим множества классицизм, ампир и классицизм в виде
кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Представим множества классицизм, ампир и классицизм в виде
кругов Эйлера, обозначим сектора буквами (А, Б, В, Г). Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Гбарокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1
Задача №5В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | канарейки | терьеры | содержание |
| 2 | канарейки & содержание |
| 3 | канарейки & щеглы & содержание |
| 4 | разведение & содержание & канарейки & щеглы |
Решение задачи №5
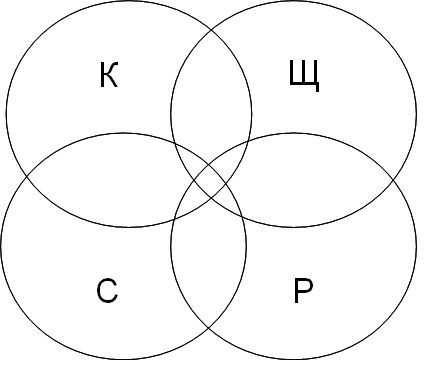
Для решения задачи представим запросы в виде кругов Эйлера.
K — канарейки,
Щ – щеглы,
С – содержание,
Р – разведение.
Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
| канарейки | терьеры | содержание | канарейки & содержание | канарейки & щеглы & содержание | разведение & содержание & канарейки & щеглы |
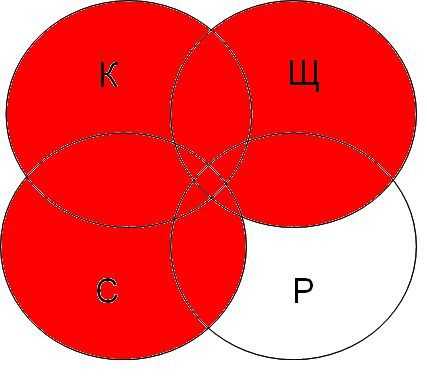 | 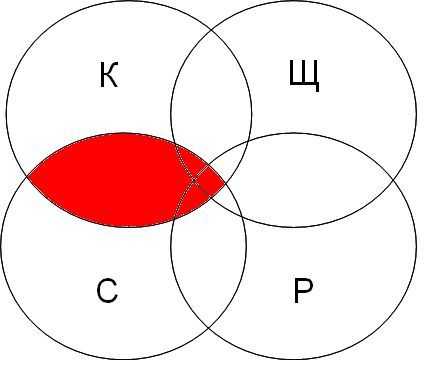 | 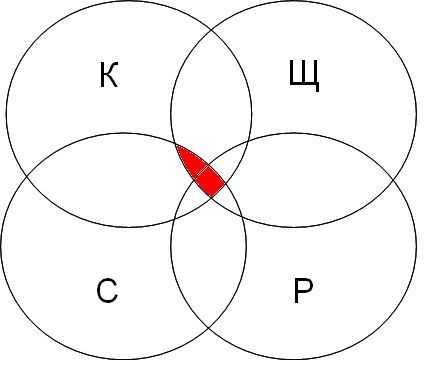 | 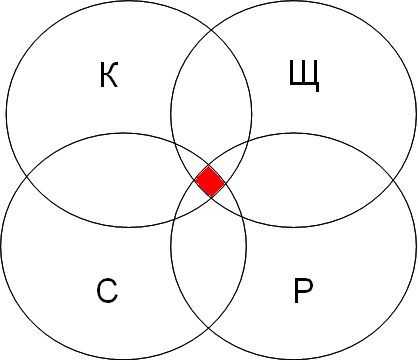 |
Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что правильно решили задачу.
Задачи для самостоятельного решения
Задача №6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | принтеры & сканеры & продажа |
| 2 | принтеры & продажа |
| 3 | принтеры | продажа |
| 4 | принтеры | сканеры | продажа |
Задача №7
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | физкультура |
| 2 | физкультура & подтягивания & отжимания |
| 3 | физкультура & подтягивания |
| 4 | физкультура | фитнесс |
Использованные материалы >>>
Решение подобных задач по информатике >>>
Ответы к задачам для самостоятельного решения
| Номер задачи | Ответ |
| 6 | ГБВА |
| 7 | БВАГ |
saitsewanatalia.blogspot.com
Сборник текстовых задач на круги Эйлера
Задачи на круги Эйлера
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. По запросам было выдано следующее количество страниц(в тысячах)
Берн — 4220
Цюрих — 3600
Цюрих | Берн — 5900
Какое количество страниц (в тысячах) будет найдено по запросу Цюрих & Берн?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
По запросам некоторого сегмента в сети Интернет было выдано следующее количество страниц(в тысячах)
Куница — 4300
Соболь — 3700
Соболь | Куница — 6500
Какое количество страниц (в тысячах) будет найдено по запросу Куница & Соболь?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
По запросам некоторого сегмента в сети Интернет было выдано следующее количество страниц(в тысячах)
Шахматы & Теннис — 1000
Теннис — 5500
Теннис | Шахматы — 7770
Какое количество страниц (в тысячах) будет найдено по запросу Шахматы?
По запросам некоторого сегмента в сети Интернет было выдано следующее количество страниц(в тысячах)
Мопс | Бульдог — 5500
Мопс — 2500
Мопс &Бульдог — 1000
Какое количество страниц (в тысячах) будет найдено по запросу Бульдог ?
По запросам некоторого сегмента в сети Интернет было выдано следующее количество страниц(в тысячах)
Мопс | Бульдог — 4000
Бульдог — 3500
Мопс — 2000
Какое количество страниц (в тысячах) будет найдено по запросу Мопс &Бульдог ?
По запросам некоторого сегмента в сети Интернет было выдано следующее количество страниц(в тысячах)
Мопс &Бульдог- 500
Бульдог — 2000
Мопс — 3200
Какое количество страниц (в тысячах) будет найдено по запросу Мопс | Бульдог
В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. По запросам было выдано следующее количество страниц(в тысячах)
Корвет| Субмарина — 3000
Корвет & Субмарина — 600
Субмарина 2000
Какое количество страниц (в тысячах) будет найдено по запросу Корвет?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.
В классе 36 человек. Ученики этого класса посещают такие кружки: математический -18 чел, физический – 14 чел, и химический – 10 чел. Кроме того, известно, что 2 человека посещают все кружки, 8-и математику и физику, 5 – математику и химию, 3- физику и химию. Сколько человек в классе не посещают никаких кружков? (8 чел)
Ресторан за день посетили 50 человек. На кухне было приготовлено следующее количество вторых блюд: грибы- 25 порций, мясо – 29 порций, рыба- 24 порции. Известно, что 3 человека заказывали сразу все блюда, 8 человек — рыбу и грибы, 11 человек- рыбу и мясо и 15 человек – грибы и мясо. Сколько посетителей вообще отказались от второго блюда? (3)
После зимних каникул учитель спросил, как дети их провели. Оказалось, что из 36 учащихся 2 – не были нигде, 25 человек — в кино, 11 — в театре, 17 — в цирке. И в кино и в театре — 6 чел, и в кино и в цирке- 10, и в театре и в цирке -4 чел. Сколько человек побывало везде? (1 чел)
В параллели 10 классов 70 человек. 32 человека посещают секцию баскетбол, 35- волейбола, 29- футбола. 12 человек ходят и баскетбол и волейбол, 7 учащихся – на волейбол и футбол, 10 – на баскетбол и футбол. Сколько человек ходят сразу на все 3 секции? (3)
В здании 55 кабинетов. 24 из них оснащены вентиляцией, 31 кабинет имеет железные двери, и в 22 стоят компьютеры. В 9 кабинетах есть вентиляция и компьютеры, в 12 — компьютеры и железные двери, в 11 – вентиляция и железные двери. В 5 кабинетах нет ничего из вышеперечисленного. В скольких кабинетах есть сразу все? (5)
В классе 35 учеников. 24 из них занимаются спортом, 12 – музыкой, 18 –посещают факультативы. 10 учеников одновременно занимаются спортом и учебой, 8- спортом и музыкой, 5 учебой и музыкой. Сколько учеников занимаются всем? (4)
В социологическом опросе участвовало 100 человек. 15% опрошенных сказали что у нас прекрасный город. 50 % заявили что город грязный, 48% — что дороги плохие, 20% что и грязь и дороги, 16%- что молодежи нечем заняться в городе, и вокруг грязь, 14% — что плохие дороги и мало развлечений для молодежи. Сколько человек говорили про молодежь? ()
Среди 50 опрошенных 21 человека слушают только поп-музыку, 19 – только рэп, 17 – только рок и 8 человек вообще не любят эти направления. Тех, кто любит поп и рэп и терпеть не могут рок – 6 человек. Тех кто любит рэп и рок вместе – 5 человек, а тех, кто готов слушать все, что угодно- 2 человека. Сколько человек любят поп и рок и терпеть не могут рэп? (2)
При опросе 50 человек оказалось, что 17 любят попугайчиков, 28 –собак, 7 –попугаев и кошек, 13 –кошек и собак, 3 – любят попугаев и собак и терпеть не могут кошек, 5 любят всех животных вообще и 3 — не любят никого. Сколько человек любят исключительно кошек? (10)
Из 90 опрошенных 30 человек сказали, что проводят выходные на природе, еще 40 – что встречаются с друзьями, 13 – что кроме природы ходят в развлекательные заведения, 4 – приглашают друзей на природу, а развлекательные заведения не любят, 12 – встречаются с друзьями в клубах а на природу не ездят вообще, 6 – отдыхают сразу везде, и 11- проводят дома у телевизора. Сколько людей посещают развлекательные учреждения?
На 3 курсе факультета обучается 81 студент. Многие из них выбрали одинаковые дисциплины, посещают одни и те же лекции и хорошо знают друг друга. 43 студента посещают лекции по философии, 32 — по логике и 41 — по естествознанию. Философию и логику выбрали 11 человек. Философию и естествознание посещает 21 студент, а логику и естествознание — 16. 4 человека выбрали только философию и логику. Сколько студентов посещают лекции: По всем трем предметам? Только по философии и естествознанию? Только по логике и естествознанию? Только по философии? Только по естествознанию? Только по логике? Не выбрали ни одну из этих дисциплин?
Коллектив фирмы из 47 человек решил весело встретить новый год. 26 человек хотели бы встретить его в ресторане, 15- уехать на дачу, 27 – устроить праздник в офисе фирмы, а 8 – не собирались встречать праздник с коллективом. При этом 9 человек колебались между рестораном и дачей, 6 – между рестораном и офисом, 3 – между офисом и дачей. Сколько человек были готовы встретить праздник где угодно, но с коллективом? (1)
В туристическую фирму обратилось за месяц 70 человек. 34 из них заказали путевки в Россию, 30 — в Турцию, 21- на Кипр, а 8 – в другие страны. Известно, что и в России и на Кипре успело отдохнуть 9 человек, в России и в Турции -11 человек, в Турции и на Кипре -7 человек. Сколько клиентов ухитрилось съездить в отпуск и на Кипр и в Турцию и еще успеть отдохнуть в России.
В кружок по рисованию ходят 11 первоклассников, по пению — 14, по труду -9. известно, что на рисование и пение ходят 4 человека, на рисование и труды – 3, на труды и пение – 3. Сколько человек ходят сразу в три кружка, если в классе 27 человек и двое не посещают никаких кружков
Начало формы
infourok.ru
Решение задач с помощью кругов Эйлера
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
Решение задачи №1

Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б,В).
Из условия задачи следует:
Торты │Пироги = А+Б+В = 12000
Торты & Пироги = Б = 6500
Пироги = Б+В = 7700
Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.
Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300
Сектор А равен 4300, следовательно
Торты = А+Б = 4300+6500 = 10800
Задача №2
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросу Выпечка?
Считается, что все запросы выполнялись практически одновременно, так что набор страниц, содержащих все искомые слова, не изменялся за время выполнения запросов.Решение задачи №2

Для решения задачи отобразим множестваПироженых и Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б,В).
Из условия задачи следует:
Пироженое & Выпечка = Б = 5100
Пироженое = А+Б = 9700
Пироженое │ Выпечка = А+Б+В = 14200
Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти сектор В, для этого из общего множества (Пироженое │ Выпечка ) отнимем множествоПироженое.
Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500Сектор В равен 4500, следовательно Выпечка = Б + В = 4300+5100 = 9400
Задача №3
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | спаниели | (терьеры & овчарки) |
| 2 | спаниели | овчарки |
| 3 | спаниели | терьеры | овчарки |
| 4 | терьеры | овчарки |
Решение задачи №3

Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
спаниели │(терьеры & овчарки) = Г + Б
спаниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
терьеры & овчарки = Б
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4
Задача №4
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | барокко | классицизм | ампир |
| 2 | барокко | классицизм & ампир |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Решение задачи №4
 Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Представим множества классицизм, ампир и классицизм в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Гбарокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1
Задача №5В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | канарейки | терьеры | содержание |
| 2 | канарейки & содержание |
| 3 | канарейки & щеглы & содержание |
| 4 | разведение & содержание & канарейки & щеглы |
Решение задачи №5

Для решения задачи представим запросы в виде кругов Эйлера.
K — канарейки,
Щ – щеглы,
С – содержание,
Р – разведение.
Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что правильно решили задачу.
Задачи для самостоятельного решения
Задача №6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | принтеры & сканеры & продажа |
| 2 | принтеры & продажа |
| 3 | принтеры | продажа |
| 4 | принтеры | сканеры | продажа |
Задача №7
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | физкультура |
| 2 | физкультура & подтягивания & отжимания |
| 3 | физкультура & подтягивания |
| 4 | физкультура | фитнесс |
oge-gia.blogspot.com
Шинкаренко Евгений Александрович — Решение задач ЕГЭ с помощью кругов Эйлера
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
Решение задачи №1
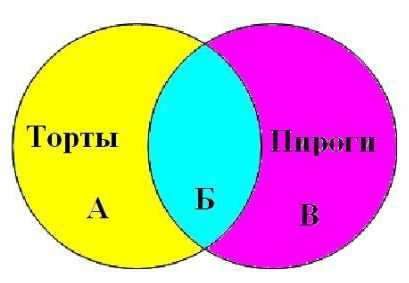
Для решения задачи отобразим множества Тортов и Пирогов в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Торты │Пироги = А+Б+В = 12000
Торты & Пироги = Б = 6500
Пироги = Б+В = 7700
Чтобы найти количество Тортов (Торты = А+Б), надо найти сектор А, для этого из общего множества (Торты│Пироги) отнимем множество Пироги.
Торты│Пироги – Пироги = А+Б+В-(Б+В) = А = 1200 – 7700 = 4300
Сектор А равен 4300, следовательно
Торты = А+Б = 4300+6500 = 10800
Задача №2
В языке запросов поискового сервера для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| Запрос | Найдено страниц (в тысячах) |
| Пироженое & Выпечка | 5100 |
| Пироженое | 9700 |
| Пироженое | Выпечка | 14200 |
Какое количество страниц (в тысячах) будет найдено по запросу Выпечка?
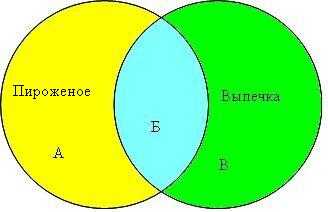
Для решения задачи отобразим множества Пироженых и Выпечек в виде кругов Эйлера.
Обозначим каждый сектор отдельной буквой (А, Б, В).
Из условия задачи следует:
Пироженое & Выпечка = Б = 5100
Пироженое = А+Б = 9700
Пироженое │ Выпечка = А+Б+В = 14200
Чтобы найти количество Выпечки (Выпечка = Б+В), надо найти сектор В, для этого из общего множества (Пироженое │ Выпечка ) отнимем множество Пироженое.
Пироженое │ Выпечка – Пироженное = А+Б+В-(А+Б) = В = 14200–9700 = 4500Сектор В равен 4500, следовательно Выпечка = Б + В = 4300+5100 = 9400
Задача №3
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке убывания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | спаниели | (терьеры & овчарки) |
| 2 | спаниели | овчарки |
| 3 | спаниели | терьеры | овчарки |
| 4 | терьеры | овчарки |
Решение задачи №3
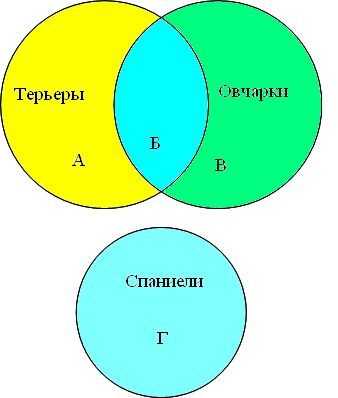
Представим множества овчарок, терьеров и спаниелей в виде кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
спаниели │(терьеры & овчарки) = Г + Б
спаниели│овчарки = Г + Б + В
спаниели│терьеры│овчарки = А + Б + В + Г
терьеры & овчарки = Б
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке убывания количества страниц: 3 2 1 4
Задача №4
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | барокко | классицизм | ампир |
| 2 | барокко | классицизм & ампир |
| 3 | классицизм & ампир |
| 4 | барокко | классицизм |
Решение задачи №4
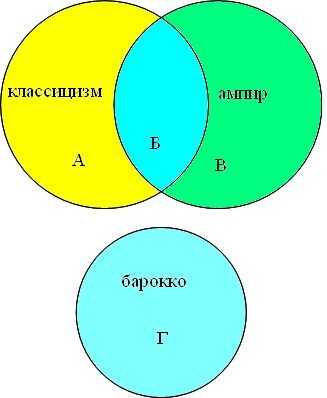 Представим множества классицизм, ампир и классицизм в виде
кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Представим множества классицизм, ампир и классицизм в виде
кругов Эйлера, обозначим сектора буквами (А, Б, В, Г).
Преобразим условие задачи в виде суммы секторов:
барокко│ классицизм │ампир = А + Б + В + Гбарокко │(классицизм & ампир) = Г + Б
классицизм & ампир = Б
барокко│ классицизм = Г + Б + А
Из сумм секторов мы видим какой запрос выдал больше количества страниц.
Расположим номера запросов в порядке возрастания количества страниц: 3 2 4 1
Задача №5
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возврастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | канарейки | терьеры | содержание |
| 2 | канарейки & содержание |
| 3 | канарейки & щеглы & содержание |
| 4 | разведение & содержание & канарейки & щеглы |
Решение задачи №5
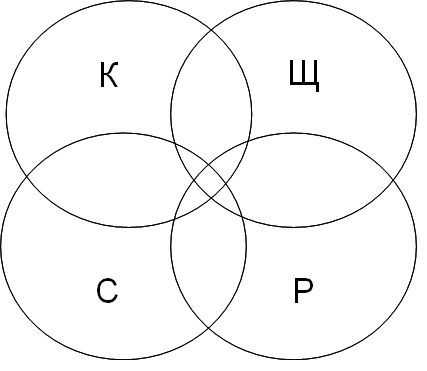
Для решения задачи представим запросы в виде кругов Эйлера.
K — канарейки,
Щ – щеглы,
С – содержание,
Р – разведение.
Далее будем закрашивать красным цветом сектора согласно запросам, наибольший по величине сектор даст большее количество страниц на запрос.
канарейки | терьеры | содержание канарейки & содержание канарейки & щеглы & содержание разведение & содержание & канарейки & щеглы 



Самая большая область закрашенных секторов у первого запроса, затем у второго, затем у третьего, а у четвертого запроса самый маленький.
В порядке возрастания по количеству страниц запросы будут представлены в следующем порядке: 4 3 2 1
Обратите внимание что в первом запросе закрашенные сектора кругов Эйлера содержат в себе закрашенные сектора второго запроса, а закрашенные сектора второго запроса содержат закрашенные сектора третьего запроса, закрашенные сектора третьего запроса содержат закрашенный сектор четвертого запроса.
Только при таких условиях мы можем быть уверены, что
правильно решили задачу.
Задачи для самостоятельного решения
Задача №6
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | принтеры & сканеры & продажа |
| 2 | принтеры & продажа |
| 3 | принтеры | продажа |
| 4 | принтеры | сканеры | продажа |
Задача №7
В таблице приведены запросы к поисковому серверу. Расположите номера запросов в порядке возрастания количества страниц, которые найдет поисковый сервер по каждому запросу.
Для обозначения логической операции «ИЛИ» используется символ «|», а для логической операции «И» — символ «&».
| 1 | физкультура |
| 2 | физкультура & подтягивания & отжимания |
| 3 | физкультура & подтягивания |
| 4 | физкультура | фитнесс |
Ответы к задачам для самостоятельного решения
| Номер задачи | Ответ |
| 6 | ГБВА |
| 7 | БВАГ |
shinkarenkoea.ucoz.ru
