Системы линейных неравенств и выпуклые множества точек
Неравенство — это два числа или математических выражения, соединённых одним из знаков: > (больше, в случае строгих неравенств), < (меньше, в случае строгих неравенств), ≥ (больше или равно, в случае нестрогих неравенств), ≤ (меньше или равно, в случае нестрогих неравенств).
Неравенство является линейным при тех же условиях, что и уравнение: оно содержит переменные только в первой степени и не содержит произведений переменных.
Решение линейных неравенств и систем линейных неравенств неразрывно связано
с их геометрическим смыслом: решением линейного неравенства является некоторая полуплоскость,
на которые всю плоскость делит прямая, уравнением которой задано линейное неравенство. Эту
полуплоскость, а в случае системы линейных неравенств — часть плоскости, ограниченную
несколькими прямыми, требуется найти на чертеже.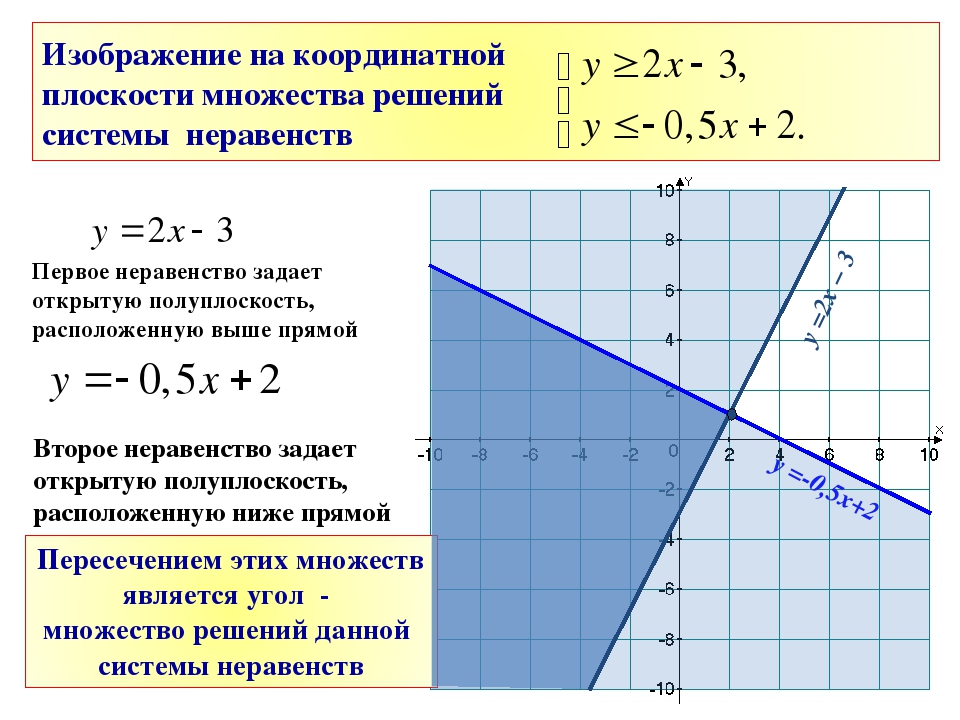
К решению систем линейных неравенств с большим числом переменных сводятся многие экономические задачи, в частности, задачи линейного программирования, в которых требуется найти максимум или минимум функции.
Одно неравенство с двумя неизвестными, так же как и уравнение, имеет бесчисленное множество решений. Решением данного неравенства назовём пару чисел , удовлетворяющих этому неравенству. Геометрически множество решений неравенства изображается в виде полуплоскости, ограниченной прямой
,
которую назовём граничной прямой.
Шаг 1. Построить прямую, ограничивающую множество решений линейного неравенства
Для этого надо знать какие-либо две точки этой прямой. Найдём точки
пересечения с осями координат. Ордината точки пересечения A равна нулю (рисунок 1).
Числовые значения на осях на этом рисунке относятся к примеру 1, который разберём сразу
после этого теретического экскурса.
Абсциссу найдём, решая как систему уравнение прямой с уравнением оси .
Найдём пересечение с осью :
Подставляя значение в первое уравнение, получаем
, откуда .
Таким образом, нашли абсциссу точки A .
Найдём координаты точки пересечения с осью .
Абсцисса точки B равна нулю. Решим уравнение граничной прямой с уравнением оси координат:
Решение:
,
следовательно, координаты точки
Шаг 2. Начертить прямую, ограничивающую множество решений неравенства. Зная точки A и B пересечения граничной прямой с осями
координат, можем начертить эту прямую. Прямая (снова рисунок 1) делит всю плоскость на две
части, лежащие справа и слева (выше и ниже) от этой прямой.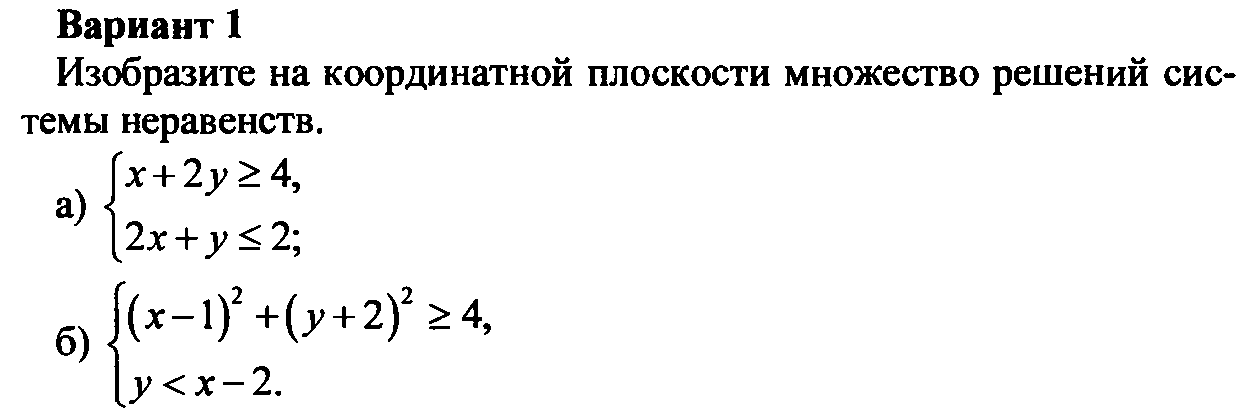
Шаг 3. Установить, которая из полуплоскостей является решением данного неравенства. Для этого нужно в это неравенство подставить начало координат (0; 0). Если координаты начала удовлетворяют неравенству, то решением неравенства является полуплоскость, в которой находится начало координат. Если же координаты не удовлетворяют неравенству, то решением неравенства является полуплоскость, которая не содержит начала координат. Полуплоскость решения неравенства будем обозначать штрихами от прямой внутрь полуплоскости, как на рисунке 1.
Если решаем систему линейных неравенств, то каждый шаг выполняется для каждого из неравенств системы.
Пример 1. Решить неравенство
Решение. Начертим прямую
Подставив в уравнение прямой ,
получим , а
подставив ,
получим . Следовательно, координаты точек пересечения с осями будут A(3; 0),
B(0; 2). Через эти точки проведём прямую (опять рисунок 1).
Следовательно, координаты точек пересечения с осями будут A(3; 0),
B(0; 2). Через эти точки проведём прямую (опять рисунок 1).
Выберем полуплоскость решений неравенства. Для этого в неравенство подставим координаты начала (0; 0):
,
получим , т. е. координаты начала удовлетворяют данному неравенству. Следовательно, решением неравенства является полуплоскость, содержащая в себе начало координат, т. е. левая (она же нижняя) полуплоскость.
Если бы данное неравенство было строгим, то есть имело бы вид
,
то точки граничной прямой не являлись бы решением, так как они не удовлетворяют неравенству.
Теперь рассмотрим систему линейных неравенств с двумя неизвестными:
Каждое из неравенств этой системы на плоскости определяет полуплоскость. Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и
несовместной, если она не имеет решений. Решением системы линейных неравенств называется
любая пара чисел (),
удовлетворяющая всем неравенствам данной системы.
Система линейных неравенств называется совместной, если она имеет хотя бы одно решение, и
несовместной, если она не имеет решений. Решением системы линейных неравенств называется
любая пара чисел (),
удовлетворяющая всем неравенствам данной системы.
Пример 2. Решить систему линейных неравенств
Решение. Итак, требуется найти многоугольник решений этой системы неравенств. Построим граничную прямую для первого неравенства, то есть прямую ,
и граничную прямую для второго неравенства, то есть прямую .
Построим граничную прямую для первого неравенства, то есть прямую ,
и граничную прямую для второго неравенства, то есть прямую .
Делаем это пошагово, как было показано в теоретической справке и в примере 1, тем более, что в примере 1 строили граничную прямую для неравенства, которое является первым в данной системе.
Полуплоскости решений, соответствующие неравенствам данной системы, на рисунке 2 заштрихованы вовнутрь. Общая часть полуплоскостей решений представляет собой открытый угол ABC. Это означает, что множество точек плоскости, составляющих открытый угол ABC, является решением как первого, так и второго неравенства системы, то есть, является решением системы двух линейных неравенств. Иначе говоря, кординаты любой точки из этого множества удовлетворяют обоим неравенствам системы.
Пример 3. Решить систему линейных неравенств
Решение. Построим граничные прямые, соответствующие неравенствам системы.
Делаем это, выполняя шаги, данные в теоретической справке, для каждого неравенства. Теперь
определим полуплоскости решений для каждого неравенства (рисунок 3).
Построим граничные прямые, соответствующие неравенствам системы.
Делаем это, выполняя шаги, данные в теоретической справке, для каждого неравенства. Теперь
определим полуплоскости решений для каждого неравенства (рисунок 3).
Полуплоскости решений, соответствующие неравенствам данной системы, заштрихованы вовнутрь. Пересечение полуплоскостей решений изображается, как показано на рисунке, в виде четырёхугольника ABCE. Получили, что многоугольник решений системы линейных неравенств с двумя переменными является четырёхугольником ABCE.
Всё описанное выше о системах линейных неравенств с двумя неизвестными
относится и к системе неравенств с любым числом неизвестных, с той лишь разницей, что решением
неравенства с n неизвестными будет совокупность n чисел (),
удовлетворяющих всем неравенствам, а вместо граничной прямой будет граничная гиперплоскость
n-мерного пространства.
Так же, как и в двухмерном пространстве (на плоскости), каждое из неравенств системы определяет n-мерное полупространство. Пересечение всех этих полупространств образует многогранник решений. Но изобразить этот многогранник (называемый симплексом) геометрически невозможно. Лишь в случае, когда число неизвестных не больше трёх, то есть в действительном пространстве, многогранник решений можно изобразить геометрически.
Множество решений линейных неравенств геометрически составляет выпуклый многогранник или выпуклое множество точек.
Как уже отмечалось, системы линейных неравенств играют важную роль в линейном программировании. Теоремы линейного программирования содержат такие понятия, как выпуклые множества и крайние точки. Разберёмся бегло, о чём речь.
Множество точек называется выпуклым, если вместе с его любыми двумя
точками ему принадлежит и весь отрезок, соединяющий их. Если же существует хотя бы такая
пара точек множества, что отрезок, соединяющий эти точки, не принадлежит целиком этому
множеству, то такое множество называется невыпуклым. На рисунке 4 слева изображено
выпуклое множество, а справа — невыпуклое.
Если же существует хотя бы такая
пара точек множества, что отрезок, соединяющий эти точки, не принадлежит целиком этому
множеству, то такое множество называется невыпуклым. На рисунке 4 слева изображено
выпуклое множество, а справа — невыпуклое.
Выпуклые множества обладают важным свойством, которое устанавливается следующей теоремой.
Теорема. Пересечение двух выпуклых множеств — также выпуклое множество.
Через любую внутреннюю точку выпуклого множества можно провести отрезок, для которого она является внутренней, а сам отрезок целиком принадлежит этому множеству. Но есть точки (для выпуклого многоугольника это его вершины), для которых такое построение выполнить нельзя: нет ни одного отрезка, для которого вершина являлась бы внутренней, а отрезок целиком бы принадлежал мноргоугольнику.
Точка выпуклого множества называется угловой (или крайней), если через
неё нельзя провести ни одного отрезка, состоящего только из точек данного множества и для
которого она была бы внутренней.
Продолжение темы «Систем уравнений и неравенств»
Начало темы «Линейная алгебра»
Поделиться с друзьями
Решение задач по математике
Каталог примеров
- Категория: PHP
- Категория: Алгебраические преобразования, уравнения, неравенства
- Как упростить выражение с дробями на тестах по математике
- Решение дробно-рационального уравнения высшей степени методом замены переменной
- Решение неравенств онлайн, пример с высшими степенями
- Решение неравенства с многочленами высших степеней.
- Решение системы неравенств
- Решение уравнения с двумя параметрами
- Решить неравенство, содержащее кубическую функцию.
- Упростить выражение, примеры. Упростить выражение с дробными функциями
- Упростить выражение наиболее оптимальным способом
- Решение системы неравенств с тремя неравенствами, содержащими квадратичную и кубическую функции
- Возведение одночленов в степень
- Деление простейших рациональных дробей со знаменателями-одночленами высших степеней.

- Докажите, что при любых любых значениях истинны неравенства
- Иррациональные уравнения примеры.
- Использование формулы разности кубов при упрощении выражений
- Исследование функции онлайн 4 степени
- Исследование функции онлайн с квадратичной функцией в числителе и знаменателе
- Исследование функции онлайн, содержащей квадратичную функцию в числителе и знаменателе.
- Исследование функции онлайн, функции третьей , четвертой степени
- Исследование функции с квадратичной функцией в числителе и линейной в знаменателе
- Исследовать полином шестой степени и построить ее график
- исследовать функцию второй степени и построить ее график
- Исследуем функцию в знаменетеле которой произведение линейных функций
- Как решать кубические уравнения
- Как решить неравенство с дробями
- Нахождение множества решений неравенства
- Необходимо упростить выражение.
- Необходимо построить график графики функций, заданную вот такой формулой
- Нестандартные способы решения решение квадратных уравнений.
 Метод замены
Метод замены - Построить график функции заданной формулой
- Построить график функции, провести ее полное исследование
- Пример на упрощение выражений
- Пример на упрощение выражения
- Пример на упрощение выражения
- Пример решения дробно рациональных уравнений
- Примеры как решать биквадратные уравнения
- примеры построения графиков
- Примеры решения системы линейных уравнений.
- Провести полное исследование и построить график функции седьмой степени
- Разложение многочлена на множители
- Разложение многочленов на множители. Применение различных способов
- разложить на множители
- Решаем неравенств, имеющих в левой левой части дробное выражение с квадратичными функциями
- Решаем неравенство с четвертой степенью интервалов
- Решение иррациональных уравнений с переменной z
- Решение биквадратного уравнения методом замены
- Решение биквадратного уравнения методом замены переменной
- Решение биквадратного уравнения методом замены переменной
- Решение биквадратных уравнений онлайн
- Решение биквадратных уравнений онлайн
- Решение двойного неравенства онлайн с модулем в числителе и знаменателе
- Решение двойных неравенств на тестах по математике
- решение дробно-рациональных выражений, приводящих к квадратным
- Решение дробно-рациональных уравнений с параметрами
- Решение дробно-рациональных уравнений, сводящихся к квадратным
- Решение задач на округление с недостатком
- Решение иррациональное уравнение с параметрами.

- Решение иррациональных уравнений, содержащих кубический корень.
- Решение квадратичного неравенства с модулем
- Решение квадратичных неравенств онлайн с модулем
- Решение квадратного уравнения с квадратичными многочленами в числителе и знаменателе
- Решение квадратных уравнений методом замены переменной
- Решение квадратных уравнений по формуле дискриминанта
- Решение квадратных уравнений с квадратным трехчленом в числителе и знаменателе
- Решение квадратных уравнений с модулями
- Решение квадратных уравнений с преобразованием левой и правой части уравнения.
- Решение квадратных уравнений, содержащих алгебраические преобразования.
- Решение линейных неравенств онлайн с модулем в знаменателе
- Решение линейных неравенств с дробными выражениями
- решение линейных неравенств, содержащих модуль
- Решение линейных уравнений с дробями в левой и правой части
- Решение на тестах по математике неравенств онлайн, содержащих модуль
- Решение на тестах по математике неравенств содержащих модуль и кубическую функцию в правой части
- Решение неравенств c кубическими степенями
- Решение неравенств онлайн с дробями наиболее оптимальным способом
- Решение неравенств высших степеней онлайн .

- Решение неравенств онлайн методом замены переменных
- Решение неравенств онлайн на тестах по математике, имеющих очень большую степень
- Решение неравенств онлайн с двумя квадратичными функциями в знаменателе
- Решение неравенств онлайн с квадратичными функциями в знаменателе дроби
- Решение неравенств онлайн со сложными дробно-рациональными дробями
- Решение неравенств онлайн, содержащих в числителе и знаменателе произведение квадратных трехчленов
- Решение неравенств онлайн, содержащих многочлен четвертой степени в левой части
- Решение неравенств онлайн, содержащих модуль в знаменателе и квадратичную функцию в числителе
- Решение неравенств онлайн, содержащих модуль.
- Решение неравенств онлайн, содержащих произведение квадратичных функций
- Решение неравенств онлайн, содержащих произведение функций в левой части и линейную функцию в правой
- Решение неравенств онлайн, содержащих разность дробей
- Решение неравенств онлайн.
 Дробно-рациональное неравенство
Дробно-рациональное неравенство - Решение неравенств онлайн. Применение группировки для решения неравенств
- Решение неравенств онлайн. Решение квадратичных неравенств.
- Решение неравенств с выносом за скобки многочлена
- Решение неравенств с квадратичной функцией под модулем.
- Решение неравенств с квадратичной функцией в числителе и знаменателе
- Решение неравенств с квадратичной функцией в числителе и знаменателе.
- Решение неравенств с линейной функцией в правой части
- Решение неравенств с линейными и квадратичными функциями в знаменателе
- Решение неравенств с линейными функциями в модулях
- Решение неравенств с многочленом пятой степени
- Решение неравенств с модулем в знаменателе.
- Решение неравенств с модулем. Квадратичная функция в модуле.
- Решение неравенств с применением разности кубов
- Решение неравенств с применением формул сокращенного умножения
- Решение неравенств с применением формулы разности квадратов
- Решение неравенств с произведением многочленов в числителе и знаменателе
- Решение неравенств с произведением квадратичных функций в числителе и знаменателе
- Решение неравенств содержащих параметр
- Решение неравенств третьей степени онлайн методом замены
- Решение неравенств четвертой степени заменой
- Решение неравенств, содержащих куб суммы
- Решение неравенств, содержащих линейные функции в числителе дроби в левой части
- Решение неравенства 3 степени
- Решение неравенства онлайн с квадратичной функцией под модулем в левой части и линейной под модулем в правой
- Решение неравенства онлайн с модулем и квадратичной функцией в левой части
- Решение неравенства онлайн.
 Пример, в котором нужно решить систему
Пример, в котором нужно решить систему - Решение неравенства с 4 квадратичными функциями
- Решение неравенства с двумя модулями
- Решение неравенства с квадратичной функцией под модулем.
- Решение неравенства с модулем
- Решение неравенства с модулем
- Решение неравенства с модулем в знаменателе
- Решение неравенства с модулем квадратичной функциии в знаменателе
- Решение неравенства с модулями и дробями
- Решение неравенства с одинаковой квадратичной функцией
- Решение неравенства, содержащего произведение многочленов в числителе и знаменателе
- Решение нескольких линейных уравнений с параметром и модулем
- Решение показательных уравнений онлайн с применением свойств степеней с рациональным показателем и свойств показательной функции
- Решение показательных уравнений онлайн.
- Решение показательных уравнений с линейными функциями в степенях
- Решение примеров с отрицательными степенями
- Решение примеров с упрощением радикалов на тестах по математике
- Решение рациональных уравнений, сводящихся к квадратным
- Решение систем квадратных неравенств
- Решение систем линейных неравенств
- Решение систем линейных уравнений второй степени методом выражения неизвестной
- Решение систем линейных уравнений с двойными неравенствами
- Решение систем линейных уравнений с дробными коэффициентами
- Решение систем линейных уравнений с модулями
- Решение систем неравенств
- Решение систем неравенств на тестах по математике
- Решение систем неравенств онлайн на тестах по математике
- Решение систем неравенств онлайн с квадратичными функциями
- Решение систем неравенств с квадратичными функциями
- Решение систем уравнений , в которой одна из переменных в квадрате
- Решение систем уравнений с 3 неизвестными
- Решение систем уравнений с 4 неизвестными
- Решение систем уравнений с дробями повышенного уровня сложности
- Решение систем уравнений с переменными с высшими степенями
- Решение систем уравнений с произведением многочленов
- Решение систем уравнений с суммой и произведением неизвестных
- Решение систем уравнений уравнений с x и у в числителе дроби
- Решение системы линейных уравнений
- Решение системы неравенств c линейными функциями в каждом неравенстве
- Решение системы неравенств онлайн
- Решение системы неравенств онлайн с квадратичными функциями
- Решение системы неравенств, содержащее кубическое неравентсво
- Решение сложного дробно-рационального уравнения
- Решение сложного неравенства с применением формул сокращенного умножения
- Решение сложных дробно-рациональных неравенств
- Решение сложных квадратных уравнений онлайн
- решение сложных неравенств
- Решение уравнений высших степеней с дробями
- Решение уравнений методом замены переменной
- Решение уравнений онлайн с большим числом многочленов
- Решение уравнений онлайн с квадратичной функцией в знаменателе под знаком модуля
- Решение уравнений с двумя множителями, в которых стоят квадратичные функции
- Решение уравнений с модулем и параметром
- Решение уравнений с параметрами
- Решение уравнений третьей степени с дробной частью
- Решение уравнений, сводящихся к квадратным
- Решение уравнений, сводящихся к квадратным применением свойств сокращенного умножения.

- Решение уравнения с заменой переменных
- Решении неравенств методом подбора
- Решения задач на свойства степеней
- Решить неравенство онлайн методом интервалов,применив при этом метод группировки слагаемых.
- Решить биквадратное уравнение.
- Решить дробно-рациональное кубическое уравнение наиболее оптимальным способом.
- Решить Дробно-рациональное неравенство онлайн
- Решить дробно-рациональное уравнение высшей степени с дробями.
- Решить квадратное уравнение наиболее оптимальным способом.
- Решить линейное неравенство, содержащее дроби в обеих частях
- Решить неравенство онлайн наиболее оптимальным способом
- Решить неравенство с дробями
- Решить неравенство высших степеней методом интервалов
- Решить неравенство онлайн наиболее оптимальным методом
- Решить неравенство онлайн с многочленом третьей степени
- Решить неравенство онлайн, содержащее произведение многочленов
- Решить неравенство онлайн, содержащее высшие степени
- Решить неравенство онлайн, содержащее высшие степени
- Решить неравенство онлайн, содержащее дробно-рациональные выражения
- Решить неравенство онлайн, содержащее модуль.

- Решить неравенство онлайн, содержащее произведение многочленов высших степеней.
- Решить неравенство онлайн, содержащее произведение многочленов
- Решить неравенство онлайн, содержащее сумму дробно-рациональных функций
- Решить неравенство онлайн. Квадратичная функция.
- Решить неравенство онлайн. Неравенство высших степеней.
- Решить неравенство онлайн. Дробно-рациональные функции
- Решить неравенство оптимальным способом
- Решить неравенство с модулем
- Решить неравенство, содержащее высокую степень, методом интервалов
- Решить неравенство, содержащее дробно-рациональную функцию
- Решить неравенство, содержащее дробно-рациональные выражения в левой и правой части
- Решить неравенство, содержащее произведение кубической и квадратной функций.
- Решить неравенство, содержащее произведение многочленов.
- Решить неравенство, содержащее произведении многочленов
- Решить неравенство, содержащую высшую степень методом интервалов
- Решить систему неравенств наиболее оптимальным способом.

- Решить систему неравенств с модулями
- Решить систему неравенств, содержащую неравенства второй степени
- Решить систему неравенств.
- Решить систему неравенств.
- Решить систему уравнений с тремя неизвестными методом выражения неизвестной величины
- Решить систему уравнений, выразив x,y,z через u и v.
- Решить уравнение высшей степени
- Решить уравнение высшей степени, используя метод замены переменных
- Решить уравнение онлайн, используя замену переменной
- Решить уравнение онлайн, содержащее в левой и правой части дробно-рациональные выражения с квадратичными функциями.
- Решить уравнение онлайн, содержащее выражения под знаком модуля в левой и правой части уравнения
- Решить уравнение четвертой степени, используя группировку и вынесение общего множителя
- Тождественное преобразование рациональных выражений с использованием формулы разницы квадратов
- Тождественные преобразования рациональных выражений
- Упросить выражение оптимальным способом
- Упростить выражение примеры
- Упростить выражение примеры.
 Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с одинаковыми знаменателями - Упростить выражение примеры. Упрощение дробно-рациональных выражений.
- Упростить выражение с дробями.
- Упростить выражение с помощью преобразований
- Упростить выражение типичные примеры для тестов по математике
- Упростить выражение, содержащее дробные выражения
- Упрощение выражение с радикалами
- Упрощение выражений на тестах по математике доказательство с использованием тождественных преобразований.
- Упрощение выражений на тестах по математике. Сложение и вычитание дробей с разными знаменателями. Простейшие примеры
- Упрощение выражений при умножении рациональных дробей
- Упрощение выражений с корнями
- Упрощение выражений с кубическими корнями
- Упрощение выражений с многоэтажными дробями
- Упрощение выражений с помощью разности квадратов
- Упрощение выражений с помощью формул квадрата суммы.
- Упрощение выражений с помощью формулы разности квадратов
- Упрощение выражений с помощью формулы умножения дробей
- Упрощение выражений с применением формул разложения квадратного трехчлена на множители
- Упрощение выражений с применением формулы суммы кубов и куб разности
- Упрощение выражений с радикалами.

- Упрощение выражений с тремя действиями
- Упрощение выражений, возведение рационального выражения в степень.
- Упрощение выражений, сложение рациональных дробей с многочленами в знаменателе
- Упрощение выражений, содержащих деление многочленов
- Упрощение выражений, содержащих деление рациональных дробей
- Упрощение выражений, содержащих степень с рациональным показателем
- Упрощение выражений, содержащих умножение дробей с квадратичными функциями
- Упрощение выражения, содержащего операции деления
- Категория: Другое
- Категория: Логарифмические, показательные уравнения , неравенства
- Категория: Начала анализа
- Задача на нахождение числа касательных.
- Исследование и построение графика функции четвертой степени
- Исследование функции онлайн, содержащей многочлен пятой степени в числителе и седьмой в знаменателе.
- Исследование графика функции с многочленом четвертой степени в знаменателе
- Исследование дробно-рациональной функции и построения ее графика
- Исследование дробной функции и построение ее графика
- Исследование онлайн функции с кубом в знаменателе
- Исследование рациональной функции и с построение ее графика
- Исследование функции десятой степени
- Исследование функции онлайн с кубической функцией в числителе
- Исследование функции онлайн с числителем шестой степени
- Исследование функции онлайн, заданной частным квадратичной и кубичной функций
- Исследование функции пятой степени
- Исследование функции с линейной функцией в числителе и знаменателе
- Исследование функции с многочленом шестой степени в числителе
- Исследование функции с числителем пятой степени
- Исследовать график дробно-линейной функции и правильно построить график
- Исследовать функцию 4 степени и построить график
- Исследовать функцию высших степеней и построить ее график
- Исследовать функцию и построить ее график
- Исследовать функцию и построить ее график онлайн.

- Исследуем онлайн функцию, заданную многочленом четвертой степени в числителе
- Исследуем функцию, в которой в знаменателе произведение квадратичных функций
- Исследуем функцию, заданную многочленом четвертой степени
- на исследование функций
- Найти значение производной в точке
- Нахождение производной сложной функции и построение её графика
- Полное исследование сложной функции и построение ее графика
- Построение график функции с кубом в числителе и знаменателе
- Построение графика дробно-линейной функции
- Построение графика кубической функции
- Построение графика с квадратичными функциями в числителе и знаменателе
- Построение графика с кубической функцией в числителе и линейной в знаменателе
- Построение графика с функцией шестой степени в числителе
- Построение графика функции с полным исследованием
- Построение графика функции с квадратичной функцией в числителе и линейной в знаменателе
- Построение графика функции с многочленом пятой степени в знаменателе
- Построение графика функции, в знаменателе которой многочлен пятой степени
- Построение графиков на тестах по математике
- Построение графиков функций онлайн.
 Нахождение производной в точке
Нахождение производной в точке - Построить график функции и провести ее полное исследование. Функция дробно-рациональная
- Построить график дробной-линейной функции и провести ее полное исследование.
- Построить график квадратичной функции методом полного исследования
- Построить график кубической функции
- Построить график кубической функции, проведя ее полное исследование
- Построить график функции дробной функции, содержащей функцию четвертой степени в знаменателе, проведя полное исследование.
- Построить график функции и провести ее полное исследование
- Построить график функции онлайн, заданной следующей формулой
- Построить график функции пятой степени
- Построить график функции, содержащей дроби.
- Построить и исследовать график функции, заданной такой формулой.
- Провести исследование функции и построить ее график
- Провести исследование функции и построить ее график.
- Провести полное исследование функции .
 После этой исследования построить ее график.
После этой исследования построить ее график. - Производная дроби примеры
- Укажите график нечетной функции
- Категория: Планиметрия
- Категория: Прогрессии
- Категория: Стереометрия
- Категория: Текстовые задачи
- Категория: Тригонометрия
- Категория: Числа и выражения
Каждый год выпускники стараются успешно завершить обучение и успешно сдать вступительные экзамены, чтобы поступить в высшие учебные заведения и стать студентами.
Многие ищут решение задач по математике, чтобы к этому подготовиться.
В данный момент аттестация проводится в форме внешнего независимого
оценивания (ЗНО). Результат тестов по математике засчитывается как балл государственной итоговой
аттестации (ДПА) . Выпускникам, которые прошли ЕГЭ по математике, алгебре, геометрии выдается сертификат
с его результатами, в соответствии с которым вносится соответствующая запись в дополнение к аттестату.
Чтобы набрать необходимое количество баллов недостаточно формально овладеть школьным материалом –
необходимы углубленные знания, практика в решении задач, умение правильно и четко изложить на бумаге
решение задачи, сопровождая его необходимыми схемами, рисунками, формулами.
Выпускникам, которые прошли ЕГЭ по математике, алгебре, геометрии выдается сертификат
с его результатами, в соответствии с которым вносится соответствующая запись в дополнение к аттестату.
Чтобы набрать необходимое количество баллов недостаточно формально овладеть школьным материалом –
необходимы углубленные знания, практика в решении задач, умение правильно и четко изложить на бумаге
решение задачи, сопровождая его необходимыми схемами, рисунками, формулами.
Этот сайт с решениями задач по математике поможет в комплексной подготовке абитуриента к независимому внешнему тестированию по математике. Он решит с вами задачи, которые в разное время предлагались для решения школьникам и абитуриентам при поступлении в высшие учебные заведения.
Разбор задач , уроки позволят вам успешно сдать непростые экзамены и легко
овладеть такими науками, как алгебра и геометрия. Вы научитесь выполнять алгебраические преобразования,
сможете упростить любое выражение, изучите алгебраические формулы. Вы успешно освоите решение уравнений,
систем уравнений, неравенств, систем неравенств (квадратные, иррациональные, показательные,
логарифмические, тригонометрические).
Вы научитесь выполнять алгебраические преобразования,
сможете упростить любое выражение, изучите алгебраические формулы. Вы успешно освоите решение уравнений,
систем уравнений, неравенств, систем неравенств (квадратные, иррациональные, показательные,
логарифмические, тригонометрические).
Сложности в решение задач на составление уравнений? На сайте приведены решения задач с полным описанием. Геометрия дается сложнее, чем алгебра? На сайте приведены решения задач из разделов планиметрия и стереометрия, разобраны примеры решения на нахождение неизвестных геометрических элементов, площадей фигур, методики доказательств утверждений.
Сайт- хороший помощник при подготовке домашних заданий и подготовке к тестам
Сайт нужен для получения и лучшего усвоения большего количества информации,
более глубоких знаний, а также приобретения навыков по реализации полученных знаний на практике. Специалиста можно найти, обратившись в специальные агентства, поместив объявление в средствах массовой
информации. Однако , попав на этот сайт, вы уже нашли то, что искали. У автора — большой опыт подготовки
к ЗНО по математике, ДПА по математике, ЗНО по физике, ДПА по физике. Вы можете посмотреть отзывы на
соответствующей странице. Все мои ученики успешно сдавали ЗНО с результатом от 180 баллов, а результат
ДПА всегда был не ниже 9. Поэтому вы можете быть уверены в результативности занятий.
Специалиста можно найти, обратившись в специальные агентства, поместив объявление в средствах массовой
информации. Однако , попав на этот сайт, вы уже нашли то, что искали. У автора — большой опыт подготовки
к ЗНО по математике, ДПА по математике, ЗНО по физике, ДПА по физике. Вы можете посмотреть отзывы на
соответствующей странице. Все мои ученики успешно сдавали ЗНО с результатом от 180 баллов, а результат
ДПА всегда был не ниже 9. Поэтому вы можете быть уверены в результативности занятий.
Примеры решения нелинейных систем неравенств с двумя переменными
Примеры с решениями
Пример №323.Изобразить на координатной плоскости
фигуру , заданную системой неравенств, и найти площадь этой фигуры.Решение:
а) Неравенство
задает множество точек, лежащих внутри окружности с центром в начале координат и радиусом 2 (рис. 27.1), а неравенство — множество точек, расположенных выше прямой
27.1), а неравенство — множество точек, расположенных выше прямойЭта прямая пересекает окружность в точках
и а фигура представляет собой сегмент (рис. 27.1). Искомая площадь равна разности между площадью четверти круга и площадью треугольникаТак как
тоб) Фигура
— это множество точек, лежащих внутри окружности с центром в точке и радиусом 2, но вне окружности с центром в точке и радиусом 1 (рис. 27.2). Значит, площадь фигуры равнаПример №324.Найти площадь фигуры
, которая задается на координатной плоскости системой неравенствРешение:
Неравенство (1) определяет множество точек, лежащих вне и на границе круга с центром в точке
и радиусом (рис. 27.3).Решив неравенство (2), получим
Поэтому неравенство (2) задает вертикальную полосу, лежащую между прямыми и (включая и точки этих прямых).
Наконец, неравенству (3) удовлетворяют точки множества
, которое состоит из двух острых вертикальных углов, образованных прямыми и (включая и точки этих прямых), так как в точке принадлежащей множеству , левая часть неравенства (3) положительна. Множество заштриховано на рис. 27.3, а указанные прямые обозначены и .Прямая
пересекается с прямыми и в точках и , а прямая пересекается с теми же прямыми в точках Далее, прямая касается окружности так как система уравненийимеет единственное решение
наконец, прямая проходит через центр этой окружности.Итак, фигура
— это трапеция из которой удален полукруг радиуса с центром в точке . Искомая площадьгде
Ответ.
Пример №325.На координатной плоскости рассматривается фигура
, состоящая из всех точек, координаты которых удовлетворяют системе неравенствИзобразить фигуру
и найти ее площадь.
Решение:
Неравенство (5), равносильное неравенству
является верным в тех и только в тех точках плоскости
, которые лежат вне круга радиуса 12 с центром и внутри круга радиуса 25 с центром в точке (рис. 27.4). Неравенство (4) имеет смысл, еслит. е. для точек I и III квадрантов. Считая условие (6) выполненным, рассмотрим два возможных случая:
1) Если
то неравенство (4) является верным. Система неравенств (7) задает множество точек I и III квадрантов, лежащих ниже прямой
2) Если
то неравенство (4) равносильно каждому из неравенств
Условиями (8), (9) определяется множество тех точек I квадранта, которые заключены между прямыми
ии точек III квадранта, которые заключены между прямыми иЗаметим, что прямая
имеет единственную общую точку с окружностью и, следовательно, касается этой окружности. Площадь фигуры равна где —сумма площадей двух секторов (им соответствуют центральные углы и ), a — площадь полукруга радиуса 12.
Площадь фигуры равна где —сумма площадей двух секторов (им соответствуют центральные углы и ), a — площадь полукруга радиуса 12.Ответ.
Пример №326.Найти площадь фигуры
, которая задается на координатной плоскости системой неравенствРешение:
Область определения неравенства (10), а значит, и системы (10), (11) задается условием
т. е.Неравенство (12) определяет область, внешнюю по отношению к кругу с центром в начале координат и радиусом 1 (включая границу круга, рис. 27.5).
Возможны два случая:
1) Если
т. е.то неравенство (10) является верным на множестве
2) Если
т. е.
е.то неравенство (10) равносильно каждому из неравенств
Прямые
и заданные соответственно уравнениямипроходят через точку
Прямая касается окружности в точке так как система уравненийимеет единственное решение
Прямая I2, симметричная прямой относительно оси , касается этой же окружности в точкеВ точке
левая часть неравенства (15) положительна и поэтому указанное неравенство справедливо в двух вертикальных углах с вершиной в точке , содержащих ось .Рассмотрим неравенство (11). Уравнение
задает два луча, выходящие из точки
и пересекающиеся прямые и в точках и Неравенству (11) удовлетворяют точки, находящиеся внутри и на границе углаИтак, множеством точек, удовлетворяющих системе неравенств (10), (11) является фигура
, выделенная штриховкой на рис. 27.5. Ее граница состоит из отрезков и дуги окружности
27.5. Ее граница состоит из отрезков и дуги окружностиПлощадь фигуры
равнагде
—площадь треугольника — площадь треугольника — площадь сектора Здесь(так как
),Ответ.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Решение задач по математике
Возможно вам будут полезны эти страницы:
Алгебра: уроки, тесты, задания.
Алгебра: уроки, тесты, задания.-
Информация о разделе
-
-
Числовые выражения.
 Алгебраические выражения
Алгебраические выражения
-
Математический язык
-
Математические модели реальных ситуаций
-
Линейное уравнение с одной переменной. Алгоритм решения
-
Координатная прямая.
 Числовые промежутки
Числовые промежутки
-
-
-
Координатная плоскость. Координаты точки
-
Линейное уравнение ax + by + c = 0. График линейного уравнения
-
Линейная функция y = kx + m. График линейной функции
-
Линейная функция y = kx, её свойства
-
Взаимное расположение графиков линейных функций
-
-
-
Понятие системы линейных уравнений с двумя переменными
-
Решение систем линейных уравнений.
 Метод подстановки
Метод подстановки
-
Решение систем линейных уравнений. Метод сложения
-
Система линейных уравнений как математическая модель
-
-
-
Понятие степени с натуральным показателем
-
Часто используемые степени
-
Базовые свойства степеней с натуральным показателем
-
Умножение и деление степеней с одинаковыми натуральными показателями
-
Понятие степени с нулевым показателем
-
-
-
Понятие одночлена.
 Приведение одночлена к стандартному виду
Приведение одночлена к стандартному виду
-
Сложение и вычитание подобных одночленов
-
Произведение одночленов и возведение одночлена в степень
-
Деление одночленов
-
-
-
Понятие многочлена.
 Приведение многочлена к стандартному виду
Приведение многочлена к стандартному виду
-
Как складывать и вычитать многочлены
-
Как умножать многочлен на одночлен
-
Как умножать многочлен на многочлен
-
Применение формул сокращённого умножения
-
Как делить многочлен на одночлен
-
-
-
Понятие разложения многочленов на множители
-
Разложение на множители.
 Вынесение общего множителя за скобки
Вынесение общего множителя за скобки
-
Разложение на множители. Способ группировки
-
Разложение на множители. Использование формул сокращённого умножения
-
Разложение на множители. Сочетание различных приёмов
-
Применение разложения на множители для сокращения алгебраических дробей
-
Понятие тождества
-
-
-
Квадратичная функция y = x² и её график
-
Решение уравнений графическим методом
-
Запись функции в виде у = f(x)
-
-
-
Понятие алгебраической дроби
-
Применение основного свойства алгебраической дроби
-
Как складывать и вычитать алгебраические дроби с равными знаменателями
-
Как складывать и вычитать алгебраические дроби с разными знаменателями
-
Как умножать, делить и возводить в степень алгебраические дроби
-
Упрощение рациональных выражений
-
Решение рациональных уравнений
-
-
-
Квадратичная функция y = kx² и её свойства.
 Парабола
Парабола
-
Функция y = k/x и её свойства. Гипербола
-
Как построить график функции у = f(x + l)
-
Как построить график функции у = f(x) + m
-
Как построить график функции y = f(x + l) + m
-
Квадратичная функция y = ax² + bx + c
-
Решение квадратных уравнений с помощью графиков функций
-
-
-
Понятие квадратного корня
-
Функция квадратного корня y = √x, её свойства и график
-
Множество рациональных чисел
-
Базовые свойства квадратных корней
-
Преобразование иррациональных выражений
-
-
-
Какие бывают квадратные уравнения
-
Способы решения квадратных уравнений
-
Решение рационального уравнения, сводящегося к квадратному
-
Использование рациональных уравнений для решения задач
-
Упрощённая формула для решения квадратного уравнения
-
Применение теоремы Виета
-
Решение иррационального уравнения, сводящегося к квадратному
-
-
-
Множества натуральных чисел, целых чисел, рациональных чисел
-
Понятие иррационального числа
-
Множество действительных чисел и её геометрическая модель
-
Модуль действительного числа и его геометрический смысл
-
Приближённые значения по недостатку (по избытку)
-
Понятие степени с отрицательным целым показателем
-
Стандартный вид положительного числа
-
-
-
Понятие числовых промежутков
-
Свойства числовых неравенств.
 Свойства неравенств одинакового смысла
Свойства неравенств одинакового смысла
-
Как решать линейное неравенство
-
Методы решения квадратных неравенств
-
Понятие монотонности функции. Исследование функций на монотонность
-
-
Международная оценка образовательных достижений учащихся (PISA)
-
-
Повторим способы решения линейных и квадратных неравенств
-
Решение рациональных неравенств методом интервалов
-
Множества и подмножества.
 Объединение и пересечение множеств
Объединение и пересечение множеств
-
Системы рациональных неравенств
-
-
-
Понятие системы рациональных уравнений
-
Методы решения систем рациональных уравнений
-
Использование систем рациональных уравнений для решения задач
-
-
-
Определение числовой функции и способы её задания
-
Свойства основных функций
-
Чётные и нечётные функции.
 Определение чётности и нечётности
Определение чётности и нечётности
-
Степенная функция с натуральным показателем
-
Степенная функция с отрицательным целым показателем
-
Функция кубического корня
-
-
-
Понятие числовой последовательности.
 Способы задания последовательностей
Способы задания последовательностей
-
Арифметическая прогрессия. Свойства арифметической прогрессии
-
Геометрическая прогрессия. Свойства геометрической прогрессии
-
-
-
Злементы комбинаторики.
 Комбинаторные задачи
Комбинаторные задачи
-
Элементы статистики. Методы обработки информации
-
Элементы теории вероятности. Нахождение вероятности
-
Относительная частота и статистическая вероятность события
-
-
-
Натуральные числа.
 Повторение
Повторение
-
Рациональные числа. Повторение
-
Иррациональные числа. Повторение
-
-
-
Обратимая и обратная функции
-
Понятие периодической функции (профильный)
-
-
-
Числовая окружность на координатной плоскости
-
Нахождение значений синуса и косинуса, тангенса и котангенса
-
Числовой аргумент тригонометрических функций
-
Угловой аргумент тригонометрических функций
-
Свойства функции y = sin x и её график
-
Свойства функции y = cos x и её график
-
Периодичность тригонометрических функций, чётность, нечётность
-
Гармонические колебания (профильный)
-
Свойства функций y = tg x, y = ctg x и их графики
-
Функции y = arcsin a, y = arccos a, y = arctg a, y = arcctg a (профильный)
-
-
-
Арккосинус и решение уравнения cos х = a
-
Арксинус и решение уравнения sin x = a
-
Арктангенс и арккотангенс.
 Решение уравнений tg x = a, ctg x = a
Решение уравнений tg x = a, ctg x = a
-
Методы, используемые для решения тригонометрических уравнений
-
-
-
Формулы синуса суммы и разности, косинуса суммы и разности
-
Тангенс суммы и разности
-
Формулы приведения.
 Общее правило
Общее правило
-
Формулы синуса, косинуса, тангенса двойного угла
-
Формулы понижения степени, или формулы половинного угла (профильный)
-
Формулы сумм тригонометрических функций
-
Формулы произведений тригонометрических функций
-
Метод введения вспомогательного угла (профильный)
-
-
-
Числовые последовательности и их свойства
-
Понятие предела числовой последовательности
-
Как найти сумму бесконечной геометрической прогрессии
-
Предел функции в точке.
 Предел функции на бесконечности
Предел функции на бесконечности
-
Определение производной. Геометрический и физический смысл производной
-
Вычисление производных. Правила дифференцирования
-
Как получить уравнение касательной к графику функции
-
Исследование функций на монотонность и экстремумы
-
Исследование выпуклости и перегиба, построение графиков функции
-
Применение производной для отыскания наибольших и наименьших величин
-
-
-
Понятие корня n-й степени из действительного числа
-
Функция корня n-й степени
-
Свойства корня n-й степени.
 Преобразование иррациональных выражений
Преобразование иррациональных выражений
-
Способы упрощения выражений, содержащих радикалы
-
Понятие степени с рациональным показателем, свойства степеней
-
Свойства степенных функций и их графики
-
-
-
Свойства показательной функции и её график
-
Методы решения показательных уравнений
-
Методы решения показательных неравенств
-
Понятие логарифма.
 Основное логарифмическое тождество
Основное логарифмическое тождество
-
Свойства логарифмической функции и её график
-
Базовые свойства логарифмов
-
Методы решения логарифмических уравнений
-
Методы решения логарифмических неравенств
-
Переход к новому основанию логарифма
-
Системы показательных и логарифмических уравнений
-
Системы логарифмических и показательных неравенств
-
Производная показательной и логарифмической функции
-
-
-
Понятие первообразной
-
Неопределённые и определённые интегралы.
 Методы интегрирования
Методы интегрирования
-
Вычисление площадей с помощью интегралов
-
-
-
Правило суммы
-
Правило произведения
-
Перестановки.
 Перестановки без повторений
Перестановки без повторений
-
Размещения. Размещения с повторениями
-
Сочетания и их свойства
-
Треугольник Паскаля. Бином Ньютона
-
-
-
Какие бывают случайные события
-
Комбинации событий.
 Противоположные события
Противоположные события
-
Вероятность события
-
Сложение вероятностей
-
Независимые события. Умножение вероятностей
-
Статистическая вероятность
-
-
-
Случайные величины
-
Центральные тенденции
-
Меры разброса
-
Закон распределения вероятностей.
 Закон больших чисел
Закон больших чисел
-
-
-
Равносильность уравнений. Теоремы о равносильности уравнений
-
Общие методы решения уравнений
-
Равносильность неравенств. Системы и совокупности неравенств
-
Уравнения и неравенства с двумя переменными
-
Общие методы решения систем уравнений
-
Уравнения и неравенства с параметром
-
-
Коллекция интерактивных моделей
Тест.
 Системы неравенств с двумя переменными Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!
Системы неравенств с двумя переменными Будьте внимательны! У Вас есть 10 минут на прохождение теста. Система оценивания — 5 балльная. Разбалловка теста — 3,4,5 баллов, в зависимости от сложности вопроса. Порядок заданий и вариантов ответов в тесте случайный. С допущенными ошибками и верными ответами можно будет ознакомиться после прохождения теста. Удачи!Список вопросов теста
Вопрос 1
Является ли пара чисел (1;-3) решением системы неравенств
В ответе укажите: да или нет (без пробелов).
Вопрос 2
Пара чисел является решением системы неравенств, если она обращает в верное числовое неравенство … .
Варианты ответов
- первое неравенство системы
- второе неравенство системы
- каждое неравенство системы
Вопрос 3
Какая пара чисел является решением системы неравенств
Варианты ответов
Вопрос 4
Какое количество множеств является решением системы неравенств
В ответе кажите только число.
Вопрос 5
Укажите номер множества являющегося решением системы
Варианты ответов
Вопрос 6
Решение какой системы изображено на рисунке?
Варианты ответов
Вопрос 7
Установите соответствие между системами и парами значений, являющимися их решениями.
Варианты ответов
Вопрос 8
Какую фигуру задаёт множество решений системы
Варианты ответов
- квадрат
- прямоугольник
- треугольник
- круг
Вопрос 9
Выберите системы, решением которых является пара чисел (-1;5).
Варианты ответов
Вопрос 10
Выберите пары чисел, являющиеся решением системы
Варианты ответов
- (4;2)
- (-5;1)
- (-2;-1)
- (6;-5)
Уравнения и неравенства с двумя переменными.
 2=0$ имеет всего одно решение $х=-2$ и $у=-4$. Поскольку, сумма двух не отрицательных чисел может равняться нулю, когда они одновременно равны нулю. В данном примере мы получили всего одно решение.
2=0$ имеет всего одно решение $х=-2$ и $у=-4$. Поскольку, сумма двух не отрицательных чисел может равняться нулю, когда они одновременно равны нулю. В данном примере мы получили всего одно решение.Если дано целое рациональное уравнение с несколькими переменными и целочисленными коэффициентами, и также требуется найти целые (или рациональные) решения данного уравнения, то принято говорить, что задано диофантово уравнение.
Диофантовы уравнения решаются довольно трудно, и не всегда сразу можно придумать ходы решения. Часто помогает теория делимости целых чисел. Также отмечу, что современные методы программирования позволяют решать многие уравнения на компьютерах, используя так называемые численные методы.
Пример.
Найти целочисленные решения уравнения: $5x+4y=17$.
Решение.
В общем случае мы могли бы на декартовой системе координат изобразить прямую и получить множество всех решений, но нам требуется найти только целочисленные решения.
Воспользуемся известными предложениями теории делимости целых чисел.
Приведем наше уравнение к виду: $y=\frac{17-5x}{4}$.
Целое число $17-5х$ должно делиться без остатка на 4.
При делении на 4 возможны четыре случая:
а) остаток от деления на 4 равен нулю, то есть $х=4k$.
б) остаток от деления на 4 равен единице, то есть $х=4k+1$.
в) остаток от деления на 4 равен двум, то есть $х=4k+2$.
г) остаток от деления на 4 равен трем, то есть $х=4k+3$, где k — целое число.
Рассмотрим каждый случай отдельно:
а) Если $х=4k$, то $17-5x=17-20k$ не делится нацело на 4, т.к. каждый член разности должен делиться на 4, а число 17 не делится на 4.
б) Если $х=4k+1$, то $17-5x=17-20k-5=12-20k$ делится нацело на 4.
в) Если $х=4k+2$, то $17-5x=17-20k-10=7-20k$ не делится на 4.
г) Если $х=4k+3$, то $17-5x=17-20k-15=2-20k$ не делится на 4.
Среди всех возможных вариантов нам подошел лишь один вариант: $х=4k+1$.
Найдем y: $y=\frac{17-5x}{4}=\frac{17-20k-5}{4}=3-5k.$
Целым решением нашего уравнения является любая пара чисел $(4k+1;3-5k)$,
где k – любое целое число. 2=13$.
2=13$.
Решение.
Воспользуемся формулой разности квадратов: $(4x-2y)(4x+2y)=13$.
Мы получили произведение двух чисел в левой части уравнения. Заметим, что в правой части уравнения получилось простое число, которое делится только на себя и единицу по модулю.
Число 13 получается лишь в четырех случаях при произведении двух чисел:
а) Первый сомножитель равен 1, второй сомножитель равен 13.
б) Первый сомножитель равен 13, второй сомножитель равен 1.
в) Первый сомножитель равен -1, второй сомножитель равен -13.
г) Первый сомножитель равен -13, второй сомножитель равен -1.
Значит, нам надо решить совокупность 4 систем.
а)$\begin {cases} 4x-2y=1, \\ 4x+2y=13 \end {cases}$.
б)$\begin {cases} 4x-2y=13, \\ 4x+2y=1 \end {cases}$.
в)$\begin {cases} 4x-2y=-1, \\ 4x+2y=-13 \end {cases}$.
г) $\begin {cases} 4x-2y=-13, \\ 4x+2y=-1 \end {cases}$.
Решением каждой системы является пара чисел: а) $(1,75;3)$; б) $(1,75;-3)$;
в) $(-1,75;-3)$; г) $(-1,75;3)$.
Получается, что в данном примере целочисленных решений нет, но суть метода решения должна быть ясна.
Ответ: целочисленных решений нет.
Неравенства
Неравенства вида $p(x;y)>0$, $p(x;y)Решением неравенства $p(x;y)>0$ называют всякую пару чисел, которые удовлетворяют данному неравенству (неравенство превращается в верное числовое неравенство). Решения неравенств с двумя переменными также проще изображать на графиках в декартовой системе координат. Рассмотрим несколько примеров.
Пример.
Решить неравенство: $2x+5y>7$.
Решение.
Для начала выразим у через х: $y>\frac{7-2x}{5}$.
Построим прямую $y=\frac{7-2x}{5}$. Множество всех решений неравенства расположено, либо выше, либо ниже данной прямой.
Можно подставить любую пару чисел и проверить: выполнилось неравенство или нет. Если неравенство выполнилось, то мы выбираем в качестве решения ту область, которой принадлежат эти пара чисел, если не выполнилось, то выбираем противоположную область. 2-6x+2, \\ y≤x+5 \end {cases}$.
2-6x+2, \\ y≤x+5 \end {cases}$.
Как решить неравенство онлайн с подробным решением
Как решать неравенства
Любое неравенство или система неравенств может быть решена на нашем сайте используя Калькулятор за пару секунд. Решить неравенство с помощью калькулятора просто. Чтобы ввести неравенство, нажмите «+условие»
Например:
x+5
Нажав кнопку Решить вы получите подробное решение неравенств.
Неравенством в математике именуют все уравнения, где знак «=» заменяется на любой из этих значков: \[ > \] \[ \geq \] \[
* линейным;
* квадратным;
* дробным;
* показательным;
* тригонометрическим;
* логарифмическим.
В зависимости от этого и неравенства называются линейными, дробными и т. д.
д.
Об этих знаках нужно знать следующее:
* неравенства со значком больше (>), или меньше (
* неравенства со значками больше или равно \[ \geq \], меньше или равно \[\leq \] называются нестрогими;
* значок не равно \[ \ne \] стоит особняком, но решать примеры с таким значком тоже приходится постоянно.
Неравенства также можно разделить на верные неравенства и неверные неравенства. Например на уроке в школе вы можете часто услышать «запишите верное неравенство»
Как решить неравенство?
Решаются данного рода неравенства при помощи тождественных преобразований.
Допустим, дано неравенство такого вида:
\[x+3 > 5x-5\]
Оно решается точно так же, как и линейное уравнение, но необходимо внимательно следить за знаком неравенства. Изначально выполним перенос членов с неизвестной в левую сторону, с известной в правую, меняя знаки на противоположные:
\[x-5x > -5-3\]
\[-4x > -8\]
Далее выполним деление обеих частей на -4 и меняем знак неравенства на противоположный:
\[x
Это и будет неравенства решение.
Где можно решить неравенства онлайн калькулятор?
Решить неравенства вы можете на нашем сайте. Бесплатный онлайн решатель позволит решить неравенства x онлайн любой сложности за считанные секунды. Все, что вам необходимо сделать — это просто ввести свои данные в решателе. Так же вы можете посмотреть видео инструкцию и узнать, как вводить задачи на нашем сайте. А если у вас остались вопросы, то вы можете задать их в нашей групе Вконтакте http://vk.com/pocketteacher. Вступайте в нашу группу, мы всегда рады помочь вам.
Так же читайте нашу статью «Решить целое уравнение онлайн решателем»
Решение неравенств с двумя переменными
Решения неравенств с двумя переменными
Мы знаем, что линейное уравнение с двумя переменными имеет бесконечно много упорядоченных парных решений, которые на графике образуют линию. Линейное неравенство с двумя переменными Неравенство, связывающее линейные выражения с двумя переменными. Набор решений — это область, определяющая половину плоскости., С другой стороны, имеет набор решений, состоящий из области, определяющей половину плоскости.
Линейное неравенство с двумя переменными Неравенство, связывающее линейные выражения с двумя переменными. Набор решений — это область, определяющая половину плоскости., С другой стороны, имеет набор решений, состоящий из области, определяющей половину плоскости.
Линейное уравнение | Линейное неравенство |
|---|---|
y = 32x + 3 | y≤32x + 3 |
Для неравенства линия определяет границу заштрихованной области.Это означает, что любая упорядоченная пара в заштрихованной области, включая граничную линию, будет удовлетворять неравенству. Чтобы убедиться, что это так, выберите несколько контрольных точек — точку не на границе линейного неравенства, используемую в качестве средства для определения, в какой полуплоскости лежат решения. и подставляем их в неравенство.
Чтобы убедиться, что это так, выберите несколько контрольных точек — точку не на границе линейного неравенства, используемую в качестве средства для определения, в какой полуплоскости лежат решения. и подставляем их в неравенство.
Контрольная точка | y≤32x + 3 |
(0, 0) | 0≤32 (0) + 30≤3 ✓ |
(2, 1) | 1≤32 (2) + 31≤3 + 31≤6 ✓ |
(−2, −1) | −1≤32 (−2) + 3−1≤ − 3 + 3−1≤0 ✓ |
Также мы можем видеть, что упорядоченные пары вне заштрихованной области не решают линейное неравенство.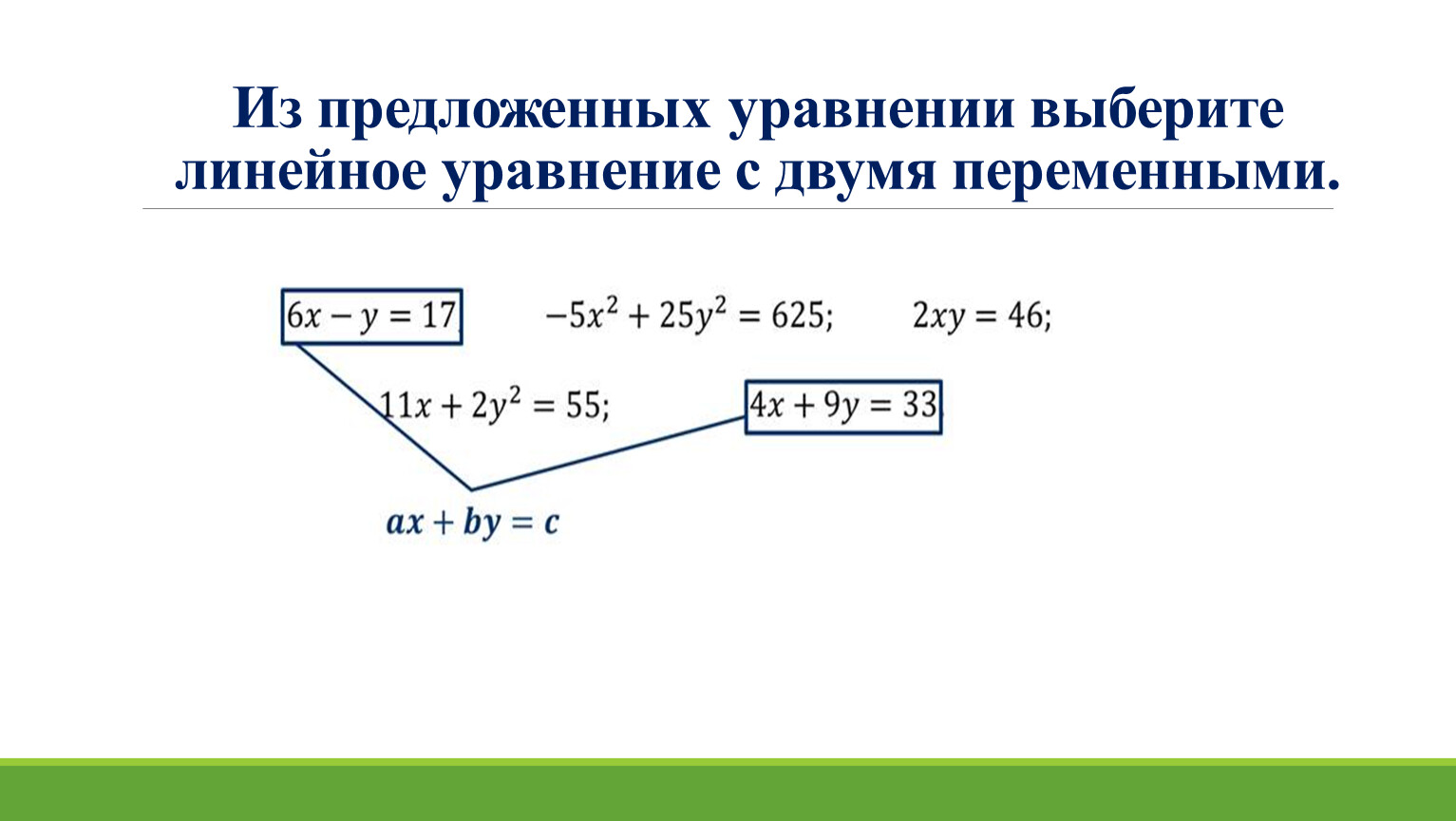
Контрольная точка | y≤32x + 3 |
(-2, 3) | 3≤32 (−2) + 33≤ − 3 + 33≤0 ✗ |
График решения, установленного для линейного неравенства, всегда является областью. Однако граница не всегда может быть включена в этот набор.В предыдущем примере линия была частью набора решений из-за части «или равно» в инклюзивном неравенстве ≤. Если дано строгое неравенство <, мы использовали бы пунктирную линию, чтобы указать, что эти точки не включены в набор решений.
Неисключительная граница | Включая Граница |
|---|---|
y <32x + 3 | y≤32x + 3 |
Рассмотрим точку (0, 3) на границе; эта упорядоченная пара удовлетворяет линейному уравнению.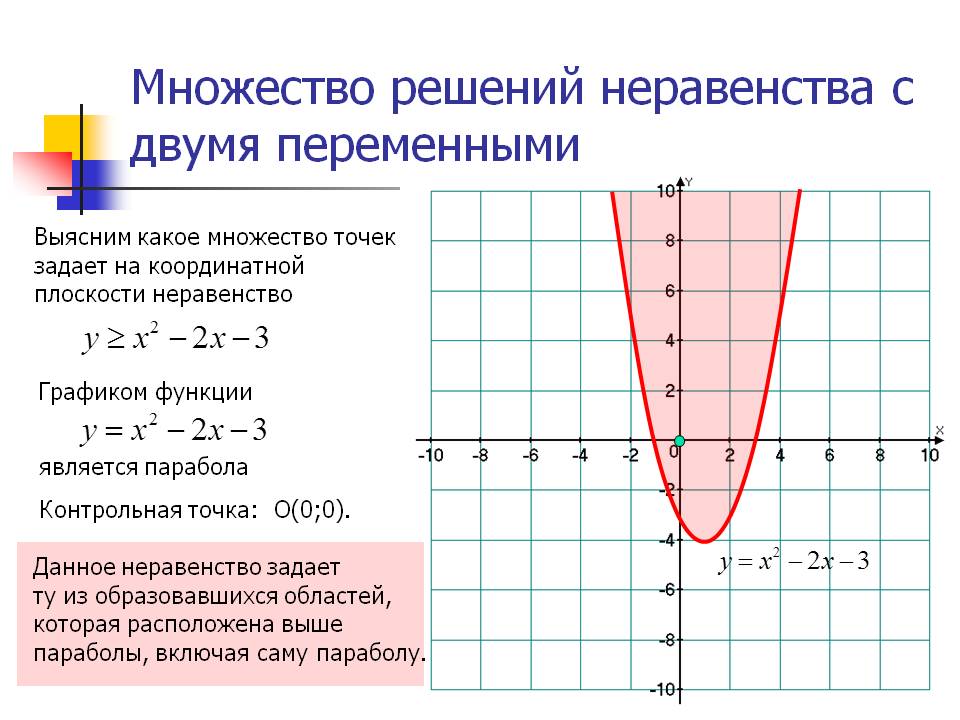 Именно часть инклюзивного неравенства «или равно» делает упорядоченную пару частью множества решений.
Именно часть инклюзивного неравенства «или равно» делает упорядоченную пару частью множества решений.
y <32x + 3 | y≤32x + 3 |
3 <32 (0) +33 <0 + 33 <3 ✗ | 3≤32 (0) + 33≤0 + 33≤3 ✓ |
До сих пор мы видели примеры неравенства, которое было «меньше чем.”Теперь рассмотрим следующие графы с той же границей:
Больше, чем (вверху) | Меньше (ниже) |
|---|---|
y≥32x + 3 | y≤32x + 3 |
Учитывая приведенные выше графики, чего можно ожидать, если мы используем начало координат (0, 0) в качестве контрольной точки?
y≥32x + 3 | y≤32x + 3 |
0≥32 (0) + 30≥0 + 30≥3 ✗ | 0≤32 (0) + 30≤0 + 30≤3 ✓ |
Пример 1
Определите, является ли (2,12) решением 5x − 2y <10.
Решение:
Подставьте значения x и y в уравнение и посмотрите, получится ли истинное утверждение.
5x − 2y <105 (2) −2 (12) <10 10−1 <109 <10 ✓
Ответ: (2,12) — это решение.
Эти идеи и методы распространяются на нелинейные неравенства с двумя переменными. Например, все решения для y> x2 затенены на графике ниже.
Граница области представляет собой параболу, показанную пунктирной кривой на графике, и не является частью набора решений.Однако, исходя из графика, мы ожидаем, что упорядоченная пара (−1,4) будет решением. Кроме того, мы ожидаем, что упорядоченные пары, которые не находятся в заштрихованной области, например (−3, 2), не будут удовлетворять неравенству.
Чек (-1,4) | Чек (−3, 2) |
|---|---|
y> x24> (- 1) 24> 1 ✓ | y> x22> (- 3) 22> 9 ✗ |
Ниже приведены графики наборов решений неравенств с инклюзивными параболическими границами.
y≤ (x − 1) 2−2 | y≥ (x − 1) 2−2 |
Вам предлагается проверять точки в каждом наборе решений, изображенном на графике выше.
Попробуй! Является ли (−3, −2) решением 2x − 3y <0?
Ответ: Нет
Графические решения неравенств с двумя переменными
Решения линейных неравенств представляют собой заштрихованную полуплоскость, ограниченную сплошной или пунктирной линией.Эта граница либо входит в решение, либо нет, в зависимости от заданного неравенства. Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано инклюзивное неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги для построения графика набора решений для неравенства с двумя переменными показаны в следующем примере.
Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано инклюзивное неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги для построения графика набора решений для неравенства с двумя переменными показаны в следующем примере.
Пример 2
Изобразите набор решений y> −3x + 1.
Решение:
Шаг 1: Постройте границу. Из-за строгого неравенства мы построим границу y = −3x + 1 с помощью пунктирной линии. Мы можем видеть, что наклон равен m = −3 = −31 = riserun, а точка пересечения y равна (0, 1).
Шаг 2: Протестируйте точку на границе , а не .Обычная контрольная точка — это начало координат (0, 0).
 Контрольная точка помогает нам определить, какую половину плоскости затенить.
Контрольная точка помогает нам определить, какую половину плоскости затенить.Контрольная точка
г> −3x + 1
(0, 0)
0> −3 (0) +10> 1 ✗
- Шаг 3: Закрасьте область, содержащую растворы.Поскольку контрольная точка (0, 0) не была решением, она не лежит в области, содержащей все упорядоченные парные решения. Поэтому заштрихуйте половину плоскости, на которой нет этой контрольной точки. В этом случае заштрихуйте линию выше границы.
Ответ:
Рассмотрим проблему затенения выше или ниже граничной линии, когда неравенство имеет форму пересечения уклона. Изобразите набор решений 2x − 5y≥ − 10. Решение: Здесь граница определяется линией 2x − 5y = −10. Поскольку неравенство носит инклюзивный характер, мы обозначим границу сплошной линией. В этом случае нарисуйте граничную линию, используя точки пересечения. Чтобы найти точку пересечения x , установите y = 0. Чтобы найти точку пересечения y , установите x = 0. 2x − 5y = −10 2x − 5 (0) = — 102x = −10x = −5 2x − 5y = −10 2 (0) −5y = −10−5y = −10y = 2 x -перехват: (−5, 0) y -перехват: (0, 2) Затем проверьте точку; это помогает решить, какую область затенять. Контрольная точка 2x − 5y≥ − 10 (0, 0) 2 (0) −5 (0) ≥ − 100≥ − 10 ✓ Так как контрольная точка находится в наборе решений, заштрихуйте половину плоскости, которая ее содержит. Ответ: В этом примере обратите внимание, что набор решений состоит из всех упорядоченных пар ниже граничной линии. Это может показаться нелогичным, поскольку исходное неравенство включало «больше, чем» ≥. Это показывает, что лучше всего проверить точку. Решите относительно и , и вы увидите, что затенение правильное. 2x − 5y≥ − 102x − 5y − 2x≥ − 10−2x − 5y≥ − 2x − 10−5y − 5≤ − 2x − 10−5 Обратить неравенство. В форме пересечения откоса вы можете видеть, что область под линией границы должна быть заштрихована. Альтернативный подход состоит в том, чтобы сначала выразить границу в форме пересечения наклона, нанести ее на график, а затем заштриховать соответствующую область. Изобразите набор решений y <2. Решение: Сначала изобразите граничную линию y = 2 пунктирной линией из-за строгого неравенства.Затем проверьте точку. Контрольная точка г <2 (0, 0) 0 <2 ✓ В этом случае закрасьте область, содержащую тестовую точку. Ответ: Попробуй! Изобразите набор решений 2x − 3y <0. Ответ: Шаги такие же для нелинейных неравенств с двумя переменными. Сначала нарисуйте границу, а затем проверьте точку, чтобы определить, в какой области находятся решения. Изобразите набор решений y <(x + 2) 2−1. Решение: Граница представляет собой базовую параболу, смещенную на 2 единицы влево и на 1 единицу вниз.Начните с рисования пунктирной параболической границы из-за строгого неравенства. Затем проверьте точку. Контрольная точка y <(x + 2) 2−1 (0, 0) 0 <(0 + 2) 2−10 <4−10 <3 ✓ В этом случае закрасьте область, содержащую тестовую точку (0,0). Ответ: Изобразите набор решений y≥x2 + 3. Решение: Граница представляет собой базовую параболу, смещенную на 3 единицы вверх. Он изображен сплошной кривой из-за включенного неравенства. Затем проверьте точку. Контрольная точка y≥x2 + 3 (0, 0) 0≥02 + 30≥3 ✗ В этом случае закрасьте область, которая не содержит контрольную точку (0,0). Ответ: Попробуй! Изобразите набор решений y <| x − 1 | −3. Ответ: Является ли упорядоченная пара решением данного неравенства? 5x − y> −2; (−3, −4) 4x − y <−8; (−3, −10) 6x − 15y≥ − 1; (12, −13) х − 2y≥2; (23, −56) 34x − 23y <32; (1, −1) 25x + 43y> 12; (−2,1) y≤x2−1; (-1,1) y≥x2 + 3; (−2,0) y≥ (x − 5) 2 + 1; (3,4) y≤2 (x + 1) 2−3; (-1, -2) у> 3− | х |; (−4, −3) у <| х | −8; (5, −7) у> | 2x − 1 | −3; (-1,3) у <| 3x − 2 | +2; (-2,10) Постройте график набора решений. 16x + 110y≤12 38x + 12y≥34 112x − 16y <23 13x − 19y> 43 2x≥6−9y Напишите неравенство, описывающее все точки в верхней полуплоскости выше оси x . Напишите неравенство, описывающее все точки в нижней полуплоскости ниже оси x . Напишите неравенство, описывающее все точки в полуплоскости слева от оси y . Напишите неравенство, описывающее все точки в полуплоскости справа от оси y . Напишите неравенство, описывающее все упорядоченные пары, у которых координата y составляет не менее k единиц. Напишите неравенство, описывающее все упорядоченные пары, у которых координата x составляет не более k единиц. Изобразите набор решений. Прямоугольный загон должен иметь ограждение не более 200 футов.Запишите линейное неравенство для длины l и ширины w . Нарисуйте график всех возможных решений этой проблемы. Компания продает один продукт за 8 долларов, а другой за 12 долларов. Сколько каждого продукта необходимо продать, чтобы выручка составила не менее 2400 долларов? Пусть x представляет количество продуктов, проданных по 8 долларов, а y — количество продуктов, проданных по 12 долларов.Напишите линейное неравенство в терминах x и y и нарисуйте график всех возможных решений. Чтобы построить линейный
неравенство
в двух переменных (скажем,
Икс
а также
y
), сначала получите
y
один на одной стороне. Затем рассмотрим соответствующее уравнение, полученное заменой знака неравенства на знак равенства.График этого уравнения представляет собой линию. Если неравенство строгое ( <
или же
> ), начертите штриховой линией. Если неравенство не строгое
(
≤
или же
≥
), начертите сплошной линией. Наконец, выберите одну точку, которая не находится ни на одной строке (
(
0
,
0
)
обычно самый простой) и решите, удовлетворяют ли эти координаты неравенству или нет. Если это так, заштрихуйте полуплоскость, содержащую эту точку.Если нет, закройте другую полуплоскость. Аналогичным образом изобразите каждое из неравенств в системе. Решение
система неравенства
— область пересечения всех решений в системе. Пример 1: Решите систему неравенств, построив графики: y
≤
Икс
—
2
y
>
—
3
Икс
+
5 Сначала изобразим неравенство
y
≤
Икс
—
2
.Связанное уравнение
y
знак равно
Икс
—
2
. Поскольку неравенство
≤
, не строгий, граница сплошная. Постройте прямую линию. Рассмотрим точку, которая не находится на линии — скажем,
(
0
,
0
)
— и подставляем в неравенство
y
≤
Икс
—
2
. 0
≤
0
—
2
0
≤
—
2 Это неправда.Итак, решение не содержит точки
(
0
,
0
)
. Заштрихуйте нижнюю половину линии. Аналогичным образом нарисуйте пунктирную линию для соответствующего уравнения второго неравенства
y
>
—
3
Икс
+
5
которое имеет строгое неравенство. Точка
(
0
,
0
)
не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точки
(
0
,
0
)
. Решение системы неравенств — это область пересечения решений двух неравенств. Пример 2: Решите систему неравенств, построив графики: 2
Икс
+
3
у
≥
12
8
Икс
—
4
у
>
1
Икс <
4 Перепишем первые два неравенства с
у
один на одной стороне. 3
у
≥
—
2
Икс
+
12
у
≥
—
2
3
Икс
+
4
—
4
у
>
—
8
Икс
+
1
у <
2
Икс
-
1
4 Теперь изобразим неравенство
у
≥
—
2
3
Икс
+
4
.Связанное уравнение
у
знак равно
—
2
3
Икс
+
4
. Поскольку неравенство
≥
, не строгий, граница сплошная. Постройте прямую линию. Рассмотрим точку, которая не находится на линии — скажем,
(
0
,
0
)
— и подставляем в неравенство. 0
≥
—
2
3
(
0
)
+
4
0
≥
4 Это неправда.Итак, решение не содержит точки
(
0
,
0
)
. Заштрихуйте верхнюю половину линии. Аналогично нарисуйте пунктирную линию соответствующего уравнения второго неравенства
у <
2
Икс
-
1
4
которое имеет строгое неравенство. Точка
(
0
,
0
)
не удовлетворяет неравенству, поэтому заштрихуйте половину, не содержащую точки
(
0
,
0
)
. Нарисуйте пунктирную вертикальную линию
Икс
знак равно
4
которое является родственным уравнением третьего неравенства. Здесь точка
(
0
,
0
)
удовлетворяет неравенству, поэтому заштрихуйте половину, содержащую точку. Решение системы неравенств — это область пересечения решений трех неравенств. Знаете ли вы, что при совершении покупок в Интернете вы используете линейное неравенство? Когда вы используете опцию для просмотра товаров в определенном ценовом диапазоне, вы просите поисковую систему использовать линейное неравенство, основанное на цене.По сути, вы говорите «покажите мне все товары на продажу от 50 до 100 долларов», что можно записать как [латекс] {50} \ le {x} \ le {100} [/ latex], где x цена. В этом разделе вы примените все, что вы знаете о построении графиков линейных уравнений, для построения графиков линейных неравенств. Так как же перейти от алгебраической формы неравенства, такой как [latex] y> 3x + 1 [/ latex], к графику этого неравенства? Построить график неравенства довольно просто, если вы выполните пару шагов. Чтобы построить график неравенства: Построим график неравенства [latex] x + 4y \ leq4 [/ latex]. Чтобы построить граничную линию, найдите по крайней мере два значения, которые лежат на линии [латекс] x + 4y = 4 [/ latex]. Вы можете использовать интерцепты x и y для этого уравнения, подставив сначала 0 вместо x и найдя значение y ; затем подставьте 0 вместо y и найдите x . Постройте точки [latex] (0,1) [/ latex] и [latex] (4,0) [/ latex] и проведите через эти две точки линию границы. Линия сплошная, потому что ≤ означает «меньше или равно», поэтому все упорядоченные пары вдоль линии включены в набор решений. Следующий шаг — найти область, содержащую решения. Это выше или ниже границы? Чтобы определить область, в которой выполняется неравенство, вы можете протестировать пару упорядоченных пар, по одной с каждой стороны граничной линии. Если вы замените [latex] (- 1,3) [/ latex] на [latex] x + 4y \ leq4 [/ latex]: [латекс] \ begin {array} {r} −1 + 4 \ left (3 \ right) \ leq4 \\ — 1 + 12 \ leq4 \\ 11 \ leq4 \ end {array} [/ latex] Это ложное утверждение, поскольку 11 не меньше или равно 4. С другой стороны, если вы замените [latex] (2,0) [/ latex] на [latex] x + 4y \ leq4 [/ latex]: [латекс] \ begin {array} {r} 2 + 4 \ left (0 \ right) \ leq4 \\ 2 + 0 \ leq4 \\ 2 \ leq4 \ end {array} [/ latex] Это правда! Область, которая включает [latex] (2,0) [/ latex], должна быть заштрихована, так как это область растворов. И вот он — график множества решений для [latex] x + 4y \ leq4 [/ latex]. Изобразите неравенство [latex] 2y> 4x – 6 [/ latex]. Решите относительно и . [латекс] \ displaystyle \ begin {array} {r} 2y> 4x-6 \\\\\ frac {2y} {2}> \ frac {4x} {2} — \ frac {6} {2} \ \\\ y> 2x-3 \\\ end {array} [/ latex] Создайте таблицу значений, чтобы найти две точки на линии [latex] \ displaystyle y = 2x-3 [/ latex], или изобразите ее на основе метода пересечения наклона, значения b из y — перехват — [латекс] -3 [/ латекс], а наклон равен 2. Постройте точки и нанесите линию на график. Линия пунктирна, потому что знак в неравенстве>, а не ≥, и поэтому точки на линии не являются решениями неравенства. [латекс] \ displaystyle y = 2x-3 [/ латекс] Найдите упорядоченную пару по обе стороны от ограничивающей линии.Вставьте значения x и y в неравенство [латекс] \ begin {array} {l} 2y> 4x – 6 \\\\\ text {Test} 1: \ left (−3,1 \ right) \\ 2 \ left (1 \ right)> 4 \ left (−3 \ right) –6 \\\, \, \, \, \, \, \, 2> –12–6 \\\, \, \, \, \, \, \, 2> −18 \\\ text {TRUE} \\\\\ text {Test} 2: \ left (4,1 \ right) \\ 2 (1)> 4 \ left (4 \ right) — 6 \\\, \, \, \, \, \, 2> 16–6 \\\, \, \, \, \, \, 2> 10 \\\ text {FALSE} \ end {array} [/ latex] График неравенства [латекс] 2y> 4x – 6 [/ латекс] равен: Краткое примечание о проблеме выше — обратите внимание, что вы можете использовать точки [latex] (0, −3) [/ latex] и [latex] (2,1) [/ latex] для построения граничной линии, но это эти точки не входят в область решений, так как область не включает граничную линию! На графике ниже показана область значений, которая делает неравенство [латекс] 3x + 2y \ leq6 [/ latex] истинным (закрашено красным), граничная линия [латекс] 3x + 2y = 6 [/ latex], а также горстка заказанных пар.Граничная линия сплошная, потому что точки на граничной линии [латекс] 3x + 2y = 6 [/ latex] сделают неравенство [латекс] 3x + 2y \ leq6 [/ latex] истинным. Вы можете подставить значения x- и y- в каждую из упорядоченных пар [latex] (x, y) [/ latex] в неравенство, чтобы найти решения. Иногда для более сложных неравенств имеет смысл составить таблицу значений. [латекс] 3x + 2y \ leq6 [/ латекс] истинное заявление [латекс] 3x + 2y \ leq6 [/ латекс] ложное заявление Если замена [latex] (x, y) [/ latex] в неравенство дает истинное утверждение, то упорядоченная пара является решением неравенства, и точка будет нанесена на заштрихованную область или точку будет частью сплошной границы.Ложное утверждение означает, что упорядоченная пара не является решением, и точка будет отображаться вне заштрихованной области, или точка будет частью пунктирной линии границы. Используйте график, чтобы определить, какие упорядоченные пары, изображенные ниже, являются решениями неравенства [латекс] x – y <3 [/ latex]. будут расположены в затененной области. Поскольку это проблема «меньше чем», упорядоченные пары на граничной линии не включаются в набор решений. Эти значения расположены в заштрихованной области, как и решения. (При подстановке в неравенство [латекс] x – y <3 [/ latex] они дают истинные утверждения.) [латекс] (- 1,1) [/ латекс] [латекс] (- 2, −2) [/ латекс] Эти значения не находятся в затененной области, поэтому не являются решениями. (При подстановке в неравенство [латекс] x-y <3 [/ latex] они дают ложные утверждения.) [латекс] (1, −2) [/ латекс] [латекс] (3, -2) [/ латекс] [латекс] (4,0) [/ латекс] [латекс] (- 1,1) \, \, \, (- 2, −2) [/ латекс] В следующем видео показан пример определения того, является ли упорядоченная пара решением неравенства. Является ли [latex] (2, −3) [/ latex] решением неравенства [latex] y <−3x + 1 [/ latex]? Если [latex] (2, −3) [/ latex] является решением, тогда оно даст истинное утверждение при подстановке в неравенство [latex] y <−3x + 1 [/ latex]. [латекс] y <−3x + 1 [/ латекс] Заменить [латекс] x = 2 [/ латекс] и [латекс] y = −3 [/ латекс] в неравенство. [латекс] −3 <−3 \ влево (2 \ вправо) +1 [/ латекс] Оценить. [латекс] \ begin {массив} {l} −3 <−6 + 1 \\ - 3 <−5 \ end {array} [/ latex] Это утверждение не , поэтому упорядоченная пара [latex] (2, −3) [/ latex] — это , а не решение. [latex] (2, −3) [/ latex] не является решением. В следующем видео показан еще один пример определения того, является ли упорядоченная пара решением неравенства. Рассмотрим график неравенства [латекс] y <2x + 5 [/ латекс]. Пунктирная линия [латекс] y = 2x + 5 [/ latex]. Каждая упорядоченная пара в заштрихованной области под линией является решением [latex] y <2x + 5 [/ latex], поскольку все точки под линией делают неравенство истинным. Если вы сомневаетесь в этом, попробуйте подставить координаты x и y точек A и B в неравенство — вы увидите, что они работают. Итак, заштрихованной областью показаны все решения этого неравенства. Граничная линия делит координатную плоскость пополам.В этом случае он показан пунктирной линией, поскольку точки на линии не удовлетворяют неравенству. Если бы неравенство было [латекс] y \ leq2x + 5 [/ латекс], то граница была бы сплошной. Изобразим еще одно неравенство: [latex] y> −x [/ latex]. Вы можете проверить пару точек, чтобы определить, какую сторону границы нужно заштриховать. Контрольные точки M и N дают верные утверждения. Итак, заштриховываем область над линией. Линия пунктирна, поскольку точки на линии не соответствуют действительности. Чтобы создать систему неравенств, вам необходимо построить график двух или более неравенств вместе.Давайте использовать [latex] y <2x + 5 [/ latex] и [latex] y> −x [/ latex], поскольку мы уже изобразили каждый из них. Фиолетовая область показывает, где перекрываются решения двух неравенств. Эта область является решением системы неравенств . Любая точка в этой фиолетовой области будет верна как для [latex] y> −x [/ latex], так и для [latex] y <2x + 5 [/ latex]. В следующих видео-примерах мы покажем, как построить график системы линейных неравенств и определить область решения. В следующем разделе мы увидим, что точки могут быть решениями систем уравнений и неравенств. Проверим алгебраически, является ли точка решением линейного уравнения или неравенства. На приведенном выше графике вы можете видеть, что точки B и N являются решениями для системы, потому что их координаты делают оба неравенства истинными. Напротив, точки M и A лежат за пределами области решения (фиолетовый). Хотя точка M является решением неравенства [latex] y> −x [/ latex], а точка A является решением неравенства [latex] y <2x + 5 [/ latex], ни одна из точек не является решением для система . В следующем примере показано, как проверить точку, чтобы увидеть, является ли она решением системы неравенств. Является ли точка (2, 1) решением системы [латекс] x + y> 1 [/ latex] и [latex] 2x + y <8 [/ latex]? [латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex] (2, 1) — решение для [латекса] x + y> 1 [/ latex]. [латекс] \ begin {array} {r} 2x + y <8 \\ 2 \ left (2 \ right) +1 <8 \\ 4 + 1 <8 \\ 5 <8 \\\ text {TRUE} \ end {array} [/ latex] (2, 1) — решение для [латекса] 2x + y <8. [/ Latex] Поскольку (2, 1) является решением каждого неравенства, оно также является решением системы. Точка (2, 1) является решением системы [латекс] x + y> 1 [/ latex] и [latex] 2x + y <8 [/ latex]. Вот график системы в примере выше. Обратите внимание, что (2, 1) находится в фиолетовой области, которая является областью перекрытия для двух неравенств. Является ли точка (2, 1) решением системы [латекс] x + y> 1 [/ latex] и [latex] 3x + y <4 [/ latex]? Отметьте точку с каждым неравенством.Замените 2 на x и 1 на y . Является ли дело решением обоих неравенств? [латекс] \ begin {массив} {r} x + y> 1 \\ 2 + 1> 1 \\ 3> 1 \\\ text {TRUE} \ end {array} [/ latex] (2, 1) — решение для [латекса] x + y> 1 [/ latex]. [латекс] \ begin {array} {r} 3x + y <4 \\ 3 \ left (2 \ right) +1 <4 \\ 6 + 1 <4 \\ 7 <4 \\\ text {FALSE} \ end {array} [/ latex] (2, 1) — это , а не решение для [латекса] 3x + y <4 [/ latex]. Поскольку (2, 1) — это , а не решение одного из неравенств, оно не является решением системы. Точка (2, 1) не является решением системы [латекс] x + y> 1 [/ latex] и [latex] 3x + y <4 [/ latex]. Вот график этой системы. Обратите внимание, что (2, 1) не находится в фиолетовой области, которая является перекрывающейся областью; это решение одного неравенства (красная область), но не решение второго неравенства (синяя область). В следующем видео мы показываем еще один пример определения, находится ли точка в решении системы линейных неравенств. Как показано выше, нахождение решений системы неравенств может быть выполнено путем графического отображения каждого неравенства и определения области, в которой они находятся. Ниже приведены дополнительные примеры, показывающие весь процесс определения области решений на графике для системы двух линейных неравенств. Общие шаги описаны ниже: В следующем примере мы покажем решение системы двух неравенств, граничные линии которых параллельны друг другу.Когда графики системы двух линейных уравнений параллельны друг другу, мы обнаружили, что у системы нет решения. Мы получим аналогичный результат для следующей системы линейных неравенств. Постройте график системы [latex] \ begin {array} {c} y \ ge2x + 1 \\ y \ lt2x-3 \ end {array} [/ latex] Граничные линии этой системы параллельны друг другу, обратите внимание, как они имеют одинаковый уклон. [латекс] \ begin {array} {c} y = 2x + 1 \\ y = 2x-3 \ end {array} [/ latex] Построение граничных линий даст график ниже.Обратите внимание, что неравенство [latex] y \ lt2x-3 [/ latex] требует рисования пунктирной линии, а неравенство [latex] y \ ge2x + 1 [/ latex] требует сплошной линии. Теперь нам нужно добавить регионы, представляющие неравенства. Для неравенства [латекс] y \ ge2x + 1 [/ latex] мы можем проверить точку по обе стороны от линии, чтобы увидеть, какую область закрасить. Давайте проверим [латекс] \ left (0,0 \ right) [/ latex], чтобы упростить задачу. Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ ge2x + 1 [/ latex] [латекс] \ begin {array} {c} y \ ge2x + 1 \\ 0 \ ge2 \ left (0 \ right) +1 \\ 0 \ ge {1} \ end {array} [/ latex] Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [latex] y \ ge2x + 1 [/ latex].График теперь будет выглядеть так: Теперь закрасим область, которая показывает решения неравенства [latex] y \ lt2x-3 [/ latex]. Опять же, мы можем выбрать [latex] \ left (0,0 \ right) [/ latex] для тестирования, потому что это упрощает алгебру. Заменить [латекс] \ left (0,0 \ right) [/ latex] на [latex] y \ lt2x-3 [/ latex] [латекс] \ begin {array} {c} y \ lt2x-3 \\ 0 \ lt2 \ left (0, \ right) x-3 \\ 0 \ lt {-3} \ end {array} [/ latex ] Это неправда, поэтому мы знаем, что нам нужно заштриховать другую сторону граничной линии для неравенства [латекс] y \ lt2x-3 [/ latex].График теперь будет выглядеть так: У этой системы неравенства нет общих черт. В следующих примерах мы продолжим практиковаться в графическом построении области решения для систем линейных неравенств. Мы также построим график решений системы, которая включает составное неравенство. Закрасьте область графика, которая представляет решения для обоих неравенств. [латекс] x + y \ geq1 [/ латекс] и [латекс] y – x \ geq5 [/ латекс]. Найдите упорядоченную пару по обе стороны от ограничивающей линии. Вставьте значения x и y в неравенство [latex] x + y \ geq1 [/ latex] и посмотрите, какая упорядоченная пара дает истинное утверждение. [латекс] \ begin {array} {r} \ text {Test} 1: \ left (−3,0 \ right) \\ x + y \ geq1 \\ — 3 + 0 \ geq1 \\ — 3 \ geq1 \\\ text {FALSE} \\\\\ text {Test} 2: \ left (4,1 \ right) \\ x + y \ geq1 \\ 4 + 1 \ geq1 \\ 5 \ geq1 \\\ текст {ИСТИНА} \ end {array} [/ latex] Поскольку (4, 1) приводит к истинному утверждению, область, которая включает (4, 1), должна быть заштрихована. Проделайте то же самое со вторым неравенством. Постройте граничную линию, затем проверьте точки, чтобы определить, какая область является решением неравенства. В этом случае граница [латекс] y – x = 5 \ left (\ text {или} y = x + 5 \ right) [/ latex] сплошная.Контрольная точка (−3, 0) не является решением [latex] y – x \ geq5 [/ latex], а контрольная точка (0, 6) является решением. Фиолетовая область на этом графике показывает набор всех решений системы. В следующих видеороликах показаны другие примеры построения графиков множества решений системы линейных неравенств. Система в нашем последнем примере включает составное неравенство. Мы увидим, что вы можете относиться к составному неравенству как к двум линиям, когда строите их график. Найдите решение системы 3 x + 2 y <12 и −1 ≤ y ≤ 5. Изобразите одно неравенство. Сначала нарисуйте граничную линию, затем контрольные точки. Помните, поскольку неравенство 3 x + 2 y <12 не включает знак равенства, проведите пунктирную линию границы. Проверка точки (например, (0, 0) покажет, что область под линией является решением этого неравенства. Неравенство −1 ≤ y ≤ 5 на самом деле представляет собой два неравенства: −1 ≤ y и y ≤ 5. Другой способ представить это: y должно быть между −1 и 5. Граница линии для обоих горизонтальные. Область между этими двумя линиями содержит решения −1 ≤ y ≤ 5. Мы делаем линии сплошными, потому что мы также хотим включить y = −1 и y = 5. Изобразите эту область на тех же осях, что и другое неравенство. Фиолетовая область на этом графике показывает набор всех решений системы. В следующем видео мы покажем, как решить еще одну систему неравенств. В нашем первом примере мы покажем, как написать и изобразить систему линейных неравенств, которая моделирует объем продаж, необходимых для получения определенной суммы денег. Кэти продает рожки мороженого на школьном мероприятии по сбору средств.Она продает два размера: маленький (в котором 1 мерная ложка) и большой (в котором 2 мерные ложки). Она знает, что может получить максимум 70 шариков мороженого из своего запаса. Она берет 3 доллара за маленький конус и 5 долларов за большой. Кэти хочет заработать не менее 120 долларов, чтобы отдать их школе. Напишите и изобразите систему неравенств, которая моделирует эту ситуацию. Сначала определите переменные. Есть две переменные: количество маленьких шишек и количество больших шишек. s = маленький конус л = большой конус Напишите первое уравнение: максимальное количество ложек, которое она может выдать. Количество совков, имеющихся у нее в наличии (70), должно быть больше или равно количеству совков для маленьких конусов ( s ) и больших конусов (2 l ), которые она продает. [латекс] s + 2l \ le70 [/ латекс] Напишите второе уравнение: сумму денег, которую она собирает. Она хочет, чтобы общая сумма денег, заработанных на маленьких шишках (3 x ) и больших (5 l ), составляла не менее 120 долларов. [латекс] 3s + 5l \ ge120 [/ латекс] Запишите систему. [латекс] \ begin {case} s + 2l \ le70 \\ 3s + 5l \ ge120 \ end {case} [/ latex] Теперь изобразите систему. Переменные x и y заменены на s и l ; график s по оси x и l по оси y . Сначала нарисуйте область s + 2 l ≤ 70. Постройте граничную линию, а затем проверьте отдельные точки, чтобы увидеть, какую область закрасить.График показан ниже. Теперь нарисуйте область [латекс] 3s + 5l \ ge120 [/ latex] Постройте граничную линию, а затем проверьте отдельные точки, чтобы увидеть, какую область закрасить. График показан ниже. Изобразив регионы вместе, вы обнаружите следующее: И представленный так же, как перекрывающаяся область, у вас есть: Область фиолетового цвета — это решение. Пока комбинация маленьких и больших рожков, которые продает Кэти, может быть нанесена на карту в фиолетовой области, она заработает не менее 120 долларов и не потратит более 70 шариков мороженого. В предыдущем примере поиска решения системы линейных уравнений мы ввели уравнения затрат и доходов производителя: Стоимость: [латекс] y = 0,85x + 35,000 [/ латекс] Доход: [латекс] y = 1,55x [/ латекс] Уравнение затрат показано синим цветом на графике ниже, а уравнение доходов — оранжевым. Точка пересечения двух линий называется точкой безубыточности, мы узнали, что это решение системы линейных уравнения, которые в данном случае включают уравнения затрат и доходов. Заштрихованная область справа от точки безубыточности представляет объемы, от которых компания получает прибыль. Область слева представляет количества, по которым компания терпит убытки. В следующем примере вы увидите, как информацию, которую вы узнали о системах линейного неравенства, можно применить для ответа на вопросы о затратах и доходах. Обратите внимание, как заштрихованная синим цветом область между уравнениями затрат и доходов обозначена как «Прибыль». Это «золотая середина», которую компания хочет достичь, когда они производят достаточное количество велосипедных рам с минимальными затратами, чтобы зарабатывать деньги.Они не хотят, чтобы выходило больше денег, чем приходило! Определите область прибыли для бизнеса по производству скейтбордов с помощью неравенств, учитывая систему линейных уравнений: Стоимость: [латекс] y = 0,85x + 35,000 [/ латекс] Доход: [латекс] y = 1,55x [/ латекс] Мы знаем, что графически решения линейных неравенств представляют собой целые области, и мы узнали, как графически отображать системы линейных неравенств ранее в этом модуле.Основываясь на приведенном ниже графике и уравнениях, определяющих затраты и выручку, мы можем использовать неравенства для определения региона, в котором производитель скейтбордов будет получать прибыль. Начнем с уравнения дохода. Мы знаем, что точка безубыточности находится на (50,000, 77,500), а область прибыли — это синяя область. Если мы выберем точку в регионе и протестируем ее, как мы это делали для поиска областей решения неравенств, мы будем знать, какой знак неравенства использовать. Давайте проверим точку [латекс] \ влево (65,00,100,000 \ вправо) [/ латекс] в обоих уравнениях, чтобы определить, какой знак неравенства использовать. Стоимость: [латекс] \ begin {array} {l} y = 0,85x + {35 000} \\ {100 000} \ text {? } 0,85 \ влево (65,000 \ вправо) +35,000 \\ 100,000 \ text {? } 90,250 \ end {array} [/ latex] Нам нужно использовать>, потому что 100,000 больше 90,250 Неравенство затрат, которое обеспечит получение компанией прибыли, а не только безубыточности, составляет [латекс] y> 0,85x + 35,000 [/ латекс] Теперь проверьте точку в уравнении доходов: Выручка: [латекс] \ begin {array} {l} y = 1.55x \\ 100,000 \ text {? } 1,55 \ влево (65 000 \ вправо) \\ 100 000 \ text {? } 100,750 \ end {array} [/ latex] Нам нужно использовать <, потому что 100,000 меньше 100,750 Неравенство доходов, которое обеспечит получение компанией прибыли, а не только безубыточности, составляет [латекс] y <1,55x [/ латекс] Система неравенств, определяющая область прибыли производителя велосипеда: [латекс] \ begin {array} {l} y> 0,85x + 35,000 \\ y <1,55x \ end {array} [/ latex] Стоимость производства 50 000 единиц составляет 77 500 долларов США, а выручка от продажи 50 000 единиц также составляет 77 500 долларов США.Чтобы получить прибыль, бизнес должен произвести и продать более 50 000 единиц. Система линейных неравенств, которая представляет количество единиц, которые компания должна произвести, чтобы получить прибыль: [латекс] \ begin {array} {l} y> 0,85x + 35,000 \\ y <1,55x \ end {array} [/ latex] В следующем видео вы увидите пример того, как найти точку безубыточности для небольшого бизнеса по производству снобоксов. А вот еще один видео-пример решения приложения с использованием системы линейных неравенств. Мы увидели, что системы линейных уравнений и неравенств могут помочь определить поведение рынка, которое очень полезно для бизнеса. Пересечение уравнений затрат и доходов дает точку безубыточности, а также помогает определить регион, в котором компания будет получать прибыль. Прежде чем решать системы линейных неравенств , давайте посмотрим, что означает неравенство.Слово неравенство означает математическое выражение, в котором стороны не равны друг другу. Как правило, для представления уравнений неравенства используются пять символов неравенства. Это меньше (<), больше (>), меньше или равно (≤), больше или равно (≥) и символ «не равно» (≠). Неравенства используются для сравнения чисел и определения диапазона или диапазонов значений, которые удовлетворяют условиям данной переменной. Система линейных неравенств — это система уравнений линейных неравенств, содержащих одинаковые переменные. Несколько методов решения систем линейных уравнений переводятся в систему линейных неравенств. Однако решение системы линейных неравенств несколько отличается от линейных уравнений, потому что знаки неравенства мешают нам решить с помощью метода замены или исключения. Возможно, лучший метод решения систем линейных неравенств — это графическое отображение неравенств. Ранее вы научились решать простое линейное неравенство с помощью построения графиков.В этой статье мы узнаем, как найти решения для системы линейных неравенств путем одновременного построения графиков двух или более линейных неравенств. Решением системы линейных неравенств является область, в которой пересекаются графики всех линейных неравенств в системе. Чтобы решить систему неравенств, изобразите каждое линейное неравенство в системе на одной оси x-y, выполнив следующие шаги: : Давайте рассмотрим пару примеров, чтобы понять эти шаги. Пример 1 Изобразите следующую систему линейных неравенств: y ≤ x — 1 и y <–2x + 1 Решение Изобразите первое неравенство y ≤ x — 1. Следовательно, решением этой системы неравенств является более темная заштрихованная область, продолжающаяся вечно в направлении вниз, как показано ниже. Пример 2 Решите следующую систему неравенств: x — 5y ≥ 6 3x + 2y> 1 Решение Для x — 5y ≥ 6; => x ≥ 6 + 5y => 5y ≤ x — 6 => y ≤ 0.2 x — 1,2 А для 3x + 2y> 1; => 2y> 1 — 3x => y> 0,5 — 1,5x Решение системы неравенства — более темная заштрихованная область, которая является перекрытием двух отдельных областей решения. Пример 3 Изобразите следующую систему линейных неравенств. y ≤ (1/2) x + 1, y ≥ 2x — 2, y ≥ — (1/2) x — 3. Решение Эта система неравенств имеет три уравнения, которые все связаны символом «равно». Это говорит нам о том, что все границы будут прочными. График трех неравенств показан ниже. Заштрихованная область трех уравнений перекрывается прямо в средней части. Следовательно, решения системы лежат в ограниченной области, как показано на графике. Пример 4 Изобразите следующую систему линейных неравенств: x + 2y <2, y> –1, x ≥ –3. Решение Выделите переменную y в первом неравенстве, чтобы получить; y <- x / 2 +1 Обратите внимание, что неравенства y> –1 и x ≥ –3 будут иметь горизонтальные и вертикальные граничные линии соответственно. Давайте изобразим три неравенства, как показано ниже. Более темная заштрихованная область, ограниченная двумя сегментами пунктирной линии и одним сегментом сплошной линии, дает три неравенства. Пример 5 Решите следующую систему линейных неравенств: –2x -y <-1 4x + 2y ≤-6 Решение Изолировать переменную y в каждом неравенство. –2x -y <-1 => y> –2x + 1 4x + 2y ≤ -6 => y ≤ -2x -3 Давайте продолжим и построим график y> –2x + 1 и y ≤ — 2x -3: Поскольку заштрихованные области двух неравенств не перекрываются, мы можем сделать вывод, что система неравенств не имеет решения. Методы решения систем линейных неравенств отличаются от методов решения линейных уравнений, потому что знаки неравенства не позволяют нам выполнять замену, как мы это делаем с уравнениями. Тем не менее, мы все еще можем решить эти проблемы. Ключевые термины o Система линейных неравенств o Линейная оптимизация o Линейное программирование Цели o Научиться решать задачи, связанные с системами линейных неравенств o Понять базовый подход к решению задач линейной оптимизации. Системы линейных неравенств Система линейных неравенств включает несколько выражений, решение которых может дать ряд решений. Многие концепции, которые мы усвоили при изучении систем линейных уравнений, можно преобразовать в решение системы линейных неравенств, но этот процесс может быть несколько сложным. Возможно, наиболее наглядный способ одновременного решения набора линейных неравенств — использование графиков.Давайте сразу рассмотрим пример в двух измерениях. 2 x -5 y ≤ 3 y — 3 x ≤ 1 Из-за неравенства мы не можем использовать подстановку так же, как мы это делали с системами линейных уравнений. Посмотрим на графики этих неравенств. Во-первых, мы упрощаемся до формы, которую легко построить графически. 2 x -5 y ≤ 3 y -3 x ≤ 1 2 x ≤ 3 + 5 y y ≤ 3 x + 1 5 y ≥ 2 x — 3 y ≥ 0.4 х — 0,6 Теперь построим график этих неравенств. На графике видно, что есть две заштрихованные области, соответствующие решениям каждого неравенства. Линии заштрихованы, потому что неравенства не строгие (используются ≥ и ≤). Решением системы неравенств является более темная заштрихованная область, которая представляет собой перекрытие двух отдельных областей, и части линий (лучей), которые граничат с этой областью.Символически мы, пожалуй, лучше всего можем выразить решение в этом случае как 0,4 x — 0,6 ≤ y ≤ 3 x + 1 Решение систем неравенств в трех или более измерениях возможно, но это намного сложнее — построить графики твердых областей, которые составляют решения, также сложнее. Практическая задача: Найдите и изобразите на графике множество решений следующей системы неравенств: x -5 y ≥ 6 3 x + 2 y > 1 Решение : Сначала решим выражения для y . x — 5 y ≥ 6 3 x + 2 y > 1 x ≥ 6 + 5 y 2 y > 1-3 x 5 y ≤ x — 6 y > 0,5 — 1,5 x y ≤ 0,2 x — 1,2 Тогда мы можем выразить решение этой системы неравенств следующим образом: 0.5 — 1,5 x < y ≤ 0,2 x — 1,2 Построим график набора решений. Сначала мы нанесем на график линии, соответствующие двум отдельным неравенствам (и выберем сплошную линию для первого и ломаную для второго), а затем соответствующим образом закрасим две области. Решение представляет собой более темную заштрихованную область (которая является перекрытием двух отдельных областей решения), но давайте изобразим ее отдельно, чтобы было немного четче. Линейная оптимизация Мы можем применить то, что мы узнали выше, к линейной оптимизации (также называемой линейным программированием ), которая представляет собой процесс поиска максимального или минимального значения для некоторой функции при определенных условиях (например, линейных неравенствах). Решение задач, связанных с линейной оптимизацией, не требует от вас приобретения каких-либо новых навыков; они просто требуют, чтобы вы применяли то, что уже знаете.Итак, перейдем к практической задаче. Практическая задача: Найдите максимальное значение y при –3 x + 2 y ≤ 4 и x + y ≤ 1 при условии, что x ≥ 0. Решение: Нам дана система неравенств, для которой мы должны сначала найти соответствующее множество решений. В этом наборе решений мы можем найти максимальное значение y .Итак, мы можем сначала применить то, что мы уже знаем: давайте перестроим неравенства в форму, которую мы можем легко изобразить. –3 x + 2 y ≤ 4 x + y ≤ 1 x ≥ 0 2 y ≤ 3 x + 4 y ≤ 1- x y ≤ 1,5 x + 2 Теперь давайте изобразим каждое из этих неравенств, отмечая, что мы должны использовать сплошные линии в каждом случае. Самая темная заштрихованная область (клин в правом нижнем углу графика) удовлетворяет всем ограничениям задачи. Затем мы хотим найти максимальное значение y , которое явно равно 1. (Мы также можем найти это значение, подставив x = 0 в x + y ≤ 1 и найдя максимальное значение y. , что также явно 1.) Мы знаем, что линейное уравнение с двумя переменными имеет бесконечно много упорядоченных парных решений, которые на графике образуют линию.С другой стороны, линейное неравенство с двумя переменными имеет набор решений, состоящий из области, определяющей половину плоскости. Рисунок \ (\ PageIndex {1} \) Рисунок \ (\ PageIndex {2} \) Для неравенства линия определяет одну границу заштрихованной области.Это означает, что любая упорядоченная пара, находящаяся в заштрихованной области, включая граничную линию, будет удовлетворять неравенству. Чтобы убедиться в этом, выберите несколько контрольных точек и подставьте их в неравенство. Кроме того, мы можем видеть, что упорядоченные пары вне заштрихованной области не решают линейное неравенство. \ (\ begin {array} {c | c} {\ underline {\ color {Cerulean} {Test \: point}}} & {\ underline {y \ leq \ frac {3} {2} x + 3} } \\ {(- 2,3)} & {3 \ leq \ frac {3} {2} (- 2) +3} \\ {} & {3 \ leq -3 + 3} \\ {} & {3 \ leq 0 \ quad \ color {red} {x}} \ end {array} \) График решения, установленного для линейного неравенства, всегда является областью. Однако граница не всегда может быть включена в этот набор. В предыдущем примере линия была частью набора решений из-за части «или равно» во включительном неравенстве \ (≤ \).Если у нас есть строгое неравенство \ (<\), мы использовали бы пунктирную линию, чтобы указать, что эти точки не включены в набор решений. Рисунок \ (\ PageIndex {3} \) Рисунок \ (\ PageIndex {4} \) Рассмотрим точку \ ((0, 3) \) на границе; эта упорядоченная пара удовлетворяет линейному уравнению.Это часть инклюзивного неравенства «или равно» делает его частью набора решений. \ (\ begin {array} {c | c} {\ underline {y <\ frac {3} {2} x + 3}} & {\ underline {y \ leq \ frac {3} {2} x + 3}} \\ {3 <\ frac {3} {2} (0) +3} & {3 \ leq \ frac {3} {2} (0) +3} \\ {3 <0 + 3} & {3 \ leq 0 + 3} \\ {3 <3 \ quad \ color {red} {x}} & {3 \ leq 3 \ quad \ color {Cerulean} {\ checkmark}} \ end {array} \ ) До сих пор мы видели примеры неравенства «меньше». Теперь рассмотрим следующие графы с той же границей: Рисунок \ (\ PageIndex {5} \) Рисунок \ (\ PageIndex {6} \) Учитывая приведенные выше графики, чего можно ожидать, если мы используем начало координат \ ((0, 0) \) в качестве контрольной точки? \ (\ begin {array} {c | c} {\ underline {y \ geq \ frac {3} {2} x + 3}} & {\ underline {y \ leq \ frac {3} {2} x +3}} \\ {0 \ geq \ frac {3} {2} (0) +3} и {0 \ leq \ frac {3} {2} (0) +3} \\ {0 \ geq 0 +3} & {0 \ leq0 + 3} \\ {0 \ geq 3 \ quad \ color {red} {x}} & {0 \ leq 3 \ quad \ color {Cerulean} {\ checkmark}} \ end { массив} \) Упражнение \ (\ PageIndex {1} \) Какая из упорядоченных пар \ ((- 2, −1), (0, 0), (−2, 8), (2, 1), \) и \ ((4, 2) \) решает неравенство \ (y> — \ frac {1} {2} x + 2 \)? \ ((- 2, 8) \) и \ ((4, 2) \) Решения линейных неравенств представляют собой заштрихованную полуплоскость, ограниченную сплошной или пунктирной линией.Эта граница либо входит в решение, либо нет, в зависимости от заданного неравенства. Если нам дано строгое неравенство, мы используем пунктирную линию, чтобы указать, что граница не включена. Если нам дано инклюзивное неравенство, мы используем сплошную линию, чтобы указать, что оно включено. Шаги для построения графика набора решений для неравенства с двумя переменными описаны в следующем примере. Пример \ (\ PageIndex {1} \) График набора решений: \ (у> −3x + 1 \). Решение : Шаг 1 : Постройте граничную линию. В этом случае изобразите пунктирную линию \ (y = −3x + 1 \) из-за строгого неравенства. При осмотре мы видим, что наклон равен \ (m = −3 = — \ frac {3} {1} = \ frac {rise} {run} \), а точка пересечения \ (y \) — \ ((0 , 1) \). Рисунок \ (\ PageIndex {7} \) Шаг 2 : Проверьте точку , а не на границе. Обычная контрольная точка — начало координат \ ((0, 0) \).Контрольная точка помогает нам определить, какую половину плоскости затенить. \ (\ begin {array} {c | c} {\ underline {\ color {Cerulean} {Test \: point}}} & {\ underline {y> -3x + 1}} \\ {(0,0 )} & {0> -3 (0) +1} \\ {} & {0> 1 \ quad \ color {red} {x}} \ end {array} \) Шаг 3 : Закрасьте область, содержащую растворы. Поскольку контрольная точка \ ((0, 0) \) не была решением, она не лежит в области, содержащей все упорядоченные парные решения. Поэтому заштрихуйте половину плоскости, на которой нет этой контрольной точки.В этом случае заштрихуйте линию выше границы. Ответ : Рисунок \ (\ PageIndex {8} \) Рассмотрим проблему затенения выше или ниже граничной линии, когда неравенство имеет форму пересечения уклона. Если \ (y> mx + b \), то заштрихуйте над линией. Если \ (y Пример \ (\ PageIndex {2} \) График набора решений: \ (2x − 5y≥ − 10 \). Решение : Здесь граница определяется линией \ (2x − 5y = −10 \). Поскольку неравенство носит инклюзивный характер, мы обозначим границу сплошной линией. В этом случае нарисуйте граничную линию, используя точки пересечения. Рисунок \ (\ PageIndex {9} \) Затем проверьте точку; это помогает решить, какую область затенять. \ (\ begin {array} {c | c} {\ underline {\ color {Cerulean} {Test \: point}}} & {\ underline {2x-5y \ geq -10}} \\ {(0, 0)} & {2 (0) -5 (0) \ geq -10} \\ {} & {0 \ geq -10 \ quad \ color {Cerulean} {\ checkmark}} \ end {array} \) Так как контрольная точка находится в наборе решений, заштрихуйте половину плоскости, которая ее содержит. Ответ : Рисунок \ (\ PageIndex {10} \) В этом примере обратите внимание, что набор решений состоит из всех упорядоченных пар ниже граничной линии. Это может показаться нелогичным из-за исходного \ (≥ \) в неравенстве. Это показывает, что лучше всего проверить точку. Решите для \ (y \), и вы увидите, что затенение правильное. В форме пересечения откоса вы можете видеть, что область под линией границы должна быть заштрихована.Альтернативный подход состоит в том, чтобы сначала выразить границу в форме пересечения наклона, нанести ее на график, а затем заштриховать соответствующую область. Пример \ (\ PageIndex {3} \) График набора решений: \ (у <2 \). Решение : Сначала изобразите граничную линию \ (y = 2 \) пунктирной линией из-за строгого неравенства. Рисунок \ (\ PageIndex {11} \) Теперь проверьте точку. \ (\ begin {array} {c | c} {\ underline {\ color {Cerulean} {Test \: point}}} & {\ underline {y <2}} \\ {(0,0)} & {0 <2 \ quad \ color {Cerulean} {\ checkmark}} \ end {array} \) В этом случае закрасьте область, содержащую тестовую точку. Ответ : Рисунок \ (\ PageIndex {12} \) Упражнение \ (\ PageIndex {2} \) График набора решений: \ (5x − y≤10 \). Рисунок \ (\ PageIndex {13} \) Линейные неравенства с двумя переменными имеют бесконечные множества или бесконечное множество упорядоченных парных решений. Эти упорядоченные пары или наборы решений можно изобразить в соответствующей половине прямоугольной координатной плоскости. Помогите Бобу определить, является ли (2,1 / 5) решением \ [2x + 5y <10 \] Решение Положим эти значения (2,1 / 5) в данное линейное неравенство. Это дает \ begin {уравнение} \ begin {уравнение} 4 + 1 <10 \ end {уравнение} \ begin {уравнение} 5 <10 \ end {уравнение} что верно. Мать Брука вручает ему 7 долларов на шоколадные конфеты. Она говорит ему потратить всего 7 долларов или меньше. Молочный шоколад стоит 2 доллара, а ореховый шоколад — 33 доллара. Пусть x будет количеством шоколадных конфет, а y — количеством шоколадных конфет с орехами. Сформируйте неравенство, соответствующее описанной выше ситуации, и нанесите его на график. Решение \ [2x + 3y ≤ 7 \] будет неравенством, соответствующим описанной выше ситуации. В этом случае мы построим сплошную линию как границу, соединяющую точки, которые удовлетворяют линейному уравнению \ [2x + 3y = 7 \] Для \ [2x + 3y = 7 \] Для неравенства \ [2x + 3y ≤ 7 \] Теперь положим x = 0, y = 0 Это дает 2 (0) + 3 (0) ≤ 7, что удовлетворяет неравенству. Итак, заштрихуйте полуплоскость на приведенном ниже графике линейного неравенства, который включает точку (0,0). Изобразите набор решений для \ [y> -5x + 2 \] Решение: \ [y> -5x + 2 \] — неравенство в форме пересечения наклона; наклон = -5, точка пересечения = 2. В этом случае мы построим пунктирную линию из-за того, что равенство меньше или равно равенству, как граница, соединяющая точки, которые удовлетворяют линейному уравнению \ [y = -5x + 2 \] Для \ [y = -5x + 2 \] Для неравенства \ [y> -5x + 2 \] Для \ [y> -5x + 2 \] положим x = 0, y = 0 Это дает 0> -5 (0) +2 , что дополнительно дает 0> 2 Это неверно для данного неравенства. Итак, закрасьте полуплоскость на приведенном ниже графике линейного неравенства, который не включает точку (0,0). Вот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат. Мы надеемся, что вам понравилось узнать, что такое линейные неравенства с двумя переменными, решение линейных неравенств с двумя переменными, построение графиков неравенств с двумя переменными, бесконечные множества, упорядоченные пары, больше или равно &, меньше или равно с помощью интерактивных вопросов. Теперь вы сможете легко находить ответы на линейные неравенства с двумя переменными и знать о решениях линейных неравенств. Мини-урок был посвящен увлекательной концепции линейного неравенства по двум переменным. Математическое путешествие по линейному неравенству по двум переменным начинается с того, что студент уже знает, и переходит к творческому созданию новой концепции в молодых умах. Сделано таким образом, чтобы не только было понятно и легко понять, но и навсегда осталось с ними. В этом заключается магия Куэмат. В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов! Благодаря интерактивному и увлекательному подходу к обучению-обучению-обучению учителя исследуют тему со всех сторон. Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, мы в Cuemath верим в логическое мышление и интеллектуальный подход к обучению. Система линейных неравенств с двумя переменными относится к набору как минимум двух линейных неравенств с одинаковыми переменными. График линейных уравнений включает сплошную линию в каждой ситуации, тогда как в случае линейных неравенств график включает пунктирную или сплошную линию. Кроме того, линейные неравенства включают заштрихованные области, а линейные уравнения — нет. Примером линейного неравенства может быть любое линейное уравнение, но с такими символами, как <,>, ≤ или ≥ вместо =. В линейных неравенствах используются следующие символы: <, ≤,> и ≥. Линейное неравенство — это неравенство, имеющее линейную функцию, состоящую из одного из символов неравенства. Когда две стороны уравнения имеют знак, отличный от равного. Система линейных неравенств часто используется для определения максимальных или минимальных значений ситуации с множественными ограничениями. Пять символов неравенства: ≠ = не равно,> = больше, <= меньше, ≥ = больше или равно & ≤ = меньше или равно. В неравенствах R соответствует действительным числам и включает все действительные числа. Если y> mx + b, то заштрихуйте над линией.Если y
Если y> mx + b, то заштрихуйте над линией.Если y Пример 3

 у≤25x + 2
у≤25x + 2 Пример 4

Пример 5

Пример 6
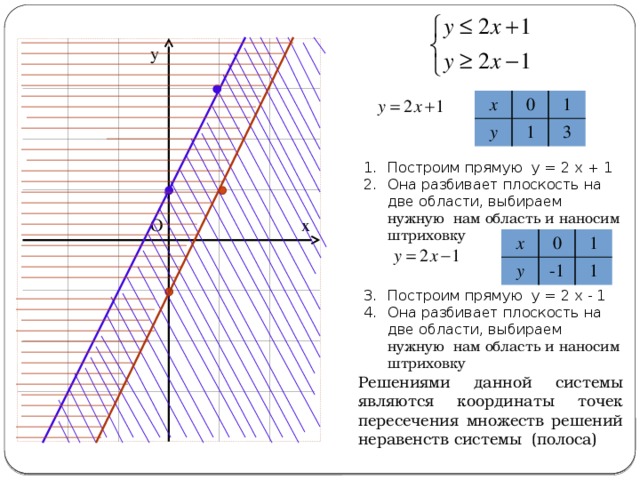
Основные выводы
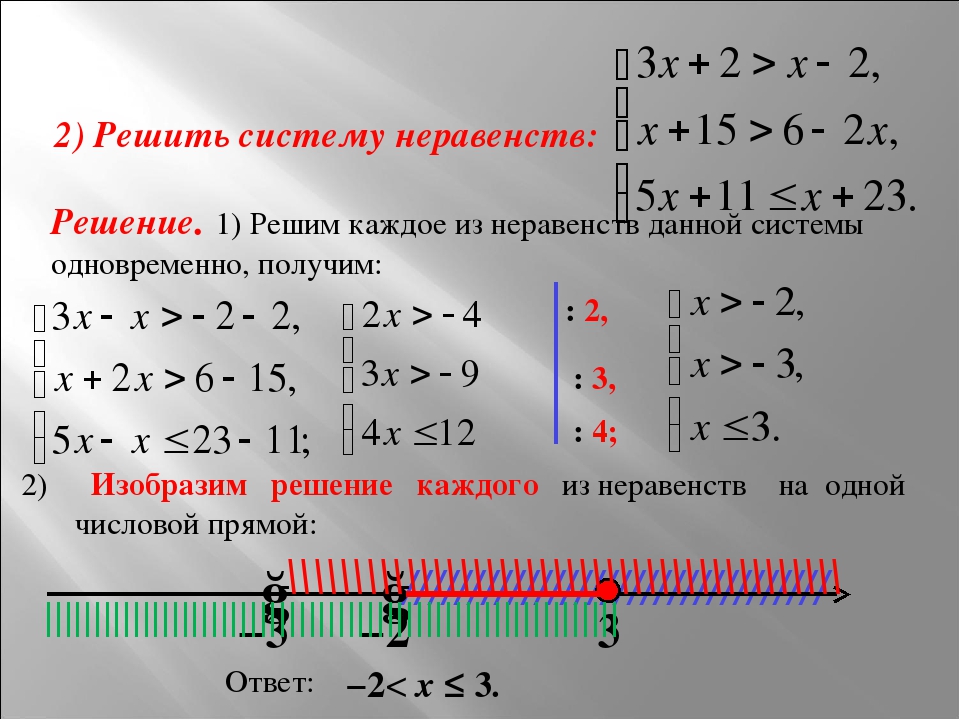
Тематические упражнения
Часть A: Решение неравенств с двумя переменными
Часть B: Графические решения неравенств с двумя переменными.

Графические системы линейных неравенств
Линейные неравенства и системы линейных неравенств от двух переменных
Цели обучения
Неравенства по двум переменным
Графическое изображение неравенств
Графическое изображение линейных неравенств с двумя переменными
Пример
x y 0 [латекс] −3 [/ латекс] 2 1
[latex] 2y> 4x – 6 [/ latex] и посмотрите, какая упорядоченная пара дает истинное утверждение. Поскольку [latex] (- 3,1) [/ latex] приводит к истинному утверждению, область, которая включает [latex] (- 3,1) [/ latex], должна быть заштрихована. Ответ
Наборы решений неравенств
Заказанная пара Делает неравенство Делает неравенство [латекс] (- 5, 5) [/ латекс] [латекс] \ begin {array} {r} 3 \ left (−5 \ right) +2 \ left (5 \ right) \ leq6 \\ — 15 + 10 \ leq6 \\ — 5 \ leq6 \ end {массив } [/ латекс] [латекс] (- 2, -2) [/ латекс] [латекс] \ begin {array} {r} 3 \ left (−2 \ right) +2 \ left (–2 \ right) \ leq6 \\ — 6+ \ left (−4 \ right) \ leq6 \\ –10 \ leq6 \ end {array} [/ latex] [латекс] (2,3) [/ латекс] [латекс] \ begin {array} {r} 3 \ left (2 \ right) +2 \ left (3 \ right) \ leq6 \\ 6 + 6 \ leq6 \\ 12 \ leq6 \ end {array} [/ латекс] [латекс] (2,0) [/ латекс] [латекс] \ begin {array} {r} 3 \ left (2 \ right) +2 \ left (0 \ right) \ leq6 \\ 6 + 0 \ leq6 \\ 6 \ leq6 \ end {array} [/ латекс] [латекс] (4, -1) [/ латекс] [латекс] \ begin {array} {r} 3 \ left (4 \ right) +2 \ left (-1 \ right) \ leq6 \\ 12+ \ left (-2 \ right) \ leq6 \\ 10 \ leq6 \ end {array} [/ latex] Пример
Ответ
Пример
Ответ
Изобразите систему двух неравенств
Определить, является ли упорядоченная пара решением системы линейных неравенств
Пример
Ответ
Пример
Ответ
Системы без решений
Примеры
Пример
Ответ
Пример
Ответ
Приложения
Пример
Ответ
Пример
Ответ
Система линейных неравенств — объяснение и примеры
Что такое система линейных неравенств?
Как решать системы линейных неравенств?
Решение систем линейных неравенств
3.8: Линейные неравенства (две переменные)
Решения линейных неравенств
Линейное уравнение Линейное неравенство \ (y = \ frac {3} {2} x + 3 \) \ (у \ leq \ frac {3} {2} x + 3 \) \ (\ color {Cerulean} {Test \: point} \) \ (у \ leq \ frac {3} {2} x + 3 \) \ ((0,0) \) \ (\ begin {align} 0 & \ leq \ frac {3} {2} (0) +3 \\ 0 & \ leq 3 \ quad \ color {Cerulean} {\ checkmark} \ end {align} \) \ ((2,1) \) \ (\ begin {align} 1 & \ leq \ frac {3} {2} (2) +3 \\ 1 & \ leq 3 + 3 \\ 1 & \ leq 6 \ quad \ color {Cerulean} {\ checkmark} \ конец {выровнен} \) \ ((- 2, -1) \) \ (\ begin {align} -1 & \ leq \ frac {3} {2} (- 2) +3 \\ -1 & \ leq -3 + 3 \\ -1 & \ leq 0 \ quad \ color {Cerulean} {\ checkmark} \ end {align} \) Неисключительная граница Граница включительно \ (y <\ frac {3} {2} x + 3 \) \ (у \ leq \ frac {3} {2} x + 3 \) Больше, чем (вверху) Меньше (ниже) \ (y \ geq \ frac {3} {2} x + 3 \) \ (у \ leq \ frac {3} {2} x + 3 \) Графические решения линейных неравенств
линейных неравенств по двум переменным | Графики и уравнения | Примеры
Решенные примеры
2 (2) +5 (1/5) <10
\ end {Equation} \ (\ следовательно \) Таким образом (2,1 / 5) является решением \ [2x + 5y <10 \] x 2 5 -7 л 1 -1 7 x 0 1 2 -1 л 2 -3 -8 7
Интерактивные вопросы
Подведем итоги
Часто задаваемые вопросы о n Линейные неравенства в двух переменных 1. Что такое система линейных неравенств двух переменных?
2.Как отличить линейные неравенства с двумя переменными от линейных уравнений с двумя переменными?
3. Какой пример линейного неравенства?
4. Какие символы используются в линейных неравенствах?
5. Что означают линейные неравенства?
6. Как определить линейное неравенство?
7. Какая польза от линейных неравенств?
8. Какие 5 символов неравенства?
9. Что означает R в неравенстве?


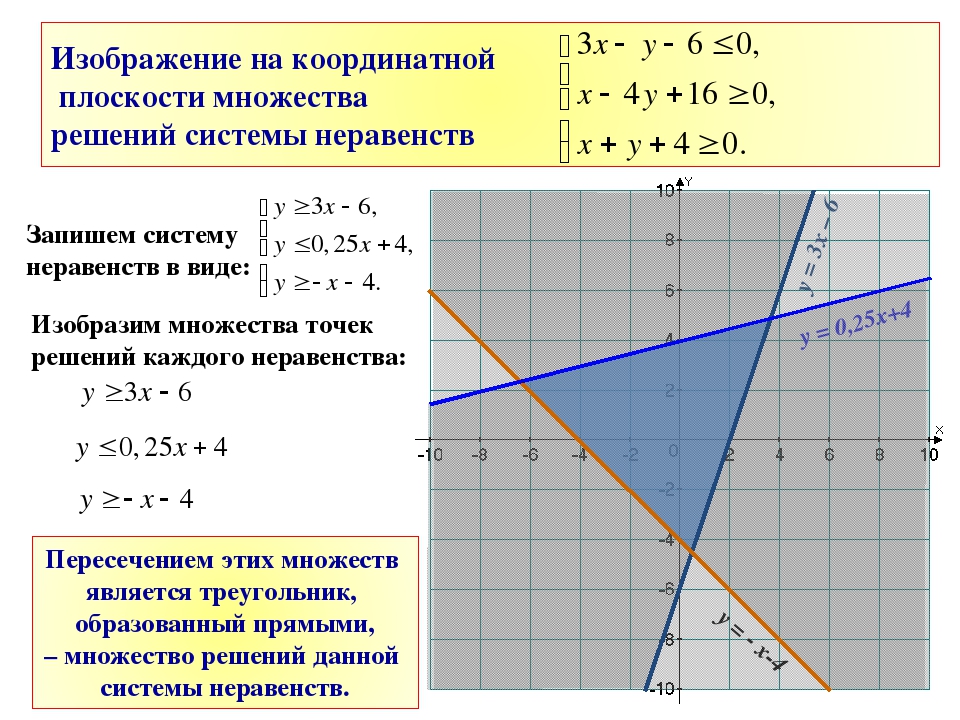 Метод замены
Метод замены

 Дробно-рациональное неравенство
Дробно-рациональное неравенство Пример, в котором нужно решить систему
Пример, в котором нужно решить систему


 Сложение и вычитание рациональных дробей с одинаковыми знаменателями
Сложение и вычитание рациональных дробей с одинаковыми знаменателями
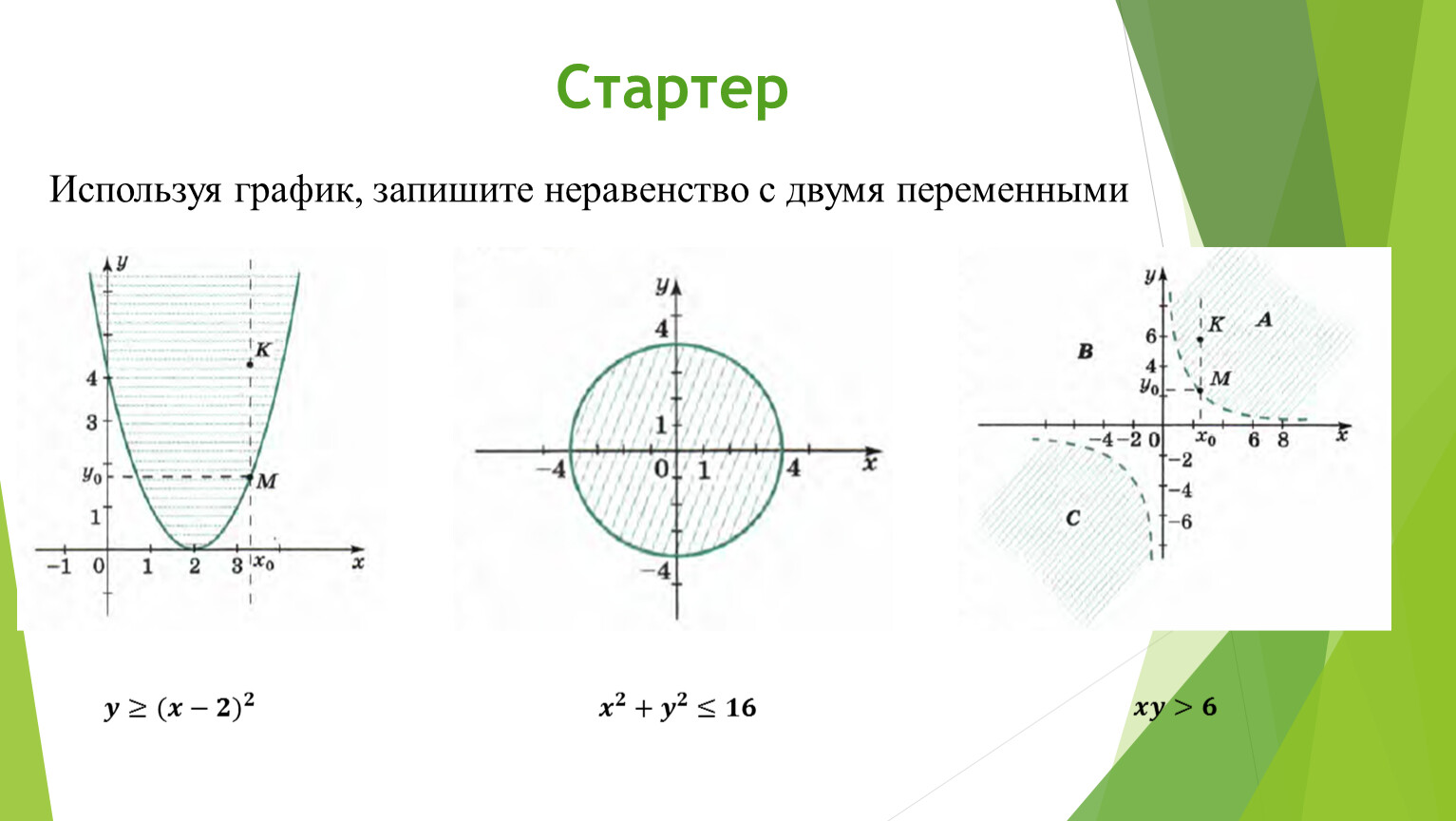
 Нахождение производной в точке
Нахождение производной в точке После этой исследования построить ее график.
После этой исследования построить ее график. Алгебраические выражения
Алгебраические выражения
 Числовые промежутки
Числовые промежутки
 Метод подстановки
Метод подстановки
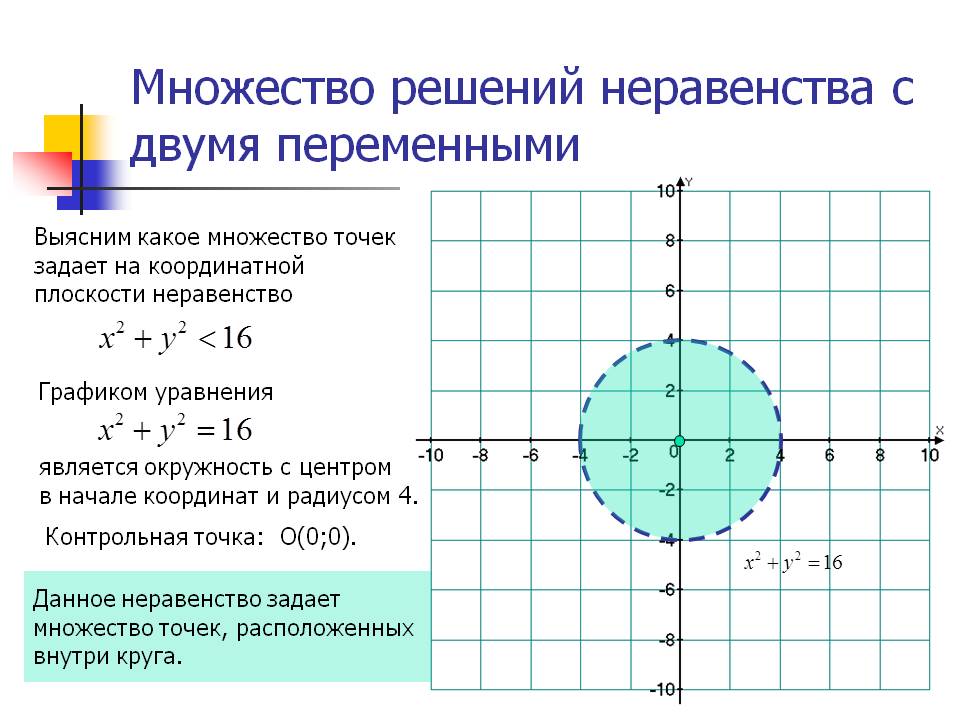 Приведение одночлена к стандартному виду
Приведение одночлена к стандартному виду
 Приведение многочлена к стандартному виду
Приведение многочлена к стандартному виду
 Вынесение общего множителя за скобки
Вынесение общего множителя за скобки
 Парабола
Парабола
 Свойства неравенств одинакового смысла
Свойства неравенств одинакового смысла
 Объединение и пересечение множеств
Объединение и пересечение множеств
 Определение чётности и нечётности
Определение чётности и нечётности
 Способы задания последовательностей
Способы задания последовательностей
 Комбинаторные задачи
Комбинаторные задачи
 Повторение
Повторение
 Решение уравнений tg x = a, ctg x = a
Решение уравнений tg x = a, ctg x = a
 Общее правило
Общее правило
 Предел функции на бесконечности
Предел функции на бесконечности
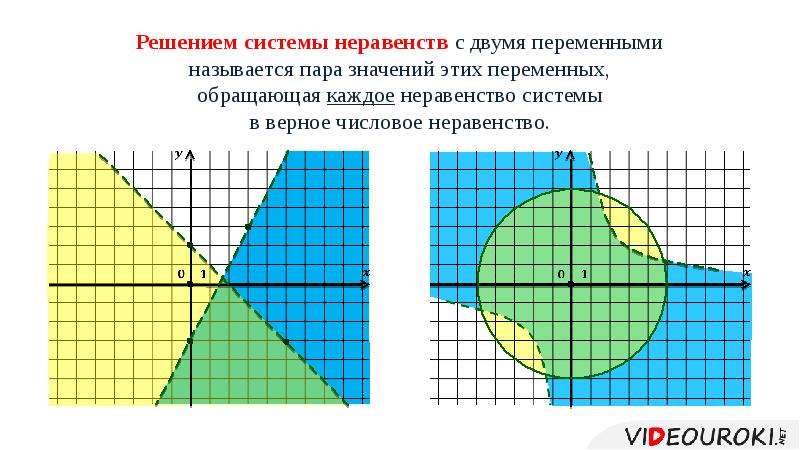 Преобразование иррациональных выражений
Преобразование иррациональных выражений
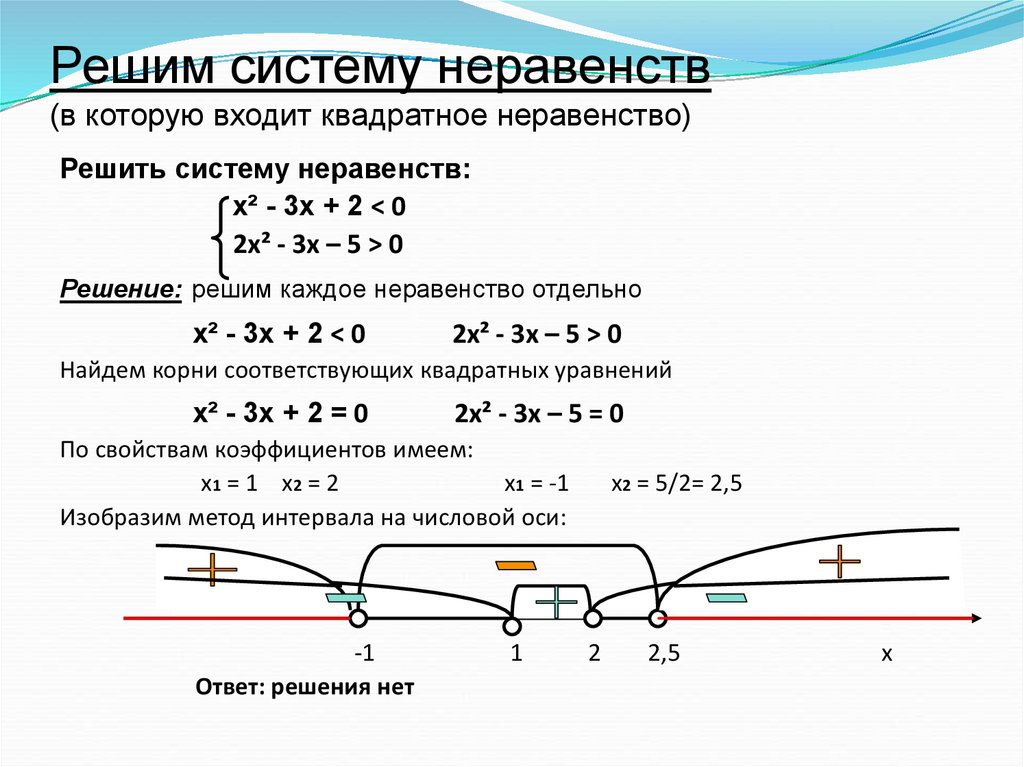 Основное логарифмическое тождество
Основное логарифмическое тождество
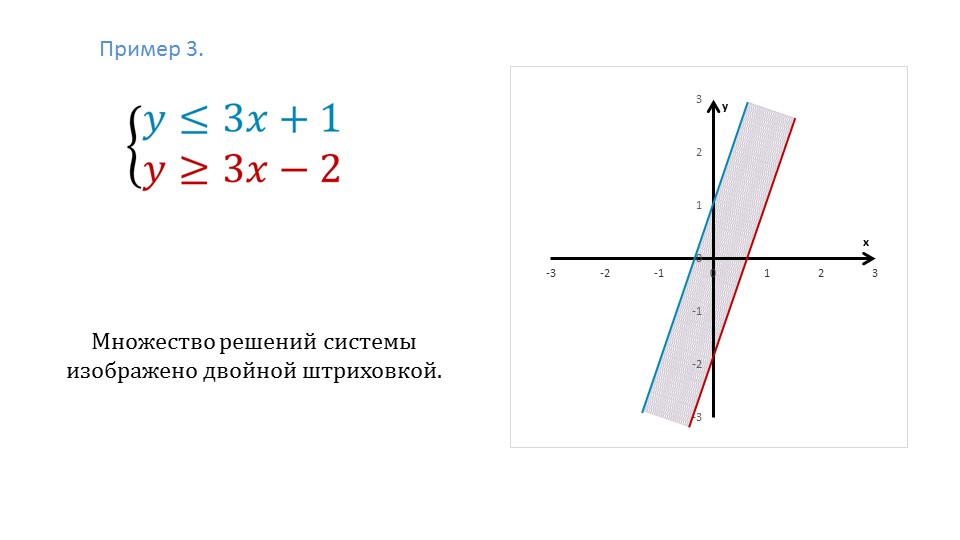 Методы интегрирования
Методы интегрирования
 Перестановки без повторений
Перестановки без повторений
 Противоположные события
Противоположные события
 Закон больших чисел
Закон больших чисел
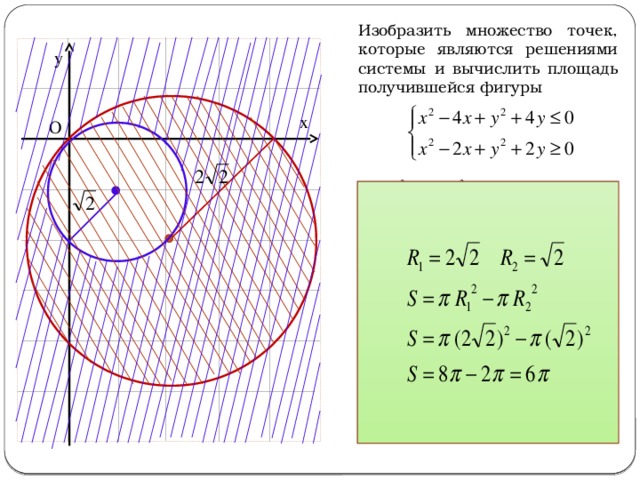 Контрольная точка помогает нам определить, какую половину плоскости затенить.
Контрольная точка помогает нам определить, какую половину плоскости затенить.