Производная функции, заданной неявно
Будем учиться находить производные функций, заданных неявно, то есть заданных некоторыми уравнениями, связывающими между собой переменные x и y. Примеры функций, заданных неявно:
,
,
,
,
.
Производные функций, заданных неявно, или производные неявных функций, находятся довольно просто. Сейчас же разберём соответствующее правило и пример, а затем выясним, для чего вообще это нужно.
Для того, чтобы найти производную функции, заданной неявно, нужно продифференцировать обе части уравнения по иксу. Те слагаемые, в которых присутствует только икс, обратятся в обычную производную функции от икса. А слагаемые с игреком нужно дифференцировать, пользуясь правилом дифференцирования сложной функции, так как игрек — это функция от икса. Если совсем просто, то в полученной производной слагаемого с иксом должно получиться: производная функции от игрека, умноженная на производную от игрека. Например, производная слагаемого запишется как , производная слагаемого запишется как . Далее из всего этого нужно выразить этот «игрек штрих» и будет получена искомая производная функции, заданной неявно. Разберём это на примере.
Пример 1. Найти производную функции, заданной неявно:
.
Решение. Дифференцируем обе части уравнения по иксу, считая, что игрек — функция от икса:
.
Отсюда получаем производную, которая требуется в задании:
.
Теперь кое-что о неоднозначном свойстве функций, заданных неявно, и почему нужны особенные правила их дифференцирования. В части случаев можно убедиться, что подстановка в заданное уравнение (см. примеры выше) вместо игрека его выражения через икс приводит к тому, что это уравнение обращается в тождество. Так. приведённое выше уравнение неявно определяет следующие функции:
,
.
После подстановки выражения игрека в квадрате через икс в первоначальное уравнение получаем тождество:
.
Выражения, которые мы подставляли, получились путём решения уравнения относительно игрека.
Если бы мы стали дифференцировать соответствующую явную функцию
,
то получили бы ответ как в примере 1 — от функции, заданной неявно:
.
Но не всякую функцию, заданную неявно, можно представить в виде y = f(x). Так, например, заданные неявно функции
и
не выражаются через элементарные функции, то есть эти уравнения нельзя разрешить относительно игрека. Поэтому и существует правило дифференцирования функции, заданной неявно, которое мы уже изучили и далее будем последовательно применять в других примерах.
Пример 2. Найти производную функции, заданной неявно:
.
Решение. Дифференцируем обе части уравнения по иксу:
.
Выражаем игрек штрих и — на выходе — производная функции, заданной неявно:
.
Пример 3. Найти производную функции, заданной неявно:
.
Решение. Дифференцируем обе части уравнения по иксу:
.
Выражаем и получаем производную:
.
Пример 4.
Найти производную функции, заданной неявно:.
Решение. Дифференцируем обе части уравнения по иксу:
.
Выражаем и получаем производную:
.
Пример 5. Найти производную функции, заданной неявно:
.
Решение. Переносим слагаемые в правой части уравнение в левую часть и справа оставляем ноль. Дифференцируем обе части уравнения по иксу:
Путь к ответу и в конец сам ответ:
Поделиться с друзьями
Производные
Функции несольких переменных
function-x.ru
Производная неявной функции, формула и примеры
ОПРЕДЕЛЕНИЕ Если функция задана уравнением то говорят, что она задана неявно.Для нахождения производной неявно заданной функции нет необходимости преобразовывать ее в явную форму (и это не всегда возможно сделать). Для этого, зная уравнение достаточно выполнить следующие действия:
- Сначала необходимо продифференцировать обе части уравнения по независимой переменной предполагая, что – это дифференцируемая по функция. Для нахождения производной используется правило вычисления производной от сложной функции. В правой части равенства получаем 0, как производную от константы.
Замечание. Если правая часть отлична от нуля, то есть неявное уравнение имеет вид то функцию следует перенести влево и свести исходное уравнение к виду
- Решить полученное уравнение относительно производной
Примеры вычисления производных неявных функций
ПРИМЕР 1| Задание | Найти производную от функции заданной неявно. |
| Решение | Перенесем выражение стоящее в правой части равенства, в левую часть:
Далее дифференцируем левую и правую часть последнего равенства:
Используя свойство линейности производной, получим:
Первое слагаемое дифференцируем как произведение:
при этом считаем, что есть функция от поэтому производную от него находим как производную от сложной функции:
Будем иметь:
Было учтено, что Итак, для заданной функции имеем:
Решаем полученное уравнение относительно функции
|
| Ответ |
| Задание | Найти производную от функции заданной неявно. |
| Решение |
Производная от суммы/разности функций равна сумме/разности производных, а также константу можно выносить за знак производной:
Находим производную каждого слагаемого в левой части последнего равенства:
Разрешаем полученное равенство относительно искомой производной
Отсюда
|
| Ответ |
| Понравился сайт? Расскажи друзьям! | |||
Производная неявно заданной функции
В предыдущей статье был рассмотрен вопрос нахождения производной функции, заданной в явном виде, то есть . Сейчас мы научимся находить производную от неявной функции.
Неявной называют функцию, заданную уравнением . То есть и связаны между собой, однако выразить отсюда не представляется возможным. Как в этом случае будет находиться производная?
Алгоритм такой:
- Дифференцируем левую и правую часть по , при этом дифференцируем как сложную функцию от (производная от будет ).
- Решаем полученное уравнение относительно производной, то есть выражаем .
Стоит заметить, что на практике в правой части уравнения совсем необязательно будет именно . Там можем быть и некоторое выражение от , . Понятно, что это выражение можно без проблем перенести влево и получить уравнение вида .
Пример 1. Найти производную функции
Решение
Действуем строго по алгоритму — дифференцируем левую и правую часть уравнения:
Первая часть работы выполнена. Теперь выражаем отсюда :
Всё, производная успешно найдена. В ответ запишем
[свернуть]
Пример 2. Найти производную функции
Решение
Снова дифференцируем и не забываем, что — сложная функция.
Решаем уравнение относительно :
[свернуть]
Пример 3. Найти производную функции
Решение
Теперь аккуратно выразим :
[свернуть]
Пример 4. Найти производную функции
РешениеЕсли продифференцировать левую и правую часть уравнения, то увидим, что получатся два выражения, производные от которые в таблице производных отсутствуют. Поступим следующим образом: прологарифмируем левую и правую часть, полагая, что , и , .
Теперь по свойству логарифма получаем:
Всё, сейчас с дифференцированием проблем быть не должно — нужно просто найти производные от двух произведений по соответствующей формуле:
И выражаем :
[свернуть]
Помимо первой производной, у неявной функции можно найти производные высших порядков (то есть 2го, 3го, 4го и т.д.). Покажем на паре примеров как это делается.
Пример 5. Найти вторую производную функции
Решение
Дифференцируем левую и правую часть уравнения:
Теперь выражаем отсюда :
Первая производная найдена, но нам нужна вторая. Поэтому дифференцируем еще раз исходное уравнение:
Решаем уравнение относительно :
Осталось лишь избавиться в правой части от , которое уже было найдено раньше. То есть вместо подставим :
Итак, вторая производная найдена. С ответом можно, конечно, попытаться поработать, сделать красивее, но мы этого делать не будем — лучше решим еще один пример 😉
[свернуть]
Пример 6. Найти третью производную функции
Решение
Вновь имеем дело с неявно заданной функцией. Дифференцируем:
Отсюда
Дифференцируем уравнение еще раз:
Выражаем :
Избавимся сразу от первой производной, используя равенство .
И, наконец, третий раз дифференцируем уравнение (не просчитаться бы 🙂 ).
Мда, задачи я придумал, конечно… Предлагаю, если у Вас есть желание, самостоятельно окончательно расписать эту третью производную. Добавлю только, что .
[свернуть]
На этом всё, принцип понятен. Тема несложная, если не связываться с производными высших порядков, а там нужно считать очень внимательно.
Удачи!
higher-math.ru
Производная неявной функции — доказательство
Производная первого порядка
Пусть функция задана неявным образом с помощью уравнения
(1) .
И пусть это уравнение, при некотором значении , имеет единственное решение . Пусть функция является дифференцируемой функцией в точке , причем
.
Тогда, при этом значении , существует производная , которая определяется по формуле:
(2) .
Доказательство
Для доказательства рассмотрим функцию как сложную функцию от переменной :
.
Применим правило дифференцирования сложной функции и найдем производную по переменной от левой и правой частей уравнения
(3) :
.
Поскольку производная от постоянной равна нулю и , то
(4) ;
.
Формула доказана.
Производные высших порядков
Перепишем уравнение (4), используя другие обозначения:
(4) .
При этом и являются сложными функциями от переменной :
;
.
Зависимость определяет уравнение (1):
(1) .
Находим производную по переменной от левой и правой части уравнения (4).
По формуле производной сложной функции имеем:
;
.
По формуле производной произведения:
.
По формуле производной суммы:
.
Поскольку производная правой части уравнения (4) равна нулю, то
(5) .
Подставив сюда производную , получим значение производной второго порядка в неявном виде.
Дифференцируя, аналогичным образом, уравнение (5), мы получим уравнение, содержащее производную третьего порядка :
.
Подставив сюда найденные значения производных первого и второго порядков, найдем значение производной третьего порядка.
Продолжая дифференцирование, можно найти производную любого порядка.
Примеры
Пример 1
Найдите производную первого порядка от функции, заданной неявно уравнением:
(П1) .
Решение по формуле 2
Находим производную по формуле (2):
(2) .
Перенесем все переменные в левую часть, чтобы уравнение приняло вид .
.
Отсюда .
Находим производную по , считая постоянной.
;
;
;
.
Находим производную по переменной , считая переменную постоянной.
;
;
;
.
По формуле (2) находим:
.
Мы можем упростить результат если заметим, что согласно исходному уравнению (П.1), . Подставим :
.
Умножим числитель и знаменатель на :
.
Решение вторым способом
Решим этот пример вторым способом. Для этого найдем производную по переменной левой и правой частей исходного уравнения (П1).
Применяем формулу производной сложной функции:
.
Применяем формулу производной дроби:
;
.
Применяем формулу производной сложной функции:
.
Дифференцируем исходное уравнение (П1).
(П1) ;
;
.
Умножаем на и группируем члены.
;
.
Подставим (из уравнения (П1)):
.
Умножим на :
.
Ответ
Пример 2
Найти производную второго порядка от функции , заданной неявно с помощью уравнения:
(П2.1) .
Решение
Дифференцируем исходное уравнение, по переменной , считая что является функцией от :
;
.
Применяем формулу производной сложной функции.
.
Дифференцируем исходное уравнение (П2.1):
;
.
Из исходного уравнения (П2.1) следует, что . Подставим :
.
Раскрываем скобки и группируем члены:
;
(П2.2) .
Находим производную первого порядка:
(П2.3) .
Чтобы найти производную второго порядка, дифференцируем уравнение (П2.2).
;
;
;
.
Подставим выражение производной первого порядка (П2.3):
.
Умножим на :
;
.
Отсюда находим производную второго порядка.
Ответ
Пример 3
Найти производную третьего порядка при от функции , заданной неявно с помощью уравнения:
(П3.1) .
Решение
Дифференцируем исходное уравнение по переменной считая, что является функцией от .
;
;
;
;
;
;
(П3.2) ;
Дифференцируем уравнение (П3.2) по переменной .
;
;
;
;
;
(П3.3) .
Дифференцируем уравнение (П3.3).
;
;
;
;
;
(П3.4) .
Из уравнений (П3.2), (П3.3) и (П3.4) находим значения производных при .
;
;
.
Ответ
.
Автор: Олег Одинцов. Опубликовано:
1cov-edu.ru
Найти производную неявно заданной функции
Неявная функция — это функция у от аргумента x, заданная уравнением F(x;y)=0, не разрешенным относительно y.
Чтобы найти производную неявно заданной функции:
1. Находим производную по x от левой части уравнения F(x;y)=0, с учетом того, что у — функция от x;
2. Полученное выражение приравниваем к нулю и решаем как уравнение относительно y’, то есть выражаем y’ через y и x.
Примеры. Найти производную неявно заданной функции:
1) x³+xy²+y³=0.
1. Это — неявная функция. Находим производную по x левой части равенства с учетом того, что y — функция от x:
(x³+xy²+y³)’=3x²+x’·y²+(y²)’·x+3y²·y’=3x²+y²+2y·y’·x+3y²·y’
2. Полученное выражение приравниваем к нулю и из него находим y’:
3x²+y²+2y·y’·x+3y²·y’=0
3x²+y²+y'(2xy+3y²)=0
y'(2xy+3y²)=-3x²-y²
2) siny=xy
1. Приводим зависимость к виду F(x;y)=0. Для этого переносим все слагаемые в левую часть: siny-xy=0. Теперь находим производную по x от левой части (не забывая о том, что y — функция от x):
(siny-xy)’=cosy-(x’·y+y’·x)=cosy-y-xy’.
2. Полученное выражение приравниваем к 0 и находим y’:
cosy-y-xy’=0
xy’=cosy-y
1. Приводим выражение к виду F(x;y)=0:
Теперь находим производную по x левой части (y=y(x)!):
2. Приравниваем получившееся выражение к нулю и решаем уравнение относительно y’:
Примеры для самопроверки. Найти производную неявно заданной функции:
1) xy²+x²y=5;
2) arctg(x+y)=y.
Показать решение
1) 1. xy²+x²y-5=0(xy²+x²y-5)’=x’·y²+(y²)’·x+(x²)’·y+y’·x²-0=y²+2yy’·x+2xy+x²y’=y'(2xy+x²)+y²+2xy.
2. y'(2xy+x²)+y²+2xy=0
y'(2xy+x²)=-y²-2xy
2) arctg(x+y)-y=0
www.matematika.uznateshe.ru
Производная неявно заданной функции, формулы и примеры решений
Задание. Найти вторую производную неявной функции .
Решение. Продифференцируем левую и правую часть заданного равенства, при этом помним, что является функцией переменной , поэтому производную от нее будем брать как производную от сложной функции. В итоге получаем:
Из полученного равенства выражаем :
Для нахождения второй производной продифференцируем равенство еще раз:
Подставив вместо найденное выше выражение, получаем:
После упрощения получаем:
Из полученного равенства выражаем вторую производную :
Ответ.
Больше примеров решений Решение производных онлайнwww.webmath.ru
4. Производная неявной функции
Определение 2. Если функция у = f(x), определенная на некотором интервале (а; b), такова, что уравнение F(x; y) = 0 при подстановке в него у = f(x) обращается в тождество относительно х, то функция y = f(x) называется неявно заданной уравнением F(x; y) = 0.
Чтобы
найти производную неявной функции у по
аргументу х, заданной уравнением F(x;
y)=0, необходимо продифференцировать
левую и правую части этого уравнения,
считая у функцией от х
.
Из полученного линейного уравнения
находим искомую производную .
.
Пример 3. Вычислить производную неявной функции.
x2 + x2y + y2x + y2 + 3 = 0.
Решение
2x
+ 2xy + x2
2y= 0
2y= 0
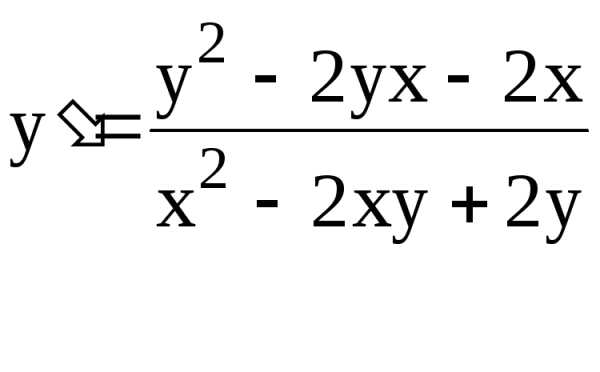
Вычислить производные неявных функций
75. x3 + y3 3xy = 0 76. x2 + y2 = 4
77. x4 6x2y2 + 9y4 = 100 78. Ax2 + 2Bxy + Cy2 = F
79. x sin y + y sin x = 0 80. ex + ey 2xy 1 = 0
81. 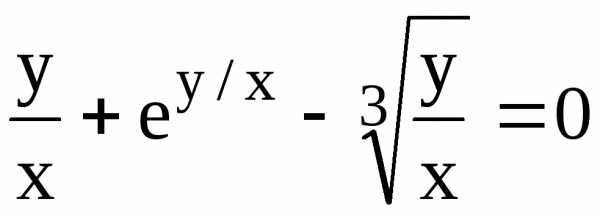 82. x2 sin
y + y2 cos x = 0
82. x2 sin
y + y2 cos x = 0
83. 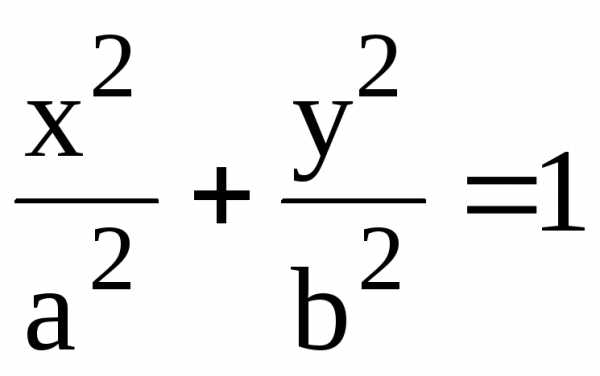 84. еу/х
ex/y = 1
84. еу/х
ex/y = 1
85. xy + yx = 0 86. + y2 ln x = 4
5. Производные высших порядков
Определение
3. Производная  называется производной первого порядка.
называется производной первого порядка.
Производная
от 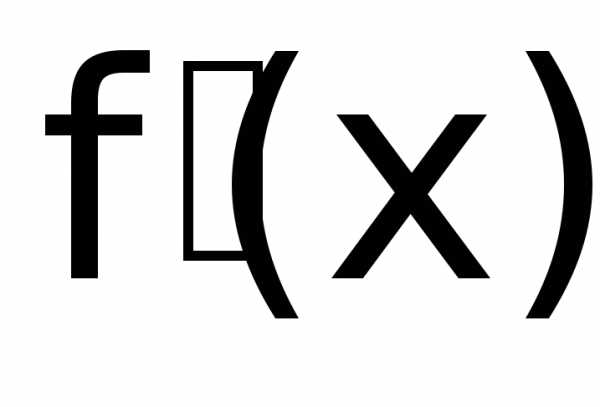 называется производной второго порядка
или второй производной от функции f(x)
и обозначается
называется производной второго порядка
или второй производной от функции f(x)
и обозначается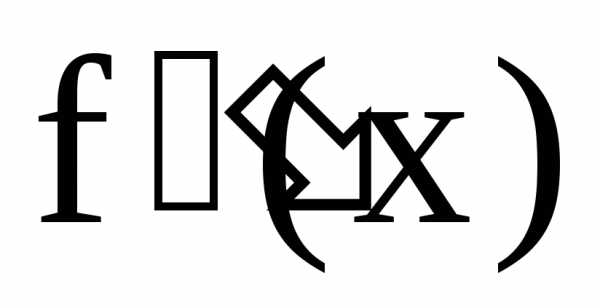 ,
, ,
,
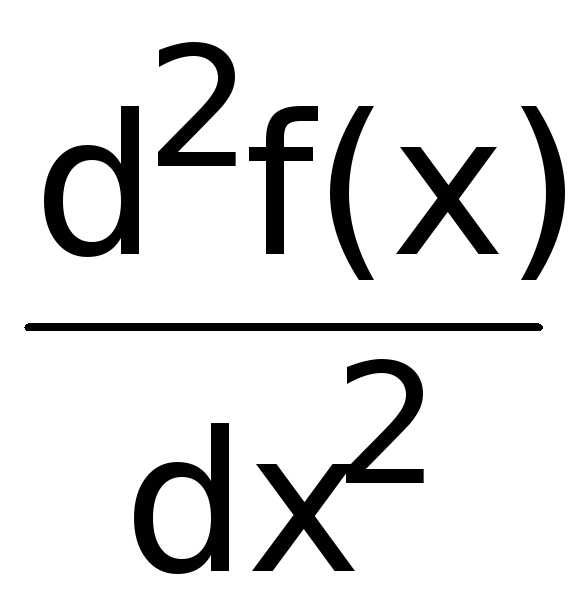 или
или 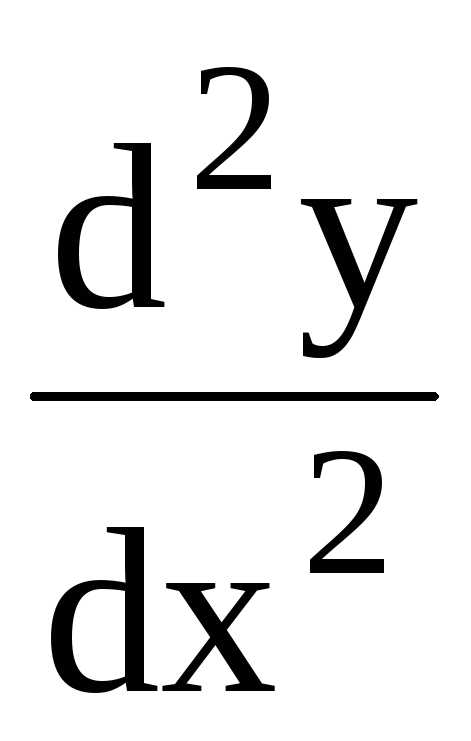 .
.
Производная
от  называется производной третьего порядка
или третьей производной от функции f(x)
и обозначается
называется производной третьего порядка
или третьей производной от функции f(x)
и обозначается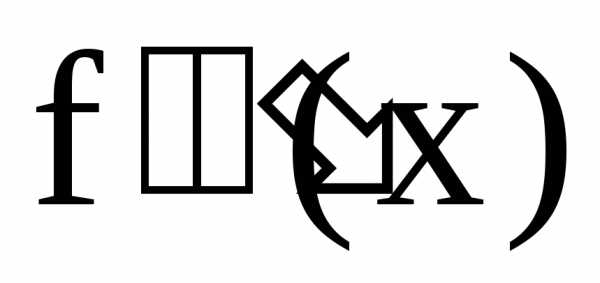 ,
,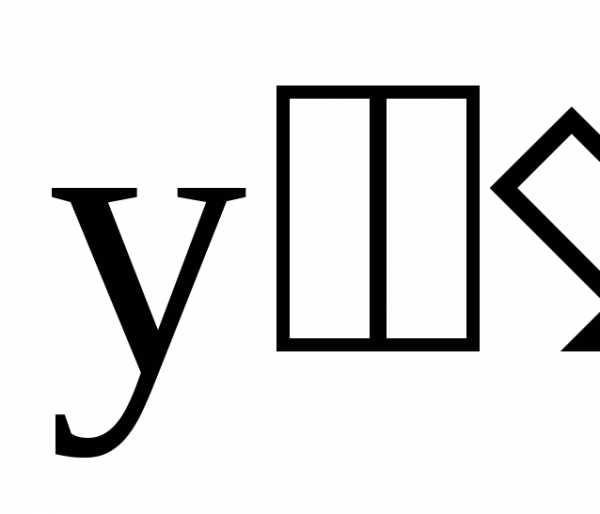 ,
,
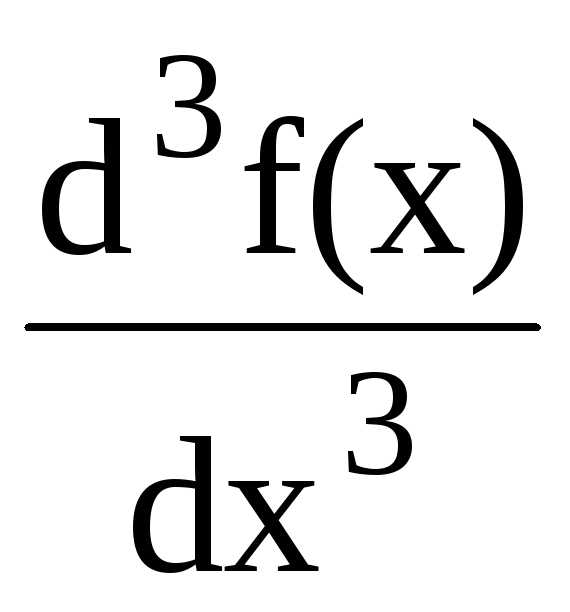 или
или  и т.д.
и т.д.
Производная n-го порядка есть производная от производной (n-1)-го порядка, т.е. .
Пример 4. Найти производную второго порядка от функции
у=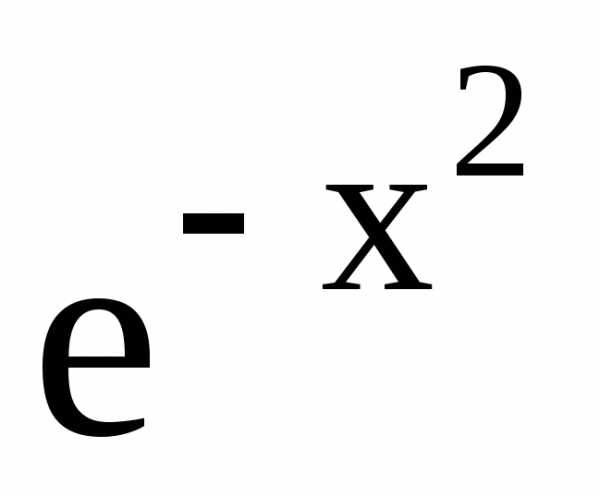 .
.
Решение
Найти производные второго порядка от функций:
87. у = tg x 88. y = ctg x
89. y = sin2x 90. y = cos2x
91.
y =  92. y = ln (2x3)
92. y = ln (2x3)
93.
y = x sin x 94. y = 
95. y = 2x 96. y = e1/x
97. y = x2 ln x 98. y = ax x3
99. 100. y
= ln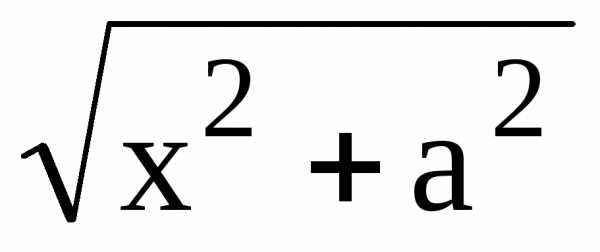
6. Правило Лопиталя Устранение неопределенностей вида ,
Правило
Лопиталя. Если
функции f(x) и g(x) дифференцируемы в
некоторой окрестности точки x0 за исключением, быть может самой точки
x0,
причем, в этой окрестности 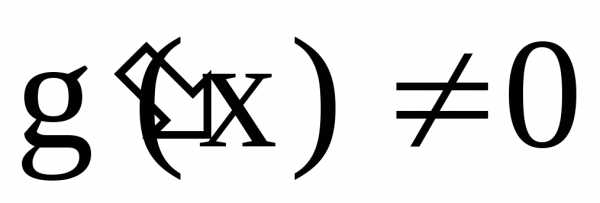 и, если
и, если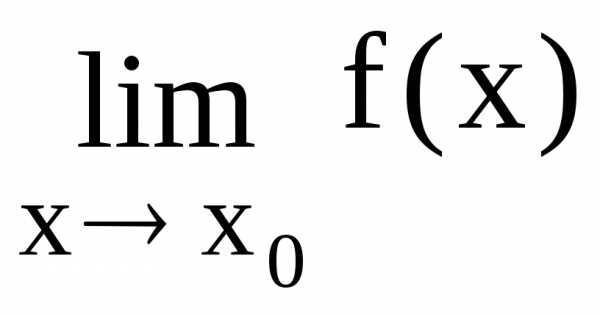 =
=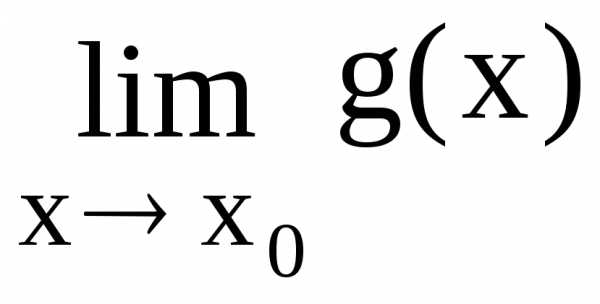 = 0 или
= 0 или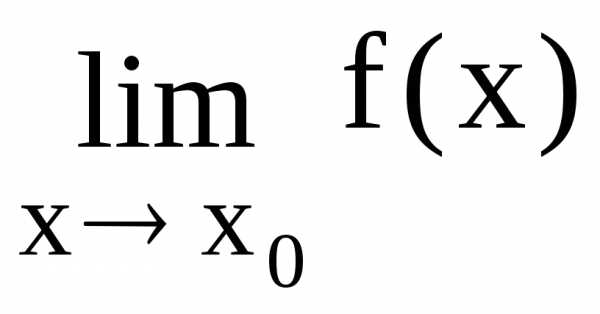 =
=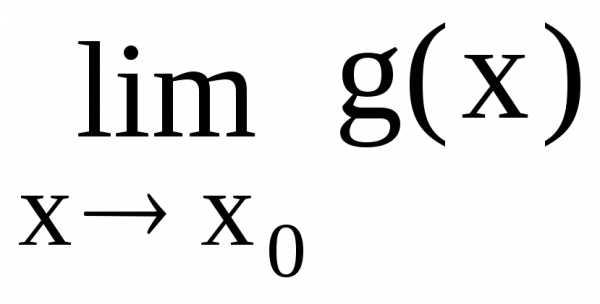 =
, то
=
, то
,
если последний предел существует.
Иными
словами, для неопределенностей вида  или
или предел отношения двух функций равен
пределу отношения их производных, если
последний существует (конечный или
бесконечный).
предел отношения двух функций равен
пределу отношения их производных, если
последний существует (конечный или
бесконечный).
Здесь
x0 может
быть числом, + ,
либо.
,
либо.
Пример
5. Вычислить
предел 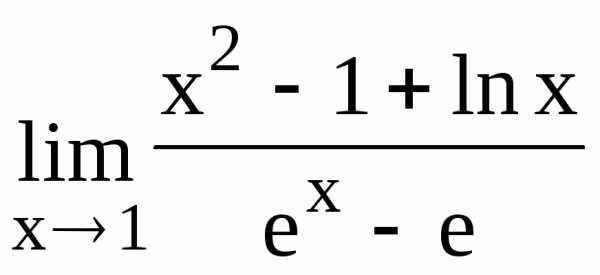 .
.
Решение. Имеем неопределенность вида 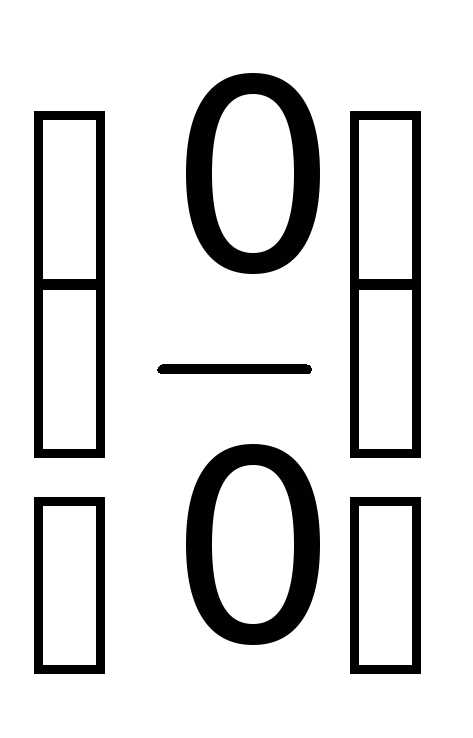 .
Для ее устранения воспользуемся правилом
Лопиталя
.
Для ее устранения воспользуемся правилом
Лопиталя
Пример 6. Вычислить предел 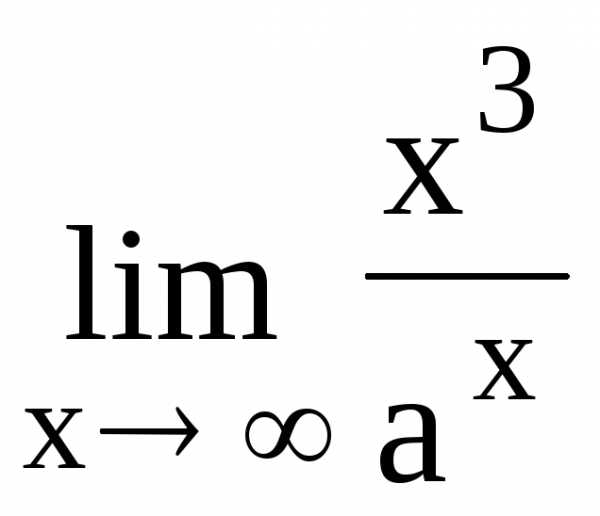 .
.
Решение. Имеем неопределенность вида 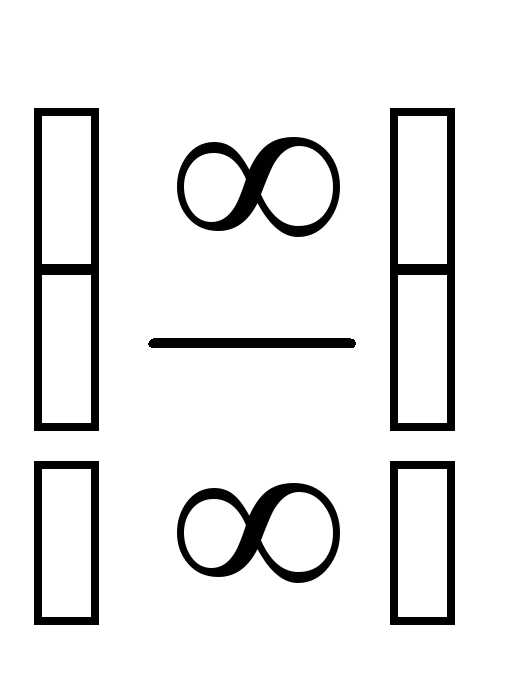 .
Применяя трижды правило Лопиталя,
получим
.
Применяя трижды правило Лопиталя,
получим
.
Вычислить пределы
101. 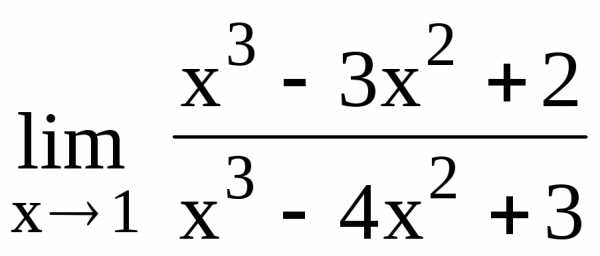 102.
102.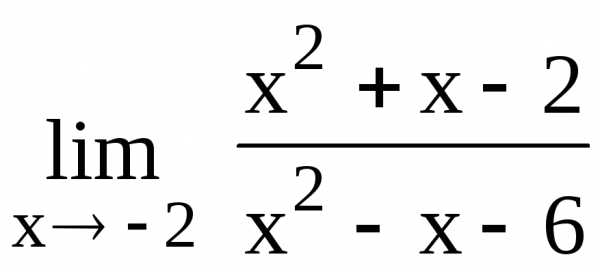
103.  104.
104.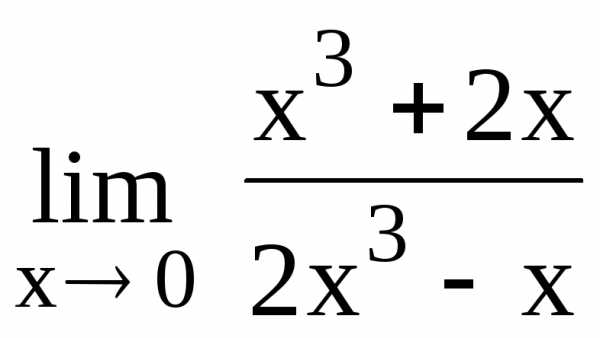
105. 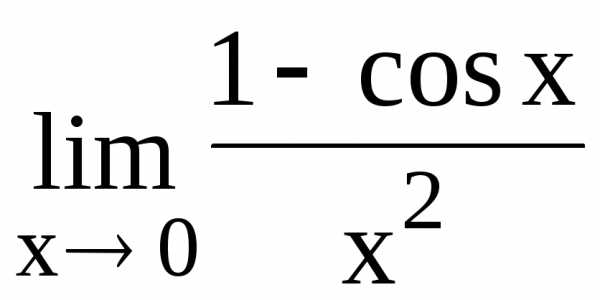 106.
106.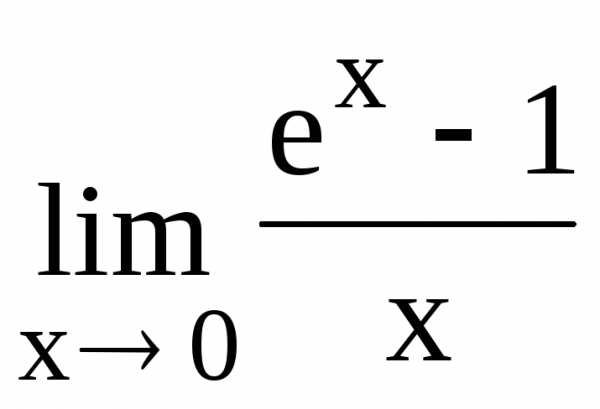
107. 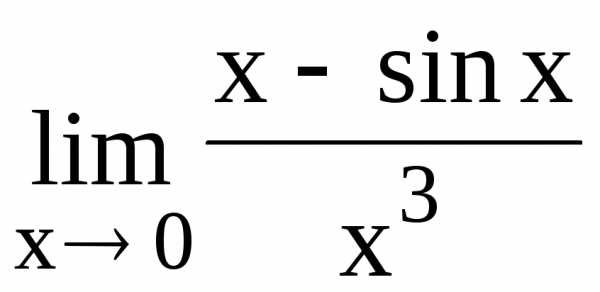 108.
108.
109. 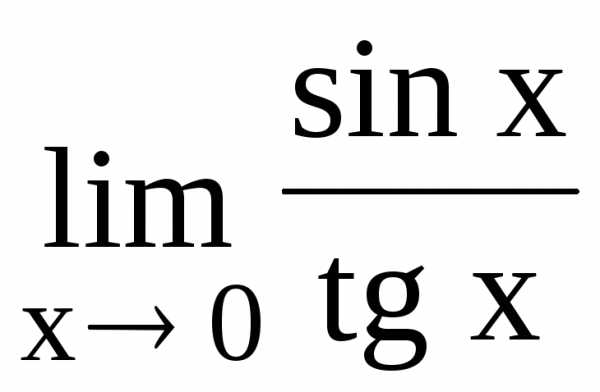 110.
110.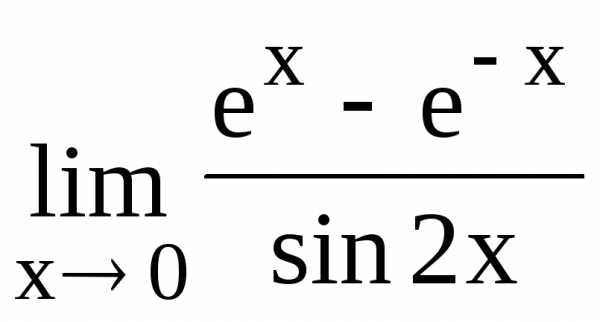
111. 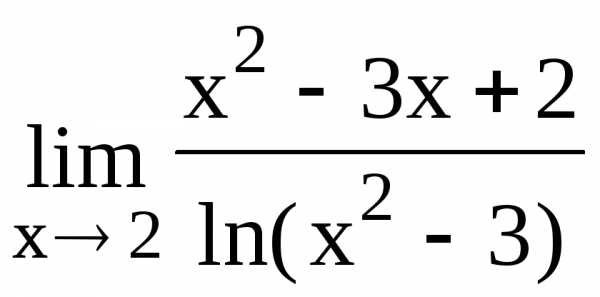 112.
112.
113.  114.
114.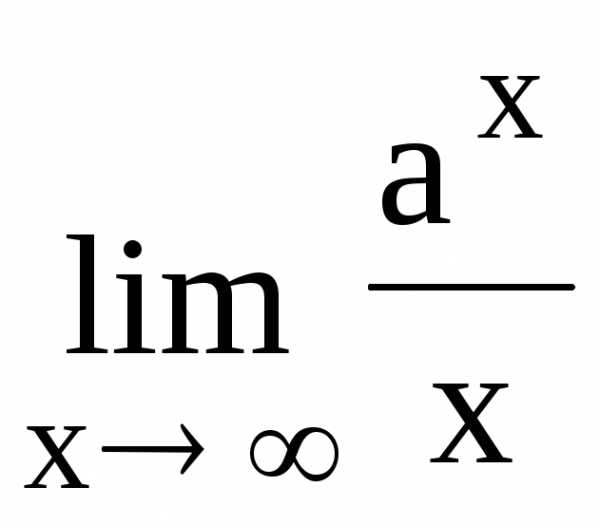 ,
a >1
,
a >1
115. 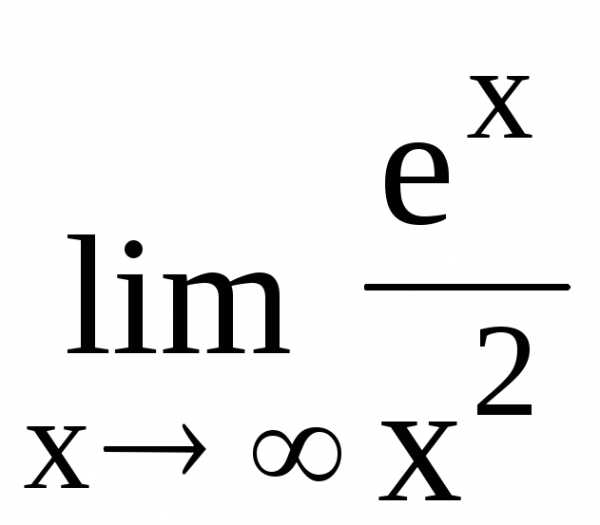 116.
116.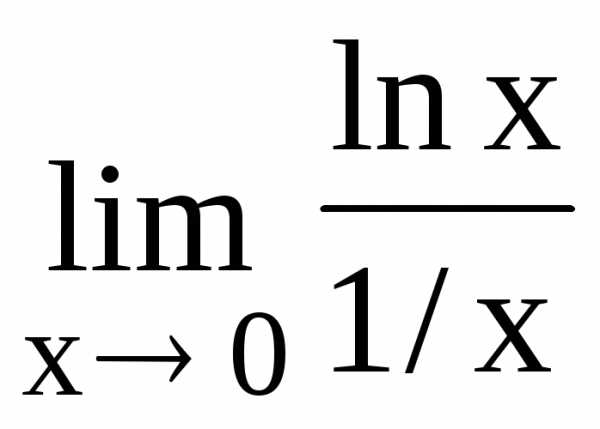
117. 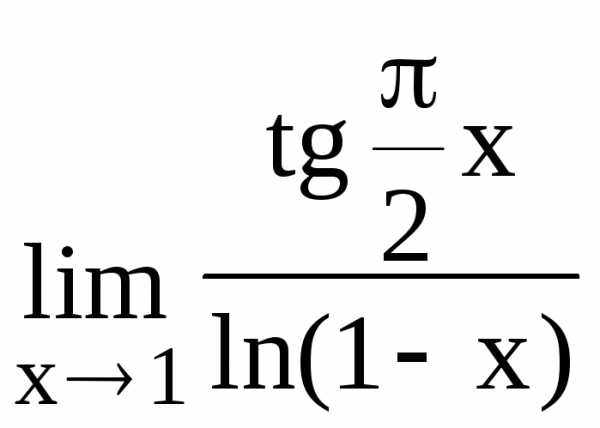 118.
118.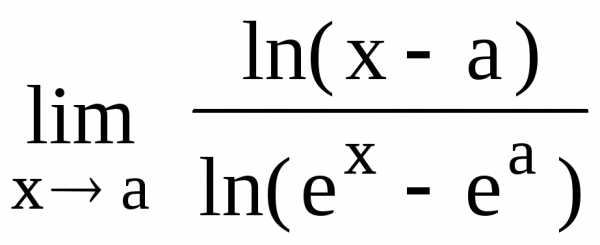
119. 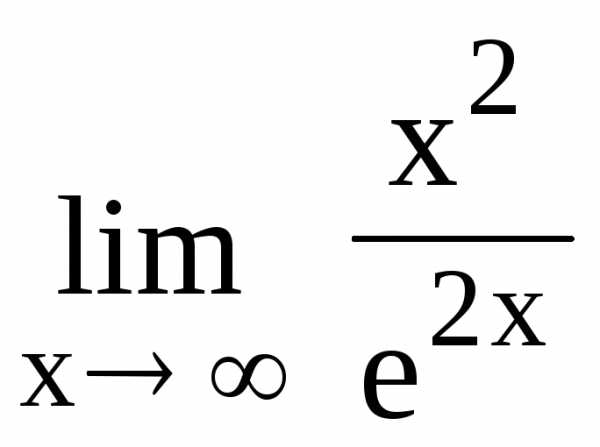 120.
120.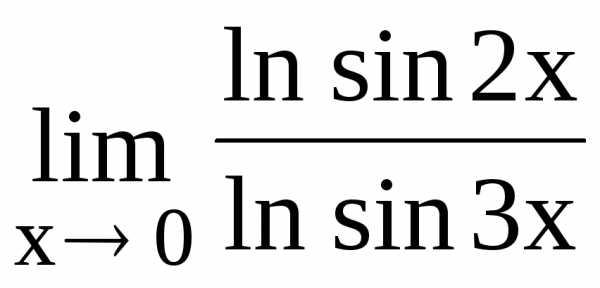
121. 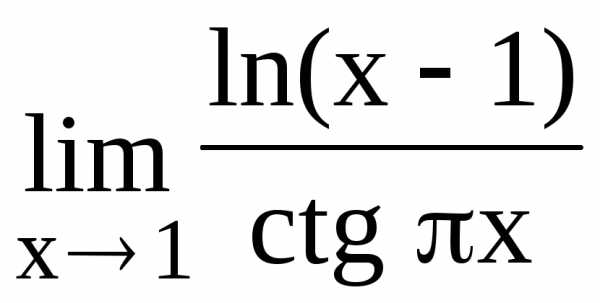 122.
122.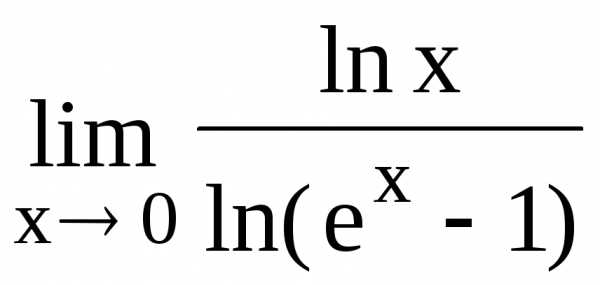
7. Неопределенности вида 0 , 00, 1, 0 и их устранение
Неопределенность
вида 0
сводится путем алгебраических
преобразований к неопределенностям
вида 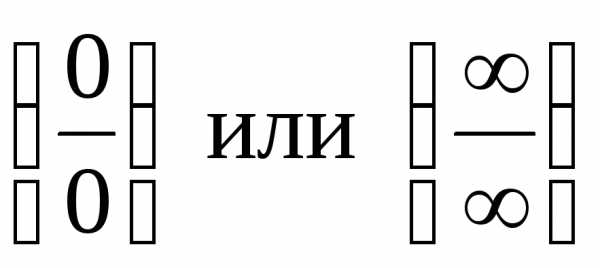 ,
а затем раскрываются с помощью правила
Лопиталя.
,
а затем раскрываются с помощью правила
Лопиталя.
Неопределенности вида 00, 1, 0 с помощью тождества
f(x)g(x) eg(x) lnf(x)сводятся к неопределенности вида 0 .
Пример
7. Вычислить
предел 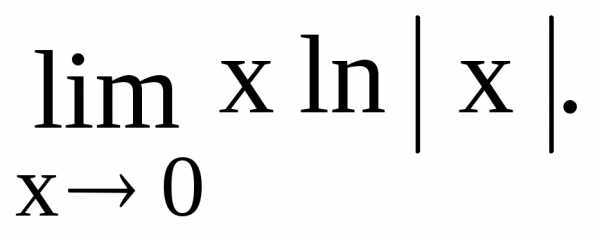
Решение. Имеем неопределенность вида 0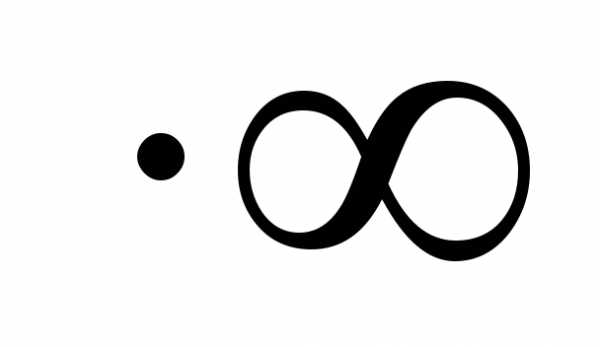 .
Но x ln |x| =
.
Но x ln |x| =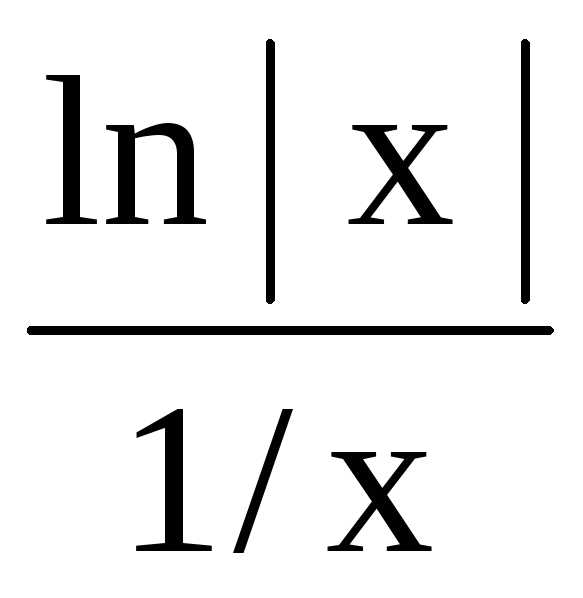
получена неопределенность вида
получена неопределенность вида 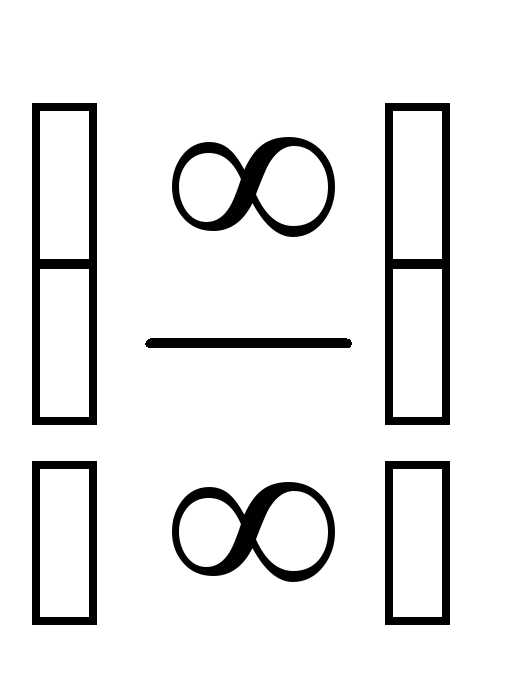 .
Применяя правило Лопиталя, получим=.
.
Применяя правило Лопиталя, получим=.
Пример
8. Вычислить
предел 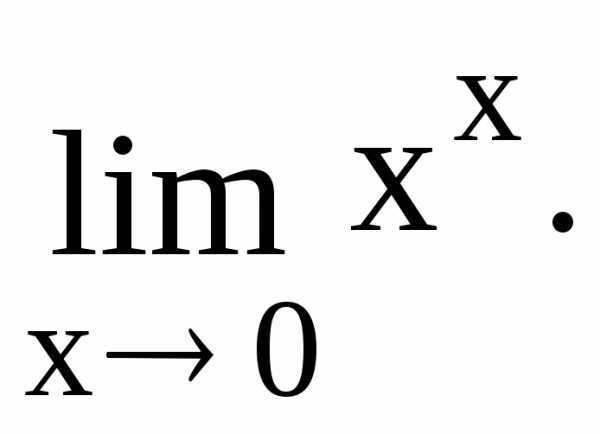
Решение. Имеем неопределенность вида 00. Но xx = ex ln x и получаем в показателе степени неопределенность вида 0 , которая рассмотрена в предыдущем примере. Следовательно
.
Пример
9. Вычислить 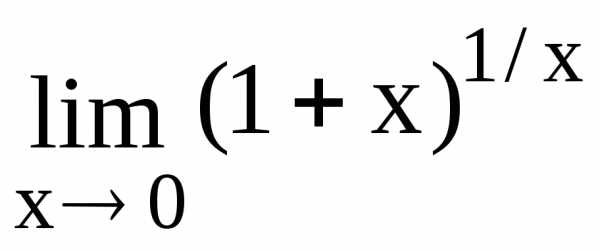 .
.
Решение. Имеем неопределенность вида 1. Но (1 + x)1/x = e1/xln(1+x)
и
в показателе степени получена
неопределенность вида 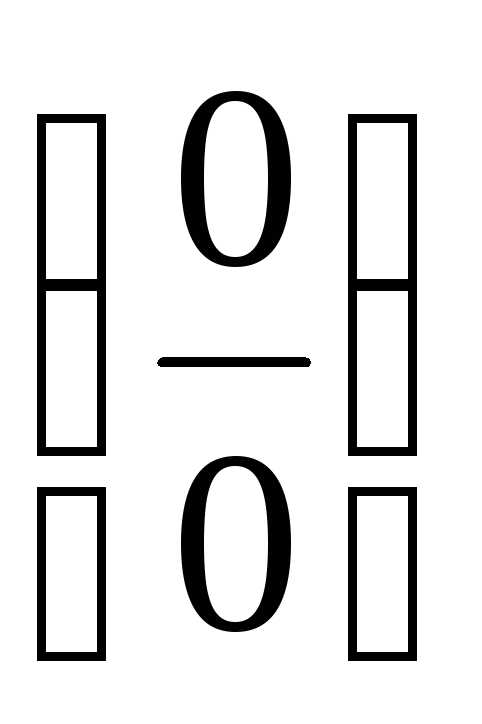 .
Устраним ее, используя правило Лопиталя.
.
Устраним ее, используя правило Лопиталя.
.
Пример
10. Вычислить 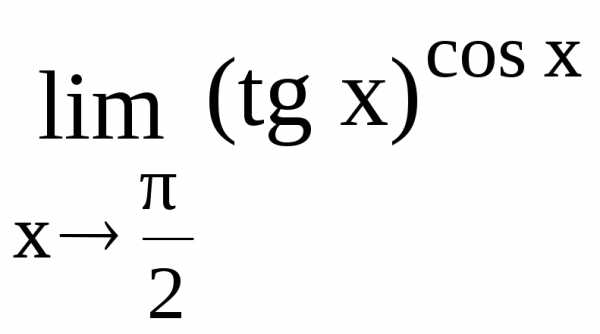 .
.
Решение. Имеем неопределенность вида 0.
Но
и
в показателе степени получена
неопределенность вида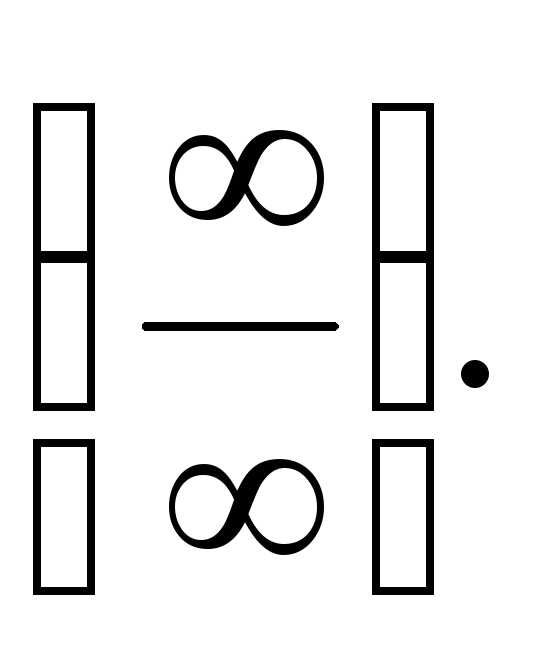 Применяя правило Лопиталя, находим
Применяя правило Лопиталя, находим
Следовательно .
Вычислить пределы
123. 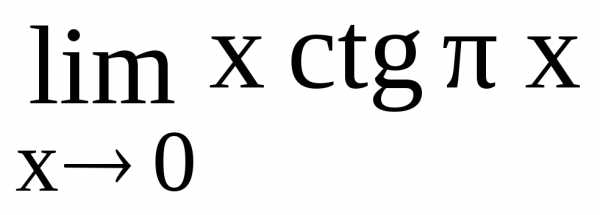 124.
124.
125. 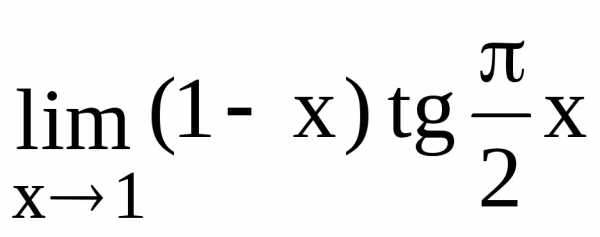 126.
126.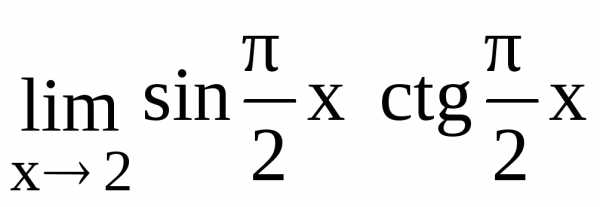
127. 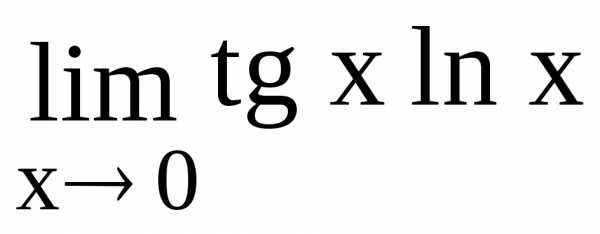 128.
128.
129. 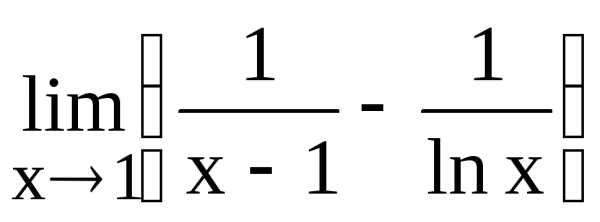 130.
130.
131. 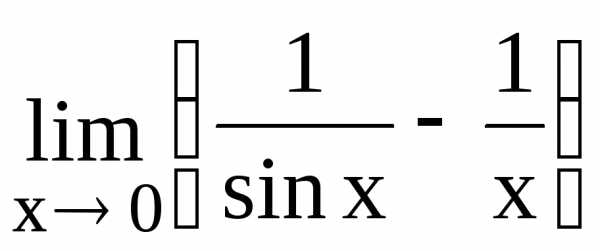 132.
132.
133.  134.
134.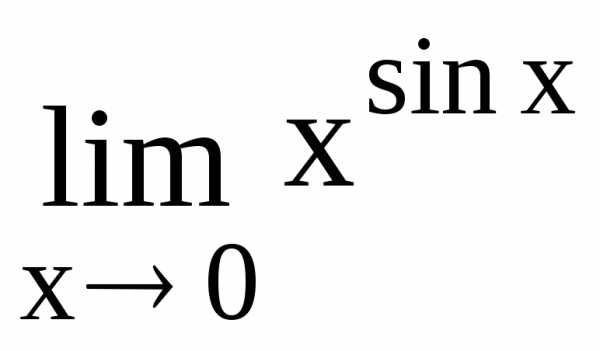
135. 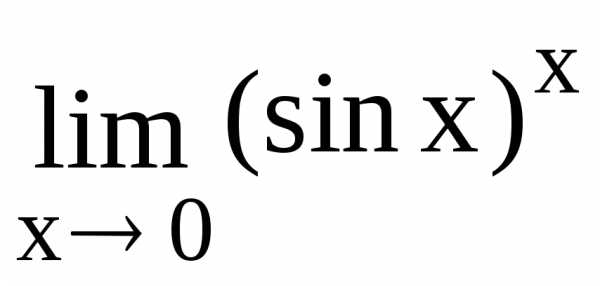 136.
136.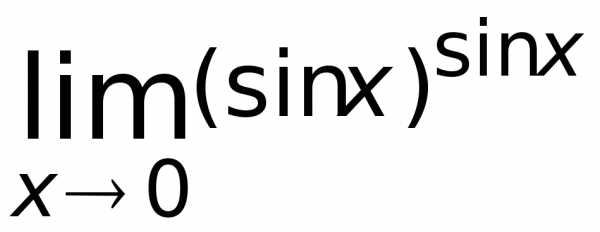
137. 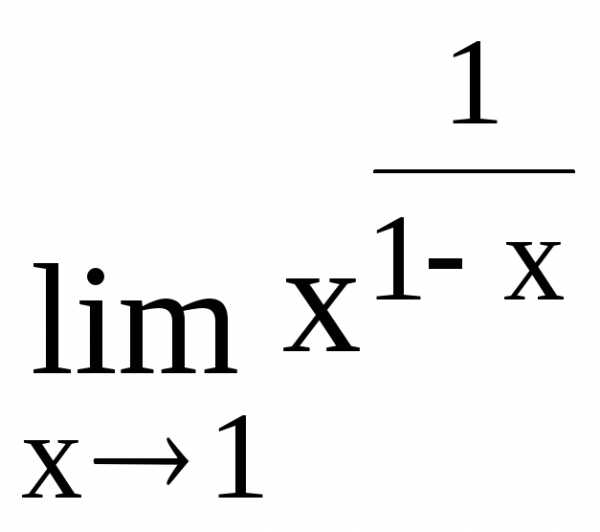 138.
138.
139. 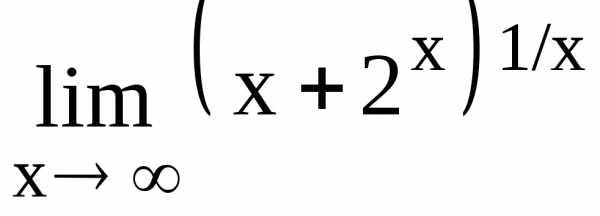 140.
140.
141. 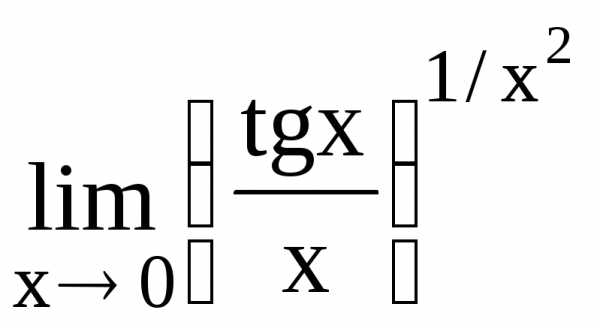 142.
142.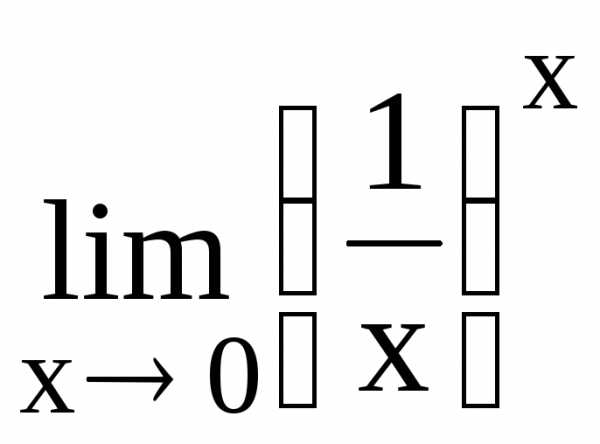
studfiles.net
