а это противоречит определению модуля.
Следовательно, таких \( x;y\in \mathbb{R}\) не существует, а значит, при всех \( x,\text{ }y\in \mathbb{R}\) выполняется неравенство \( \left| x+y \right|\le \left| x \right|+\left| y \right|.\)
Примеры для самостоятельного решения:
1) Докажите свойство №6.
2) Упростите выражение \( \left| \frac{31}{8}-\sqrt{15} \right|+\left| \frac{15}{4}-\sqrt{15} \right|\).
Ответы:
1) Воспользуемся свойством №3: \( \left| c\cdot x \right|=\left| c \right|\cdot \left| x \right|\), а поскольку \( c>0\text{ }\Rightarrow \text{ }\left| c \right|=c\), тогда
\( \left| cx \right|=c\cdot \left| x \right|\), ч.т.д.
2) \( \left| \frac{31}{8}-\sqrt{15} \right|+\left| \frac{15}{4}-\sqrt{15} \right|\).
\( \frac{15}{4}-\sqrt{15}\text{ }<0\text{ }\Rightarrow \text{ }\left| \frac{15}{4}-\sqrt{15} \right|=\sqrt{15}-\frac{15}{4}\).
Складываем значения модулей:
\( \displaystyle \left| \frac{31}{8}-\sqrt{15} \right|+\left| \frac{15}{4}-\sqrt{15} \right|=\frac{31}{8}-\sqrt{15}+\sqrt{15}-\frac{15}{4}=\frac{1}{8}=0.125\)
6.2.4. Модуль числа
Автор Татьяна Андрющенко На чтение 2 мин. Просмотров 5k. Опубликовано
Модулем числа а (записывают |a|) называют расстояние от начала отсчета до точки, соответствующей данному числу а.
Значение модуля любого числа неотрицательно. |3|=3; |-3|=3, т.к. расстояние от начала отсчета и до числа -3, и до числа 3 равно трем единичным отрезкам.
По определению модуля числа: |a|=a, если a≥0 и |a|=-a, если а<0. Читают: модуль неотрицательного числа равен самому этому числу; модуль отрицательного числа равен противоположному числу.
Примеры.
1. Вычислить: а) |5|-2; б) |-12| : 6; в) |-24| + |13|; г) |65|-|-45|.
Решение. а) |5|-2=5-2=3;
б) |-12| : 6=12 : 6=2;
в) |-24|+|13|=24+13=37;
г) |65|-|-45|=65-45=20.
2. Решить уравнение: а) |m|+4=10;
Решение.
а) |m|+4=10;
|m|=10-4; из суммы вычли известное слагаемое;
|m|=6. Так как |-6|=6 и |6|=6, то m=-6 или m=6.
Ответ: -6; 6.
б) 6-|x|=2.
|x|=6-2;
|x|=4, отсюда х=-4 или х=4.
Ответ: -4; 4.
3. Записать перечислением элементов множество целых чисел А, модуль которых меньше числа 5.
Решение. По определению модуля числа 5 искомые числа должны отстоять от начала отсчета как вправо, так и влево на расстояние, меньшее пяти единичных отрезков. В этом промежутке (показан штриховкой на рисунке) бесконечно много чисел, но нам нужно выбрать из них лишь все целые числа. Берем числа: -4, -3, -2, -1, 0, 1, 2, 3, 4. Числа -5 и 5 не подходят по условию.
Ответ: множество А={-4, -3, -2, -1, 0, 1, 2, 3, 4}.
4. Записать перечислением множество натуральных чисел В, модуль которых меньше числа 5.
Решение. Из всех чисел, показанных на рисунке штриховкой, нам нужно выбрать натуральные, т. е. только те числа, которые употребляются при счете предметов. Ответ: B={1, 2, 3, 4}.
е. только те числа, которые употребляются при счете предметов. Ответ: B={1, 2, 3, 4}.
Модуль
Модулем положительного числа называют само это число; модулем отрицательного числа называют число, ему противоположное; модуль нуля равен нулю.\(|a|=\begin{cases} a, \;\; если \; a>0 \\ 0, \; если\;\; a=0\\ -a,\; если \;\; a<0 \end{cases}\)
Второе название модуля – «абсолютное значение действительного числа».
Фактически модуль делает всё, что находится внутри него положительным. Поэтому чтобы правильно его раскрыть, необходимо сначала выяснить знак выражения внутри него:
— если подмодульное выражение положительно, модуль просто убирается. При этом само выражение не меняется.
— если же оно отрицательно, то при снятии модуля перед подмодульным выражением надо добавить знак «минус», чтобы сделать его положительным. 4+1\)
4+1\)
Пример. Вычислить значение выражения \(|7-x|-|x+3|\), при \(x>12\).
Решение: При любом \(x\) большем \(12\), первое подмодульное выражение будет отрицательно, а второе – положительно. Соответственно, первый модуль будет раскрываться с минусом, а второй – с плюсом (значит перед ним останется минус, который стоял перед ним до раскрытия):
\(|7-x|-|x+3|=-(7-x)-(x+3)=-7+x-x-3=-10\)Ответ: \(-10\)
Геометрическое определение модуля
\(|a|\) — это расстояние от \(0\) до числа \(a\) на числовой оси
Пример. Чему равен \(|5|\) и \(|-5|\)?
Представим числовую ось и отметим на ней точки \(5\) и \(-5\). Какое будет расстояние от нуля до этих точек? Очевидно \(5\).
Значит ответ: \(|5|=5\), \(|-5|=5\).
Так как модуль это расстояние, а расстояние не может выражаться отрицательным числом, то он всегда положителен.
Понимать легче второе определение, но практике удобнее использовать первое.
Решение простейших уравнений с модулем
Уравнения вида \(|f|=g\) решается с помощью перехода к совокупности \( \left[ \begin{gathered}f= g\\ f=-g\end{gathered}\right.\) , при условии, что \(g≥0\).
Сначала об условии \(g≥0\). Откуда оно берется? Из определения модуля, ведь модуль всегда неотрицателен (то есть, положителен или равен нулю). Поэтому условие \(g≥0\) обязательно. Иначе уравнение не будет иметь решения.
Теперь о совокупности. Почему уравнение распадается на два? Давайте, к примеру, рассмотрим уравнение \(|x|=3\). Какое число под модулем будет равно \(3\)? Конечно \(3\) и \(-3\), потому что \(|3|=3\), \(|-3|=3\). Корни уравнения \(|x|=3\): \(3\) и \(-3\). Логично? Логично! В общем виде получается, что подмодульное выражение \(f\) должно быть равно \(g\) и \(-g\). Иначе равенство не получится.
Пример.
 Решить уравнение:
Решить уравнение:|
\(|x-1|=3x\) |
Найдем ограничения уравнения. Запишем его немного правее от основного решения |
|
|
\(3x≥0\) |
Когда ограничение записано — можно со спокойной душой решать уравнение. Избавимся от модуля и перейдем к совокупности уравнений |
|
|
\( \left[ \begin{gathered}x-1=3x\\ x-1=-3x\end{gathered}\right.\) |
Перед нами 2 линейных уравнения. Решаем их с помощью известного заклинания: «иксы влево, числа вправо» |
|
|
\( \left[ \begin{gathered}x-3x=1\\ x+3x=1\end{gathered}\right. |
Приведем подобные слагаемые | |
|
\( \left[ \begin{gathered}-2x=1\\ 4x=1\end{gathered}\right.\) |
|
Поделим первое уравнение на \(-2\), второе на \(4\). |
|
\( \left[ \begin{gathered} x=-\frac{1}{2}\\ x=\frac{1}{4}\end{gathered}\right.\) |
|
Корень \(-\)\(\frac{1}{2}\) – не подходит, т.к. \(x≥0\). Остается корень \(\frac{1}{4}\), его и запишем в ответ |
Ответ: \(\frac{1}{4}\)
Решение простейших неравенств с модулем
Неравенство вида \(|f|< c\) решается с помощью перехода к двойному неравенству \( -c< f< c\) , при условии, что \(c>0\).

Начнем опять с условия. Почему \(c>0\)? Потому что, иначе неравенство не будет иметь решения. Здесь все также как в уравнениях. В самом деле, когда, например, модуль икса меньше \(-7\)? Никогда!
Теперь разберем неравенство \(|x|<3\). Какие иксы нам подойдут? Все от \(-3\) до \(3\). Иначе говоря, икс должен лежать между \(-3\) и \(3\). Это утверждение можно записать вот так \(-3< x <3\) либо системой \(\begin{cases}x<3\\x > -3\end{cases}\). В любом случае ответ будет \(xϵ (-3;3)\).
Неравенство вида \(|f|>c\) решается с помощью перехода к совокупности неравенств \( \left[ \begin{gathered} f>c\\ f< -c\end{gathered}\right.\), при условии, что \(c≥0\).
А здесь почему \(c≥0\)? Потому что иначе решать нечего: если \(c\) отрицательно, то модуль абсолютно любого икса нам подойдет. И значит ответ, икс – любое число.
Теперь о переходе. Рассмотрим неравенство \(|x|>3\). Какие иксы нам подойдут? Все, модуль которых больше трех, то есть от минус бесконечности до \(-3\) и от \(3\) до плюс бесконечности. Записывая системой получим \(\begin{cases}x>3\\x < -3\end{cases}\). Ответ будет \(x ϵ (-∞;-3)⋃(3;∞)\).
Какие иксы нам подойдут? Все, модуль которых больше трех, то есть от минус бесконечности до \(-3\) и от \(3\) до плюс бесконечности. Записывая системой получим \(\begin{cases}x>3\\x < -3\end{cases}\). Ответ будет \(x ϵ (-∞;-3)⋃(3;∞)\).
\(|3x-7|≤8\) |
\(|3x-11|≥11\) |
|
|
\(-8≤3x-7≤8\) \(|+7\) |
\( \left[ \begin{gathered}3x-11≥11\\ 3x-11≤-11\end{gathered}\right.\) |
|
|
\(-1≤3x≤15\) |
\( \left[ \begin{gathered}3x≥22\\ 3x≤0\end{gathered}\right.\) |
|
|
\(-\frac{1}{3}≤x≤5\) |
\( \left[ \begin{gathered}x≥\frac{22}{3}\\ x≤0\end{gathered}\right. |
|
|
Ответ: \([ -\frac{1}{3};5]\) |
Ответ: \( (-\infty;0]\cup [ \frac{22}{3};\infty)\) |
Смотрите также:
Свойства модуля
Внеклассный урок — Модуль числа
Модуль числаМодулем числа называется само это число, если оно неотрицательное, или это же число с противоположным знаком, если оно отрицательное.
Например, модулем числа 5 является 5, модулем числа –5 тоже является 5.
То есть под модулем числа понимается абсолютная величина, абсолютное значение этого числа без учета его знака.
Обозначается так: |5|, |х|, |а| и т.д.
Правило:
|а| = а, если а ≥ 0. |а| = –а, если а < 0. |
Пояснение:
|5| = 5
Читается так: модулем числа 5 является 5.
|–5| = –(–5) = 5
Читается так: модулем числа –5 является 5.
|0| = 0
Читается так: модулем нуля является ноль.
Свойства модуля:
1) Модуль числа есть неотрицательное число: |а| ≥ 0 2) Модули противоположных чисел равны: |а| = |–а| 3) Квадрат модуля числа равен квадрату этого числа: |а|2 = a2 4) Модуль произведения чисел равен произведению модулей этих чисел: |а · b| = |а| · |b| 6) Модуль частного чисел равен отношению модулей этих чисел: |а : b| = |а| : |b| 7) Модуль суммы чисел меньше или равен сумме их модулей: |а + b| ≤ |а| + |b| 8) Модуль разности чисел меньше или равен сумме их модулей: |а – b| ≤ |а| + |b| 9) Модуль суммы/разности чисел больше или равен модулю разности их модулей: |а ± b| ≥ ||а| – |b|| 10) Постоянный положительный множитель можно вынести за знак модуля: |m · a| = m · |а|, m >0 11) Степень числа можно вынести за знак модуля: |аk| = |а|k, если аk существует 12) Если |а| = |b|, то a = ± b |
Геометрический смысл модуля.
Модуль числа – это величина расстояния от нуля до этого числа.
Для примера возьмем снова число 5. Расстояние от 0 до 5 такое же, что и от 0 до –5 (рис.1). И когда нам важно знать только длину отрезка, то знак не имеет не только значения, но и смысла. Впрочем, не совсем верно: расстояние мы измеряем только положительными числами – или неотрицательными числами. Пусть цена деления нашей шкалы составляет 1 см. Тогда длина отрезка от нуля до 5 равна 5 см, от нуля до –5 тоже 5 см.
На практике часто расстояние отмеряется не только от нуля – точкой отсчета может быть любое число (рис.2). Но суть от этого не меняется. Запись вида |a – b| выражает расстояние между точками а и b на числовой прямой.
Пример 1. Решить уравнение |х – 1| = 3.
Решение.
Смысл уравнения в том, что расстояние между точками х и 1 равно 3 (рис.2). Поэтому от точки 1 отсчитываем три деления влево и три деления вправо – и наглядно видим оба значения х:
х1 = –2, х2 = 4.
Можем и вычислить.
│х – 1 = 3
│х – 1 = –3
↕
│х = 3 + 1
│х = –3 + 1
↕
│х = 4
│ х = –2.
Ответ: х1 = –2; х2 = 4.
Пример 2. Найти модуль выражения:
3√5 – 10.
Решение.
Сначала выясним, является ли выражение положительным или отрицательным. Для этого преобразуем выражение так, чтобы оно состояло из однородных чисел. Не будем искать корень из 5 – это довольно сложно. Поступим проще: возведем в корень 3 и 10. Затем сравним величину чисел, составляющих разность:
3 = √9. Следовательно, 3√5 = √9 · √5 = √45
10 = √100.
Мы видим, что первое число меньше второго. Значит, выражение отрицательное, то есть его ответ меньше нуля:
3√5 – 10 < 0.
Но согласно правилу, модулем отрицательного числа является это же число с противоположным знаком. У нас отрицательное выражение. Следовательно, надо поменять его знак на противоположный. Выражением, противоположным 3√5 – 10, является –(3√5 – 10). Раскроем в нем скобки – и получим ответ:
Следовательно, надо поменять его знак на противоположный. Выражением, противоположным 3√5 – 10, является –(3√5 – 10). Раскроем в нем скобки – и получим ответ:
–(3√5 – 10) = –3√5 + 10 = 10 – 3√5.
Ответ:
|3√5 – 10| = 10 – 3√5.
модуль числа на примерах с int и float, синтаксис функции
Встроенная функция abs(x) в Python возвращает абсолютное значение аргумента x, который может быть целым или числом с плавающей точкой, или же объектом, реализующим функцию __abs__(). Для комплексных чисел функция возвращает их величину. Абсолютное значение любого числового значения -x или +x — это всегда соответствующее положительное +x.
| Аргумент | x | целое число, число с плавающей точкой, комплексное число, объект, реализующий __abs__() |
| Возвращаемое значение | |x| | возвращает абсолютное значение входящего аргумента |
Пример abs() с целым числом
Следующий код демонстрирует, как получить абсолютное значение 42 положительного числа 42.
x = 42
abs_x = abs(x)
print(f"Абсолютное значение {x} это {abs_x}")
# Вывод: Абсолютное значение 42 это 42
Вывод: «Абсолютное значение 42 это 42».
То же самое, но уже с отрицательным -42.
x = -42
abs_x = abs(x)
print(f"Абсолютное значение {x} это {abs_x}")
# Вывод: Абсолютное значение -42 это 42
Пример с числом float
Вот как получить абсолютное значение 42.42 и для -42.42:
x = 42.42
abs_x = abs(x)
print(f"Абсолютное значение {x} это {abs_x}")
# Абсолютное значение 42.42 это 42.42
x = -42.42
abs_x = abs(x)
print(f"Абсолютное значение {x} это {abs_x}")
# Абсолютное значение -42.42 это 42.42
Комплексное число
Абсолютное значение комплексного числа (3+10j).
complex_number = (3+10j)
abs_complex_number = abs(complex_number)
print(f"Абсолютное значение {complex_number} это {abs_complex_number}")
# Абсолютное значение (3+10j) это 10. 44030650891055
44030650891055
abs() vs fabs()
abs(x) вычисляет абсолютное значение аргумента x. По аналогии функция fabs(x) модуля math вычисляет то же значение. Разница лишь в том, что math.fabs(x) возвращает число с плавающей точкой, а abs(x) вернет целое число, если в качестве аргумента было целое число. Fabs расшифровывается как float absolute value.
Пример c fabs():
x = 42
print(abs(x))
# 42
import math
print(math.fabs(x))
# 42.0
abs() vs. np.abs()
И abs() в Python, и np.abs() в NumPy вычисляют абсолютное значение числа, но есть два отличия. np.abs(x) всегда возвращает число с плавающей точкой. Также np.abs(x) принимает массив NumPy, вычисляя значение для каждого элемента коллекции.
Пример:
x = 42
print(abs(x))
# 42
import numpy as np
print(np. fabs(x))
# 42.0
a = np.array([-1, 2, -4])
print(np.abs(a))
# [1 2 4]
fabs(x))
# 42.0
a = np.array([-1, 2, -4])
print(np.abs(a))
# [1 2 4]
abs и np.abs абсолютно идентичны. Нет разницы какой использовать. У первой преимущество лишь в том, что ее вызов короче.
Вывод
Функция abs() — это встроенная функция, возвращающая абсолютное значение числа. Она принимает целые, с плавающей точкой и комплексные числа на вход.
Если передать в abs() целое число или число с плавающей точкой, то функция вернет не-отрицательное значение n и сохранит тип. Для целого числа — целое число. Для числа с плавающей точкой — число с плавающей точкой.
>>> abs(20)
20
>>> abs(20.0)
20.0
>>> abs(-20.0)
20.0
Комплексные числа состоят из двух частей и могут быть записаны в форме a + bj, где a и b — это или целые числа, или числа с плавающей точкой. Абсолютное значение a + bj вычисляется математически как math.sqrt(a**2 + b**2).
Абсолютное значение a + bj вычисляется математически как math.sqrt(a**2 + b**2).
>>> abs(3 + 4j)
5.0
>>> math.sqrt(3**2 + 4**2)
5.0
Таким образом, результат всегда положительный и всегда является числом с плавающей точкой.
Модуль числа, сравнение чисел
Модуль числа
Модуль числа а обозначают $|a|$. Вертикальные черточки справа и слева от числа образуют знак модуля.
Например, модуль любого числа (натурального, целого, рационального или иррационального) записывается так: $|5|$, $|-11|$, $|2,345|$, $|\sqrt[4]{45}|$.
Определение 1
Модуль числа a равен самому числу $a$, если $a$ является положительным, числу $−a$, если $a$ является отрицательным, или $0$, если $a=0$.
Данное определение модуля числа можно записать следующим образом:
$|a|= \begin{cases} a, & a > 0, \\ 0, & a=0,\\ -a, &a
Можно использовать более краткую запись:
$|a|=\begin{cases} a, & a \geq 0 \\ -a, & a
Пример 1
Вычислить модуль чисел $23$ и $-3,45$.
Решение.
Найдем модуль числа $23$.
Число $23$ – положительное, следовательно, по определению модуль положительного числа равен этому числу:
$|23|=23$.
Найдем модуль числа $–3,45$.
Число $–3,45$ – отрицательное число, следовательно согласно определению модуль отрицательного числа равен числу, противоположному данному:
$|-3,45|=3,45$.
Ответ: $|23|=23$, $|-3,45|=3,45$.
Определение 2
Модуль числа является абсолютной величиной числа.
Таким образом, модуль числа – число под знаком модуля без учета его знака.
Модуль числа как расстояние
Геометрическое значение модуля числа: модуль числа – это расстояние.
Определение 3
Модуль числа a – это расстояние от точки отсчета (нуля) на числовой прямой до точки, которая соответствует числу $a$.
Пример 2
Например, модуль числа $12$ равен $12$, т. 2}=14$.
2}=14$.
Ответ: $|-14|=14$.
Сравнение отрицательных чисел
Сравнение отрицательных чисел основывается на сравнении модулей этих чисел.
Замечание 1
Правило сравнения отрицательных чисел:
- Если модуль одного из отрицательных чисел больше, то такое число является меньшим;
- если модуль одного из отрицательных чисел меньше, то такое число является большим;
- если модули чисел равны, то отрицательные числа равны.
Замечание 2
На числовой прямой меньшее отрицательное число располагается левее большего отрицательного числа.
Пример 4
Сравнить отрицательные числа $−27$ и $−4$.
Решение.
Согласно правилу сравнения отрицательных чисел найдем сначала модули чисел $–27$ и $–4$, а затем сравним полученные положительные числа.
$|-27|=27$
$|-4|=4$
Сравним полученные натуральные числа:
$27 > 4$.
Таким образом, получаем, что $–27 |-4|$.
Ответ: $–27
При сравнении отрицательных рациональных чисел необходимо преобразовать оба числа к виду обыкновенных дробей или десятичных дробей.
Сравнение чисел с противоположными знаками
Замечание 3
Правило сравнения чисел с противоположными знаками:
Положительное число всегда больше отрицательного, а отрицательное число всегда меньше положительного.
Пример 5
Сравнить целые числа $−53$ и $8$.
Решение.
Числа имеют противоположные знаки. Согласно правилу сравнения чисел с противоположными знаками получаем, что отрицательное число $−53$ меньше положительного числа $8$.
Ответ: $−53
Пример 6
Сравнить числа $3 \frac{11}{13}$ и $–5,(123)$.
Решение.
Согласно правилу сравнения чисел с противоположными знаками отрицательное число всегда меньше положительного. Следовательно, $–5,(123)
Ответ: $–5,(123)
По данному правилу можно сравнивать также и действительные числа с противоположными знаками.
Если числа заданы как числовые выражения, то сразу невозможно определить какие они имеют знаки. В таком случае нужно вычислить значение этих выражений и затем определить, какое из правил сравнения можно применить.
Решение уравнений с модулем
Решение уравнений и неравенств с модулем часто вызывает затруднения. Однако, если хорошо понимать, что такое модуль числа, и как правильно раскрывать выражения, содержащие знак модуля, то наличие в уравнении выражения, стоящего под знаком модуля, перестает быть препятствием для его решения.
Немного теории. Каждое число имеет две характеристики: абсолютное значение числа, и его знак.
Например, число +5, или просто 5 имеет знак «+» и абсолютное значение 5.
Число -5 имеет знак «-» и абсолютное значение 5.
Абсолютные значения чисел 5 и -5 равны 5.
Абсолютное значение числа х называется модулем числа и обозначается |x|.
Как мы видим, модуль числа равен самому числу, если это число больше или равно нуля, и этому числу с противоположным знаком, если это число отрицательно.
Это же касается любых выражений, которые стоят под знаком модуля.
Правило раскрытия модуля выглядит так:
|f(x)|= f(x), если f(x) ≥ 0, и
|f(x)|= — f(x), если f(x) < 0
Например |x-3|=x-3, если x-3≥0 и |x-3|=-(x-3)=3-x, если x-3<0.
Чтобы решить уравнение , содержащее выражение, стоящее под знаком модуля, нужно сначала раскрыть модуль по правилу раскрытия модуля.
Тогда наше уравнение или неравенство преобразуется в два различных уравнения, существующих на двух различных числовых промежутках.
Одно уравнение существует на числовом промежутке, на котором выражение, стоящее под знаком модуля неотрицательно.
А второе уравнение существует на промежутке, на котором выражение, стоящее под знаком модуля отрицательно.
Рассмотрим простой пример.
Решим уравнение:
|x-3|=-x2+4x-3
1. Раскроем модуль.
Раскроем модуль.
|x-3|=x-3, если x-3≥0, т.е. если х≥3
|x-3|=-(x-3)=3-x, если x-3<0, т.е. если х<3
2. Мы получили два числовых промежутка: х≥3 и х<3.
Рассмотрим, в какие уравнения преобразуется исходное уравнение на каждом промежутке:
А) При х≥3 |x-3|=x-3, и наше уранение имеет вид:
x-3=-x2+4x-3
Внимание! Это уравнение существует только на промежутке х≥3!
Раскроем скобки, приведем подобные члены:
x2 -3х=0
и решим это уравнение.
Это уравнение имеет корни:
х1=0, х2=3
Внимание! поскольку уравнение x-3=-x2+4x-3 существует только на промежутке х≥3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х2=3.
Б) При x<0 |x-3|=-(x-3) = 3-x, и наше уравнение приобретает вид:
3-x=-x2+4x-3
Внимание! Это уравнение существует только на промежутке х<3!
Раскроем скобки, приведем подобные члены. Получим уравнение:
Получим уравнение:
x2-5х+6=0
х1=2, х2=3
Внимание! поскольку уравнение 3-х=-x2+4x-3 существует только на промежутке x<3, нас интересуют только те корни, которые принадлежат этому промежутку. Этому условию удовлетворяет только х1=2.
Итак: из первого промежутка мы берем только корень х=3, из второго — корень х=2.
Ответ: х=3, х=2
Модуль 1: Местная ценность — Пути обучения математике
Учебная деятельность 1
Расширитель числовых значений разрядных значений
Посмотрите следующее видео:
Dr Paul Swan — расширитель числа
Что вы узнали из этого видео о числовой ценности?
Сначала запишите свою мысль на листе бумаги, а затем переходите к разделу «Понимание 1 и 2».
Понимание 1
Каждая цифра в номере имеет разрядное значение в зависимости от его положения
Например, посмотрите на это число и определите каждое разрядное значение:
604
Проверьте свой ответ здесь
Понимание 2
Числа могут быть разделены и переименованы в зависимости от положения каждой цифры.
Вот еще пример:
Число 25 604.378 разделено или разбито, чтобы показать значение цифр.
2 находится в разряде десятков тысяч , поэтому значение 2 составляет 20000 (2 x 10 000)
5 находится в разряде тысяч , поэтому значение 5 равно 5 000 (5 x 1 000)
6 находится в разряде сотен , поэтому значение 6 равно 600 (6 x 100)
0 действует как заполнитель в разряде десятков , указывая, что в разряде десятков нет десятков
4 находится на месте единиц , поэтому его значение равно 4 (4 x 1)
3 находится на десятом месте , поэтому значение 3 составляет 3 десятых или 0. 3 (3 х 110)
3 (3 х 110)
7 находится на разряде сотых , поэтому он представляет 7 сотых или 0,07 (7 x 1100)
8 находится на тысячных разрядах , поэтому он представляет 8 тысячных или 0,008 (8 x 11000)
Таким образом, число может быть переименовано или выражено по-другому, с точки зрения его частей значения позиции.
25 604,378 = 2 десятка + 5 тысяч + 6 сотен + 4 единицы +3 десятые + 7 сотых + 8 тысячных
или
25 604.378 = (2 x 10 000) + (5 x 1000) + (6 x 100) + (4 x 1) + (3 x 0,1) + (7 x 0,01) + (8 x 0,001)
или
25 604,378 = 20 000 + 5 000 + 600 + 4 + 0,3 + 0,07 + 0,008
Выше приведены примеры расширенной записи.
Понимание 3
Числа могут быть разделены и перегруппированы в различные значения с основанием десять, чтобы облегчить вычисления.

Число 6 512 можно выразить по-разному, например:
Шесть тысяч пятьсот двенадцать единиц | Все число выражается в единицах. |
Шестьсот пятьдесят одна десятка и две единицы | Вместо разделения чисел на отдельные группы тысяч, сотен и десятков, тысячи и сотни были заменены на десятки. Таким образом, число можно переименовать в 651 десятку и две единицы. |
Шестьдесят пять сотен и 12 | Тысячи и сотни были объединены в одну группу путем обмена десять сотен на каждую тысячу. |
Что мы здесь сделали, так это разделили целое число, и они перегруппировали его в разные значения с основанием десяти (например, обменяли тысячи и сотни на десятки)
Это понимание поможет решать следующие повседневные задачи. Задача проще:
Задача проще:
2 750 долларов снимается наличными, причем запрос касается банкнот 100 долларов, максимально возможного достоинства.
Сколько стодолларовых банкнот будет выдано?
Вы заметили : в приведенном выше примере используется запятая (2750 долларов США), но не в других числах? Причина этого в том, что, когда мы говорим о деньгах, мы используем запятую для разделения сотен и тысячных разрядов, а также стотысячных и миллионов разрядов.Например, мы записываем 12 миллионов долларов как 12 000 000 долларов.
Проверьте свой ответ здесь
Понимание 4
Стоимость разрядов увеличивается в степени 10 справа налево и уменьшается в степени 10 слева направо. Десятичная точка отделяет целые числовые значения от десятичных значений.
Мы знаем, что каждая цифра в числе имеет разрядное значение в зависимости от ее положения.
На диаграмме ниже показаны значения позиций в столбцах по обе стороны от десятичной точки.Десятичная точка отделяет целые числа от десятичных.
Таблица стоимости
Цифры справа от десятичной точки являются десятичными, а не целыми числами.
Наша десятичная система значений использует цифры от 0 до 9 для обозначения чисел с десятью в качестве основы. Значение разрядов увеличивается в степени 10 справа налево и уменьшается в степени 10 слева направо.
Это может быть продемонстрировано в таблице ниже, где используются единицы до тысяч, чтобы показать увеличение в десять раз при каждом перемещении позиции влево или увеличение в десять раз при каждом движении позиции вправо.
тыс. | сот | Десятки | Единицы |
|---|---|---|---|
1000 = 10x10x10 = 10 3 | 100 = 10×10 = 10 2 | 10 = 10 1 | 1 = 10 0 |
Взгляните на число 2 385 на приведенной ниже таблице значений разряда. Положение на диаграмме показывает значение каждой цифры. Цифра с наибольшим значением считывается первой, поэтому мы читаем число слева направо.
Положение на диаграмме показывает значение каждой цифры. Цифра с наибольшим значением считывается первой, поэтому мы читаем число слева направо.
тыс. | сот | Десятки | Единицы |
|---|---|---|---|
2 | 3 | 8 | 5 |
Мы читаем это как число: две тысячи триста восемьдесят пять
Используя расширенные обозначения, 2385 можно выразить несколькими способами, например:
2 тысячи, 3 сотни, 8 десятков и 5 единиц
Используя расширенные обозначения, число можно также представить как:
(2 x 1 000) + (3 x 100) + (8 x 10) + (5 x 1)
Используя расширенные обозначения со степенями десяти, число можно кратко представить как:
(2 x 10 3 ) + (3 x 10 2 ) + (8 x 10 1 ) + 5
Взгляните на число 67 на приведенной ниже диаграмме разряда. 51
51
Позиция на диаграмме показывает значение каждой цифры с десятичной точкой, отделяющей целые числа от десятичных. Цифра с наибольшим значением считывается первой, поэтому мы читаем число слева направо.
Десятки | Единицы | . | десятые | сотых |
|---|---|---|---|---|
6 | 7 | . | 5 | 1 |
Мы читаем это как число: шестьдесят семь целых пять сотых один
67,51 можно выразить несколькими способами с помощью расширенной записи, например:
6 десятков, 7 единиц, 5 десятых и 1 сотая
или
(6 х 10) + (7 х 1) + (5 х 0. 1) + (1 х 0,01)
1) + (1 х 0,01)
Используя расширенные обозначения со степенями десяти, число можно представить как:
(6 x 10 1 ) + (7 x 10 0 ) + (5 x 10 -1 ) + (1 x 10 -2 )
Что означают 10 -1 и 10 -2 ?
Практическое задание 1 (проверка понимания 1 и 4)
Напишите следующие числа цифрами.
a) Пятьдесят восемь тысяч пять
b) Шесть миллионов четыреста двенадцать тысяч двести двадцать
c) Семьдесят пять целых две целых пять сотых
d) Четыреста восемь целых ноль два
e ) Сто шестьдесят две и пятнадцать тысячных
f) Двести семь миллионов двадцать
Проверьте свой ответ здесь
Практическое задание 2 (тестирование понимания 1, 2 и 4)
Пример: Express 6 548 с использованием расширенной записи
6548 = 6000 + 500 + 40 + 8
6 548 = (6 x 1000) + (5 x 100) + (4 x 10) + 8
Теперь выполните следующие практические задания.
Выразите следующие числа как минимум двумя другими способами, используя расширенную нотацию.
a) 25 408
b) 6 357250
c) 92,5
d) 6,25
Проверьте свои ответы здесь
Практическое задание 3 (тестирование Понимание 3)
Пример: сколько десятков в 43 560?
Помните, что здесь спрашивается, сколько десятков во всем числе, а не в разряде десятков.Ответ — 4 356. Мы можем проверить это, умножив 4 356 на 10 (43 560).
Теперь выполните следующие практические задания.
Сколько десятков в:
а) Сколько сотен в 120 800?
б) Сколько единиц в 609?
в) Сколько десятков в 2 530?
г) Сколько тысяч в 9 689 000?
Проверьте свои ответы здесь
Практическое задание 4 (тестирование понимания 1,2, 3 и 4)
Пример: разделить и переименовать номер 4 506 с помощью перегруппировки
4 506 = 4 000 + 500 + 6
4 506 = 45 соток + 6
4 506 = 450 десятков + 6
Теперь выполните следующие практические задания.
Разделите и переименуйте следующие номера с помощью перегруппировки.
Сколько разных способов это сделать?
a) 3 651
b) 9 005
c) 15 508
d) 650 432
e) 98,4
f) 9,15
Проверьте свои ответы здесь
Для вашего интереса …
В таблице ниже показаны числа от десяти до миллиона (10 6 ).
Попробуйте представить себе огромную величину такого числа, как 10 24 .Кажется, это невозможно понять!
С другой стороны, 10 -3 равно (десятая часть десятой десятой) или 0,1 x 0,1 x 0,1, что составляет 0,001 или одну тысячную. Теперь попробуем осмыслить размер 10 -16 .
Когда можно было бы использовать числа такой малой или большой величины?
Следующее увлекательное видео помогает нам понять величину этих чисел.
| Миллион | 1 000 000 | 10 х 10 х 10 х 10 х 10 х 10 | 10 6 (десять в степени шесть) |
| Сто тысяч | 100 000 | 10 х 10 х 10 х 10 х 10 | 10 5 (десять в степени пяти) |
| Десять тысяч | 10 000 | 10 х 10 х 10 х 10 | 10 4 (десять в степени четыре) |
| Тысяча | 1 000 | 10 х 10 х 10 | 10 3 (десять в степени тройки) |
| Сотня | 100 | 10 х 10 | 10 2 (десять в степени два) |
| Тен | 10 | 1 х 10 | 10 1 (десять в большей степени) |
| Один | 1 | х 10 | 10 0 (десять до нуля) |
| Десятая | 0. 1 1 | х 10 | 10 -1 (десять в отрицательной степени 1) |
| сотка | 0,01 | х 10 | 10 -2 (десять в отрицательной степени 2) |
| Тысячная | 0,001 | х 10 | 10 -3 (десять в степени отрицательной 3) |
Проверьте свое понимание системы Base-Ten
Целью данного раздела было продемонстрировать следующие четыре понимания:
1.Каждая цифра в числе имеет разрядное значение в зависимости от ее положения.
2. Числа могут быть разделены и переименованы в зависимости от положения каждой цифры.
3. Числа могут быть разделены и перегруппированы в различные десятичные значения для облегчения вычислений.
4. Значение разрядов увеличивается в степени 10 справа налево и уменьшается в степени 10 слева направо. Десятичная точка отделяет целые числовые значения от десятичных значений.
Десятичная точка отделяет целые числовые значения от десятичных значений.
Имеет ли это смысл для вас сейчас?
Перейдите к следующая вкладка
Как использовать оператор% — Real Python
Python поддерживает широкий спектр арифметических операторов, которые вы можете использовать при работе с числами в вашем коде.Одним из этих операторов является оператор по модулю (% ), который возвращает остаток от деления двух чисел.
Оператор модуля Python иногда может быть упущен из виду. Но хорошее понимание этого оператора даст вам бесценный инструмент в вашем арсенале инструментов Python.
Модуль математики
Термин по модулю происходит от раздела математики, называемого модульной арифметикой. Модульная арифметика имеет дело с арифметикой целых чисел на круговой числовой строке с фиксированным набором чисел.Все арифметические операции, выполняемые на этой числовой строке, будут повторяться, когда они достигнут определенного числа, называемого модулем .
Классическим примером модульной арифметики являются двенадцатичасовые часы. Двенадцатичасовые часы имеют фиксированный набор значений от 1 до 12. При подсчете двенадцатичасовых часов вы считаете до модуля 12, а затем возвращаетесь к 1. Двенадцатичасовые часы можно классифицировать как « по модулю 12 », иногда сокращается до« по модулю 12 ».
Оператор по модулю используется, когда вы хотите сравнить число с модулем и получить эквивалентное число, ограниченное диапазоном модуля.
Например, предположим, что вы хотите определить, сколько времени будет через девять часов после 8:00. В двенадцатичасовых часах вы не можете просто добавить 9 к 8, потому что вы получите 17. Вам нужно взять результат 17, и используйте мод , чтобы получить эквивалентное значение в двенадцатичасовом контексте:
8 часов + 9 = 17 часов
17 мод 12 = 5
17 mod 12 возвращает 5 . Это означает, что девять часов после 8:00 — это 17:00.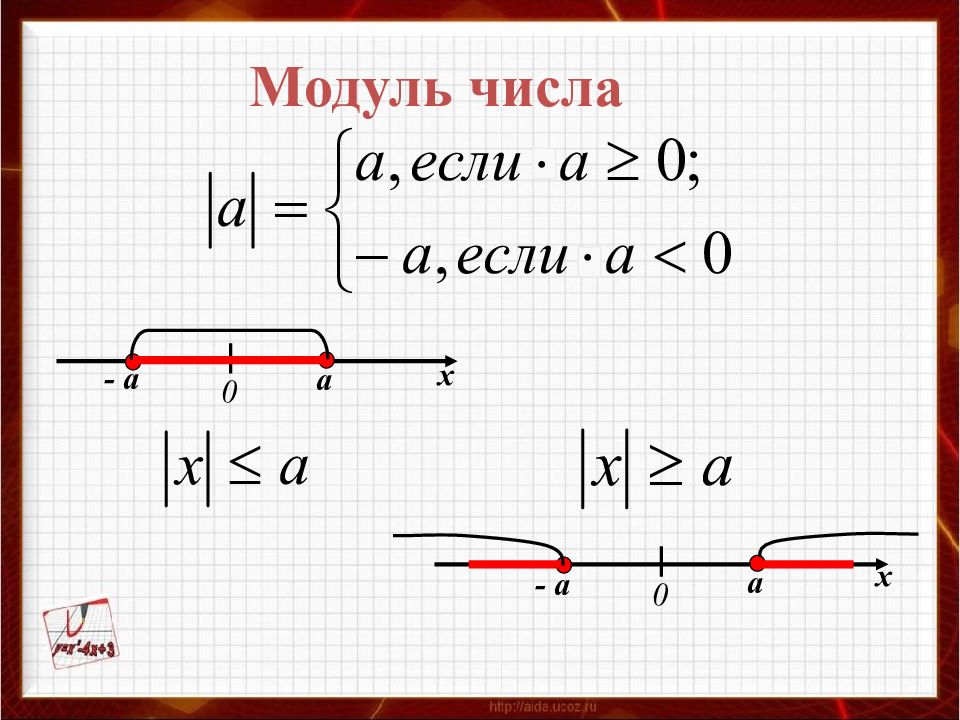 Вы определили это, взяв число
Вы определили это, взяв число 17 и применив его к контексту mod 12 .
Теперь, если подумать, 17 и 5 эквивалентны в контексте mod 12 . Если бы вы посмотрели на часовую стрелку в 5:00 и 17:00, она была бы в том же положении. В модульной арифметике есть уравнение, описывающее эту взаимосвязь:
Это уравнение гласит: « a и b равны по модулю n ». Это означает, что a и b эквивалентны в mod n , поскольку они имеют одинаковый остаток при делении на n .В приведенном выше уравнении n — это модуль упругости как для a , так и для b . Используя значения 17 и 5 из предыдущих, уравнение будет выглядеть так:
Это гласит: « 17 и 5 равны по модулю 12 ». 17 и 5 имеют одинаковый остаток, 5 , при делении на 12 . Итак, в
Итак, в mod 12 числа 17 и 5 эквивалентны.
Подтвердить это можно с помощью деления:
17/12 = 1 R 5
5/12 = 0 R 5
Обе операции имеют одинаковый остаток, 5 , поэтому они эквивалентны по модулю 12 .
Теперь это может показаться сложным математическим делом для оператора Python, но эти знания подготовят вас к использованию оператора по модулю в примерах далее в этом руководстве. В следующем разделе вы познакомитесь с основами использования оператора Python по модулю с числовыми типами int и float .
Основы операторов Python по модулю
Оператор по модулю, как и другие арифметические операторы, может использоваться с числовыми типами int и float . Как вы увидите позже, его также можно использовать с другими типами, такими как math.fmod () , decimal.Decimal и вашими собственными классами.
Оператор по модулю с
int В большинстве случаев вы будете использовать оператор по модулю с целыми числами. Оператор по модулю, когда он используется с двумя положительными целыми числами, вернет остаток от стандартного евклидова деления:
>>> >>> 15% 4
3
>>> 17% 12
5
>>> 240% 13
6
>>> 10% 16
10
Будьте осторожны! Как и в случае с оператором деления (/), Python вернет ZeroDivisionError , если вы попытаетесь использовать оператор по модулю с делителем 0 :
>>> 22% 0
ZeroDivisionError: целочисленное деление или по модулю нуля
Далее вы познакомитесь с использованием оператора по модулю с плавающей точкой .
Оператор по модулю с поплавком
Подобно int , оператор по модулю, используемый с float , вернет остаток от деления, но как значение float :
>>> 12,5% 5,5
1. 5
>>> 17,0% 12,0
5.0
5
>>> 17,0% 12,0
5.0
Альтернативой использованию числа с плавающей запятой с оператором по модулю является использование math.fmod () для выполнения операций по модулю для значений с плавающей запятой :
>>> импорт математики
>>> математика.fmod (12.5, 5.5)
1.5
>>> math.fmod (8.5, 2.5)
1.0
Официальные документы Python предлагают использовать math.fmod () вместо оператора Python по модулю при работе со значениями float , поскольку math.fmod () вычисляет результат операции по модулю. Если вы используете отрицательный операнд, вы можете увидеть разные результаты между math.fmod (x, y) и x% y . В следующем разделе вы более подробно исследуете использование оператора по модулю с отрицательными операндами.
Как и другие арифметические операторы, оператор по модулю и math.fmod () могут столкнуться с проблемами округления и точности при работе с арифметикой с плавающей запятой:
>>> 13,3% 1,1
0,09999999999999964
>>> импорт математики
>>> math. fmod (13.3, 1.1)
0,09999999999999964
fmod (13.3, 1.1)
0,09999999999999964
Если для вашего приложения важно поддерживать точность с плавающей запятой, вы можете использовать оператор по модулю с десятичным числом .Десятичный . Вы рассмотрите это позже в этом руководстве.
Оператор по модулю с отрицательным операндом
Все операции по модулю, которые вы видели до этого момента, использовали два положительных операнда и возвращали предсказуемые результаты. Когда вводится отрицательный операнд, все становится сложнее.
Как оказалось, способ, которым компьютеры определяют результат операции по модулю с отрицательным операндом, оставляет неоднозначность относительно того, должен ли остаток принимать знак делимого (делимое число) или знак делителя (число, на которое делится дивиденд).Разные языки программирования обрабатывают это по-разному.
Например, в JavaScript остаток примет знак делимого:
Остаток в этом примере, 2 , положительный, поскольку принимает знак дивиденда 8 . В Python и других языках остаток примет знак делителя:
В Python и других языках остаток примет знак делителя:
Здесь вы можете видеть, что остаток -1 принимает знак делителя -3 .
Вы можете спросить, почему остаток в JavaScript равен 2 , а остаток в Python равен -1 .Это связано с тем, как разные языки определяют результат операции по модулю. Языки, в которых остаток принимает знак делимого, используют следующее уравнение для определения остатка:
Это уравнение состоит из трех переменных:
-
r— остаток. -
a— дивиденды. -
n— делитель.
trunc () в этом уравнении означает, что используется усеченное деление , которое всегда округляет отрицательное число до нуля.Для получения дополнительных пояснений см. Шаги операции по модулю ниже, используя 8 в качестве делимого и -3 в качестве делителя:
r = 8 - (-3 * усечение (8 / -3))
r = 8 - (-3 * усечение (-2,666666666667))
r = 8 - (-3 * -2) # Округление в сторону 0
г = 8 - 6
г = 2
Здесь вы можете увидеть, как такой язык, как JavaScript, получает остаток 2 . Python и другие языки, в которых остаток принимает знак делителя, используют следующее уравнение:
Python и другие языки, в которых остаток принимает знак делителя, используют следующее уравнение:
floor () в этом уравнении означает, что используется разделение этажа .При положительных числах деление этажа вернет тот же результат, что и усеченное деление. Но при отрицательном числе деление по этажам округляет результат в меньшую сторону, в сторону от нуля:
r = 8 - (-3 * этаж (8 / -3))
r = 8 - (-3 * этаж (-2.666666666667))
r = 8 - (-3 * -3) # Округление от 0
г = 8 - 9
г = -1
Здесь видно, что результат: -1 .
Теперь, когда вы понимаете, откуда берется разница в остатке, вам может быть интересно, почему это важно, если вы используете только Python.Как оказалось, не все операции по модулю в Python одинаковы. В то время как модуль, используемый с типами int и float , принимает знак делителя, другие типы — нет.
Вы можете увидеть пример этого, сравнив результаты 8. и  0% -3.0
0% -3.0 math.fmod (8.0, -3.0) :
>>> 8,0% -3
-1,0
>>> импорт математики
>>> math.fmod (8.0, -3.0)
2.0
математ.fmod () принимает знак делимого с использованием усеченного деления, тогда как float использует знак делителя. Позже в этом руководстве вы увидите другой тип Python, который использует знак делимого, десятичное число . Десятичное число .
Оператор по модулю и
divmod () Python имеет встроенную функцию divmod () , которая внутренне использует оператор по модулю. divmod () принимает два параметра и возвращает кортеж, содержащий результаты деления по этажу и по модулю с использованием предоставленных параметров.
Ниже приведен пример использования divmod () с 37 и 5 :
>>> divmod (37, 5)
(7, 2)
>>> 37 // 5
7
>>> 37% 5
2
Вы можете видеть, что divmod (37, 5) возвращает кортеж (7, 2) .
7 является результатом разделения этажей на 37 и 5 . 2 является результатом 37 по модулю 5 .
Ниже приведен пример, в котором второй параметр — отрицательное число. Как обсуждалось в предыдущем разделе, когда оператор по модулю используется с int , остаток примет знак делителя:
>>> divmod (37, -5)
(-8, -3)
>>> 37 // -5
-8
>>> 37% -5
-3 # Результат имеет знак делителя
Теперь, когда у вас была возможность увидеть оператор по модулю, используемый в нескольких сценариях, важно взглянуть на то, как Python определяет приоритет оператора по модулю при использовании с другими арифметическими операторами.
Приоритет оператора по модулю
Как и другие операторы Python, для оператора по модулю существуют особые правила, определяющие его приоритет при вычислении выражений. Оператор по модулю (% ) имеет тот же уровень приоритета, что и операторы умножения ( * ), деления (/) и деления по полу ( // ).
Взгляните на пример приоритета оператора по модулю ниже:
>>> >>> 4 * 10% 12 - 9
-5
Операторы умножения и по модулю имеют одинаковый уровень приоритета, поэтому Python будет оценивать их слева направо.Вот шаги для вышеуказанной операции:
-
4 * 10оценивается, в результате получается40% 12 - 9. -
40% 12оценивается, в результате получается4 - 9. -
4 - 9вычисляется, в результате получается-5.
Если вы хотите переопределить приоритет других операторов, вы можете заключить в круглые скобки операцию, которую вы хотите оценить первой:
>>> >>> 4 * 10% (12-9)
1
В этом примере сначала оценивается (12–9) , затем 4 * 10 и, наконец, 40% 3 , что равно 1 .
Оператор модуля Python на практике
Теперь, когда вы познакомились с основами оператора Python по модулю, вы рассмотрите несколько примеров его использования для решения реальных задач программирования. Иногда бывает трудно определить, когда использовать в коде оператор по модулю. Приведенные ниже примеры дадут вам представление о многих способах его использования.
Иногда бывает трудно определить, когда использовать в коде оператор по модулю. Приведенные ниже примеры дадут вам представление о многих способах его использования.
Как проверить, четное или нечетное число
В этом разделе вы увидите, как использовать оператор по модулю, чтобы определить, является ли число четным или нечетным.Используя оператор по модулю с модулем 2 , вы можете проверить любое число, чтобы узнать, делится ли оно без остатка на 2 . Если оно делится без остатка, то это четное число.
Взгляните на is_even () , который проверяет, является ли параметр num четным:
def is_even (число):
вернуть число% 2 == 0
Здесь num% 2 будет равно 0 , если num четное, и 1 , если num нечетное.Проверка против 0 вернет логическое значение Истина или Ложь в зависимости от того, является ли num четным.
Проверка на нечетные числа очень похожа. Чтобы проверить нечетное число, вы инвертируете проверку равенства:
def is_odd (число):
вернуть число% 2! = 0
Эта функция вернет True , если num% 2 не равно 0 , что означает, что остаток доказывает, что num — нечетное число.Теперь вам может быть интересно, можно ли использовать следующую функцию, чтобы определить, является ли num нечетным числом:
def is_odd (число):
вернуть число% 2 == 1
Ответ на этот вопрос — да и нет. Технически эта функция будет работать так же, как Python вычисляет по модулю с целыми числами. Тем не менее, вам следует избегать сравнения результата операции по модулю с 1 , поскольку не все операции по модулю в Python возвращают тот же остаток.
Вы можете понять, почему, в следующих примерах:
>>> >>> -3% 2
1
>>> 3% -2
-1
Во втором примере остаток принимает знак отрицательного делителя и возвращает -1 . В этом случае логическая проверка
В этом случае логическая проверка 3% -2 == 1 вернет False .
Однако, если вы сравните операцию по модулю с 0 , то не имеет значения, какой операнд отрицательный. Результатом всегда будет Истинно , когда это четное число:
>>> -2% 2
0
>>> 2% -2
0
Если вы будете сравнивать операцию Python по модулю с 0 , то у вас не должно возникнуть проблем с проверкой четных и нечетных чисел или любых других кратных чисел в вашем коде.
В следующем разделе вы узнаете, как можно использовать оператор по модулю с циклами для управления потоком вашей программы.
Как запускать код с определенными интервалами в цикле
С помощью оператора Python по модулю вы можете запускать код через определенные промежутки времени внутри цикла. Это делается путем выполнения операции по модулю с текущим индексом цикла и модулем. Номер модуля определяет, как часто код, зависящий от интервала, будет выполняться в цикле. 15}», end = «»)
если индекс% модуля == 0:
Распечатать()
Распечатать()
15}», end = «»)
если индекс% модуля == 0:
Распечатать()
Распечатать()
Этот код определяет split_names_into_rows () , который принимает два параметра. список_имён — это список имен, который следует разбить на строки. Модуль устанавливает модуль для операции, эффективно определяя, сколько имен должно быть в каждой строке. split_names_into_rows () будет перебирать name_list и начинать новую строку после достижения значения модуля .
Прежде чем разбирать функцию более подробно, взгляните на нее в действии:
>>> >>> names = ["Пикард", "Райкер", "Трой", "Крашер", "Ворф", "Дейта", "Ла Форж"]
>>> split_names_into_rows (имена)
---- Пикард ----- ----- Райкер ----- ----- Трой ------
---- Дробилка ---- ----- Worf ------ ----- Данные ------
--- Ла Форж ----
Как видите, список имен разделен на три строки, максимум по три имени в каждой строке. Модуль упругости
Модуль упругости по умолчанию равен 3 , но вы можете указать любое число:
>>> split_names_into_rows (имена, модуль = 4)
---- Пикард ----- ----- Райкер ----- ----- Трой ------ ---- Крашер ----
----- Ворф ------ ----- Данные ------ --- Ла Форж ----
>>> split_names_into_rows (имена, модуль = 2)
---- Пикард ----- ----- Райкер -----
----- Трой ------ ---- Дробилка ----
----- Worf ------ ----- Данные ------
--- Ла Форж ----
>>> split_names_into_rows (имена, модуль = 1)
---- Пикард -----
----- Райкер -----
----- Трой ------
----Дробилка----
----- Ворф ------
-----Данные------
--- Ла Форж ----
Теперь, когда вы увидели код в действии, вы можете разобрать, что он делает.Во-первых, он использует enumerate () для перебора name_list , присваивая текущий элемент в списке имени и значению счетчика index . Вы можете видеть, что необязательный аргумент start для enumerate () имеет значение 1 . Это означает, что счетчик индекса
Это означает, что счетчик индекса начнется с 1 вместо 0 :
для индекса, имя в перечислении (name_list, start = 1):
Затем внутри цикла функция вызывает print () для вывода name в текущую строку.15 Синтаксис указывает print () выполнить следующие действия:
- Выведите не менее
15символов, даже если строка короче 15 символов. - Выровняйте строку по центру.
- Заполните любое пространство справа или слева от строки символом дефиса (
-).
Теперь, когда имя напечатано в строке, взглянем на основную часть split_names_into_rows () :
, если индекс% модуля == 0:
Распечатать()
Этот код принимает индекс текущей итерации и, используя оператор по модулю, сравнивает его с модулем .Если результат равен 0 , то он может запустить код, зависящий от интервала. В этом случае функция вызывает
В этом случае функция вызывает print () , чтобы добавить новую строку, которая начинает новую строку.
Приведенный выше код является только одним примером. Использование шаблона index% modulus == 0 позволяет запускать другой код через определенные промежутки времени в ваших циклах. В следующем разделе вы немного углубитесь в эту концепцию и рассмотрите циклическую итерацию.
Как создать циклическую итерацию
Циклическая итерация описывает тип итерации, которая сбрасывается при достижении определенной точки.Как правило, этот тип итерации используется для ограничения индекса итерации определенным диапазоном.
Вы можете использовать оператор по модулю для создания циклической итерации. Взгляните на пример использования библиотеки turtle для рисования формы:
импортная черепаха
случайный импорт
def draw_with_cyclic_iteration ():
colors = ["зеленый", "голубой", "оранжевый", "фиолетовый", "красный", "желтый", "белый"]
turtle. bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.выбор (цвета)) # Первый цвет случайный
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
turtle.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.выбор (цвета)) # Первый цвет случайный
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
turtle.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
В приведенном выше коде используется бесконечный цикл для рисования повторяющейся формы звезды. После каждых шести итераций он меняет цвет пера. Размер пера увеличивается с каждой итерацией, пока значение i не будет сброшено обратно на 0 .Если запустить код, то должно получиться примерно следующее:
Важные части этого кода выделены ниже:
импортная черепаха
случайный импорт
def draw_with_cyclic_iteration ():
colors = ["зеленый", "голубой", "оранжевый", "фиолетовый", "красный", "желтый", "белый"]
turtle. bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.choice (цвета))
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
черепаха.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.choice (цвета))
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
черепаха.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
Каждый раз при прохождении цикла i обновляется на основе результатов (i + 1)% 6 . Это новое значение i используется для увеличения .pensize с каждой итерацией. Как только i достигнет 5 , (i + 1)% 6 будет равно 0 , а i вернется к 0 .
Вы можете увидеть шаги итерации ниже для более ясного понимания:
я = 0: (0 + 1)% 6 = 1
я = 1: (1 + 1)% 6 = 2
я = 2: (2 + 1)% 6 = 3
я = 3: (3 + 1)% 6 = 4
я = 4: (4 + 1)% 6 = 5
i = 5: (5 + 1)% 6 = 0 # Сброс
Когда i сбрасывается обратно на 0 , . изменяется на новый случайный цвет, как показано ниже: pencolor
pencolor
если i == 0:
turtle.pencolor (random.choice (цвета))
Код в этом разделе использует 6 в качестве модуля, но вы можете установить его на любое число, чтобы настроить, сколько раз цикл будет повторяться перед сбросом значения i .
Как преобразовать единицы
В этом разделе вы узнаете, как использовать оператор по модулю для преобразования единиц. В следующих примерах единицы меньшего размера преобразуются в единицы большего размера без использования десятичных знаков. Оператор по модулю используется для определения любого остатка, который может существовать, когда меньшая единица не делится без остатка на большую единицу.
В этом первом примере вы преобразуете дюймы в футы. Оператор по модулю используется для получения оставшихся дюймов, которые неравномерно не делятся на футы.Оператор деления пола ( // ) используется для округления общего количества футов в меньшую сторону:
def convert_inches_to_feet (total_inches):
дюймы = total_inches% 12
футов = total_inches // 12
print (f "{total_inches} дюймов = {футов} футов и {дюймов} дюймов")
Вот пример используемой функции:
>>> >>> convert_inches_to_feet (450)
450 дюймов = 37 футов 6 дюймов
Как видно из выходных данных, 450% 12 возвращает 6 , то есть оставшиеся дюймы, которые не были равномерно разделены на футы. Результатом
Результатом 450 // 12 является 37 , что представляет собой общее количество футов, на которое дюймы были равномерно разделены.
В следующем примере вы можете пойти немного дальше. convert_minutes_to_days () принимает целое число, total_mins , представляющее количество минут, и выводит период времени в днях, часах и минутах:
def convert_minutes_to_days (total_mins):
дней = total_mins // 1440
extra_minutes = total_mins% 1440
часы = extra_minutes // 60
минут = дополнительные_минуты% 60
print (f "{total_mins} = {days} дней, {часов} часов и {минут} минут")
Разбив это, вы можете увидеть, что функция выполняет следующее:
- Определяет общее количество равномерно делимых дней с
total_mins // 1440, где1440- количество минут в дне - Вычисляет любые
extra_minutesоставшиеся сtotal_mins% 1440 - Использует
дополнительных_минут, чтобы получить равномерно делимыечасови любые дополнительныеминут
Вы можете увидеть, как это работает, ниже:
>>> >>> convert_minutes_to_days (1503)
1503 = 1 день, 1 час и 3 минуты
>>> convert_minutes_to_days (3456)
3456 = 2 дня, 9 часов и 36 минут
>>> convert_minutes_to_days (35000)
35000 = 24 дня, 7 часов и 20 минут
Хотя приведенные выше примеры относятся только к преобразованию дюймов в футы и минут в дни, вы можете использовать любой тип единиц с оператором по модулю, чтобы преобразовать меньшую единицу в большую единицу.
Примечание : Оба приведенных выше примера можно изменить, чтобы использовать divmod () , чтобы сделать код более лаконичным. Если вы помните, divmod () возвращает кортеж, содержащий результаты деления этажа и по модулю с использованием предоставленных параметров.
Ниже операторы деления по этажам и по модулю были заменены на divmod () :
def convert_inches_to_feet_updated (total_inches):
футы, дюймы = divmod (total_inches, 12)
print (f "{total_inches} дюймов = {футов} футов и {дюймов} дюймов")
Как видите, divmod (total_inches, 12) возвращает кортеж, который распакован в футов и дюймов .
Если вы попробуете эту обновленную функцию, то получите те же результаты, что и раньше:
>>> >>> convert_inches_to_feet (450)
450 дюймов = 37 футов 6 дюймов
>>> convert_inches_to_feet_updated (450)
450 дюймов = 37 футов 6 дюймов
Вы получите тот же результат, но теперь код более лаконичный. Вы также можете обновить
Вы также можете обновить convert_minutes_to_days () :
def convert_minutes_to_days_updated (total_mins):
дней, extra_minutes = divmod (total_mins, 1440)
часы, минуты = divmod (extra_minutes, 60)
print (f "{total_mins} = {days} дней, {часов} часов и {минут} минут")
При использовании divmod () функция легче читается, чем предыдущая версия, и возвращает тот же результат:
>>> convert_minutes_to_days (1503)
1503 = 1 день, 1 час и 3 минуты
>>> convert_minutes_to_days_updated (1503)
1503 = 1 день, 1 час и 3 минуты
Использование divmod () необязательно для всех ситуаций, но здесь имеет смысл, поскольку при расчетах преобразования единиц используется как деление по этажам, так и по модулю.
Теперь, когда вы узнали, как использовать оператор по модулю для преобразования единиц, в следующем разделе вы узнаете, как можно использовать оператор по модулю для проверки простых чисел.
Как определить, является ли число простым числом
В следующем примере вы посмотрите, как можно использовать оператор Python по модулю, чтобы проверить, является ли число простым числом . Простое число - это любое число, которое содержит только два делителя: 1 и само себя. Примеры простых чисел: 2 , 3 , 5 , 7 , 23 , 29 , 59 , 83 и 97 .
Код ниже представляет собой реализацию для определения простоты числа с помощью оператора по модулю:
def check_prime_number (число):
если число <2:
print (f "{число} должно быть больше или равно 2, чтобы быть простым.")
возвращаться
факторы = [(1, число)]
я = 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
если len (факторы)> 1:
print (f "{число} не является простым. Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
Этот код определяет check_prime_number () , который принимает параметр num и проверяет, является ли это простым числом.Если это так, то отображается сообщение о том, что num - простое число. Если это не простое число, отображается сообщение со всеми множителями числа.
Примечание: Приведенный выше код не самый эффективный способ проверки простых чисел. Если вы хотите копнуть глубже, посмотрите Сито Эратосфена и Сито Аткина, где можно найти примеры более эффективных алгоритмов поиска простых чисел.
Прежде чем вы внимательно посмотрите на функцию, вот результаты с использованием некоторых других чисел:
>>> >>> check_prime_number (44)
44 не простое.Он имеет следующие факторы: [(1, 44), (2, 22), (4, 11)]
>>> check_prime_number (53)
53 - простое число
>>> check_prime_number (115)
115 не простое. Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number (997)
997 - простое число
Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number (997)
997 - простое число
Углубившись в код, вы увидите, что он начинается с проверки, меньше ли num 2 . Простые числа могут быть не более 2 . Если num меньше 2 , то выполнение функции не требуется.Он будет print () сообщение и вернет :
если число <2:
print (f "{число} должно быть больше или равно 2, чтобы быть простым.")
возвращаться
Если num больше 2 , то функция проверяет, является ли num простым числом. Чтобы проверить это, функция выполняет итерацию по всем числам от 2 до квадратного корня из num , чтобы увидеть, делятся ли они на num равномерно. Если одно из чисел делится равномерно, значит, был найден множитель, и num не может быть простым числом.
Вот основная часть функции:
факторов = [(1, число)]
я = 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
Здесь есть что распаковать, так что давайте рассмотрим это шаг за шагом.
Сначала создается список факторов с начальными факторами (1, число) . Этот список будет использоваться для хранения любых других найденных факторов:
Затем, начиная с 2 , код увеличивает i , пока не достигнет квадратного корня из num .На каждой итерации он сравнивает num с i , чтобы увидеть, делится ли оно без остатка. Коду нужно только проверить квадратный корень из num включительно, потому что он не будет содержать никаких множителей выше этого:
я = 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
Вместо того, чтобы пытаться определить квадратный корень из num , функция использует цикл while , чтобы проверить, является ли i * i <= num . Пока
Пока i * i <= num , цикл не достиг квадратного корня из num .
Внутри цикла while оператор по модулю проверяет, делится ли num без остатка на i :
факторов = [(1, число)]
i = 2 # Начать начальный индекс с 2
в то время как я * я <= число:
если num% i == 0:
Factors.append ((i, num // i))
я + = 1
Если число делится без остатка на i , тогда i является множителем число , и кортеж множителей добавляется к списку множителей .
После завершения цикла и код проверяет, были ли найдены какие-либо дополнительные факторы:
если len (факторы)> 1:
print (f "{число} не является простым. Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
Если в списке факторов существует более одного кортежа, то num не может быть простым числом. Для непростых чисел коэффициенты распечатываются. Для простых чисел функция выводит сообщение о том, что
Для непростых чисел коэффициенты распечатываются. Для простых чисел функция выводит сообщение о том, что num - простое число.
Как реализовать шифры
Оператор модуля Python может использоваться для создания шифров. Шифр - это тип алгоритма для выполнения шифрования и дешифрования входных данных, обычно текста. В этом разделе вы познакомитесь с двумя шифрами: шифром Цезаря и шифром Виженера .
Цезарь Шифр
Первый шифр, на который вы посмотрите, - это шифр Цезаря, названный в честь Юлия Цезаря, который использовал его для тайной передачи сообщений.Это шифр подстановки, который использует подстановку букв для шифрования строки текста.
Шифр Цезаря работает, взяв зашифровываемую букву и сдвинув ее на определенное количество позиций влево или вправо в алфавите. Какая бы буква ни находилась в этой позиции, используется как зашифрованный символ. Это же значение сдвига применяется ко всем символам в строке.
Например, если сдвиг был 5 , то A сместился бы на пять букв вверх и стал бы F , B стал бы G и так далее.Ниже вы можете увидеть процесс шифрования текста REALPYTHON со сдвигом 5 :
В результате получается шифр WJFQUDYMTS .
Расшифровка шифра выполняется реверсированием сдвига. Процессы шифрования и дешифрования можно описать следующими выражениями, где char_index - это индекс символа в алфавите:
encrypted_char_index = (char_index + shift)% 26
decrypted_char_index = (char_index - сдвиг)% 26
Этот шифр использует оператор по модулю, чтобы гарантировать, что при сдвиге буквы индекс будет повторяться, если будет достигнут конец алфавита.Теперь, когда вы знаете, как работает этот шифр, взгляните на его реализацию:
импортная строка
def caesar_cipher (текст, сдвиг, расшифровка = ложь):
если не text. isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = прописные буквы.индекс (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = прописные буквы.индекс (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
Этот код определяет функцию с именем caesar_cipher () , которая имеет два обязательных параметра и один необязательный параметр:
-
текст- текст, который нужно зашифровать или расшифровать. -
сдвиг- количество позиций для сдвига каждой буквы. -
decrypt- логическое значение, устанавливаемое, еслитекстдолжен быть расшифрован.
decrypt включен, чтобы можно было использовать одну функцию для обработки как шифрования, так и дешифрования. Эта реализация может обрабатывать только буквенные символы, поэтому функция сначала проверяет, является ли текст буквенным символом в кодировке ASCII:
def caesar_cipher (text, shift, decrypt = False):
если не text.isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
Затем функция определяет три переменные для хранения строчных символов ASCII, прописных символов ASCII и результатов шифрования или дешифрования:
нижний регистр = строка.ascii_lowercase # "abcdefghijklmnopqrstuvwxyz"
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результат = ""
Затем, если функция используется для расшифровки текста , она умножает shift на -1 , чтобы сдвинуть назад:
если расшифровать:
сдвиг = сдвиг * -1
Наконец, caesar_cipher () перебирает отдельные символы в тексте и выполняет следующие действия для каждого символа :
- Проверьте, является ли
charстрочными или прописными буквами.
- Получите индекс
charв спискахнижнего регистраиливерхнего регистраASCII. - Добавьте сдвиг
- Используйте
% 26, чтобы убедиться, что сдвиг вернется к началу алфавита. - Добавить зашифрованный символ к строке результата
После того, как цикл завершает итерацию по значению текста , возвращается результат :
для символов в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
Вот еще раз полный код:
импортная строка
def caesar_cipher (текст, сдвиг, расшифровка = ложь):
если не text. isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
прописные буквы = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
прописные буквы = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
Теперь запустите код в Python REPL, используя текст meetMeAtOurHideOutAtTwo со сдвигом 10 :
>>> caesar_cipher ("meetMeAtOurHideOutAtTwo", 10)
woodWoKdYebRsnoYedKdDgy
Зашифрованный результат: woodWoKdYebRsnoYedKdDgy .Используя этот зашифрованный текст, вы можете запустить расшифровку, чтобы получить исходный текст:
>>> caesar_cipher ("woodWoKdYebRsnoYedKdDgy", 10, decrypt = True)
MeetMeAtOurHideOutAtTwo
С шифром Цезаря интересно поиграть для введения в криптографию. Хотя шифр Цезаря редко используется сам по себе, он является основой для более сложных подстановочных шифров. В следующем разделе вы познакомитесь с одним из потомков шифра Цезаря, шифром Виженера.
Хотя шифр Цезаря редко используется сам по себе, он является основой для более сложных подстановочных шифров. В следующем разделе вы познакомитесь с одним из потомков шифра Цезаря, шифром Виженера.
Шифр Виженера
Шифр Виженера представляет собой полиалфавитный замещающий шифр. Для шифрования он использует разные шифры Цезаря для каждой буквы входящего текста. Шифр Виженера использует ключевое слово, чтобы определить, какой шифр Цезаря следует использовать для поиска буквы шифра.
Вы можете увидеть пример процесса шифрования на следующем изображении. В этом примере входной текст REALPYTHON зашифрован с использованием ключевого слова MODULO :
Для каждой буквы входящего текста, REALPYTHON , используется буква ключевого слова MODULO , чтобы определить, какой столбец шифра Цезаря следует выбрать.Если ключевое слово короче вводимого текста, как в случае с MODULO , то буквы ключевого слова повторяются до тех пор, пока все буквы вводимого текста не будут зашифрованы.
Ниже представлена реализация шифра Виженера. Как вы увидите, оператор по модулю используется в функции дважды:
импортная строка
def vigenere_cipher (текст, ключ, decrypt = False):
если не text.isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
Вы могли заметить, что подпись для vigenere_cipher () очень похожа на caesar_cipher () из предыдущего раздела:
def vigenere_cipher (текст, ключ, decrypt = False):
если не текст. isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
верхний регистр = строка.ascii_uppercase
результаты = ""
isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
верхний регистр = строка.ascii_uppercase
результаты = ""
Основное отличие состоит в том, что вместо параметра shift , vigenere_cipher () принимает параметр key , который является ключевым словом, используемым во время шифрования и дешифрования. Еще одно отличие - добавление text.isupper () . На основе этой реализации vigenere_cipher () может принимать только вводимый текст в верхнем регистре.
Подобно caesar_cipher () , vigenere_cipher () выполняет итерацию по каждой букве входного текста, чтобы зашифровать или расшифровать его:
для i, символ в перечислении (текст):
current_key = ключ [i% len (ключ)]
В приведенном выше коде вы можете увидеть, как функция впервые использовала оператор по модулю:
current_key = ключ [i% len (ключ)]
Здесь значение current_key определяется на основе индекса, возвращенного из i% len (key) . Этот индекс используется для выбора буквы из строки ключа , например
Этот индекс используется для выбора буквы из строки ключа , например M из MODULO .
Оператор по модулю позволяет использовать ключевое слово любой длины независимо от длины текста , который нужно зашифровать. Как только индекс i , индекс символа, который в настоящее время зашифрован, равен длине ключевого слова, он начнется с начала ключевого слова.
Для каждой буквы входящего текста несколько шагов определяют, как ее зашифровать или расшифровать:
- Определите
char_indexна основе индексаcharвнутриверхнего регистра. - Определите
key_indexна основе индексаcurrent_keyвнутрив верхнем регистре. - Используйте
char_indexиkey_index, чтобы получить индекс для зашифрованного или дешифрованного символа.
Взгляните на эти шаги в приведенном ниже коде:
char_index = uppercase. index (char)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
index (char)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
Как видите, индексы для расшифровки и шифрования рассчитываются по-разному.Поэтому в этой функции используется расшифровка . Таким образом, вы можете использовать эту функцию как для шифрования, так и для дешифрования.
После определения индекса вы обнаружите, что функция использует второй оператор по модулю:
результаты + = верхний регистр [индекс% 26]
index% 26 гарантирует, что индекс символа не превышает 25 , что гарантирует, что он остается внутри алфавита. С помощью этого индекса зашифрованный или дешифрованный символ выбирается из прописных букв и добавляется к результатам .
Вот еще раз полный код шифра Виженера:
импортная строка
def vigenere_cipher (текст, ключ, decrypt = False):
если не text. isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = прописные буквы.индекс (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = прописные буквы.индекс (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
Теперь запустите его в Python REPL:
>>> >>> vigenere_cipher (text = "REALPYTHON", key = "MODULO")
DSDFAMFVRH
>>> encrypted = vigenere_cipher (text = "REALPYTHON", key = "MODULO")
>>> печать (в зашифрованном виде)
DSDFAMFVRH
>>> vigenere_cipher (зашифровано, "MODULO", decrypt = True)
РЕАЛПИТОН
Отлично! Теперь у вас есть рабочий шифр Виженера для шифрования текстовых строк.
Расширенное использование оператора модуля Python в Python
В этом последнем разделе вы поднимете свои знания об операторах по модулю на новый уровень, используя их с десятичным числом . Десятичное число . Вы также узнаете, как добавить .__ mod __ () к своим пользовательским классам, чтобы их можно было использовать с оператором по модулю.
Использование оператора Python по модулю с десятичным числом
. Десятичное число Ранее в этом руководстве вы видели, как можно использовать оператор по модулю с числовыми типами, такими как int и float , а также с математикой .fmod () . Вы также можете использовать оператор по модулю с Decimal из модуля decimal . Вы используете decimal.Decimal , когда вам нужно дискретное управление точностью арифметических операций с плавающей запятой.
Вот несколько примеров использования целых чисел с десятичным числом , десятичным числом и оператором по модулю:
>>> импортировать десятичный
>>> десятичное. Десятичное (15)% десятичное.Десятичное (4)
Десятичный ('3')
>>> десятичный.Десятичный (240)% десятичный. Десятичный (13)
Десятичный ('6')
Десятичное (15)% десятичное.Десятичное (4)
Десятичный ('3')
>>> десятичный.Десятичный (240)% десятичный. Десятичный (13)
Десятичный ('6')
Вот некоторые числа с плавающей запятой, используемые с десятичным числом . Десятичное число и оператор по модулю:
>>> decimal.Decimal ("12,5")% decimal.Decimal ("5,5")
Десятичный ('1,5')
>>> decimal.Decimal ("13.3")% decimal.Decimal ("1.1")
Десятичный ('0,1')
Все операции по модулю с десятичным числом . Десятичное число возвращают те же результаты, что и другие числовые типы, за исключением случаев, когда один из операндов отрицательный.В отличие от int и float , но как math.fmod () , decimal. Decimal использует знак делимого для результатов.
Взгляните на приведенные ниже примеры, в которых сравниваются результаты использования оператора по модулю со стандартными значениями int и float и с десятичным числом .: Decimal
Decimal
>>> -17% 3
1 # Знак делителя
>>> десятичное.Десятичное (-17)% десятичное.Десятичное (3)
Десятичный (-2) # Знак дивиденда
>>> 17% -3
-1 # Знак делителя
>>> десятичный.Десятичный (17)% десятичный. Десятичный (-3)
Десятичный ("2") # Знак дивиденда
>>> -13,3% 1,1
1.0000000000000004 # Знак делителя
>>> decimal.Decimal ("- 13,3")% decimal.Decimal ("1,1")
Десятичный ("- 0,1") # Знак дивиденда
По сравнению с math.fmod () , десятичное. Десятичное число будет иметь тот же знак, но точность будет другой:
>>> decimal.Decimal ("- 13,3")% decimal.Decimal ("1,1")
Десятичный ("- 0,1")
>>> математика.fmod (-13,3, 1,1)
-0,09999999999999964
Как видно из приведенных выше примеров, работа с десятичным числом , десятичным числом и оператором по модулю аналогична работе с другими числовыми типами. Просто нужно иметь в виду, как он определяет знак результата при работе с отрицательным операндом.
В следующем разделе вы узнаете, как можно переопределить оператор по модулю в своих классах, чтобы настроить его поведение.
Использование оператора Python по модулю с настраиваемыми классами
Модель данных Python позволяет вам переопределить встроенные методы в объекте Python, чтобы настроить его поведение.В этом разделе вы узнаете, как переопределить .__ mod __ () , чтобы вы могли использовать оператор по модулю со своими собственными классами.
В этом примере вы будете работать с классом Student . Этот класс будет отслеживать количество времени, которое студент учился. Вот начальный класс Student :
класс Студент:
def __init __ (я, имя):
self.name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
себя.study_sessions + = сеансы
Класс Student инициализируется параметром name и начинается с пустого списка study_sessions , который будет содержать список целых чисел, представляющих количество минут, изученных за сеанс. Также существует
Также существует .add_study_sessions () , который принимает параметр sessions , который должен быть списком учебных сессий, который нужно добавить к study_sessions .
Теперь, если вы помните из раздела преобразования единиц выше, convert_minutes_to_day () использовал оператор Python по модулю для преобразования total_mins в дни, часы и минуты.Теперь вы реализуете модифицированную версию этого метода, чтобы увидеть, как можно использовать собственный класс с оператором по модулю:
def total_study_time_in_hours (студент, всего_мин.):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Эту функцию можно использовать с классом Student для отображения общего количества часов, которые изучил Student . В сочетании с классом Student , приведенным выше, код будет выглядеть следующим образом:
класс Студент:
def __init __ (я, имя):
себя. name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def total_study_time_in_hours (студент, total_mins):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def total_study_time_in_hours (студент, total_mins):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Если вы загрузите этот модуль в Python REPL, то можете использовать его так:
>>> >>> jane = Студент ("Джейн")
>>> jane.add_study_sessions ([120, 30, 56, 260, 130, 25, 75])
>>> total_mins = сумма (джейн.study_sessions)
>>> total_study_time_in_hours (Джейн, total_mins)
Джейн занималась 11 часов 36 минут
Приведенный выше код распечатывает общее количество часов, которые изучала Джейн . Эта версия кода работает, но требует дополнительного шага суммирования study_sessions , чтобы получить total_mins перед вызовом total_study_time_in_hours () .
Вот как можно изменить класс Student , чтобы упростить код:
класс Студент:
def __init __ (я, имя):
себя. name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (сам, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (сам, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
Переопределив .__ mod __ () и .__ floordiv __ () , вы можете использовать экземпляр Student с оператором по модулю. Вычисление суммы () из study_sessions также включен в класс Student .
С этими изменениями вы можете использовать экземпляр Student непосредственно в total_study_time_in_hours () . Поскольку total_mins больше не нужен, вы можете удалить его:
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Вот полный код после изменений:
класс Студент:
def __init __ (я, имя):
себя. name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (сам, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (сам, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
Теперь, вызвав код в Python REPL, вы увидите, что он гораздо лаконичнее:
>>> >>> jane = Студент ("Джейн")
>>> Джейн.add_study_sessions ([120, 30, 56, 260, 130, 25, 75])
>>> total_study_time_in_hours (Джейн)
Джейн занималась 11 часов 36 минут
Переопределяя .__ mod __ () , вы позволяете своим пользовательским классам вести себя больше как встроенные числовые типы Python.
Заключение
На первый взгляд, оператор по модулю Python может не привлечь ваше внимание. Тем не менее, как вы видели, в этом скромном операторе есть так много всего. От проверки четных чисел до шифрования текста - вы видели множество различных применений оператора по модулю.
Тем не менее, как вы видели, в этом скромном операторе есть так много всего. От проверки четных чисел до шифрования текста - вы видели множество различных применений оператора по модулю.
Из этого руководства вы узнали, как:
- Используйте оператор по модулю с
int,float,math.fmod (),divmod ()иdecimal. Decimal - Вычислить результаты операции по модулю
- Решите реальных проблем с помощью оператора по модулю
- Переопределите
.__ mod __ ()в ваших собственных классах, чтобы использовать их с оператором по модулю
Знания, полученные в этом руководстве, позволяют теперь с большим успехом начать использовать оператор по модулю в собственном коде.Удачного питонинга!
Детский сад Математика - обучение и практика по математике для детских садов
Все приложения
[«« # »,« Моя учетная запись »] От распознавания чисел до счета и операций, учащиеся развивают чувство числа и концептуальное понимание, которое им понадобится в 1 классе .
МОДУЛЬ 1 Числа до 10
Тема A: Определение одинаковых, разных и похожих
Ученики рассматривают размер, форму и цвет предметов, чтобы определить, одинаковы ли они, разные , или подобное.Кроме того, они представлены разнородным объектам, которые «совпадают» из-за связанной функции, например, носку и обуви.
Определите два из трех одинаковых объектов.
На изображении трех существ выберите два одинаковых. Нажмите на те, которые точно такие же. Тот, который отличается, будет другого цвета, иметь другие особенности и другую позу.
Определите два из трех разных объектов.
Узнайте, как определить, есть ли различия.На изображении трех существ выберите два, которые не совпадают. Два будут точно такими же. Тот, который отличается, будет другого цвета, иметь разные особенности и другую позу
Определите различия между двумя похожими изображениями
Сравните два изображения и найдите 5 различий между ними
Определите элементы, которые принадлежат друг другу, в зависимости от их использования
Сопоставляйте предметы, которые используются вместе. Выберите элемент из трех вариантов, который используется с данным элементом.Переместите нужный элемент рядом с изображением. Затем сопоставьте три изображения с предметами, с которыми они обычно используются.
Выберите элемент из трех вариантов, который используется с данным элементом.Переместите нужный элемент рядом с изображением. Затем сопоставьте три изображения с предметами, с которыми они обычно используются.
Определите, имеют ли два объекта одинаковую форму (с разными цветами и узорами).
Укажите, имеют ли два объекта одинаковую форму. Дается одна форма, затем рядом с ней прокручиваются разные формы разного цвета и узоров. Щелкните галочку или x, чтобы указать, совпадают ли формы
Определите, имеют ли два объекта одинаковый цвет (с разными формами и узорами)
Научитесь сравнивать цвета двух объектов.Предметы могут быть одноцветными или двухцветными. Щелкните Проверить или X, чтобы указать, совпадают ли цвета двух фигур.
Определить, имеют ли два объекта одинаковый узор (с разными формами и цветами)
Сравните узор на двух объектах. Совместите каждую из трех фигур с одним и тем же узором серого цвета, перетащив серый узор вверх к его партнеру. Затем нажмите «Проверить» или «X», чтобы указать, совпадают ли рисунки двух фигур.
Затем нажмите «Проверить» или «X», чтобы указать, совпадают ли рисунки двух фигур.
Определить, одинаковы ли форма, цвет или рисунок у двух объектов.
Определить схожие характеристики двух фигур.Фигуры могут различаться по форме, рисунку и цвету.
Тема B: Сортировка и подсчет похожих объектов
Учащиеся сортируют похожие предметы по узким категориям (например, «медведи»), широким категориям (например, «одежда») и самоопределяемые категории. Они идентифицируют объекты, не принадлежащие к группе, без присвоения имени категории. Наконец, студенты считают, чтобы определить общее количество предметов в группе.
Тема C: Числа до 5 в различных конфигурациях, математические рисунки и выражения
Учащиеся считают последовательно, чтобы определить позицию, или суммируют до 5.Они связывают объекты с цифрами и видят цифры в различных шрифтах. Они работают с выровненными объектами, разбросанными объектами, пальцами и числовой линией. Учащиеся изучают стратегии подсчета при совпадении 1: 1 и узнают, что наборы предметов с одинаковым итогом можно выравнивать по-разному.
Сопоставьте пронумерованный набор из 1, 2 или 3 кубиков с одинаковым пронумерованным набором кубиков
Сопоставьте наборы кубиков. Показан человек с 1-3 кубиками. Затем есть еще трое людей с наборами кубиков.Выберите набор, соответствующий первому набору. Числа написаны разными шрифтами, чтобы практиковаться в распознавании чисел.
Сопоставьте нумерованные и ненумерованные наборы кубиков с числом 1-3
Выберите изображения, на которых показано указанное количество (1, 2 или 3) кубиков. В каждой задаче дано по четыре рисунка. Цифры написаны разными шрифтами, чтобы научиться распознавать числа. Некоторые числа затемнены, чтобы облегчить подсчет кубиков.
Сопоставьте наборы кубиков с числами 1-3
При наличии изображений с числами 1-3 и карточек с наборами кубиков перетащите правильный набор кубиков к каждому числу.Цифры и наборы расположены в случайном порядке. Одновременно отображаются три набора кубиков и чисел.
Сопоставьте числа 1-3 с их позициями на числовой строке, помеченной числами и точечными узорами.

Поместите числа в числовую строку. Перетащите числа 1-3 в соответствующее место на числовой строке. Числовая линия охватывает числа от 0 до 10 и помечена числами и точечными рисунками каждого числа. Цифры представлены различными шрифтами.
Определите пронумерованный набор кубиков, который соответствует идентичному набору из 4 или 5 пронумерованных кубов
Сопоставьте наборы кубиков.Показан один человек с 4 или 5 кубиками. Затем есть еще три человека с наборами кубиков от 2 до 5. Выберите набор, соответствующий первому набору. Числа написаны разными шрифтами, чтобы практиковаться в распознавании чисел.
Сопоставьте нумерованные и ненумерованные наборы кубиков с номером 4 или 5
Выберите картинки, на которых показано указанное количество (4 или 5) кубиков. В каждой задаче дано по четыре рисунка. Цифры написаны разными шрифтами, чтобы научиться распознавать числа.Некоторые числа затемнены, чтобы стимулировать подсчет кубиков
Подсчитайте 2-5 выровненных объектов, чтобы определить общее количество
Для ряда из 2-5 кубиков введите или выберите количество отображаемых кубиков
Сопоставьте числа 1-5 с расположением пальцы, отображаемые на руке
Сопоставьте руку с количеством отображаемых пальцев с правильной цифрой. Одновременно отображаются три числа и руки.
Одновременно отображаются три числа и руки.
Сопоставьте наборы кубиков с числами 1-5
Сопоставьте набор объектов с номером.Учитывая изображения с числами 1-5 и карточки с наборами кубиков, перетащите правильный набор кубиков на каждое число. Цифры и наборы расположены в случайном порядке. Одновременно отображаются три набора кубиков и чисел.
Определите пронумерованные наборы кубиков, которые соответствуют заданной сумме до 5
Выберите изображения, на которых показано указанное количество (1-5) кубиков. В каждой задаче даны четыре картинки с наборами кубиков. Более чем одно изображение может содержать желаемое количество кубиков, поэтому выберите все, которые применяют
Сопоставление чисел 1-5 к их позициям на числовой строке, помеченной числами и точечными узорами
Перетащите числа 1-5 в соответствующее место на числовая строка.Числовая линия охватывает числа от 0 до 10 и помечена числами и точечными рисунками каждого числа. Числа для перетаскивания представлены различными шрифтами.
Выровняйте разбросанные объекты для подсчета и определения общей суммы
Представлен случайный набор объектов (1-5). Перетащите объекты в коробку, чтобы выровнять их, чтобы было легче считать. Затем введите или выберите показанное число
Подсчет, чтобы найти общее количество разбросанных объектов, сопоставив числа 1: 1 с объектами
Подсчитайте количество показанных объектов.Нажмите на них, чтобы изменить их цвет, чтобы отметить, что они были подсчитаны. Затем выберите число
Определите набор разбросанных объектов, который соответствует заданному общему количеству до 5
Подсчитайте количество показанных объектов. Введите или выберите номер. Затем, учитывая указание количества объектов, которые нужно найти, выберите контейнер с правильным количеством элементов в нем
Тема D: Концепция нуля и работа с числами 0–5
Учащиеся используют цифры 1–5 для последовательности объектов и определить позицию или сумму.Они работают с выровненными объектами, разбросанными объектами и числовой линией. Они исследуют состав числа 3 и начинают использовать знаки +, - и =.
Они исследуют состав числа 3 и начинают использовать знаки +, - и =.
Тема E: Работа с числами 6–8 в различных конфигурациях
Учащиеся считают последовательно, чтобы определить позицию или общее количество до 9. Они связывают объекты с цифрами и видят цифры в различных шрифтах. Они работают с выровненными объектами, разбросанными объектами, пальцами и числовой линией. Учащиеся изучают стратегии подсчета при совпадении 1: 1 и узнают, что наборы предметов с одинаковым итогом можно выравнивать по-разному.
Учтите, что на единицу больше 5 составляет 6
Выучите число 6. Показаны пять элементов. Выберите правильную цифру, чтобы представить это. Затем добавляется еще один элемент, показывающий, что цифра 6 идет после 5
. Распознайте, что одно больше 6 - это 7
. Выучите число 7. Отображаются шесть элементов. Выберите правильную цифру, чтобы представить это. Затем добавляется еще один элемент, показывающий, что цифра 7 стоит после 6
Определить количество пальцев до 7, отображаемых на двух руках
Отображаются две руки, показывающие от 0 до 7 пальцев. Щелкните или введите количество показанных пальцев
Щелкните или введите количество показанных пальцев
Сопоставьте числа 0-7 с расположением пальцев, отображаемым на двух руках
Показаны три числа и три изображения рук с пальцами. Сопоставьте руки с числами 0-7
Определите набор выровненных объектов, который соответствует заданной сумме до 7
Определите изображение, показывающее до 7 кубиков. Даны три варианта ряда кубиков. Нажмите на тот, который соответствует номеру
Сопоставьте пронумерованные образцы точек с одинаковыми пронумерованными образцами точек до 7
Сопоставьте пронумерованные образцы точек.Маленькие осьминоги держат флаги с числами и точечными узорами. Перетащите к нему все, что соответствует номеру и рисунку отца осьминога. Цифры написаны различными шрифтами.
Определите наборы пронумерованных кубиков, которые соответствуют заданной сумме 6 или 7 (Часть 1)
Определите количество показанных кубиков из двух вариантов. Затем добавляется куб. Снова определите число, чтобы получилось 6 или 7. Выберите картинки с таким же общим количеством кубиков. Цифры на рисунках написаны различными шрифтами.
Выберите картинки с таким же общим количеством кубиков. Цифры на рисунках написаны различными шрифтами.
Определите наборы пронумерованных кубиков, которые соответствуют заданной сумме 6 или 7 (Часть 2)
Выберите наборы, содержащие указанную сумму.Выделите все картинки, содержащие заданное количество кубиков (6 или 7). Цифры на рисунках написаны различными шрифтами, а кубики расположены в различных конфигурациях
Сопоставьте числа 1-7 с их позициями на числовой строке, помеченной числами и точечными узорами
Для данной числовой строки перетащите два числа от 1 до 7 до их правильного местоположения на линии. Числовая строка помечена числами от 0 до 10 и точечными узорами, представляющими числа. Цифры, которые нужно перетаскивать, написаны различными шрифтами.
Подсчитайте объекты по мере их удаления от набора и определите общее число
Птицы улетают от дерева по одной.Подсчитайте количество улетевших птиц и введите или выберите количество улетевших
Подсчитайте разбросанные объекты двумя разными способами, чтобы получить одинаковую сумму
Узнайте, что порядок, в котором подсчитывается группа, не влияет на общую сумму. Следуя стрелкам, нажимайте на бусинки, чтобы изменить их цвет, и сосчитайте их. Затем введите номер. Подсчитайте элементы в другом порядке и введите число еще раз.
Следуя стрелкам, нажимайте на бусинки, чтобы изменить их цвет, и сосчитайте их. Затем введите номер. Подсчитайте элементы в другом порядке и введите число еще раз.
Обратите внимание на то, что одно число больше 7 равно 8
Выучите число 8. Показаны семь элементов.Выберите правильную цифру, чтобы представить это. Затем добавляется еще один элемент, показывающий, что цифра 8 идет после 7
Определить количество пальцев до 8, отображаемых на двух руках
Отображаются две руки, показывающие от 0 до 8 пальцев. Щелкните или введите количество показанных пальцев
Сопоставьте числа от 0 до 8 с расположением пальцев, отображаемым на двух руках
Показаны три числа и три изображения рук с пальцами. Сопоставьте руки с числами 0-8
Определите набор выровненных объектов, который соответствует заданной сумме до 8
Определите изображение, показывающее до 8 кубиков.Даны три варианта ряда кубиков. Нажмите на тот, который соответствует номеру
Определите наборы пронумерованных кубиков, которые соответствуют заданному общему количеству до 9 (Часть 1)
Определите количество показанных кубиков из двух вариантов. Затем добавляется по одному кубу. Снова определите число, всего 8. Затем будут показаны три или четыре изображения. Выберите те, у которых одинаковое количество кубиков. Цифры на рисунке
Затем добавляется по одному кубу. Снова определите число, всего 8. Затем будут показаны три или четыре изображения. Выберите те, у которых одинаковое количество кубиков. Цифры на рисунке
Определите наборы пронумерованных кубиков, которые соответствуют заданной сумме до 9 (Часть 2)
Выберите все изображения, содержащие заданное количество кубиков, до 9.Цифры на рисунках написаны различными шрифтами, а кубы расположены в различных конфигурациях.
Подсчитайте объекты по мере их удаления от набора и определите общее количество
Птиц, отлетающих от дерева, по одной. Подсчитайте количество улетевших птиц и введите или выберите общее количество улетевших
Подсчитайте разбросанные объекты двумя разными способами, чтобы получить одинаковую сумму
Узнайте, что порядок, в котором подсчитывается группа, не влияет на общую сумму. Следуя стрелкам, нажимайте на бусинки, чтобы изменить их цвет, и сосчитайте их.Затем введите номер. Подсчитайте их еще раз в другом порядке и снова введите число
Определите общее количество разбросанных объектов после того, как известное общее количество было преобразовано
Узнайте, что количество объектов не меняется при их перемещении. Подсчитайте количество предметов в контейнере и введите сумму. Затем предметы перемещаются. Подсчитайте их еще раз и введите общее
Подсчитайте количество предметов в контейнере и введите сумму. Затем предметы перемещаются. Подсчитайте их еще раз и введите общее
Тема F: Работа с числами 9–10 в различных конфигурациях
Учащиеся все больше работают с 0 и числами 6–10, чтобы определять итоги и распознавать цифры.Они работают с разрозненными объектами, неидентичными объектами, пальцами и числовой линией.
Тема G: Еще одно с числами 0–10
Учащиеся используют знакомые представления (объекты, блоки с основанием 10, числовая прямая и уравнения), чтобы изучить концепцию еще одного. Они начинают рассчитывать, а не считать все.
Тема H: На один меньше с числами 0–10
Учащиеся используют знакомые представления (объекты, блоки с основанием 10, числовая линия и уравнения), чтобы изучить концепцию «на единицу меньше».Для решения задач они чередуются между +1 и -1.
Определите недостающие числа в числовой строке с номером 9-1
Научитесь считать в обратном порядке. Введите два пропущенных числа в строке с обратным номером
Введите два пропущенных числа в строке с обратным номером
Определите на один больше и на один меньше в строке чисел
Укажите число на единицу больше и на единицу меньше заданного числа в строке числа. Числовая строка помечена цифрами 0 и 10 и начальным значением. Введите число слева и справа от начального значения
Продолжить последовательность счета в числовой строке от заданной точки, отсчитывая назад
Обратный отсчет в пределах от 10 до 0.Учитывая числовую строку, отсчитайте в обратном порядке от 10 до 0 один раз. Затем потренируйтесь считать два числа слева от заданного числа, вводя второе число
Решите -1 уравнения на основе модели блоков с основанием 10
Выучите вычитание 1. Отображается ряд кубиков и последний один выскакивает при нажатии. Введите количество оставшихся кубиков и ответ на уравнение вычитания
Решите уравнения -1 на основе модели числовой линии
Используйте числовую линию, чтобы найти ответ на уравнение -1.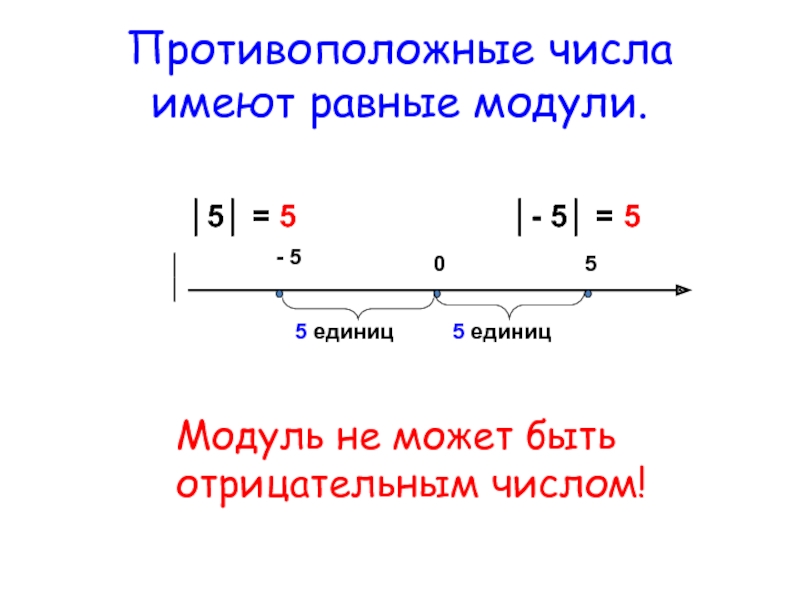 На числовой строке обозначены только числа 0, 5 и 10. Сверчок прыгает на одну цифру влево. Введите число, на которое он приземляется, затем введите это же число в качестве ответа на уравнение
На числовой строке обозначены только числа 0, 5 и 10. Сверчок прыгает на одну цифру влево. Введите число, на которое он приземляется, затем введите это же число в качестве ответа на уравнение
Решите -1 уравнения (Уровень 1)
Практикуйтесь вычитанием 1. Дана либо модель с кубиками, либо числовая линия, чтобы помочь найти ответ
Решите -1 задачу на основе известной суммы и сценария с использованием объектов
Подсчитайте количество предметов в банке и введите число. Затем отображается вторая банка, в которой элементы переставляются, и один объект удаляется.В некоторых задачах первая сумма написана на банке, скрывая предметы, и один предмет удаляется. Введите новую сумму
Решите -1 проблемы на основе известной суммы и сценария с использованием объектов
Укажите общую сумму после удаления одного объекта из известного числа. Показана банка с указанием количества в ней. Один элемент удален. Введите новую сумму
Решите -1 уравнение (Уровень 2)
Практикуйте вычитание 1. Отображается только уравнение вычитания. Введите сумму
Решите уравнения +1 и -1 на основе модели блоков с основанием 10
Попрактикуйтесь в сочетании задач, используя сложение и вычитание 1.Блоки используются для моделирования решаемого уравнения. Введите количество блоков и ответ на уравнение
Решите уравнения +1 и -1 на основе модели числовой линии
Попрактикуйтесь в сочетании задач, используя сложение и вычитание 1. Числовая линия от 0 до 10 используется для смоделировать решаемое уравнение. Введите количество блоков и ответ на уравнение
Решите задачи +1 и -1 на основе известной суммы и сценария с использованием объектов
Попрактикуйтесь в сочетании задач, используя сложение и вычитание 1.Банку с предметами используют для моделирования решаемого уравнения. Введите количество блоков и ответ на уравнение
Решите уравнения +1 и -1
Решите уравнения, включающие сложение или вычитание 1. Модель не используется. Отображается только уравнение. Введите ответ
МОДУЛЬ 2 Двумерные и трехмерные формы
Тема A: Двумерные плоские формы
Учащиеся знакомятся с внешним видом и названиями двумерных фигур. Они работают с квадратами, кругами, треугольниками, прямоугольниками и шестиугольниками.Учащиеся выделяют примеры из числа не являющихся примерами. Наша звуковая функция позволяет не читателям получать доступ к именам фигур.
Определение положения над и под объектом
Научитесь определять положение как над или под объектом. Выберите указанное местоположение, щелкнув правильное положение.
Расположить объекты выше и ниже объекта
Позиционировать 1 или 2 объекта выше или ниже неподвижного объекта. Выберите правильное местоположение и правильный цвет в соответствии с указаниями.
Поместите объект перед объектом или позади него (Часть 1)
Научитесь определять положение как перед объектом, так и позади него.Выберите указанное местоположение, щелкнув правильное положение.
Поместите объект перед или за объектом (Часть 2)
Определите местоположение как «перед» или «за» объектом. Перетащите символ в указанную позицию
Определите линии
Научитесь определять линии. Выберите линии с различной ориентацией из группы, содержащей линии и кривые
Определить изогнутые линии
Научитесь определять кривые. Выберите кривые в различных ориентациях и формах из группы, содержащей линии и кривые
Определите прямоугольники, треугольники или круги из набора фигур
Определите прямоугольники, треугольники и круги из наборов фигур.Нажмите на фигуры, которые соответствуют указанному рисунку
Определите свойства треугольников
Узнайте характеристики треугольника. Затем выберите те формы, которые являются треугольниками.
Определение свойств прямоугольников
Изучите характеристики прямоугольника. Затем выберите те формы, которые являются прямоугольниками.
Определите шестиугольники из набора форм.
Определите, какая из двух форм является шестиугольником. Затем выберите все шестиугольники из множества форм
Определите свойства шестиугольников
Узнайте характеристики шестиугольника.Затем выберите те формы, которые являются шестиугольниками, чтобы завершить изображение.
Определите отдельные 2D-формы на большом изображении.
Используйте разные цвета для обозначения фигур. Следуйте инструкциям, чтобы раскрасить каждый тип формы в указанный цвет
Идентифицировать объекты реального мира, состоящие из двумерных фигур
Выберите объекты реального мира, содержащие заданную форму, из набора из 6 объектов. Фигуры включают круги, прямоугольники и треугольники.
Сопоставьте объекты реального мира с их двухмерными формами.
Выберите правильную двухмерную фигуру, моделирующую объекты реального мира.Объект и соответствующая фигура могут быть ориентированы в разных направлениях.
Сопоставьте двухмерную форму с ее именем.
С учетом имени формы сопоставьте ее с правильной формой. Щелкните значок x или галочку рядом с каждой из трех фигур, чтобы указать, соответствует ли она слову
Определить фигуры с заданным количеством сторон, углов или изогнутых линий
Выберите фигуры с указанными характеристиками. Из набора из 5 фигур выберите те, которые имеют заданное количество сторон или углов.
Определите двухмерные формы и переместите их в положения выше, ниже, впереди и сзади.
Практикуйте двухмерные формы и положение.Перетащите указанную фигуру в указанное место относительно статического изображения
Тема B: Трехмерные твердые формы
Учащиеся знакомятся с внешним видом и названиями трехмерных фигур. Они работают с кубами, сферами, конусами и цилиндрами. Студенты также укрепляют свое понимание позиций (вверху, внизу, впереди, рядом и позади). Наша звуковая функция позволяет не читателям получать доступ к именам фигур.
Сортировка фигур по категориям плоские и цельные
Научитесь различать двухмерные и трехмерные фигуры.Затем отсортируйте их по категориям
Сопоставьте формы с реальными объектами
Сопоставьте реальные объекты с трехмерными сплошными фигурами
Определите цилиндры среди трехмерных фигур
Научитесь определять цилиндры из набора из трех -мерные тела. Щелкните цилиндры среди группы других твердых тел
Определите конусы среди трехмерных фигур
Практикуйтесь в определении конусов из набора трехмерных тел. Щелкните конусы среди группы других твердых тел
Определите кубы среди трехмерных фигур
Научитесь определять кубы из набора трехмерных тел.Щелкните кубы среди группы других твердых тел
Определите сферы среди трехмерных фигур
Практикуйтесь в определении сфер из набора трехмерных тел. Щелкните сферы среди группы других тел
Определите трехмерные формы по имени
Выберите правильное имя для данного твердого тела. Будет предложено два варианта выбора
Определить трехмерные формы среди реальных объектов
Найдите основные трехмерные твердые формы, используемые в изображениях реальных объектов. Если представлен набор из менее чем 10 изображений, щелкните те, которые содержат заданные твердые тела
Положение 3-D фигуры выше, ниже, спереди и сзади объекта
Практикуйте трехмерные тела и положение.Перетащите указанное твердое тело в указанное место относительно статического изображения
Определите объекты в положениях выше, ниже, рядом и перед ним
Попрактикуйтесь в словах положения «выше», «ниже», «рядом с», и «перед». Щелкните один из двух символов, которые находятся в правильном положении относительно указанного символа.
Тема C: Двумерные и трехмерные формы
Учащиеся применяют свое предыдущее понимание плоских и твердых форм, чтобы различать их.
МОДУЛЬ 3 Сравнение длины, веса, вместимости и чисел с 10
Тема A: Сравнение длины и роста
Используя знакомые реальные предметы, учащиеся используют язык сравнения (самый высокий, высокий, самый длинный, длинный, самый короткий , короче), поскольку они исследуют длину.
Тема B: Сравнение длины и высоты соединяющих палочек куба в пределах 10
Учащиеся работают со знакомыми соединяющими кубиками для подсчета кубиков и определения длины палочек. Они сравнивают длину, используя более длинные, короткие и такие же, как.
Тема C: Сравнение веса
Используя знакомые, реальные предметы, учащиеся используют язык сравнения (тяжелее, легче, примерно такой же) при изучении веса. Для этого они используют виртуальную шкалу баланса для сравнения.
Тема D: Сравнение тома
Учащиеся выучивают слово «вместимость» и используют его для измерения количества жидкости, которое может вместить контейнер. Используя единицу «стаканы», они измеряют, переливая стаканы в большую емкость и переливая из большей емкости в стаканы.Они также сравнивают измеренную вместимость двух контейнеров.
Тема E: Достаточно?
Чтобы подготовиться к сравнению чисел, учащиеся работают с объектами реального мира, чтобы определить, «достаточно» ли их, чтобы составить пары. Затем они определяют, имеет ли набор реальных объектов больше, меньше или столько же, что и другой набор объектов.
Тема F: Сравнение наборов из 10
Учащиеся сравнивают два набора объектов, используя слова больше, меньше и тот же. Они работают с похожими объектами, как выровненными, так и разбросанными.
Тема G: Сравнение цифр
Учащиеся сравнивают два набора предметов, используя слова больше, меньше и тот же. Они работают с похожими и разными объектами, как выровненными, так и разбросанными, с вертикальным и горизонтальным выравниванием. Наконец, они начинают сравнивать числа.
МОДУЛЬ 4 Числовые пары, сложение и вычитание до 10
Тема A: Композиции и разложения 2, 3, 4 и 5
Учащиеся используют знакомые блоки с основанием 10, сценарии с объектами, числовую линию и уравнения для изучить основные концепции сложения.Студенты определяют как суммы, так и недостающие слагаемые, постепенно переходя от конкретных моделей к абстрактным уравнениям.
Тема B: Разложение 6, 7 и 8 на числовые пары
Учащиеся расширяют свое понимание числовых связей до сумм 6, 7 и 8. Они работают с наборами похожих объектов двух цветов для подсчета частей (на цвет) и общ. Затем они используют эти числа для построения числовых связей на основе изображения объектов.
Создание числовой связи на основе набора объектов; Определите добавление в числовой связи
Создайте числовую связь, используя изображение объектов двух разных цветов.Определите сумму и слагаемые, затем перетащите их в нужное место в облигации. Кроме того, заполните недостающее дополнение в устной выписке облигации
Определите недостающий номер в числовой связи на основе набора объектов
Заполните недостающее значение на числовой связи. Затем также заполните устное заявление о залоге. Предусмотрено изображение объектов в двух цветах.
Построение числовой связи на основе набора объектов; Определите общую сумму в числовой связке (всего 6)
Создайте числовую связь из объектов двух цветов, найденных на монохроматическом изображении.Заполните все числа в номере-связке. Кроме того, заполните словесное заявление о взаимосвязи между числами
Раскрасьте набор объектов в два цвета, чтобы представить данное число bond
Раскрасьте набор кругов в два разных цвета, чтобы соответствовать заданному числу bond
Построить число облигация на основе набора предметов; Определите общее количество облигаций (всего 7)
Практическое число облигаций для набора из 7 яиц. Для начала выберите цвет и рисунок яиц.Затем запишите номер для показанного набора яиц. Кроме того, завершите словесное заявление о взаимосвязи между числами
Создайте связь чисел на основе набора предметов; Определите общую сумму в числовой связи (всего 8)
Запишите числовые связи для набора из 8 объектов в двух цветах. Кроме того, заполните словесную формулировку взаимосвязи между числами
Запишите числовую связь на основе модели, которую создают учащиеся (всего 7 или 8).
Напишите числовую связь для набора из 7 или 8 предметов.Раскрасьте кружки, используя два цвета, затем заполните числовую связь, соответствующую цветовой конфигурации. Кроме того, заполните пробел в выписке о числовом связывании
Тема C: Сложение с итогами 6, 7 и 8
Учащиеся углубят свое понимание сложения, укрепив связь между конкретными объектами, блоками с основанием 10 и уравнениями. Они определяют как суммы, так и недостающие слагаемые. Они записывают уравнения, включая символ +.
Определите недостающее слагаемое и суммируйте уравнения сложения до 5 на основе сценария с объектами
Заполните уравнение сложения.Анимация с набором стационарных объектов и набором добавляемых объектов дается в общей сложности до 5. Заполните пробелы в уравнении сложения
Используйте кубы для представления сценария добавления на основе объектов и сопоставления шаблонов кубов к добавлению сценариев
Практика индивидуальной переписки. Смоделируйте сценарий сложения с кубиками двух разных цветов
Решите уравнения сложения для 5 на основе модели блоков с основанием 10
Смоделируйте задачу сложения с кубиками.Во-первых, изобразите недостающее слагаемое кубиками. Введите новую сумму после каждого добавленного куба, затем введите решение уравнения. В других задачах используется модель куба, поэтому просто введите сумму
Определите недостающие слагаемые в уравнениях с суммой 4
Напишите уравнение для данной модели куба. Даны кубики двух цветов. Напишите уравнение сложения, представляющее модель. Подсказки даются для каждого бланка
Решите +/- уравнения в пределах 5 на основе перемещений в числовой строке
Представьте задачу сложения слов в числовой строке.Начиная с заданного значения числовой строки, переместите дополнительную сумму, чтобы получить общее количество до 5. Соответствующее уравнение сложения отображается после правильного перемещения по числовой строке
Определите недостающее слагаемое в уравнениях с суммой 4
Найти недостающий член в уравнении сложения с суммой 4. Сначала предоставляется модель куба. Затем заполните пропуски без модели
Определите недостающее слагаемое в уравнениях с суммой 5
Найдите недостающее слагаемое в уравнении сложения с суммой 5.Во-первых, предоставляется модель куба. Затем заполните пробелы без модели.
Запишите сценарии сложения с объектами в виде уравнений для 5
Напишите уравнение сложения для анимации с суммой 5. Показан ряд неподвижных объектов. Затем появляются дополнительные объекты. Напишите уравнение с подсказками для каждого бланка
Используйте блоки base-10 для представления сценариев сложения с объектами 5
Смоделируйте задачу сложения с кубиками и напишите уравнение. Изобразите ситуацию сложения с кубиками.Затем заполните уравнение сложения без каких-либо подсказок для пробелов
Напишите уравнение для сопоставления числовой связи (всего 3, 4 или 5)
Напишите уравнение, представленное числовой связью с суммой 3, 4, или 5. Введите числа из связи в уравнение
Заполните уравнения сложения с суммой 6 на основе модели блоков с основанием 10
Заполните все уравнения, которые имеют сумму 6. Создайте модель куба a каждой пары слагаемых. Заполните пропуски в уравнениях, которые соответствуют моделям
Сценарии сложения модели до 6 на числовой прямой и решите соответствующее уравнение
Представьте задачу сложения слов на числовой прямой.Начиная с заданного значения числовой строки, переместите дополнительную сумму, чтобы в итоге получилось 6. Также завершите уравнение сложения, которое представлено числовой строкой
Напишите уравнение для сопоставления числовой связи (всего 6)
Напишите уравнение, представленное числовой связью с суммой 6. Введите числа из связи в уравнение
Представьте сценарии сложения с объектами, используя блоки с основанием 10, и запишите как уравнение с суммой 6
Напишите Уравнение сложения для картинки с суммой 6.Сначала создайте кубическую модель ситуации. Затем запишите уравнение, представленное кубиками.
Определите недостающее слагаемое в уравнениях с суммой 6
Найдите недостающее слагаемое в уравнении сложения с суммой 6. Сначала предоставляется модель куба. Затем заполните пробелы без модели
Разложите набор из 7 объектов на две группы и определите их как слагаемые в уравнении
Заполните все уравнения, сумма которых равна 7. Создайте модель куба для каждой пары слагаемых. .Заполните пропуски в уравнениях, соответствующих моделям.
Сценарии сложения модели до 7 на числовой прямой и решите соответствующее уравнение.
Изобразите задачу сложения слов на числовой прямой. Начиная с заданного значения числовой строки, переместите дополнительную сумму, чтобы в итоге получилось 7. Также завершите уравнение сложения, которое представлено числовой строкой
Напишите уравнение для сопоставления числовой связи (всего 7)
Напишите уравнение, представленное числовой связью с суммой 7.Введите числа из облигации в уравнение
Представьте сценарии сложения с объектами, используя блоки с основанием 10, и запишите в виде уравнения с суммой 7
Напишите уравнение сложения для изображения с суммой 7. Сначала создайте кубическая модель анимации. Затем запишите уравнение, представленное кубами.
Определите недостающее слагаемое в уравнениях с суммой 7
Найдите недостающее слагаемое в уравнении сложения с суммой 7. Сначала предоставляется модель куба.Затем заполните пропуски без модели
Заполните уравнения сложения с суммой 8 на основе модели блоков по основанию 10
Заполните все уравнения, которые имеют сумму 8. Создайте модель куба для каждой пары добавляет. Заполните пропуски в уравнениях, которые соответствуют моделям
Сценарии сложения модели до 8 на числовой прямой и решите соответствующее уравнение
Представьте задачу сложения слов на числовой прямой. Начиная с заданного значения числовой строки, переместите дополнительную сумму до 8.Кроме того, заполните уравнение сложения, которое представлено числовой строкой
Напишите уравнение для сопоставления числовой связи (всего 8)
Напишите уравнение, представленное числовой связью с суммой 8. Введите числа из связи в уравнение
Представьте сценарии сложения с объектами с использованием блоков base-10 и запишите в виде уравнения с суммой 8
Напишите уравнение сложения для изображения с суммой 8. Сначала создайте модель куба анимации.Затем запишите уравнение, представленное кубами.
Определите недостающее слагаемое в уравнениях с суммой 8
Найдите недостающее слагаемое в уравнении сложения с суммой 8. Сначала предоставляется модель куба. Затем заполните пропуски без модели.
Тема D: Вычитание из чисел до 8
Учащиеся используют знакомые блоки с основанием 10, сценарии с объектами, числовую линию и уравнения, чтобы изучить основные концепции вычитания. Студенты определяют как различия, так и недостающие вычитания, постепенно переходя от конкретных моделей к абстрактным уравнениям.Они также связывают вычитание и сложение посредством исследования семейств фактов.
Тема E: Разложение 9 и 10 на пары чисел
Учащиеся используют знакомые сценарии с объектами, блоками с основанием 10 и уравнениями, чтобы расширить свое понимание сложения и вычитания, включив в него 9 и 10. Учащиеся изучают состав этих итогов. чтобы повысить их осведомленность о числовых связях.
Запишите числовую связь на основе сценария с 9 реальными объектами (начните с общего числа)
Узнайте, как записывать числовые связи.Определите общее количество объектов и перенесите эту информацию в графическое изображение с номерами. Затем определите, сколько показано каждого из двух типов, и введите его в графическое изображение с числовой связью. Также заполните выписку
Запишите числовую связь на основе сценария с 9 реальными объектами (не выровненными)
Завершите числовую связь для набора из 9 разрозненных объектов. Заполните недостающие числа в числовой связке на основе данной картинки. Предлагаются подсказки, помогающие ввести правильные числа.Кроме того, заполните выписку о числовой связи
Запишите числовую связь на основе сценария с 9 реальными объектами (общее количество отсутствует)
Запишите числовую связь для набора из 9 объектов. Заполните недостающие числа в числовой связке на основе данной картинки. Помощь в заполнении пропусков не оказывается. Кроме того, заполните выписку по номеру связи
Запишите числовую связь на основе сценария с 9 реальными объектами
Завершите числовую связь для изображения 9 объектов в строках. Заполните все значения в нужных местах без дополнительной помощи.Кроме того, заполните пробел в выписке по номеру связи
Запишите цифровую связь на основе сценария с 9 реальными объектами (не выровненными)
Завершите числовую связь для изображения 9 разбросанных объектов. Заполните все значения в нужных местах без дополнительной помощи. Кроме того, заполните пробел в выписке по количеству облигаций
Запишите числовую связь на основе сценария с 10 реальными объектами (начинаются с общего количества)
Узнайте, как записать числовые облигации. Определите общее количество объектов и перенесите эту информацию в графическое изображение с номерами.Затем определите, сколько показано каждого из двух типов, и введите его на графике с числовыми связями. Также заполните выписку
Запишите числовую связь на основе сценария с 10 реальными объектами (отсутствующий элемент)
Завершите числовую связь для набора из 10 разрозненных объектов. Заполните недостающие числа в числовой связке на основе данной картинки. Предлагаются подсказки, помогающие ввести правильные числа. Кроме того, заполните выписку о числовой привязке
Запишите числовую связь на основе сценария с 10 реальными объектами (без добавления)
Завершите числовую связь для изображения 10 объектов в строках.Заполните все значения в нужных местах без дополнительной помощи. Кроме того, введите недостающий номер в выписке по номеру связи
Запишите числовую связь на основе сценария с 10 реальными объектами
Запишите числовую связь для изображения 10 объектов в строках. Заполните все значения в нужных местах без дополнительной помощи. Кроме того, введите недостающий номер в выписку по номеру связи.
Запишите числовую связь на основе сценария с 10 реальными объектами (невыровненными).
Завершите числовую связь для набора из 10 разрозненных объектов.Заполните недостающие числа в числовой связке на основе заданного изображения без дополнительных подсказок. Кроме того, заполните формуляр счисления
Тема F: Сложение с итогами 9 и 10
Учащиеся применяют свое понимание состава 9 и 10 для решения задач с пропущенными слагаемыми.
Тема G: Вычитание из 9 и 10
Учащиеся работают как с сложением, так и с вычитанием, чтобы укрепить понимание основных понятий. Они представляют сценарии с объектами, использующими блоки с основанием 10, и блоки с основанием 10 в виде уравнений.
Тема H: Образцы со сложением 0 и 1 и получением 10
Учащиеся продолжают выполнять знакомые задания, теперь используя 0 как добавление, вычитание или разность. Они используют сценарии с объектами, числовой линией и уравнениями.
МОДУЛЬ 5 Числа от 10 до 20 и счет до 100
Тема A: Подсчитайте 10 единиц и некоторые единицы
Учащиеся отличают «десятку» от единиц, используя десятикратную рамку или стержень. Они начинают изучать состав 2-значных чисел и числовых имен.Эти упражнения формируют основу для дальнейшего изучения методик позиционной ценности и сложения. Студенты впервые используют вертикальную числовую черту.
Тема B: Разложите числа 11–20 и сосчитайте, чтобы ответить «Сколько?»
Учащиеся углубляют свое понимание чисел подростков, применяя их к позициям числовой прямой и простым уравнениям.
Тема C: Представление и применение композиций и разложения чисел для подростков
Учащиеся сортируют, считают, складывают и вычитают десять и единицы.Они видят группу из десяти, отображаемую справа от единиц, а также слева, и видят как вертикальное, так и горизонтальное выравнивание 10 объектов. Они решают для разных позиций в +/- уравнениях, в которых все единицы или целые десять складываются или вычитаются.
Все, что вам нужно знать - настоящий Python
В этой статье вы узнаете все о модуле Python math . Математические вычисления являются неотъемлемой частью большинства разработок Python. Независимо от того, работаете ли вы над научным проектом, финансовым приложением или каким-либо другим видом программирования, вам просто не избежать математики.
Для простых математических вычислений в Python вы можете использовать встроенные математические операторы , такие как сложение ( + ), вычитание ( - ), деление (/) и умножение ( * ). . Но более сложные операции, такие как экспоненциальные, логарифмические, тригонометрические или степенные функции, не встроены. Означает ли это, что вам нужно реализовать все эти функции с нуля?
К счастью, нет. Python предоставляет модуль, специально разработанный для математических операций более высокого уровня: модуль math .
К концу этой статьи вы узнаете:
- Что такое модуль Python
math - Как использовать функции модуля
mathдля решения реальных задач - Какие константы у математического модуля , включая пи, тау и число Эйлера
- В чем разница между встроенными функциями и математическими функциями
- В чем разница между
math,cmathи NumPy:
Здесь вам пригодится математический опыт, но не волнуйтесь, если математика не ваша сильная сторона.Эта статья объяснит основы всего, что вам нужно знать.
Итак, приступим!
Знакомство с Python
math Модуль Модуль Python math - важная функция, предназначенная для работы с математическими операциями. Он поставляется в стандартной версии Python и был там с самого начала. Большинство функций модуля math представляют собой тонкие оболочки математических функций платформы C.Поскольку его основные функции написаны на CPython, модуль math эффективен и соответствует стандарту C.
Модуль Python math предлагает вам возможность выполнять общие и полезные математические вычисления в вашем приложении. Вот несколько практических применений модуля math :
- Вычисление комбинаций и перестановок с использованием факториалов
- Расчет высоты столба с помощью тригонометрических функций
- Расчет радиоактивного распада с использованием экспоненциальной функции
- Расчет кривой подвесного моста с использованием гиперболических функций
- Решение квадратных уравнений
- Моделирование периодических функций, таких как звуковые и световые волны, с помощью тригонометрических функций
Поскольку модуль math поставляется вместе с выпуском Python, вам не нужно устанавливать его отдельно.Использование - это просто импорт модуля:
Вы можете импортировать модуль Python math , используя указанную выше команду. После импорта вы можете сразу использовать его.
Константы математического модуля
Модуль Модуль Python math предлагает множество предопределенных констант . Доступ к этим константам дает несколько преимуществ. Во-первых, вам не нужно вручную жестко закодировать их в свое приложение, что сэкономит вам много времени.Кроме того, они обеспечивают согласованность всего кода. Модуль включает в себя несколько известных математических констант и важных значений:
- Пи
- Тау
- Число Эйлера
- бесконечность
- Не число (NaN)
В этом разделе вы узнаете о константах и о том, как их использовать в коде Python.
Pi
Пи (π) - это отношение длины окружности ( c ) к ее диаметру ( d ):
π = с / д
Это соотношение всегда одинаково для любого круга.
Пи - это иррациональное число , что означает, что его нельзя выразить простой дробью. Следовательно, у пи бесконечное количество десятичных знаков, но оно может быть приблизительно равно 22/7 или 3,141.
Интересный факт: Пи - самая признанная и известная математическая константа в мире. У него есть своя собственная дата празднования, называемая Днем Пи, которая приходится на 14 марта (3/14).
Вы можете получить доступ к pi следующим образом:
>>> >>> математика.Пи
3,1415589793
Как видите, число пи в Python дается с точностью до пятнадцати десятичных знаков. Количество предоставленных цифр зависит от базового компилятора C. Python по умолчанию печатает первые пятнадцать цифр, а math.pi всегда возвращает значение с плавающей запятой.
Итак, каковы некоторые из способов, которыми пи может быть вам полезен? Вы можете рассчитать длину окружности, используя 2π r , где r - радиус окружности:
>>> >>> г = 3
>>> окружность = 2 * математика.пи * р
>>> f "Окружность круга = 2 * {math.pi: .4} * {r} = {окружность: .4}"
'Окружность круга = 2 * 3,142 * 3 = 18,85'
Вы можете использовать math.pi для вычисления длины окружности. Вы также можете рассчитать площадь круга по формуле π r ² следующим образом:
>>> r = 5
>>> площадь = math.pi * r * r
>>> f "Площадь круга = {math.pi: .4} * {r} * {r} = {area: .4}"
«Площадь круга = 3.142 * 5 * 5 = 78,54 '
Вы можете использовать math.pi для вычисления площади и длины окружности. Когда вы выполняете математические вычисления с помощью Python и сталкиваетесь с формулой, в которой используется π, рекомендуется использовать значение пи, заданное модулем math , вместо жесткого кодирования значения.
Тау
Тау (τ) - отношение длины окружности к ее радиусу. Эта постоянная равна 2π, или примерно 6,28. Как и пи, тау - иррациональное число, потому что оно просто пи умноженное на два.
Во многих математических выражениях используется 2π, а использование тау может помочь упростить ваши уравнения. Например, вместо вычисления длины окружности с 2π r , мы можем подставить тау и использовать более простое уравнение τ r .
Однако использование тау в качестве постоянной окружности все еще обсуждается. Вы можете свободно использовать 2π или τ по мере необходимости.
Вы можете использовать тау, как показано ниже:
>>> >>> математика.тау
6,283185307179586
Подобно math.pi , math.tau возвращает пятнадцать цифр и является значением с плавающей запятой. Вы можете использовать тау для вычисления длины окружности с τ r , где r - радиус, следующим образом:
>>> г = 3
>>> окружность = math.tau * r
>>> f "Окружность круга = {math.tau: .4} * {r} = {окружность: .4}"
'Окружность круга = 6,283 * 3 = 18,85'
Вы можете использовать math.tau вместо 2 * math.pi , чтобы привести в порядок уравнения, содержащие выражение 2π.
Число Эйлера
Число Эйлера ( e ) - это константа, являющаяся основанием натурального логарифма , математической функции, которая обычно используется для расчета скорости роста или спада. Как и в случае с пи и тау, число Эйлера является иррациональным числом с бесконечным числом десятичных знаков. Значение e часто приблизительно равно 2,718.
Число Эйлера является важной константой, поскольку оно имеет множество практических применений, таких как расчет роста населения с течением времени или определение скорости радиоактивного распада.Вы можете получить доступ к числу Эйлера из модуля math следующим образом:
>>> math.e
2,718281828459045
Как и в случае с math.pi и math.tau , значение math.e дается с точностью до пятнадцати десятичных знаков и возвращается как значение с плавающей запятой.
бесконечность
Бесконечность не может быть определена числом. Скорее, это математическая концепция, представляющая что-то бесконечное или безграничное.Бесконечность может идти в любом направлении, в положительном или отрицательном.
Вы можете использовать бесконечность в алгоритмах , когда вы хотите сравнить заданное значение с абсолютным максимальным или минимальным значением. Значения положительной и отрицательной бесконечности в Python следующие:
>>> >>> f "Положительная бесконечность = {math.inf}"
'Положительная бесконечность = бесконечность'
>>> f "Отрицательная бесконечность = {-math.inf}"
'Отрицательная бесконечность = -inf'
Бесконечность не является числовым значением.Вместо этого он определяется как math.inf . Python представил эту константу в версии 3.5 как эквивалент float ("inf") :
>>> float ("inf") == math.inf
Правда
И float ("inf"), и math.inf представляют концепцию бесконечности, что делает math.inf больше любого числового значения:
>>> x = 1e308
>>> math.inf> x
Правда
В приведенном выше коде math.inf больше, чем значение x , 10 308 (максимальный размер числа с плавающей запятой), которое является числом с двойной точностью.
Точно так же -math.inf меньше любого значения:
>>> y = -1e308
>>> y> -math.inf
Правда
Отрицательная бесконечность меньше значения y , что составляет -10 308 . Никакое число не может быть больше или меньше отрицательной бесконечности.Вот почему математические операции с math.inf не изменяют значение бесконечности:
>>> math.inf + 1e308
инф
>>> math.inf / 1e308
инф
Как видите, ни сложение, ни деление не изменяют значение math.inf .
Не число (NaN)
Не число или NaN на самом деле не является математическим понятием. Он возник в области информатики как ссылка на значения, которые не являются числовыми.Значение NaN может быть связано с недопустимыми входными данными или может указывать на то, что переменная, в которой должно быть числовым, была повреждена текстовыми символами или символами.
Всегда рекомендуется проверять, является ли значение NaN. Если это так, то это может привести к недопустимым значениям в вашей программе. Python представил константу NaN в версии 3.5.
Вы можете увидеть значение math.nan ниже:
NaN не является числовым значением. Вы можете видеть, что значение math.nan - это nan , то же значение, что и float ("nan") .
Арифметические функции
Теория чисел - это раздел чистой математики, изучающий натуральные числа. Теория чисел обычно имеет дело с положительными целыми числами или целыми числами.
Модуль Python math предоставляет функции, которые полезны в теории чисел, а также в теории представлений , связанной области. Эти функции позволяют рассчитать ряд важных значений, включая следующие:
- Факториалы числа
- Наибольший общий делитель двух чисел
- Сумма итераций
Найдите факториалы с помощью Python
factorial () Возможно, вы встречали математические выражения вроде 7! или 4! перед.Восклицательные знаки не означают, что числа взволнованы. Скорее, "!" - это факториал , символ . Факториалы используются при поиске перестановок или комбинаций. Вы можете определить факториал числа, умножив все целые числа от выбранного числа до 1.
В следующей таблице показаны значения факториала для 4, 6 и 7:
| Символ | Словами | Выражение | Результат |
|---|---|---|---|
| 4! | Четыре факториала | 4 х 3 х 2 х 1 | 24 |
| 6! | Шесть факториалов | 6 х 5 х 4 х 3 х 2 х 1 | 720 |
| 7! | Семь факториал | 7 х 6 х 5 х 4 х 3 х 2 х 1 | 5040 |
Из таблицы видно, что 4 !, или четырехфакториал, дает значение 24 путем умножения диапазона целых чисел от 4 до 1.Аналогично 6! и 7! дают значения 720 и 5040 соответственно.
Вы можете реализовать факториальную функцию в Python, используя один из нескольких инструментов:
-
напетель - Рекурсивные функции
-
math.factorial ()
Сначала вы рассмотрим факториальную реализацию с использованием цикла для . Это относительно простой подход:
def fact_loop (число):
если число <0:
возврат 0
если num == 0:
возврат 1
факториал = 1
для i в диапазоне (1, num + 1):
факториал = факториал * я
возврат факториала
Вы также можете использовать рекурсивную функцию, чтобы найти факториал.Это сложнее, но также более элегантно, чем использование петли для . Вы можете реализовать рекурсивную функцию следующим образом:
def fact_recursion (число):
если число <0:
возврат 0
если num == 0:
возврат 1
return num * fact_recursion (число - 1)
Примечание: В Python существует ограничение на глубину рекурсии, но эта тема выходит за рамки данной статьи.
В следующем примере показано, как можно использовать для циклических и рекурсивных функций :
>>> fact_loop (7)
5040
>>> fact_recursion (7)
5040
Несмотря на то, что их реализации различны, их возвращаемые значения одинаковы.
Однако реализация собственных функций только для получения факториала числа отнимает много времени и неэффективно. Лучше использовать math.factorial () . Вот как можно найти факториал числа с помощью math.factorial () :
>>> math.factorial (7)
5040
Этот подход возвращает желаемый результат с минимальным объемом кода.
factorial () принимает только положительные целые числа.Если вы попытаетесь ввести отрицательное значение, вы получите ValueError :
>>> math.factorial (-5)
Отслеживание (последний вызов последний):
Файл "", строка 1, в
ValueError: factorial () не определен для отрицательных значений
Ввод отрицательного значения приведет к ошибке ValueError при чтении factorial (), не определенного для отрицательных значений .
factorial () также не принимает десятичные числа.Это даст вам ValueError :
>>> math.factorial (4.3)
Отслеживание (последний вызов последний):
Файл "", строка 1, в
ValueError: factorial () принимает только целые значения
Ввод десятичного значения приводит к ошибке ValueError при чтении factorial () принимает только целые значения .
Вы можете сравнить время выполнения для каждого из методов факториала, используя timeit () :
>>> импортное время
>>> timeit.timeit ("fact_loop (10)", globals = globals ())
1,063997201999996
>>> timeit.timeit ("fact_recursion (10)", globals = globals ())
1,815312818999928
>>> timeit.timeit ("math.factorial (10)", setup = "import math")
0,10671788000001925
Пример выше иллюстрирует результаты timeit () для каждого из трех факторных методов.
timeit () выполняет один миллион циклов при каждом запуске. В следующей таблице сравнивается время выполнения трех факториальных методов:
| Тип | Время выполнения |
|---|---|
| С петлями | 1.0640 с |
| С рекурсией | 1,8153 с |
С факториалом () | 0,1067 с |
Как видно из времени выполнения, factorial () работает быстрее, чем другие методы. Это из-за его базовой реализации C. Метод, основанный на рекурсии, самый медленный из трех. Хотя вы можете получить разные тайминги в зависимости от вашего CPU , порядок функций должен быть таким же.
factorial () не только быстрее, чем другие методы, но и более стабилен. Когда вы реализуете свою собственную функцию, вы должны явно кодировать случаев катастрофы , например, обработку отрицательных или десятичных чисел. Одна ошибка в реализации может привести к ошибкам. Но при использовании factorial () вам не нужно беспокоиться о случаях катастрофы, потому что функция обрабатывает их все. Поэтому по возможности рекомендуется использовать factorial () .
Найдите потолочное значение с помощью
ceil () math.ceil () вернет наименьшее целочисленное значение, которое больше или равно заданному числу. Если число является положительным или отрицательным десятичным числом, функция вернет следующее целочисленное значение, превышающее данное значение.
Например, вход 5,43 вернет значение 6, а вход -12,43 вернет значение -12. math.ceil () может принимать положительные или отрицательные действительные числа в качестве входных значений и всегда будет возвращать целочисленное значение.
Когда вы вводите целочисленное значение в ceil () , оно возвращает то же число:
>>> math.ceil (6)
6
>>> math.ceil (-11)
-11
math.ceil () всегда возвращает одно и то же значение, если на входе задано целое число. Чтобы увидеть истинную природу ceil () , вы должны ввести десятичные значения:
>>> math.ceil (4.23)
5
>>> math.ceil (-11,453)
-11
Если значение положительное (4.23), функция возвращает следующее целое число, большее значения (5). Если значение отрицательное (-11,453), функция также возвращает следующее целое число, большее значения (-11).
Функция вернет ошибку TypeError , если вы введете значение, которое не является числом:
>>> math.ceil ("x")
Отслеживание (последний вызов последний):
Файл "", строка 1, в
TypeError: должно быть действительное число, а не str
Вы должны ввести число в функцию.Если вы попытаетесь ввести любое другое значение, вы получите TypeError .
Найдите минимальное значение с
этаж () floor () вернет ближайшее целое значение, которое меньше или равно заданному числу. Эта функция ведет себя противоположно ceil () . Например, ввод 8,72 вернет 8, а ввод -12,34 вернет -13. floor () может принимать как положительные, так и отрицательные числа в качестве входных данных и возвращает целочисленное значение.
Если ввести целочисленное значение, функция вернет то же значение:
>>> >>> math.floor (4)
4
>>> math.floor (-17)
-17
Как и в случае с ceil () , когда вход для floor () является целым числом, результат будет таким же, как входное число. Вывод отличается от ввода только при вводе десятичных значений:
>>> math.floor (5.532)
5
>>> math.floor (-6.432)
-7
Когда вы вводите положительное десятичное значение (5.532), оно возвращает ближайшее целое число, которое меньше введенного числа (5). Если вы введете отрицательное число (-6,432), оно вернет следующее наименьшее целочисленное значение (-7).
Если вы попытаетесь ввести значение, не являющееся числом, функция вернет ошибку TypeError :
>>> math.floor ("x")
Отслеживание (последний вызов последний):
Файл "", строка 1, в
TypeError: должно быть действительное число, а не str
Вы не можете вводить нечисловые значения в качестве входных данных для ceil () .Это приведет к ошибке TypeError .
Усечь числа с усечением
() Когда вы получаете число с десятичной точкой, вы можете оставить только целую часть и исключить десятичную часть. Модуль math имеет функцию под названием trunc () , которая позволяет вам делать именно это.
Удаление десятичного значения - это тип округления. При использовании trunc () отрицательные числа всегда округляются в сторону увеличения до нуля, а положительные числа всегда округляются в сторону уменьшения до нуля.
Вот как функция trunc () округляет положительные или отрицательные числа:
>>> math.trunc (12.32)
12
>>> math.trunc (-43,24)
-43
Как видите, 12,32 округляется вниз до 0, что дает результат 12. Таким же образом -43,24 округляется вверх до 0, что дает значение -43. trunc () всегда округляется до нуля независимо от того, положительное или отрицательное число.
При работе с положительными числами trunc () ведет себя так же, как floor () :
>>> математика.trunc (12.32) == math.floor (12.32)
Правда
trunc () ведет себя так же, как floor () для положительных чисел. Как видите, возвращаемое значение обеих функций одинаково.
При работе с отрицательными числами trunc () ведет себя так же, как ceil () :
>>> math.trunc (-43.24) == math.ceil (-43.24)
Правда
Если число отрицательное, floor () ведет себя так же, как ceil () .Возвращаемые значения обеих функций одинаковы.
Найдите близость чисел с помощью Python
isclose () В определенных ситуациях - особенно в области науки о данных - вам может потребоваться определить, близки ли два числа друг к другу. Но для этого сначала нужно ответить на важный вопрос: насколько близко , близко ? Другими словами, каково определение слова «закрыть»?
Что ж, Мерриам-Вебстер скажет вам, что близость означает «близость во времени, пространстве, эффекте или градусе».«Не очень-то полезно, правда?
Например, возьмите следующий набор чисел: 2.32, 2.33 и 2.331. Когда вы измеряете близость по двум десятичным знакам, 2,32 и 2,33 близки. Но на самом деле 2.33 и 2.331 ближе. Таким образом, близость - понятие относительное. Невозможно определить близость без какого-либо порога.
К счастью, модуль math предоставляет функцию под названием isclose () , которая позволяет вам установить свой собственный порог, или допуск , для близости.Он возвращает Истина , если два числа находятся в пределах установленного вами допуска близости, и в противном случае возвращает Ложь .
Давайте посмотрим, как сравнить два числа, используя допуски по умолчанию:
- Относительный допуск или rel_tol - это максимальная разница, которая считается «близкой» по отношению к величине входных значений. Это процент толерантности. Значение по умолчанию - 1e-09 или 0,000000001.
- Абсолютный допуск или abs_tol - это максимальная разница, которая считается «близкой», независимо от величины входных значений.Значение по умолчанию - 0,0.
isclose () вернет Истина , если выполняется следующее условие:
абс (a-b) <= max (rel_tol * max (abs (a), abs (b)), abs_tol).
isclose использует приведенное выше выражение для определения близости двух чисел. Вы можете подставить свои собственные значения и посмотреть, близки ли какие-либо два числа.
В следующем случае 6 и 7 не близки к :
>>> >>> математика.isclose (6, 7)
Ложь
Цифры 6 и 7 не считаются близкими, поскольку относительный допуск установлен для девяти десятичных знаков. Но если вы введете 6,999999999 и 7 с одинаковым допуском, тогда они будут считаться близкими:
>>> >>> math.isclose (6.999999999, 7)
Правда
Вы можете видеть, что значение 6.999999999 находится в пределах девяти десятичных знаков 7. Следовательно, исходя из относительного допуска по умолчанию, 6.999999999 и 7 считаются близкими.
Вы можете отрегулировать относительный допуск, как хотите, в зависимости от ваших потребностей. Если установить для параметра rel_tol значение 0,2, то 6 и 7 считаются близкими:
>>> math.isclose (6, 7, rel_tol = 0.2)
Правда
Вы можете заметить, что 6 и 7 сейчас близки. Это потому, что они находятся в пределах 20% друг от друга.
Как и в случае с rel_tol , вы можете настроить значение abs_tol в соответствии с вашими потребностями. Чтобы считаться близкими, разница между входными значениями должна быть меньше или равна значению абсолютного допуска.Вы можете установить abs_tol следующим образом:
>>> math.isclose (6, 7, abs_tol = 1.0)
Правда
>>> math.isclose (6, 7, abs_tol = 0,2)
Ложь
Когда вы устанавливаете абсолютный допуск на 1, числа 6 и 7 близки, потому что разница между ними равна абсолютному допуску. Однако во втором случае разница между 6 и 7 не меньше или равна установленному абсолютному допуску 0,2.
Вы можете использовать abs_tol для очень малых значений:
>>> математика.isclose (1, 1.0000001, abs_tol = 1e-08)
Ложь
>>> math.isclose (1, 1.00000001, abs_tol = 1e-08)
Правда
Как видите, вы можете определить близость очень маленьких чисел с помощью isclose . Несколько особых случаев, касающихся близости, можно проиллюстрировать с помощью значений nan и inf :
>>> math.isclose (math.nan, 1e308)
Ложь
>>> math.isclose (math.nan, math.nan)
Ложь
>>> math.isclose (math.inf, 1e308)
Ложь
>>> math.isclose (math.inf, math.inf)
Правда
Из приведенных выше примеров видно, что nan не близко ни к какому значению, даже самому себе. С другой стороны, inf не близок ни к каким числовым значениям, даже к очень большим, а близко к себе .
Функции питания
Степенная функция принимает любое число x в качестве входных данных, увеличивает x до некоторой степени n и возвращает x n в качестве выходных данных.Модуль Python math предоставляет несколько функций, связанных с питанием. В этом разделе вы узнаете о степенных функциях, экспоненциальных функциях и функциях извлечения квадратного корня.
Вычислить степень числа с помощью
pow () Степенные функции имеют следующую формулу, где переменная x является основанием , переменная n является степенью , а a может быть любой константой :
Степенная функцияВ приведенной выше формуле значение основания x возведено в степень n .
Вы можете использовать math.pow () , чтобы получить степень числа. Существует встроенная функция pow () , которая отличается от math.pow () . Вы узнаете разницу позже в этом разделе.
math.pow () принимает два следующих параметра:
>>> math.pow (2, 5)
32,0
>>> math.pow (5, 2.4)
47,546789696
Первый аргумент - это базовое значение, а второй аргумент - это значение мощности.В качестве входных данных можно указать целое или десятичное значение, и функция всегда возвращает значение с плавающей запятой. Есть несколько особых случаев, определенных в math.pow () .
Возведение единицы с основанием 1 в степень любого числа n дает результат 1.0:
>>> >>> math.pow (1.0, 3)
1.0
Когда вы повышаете базовое значение 1 до любого значения мощности, вы всегда получите 1,0 в результате. Точно так же любое базовое число, возведенное в степень 0, дает результат 1.0:
>>> >>> math.pow (4, 0.0)
1.0
>>> math.pow (-4, 0,0)
1.0
Как видите, любое число в степени 0 даст в результате 1.0. Вы можете увидеть этот результат, даже если база равна нан :
>>> math.pow (math.nan, 0,0)
1.0
Возведение нуля в степень любого положительного числа даст в результате 0,0:
>>> >>> math.pow (0.0, 2)
0,0
>>> math.pow (0,0, 2,3)
0,0
Но если вы попытаетесь возвести 0,0 в отрицательную степень, результатом будет ValueError :
>>> math.pow (0,0, -2)
Отслеживание (последний вызов последний):
Файл "", строка 1, в
ValueError: ошибка математического домена
Ошибка ValueError возникает только тогда, когда основание равно 0. Если основание - любое другое число, кроме 0, тогда функция вернет допустимое значение мощности.
Помимо math.pow () , в Python есть два встроенных способа определения степени числа:
-
х ** у -
pow ()
Первый вариант прост. Возможно, вы уже использовали его раз или два. Тип возвращаемого значения определяется входными данными:
>>> >>> 3 ** 2
9
>>> 2 ** 3,3
9,8406759329 Когда вы используете целые числа, вы получаете целочисленное значение.Когда вы используете десятичные значения, тип возвращаемого значения изменяется на десятичное значение.
Второй вариант - универсальная встроенная функция. Вам не нужно использовать импорт, чтобы использовать его. Встроенный метод pow () имеет три параметра:
- База номер
- Мощность Номер
- Модуль упругости Номер
Первые два параметра являются обязательными, а третий - необязательным. Вы можете ввести целые или десятичные числа, и функция вернет соответствующий результат на основе ввода:
>>> >>> pow (3, 2)
9
>>> pow (2, 3.3)
9,8406759329 Встроенная функция pow () имеет два обязательных аргумента, которые работают так же, как base и power в синтаксисе x ** y . pow () также имеет третий необязательный параметр: модуль . Этот параметр часто используется в криптографии. Встроенный pow () с дополнительным параметром модуля эквивалентен уравнению (x ** y)% z . Синтаксис Python выглядит так:
>>> pow (32, 6, 5)
4
>>> (32 ** 6)% 5 == pow (32, 6, 5)
Правда
pow () возводит основание (32) в степень (6), а затем результат делится по модулю на число модуля (5).В этом случае результат будет 4. Вы можете подставить свои собственные значения и увидеть, что и pow (), и данное уравнение дают одинаковые результаты.
Несмотря на то, что все три метода расчета мощности делают одно и то же, между ними есть некоторые различия в реализации. Время выполнения для каждого метода следующее:
>>> >>> timeit.timeit ("10 ** 308")
1,00787289991
>>> timeit.timeit ("pow (10, 308)")
1.047615700008464
>>> timeit.timeit ("math.pow (10, 308)", setup = "import math")
0,1837239999877056
В следующей таблице сравнивается время выполнения трех методов, измеренное с помощью timeit () :
| Тип | Время выполнения |
|---|---|
x ** y | 1.0079 с |
pow (x, y) | 1.0476 с |
math.pow (x, y) | 0.1837 с |
Из таблицы видно, что math.pow () работает быстрее, чем другие методы, а встроенный pow () является самым медленным.
Причина эффективности math.pow () заключается в том, как она реализована. Он полагается на базовый язык C. С другой стороны, pow () и x ** y используют собственную реализацию оператора ** входного объекта. Однако math.pow () не может обрабатывать комплексные числа (что будет объяснено в следующем разделе), тогда как pow () и ** могут.
Найдите натуральную экспоненту с помощью
exp () Вы узнали о силовых функциях в предыдущем разделе. С экспоненциальными функциями дело обстоит немного иначе. Вместо основания, являющегося переменной, переменной становится мощность. Выглядит это примерно так:
Общая экспоненциальная функцияЗдесь a может быть любой константой, а x , которое является значением мощности, становится переменной.
Так что же такого особенного в экспоненциальных функциях? Значение функции быстро растет по мере увеличения значения x .Если основание больше 1, тогда значение функции непрерывно увеличивается по мере увеличения x . Особым свойством экспоненциальных функций является то, что наклон функции также непрерывно увеличивается по мере увеличения x .
Вы узнали о числе Эйлера в предыдущем разделе. Это основание натурального логарифма. Он также играет роль с экспоненциальной функцией. Когда число Эйлера включается в экспоненциальную функцию, оно становится естественной экспоненциальной функцией :
Естественная экспоненциальная функцияЭта функция используется во многих реальных ситуациях.Возможно, вы слышали о термине экспоненциальный рост , который часто используется в отношении роста человеческой популяции или скорости радиоактивного распада. Оба они могут быть вычислены с использованием естественной экспоненциальной функции.
Модуль Python math предоставляет функцию exp () , которая позволяет вычислять натуральную экспоненту числа. Вы можете найти значение следующим образом:
>>> math.exp (21)
1318815734,4832146
>>> математика.ехр (-1,2)
0,3011214
Входное число может быть положительным или отрицательным, и функция всегда возвращает значение с плавающей запятой. Если число не является числовым значением, метод вернет ошибку TypeError :
>>> math.exp ("x")
Отслеживание (последний вызов последний):
Файл "", строка 1, в
TypeError: должно быть действительное число, а не str
Как видите, если ввод является строковым значением, тогда функция возвращает ошибку TypeError , чтение должно быть действительным числом, а не str .
Вы также можете вычислить показатель степени, используя выражение math.e ** x или используя pow (math.e, x) . Время выполнения этих трех методов следующее:
>>> timeit.timeit ("math.e ** 308", setup = "import math")
0,17853009998701513
>>> timeit.timeit ("pow (math.e, 308)", setup = "import math")
0,21040189999621361
>>> timeit.timeit ("math.exp (308)", setup = "import math")
0,125878200007719
В следующей таблице сравнивается время выполнения вышеуказанных методов, измеренное с помощью timeit () :
| Тип | Время выполнения |
|---|---|
e ** x | 0.1785 с |
pow (e, x) | 0,2104 с |
math.exp (x) | 0,1259 с |
Вы можете видеть, что math.exp () быстрее, чем другие методы, а pow (e, x) - самый медленный. Это ожидаемое поведение из-за базовой реализации C модуля math .
Также стоит отметить, что e ** x и pow (e, x) возвращают одинаковые значения, но exp () возвращает немного другое значение.Это связано с различиями в реализации. В документации Python отмечается, что exp () более точен, чем два других метода.
Практический пример с
exp () Радиоактивный распад происходит, когда нестабильный атом теряет энергию из-за испускания ионизирующего излучения. Скорость радиоактивного распада измеряется с помощью периода полураспада, который представляет собой время, необходимое для распада половины количества родительского ядра. Вы можете рассчитать процесс распада по следующей формуле:
Уравнение радиоактивного распадаВы можете использовать приведенную выше формулу для расчета оставшегося количества радиоактивного элемента через определенное количество лет.Переменные данной формулы следующие:
- N (0) - исходное количество вещества.
- N (т) - это количество, которое все еще остается и еще не разложилось по прошествии некоторого времени ( т ).
- T - период полураспада распадающегося количества.
- e - число Эйлера.
Научные исследования определили период полураспада всех радиоактивных элементов.Вы можете подставить значения в уравнение, чтобы рассчитать оставшееся количество любого радиоактивного вещества. Давай попробуем сейчас.
Радиоизотоп стронций-90 имеет период полураспада 38,1 года. В пробе содержится 100 мг Sr-90. Вы можете рассчитать оставшиеся миллиграммы Sr-90 через 100 лет:
>>> >>> half_life = 38,1
>>> начальный = 100
>>> время = 100
>>> оставшийся = начальный * math.exp (-0,693 * время / период полураспада)
>>> f "Оставшееся количество Sr-90: {осталось}"
«Оставшееся количество Sr-90: 16.22044604811303 '
Как видите, период полураспада установлен на 38,1, а продолжительность установлена на 100 лет. Вы можете использовать math.exp , чтобы упростить уравнение. Подставляя значения в уравнение, вы можете обнаружить, что через 100 лет остается 16,22 мг Sr-90.
Логарифмические функции
Логарифмические функции можно рассматривать как инверсию экспоненциальных функций. Они обозначаются в следующей форме:
Общая логарифмическая функцияЗдесь a - основание логарифма, которое может быть любым числом.Вы узнали об экспоненциальных функциях в предыдущем разделе. Экспоненциальные функции могут быть выражены в виде логарифмических функций и наоборот.
Python Natural Log With
log () Натуральный логарифм числа - это его логарифм по основанию математической константы e , или числа Эйлера:
Натуральная логарифмическая функцияКак и экспоненциальная функция, натуральный логарифм использует константу e . Обычно это обозначается как f (x) = ln (x), где e неявно.
Вы можете использовать натуральный логарифм так же, как экспоненциальную функцию. Он используется для расчета таких величин, как скорость роста населения или скорость радиоактивного распада элементов.
log () имеет два аргумента. Первый является обязательным, а второй - необязательным. С одним аргументом вы можете получить натуральный логарифм (с основанием e ) входного числа:
>>> math.log (4)
1,38621198906
>>> математика.журнал (3.4)
1,2237754316221157
Однако функция возвращает ValueError , если вы вводите неположительное число:
>>> math.log (-3)
Отслеживание (последний вызов последний):
Файл "", строка 1, в
ValueError: ошибка математического домена
Как видите, в log () нельзя ввести отрицательное значение. Это связано с тем, что значения журнала не определены для отрицательных чисел и нуля.
С двумя аргументами вы можете вычислить логарифм первого аргумента по основанию второго аргумента:
>>> >>> математика.журнал (math.pi, 2)
1.6514961219
>>> math.log (math.pi, 5)
0,711260668712669
Вы можете увидеть, как значение изменяется при изменении базы журнала.
Общие сведения
log2 () и log10 () Модуль Python math также предоставляет две отдельные функции, которые позволяют вычислять значения журнала с основанием 2 и 10:
-
log2 ()используется для вычисления логарифмического значения по основанию 2. -
log10 ()используется для вычисления логарифмического значения по основанию 10.
С помощью log2 () вы можете получить значение журнала с основанием 2:
>>> math.log2 (math.pi)
1.65149612187
>>> math.log (math.pi, 2)
1.6514961219
Обе функции преследуют одну и ту же цель, но в документации Python отмечается, что log2 () более точен, чем использование log (x, 2) .
Вы можете вычислить логарифмическое значение числа по основанию 10 с помощью log10 () :
>>> математика.log10 (math.pi)
0,49714987268
>>> math.log (math.pi, 10)
0,49714987268
В документации Python также упоминается, что log10 () более точен, чем log (x, 10) , хотя обе функции имеют одну и ту же цель.
Практический пример с натуральным бревном
В предыдущем разделе вы видели, как использовать math.exp () для вычисления оставшегося количества радиоактивного элемента через определенный период времени. С математикой .log () , вы можете определить период полураспада неизвестного радиоактивного элемента, измерив массу через определенный интервал. Следующее уравнение можно использовать для расчета периода полураспада радиоактивного элемента:
Переставив формулу радиоактивного распада, вы можете сделать период полураспада ( T ) предметом формулы. Переменные данной формулы следующие:
- T - период полураспада распадающегося количества.
- N (0) - исходное количество вещества.
- N (t) - это количество, которое остается и еще не разложилось по прошествии определенного периода времени ( t ).
- ln - натуральное бревно.
Вы можете подставить известные значения в уравнение для расчета периода полураспада радиоактивного вещества.
Например, представьте, что вы изучаете образец неопознанного радиоактивного элемента.Когда это было обнаружено 100 лет назад, размер образца составлял 100 мг. После 100 лет распада осталось всего 16,22 мг. Используя формулу выше, вы можете рассчитать период полураспада этого неизвестного элемента:
>>> >>> начальное = 100
>>> Осталось = 16,22
>>> время = 100
>>> half_life = (-0,693 * время) / math.log (оставшееся / начальное)
>>> f "Период полураспада неизвестного элемента: {half_life}"
'Период полураспада неизвестного элемента: 38.098335152'
Как видите, неизвестный элемент имеет период полураспада примерно 38.1 год. Основываясь на этой информации, вы можете идентифицировать неизвестный элемент как стронций-90.
Другие важные
math Функции модуля Модуль Python math имеет множество полезных функций для математических вычислений, и в этой статье подробно рассмотрены только некоторые из них. В этом разделе вы кратко узнаете о некоторых других важных функциях, доступных в модуле math .
Вычислить наибольший общий делитель
Наибольший общий делитель (НОД) двух положительных чисел - это наибольшее положительное целое число, которое делит оба числа без остатка.
Например, НОД 15 и 25 равно 5. Вы можете разделить 15 и 25 на 5 без остатка. Нет большего числа, делающего то же самое. Если взять 15 и 30, то НОД будет 15, потому что и 15, и 30 можно разделить на 15 без остатка.
Вам не нужно реализовывать собственные функции для расчета GCD. Модуль Python math предоставляет функцию под названием math.gcd () , которая позволяет вычислить НОД двух чисел.В качестве входных данных можно указать положительные или отрицательные числа, и он вернет соответствующее значение НОД. Однако вы не можете ввести десятичное число.
Вычислить сумму итераций
Если вы когда-нибудь захотите найти сумму значений итерируемого объекта без использования цикла, то math.fsum () , вероятно, самый простой способ сделать это. Вы можете использовать итерируемые объекты, такие как массивы, кортежи или списки, в качестве входных данных, и функция возвращает сумму значений. Встроенная функция под названием sum () также позволяет вычислять сумму итераций, но fsum () более точна, чем sum () .Подробнее об этом можно прочитать в документации.
Вычислить квадратный корень
Квадратный корень числа - это значение, которое при умножении на себя дает число. Вы можете использовать math.sqrt () , чтобы найти квадратный корень из любого положительного действительного числа (целого или десятичного). Возвращаемое значение всегда является значением с плавающей запятой. Функция выдаст ValueError , если вы попытаетесь ввести отрицательное число.
Преобразование значений углов
В реальных сценариях, а также в математике, вы часто сталкиваетесь со случаями, когда вам нужно измерять углы для выполнения вычислений.Углы можно измерять в градусах или радианах. Иногда приходится переводить градусы в радианы и наоборот. Модуль math предоставляет функции, которые позволяют вам это делать.
Если вы хотите преобразовать градусы в радианы, вы можете использовать math.radians () . Он возвращает значение введенного градуса в радианах. Точно так же, если вы хотите преобразовать радианы в градусы, вы можете использовать math.degrees () .
Расчет тригонометрических значений
Тригонометрия - это изучение треугольников.Он касается отношения между углами и сторонами треугольника. Тригонометрия в основном интересует прямоугольные треугольники (в которых один внутренний угол равен 90 градусам), но ее также можно применить к другим типам треугольников. Модуль Python math предоставляет очень полезные функции, которые позволяют выполнять тригонометрические вычисления.
Вы можете вычислить значение синуса угла с помощью math.sin () , значение косинуса с помощью math.cos () и значение тангенса с помощью math.загар () . Модуль math также предоставляет функции для вычисления арксинуса с помощью math.asin () , арккосинуса с math.acos () и арктангенса с помощью math.atan () . Наконец, вы можете вычислить гипотенузу треугольника, используя math.hypot () .
Новые дополнения к математическому модулю
в Python 3.8 С выпуском Python версии 3.8 в модуль math было внесено несколько новых дополнений и изменений.Новые дополнения и изменения заключаются в следующем:
comb (n, k)возвращает количество способов выбора k элементов из n элементов без повторения и без определенного порядка .perm (n, k)возвращает количество способов выбора k элементов из n элементов без повторения и с заказом .isqrt ()возвращает целочисленный квадратный корень неотрицательного целого числа.prod ()вычисляет произведение всех элементов во входной итерации. Как и в случае сfsum (), этот метод может принимать итерации, такие как массивы, списки или кортежи.dist ()возвращает евклидово расстояние между двумя точками p и q , каждая из которых задана как последовательность (или итерация) координат. Две точки должны иметь одинаковый размер.hypot ()теперь обрабатывает более двух измерений.Ранее он поддерживал максимум два измерения.
cmath vs math Комплексное число - это комбинация действительного и мнимого числа. Он имеет формулу a + bi , где a - действительное число, а bi - мнимое число. Действительные и мнимые числа можно объяснить следующим образом:
- Действительное число - это буквально любое число, которое вы можете придумать.
- Мнимое число - это число, возведение которого в квадрат дает отрицательный результат.
Действительным числом может быть любое число. Например, 12, 4,3, -19,0 - все действительные числа. Мнимые числа отображаются как i . На следующем изображении показан пример комплексного числа:
. Комплексное числоВ приведенном выше примере 7 - действительное число, а 3i - мнимое число. Комплексные числа в основном используются в геометрии, исчислении, научных расчетах и особенно в электронике.
Функции модуля Python math не приспособлены для обработки комплексных чисел. Однако Python предоставляет другой модуль, который может специально работать с комплексными числами, модуль cmath . Модуль Python math дополняется модулем cmath , который реализует многие из тех же функций, но для комплексных чисел.
Вы можете импортировать модуль cmath следующим образом:
Поскольку модуль cmath также входит в пакет Python, вы можете импортировать его так же, как вы импортировали модуль math .Прежде чем работать с модулем cmath , вы должны знать, как определить комплексное число. Вы можете определить комплексное число следующим образом:
>>> c = 2 + 3j
>>> c
(2 + 3j)
>>> тип (c)
<класс 'сложный'>
Как видите, вы можете определить, что число действительно сложное, используя type () .
Примечание: В математике мнимая единица обычно обозначается i . В некоторых областях более привычно использовать j для того же самого.В Python вы используете j для обозначения мнимых чисел.
Python также предоставляет специальную встроенную функцию под названием complex () , которая позволяет создавать комплексные числа. Вы можете использовать комплекс () следующим образом:
>>> c = комплекс (2, 3)
>>> c
(2 + 3j)
>>> тип (c)
<класс 'сложный'>
Вы можете использовать любой метод для создания комплексных чисел. Вы также можете использовать модуль cmath для вычисления математических функций для комплексных чисел следующим образом:
>>> cmath.sqrt (c)
(1.85810721406 + 0.6727275964137814j)
>>> cmath.log (c)
(1,3622897515267103 + 0,62761967031j)
>>> cmath.exp (c)
(-16.0670844 + 12.02063434789931j) В этом примере показано, как вычислить квадратный корень, логарифмическое значение и экспоненциальное значение комплексного числа. Вы можете прочитать документацию, если хотите узнать больше о модуле cmath .
NumPy против
математики Для математических вычислений можно использовать несколько известных библиотек Python.Одна из самых известных библиотек - Numerical Python или NumPy. Он в основном используется в научных вычислениях и в областях науки о данных. В отличие от модуля math , который является частью стандартной версии Python, вам необходимо установить NumPy для работы с ним.
Сердце NumPy - это высокопроизводительная структура данных N -мерного (многомерного) массива. Этот массив позволяет выполнять математические операции со всем массивом без циклического перебора элементов.Все функции библиотеки оптимизированы для работы с объектами N-мерного массива.
Для математических вычислений можно использовать как модуль math , так и библиотеку NumPy. NumPy имеет несколько общих черт с модулем math . NumPy имеет подмножество функций, аналогичных функциям модуля math , которые имеют дело с математическими вычислениями. И NumPy, и math предоставляют функции, которые имеют дело с тригонометрическими, экспоненциальными, логарифмическими, гиперболическими и арифметическими вычислениями.
Есть также несколько фундаментальных различий между math и NumPy. Модуль Python math больше ориентирован на работу со скалярными значениями, тогда как NumPy лучше подходит для работы с массивами, векторами и даже матрицами.
При работе со скалярными значениями функции модуля math могут быть быстрее, чем их аналоги в NumPy. Это связано с тем, что функции NumPy преобразуют значения в массивы под капотом, чтобы выполнять над ними вычисления.NumPy работает намного быстрее при работе с размерными массивами N из-за оптимизации для них. За исключением fsum () и prod () , функции модуля math не могут обрабатывать массивы.
Заключение
Из этой статьи вы узнали о модуле Python math . Модуль предоставляет полезные функции для выполнения математических вычислений, которые имеют множество практических приложений.
Из этой статьи вы узнали:
- Что такое модуль Python
math - Как использовать математические функции
с практическими примерами - Какие константы математического модуля
, включая пи, тау и число Эйлера, равны - В чем разница между встроенными функциями и математическими функциями
- В чем разница между
math , cmath и NumPy:
Понимание того, как использовать математические функции , - это первый шаг.Пришло время применить полученные знания в реальных жизненных ситуациях. Если у вас есть какие-либо вопросы или комментарии, оставьте их в разделе комментариев ниже.
Математический модуль Python
Метод Описание math.acos () Возвращает арккосинус числа . math.acosh () Возвращает обратный гиперболический косинус числа . математ.asin () Возвращает арксинус числа . math.asinh () Возвращает обратный гиперболический синус числа . math.atan () Возвращает арктангенс числа в радианах. . math.atan2 () Возвращает арктангенс y / x в радианах. math.atanh () Возвращает обратный гиперболический тангенс числа . математ.ceil () Округляет число до ближайшего целого math.comb () Возвращает количество способов выбрать k элементов из n элементов без повторения и порядка math.copysign () Возвращает число с плавающей запятой, состоящее из значения первого параметра и знака второго параметра math.cos () Возвращает косинус числа . математ.cosh () Возвращает гиперболический косинус числа . математ. Град. () Преобразует угол из радиан в градусы math.dist () Возвращает евклидово расстояние между двумя точками (p и q), где p и
q - координаты этой точки math.erf () Возвращает функцию ошибки числа . математ.erfc () Возвращает дополнительную функцию ошибки числа . math.exp () Возвращает E в степени x math.expm1 () Возврат E x - 1 math.fabs () Возвращает абсолютное значение числа math.factorial () Возвращает факториал числа . математ.этаж () Округляет число до ближайшего целого math.fmod () Возвращает остаток от x / y math.frexp () Возвращает мантиссу и показатель степени указанного числа math.fsum () Возвращает сумму всех элементов в любой итерации (кортежи, массивы, списки и т. Д.) math.gamma () Возвращает гамма-функцию в x математ.gcd () Возвращает наибольший общий делитель двух целых чисел . math.hypot () Возвращает евклидову норму math.isclose () Проверяет, близки ли два значения друг к другу или нет математ. Конечн. () Проверяет, является ли число конечным или нет math.isinf () Проверяет, является ли число бесконечным математ.isnan () Проверяет, является ли значение NaN (не числом) или нет math.isqrt () Округляет квадратный корень в меньшую сторону до ближайшего целого числа math.ldexp () Возвращает значение, обратное math.frexp ().
что является x * (2 ** i) заданных чисел x и i math.lgamma () Возвращает логарифмическое значение гаммы x . математ.журнал () Возвращает натуральный логарифм числа или логарифм числа по основанию . math.log10 () Возвращает десятичный логарифм x . math.log1p () Возвращает натуральный логарифм 1 + x . math.log2 () Возвращает логарифм по основанию 2 x . math.perm () Возвращает количество способов выбрать k элементов из n элементов с порядком и без повторения математ.pow () Возвращает значение x в степени y math.prod () Возвращает произведение всех элементов в итерации математ. Радиан () Преобразует значение градуса в радианы математ. Остаток () Возвращает ближайшее значение, при котором числитель полностью делится на знаменатель. математ.грех () Возвращает синус числа . math.sinh () Возвращает гиперболический синус числа . math.sqrt () Возвращает квадратный корень из числа . math.tan () Возвращает тангенс числа . math.tanh () Возвращает гиперболический тангенс числа . математ.trunc () Возвращает усеченные целые части числа
Математический модуль Python
Некоторые из самых популярных математических функций определены в математическом модуле. К ним относятся тригонометрические функции, функции представления, логарифмические функции, функции преобразования углов и т. Д. Кроме того, в этом модуле определены две математические константы.
Пи - хорошо известная математическая константа, которая определяется как отношение длины окружности к диаметру круга, и ее значение равно 3.1415
589793. >>> импорт математики
>>> math.pi
3,1415589793
Другая известная математическая константа, определенная в математическом модуле, - это e . Оно называется числом Эйлера и является основанием натурального логарифма. Его значение - 2,718281828459045.
>>> импорт математики
>>> математика.е
2,718281828459045
Математический модуль содержит функции для вычисления различных тригонометрических соотношений для заданного угла. Для функций (sin, cos, tan и т. Д.) В качестве аргумента требуется угол в радианах.
Мы же, с другой стороны, привыкли выражать угол в градусах. Математический модуль представляет две функции преобразования углов: градусов () и радиан () , для преобразования угла из градусов в радианы и наоборот.Например, следующие инструкции преобразуют угол 30 градусов в радианы и обратно (Примечание: π радиан эквивалентно 180 градусам).
>>> импорт математики
>>> math.radians (30)
0,5235987755982988
>>> math.degrees (math.pi / 6)
29.999999999999996
Следующие утверждения показывают отношения sin, cos и tan для угла 30 градусов (0.5235987755982988 радиан):
>>> импорт математики
>>> math.sin (0.5235987755982988)
0,49999999999999994
>>> math.cos (0.5235987755982988)
0,8660254037844387
>>> math.tan (0,5235987755982988)
0,57735026257
Вы можете вспомнить, что sin (30) = 0,5 , cos (30) = 32 (что составляет 0.8660254037844387 ) и tan (30) = 13 (что составляет 0, 57735026257 ).
math.log ()
Метод math.log () возвращает натуральный логарифм заданного числа. Натуральный логарифм вычисляется по основанию e .
>>> импорт математики
>>> math.log (10)
2,3025850046
математика.log10 ()
Метод math.log10 () возвращает десятичный логарифм заданного числа. Он называется стандартным логарифмом.
>>> импорт математики
>>> math.log10 (10)
1.0
math.exp ()
Метод math.exp () возвращает число с плавающей запятой после возведения e в степень данного числа.Другими словами, exp (x) дает e ** x .
>>> импорт математики
>>> math.exp (10)
22026.4657718
Это можно проверить с помощью оператора экспоненты.
>>> импорт математики
>>> math.e ** 10
22026.4657703
математика.pow ()
Метод math.pow () получает два аргумента с плавающей запятой, повышает значение первого до второго и возвращает результат. Другими словами, pow (4,4) эквивалентно 4 ** 4.
>>> импорт математики
>>> math.pow (2,4)
16.0
>>> 2 ** 4
16
math.sqrt ()
Математика .sqrt () возвращает квадратный корень заданного числа.
>>> импорт математики
>>> math.sqrt (100)
10.0
>>> math.sqrt (3)
1.7320508075688772
Следующие две функции называются функциями представления. Функция ceil () приближает заданное число к наименьшему целому числу, которое больше или равно заданному числу с плавающей запятой.Функция floor () возвращает наибольшее целое число, меньшее или равное заданному числу.
>>> импорт математики
>>> math.ceil (4.5867)
5
>>> math.floor (4.5687)
4
Узнайте больше о математическом модуле в документации Python.
Все математические функции, определенные в модуле Math в Python 3
Что такое математический модуль в Python?
Модуль math является стандартным модулем в Python и всегда доступен.Чтобы использовать математические функции в этом модуле, вы должны импортировать модуль, используя import math .
Предоставляет доступ к базовым функциям библиотеки C. Например,
# Расчет квадратного корня
импортная математика
math.sqrt (4)
Этот модуль не поддерживает сложных типов данных . Модуль cmath - сложный аналог.
Функции в математическом модуле Python
Вот список всех функций и атрибутов, определенных в модуле math , с кратким объяснением того, что они делают.
Список функций в математическом модуле Python Функция Описание ceil (x) Возвращает наименьшее целое число, большее или равное x. копия (x, y) Возвращает x со знаком y фабрик (x) Возвращает абсолютное значение x . факториал (x) Возвращает факториал x . этаж (х) Возвращает наибольшее целое число, меньшее или равное x . fmod (x, y) Возвращает остаток от деления x на y frexp (x) Возвращает мантиссу и показатель степени x как пару (m, e) fsum (итерация) Возвращает точную сумму значений с плавающей запятой в итерируемом объекте исфинит (x) Возвращает True, если x не является ни бесконечностью, ни NaN (не числом) isinf (x) Возвращает True, если x является положительной или отрицательной бесконечностью иснан (х) Возвращает True, если x - NaN ldexp (x, i) Возвращает x * (2 ** i) modf (x) Возвращает дробную и целую части x . усечение (x) Возвращает усеченное целое число x . эксп. (X) Возврат e ** x экспм1 (x) Возврат e ** x - 1 лог (x [, b]) Возвращает логарифм x по основанию b (по умолчанию e) log1p (x) Возвращает натуральный логарифм 1 + x . log2 (x) Возвращает логарифм по основанию 2 x . log10 (x) Возвращает десятичный логарифм x . pow (x, y) Возвращает x в степени y sqrt (x) Возвращает квадратный корень из x . acos (x) Возвращает арккосинус x . asin (x) Возвращает арксинус x . атан (х) Возвращает арктангенс x . atan2 (y, x) Возвращает атан (г / х) cos (x) Возвращает косинус x . гипотеза (x, y) Возвращает евклидову норму, sqrt (x * x + y * y) грех (х) Возвращает синус x . желто-коричневый (x) Возвращает тангенс x . градусов (x) Преобразует угол x из радианов в градусы радиан (x) Преобразует угол x из градусов в радианы acosh (x) Возвращает обратный гиперболический косинус x . asinh (x) Возвращает обратный гиперболический синус x . атан (х) Возвращает гиперболический тангенс, обратный x . cosh (x) Возвращает гиперболический косинус x . sinh (x) Возвращает гиперболический косинус x . tanh (x) Возвращает гиперболический тангенс x . erf (x) Возвращает функцию ошибки в x erfc (x) Возвращает дополнительную функцию ошибки в x . гамма (x) Возвращает гамма-функцию при x lgamma (x) Возвращает натуральный логарифм абсолютного значения гамма-функции в x . пи Математическая константа, отношение длины окружности к ее диаметру (3.14159 ...) e математическая константа e (2,71828 ...)
Посетите эту страницу, чтобы узнать обо всех математических функциях, определенных в Python 3.
.

 \)
\) \)
\)

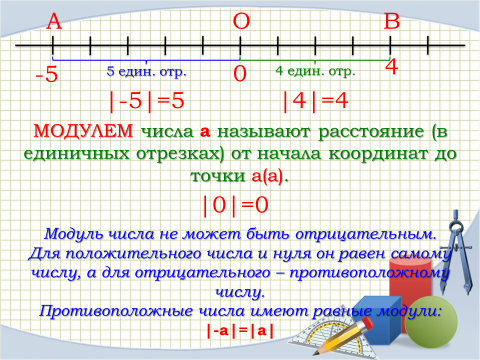 44030650891055
44030650891055
 fabs(x))
# 42.0
a = np.array([-1, 2, -4])
print(np.abs(a))
# [1 2 4]
fabs(x))
# 42.0
a = np.array([-1, 2, -4])
print(np.abs(a))
# [1 2 4]
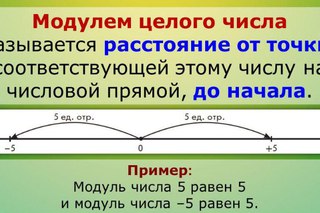 5
>>> 17,0% 12,0
5.0
5
>>> 17,0% 12,0
5.0
 fmod (13.3, 1.1)
0,09999999999999964
fmod (13.3, 1.1)
0,09999999999999964
 bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.выбор (цвета)) # Первый цвет случайный
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
turtle.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.выбор (цвета)) # Первый цвет случайный
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
turtle.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
 bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.choice (цвета))
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
черепаха.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
bgcolor ("gray8") # Hex: # 333333
turtle.pendown ()
turtle.pencolor (random.choice (цвета))
i = 0 # Начальный индекс
в то время как True:
i = (i + 1)% 6 # Обновить индекс
черепаха.pensize (i) # Установить размер pensize на i
черепаха вперед (225)
черепаха. правая (170)
# Выберите случайный цвет
если я == 0:
turtle.pencolor (random.choice (цвета))
 Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
Имеет следующие множители: {факторы}")
еще:
print (f "{num} - простое число")
 Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number (997)
997 - простое число
Он имеет следующие факторы: [(1, 115), (5, 23)]
>>> check_prime_number (997)
997 - простое число
 isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = прописные буквы.индекс (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
верхний регистр = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = прописные буквы.индекс (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат


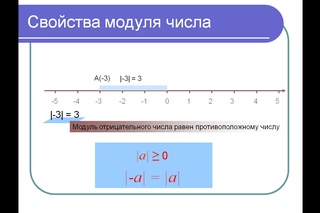 isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
прописные буквы = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
isascii () или не text.isalpha ():
Raise ValueError ("Текст должен быть в формате ASCII и не содержать чисел.")
нижний регистр = строка.ascii_lowercase
прописные буквы = строка.ascii_uppercase
результат = ""
если расшифровать:
сдвиг = сдвиг * -1
для символа в тексте:
если char.islower ():
index = lowercase.index (char)
результат + = нижний регистр [(индекс + сдвиг)% 26]
еще:
index = uppercase.index (символ)
результат + = верхний регистр [(индекс + сдвиг)% 26]
вернуть результат
 isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
верхний регистр = строка.ascii_uppercase
результаты = ""
isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
верхний регистр = строка.ascii_uppercase
результаты = ""
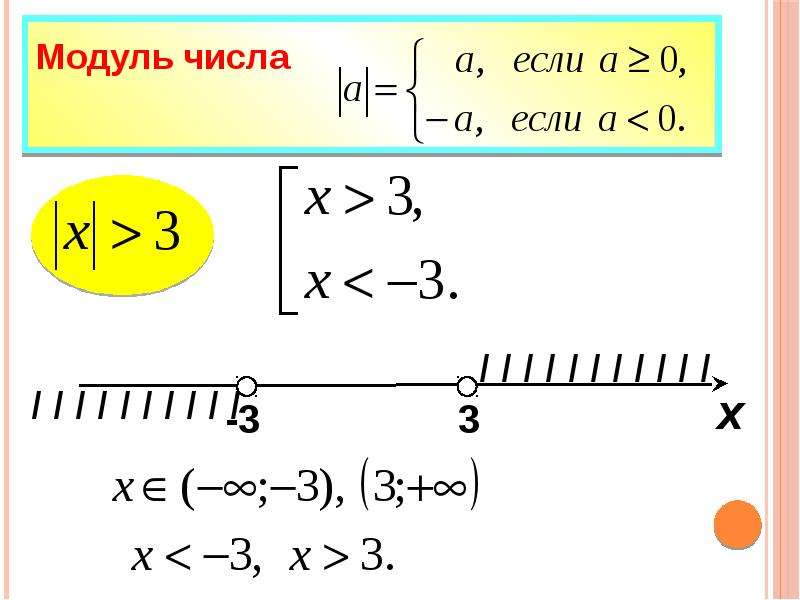 index (char)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
index (char)
key_index = uppercase.index (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
 isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = прописные буквы.индекс (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
isascii () или не text.isalpha () или не text.isupper ():
Raise ValueError ("Текст должен быть в верхнем регистре ASCII без цифр.")
uppercase = string.ascii_uppercase # "ABCDEFGHIJKLMNOPQRSTUVWXYZ"
результаты = ""
для i, char в перечислении (текст):
current_key = ключ [i% len (ключ)]
char_index = uppercase.index (символ)
key_index = прописные буквы.индекс (текущий_ключ)
если расшифровать:
index = char_index - key_index + 26
еще:
index = char_index + key_index
результаты + = верхний регистр [индекс% 26]
вернуть результаты
 Десятичное (15)% десятичное.Десятичное (4)
Десятичный ('3')
>>> десятичный.Десятичный (240)% десятичный. Десятичный (13)
Десятичный ('6')
Десятичное (15)% десятичное.Десятичное (4)
Десятичный ('3')
>>> десятичный.Десятичный (240)% десятичный. Десятичный (13)
Десятичный ('6')
 name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def total_study_time_in_hours (студент, total_mins):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def total_study_time_in_hours (студент, total_mins):
часы = total_mins // 60
минут = total_mins% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
 name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (сам, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (сам, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
 name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (сам, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")
name = имя
self.study_sessions = []
def add_study_sessions (самостоятельно, сеансы):
self.study_sessions + = сеансы
def __mod __ (сам, другое):
возвратная сумма (self.study_sessions)% other
def __floordiv __ (я, другой):
возвратная сумма (self.study_sessions) // другое
def total_study_time_in_hours (студент):
часы = студент // 60
минут = студент% 60
print (f "{student.name} изучил {часы} часы и {минуты} минуты")