Формулы и Задачи (Информатика 10) — Школа N61 г.Ульяновска
Формулы
N = 2i
N — мощность алфавита (количество знаков в алфавите)
i — информационный вес символа алфавита (количество информации в одном символе)
I — количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K — число символов в сообщении
i — информационный вес символа (количество информации в одном символе)
Q — количество разных сообщений
N — количество символов
L — длина сообщения
Формула Хартли:
I = log2N
I — количество информации, содержащееся в выбранном сообщении
N — количество сообщений
Римская система счисления
I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)
Перевод чисел из других систем счисления в десятичную систему счисления
Развернутая запись целого числа:
Правило перевода числа из любой системы счисления в десятичную систему счисления — умножаем каждую цифру исходного числа на основание системы счисления в степени разряда, в котором находится эта цифра, а затем всё складываем.
Запись через схему Горнера:
a3a2a1a0 = ((a3 * p + a2) * p + a1) * p + a0
p — основание системы счисления в котором представлено число.
Пример:
637510 = 6 * 103 + 3 * 102 + 7 * 101 + 5 * 100
637510 = ((6 * 10 + 3) * 10 + 7) * 10 + 5
12345 = 1 * 53 + 2 * 52 + 3 * 51 + 4 * 50 = 19410
12345 = ((1 * 5 + 2) * 5 + 3) * 5 + 4 = 19410
Развернутая запись дробного числа:
0,a1a2a3a4 = a1*p-1 + a2*p-2 + a3*p-3 + a4*p-4
Запись через схему Горнера:
0,a1a2a3a4 = p-1 * (a1 + p-1 * (a2 + p-1 * (a3 + p-1 * a4)))
p * (0,a1a2a3a4) = a1 + p-1 * (a2 + p-1 * (a3 + p-1 * a4))
p — основание системы счисления в котором представлено число.
Пример:
0,6375 = 6 * 10-1 + 3 * 10-2 + 7 * 10-3 + 5 * 10-4
0,6375 = 10-1 * (6 + 10-1 * (3 + 10-1 * (7 + 10-1 * 5)))
0,12345 = 1 * 5-1 + 2 * 5-2 + 3 * 5-3 + 4 * 5-4
0,12345 = 5-1 * (1 + 5-1 * (2 + 5-1 * (3 + 5-1 * 4)))
Задачи
Алфавитный подход к измерению количества информации
Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.
- информационная ёмкость символа: 256 = 28 =>> i = 8 бит = 1 байт
-
количество символов на странице:
32 * 64 = 25 * 26 = 211 -
общее количество символов:
L = 10 * 211 -
информационный объём сообщения:
I = L * i = 10 * 211 * 1 байт = 20 Кбайт
Системы счисления
X10 X16 X8 X2
0 0 0 0
1 1 1 1
2 2 2 10
3 3 3 11
4 4 4 100
5 5 5 101
6 6 6 110
7 7 7 111
8 8 10 1000
9 9 11 1001
10 A 12 1010
11 B 13 1011
12 C 14 1100
13 D 15 1101
14 E 16 1110
15 F 17 1111
16 10 20 10000
17 11 21 10001
18 12 22 10010
19 13 23 10011
20 14 24 10100
21 15 25 10101
22 16 26 10110
23 17 27 10111
24 18 30 11000
25 19 31 11001
26 1A 32 11010
27 1B 33 11011
28 1C 34 11100
29 1D 35 11101
30 1E 36 11110
31 1F 37 11111
32 20 40 100000
Логические операции
Логической операцией называется выбор решения (действия), исходя из заданной ситуации, определяемой набором факторов (условий).
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.
Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.
Таблица истинности для операции НЕ имеет вид:
| A | |
| 0 | 1 |
| 1 | 0 |
Действие, связанное с операцией НЕ можно записать следующим образом:
Логическая операция И (конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия).
B
Логическая операция ИЛИ (дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.
Таблица истинности для операции ИЛИ имеет вид:
| A | B | X=A v B |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Действие, связанное с операцией ИЛИ можно записать следующим образом:
X = A + B = A v B
Логическая операция Исключающее ИЛИ.
Таблица истинности имеет вид:
| A | B | X=AB |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:
X = A B
Действие, связанное с операцией Импликации можно записать следующим образом:
X = A → B
Таблица истинности Импликации имеет вид:
| A | B | A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операция тождество.
Операция тождество определяет тождественность аргументов.
Таблица истинности для операции тождество имеет вид:
| A | B | A Ξ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Действие, связанное с операцией тождество можно записать следующим образом:
X = A Ξ B
Диаграммы Венна (круги Эйлера)
Поиск номера сети
Необходимо найти номер сети по IP-адресу 12.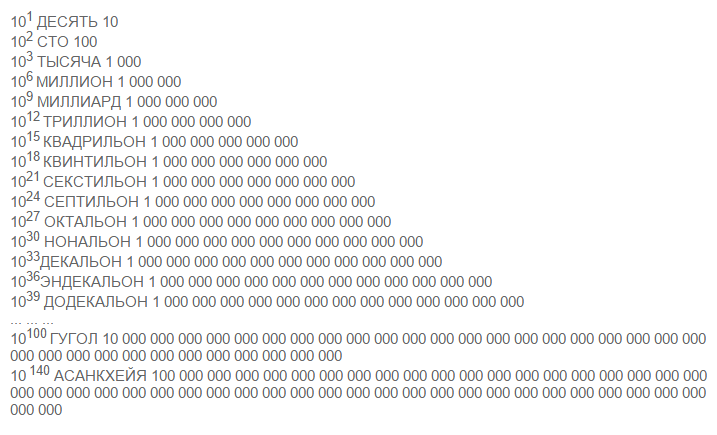
| маска сети | 255. | 255. | 224. | 0 | |
| IP-адрес | 12. | 16. | 196. | 10 | — ip-адрес (узла, компьютера и т.п.) |
| IP-адрес | 0000 1100. | 0001 0000. | 1100 0100. | 0000 1010 | |
| маска сети | 1111 1111. | 1111 1111. | 1110 0000. | 0000 0000 | |
| адрес сети | 0000 1100. | 0001 0000. | 110x xxxx. | xxxx xxxx | — эта часть относится к адресу сети — она взята из ip-адреса, но взяты те цифры, напротив которых стоят единицы остальные цифры справа надо дополнить нулями, чтобы общее число цифр стало равным 32. Получится следующее: |
| адрес сети | 0000 1100. | 0001 0000. | 1100 0000. | 0000 0000 | — полный адрес сети теперь каждую октаду (последовательность из 8 цифр, разделены точками) переводим в десятичный вид. Получаем: |
| адрес сети | 12. | 16. | 192. | 0 | — полный адрес сети (в десятичном виде) |
Формула расчёта ER в Инстаграм — как посчитать вовлечённость
Поделиться!
ER (Engagement Rate, англ. — уровень взаимодействия) — это показатель, отражающий уровень взаимодействия аудитории с вашими публикациями. Чем выше показатель ER, тем интереснее посты вашим подписчиками и они выражают это в виде лайков и комментариев. Проще говоря, если у вас 20000 подписчиков и посты набирают по 20-30 лайков — это ни есть хорошо.
В этом материале мы поговорим о том, какую формулу расчёта ER нужно использовать, расскажем на что влияет показатель вовлечённости и поделимся рекомендации по его улучшению.
Программа для раскрутки в Инстаграм — SocialKit:
- Сбор и фильтрация целевой аудитории
- Масслукинг, массфолловинг, масслайкинг
- Отложенный постинг фото, видео и историй
- Рассылка в Директ, автоответчик
Регистрация >>>
Читайте также: Как увеличить охват постов в Инстаграме
Формула расчёта ER
Для разных соцсетей ER можно и нужно рассчитывать по-разному. Да и в Инстаграме существует множество формул расчёта ER. Поэтому некорректно сравнивать показатели ER разных сервисов, так как они могут использовать различные алгоритмы.
Опишем несколько основных подходов к расчёту ER.
Один из наиболее популярных подходов — расчёт ER per post. Или средний уровень вовлечённости на один пост. Формула имеет такой вид:
ER = (лайки + комментарии) / подписчики * 100%.
Например, у вас 1000 подписчиков, а последняя публикация набрала 90 лайков и 10 комментариев.
Получается, ER = (90 + 10) / 1000 * 100% = 10%. Соответственно, чтобы рассчитать ER всего аккаунта нужно сложить ER для каждого поста и разделить на общее количество постов. Чаще всего в расчёт берутся не все посты, а 10-20 последних или все посты за последний месяц.
Данные видны под каждым постом для тех, кто перешёл на бизнес-профиль.
Ещё одна формула, которая пользуется популярностью при расчёте ER, вместо количества подписчиков учитывается охват, который получил пост.
ER = (лайки + комментарии) / охват на пост * 100%.
Этот метод подсчёта можно считать более точным, так как далеко не все подписчики видят новые публикации, а охват, отражает, как раз тех, кто видел. Например, при всё тех же показателях, что и в предыдущем примере, делить мы будет не 1000 подписчиков, а на охват, допустим он был 400. Получается, ER = (90 + 10) / 400 * 100% = 25%. Даже для 1000 подписчиков это очень высокий показатель. При дальнейшем росте аккаунта, показатель будет снижаться и это нормально.
Считать следует оба показателя. Первый говорит о качестве подписной базе в целом, второй об активности аудитории, которая видит посты.
Какой показатель ER считается нормальным
Чем больше подписчиков, тем ниже ER и это в принципе нормальное явление. Всё это происходит из-за того, что Инстаграм целенаправленно пессимизирует посты, чтобы у пользователей была мотивация запускать рекламу в Инстаграме. Возможно, что профили, которые переведены на бизнес-аккаунт, что говорит о явной коммерческой составляющей, получают пессимизацию в ещё большей степени (но это не точно).
Но здесь нужно учитывать ещё один фактор — уровень досягаемости аудитории. Её условно можно разбить на 4 группы:
- пользователи с числом подписок не более 500. Видят ваши публикации чаще остальных;
- подписчики с числом подписок от 500 до 1000. Иногда могут увидеть ваши публикации;
- число подписок у пользователя от 1000 до 2000. Вам очень повезет, если ваша публикация будет замечена;
- более 2000.
Как правило, это бизнес-аккаунты, которые подписались на вас с помощью массфоловинга. Они вообще не смотрят свою ленту. При отсутствии взаимной подписки позже удалятся.
Как правило, это бизнес-аккаунты, которые подписались на вас с помощью массфоловинга. Они вообще не смотрят свою ленту. При отсутствии взаимной подписки позже удалятся.Получается, чем больше у вас в подписчиках пользователей с небольшим количеством исходящих подписок, тем качественней ваша аудитория и тем, чаще она будет видеть ваши посты. Статья по теме: Сбор целевой аудитории в Инстаграме.
Исходя из этого, для аккаунтов с разной подписной базой будут характерны разные показатели ER (рассчитанные по второму принципу). Например для аккаунта от 5000 до 10000 подписчиков — нормальный показатель 10-20%, для аккаунтов, где свыше 10000 подписчиков это показатель обычно снижается к отметке до 5 %, всё что больше 100000 — 3%, и миллионные аккаунты до 1%.
Опять же не стоит эти показатели рассматривать, как истину в последней инстанции. Инстаграм меняется очень стремительно, поэтому меняются алгоритмы, и каждый аккаунт это отдельный случай, который нужно рассматривать индивидуально.
Как повысить ER
Действовать в этом направлении нужно улучшая качество контента и качество аудитории. Но опять же единого алгоритма, по которому можно повысить ER нет, каждая ситуация по-своему индивидуальна. Вот перечень основных рекомендаций:
- Оцените текущее положение. Проверьте какой у вас сейчас показатель ER, делаете ли вы или агентство, которое вас ведёт накрутки лайков на посты, сколько у вас ботов в подписчиках, как часто вы публикуете новый контент.
- Выявить проблему: маленький охват или низкий ER относительно охвата.
- Экспериментируйте с новым контентом — пробуйте различные варианты. Старайтесь делать фото, которые хочется обсудить, писать текст так чтобы он вызывал отклик.
- Почистите аккаунт от ботов. По ссылке можете узнать, как это сделать с помощью программы SocialKit.
- Сбор целевой аудитории в Инстаграме — соберите самую горячую и активную аудиторию, которая любит лайками и комментировать и запустите по ним накрутку подписчиков. Отфильтруйте тех, кто вряд ли увидит ваши посты (исключите тех, у кого более 1000 исходящих подписок).
- Не используйте одни и те же хэштеги к разным постам.
- Используйте только авторский контент — тот которым вы создаёте сами. Не стоит копировать, как изображения, так и текст. Тоже самое относится к репостам из пабликов.
- Не размещайте текст на фотографии. Даже в рекламе Инстаграм будет показывать посты с текстом на изображении меньшему количеству аудитории, что уже говорить об органике.
И самое главное читайте наш блог и пользуйтесь программой SocialKit для работы в Инстаграме.
Степени 10 Математическое видео для детей
ЧТО ТАКОЕ СТЕПЕНЬ 10?
Степень числа 10 равна 10, умноженному на себя любое количество раз, например 10 × 10 × 10. Степени числа 10 можно записать в экспоненциальной записи. 104 показывает, что 10 умножается на себя 4 раза.
Чтобы лучше понять степени числа 10…
ЧТО ТАКОЕ СТЕПЕНЬ 10?. Степень числа 10 равна 10, умноженному само на себя любое количество раз, например 10 × 10 × 10. Степени числа 10 можно записать в экспоненциальной записи. 104 показывает, что 10 умножается на себя 4 раза.
Чтобы лучше понять степень числа 10…
ДАВАЙТЕ РАЗЪЯСНИМ!
Чемодан с деньгами
Допустим, мы хотим представить миллион долларов, используя степени 10. Начнем с того, что соберем стопку из десяти однодолларовых купюр, что соответствует 10 долларам. Затем сделайте еще одну стопку из десяти долларовых купюр или 10 × 10 долларов, что составляет 100 долларов. В следующей стопке лежат 10 × 10 × 10 долларовых купюр, или 1000 долларов. Каждая новая стопка содержит в десять раз больше долларовых купюр, чем предыдущая стопка, поэтому наша следующая стопка содержит 10 × 10 × 10 × 10 долларовых купюр, или 10 000 долларов, а следующая стопка — 10 × 10 × 10 × 10 × 10 банкнот, что составляет 100 000 долларов. Наконец, в последней стопке долларовых купюр 10 × 10 × 10 × 10 × 10 × 10, что составляет 1 000 000 долларов. Каждый раз, когда мы умножаем на 10, цифры в нашем числе сдвигаются на один разряд влево. При работе с большими числами иногда удобнее представлять эти числа в другой форме, называемой степенью 10. Наша первая стопка банкнот — 10 долларов — может быть представлена как 10 в степени 1, или 10 9.0021 1 . Следующая стопка в 100 долларов может быть представлена как 10 в степени 2, или 10 2 , поскольку 100 = 10 × 10, или две десятки, умноженные вместе. 1000 долларов можно представить как 10 в степени 3 или 10 3 . 10 000 долларов можно представить как 10 в степени 4 или 10 4 . 100 000 долларов можно представить как 10 в степени 5 или 10 5 . 1 000 000 долларов можно представить как 10 в степени 6 или 10 6 . Мы можем записывать числа тремя различными способами: в стандартной форме (1000), в расширенной форме (10 × 10 × 10) и в экспоненциальной форме (10 3 ). Попробуйте сами: Какими тремя способами можно выразить сто долларов?
Чемодан с деньгами Допустим, мы хотим представить миллион долларов, используя степени 10. Начните с создания стопки из десяти однодолларовых купюр, что представляет собой 10 долларов. Затем сделайте еще одну стопку из десяти долларовых купюр или 10 × 10 долларов, что составляет 100 долларов. В следующей стопке лежат 10 × 10 × 10 долларовых купюр, или 1000 долларов. Каждая новая стопка содержит в десять раз больше долларовых купюр, чем предыдущая стопка, поэтому наша следующая стопка содержит 10 × 10 × 10 × 10 долларовых купюр, или 10 000 долларов, а следующая стопка — 10 × 10 × 10 × 10 × 10 банкнот, что составляет 100 000 долларов. Наконец, в последней стопке долларовых купюр 10 × 10 × 10 × 10 × 10 × 10, что составляет 1 000 000 долларов. Каждый раз, когда мы умножаем на 10, цифры в нашем числе сдвигаются на один разряд влево. При работе с большими числами иногда удобнее представлять эти числа в другой форме, называемой степенями 10. Наша первая стопка банкнот — 10 долларов — может быть представлена как 10 в степени 1, или 101. Следующая стопку в 100 долларов можно представить как 10 в степени 2 или 102, поскольку 100 = 10 × 10, или две десятки, умноженные вместе. 1000 долларов можно представить как 10 в степени 3 или 103. 10 000 долларов можно представить как 10 в степени 4 или 104. 100 000 долларов можно представить как 10 в степени 5 или 105. 1 000 000 долларов можно представить как 10 в степени 5 или 105. степень 6 или 106. Мы можем записывать числа тремя различными способами: в стандартной форме (1000), расширенной форме (10 × 10 × 10) и экспоненциальной форме (103). Попробуйте сами: как можно выразить сто долларов тремя разными способами?
Model Airline
Теперь давайте рассмотрим, как степень 10 может помочь нам умножать большие числа. Допустим, у авиакомпании десять самолетов, и в каждом самолете 162 места. Сколько всего мест? Когда вы умножаете число на 10, также представленное как 10 1 , все цифры в этом числе сдвигаются на одну позицию влево. Следуя этой схеме, 1 теперь находится в разряде тысяч, 6 — в разряде сотен, а 2 — в разряде десятков. Так как у нас нет цифры в разряде единиц, мы ставим там ноль. Это означает, что 10 умножить на 162 — это 1620, а общее количество мест в авиакомпании — 1620. Теперь предположим, что каждый из этих 1620 пассажиров платит за свой рейс 100 долларов. Сколько всего платят пассажиры? Число 100 можно представить как 10 в степени 2, 10 2 , или 10 × 10. Когда мы умножаем 1620 на 100, мы сдвигаем цифры на два разряда влево — на то же количество разрядов, что и в показателе степени (2), число, умноженное на 10, является коэффициентом 10 × 10. (2) и количество нулей в 100 (2). Теперь 1 стоит на разряде сотен тысяч, 6 — на разряде десятков тысяч, 2 — на разряде тысяч, а 0 — на разряде сотен, а так как у нас нет ни десятков, ни единиц, мы ставим нули в оба числа. места. Общая сумма, которую платят пассажиры, составляет 162 000 долларов. Теперь предположим, что на каждый рейс расходуется 100 000 литров топлива, а авиакомпания совершает 21 рейс в день. Сколько общего топлива это каждый день? Чтобы ответить на него, решите 21 × 100 000. Это выглядит сложно, но 100 000 — это то же самое, что 10 в степени 5, потому что в нем 5 нулей. Итак, мы сдвигаем цифры в числе 21 на пять знаков влево. Это дает нам 2 в разряде миллионов и 1 в разряде сотен тысяч, за которыми следуют 5 нулей. Таким образом, авиакомпания ежедневно использует 2 100 000 литров топлива. Попробуйте сами: Если каждый из 21 рейса пролетает в среднем 1000 миль каждый день, сколько всего миль пролетает авиакомпания каждый день?
Модель авиакомпании Теперь давайте рассмотрим, как степени 10 могут помочь нам умножать большие числа. Допустим, у авиакомпании десять самолетов, и в каждом самолете 162 места. Сколько всего мест? Когда вы умножаете число на 10, также представленное как 101, все цифры в этом числе сдвигаются на одну позицию влево. Следуя этой схеме, 1 теперь находится в разряде тысяч, 6 — в разряде сотен, а 2 — в разряде десятков. Так как у нас нет цифры в разряде единиц, мы ставим там ноль. Это означает, что 10 умножить на 162 — это 1620, а общее количество мест в авиакомпании — 1620. Теперь предположим, что каждый из этих 1620 пассажиров платит за свой рейс 100 долларов. Сколько всего платят пассажиры? Число 100 можно представить как 10 в степени 2, 102 или 10 × 10. Когда мы умножаем 1620 на 100, мы сдвигаем цифры на два разряда влево — на столько же разрядов, сколько и показатель степени (2), количество раз 10 является множителем 10 × 10 (2), а количество нулей в 100 (2). Теперь 1 стоит на разряде сотен тысяч, 6 — на разряде десятков тысяч, 2 — на разряде тысяч, а 0 — на разряде сотен, а так как у нас нет ни десятков, ни единиц, мы ставим нули в оба числа. места. Общая сумма, которую платят пассажиры, составляет 162 000 долларов. Теперь предположим, что на каждый рейс расходуется 100 000 литров топлива, а авиакомпания совершает 21 рейс в день. Сколько общего топлива это каждый день? Чтобы ответить на него, решите 21 × 100 000. Это выглядит сложно, но 100 000 — это то же самое, что 10 в степени 5, потому что в нем 5 нулей. Итак, мы сдвигаем цифры в числе 21 на пять знаков влево. Это дает нам 2 в разряде миллионов и 1 в разряде сотен тысяч, за которыми следуют 5 нулей. Таким образом, авиакомпания ежедневно использует 2 100 000 литров топлива. Попробуйте сами: если каждый из 21 рейса пролетает в среднем 1000 миль каждый день, сколько всего миль пролетает авиакомпания каждый день?
Мытье собак
Теперь давайте посмотрим, как степени 10 могут помочь нам умножать десятичные числа. Допустим, вы моете собак, используя ведро, вмещающее 6,85 литров воды. Сколько литров воды вмещают 10 полных ведер? Решите эту задачу, умножив 10 × 6,85. Когда мы умножаем число на десять, мы сдвигаем каждую цифру этого числа на один разряд влево. Тот же шаблон, который мы используем для умножения целого числа на степень десяти, работает, когда мы умножаем десятичное число на степень десяти. Десять в степени 1, умноженной на 6,85, равно 68,5, поэтому десять ведер воды вмещают 68,5 литров воды. Хотя перемещаются цифры, другой способ взглянуть на это состоит в том, что десятичная дробь смещается вправо на одно место. Что, если вы используете ведро, которое вмещает 9.4 литра и заполнить его 100 раз? Сколько воды вы используете? Решите задачу, умножив 9,4 × 100. Поскольку 100 равно 10 в степени 2, или 10 2 , цифры в числе 9,4 смещаются на два разряда влево. Всего 940 литров воды. Попробуйте сами: Сколько воды мы используем, если наполним ведро, вмещающее 12,5 литров воды, 1000 раз?
Мытье собак Теперь давайте посмотрим, как степень 10 может помочь нам умножать десятичные числа. Допустим, вы моете собак, используя ведро, вмещающее 6,85 литров воды. Сколько литров воды вмещают 10 полных ведер? Решите эту задачу, умножив 10 × 6,85. Когда мы умножаем число на десять, мы сдвигаем каждую цифру этого числа на один разряд влево. Тот же шаблон, который мы используем для умножения целого числа на степень десяти, работает, когда мы умножаем десятичное число на степень десяти. Десять в степени 1, умноженной на 6,85, равно 68,5, поэтому десять ведер воды вмещают 68,5 литров воды. Хотя перемещаются цифры, другой способ взглянуть на это состоит в том, что десятичная дробь смещается вправо на одно место. Что, если вы используете ведро, которое вмещает 9.4 литра и заполнить его 100 раз? Сколько воды вы используете? Решите задачу, умножив 9,4 × 100. Поскольку 100 равно 10 в степени 2, или 102, цифры в числе 9,4 смещаются на два разряда влево. Всего 940 литров воды. Попробуйте сами: сколько воды мы используем, если наполним ведро, вмещающее 12,5 литров воды, 1000 раз?
Делимся с друзьями
Давайте посмотрим, как степени 10 могут помочь разделить многозначные целые и десятичные числа. Если у вас есть 800 наклеек, которые нужно разделить между 10 друзьями, сколько наклеек получит каждый друг? Решите эту задачу, разделив 800 на 10. Когда мы делим на 10 в степени 1, или 10 1 , мы делаем число в 10 раз меньше или [ggfrac]1/10[/ggfrac] больше, чтобы все цифры сместились на одну позицию вправо. Это имеет смысл, поскольку деление противоположно умножению. Чтобы решить 800 разделить на 10, переместите все цифры на одну позицию вправо, так что наш ответ будет 80,0. Каждый из десяти ваших друзей получает по 80 наклеек. Теперь предположим, что у вас есть 250 чашек мороженого, которые нужно поровну разделить между 100 учениками. Сколько чашек мороженого получил каждый ученик? Чтобы узнать, решите 250 разделить на 100. Так как 100 равно 10 в степени 2, или 10 2 , переместите цифры в числе 250 на две позиции вправо. Это означает, что каждый студент получает 2,5 чашки мороженого. Попробуйте сами: Если у вас есть 50 чашек мороженого, которые нужно разделить поровну между 100 учениками, сколько чашек получит каждый ученик?
Делимся с друзьями Давайте посмотрим, как степени 10 могут помочь разделить многозначные целые и десятичные числа. Если у вас есть 800 наклеек, которые нужно разделить между 10 друзьями, сколько наклеек получит каждый друг? Решите эту задачу, разделив 800 на 10. Когда мы делим на 10 в степени 1 или 101, мы делаем число в 10 раз меньше или [ggfrac]1/10[/ggfrac] большим, поэтому все цифры сдвигаются на один разряд вправо. Это имеет смысл, поскольку деление противоположно умножению. Чтобы решить 800 разделить на 10, переместите все цифры на одну позицию вправо, так что наш ответ будет 80,0. Каждый из десяти ваших друзей получает по 80 наклеек. Теперь предположим, что у вас есть 250 чашек мороженого, которые нужно поровну разделить между 100 учениками. Сколько чашек мороженого получил каждый ученик? Чтобы узнать это, решите 250 разделить на 100. Поскольку 100 равно 10 в степени 2 или 102, переместите цифры в числе 250 на два разряда вправо. Это означает, что каждый студент получает 2,5 чашки мороженого. Попробуйте сами: если у вас есть 50 чашек мороженого, которые нужно разделить поровну между 100 учениками, сколько чашек получит каждый ученик?
СТЕПЕНЬ 10 СЛОВАРЬ
Разрядное значение
Числовое значение, которое имеет цифра, основанная на ее позиции в числе.
Показатель степени
Небольшое выпуклое число, используемое в экспоненциальной записи, чтобы указать, сколько раз основание используется в качестве множителя. Например, в 10 3 основание равно 10, показатель степени равен 3, а 10 3 = 10 х 10 х 10 = 1000. То же, что сила.
Степень 10
Способ записи больших чисел, записанных с использованием десяти в степени или степени.
База десяти
Система счисления, в которой каждое число в 10 раз больше числа справа от него.
Цифра
Любой из символов 0, 1, 2, 3, 4, 5, 6, 7, 8 и 9 в десятичной системе счисления.
Стандартная запись
Число, записанное в стандартном формате, например 100.
Словесная запись
Число, записанное как слово, например, сто.
Расширенная форма
Число, записанное как многократное умножение, например 10 × 10.
Экспоненциальное представление
Способ записи многократного умножения с использованием основания и степени. Например, в экспоненциальном выражении 10 2 основание 10 используется как множитель, умноженный на 2, чтобы представить 10 × 10 = 100.
СТЕПЕНЬ 10 ВОПРОСЫ ДЛЯ ОБСУЖДЕНИЯ 10, цифры в числе сдвигаются вправо или влево? Объяснять.
Цифры смещаются влево, потому что число становится больше.
При делении числа в степени 10 цифры в числе сдвигаются вправо или влево? Объяснять.
Цифры смещаются вправо, потому что число становится меньше.
Как показатель степени говорит вам, как изменяются цифры при умножении или делении на 10?
Цифры перемещаются на количество пробелов, равное целому показателю числа.
Что такое 10 × 10 × 10 × 10, записанное в экспоненциальной форме?
10 4
Объясните, что происходит с цифрами в числе 765,4, когда вы находите частное 93-8
Сколько будет 10 в 4 степени?
В математике показатели степени и степени используются, когда число умножается само на себя определенное количество раз. Например, 4 × 4 × 4 = 64. Это также может быть записано в краткой форме как 4 3 = 64. Здесь 4 3 означает, что число «4» умножается само на себя в три раза, а сокращенно форма 4 3 представляет собой экспоненциальное выражение. Число «4» — это базовое число, а число «3» — это показатель степени, и мы читаем данное показательное выражение как «4, возведенное в степень 3». В экспоненциальном выражении основание — это множитель, многократно умножаемый сам на себя, а показатель степени — это количество раз, когда множитель появляется.
Определение показателей и степеней
Если число умножается само на себя n раз , полученное выражение называется -й степенью данного числа. Между показателем степени и степенью существует очень тонкая грань. Показатель степени — это количество раз, когда данное число умножалось само на себя, а степень — это значение произведения основного числа, возведенного в степень. С помощью экспоненциальной формы чисел нам удобнее выражать чрезвычайно большие и малые числа. Например, 100000000 можно выразить как 1 × 10 8 и 0,0000000000013 можно выразить как 13 × 10 -13 . Это облегчает чтение чисел, помогает поддерживать их точность, а также экономит время.
Правила экспонент и степеней
Правила экспонент и степеней объясняют, как складывать, вычитать, умножать и делить экспоненты, а также как решать различные математические уравнения, включающие экспоненты и степени.
| Закон произведения экспонент | a m × a n =a (m+ n) | ||
|---|---|---|---|
| Quotient Rule of Exponents | a m /a n =a (m-n) | ||
| Мощность правила мощности | (A M ) N = MN | ||
| Power of A Product Rule | A | M × as × as × as as1 2121 M . | |
| Мощность правила коэффициента | A M /B M = (A /B) M | ||
| Zero Правило показания | A 10985 ZERE Правило A 10985 ZERO. Exponent Rule a -m = 1/a m | ||
| Fractional Exponent Rule | a (m/n) = n √a m |
Правило 1: Закон произведения показателей степени
В соответствии с этим законом при умножении показателей степени с одинаковыми основаниями степени складываются.
Закон о продукте показателей: A M × A N = A (M+ N)
Правило 2: Относительное правило экспонентов
Согласно этому закону, чтобы разделить два эксплуата с теми же основаниями нам нужно вычесть показатели.
Частное правило экспонент: a m /a n =a (m–n)
Правило 3. Степень степенного правила
силы умножаются.
Сила степенного правила: (a m ) n =a (m×n)
Правило 4: Сила произведения
9 надо перемножить разные основания и возвести в один и тот же показатель степени до произведения оснований.Степень правила произведения: a m × b m = (a × b) m .
Правило 5: Степень правила отношения
Согласно этому закону, нам нужно разделить различные основания и возвести один и тот же показатель степени в частное оснований.
Степень правила частного: a m ÷ b m =(a/b) m
Правило 6: Экспонента
Согласно этому закону, если значение основания, возведенного в нулевую степень, равно 1.
Правило нулевой степени: a 0 =1
Правило 7: Отрицательная степень В соответствии с этим законом, если показатель степени отрицателен, то изменение показателя степени на положительное производится путем взятия обратной величины экспоненциального числа. Правило отрицательного показателя: a -m = 1/a m Правило 8: Дробная экспонента Правило Согласно этому закону, когда у нас есть дробная экспонента, это приводит к радикалам. Правило фракционного показателя: A (1/N) = N √a A (M/N) = N √a M 11118
18 a M
a
M 9009 900318 a M 9009 118 √A в степени 4 означает?Решение:
Подсчитаем значение 10 в четвертом среднем, т.
Мы знаем, что согласно правилу степеней степени
a m = a × a × a… m умножить на
Следовательно, мы можем записать 10 4 как 10 × 10 × 10 × 10 = 10000
Следовательно,
Значение 10, поднятое к мощности 4, то есть 10 4 составляет 10000.
Проблемы выборки
Проблема 1: Найдите значение 3 6 .
Решение:
Данное выражение равно 3 6 .
Основание данного экспоненциального выражения равно «3», а показатель степени «6», т. е. данное выражение читается как «3 возводится в степень 6».
Таким образом, раскладывая 3 6 , мы получаем 3 6 = 3 × 3 × 3 × 3 × 3 × 3 = 729
Следовательно, значение 3 6 равно 729.
11 Задача 9 2: Определите показатель степени и степень выражения (12) 5 .Решение:
Данное выражение равно 12 5 .
Основание данного экспоненциального выражения равно «12», а показатель степени «5», т. е. данное выражение читается как «12 возводится в степень 5».
Задача 3: вычислить (2/7) –5 × (2/7) 7 .
Решение:
Дано: (2/7) –5 × (2/7) 7
Мы знаем, что a м × a n = a (m + n)
Итак, (2/7) –5 × (2/7) 7 = (2/7) (-5+7)
= (2/7) 2 = 4/49
Следовательно, (2/7) –5 × (2/7) 7 = 4/49
Задача 4. Найти значение x В заданном выражении: 5 3x-2 = 625.
Решение:
, 5 3x-2 = 625.
5 3x-2 = 5 4
5 3x-2 = 5 4
0003
Сравнивая показатели аналогичной базы, получаем
⇒ 3x -2 = 4
⇒ 3x = 4 + 2 = 6
⇒ x = 6/3 = 2
Следовательно, значение x равно 2.