12 и 16 общий знаменатель: Общий знаменатель 12 и 16

Содержание

Каков наибольший общий делитель чисел 12 и 16? – Обзоры Вики

GCF 12 и 16 составляет 4. Чтобы вычислить наибольший общий множитель 12 и 16, нам нужно разложить каждое число на множители (множители 12 = 1, 2, 3, 4, 6, 12; множители 16 = 1, 2, 4, 8, 16) и выбрать наибольший множитель, который точно делит и 12, и 16, т. е. 4.

Итак, каков наибольший общий делитель числа 12? К делителям числа 12 относятся: 1, 2, 3, 4, 6 и 12. Таким образом, общими делителями чисел 16 и 12 являются: 1, 2 и 4. Часто в математических задачах бывает желательно найти наибольшее общий делитель некоторых заданных чисел. В этом случае наибольшим общим множителем является 4.

Каков наибольший делитель 6 и 9? GCF 6 и 9 путем перечисления общих факторов

Есть 2 общих делителя 6 и 9: 1 и 3. Следовательно, наибольший общий делитель 6 и 9 равен 3.

Дополнительно Каков наибольший общий делитель чисел 8 и 20? Следовательно, наибольший общий делитель 8 и 20 равен 4.

Каков наибольший общий делитель чисел 8 и 10? Ответ: GCF 8 и 10 2.

Чему равен наибольший общий делитель чисел и 6?

В поисках наибольшего общего фактора

Два числа	Факторы	Наибольший общий делитель
6 и 18	6:1, 2, 3 , 6 18: 1, 2, 3, 6, 9, 18	6

Каков наибольший общий делитель 8 и 20? Ответ: GCF 8 и 20 4.

Каков наибольший общий делитель чисел 12 и 18? С точки зрения чисел наибольший общий делитель (gcf) — это наибольшее натуральное число, которое точно делит два или более заданных натуральных числа. Пример 1: 6 является наибольшим общим делителем 12 и 18.

Каков наибольший общий делитель 10 и 16?

Ответ: GCF 10 и 16 составляет 2.

Также Каков наибольший общий делитель 15 и 12? Ответ: GCF 12 и 15 3.

Каков наибольший общий делитель 12 и 6?

ВЗК 6 и 12 — 6.

Каков наибольший общий делитель 10 и 12? GCF 10 и 12 равен 2. Чтобы вычислить GCF (наибольший общий коэффициент) 10 и 12, нам нужно разложить на множители каждое число (множители 10 = 1, 2, 5, 10; множители 12 = 1, 2, 3, 4, 6, 12) и выберите наибольший множитель, который точно делит 10 и 12, т. е. 2.

Каков наибольший общий делитель 12 и 30?

HCF 12 и 30 — это 6. Чтобы вычислить Наивысший общий делитель 12 и 30, нам нужно разложить на множители каждое число (множители 12 = 1, 2, 3, 4, 6, 12; множители 30 = 1, 2, 3, 5, 6, 10, 15, 30) и выберите самый высокий множитель, который точно делит 12 и 30, то есть 6.

Какой наибольший множитель из 4 и 6?

У 2 и 4 есть 6 общих делителя, то есть 1 и 2. Следовательно, наибольший общий делитель 4 и 6 равен 2.

Каков наибольший общий делитель чисел 12 и 14? Ответ: GCF 12 и 14 2.

Каков наибольший общий делитель чисел 12 и 13? Ответ: GCF 12 и 13 1.

Каков наибольший общий делитель 18 и 12?

С точки зрения чисел наибольший общий делитель (gcf) — это наибольшее натуральное число, которое точно делит два или более заданных натуральных числа.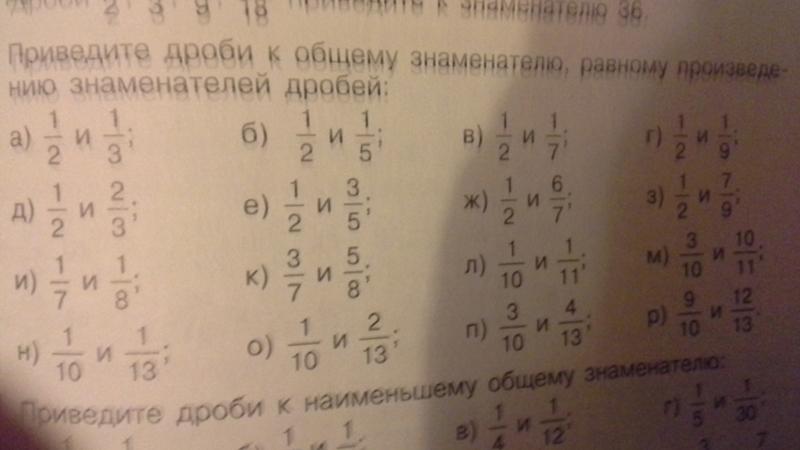 Пример 1: 6 является наибольшим общим делителем 12 и 18.

Как найти наибольший общий знаменатель? Наибольший общий множитель есть наибольший множитель что делит оба числа. Чтобы найти наибольший общий делитель, сначала перечислите простые делители каждого числа. 18 и 24 имеют один общий 2 и один 3. Мы умножаем их, чтобы получить GCF, поэтому 2 * 3 = 6 — это GCF 18 и 24.

Каков наибольший общий делитель 14 и 12?

Ответ: GCF 12 и 14 составляет 2.

Каков наибольший общий делитель чисел 8 и 16? Ответ: GCF 8 и 16 8.

Каков наибольший общий делитель 6 и 14?

Ответ: GCF 6 и 14 составляет 2.

Каков наибольший общий делитель чисел 16 и 20? Ответ: GCF 16 и 20 4.

Приведение дробей к общему знаменателю.

Общий знаменатель и дополнительный множитель.

У дробей бывают различные или одинаковые знаменатели. Одинаковый знаменатель или по-другому называют общий знаменатель у дроби. Пример общего знаменателя:

\(\frac{17}{5}, \frac{1}{5}\)

Пример разных знаменателей у дробей:

\(\frac{8}{3}, \frac{2}{13}\)

Как привести к общему знаменателю дроби?

У первой дроби знаменатель равен 3, у второй равен 13. Нужно найти такое число, чтобы делилось и на 3 и на 13. Это число 39.

Первую дробь нужно умножить на дополнительный множитель 13. Чтобы дробь не изменилась умножаем обязательно и числитель на 13 и знаменатель.

\(\frac{8}{3} = \frac{8 \times \color{red} {13}}{3 \times \color{red} {13}} = \frac{104}{39}\)

Вторую дробь умножаем на дополнительный множитель 3.

\(\frac{2}{13} = \frac{2 \times \color{red} {3}}{13 \times \color{red} {3}} = \frac{6}{39}\)

Мы привели к общему знаменателю дроби:

\(\frac{8}{3} = \frac{104}{39}, \frac{2}{13} = \frac{6}{39}\)

Наименьший общий знаменатель.

Рассмотрим еще пример:

Приведем дроби \(\frac{5}{8}\) и \(\frac{7}{12}\) к общему знаменателю.

Общий знаменатель для чисел 8 и 12 могут быть числа 24, 48, 96, 120, …, принято выбирать наименьший общий знаменатель в нашем случае это число 24.

Наименьший общий знаменатель – это наименьшее число, на которое делиться знаменатель первой и второй дроби.

Как найти наименьший общий знаменатель?
Методом перебора чисел, на которое делиться знаменатель первой и второй дроби и выбрать из них самое наименьшее.

Нам нужно дробь со знаменателем 8 умножить на 3, а дробь со знаменателем 12 умножить на 2.

\(\begin{align}&\frac{5}{8} = \frac{5 \times \color{red} {3}}{8 \times \color{red} {3}} = \frac{15}{24}\\\\&\frac{7}{12} = \frac{7 \times \color{red} {2}}{12 \times \color{red} {2}} = \frac{14}{24}\\\\ \end{align}\)

Если у вас сразу не получиться привести дроби к наименьшему общему знаменателю в этом ничего страшного нет, в дальнейшем решая пример вам может быть придется полученный ответ сократить.

Общей знаменатель можно найти для любых двух дробей это может быть произведение знаменателей этих дробей.

Например:
Приведите дроби \(\frac{1}{4}\) и \(\frac{9}{16}\) к наименьшему общему знаменателю.

Самый простой способ найти общий знаменатель – это произведение знаменателей 4⋅16=64. Число 64 это не наименьший общий знаменатель. По заданию нужно найти именно наименьший общий знаменатель. Поэтому ищем дальше. Нам нужно число, которое делиться и на 4, и на 16, это число 16. Приведем к общему знаменателю дроби, умножим дробь со знаменателем 4 на 4, а дробь со знаменателем 16 на единицу. Получим:

\(\begin{align}&\frac{1}{4} = \frac{1 \times \color{red} {4}}{4 \times \color{red} {4}} = \frac{4}{16}\\\\&\frac{9}{16} = \frac{9 \times \color{red} {1}}{16 \times \color{red} {1}} = \frac{9}{16}\\\\ \end{align}\)

Вопросы по теме:
Любые ли две дроби можно привести к одному общему знаменателю?
Ответ: да.

К какому знаменателю принято приводить дроби?
Ответ: к наименьшему общему знаменателю.

Пример №1:
Для дроби \(\frac{1}{2}\) запишите равную дробь со знаменателем: а) 12 б) 18 в) 50?

Решение:
а) Число 2 нужно умножить на 6, чтобы получить 12. Следовательно, мы всю дробь умножаем на дополнительный множитель 6.

\(\frac{1}{2} = \frac{1 \times \color{red} {6}}{2 \times \color{red} {6}} = \frac{6}{12}\)

б) Число 2 нужно умножить на 9, чтобы получить 18. Следовательно, мы всю дробь умножаем на дополнительный множитель 9.

\(\frac{1}{2} = \frac{1 \times \color{red} {9}}{2 \times \color{red} {9}} = \frac{9}{18}\)

в) Число 2 нужно умножить на 25, чтобы получить 50. Следовательно мы всю дробь умножаем на дополнительный множитель 25.

\(\frac{1}{2} = \frac{1 \times \color{red} {25}}{2 \times \color{red} {25}} = \frac{25}{50}\)

LCM Калькулятор для вычисления наименьшего общего кратного 12, 16

Бесплатный калькулятор LCM определяет наименьшее общее кратное (НОК) между 12 и 16 — наименьшее целое число, равное 48, которое делится на оба числа.

Наименьшее общее кратное (НОК) чисел 12 и 16 равно 48 .

LCM(12,16) = 48

Наименьшее общее кратное или наименьший общий знаменатель (LCD) можно вычислить тремя способами;

Наименьшее общее кратное 12 и 16 методом простых чисел
Наименьшее общее кратное 12 и 16 с формулой GCF

Имя пользователя

НОК

сообщить об этом объявлении Сначала мы вычислим простых множителей 16 и 12 .

Прайм-факторизация 16

2	16
2	8
2	4
2	2
	1

Prime factors of 16 are 2. Prime factorization of 16 in exponential form is:

16 = 2 ⁴

Prime Factorization of 12

2	12
2	6
3	3
	1

Простые множители числа 12 равны 2,3. Разложение 12 на простые множители в экспоненциальной форме:

12 = 2 ² × 3 ¹

Теперь, умножив самые высокие простые множители показателя степени, мы вычислим LCM 16 и 12 .

НОК(16,12) = 2 ⁴ ×3 ¹
НОК(16,12) = 48

Делители 16

1, 2, 4, 8, 16

Делители 12

Список положительных целых множителей числа 12, на которое 12 делится без остатка.

1, 2, 3, 4, 6, 12

Формула LCM : LCM(a,b) = (a × b) / GCF(a,b).
Нам нужно вычислить наибольший общий множитель 16 и 12, а затем применить его в уравнении НОК. (i) LCM 12 и 16 является ассоциативным

LCM 16 и 12 = LCM 12 и 16

LCM 16 и 20
LCM 16 и 21
LCM 16 и 22
LCM 16 и 23
LCM 16 и 24

LCM 12 и 16
LCM 12 и 17
LCM 12 и 18
LCM 12 и 19
LCM 12 и 20

1. Что такое LCM 16 и 12??

Ответ: НОК 16 и 12 равно 48.

2. Каковы множители числа 16?

Ответ: Делителями числа 16 являются 1, 2, 4, 8, 16. Есть 5 целых чисел, которые являются делителями числа 16. Наибольший делитель числа 16 равен 16.

3. Каковы делители числа 12?

Ответ: Делители 12 равны 1, 2, 3, 4, 6, 12. Есть 6 целых чисел, которые являются делителями 12. Наибольший делитель 12 равен 12.

4. Как найти НОК 16 и 12?

Ответ:

Наименьшее общее кратное 16 и 12 = 48

Шаг 1: Найдите простую факторизацию числа 16

16 = 2 x 2 x 2 x 2

Шаг 2: Найдите разложение числа 12 на простые множители

12 = 2 x 2 x 3

Шаг 3: Умножьте каждый множитель на большее количество раз, которое он встречается в шагах i) или ii), чтобы найти lcm:

LCM = 48 = 2 x 2 x 2 x 2 x 3

Шаг 4: Следовательно, наименьшее общее кратное 16 и 12 равно 48.

GCF 12 и 16

GCF 12 и 16, научит вас различным способам расчета GCF 12 и 16, и показать вам, для чего вы можете использовать GCF 12 и 16.
Что такое GCF 12 и 16?

GCF — это аббревиатура от Greatest Common Factor. Таким образом, GCF чисел 12 и 16 совпадает с наибольшим общим делителем. 12 и 16. GCF 12 и 16 — это наибольшее положительное целое число, на которое можно разделить как 12, так и 16. Кроме того, и 12, и 16 имеют набор факторов, и GCF является наибольшим фактором, общим для 12 и 16.
Сравните коэффициенты, чтобы получить GCF 12 и 16
В соответствии с приведенным выше определением, чтобы найти GCF 12 и 16, вы можете сравнить коэффициенты 12 с множители 16, чтобы увидеть, какой множитель больше. Когда мы это сделали, мы обнаружили что наибольший общий делитель (GCF) чисел 12 и 16 равен 4.
Используйте НОК для получения НОД 12 и 16
Наименьшее общее кратное (НОК) 12 и 16 равно 48. Вы можете найти НОД чисел 12 и 16, разделив произведение 12 и 16 на НОК 12 и 16.
Вот формула и математика:
Продукт 12 и 16
LCM 12 и 16
  =  GCF

12 × 16
48
  =  4

Используйте компьютерную таблицу, чтобы получить GCF 12 и 16
Если у вас есть компьютер, вы также можете использовать электронную таблицу в Excel или Numbers для расчета GCF 12 и 16. Вы хотите ввести =gcf(12, 16) в ячейку, чтобы получить ответ.

gcf(12, 16) = 4
Используйте НОД 12 и 16 для упрощения дроби
НОД 12 и 16 можно использовать для многих целей. Вы можете, например, упростить дробь, разделив числитель и знаменатель на GCF вот так:
12 ÷ 4
16 ÷ 4
  =

Используйте GCF, равный 12 и 16, для упрощения отношения

Аналогично, вы можете использовать GCF, равный 12 и 16, для упрощения отношения, разделив каждую часть отношения на
= 12 : 16
= (12 ÷ 4) : (16 ÷ 4)
= 3 : 4
Используйте НОК 12 и 16, чтобы найти НОК 12 и 16
Поскольку использование наименьшего общего кратного (НОК) является одним из способов найти НОК 12 и 16, вы можете использовать НОК 12 и 16, чтобы найти НОК 12 и 16. НОК 12 и 16 можно, например, использовать для сложения и вычитания дробей со знаменателем 12 и 16. НОК 12 и 16 – это произведение 12 и 16, деленное на НГК 12 и 16. Вот математика:

Продукт 12 и 16
GCF 12 и 16
  =  LCM

12 × 16
4
  =  48
Вот и все! Мы надеемся, что эта страница выполнила свою задачу по определению GCF 12 и 16, показав вам, как рассчитать GCF, примеры его использования и его отношение к LCM.
No related posts.