12 система счисления: Двенадцатеричная система счисления | это… Что такое Двенадцатеричная система счисления?

Двенадцатеричная система счисления | это… Что такое Двенадцатеричная система счисления?

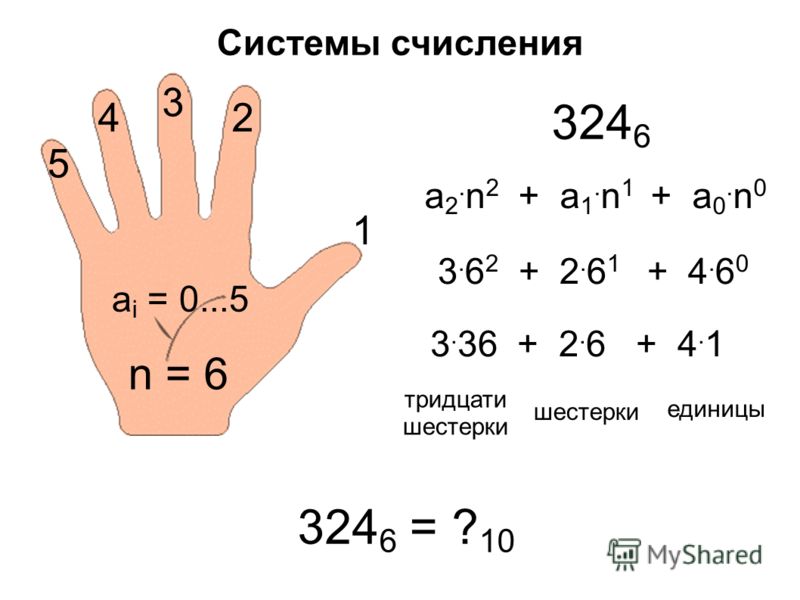
Двенадцатеричная система счисления — позиционная система счисления с основанием 12. Используются цифры 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B. Существует другая система обозначения, где для недостающих цифр используют не A и B, а T (от англ. ten, десять) или D (от лат. decim, фр. dix, десять) или X (римское десять) — и E (от англ. eleven, одиннадцать) или O (от фр. onze, одиннадцать).

Число 12 могло бы быть очень удобным основанием системы счисления, так как оно делится нацело на 2, 3, 4 и 6, в то время как число 10 — основание десятичной системы счисления — делится нацело лишь на 2 и 5.

Содержание 1 История 2 Двенадцатеричный счёт 3 Упоминание в фантастике 4 См. также 5 Примечания 6 Ссылки

История

Двенадцатеричная система счисления возникла в древнем Шумере. Предполагается, что такая система возникала исходя из количества фаланг пальцев на руке при подсчёте их большим пальцем той же руки. Фаланги пальцев использовались как простейшие счёты (текущее состояние счёта засекалось большим пальцем), вместо загибания пальцев, принятого в европейской цивилизации. Некоторые народы Нигерии и Тибета используют двенадцатеричную систему счисления в настоящее время.

Так же существует гипотеза, что до 12 считали сидя, загибая не только 10 пальцев рук, но и 2 ноги. Хотя, возможно, такое случалось, когда европейцам приходилось сталкиваться с восточным двенадцатеричным счётом.

Двенадцатые доли часто встречались и в европейских системах мер. У римлян стандартной дробью была унция (1/12). 1 английский пенс = 1/12 шиллинга, 1 дюйм = 1/12 фута и т. д.

Переход на двенадцатеричную систему счисления предлагался неоднократно. В XVII веке её сторонником был знаменитый французский естествоиспытатель Бюффон. Вольтер в «Истории Карла XII» утверждает, что этот монарх готовил указ о переходе на двенадцатеричную систему. ^[1] Во времена Великой французской революции была учреждена «Революционная комиссия по весам и мерам», которая длительный период рассматривала подобный проект, однако усилиями Лагранжа и других противников реформы дело удалось свернуть. В 1944 году было организовано «Американское двенадцатеричное общество» (англ. The Dozenal Society of America (DSA)), а в 1959 — «Английское двенадцатеричное общество» (англ. The Dozenal Society of Great Britain (DSGB)), объединившие активных сторонников одноимённой системы счисления. Однако, главным аргументом против этого всегда служили огромные затраты и неизбежная путаница при переходе.

Двенадцатеричный счёт

Элементом двенадцатеричной системы в современности может служить счёт дюжинами. Первые три степени числа 12 имеют собственные названия:

• 1 дюжина = 12 штук
• 1 гросс = 12 дюжин = 144 штуки
• 1 масса = 12 гроссов = 1728 штук

Упоминание в фантастике

Двенадцатеричная система счисления упоминается и в фантастической литературе:

• применяется эльфами в книгах Дж. Р. Р. Толкина.
• используется расой, заселившей Землю, после экспансии людей в галактику в романе Уолтера Миллера «Банк крови».
• используется людьми будущего в романе Герберта Уэллса «Когда спящий проснётся», новелле Гарри Гаррисона «История конца» и рассказе Джеймса Блиша «Маникюр».

См. также

• 12 (число)

Примечания

1. ↑ Депман И. Я. История арифметики. (1965), с. 31.

Ссылки

• Фомин С. В. Системы счисления. Серия «Популярные лекции по математике», выпуск 40. М.: Наука, 1987. 48 с.
• http://www.angelfire.com/whittenwords/measure/dozencount.htm
• http://www.earth460.com/math-naturesnumbers.html

Двенадцатеричная система счисления

Содержание:
Что такое двенадцатеричная система счисления
Как перевести целое десятичное число в двенадцатеричную систему счисления
Как перевести десятичную дробь в двенадцатеричную систему счисления
Как перевести число из двенадцатеричной системы счисления в десятичную
Как перевести дробное двенадцатеричное число в десятичное
Таблица значений десятичных чисел от 0 до 100 в двенадцатеричной системе счисления

Двенадцатеричная система счисления, является позиционной системой счисления, то есть имеется зависимость от позиции цифры в записи числа. Для записи числа в двенадцатеричной системе счисления десять цифр и две буквы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A и B. Для определения в какой системе счисления записано число, внизу, справа от числа ставят цифру, которая называется

основанием системы счисления. Например, 12B2A₁₂ или 13A₁₂

Если вам необходимо перевести число любой системы счисления в другую систему счисления, воспользуйтесь калькулятором систем счисления с подробным решением онлайн.

Как перевести целое десятичное число в двенадцатеричную систему счисления

Для того, чтобы перевести целое десятичное число в двенадцатеричную систему счисления нужно десятичное число делить на 12 до тех пор, пока неполное частное не будет равно нулю. В результате будет получено число из остатков деления записанное справа налево.

Например, переведем число 29361₁₀ в двенадцатеричную систему счисления:

29361 : 12 = 2446 остаток: 9
2446 : 12 = 203 остаток: 10, 10 = A
203 : 12 = 16 остаток: 11, 11 = B
16 : 12 = 1 остаток: 4
1 : 12 = 0 остаток: 1

29361₁₀ = 14BA9₁₂

Как перевести десятичную дробь в двенадцатеричную систему счисления

Для того чтобы перевести десятичную дробь в двенадцатеричную систему счисления необходимо сначала перевести целую часть десятичной дроби в двенадцатеричную систему счисления, а затем дробную часть, последовательно умножать на 12, до тех пор, пока в дробной части произведения не получиться ноль (результатом произведения будет целое число) или не будет достигнуто необходимое количество знаков после запятой. Если в результате умножения целая часть не равна нулю, тогда необходимо заменить значение целой части на ноль. В результате будет получено число из целых частей произведений, записанное слева направо.

Например, переведем десятичное число 14.86803144₁₀ в двенадцатеричную систему счисления:

Переведем целую часть

14 : 12 = 1 остаток: 2
1 : 12 = 0 остаток: 1

14₁₀ = 12₁₂

Переведем дробную часть

0.86803144 · 12 = 10.41637728, 10 = A
0.41637728 · 12 = 4.99652736
0.99652736 · 12 = 11.95832832, 11 = B
0.95832832 · 12 = 11.49993984, 11 = B
0.49993984 · 12 = 5.99927808
0.99927808 · 12 = 11.99133696, 11 = B
0.99133696 · 12 = 11.89604352, 11 = B
0.89604352 · 12 = 10.75252224, 10 = A
0.75252224 · 12 = 9.03026688
0.03026688 · 12 = 0.36320256

0.86803144₁₀ = 0.A4BB5BBA90₁₂

14. 86803144₁₀ = 12.A4BB5BBA90₁₂

Двенадцатеричные дроби, как и десятичные могут быть как конечными, так и бесконечными. Не всегда конечная десятичная дробь может быть представлена конечной двенадцатеричной. В данном примере получается бесконечная двенадцатеричная дробь, поэтому умножение на 12 можно производить бесконечное число раз и все равно дробная часть частного не будет равна нулю. В данном случае десятичная дробь 14.86803144 не может быть точно представлена в двенадцатеричной системе счисления. К примеру, дробь 1.5

10 может быть представлена в двенадцатеричной системе счисления в виде конечной 1.5₁₀ = 1.6₁₂.

Как перевести число из двенадцатеричной системы счисления в десятичную

Для того, чтобы перевести число из двенадцатеричной системы счисления в десятичную систему счисления, необходимо записать позиции каждой цифры в числе с права на лево начиная с нуля.

Каждая позиция цифры будет степенью числа 12, так как система счисления 12-ичная. Необходимо последовательно умножить каждое число на 12 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем число 9A36B₁₂ в десятичную систему счисления:

Позиция в числе	4	3	2	1	0
Число	9	A	3	6	B

A₁₂ = 10₁₀
B₁₂ = 11₁₀

9A36B₁₂ = 9 ⋅ 12⁴ + 10 ⋅ 12³ + 3 ⋅ 12² + 6 ⋅ 12¹ + 11 ⋅ 12⁰ = 204419₁₀

Как перевести дробное двенадцатеричное число в десятичное

Для того, чтобы перевести дробное двенадцатеричное число в десятичное, необходимо записать дробное двенадцатеричное число, убрав точку и затем сверху расставить индексы.

Индексы в дробной части числа начинаются от -1 и продолжаются на уменьшение вправо, индексы в целой части начинаются с 0 и ставятся с права на лево по возрастанию. Каждая позиция цифры (индекс) будет степенью числа 12, так как система счисления 12-ичная. Необходимо последовательно умножить каждое число на 12 в степени соответствующей позиции числа и затем сложить с последующим произведением следующего числа в степени соответствующей его позиции.

Например, переведем дробное двенадцатеричное число 9A33.34B19₁₂ в десятичное:

Позиция в числе	3	2	1	0	-1	-2	-3	-4	-5
Число	9	A	3	3	3	4	B	1	9

A₁₂ = 10₁₀
B₁₂ = 11₁₀

9A33.34B19₁₂ = 9 ⋅ 12³ + 10 ⋅ 12² + 3 ⋅ 12¹ + 3 ⋅ 12⁰ + 3 ⋅ 12^-1 + 4 ⋅ 12^-2 + 11 ⋅ 12^-3 + 1 ⋅ 12^-4 + 9 ⋅ 12^-5 = 17031. 2842279128086419753086419746₁₀

Таблица значений десятичных чисел от 0 до 100 в двенадцатеричной системе счисления

Значение числа в десятичной системе счисления	Значение числа в двенадцатеричной системе счисления
010	012
110	112
210	212
310	312
410	412
510	512
610	612
710	712
810	812
910	912
1010	A12
1110	B12
1210	1012
1310	1112
1410	1212
1510	1312
1610	1412
1710	1512
1810	1612
1910	1712
2010	1812
2110	1912
2210	1A12
2310	1B12
2410	2012
2510	2112
2610	2212
2710	2312
2810	2412
2910	2512
3010	2612
3110	2712
3210	2812
3310	2912
3410	2A12
3510	2B12
3610	3012
3710	3112
3810	3212
3910	3312
4010	3412
4110	3512
4210	3612
4310	3712
4410	3812
4510	3912
4610	3A12
4710	3B12
4810	4012
4910	4112
5010	4212

Значение числа в десятичной системе счисления	Значение числа в двенадцатеричной системе счисления
5110	4312
5210	4412
5310	4512
5410	4612
5510	4712
5610	4812
5710	4912
5810	4A12
5910	4B12
6010	5012
6110	5112
6210	5212
6310	5312
6410	5412
6510	5512
6610	5612
6710	5712
6810	5812
6910	5912
7010	5A12
7110	5B12
7210	6012
7310	6112
7410	6212
7510	6312
7610	6412
7710	6512
7810	6612
7910	6712
8010	6812
8110	6912
8210	6A12
8310	6B12
8410	7012
8510	7112
8610	7212
8710	7312
8810	7412
8910	7512
9010	7612
9110	7712
9210	7812
9310	7912
9410	7A12
9510	7B12
9610	8012
9710	8112
9810	8212
9910	8312
10010	8412

База 12: Введение | Год постройки

Люди привыкли использовать системы счисления, чтобы ориентироваться в повседневной жизни. Метрическая система, например, основана на числе, кратном 10. Есть миллиметры, сантиметры, дециметры и метры. Каждая из них увеличивается в размере в 10 раз. Вот почему метрическая система известна как десятичная система счисления.

Что такое основание 12?

Основание 12, также называемое двенадцатеричным, представляет собой систему счисления, в основе которой лежит число 12. Это контрастирует с более распространенной десятичной системой, в которой в качестве основы используется 10.

Хотя счет на основе числа 12 поначалу может показаться неудобным, мы используем различные системы с основанием 12:

Примеры систем с основанием 12

• Хронометраж: у нас 12-часовые часы и 12 месяцев в году
• Измерение : в футе 12 дюймов
• Деньги: в шиллинге 12 пенни или пенса
• Музыка: 12 клавиш (если считать и черные, и белые) в октаве
• Организация: 12 штук в дюжине и 12 дюжин в брутто
• Астрология: есть 12 знаков как в западном, так и в китайском Зодиаке

Еще от Дэвида КоффкURL Альтернативы: вводное руководство 12 очаровательны. В некоторых языках Африки и Азии есть свидетельства существования системы счета с основанием 12. Король Карл Великий, император великой Европы в средние века, также использовал систему с основанием 12 для денег своего королевства. Ранние египтяне опирались на силу основания 12. Они использовали солнечные часы и делили день на 12 частей. Древние китайцы также основывали свою концепцию земных ветвей на числе 12, потому что они обнаружили, что планете Юпитер требуется примерно 12 лет (точнее, 11,86), чтобы совершить один оборот вокруг Солнца. Из этого открытия родился китайский Зодиак.

Конечно, 12-кратное основание было не единственной математической системой, которую использовали наши древние предки. Известно, что майя использовали систему с основанием 20, а вавилоняне разработали и использовали систему с основанием 60. Эта система с основанием 60 обеспечивает легкость деления, поэтому мы до сих пор используем ее для определения времени (в минуте 60 секунд и в часе 60 минут) и для измерения углов (окружность состоит из 360 градусов).

Несмотря на простоту и мощь системы с основанием 12, ее изобретатели преподнесли пользователям сложную задачу: символы.

 

Обозначение по основанию 12

В системе счисления по основанию 12 символы, используемые для представления значений 10 и 11, представляют собой буквы A и B, греческие буквы Δ (дельта) и Λ (лямбда), а также китайские символы 什 (ши) и 佰 (bǎi). По данным Dozenal Society — ведущей глобальной организации по продвижению основания 12 — наиболее популярными буквами для обозначения чисел 10 и 11 являются X и Ɛ, которые называются «дек» и «эл» соответственно.

Эта странная причуда именования, возможно, сделана из соображений удобства. Поскольку для чисел от нуля до девяти требуется только одна цифра, система с основанием 12 также требовала, чтобы один символ представлял числа 10 и 11. 

Эта условность также является преимуществом. Использование одиночных символов для представления чисел 10 и 11 упрощает чтение и запись чисел по основанию 12.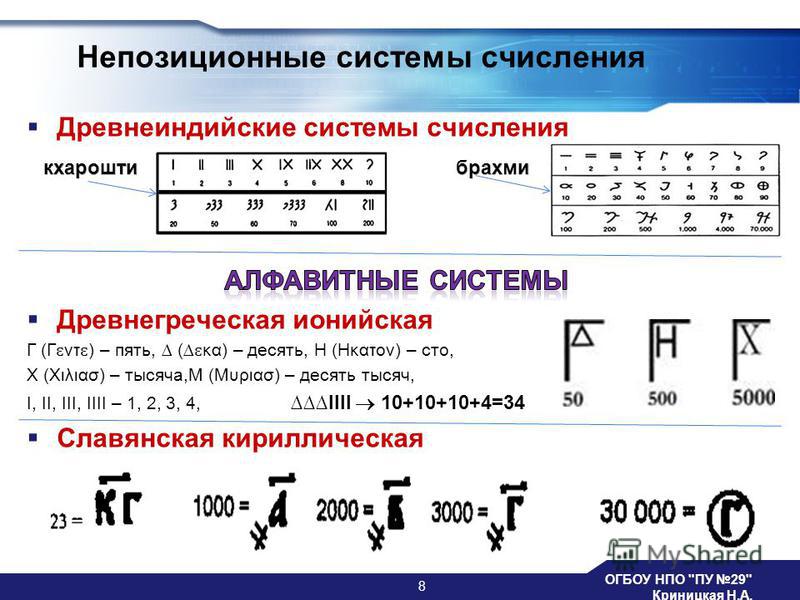 Видеть закономерности и выполнять арифметические действия в уме при работе с числами по основанию 12 также может быть проще. Но у системы есть и другие, более конкретные преимущества.

 

Преимущества основания 12

Число 12 можно разделить на шесть чисел: один, два, три, четыре, шесть и 12. Поскольку число этих шести делителей можно разделить на три, 12 называется трихотомическое число. Число 60 также является трихотомическим, поскольку его можно разделить на девять чисел: один, два, три, четыре, пять, 12, 20, 30 и 60. Для сравнения, число 10 можно разделить только на четыре числа: один , два, пять и 10. Поскольку четыре можно полностью разделить на два, 10 известно как дихотомическое число.

Математики очень предпочитают трихотомические системы счисления, потому что их гораздо проще использовать при делении. Например, проще разделить число 12 и 60 и получить целые числа, чем число 10:

Изображение создано автором.

Из-за этого трихотомические системы предпочтительнее, когда речь идет о дробях и измерениях, и эксперты хвалят их за то, что они намного легче в освоении: и в начальном обучении они были бы намного интереснее, так как маленькие дети находили бы более увлекательные занятия с двенадцатью стержнями или кубиками, чем с десятью. Любой, у кого есть эти таблицы, будет выполнять эти вычисления более чем в полтора раза быстрее в двенадцатеричной шкале, чем в десятичной. Это мой опыт; Я уверен, что тем более это был бы опыт других».

   — А. К. Эйткен, математик и член Королевского общества математика. В одном из этих недостатков нет своей вины: она не так широко используется, как стандартная десятичная система, которую используют большинство современных стран, и поэтому незнакома нематематикам. Это может привести к путанице и ошибкам, когда с ним работают новички.

Вторая проблема с основанием 12 — его ограниченная совместимость с другими системами и оборудованием. Десятичная (или десятичная) система является мировым стандартом для большинства математических и научных приложений. В результате многие инструменты, такие как калькуляторы и компьютеры, оптимизированы для использования с основанием 10, а не с основанием 12. 

Затем возникает проблема использования специальных символов в основании 12 для представления чисел 10 и 11 и любых кратных этих чисел. числа. Эти разные символы могут затруднить их распознавание и написание. Кроме того, в разных культурах используются разные символы для этих двух нестандартных чисел, поэтому не остается единого стандарта, который используется или является предпочтительным.

Перевод между основанием 12 и другими системами счисления также является более сложной задачей. Это связано с тем, что во многих случаях требуется дополнительный шаг: перевод двух дополнительных символов базы 12 в числа. Например, давайте возьмем число 11А по основанию 12 и преобразуем его в число 10 по основанию

Во-первых, нам нужно перевести символ А в его эквивалент по основанию 10, 10. Наше новое число теперь равно 1110.

Затем мы используйте стандартный метод преобразования между системами нумерации. Мы делаем это, беря каждую цифру нашего нового числа и, поскольку мы конвертируем из базы 12, умножая ее на коэффициент 12 в зависимости от ее положения в числе. Краткое напоминание о том, что любое число в нулевой степени равно единице.

Изображение: Mad for Math

Итак, 11А по основанию 12 = 168 по основанию 10. Просто, правда?

Подробнее о науке о данныхЧто такое облачная архитектура? Понимание основ.

 

Изучите основание 12

Хотя 12 основание может использоваться в будущем больше, чем сегодня, по всей вероятности, использование десятичной системы, вероятно, останется нашим глобальным стандартом. Однако остается много возможностей для понимания и использования возможностей двенадцатикратного счисления. Наши нынешние системы измерения, музыки и хронометража не изменятся в обозримом будущем. Эта возможность позволяет нам глубже понять основание 12 без необходимости изучать новые виды обозначений или преобразований.

Почему мы должны перейти на систему счета с основанием 12

Люди, по большей части, считают порциями по 10 — это основа десятичной системы. Однако, несмотря на почти повсеместное принятие, это совершенно произвольная система нумерации, возникшая по одной очень простой причине: у нас по пять пальцев на каждой руке. Но, как любят подмечать многие математики, с основанием 10 есть свои проблемы. Они утверждают, что число 12 — это то, где оно действительно находится. Вот почему мы должны были принять систему счета с основанием 12 — и как мы могли заставить ее работать.

Действительно, очень жаль, что нам не удалось разработать идеальный набор пальцев, который помог бы нам придумать систему счисления, пригодную для счета и вычислений. Вместо этого, с нашими 10 пальцами, мы застряли в неуклюжей десятичной системе.

Присмотревшись к основанию 10, мы увидим, насколько он на самом деле разочаровывающе ограничен. Десять имеет жалкие два делителя (делитель, который дает целые числа), а именно 5 и 2. Более того, эти числа не очень полезны сами по себе; 5 — это простое число, которое больше нельзя делить, а 2 — досадно маленькое целое число, с которым можно работать.

Защитники десятичной системы счисления подчеркивают ее способность допускать перемещение дробных единиц после умножения или деления, но это не исключительная черта десятичной системы. Это свойство допускает не десятичность . Точнее, это характеристика, принадлежащая всем основаниям — свойство обозначения разряда, которое мы используем для выражения чисел, наряду с символом нуля.

Интересно, что число с основанием 10 не является универсальным для всех человеческих обществ. Известно, что майя использовали систему счисления по основанию 20, а вавилоняне разработали систему с использованием наборов из 60. Также использовались системы с основанием 8 и 16 (шестнадцатеричная система), в основном для вычислительных целей (четверти и восьмые упрощаются). ).

Но эти альтернативные наборы все еще не идеальны для повседневных приложений. База 20 не подходит для подсчета пальцев; многие из нас носят обувь, когда занимаются математикой, и мы не можем двигать пальцами ног с какой-либо ловкостью. Base-8 просто слишком мал, а base-16 и base-60 слишком громоздки.

К счастью, между ними находится база — система счисления, обладающая множеством характеристик, которые просто делают ее лучшим выбором для счета и вычислений.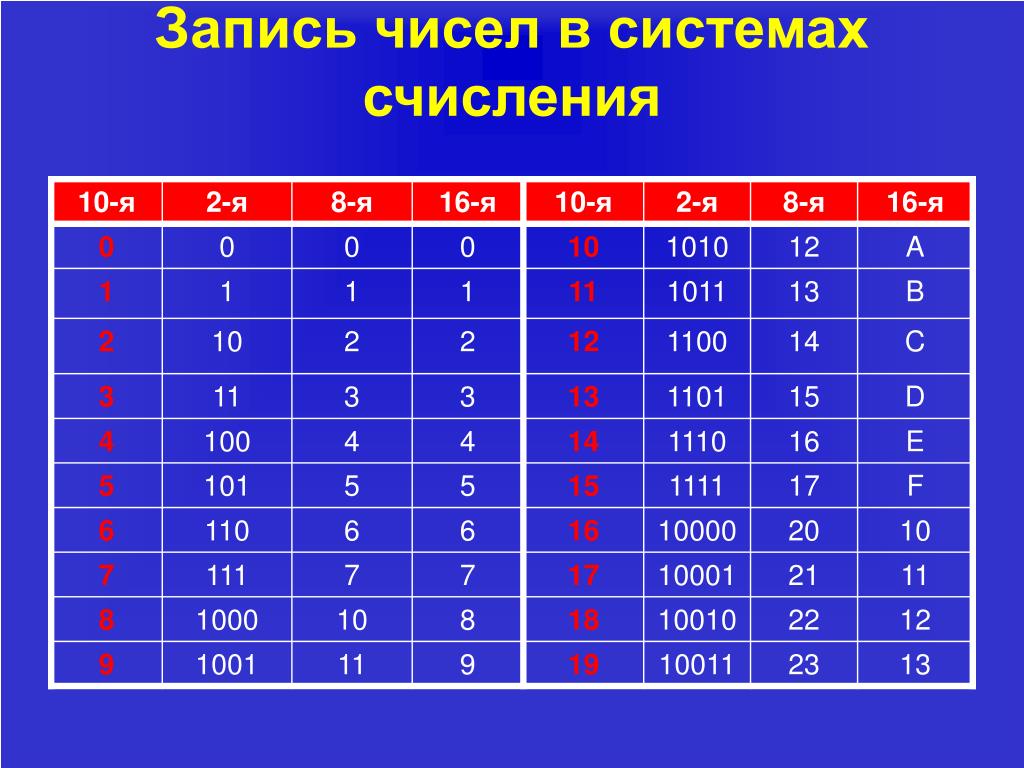

Знакомство с системой дюжин

Также называемая двенадцатеричной системой, система «дюжина» была впервые популяризирована в 17 веке, когда математики начали осознавать ограничения десятичной системы счисления.

Позже, в 1930-х годах, Ф. Эмерсон Эндрюс опубликовал книгу « Новые числа: как принятие двенадцатеричной системы счисления упростит математику », в которой он убедительно доказывал необходимость изменения. Он заметил, что из-за того, что число 12 встречается во многих традиционных единицах измерения и веса, многие из преимуществ, заявленных для метрической системы, также могут быть переняты дюжинной системой.

Действительно, примеров систем с основанием 12 предостаточно. Столярная линейка состоит из 12 делений, бакалейщики имеют дело с дюжинами и брутто (12 дюжин равны брутто), фармацевты и ювелиры используют 12 унций фунта, а чеканщики делят шиллинги на 12 пенсов. Даже наша система хронометража и датирования зависит от этого; в году 12 месяцев, и наш день измеряется 2 наборами по 12. Кроме того, в геометрии круг изобилует подмножествами и надмножествами 12 — то, что измеряется в градусах (круг 360 градусов состоит из 30 наборов по 12 ).

Также очевидно, что кто-то в нашей истории думал в этом направлении. Это самое большое число с одноморфным названием на английском языке (например, слово «двенадцать»). После этого набираем тринадцать, четырнадцать, пятнадцать и так далее — производные от трех, четырех и пяти. Очевидно, было естественно мыслить десятками.

Спустя три десятилетия после выхода книги Эндрюса блестящий математик А. К. Эйткен сделал аналогичный случай. Написав The Listen в 1962 году, он отметил:

Двенадцатеричные таблицы легко освоить, легче, чем десятичные; и в начальном обучении они были бы намного интереснее, так как маленькие дети находили бы более увлекательные занятия с двенадцатью стержнями или кубиками, чем с десятью. Любой, у кого есть эти таблицы, будет выполнять эти вычисления более чем в полтора раза быстрее в двенадцатеричной шкале, чем в десятичной. Это мой опыт; Я уверен, что тем более это был бы опыт других.

Со времен Эндрюса и Эйткена движение дюжин собрало ряд восторженных сторонников, включая появление Американского общества дюжин и Общества дюжин Великобритании.

Основной аргумент этих так называемых дюзеналистов состоит в том, что математика упрощается для осмысления и понимания, особенно для детей и студентов. Вот почему они правы.

Все дело в множителях

Прежде всего, 12 — очень сложное число — наименьшее число, имеющее ровно четыре делителя: 2, 3, 4 и 6 (шесть, если считать 1 и 12). Как уже отмечалось, 10 имеет только два. Следовательно, 12 гораздо практичнее при использовании дробей — проще разделить единицы измерения и веса на 12 частей, а именно половинки, трети и четверти.

Более того, с основанием 12 мы можем использовать эти три наиболее распространенные дроби без использования дробных обозначений. Числа 6, 4 и 3 — целые числа. С другой стороны, с основанием 10 нам приходится иметь дело с громоздкими десятичными дробями, ½ = 0,5, ¼ = 0,25 и, что хуже всего, с очень проблематичным ⅓ = 0,3333333333333333333333.

Подобно шестнадцатеричной системе с основанием 16, дюжинальная система исключительно удобна для информатики. Число 12 имеет два множителя, которые являются простыми числами, 2 и 3. Это означает, что обратные величины всех гладких чисел (числа, которые полностью делятся на маленькие простые числа), таких как 2, 3, 4, 6, 7, 8, иметь завершающее представление в двенадцатеричной системе счисления (чуть позже мы перейдем к подсчету в двенадцатеричной системе счисления). Так случилось, что двенадцать — наименьшее число с этой функцией, что делает его чрезвычайно эффективным числом для целей шифрования и вычисления дробей, включая десятичную, десятичную, двоичную, восьмеричную и шестнадцатеричную системы счисления.

Интересно, что система дюжин также облегчит определение времени. Пять минут — это 12-я часть часа, поэтому вместо «пять минут первого» мы могли бы сказать «один и двенадцатая» часа. Десять минут первого будет 1; 2, четверть первого 1; 3 и т. д. (символ «;» используется в качестве дробной точки).

Но для этого потребуются новые часы. Чтобы это работало, и часовая, и минутная стрелки должны указывать точное время. В обычных десятичных часах минутная стрелка неловко указывает на число, которое нужно умножить на пять.

Обозначения и произношение

Глядя на изображение часов слева вверху, вы, вероятно, задаетесь вопросом, что это за забавные символы и слова. Это потому, что для работы с основанием 12 нам нужно добавить два новых символа для 11 и 12 (помните, что это представления чисел, а не алфавита; число 12 получено из одного полного набора 10 (следовательно 1 в первом столбце) и дополнительное число 2 во втором столбце для обозначения двух дополнительных приращений).

Признавая преимущества системы с основанием 12, Эндрюс разработал новую систему записи для учета двух новых чисел. Вместо использования «A» и «B» для 10 и 11 (согласно шестнадцатеричной системе) Эндрюс предложил сценарий X (U + 1D4B3) и E (U + 2130), где 10 двенадцатеричных представляют 12 десятичных. Таким образом, первые 12 чисел будут выглядеть как 1, 2, 3, 4, 5, 6, 7, 8, 9, X, E, 10.

Другие предполагают, что 10 можно записать как «Т», а число одиннадцать «Э.» Математик Исаак Питман хотел использовать повернутую «2» для десяти и перевернутую «3» для одиннадцати (как на часах выше). В других схемах используется «*» для 10 и «#» для 11 (что удобно для клавиатуры телефона и компьютера).

Для дробей десятичное число 0,5 будет записано в двенадцатеричном формате как 0;6 (помните, что половина 10 отличается от половины 12).

Если это сбивает с толку, вы всегда можете использовать дюжинный/десятичный калькулятор.

Для чисел, превышающих 12, мы должны добавить префикс к значению, обозначающему количество наборов. Итак, для чисел 13, 14 и 15 мы напишем 11, 12 и 13. А для чисел 22, 23 и 24 мы напишем 1X, 1E и 20.

С точки зрения произношение, Дональд П. Гудман, президент Американского общества дюжин, говорит, что X следует называть «десятью», E — «эльвом», а 10 произносится как «unqua». Итак, при подсчете мы говорили: «…восемь, девять, десять эльфов, унква».

Интересно, что в эпизоде ​​1973 года «Маленькие двенадцать пальцев» сериала Schoolhouse Rock! В телесериале инопланетный ребенок использует систему с основанием 12 и произносит последние три числа «дек», «эль» и «до». «Dek» произошло от префикса «deca», в то время как «el» было сокращением от «одиннадцать», а «doh» — сокращением от «дюжины». Многие дюзеналисты приняли именно эту систему произношения.

Теперь, чтобы произносить числа больше 12, например двенадцатеричные 15, мы должны сказать дох-пять, что является соединением дох, что равно двенадцати, и пяти. Мы можем распространить это на другие числа, например, на двенадцатеричное 64, которое будет произноситься как шесть-до-четыре. Если мы должны были достичь и превзойти число EE (el-doh-el), нам нужно новое слово для цифр в третьем столбце.

Слово, обозначающее десятичное число 144 или дюжинное число 100, называется «гро» (буква «s» не произносится). Таким образом, трехзначное число дюжин, такое как 25X, будет произноситься как «два-гро-пять-до». -дек.» В десятичном виде это число равно 358.

Счет на пальцах

Критики дюжинной системы говорят, что это подорвет преимущества счета на пальцах.

Но, как с удовольствием отмечают дюзеналисты, каждый палец состоит из трех частей. Итак, начиная с указательного пальца и используя большой палец в качестве указателя, мы можем сразу же обозначить первые три цифры (двигаясь снизу вверх по пальцу). Тогда средний палец может обозначать 4, 5, 6, средний палец — 7, 8, 9., и так далее. Используя эту систему, наши две руки дают нам в общей сложности 24 числа для работы. Некоторые счетчики пальцев работают слева направо, обозначая кончики пальцев 1, 2, 3, 4.

Еще лучше, мы можем использовать нашу вторую руку, чтобы показать количество завершенных оснований 12. Следовательно, мы можем использовать наши пальцы, чтобы дойти до 144 (12 x 12).

Например, если вы возьмете большой палец левой руки и поместите его на средний сустав среднего пальца (что соответствует 5-му основанию 12, равному десятичному числу 60), и сделаете то же самое на правой руке (что означает 5-й приращение) получаем десятичное число 65.

Можем ли мы когда-нибудь переключиться?

К сожалению, переход на дюжинальную систему на данном этапе будет исключительно сложным и чрезмерно дорогим. Хотя долгосрочные преимущества очевидны, это, вероятно, не стоит краткосрочной боли. Но, тем не менее, жить с неоптимальной системой подсчета отсюда и до вечности кажется грустным.

Тем не менее, дюзеналисты вроде Дональда Гудмана говорят, что это не совсем невозможно. Он утверждает, что конвертация валюты будет первым и наиболее важным шагом, за которым последует организованная просветительская кампания по этому вопросу в школах (Кроме того, и в отношении этого последнего шага, именно так метрическая система была популяризирована и преподавал в Канаде; я хорошо помню тот день, когда в детстве наш учитель вошел и сказал: «Дети, отныне это метрическая система — без исключений»).

Однако Гудман скептически относится к тому, что какая-то одна процедура может работать везде, и предполагает, что ее придется адаптировать к местным условиям.