Postgres Pro Enterprise : Документация: 9.6: 9.8. Функции форматирования данных : Компания Postgres Professional
FM подавляет дополняющие пробелы и нули справа, которые в противном случае будут добавлены, чтобы результат имел фиксированную ширину. В Postgres Pro модификатор FM действует только на следующий код, тогда как в Oracle FM её действие распространяется на все последующие коды, пока не будет отключено последующим модификатором FM.
TM не затрагивает замыкающие пробелы. Функции to_timestamp и to_date игнорируют указание TM.
to_timestamp и to_date пропускают повторяющиеся пробелы во входной строке, если только не используется параметр FX. Например, to_timestamp('2000 JUN', 'YYYY MON') будет работать, но to_timestamp('2000 JUN', 'FXYYYY MON') вернёт ошибку, так как to_timestamp в данном случае ожидает только один разделяющий пробел. Приставка
Приставка FX должна быть первой в шаблоне.
to_timestamp и to_date предназначены для обработки входных форматов, для которых недостаточно простого приведения. Эти функции интерпретируют вводимые данные с послаблениями, проверяя только грубые ошибки. Хотя они выдают корректные данные, результат может отличаться от ожидаемого. В частности, входные аргументы этих функций не ограничиваются обычными диапазонами, так что to_date('20096040','YYYYMMDD') выдаёт 2014-01-17, а не ошибку. С приведением такого не происходит.
Шаблоны для функций to_char могут содержать обычный текст; он будет выведен в неизменном виде. Чтобы вывести текст принудительно, например, если в нём оказываются поддерживаемые коды, его можно заключить в кавычки. Например, в строке '"Hello Year "YYYY', код YYYY будет заменён номером года, а буква Y в слове Year останется неизменной. В функциях
В функциях to_date, to_number и to_timestamp при обработке подстроки в кавычках просто пропускаются символы входной строки по числу символов в подстроке, например для "XX" будут пропущены два символа.
Если вы хотите получить в результате кавычки, перед ними нужно добавить обратную косую черту, например так: '\"YYYY Month\"'.
Если формат года определяется менее, чем 4 цифрами, например, как YYY, и в переданном значении года тоже меньше 4 цифр, год пересчитывается в максимально близкий к году 2020, т. е. 95 воспринимается как 1995.
Функции to_timestamp и to_date воспринимают отрицательные значения годов как относящиеся к годам до н. э. Если же указать отрицательное значение и добавить явный признак BC (до н. э.), год будет относиться к н. э. Нулевое значение года воспринимается как 1 год до н. э.
В функциях to_timestamp и to_date с преобразованием YYYY связано ограничение, когда обрабатываемый год записывается более чем 4 цифрами.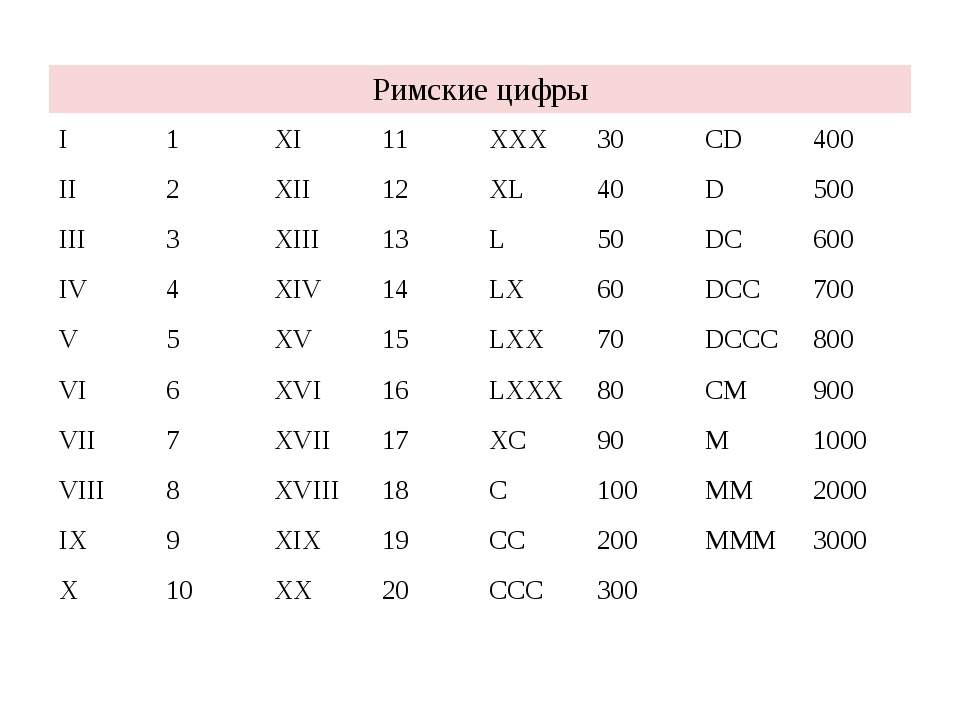 После
После YYYY необходимо будет добавить нецифровой символ или соответствующий код, иначе год всегда будет восприниматься как 4 цифры. Например, в to_date('200001131', 'YYYYMMDD') (с годом 20000) год будет интерпретирован как состоящий из 4 цифр; чтобы исправить ситуацию, нужно добавить нецифровой разделитель после года, как в to_date('20000-1131', 'YYYY-MMDD'), или код как в to_date('20000Nov31', 'YYYYMonDD').
В преобразованиях из строки в тип timestamp или date, поле CC (век) игнорируется, если шаблон включает поля YYY, YYYY или Y,YYY. Когда CC используется с YY или Y, год вычисляется как год данного столетия. Если присутствует только код столетия, без года, подразумевается первый год этого века.
Даты по недельному календарю ISO 8601 (отличающиеся от григорианских) можно передать функциям to_timestamp и to_date одним из двух способов:
Год, номер недели и дня недели: например,
to_date('2006-42-4', 'IYYY-IW-ID')возвращает дату2006-10-19. Если день недели опускается, он считается равным 1 (понедельнику).
Если день недели опускается, он считается равным 1 (понедельнику).Год и день года: например,
to_date('2006-291', 'IYYY-IDDD')также возвращает2006-10-19.
Попытка ввести дату из смеси полей григорианского и недельного календаря ISO 8601 бессмысленна, поэтому это будет считаться ошибкой. В контексте ISO 8601 понятия «номер месяца» и «день месяца» не существуют, а в григорианском календаре нет понятия номера недели по ISO.
Внимание
Тогда как to_date не примет смесь полей григорианского и недельного календаря ISO, to_char способна на это, так как форматы вроде YYYY-MM-DD (IYYY-IDDD) могут быть полезны. Но избегайте форматов типа IYYY-MM-DD; в противном случае с датами в начале года возможны сюрпризы. (За дополнительными сведениями обратитесь к Подразделу 9.9.1.)
При преобразовании из текстовой строки в timestamp, миллисекунды (MS) или микросекунды (US) воспринимаются как дробная часть числа секунд.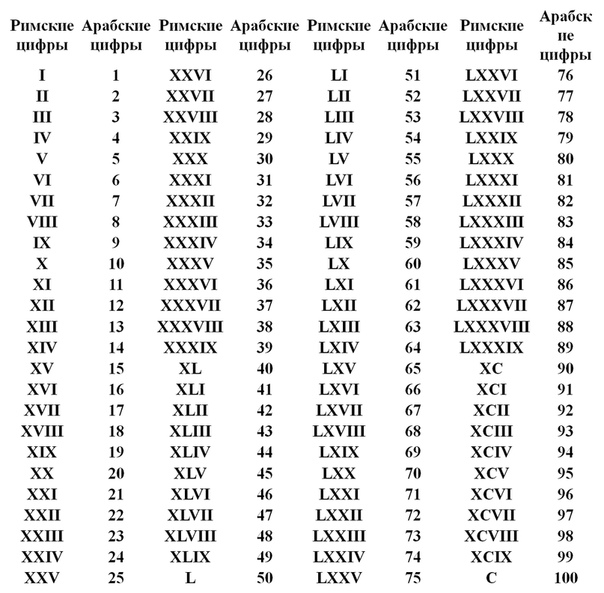 Например,
Например, to_timestamp('12:3', 'SS:MS') — это не 3 миллисекунды, а 300, так как это значение воспринимается как 12 + 0.3 сек. Это значит, что для формата SS:MS вводимые значения 12:3, 12:30 и 12:300 задают одно и то же число миллисекунд. Чтобы получить три миллисекунды, время нужно записать в виде 12:003, тогда это будет воспринято как 12 + 0.003 = 12.003 сек.
Ещё более сложный пример: to_timestamp('15:12:02.020.001230', 'Hh34:MI:SS.MS.US') будет преобразовано в 15 часов, 12 минут и 2 секунды + 20 миллисекунд + 1230 микросекунд = 2.021230 seconds.
Нумерация дней недели в to_char(..., 'ID') соответствует функции extract(isodow from ...), но нумерация to_char(..., 'D') не соответствует нумерации, принятой в extract(dow from ...).
Функция to_char(interval) обрабатывает форматы HH и Hh22 в рамках 12 часов, то есть 0 и 36 часов будут выводиться как 12, тогда как Hh34 выводит значение полностью и для интервалов выводимое значение может превышать 23.
Xix какой это век в цифрах
Какой это век XIX в цифрах
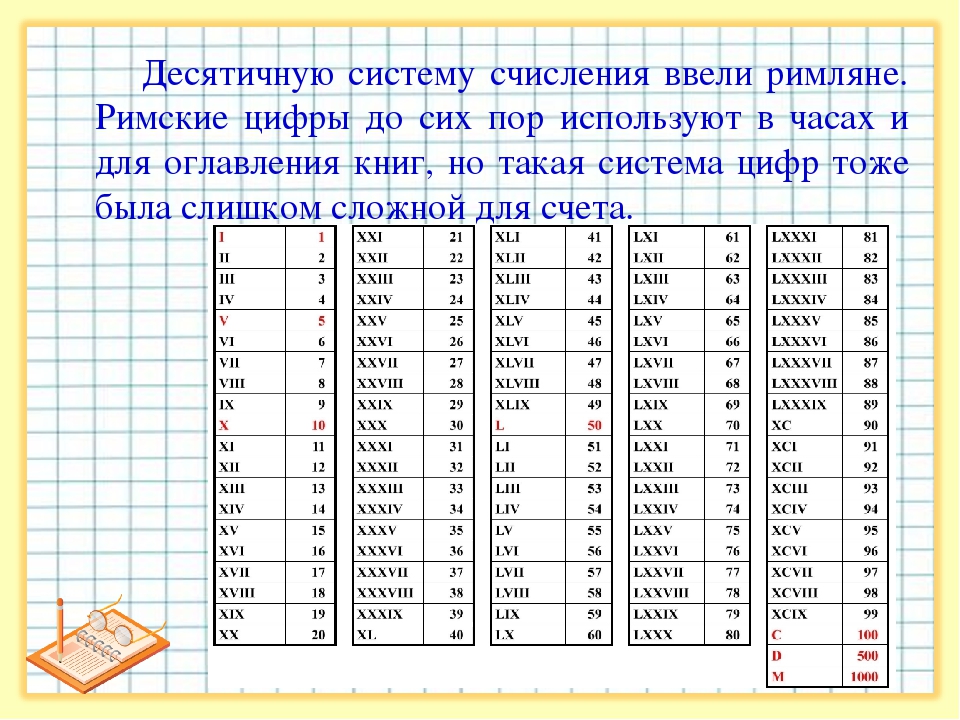
Исторически так сложилось, что в России века пишутся римскими цифрами, правда в последнее время всё чаще можно встретить использование арабских цифр для обозначения века. Происходит это из-за банальной неграмотности и незнания, как правильно писать тот или иной век римскими цифрами, также люди всё чаще задаются вопросами, какой это век XIX в цифрах?
XIX это какой век
Чтобы не просто ответить на поставленный вопрос XIX это какой век, а избавиться от подобных вопросов в будущем, нужно понять, как же читаются римские цифры. На самом деле ничего сложного здесь нет.
Итак, римские цифры обозначаются следующим образом:
• I – 1
• II – 2
• III – 3
• IV – 4
• V – 5
• VI – 6
• VII – 7
• VIII – 8
• IX – 9
• X – 10
Получается, что лишь 5 римских цифр имеют индивидуальное начертание, остальные получаются при помощи подставления I.
Обладая этими знаниями, можно легко ответить на вопрос — XIX это какой век?
XIX какой это век
И всё же, XIX какой это век? Читая эти нехитрые цифры многие разбивают их на 3 значения – X, I, X и получают какой-то весьма странный век – 10 – 1 – 10, т. е. 10 тысяч 110 век. Безусловно это не верная раскладка. Цифра XIX состоит из 2 компонентов – X и IX и расшифровывается очень просто – 1 и 9, т. е. получается 19.
Таким образом, ответом на вопрос, XIX какой это век, будет 19 век.
Как же будут выглядеть остальные века написанные римскими цифрами?
• XI – 11
• XII – 12
• XIII- 13
• XIV – 14
• XV – 15
• XVI – 16
• XVII – 17
• XVIII – 18
• XIX – 19
• XX – 20
Век, в котором мы живём сейчас обозначается как XXI.
Какой это век xix
Многие задаются вопросом, почему же в России века стали обозначать римскими цифрами, ведь всем известно, что в том же английском языке века обозначаются привычными арабскими цифрами, которые всем известны и понятны, так зачем же усложнять себе жизнь?
На самом деле всё довольно просто, дело в том, что римские цифры используются далеко не исключительно в России и не только в обозначении века. Считается, что римские цифры более торжественные и значимые чем банальные арабские, известные всем. Таким образом, римские цифры веками используются для обозначения особо значимых событий или чтобы придать некую торжественность, выделить.
Считается, что римские цифры более торжественные и значимые чем банальные арабские, известные всем. Таким образом, римские цифры веками используются для обозначения особо значимых событий или чтобы придать некую торжественность, выделить.
Убедится в том, что далеко не только век обозначается римскими цифрами довольно просто, достаточно лишь посмотреть на книжное издание сочинений в нескольких томах, где тома, наверняка, пронумерованы римскими цифрами. Во всех странах монарших особ нумеровали римскими цифрами: Пётр I, Елизавета II, Людовик XIV и т. д.
В некоторых странах римскими цифрами обозначаются даже года, что гораздо сложнее, чем выучить какой это век XIX, ведь когда добавляются сотни и тысячи, римские цифры также увеличиваются на несколько цифр – L, C, V и M. Годы, обозначенные римскими цифрами, в отличие от веков, выглядят действительно устрашающе, так 1984 записывается как MCMLXXXIV.
Также римскими цифрами обозначаются все Олимпийские игры. Таким образом в 2014 году XXI века в Сочи прошли XXII Зимние Олимпийские игры.
Таким образом в 2014 году XXI века в Сочи прошли XXII Зимние Олимпийские игры.
Таким образом, можно сказать, что не зная какой это век XIX, человек лишает себя возможности свободно читать о различных событиях, происходящих в мире.
Скорее всего, в скором времени века в России всё же будут обозначаться традиционными арабскими цифрами и вопросы типа какой это век XIX исчезнут сами собой, ведь девятнадцатый век будет записываться понятным для всех образом – 19 век.
И всё же, знать хотя бы первую сотню римских цифр для грамотного человека просто необходимо, ведь далеко не только века обозначаются ими.
Римские цифры или как правильно написать дату римскими цифрами для тату?
Для обозначения цифр в латинском языке приняты комбинации следующих семи знаков: I (1), V (5), X (10), L (50), С (100), D (500), М (1000).
Для запоминания буквенных обозначений цифр в порядке убывания придумано мнемоническое правило:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх (соответственно M, D, C, L, X, V, I).
Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее число следует прибавлять к большему, если слева, то вычитать, а именно:
VI — 6, т.е. 5 + 1
IV — 4, т.е. 5 — 1
XI — 11, т.е. 10 + 1
IX — 9, т.е. 10 — 1
LX — 60, т.е. 50 + 10
XL — 40, т.е. 50 — 10
СХ — 110, т.е. 100 + 10
ХС — 90, т.е. 100-10
Возможно различное обозначение одного и того же числа. Например, число 80 можно обозначить как LXXX (50 + 10 + 10 + 10) и как ХХС (100 — 20).
Для записи чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
I (1) — unus (унус)
II (2) — duo (дуо)
III (3) — tres (трэс)
IV (4) — quattuor (кваттуор)
V (5) — quinque (квинквэ)
VI (6) — sex (сэкс)
VII (7) — septera (сэптэм)
VIII (8) — octo (окто)
IX (9) — novem (новэм)
X (10) — decern (дэцем)
XI (11) — undecim (ундецим)
XII (12) — duodecim (дуодэцим)
ХШ (13) — tredecim (трэдэцим)
XIV (14) — quattuordecim (кваттуордэцим)
XV (15) — quindecim (квиндэцим)
XVI (16) — sedecim (сэдэцим)
XVII (17) — septendecim (сэптэндэцим)
XVIII (18) — duodeviginti (дуодэвигинти)
XIX (19) — undeviginti (ундэвигинти)
XX (20) — viginti (вигинти)
XXII (22) — duo et viginti или viginti duo и т.
 д.
д.XXVIII (28) — duodetriginta (дуодэтригинта)
XXIX (29) — undetriginta (ундэтригинта)
XXX (30) : triginta (тригинта)
XL (40) — quadraginta (квадрагинта)
L (5O) — quinquaginta (квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX (70) — septuaginta (сзлтуагинта)
LXXX180) — octoginta (октогинта)
КС (90) — nonaginta (нонагинта)
C (100) centum (центум)
CC (200) — ducenti (дуценти)
CCC (300) — trecenti (трэценти)
CD (400) — quadrigenti (квадригэнти)
D (500) — quingenti (квингэнти)
DC (600) — sescenti(сэсценти) или sexonti (сэксцонти)
DCC (700) — septigenti (сэптигэнти)
DCCC (800) — octingenti (октингэнти)
CV (DCCC) (900) — nongenti (нонгэнти)
M (1000) — mille (милле)
ММ (2000) — duo milia (дуо милиа)
V (5000) — quinque milla (квинквэ милиа)
XX (20000) — viginti milia (вигинти милиа)
C (100000) — centum milia (центум милиа)
XI (1000000) — decies centena milia (дэциэс центэна милиа).
Если вдруг любознательный человек спросит, почему для обозначения цифр 50, 100, 500 и 1000 были выбраны латинские буквы V, L, С, D, М, то сразу скажем, что это вовсе не латинские буквы, а совсем иные знаки.
Дело в том, что основой для латинского алфавита послужил алфавит западногреческий. Именно к нему восходят три знака L, С и М. Здесь они обозначали придыхательные звуки, которых не было в латинском языке. Когда оформлялся латинский алфавит, именно они оказались лишними. Их и приспособили для обозначения чисел в латинской графике. Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М (1000) — на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уж стал похож на латинскую букву. Знак V (5) являлся всего навсего верхней половиной знака X (10).
Латинские цифры от 1 до 1000. Какой это век XIX в цифрах
Мы все пользуемся римскими цифрами – отмечаем ими номера веков или месяцев года.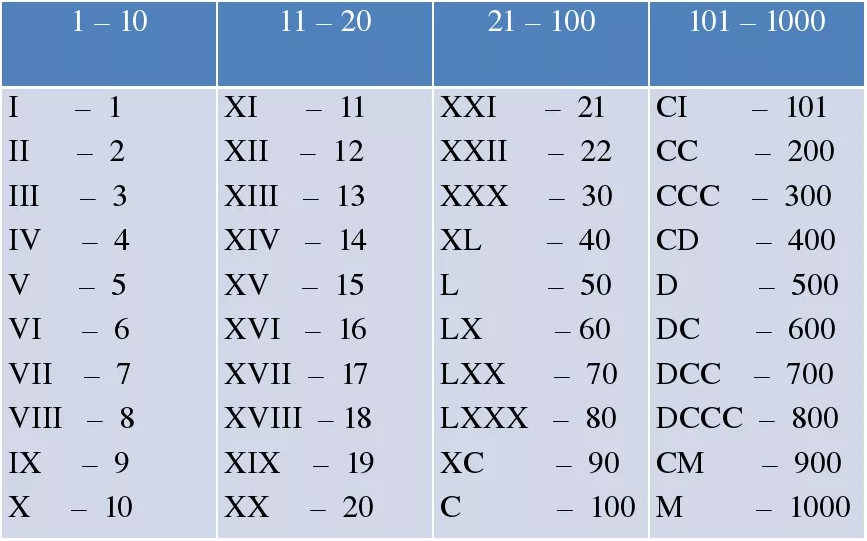 Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много.
Римские цифры находятся на часовых циферблатах, в том числе на курантах Спасской башни. Мы их используем, но знаем про них не так много.
Как устроены римские цифры
Римская система счета в ее современном варианте состоит из следующих базовых знаков:
I 1
V 5
X 10
L 50
C 100
D 500
M 1000
Чтобы запомнить цифры, непривычные для нас, пользующихся арабской системой, существует несколько специальных мнемонических фраз на русском и английском языках:
Мы Dарим Сочные Lимоны, Хватит Vсем Iх
Mы Dаем Cоветы Lишь Xорошо Vоспитанным Iндивидуумам
I Value Xylophones Like Cows Dig Milk
Система расположения этих цифр друг относительно друга такова: числа до трех включительно образуются при помощи сложения единиц (II, III), — четырехкратное повторение любой цифры запрещено. Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Важно, что любая цифра не должна повторять больше трех раз, таким образом, самое длинное число до тысячи – 888 = DCCCLXXXVIII (500+100+100+100+50+10+10+10+5+1+1+1).
Альтернативные варианты
Запрет на четвертое использование одной и той же цифры подряд стал появляться только в XIX веке. Поэтому в старинных текстах можно увидеть варианты IIII и VIIII вместо IV и IX, и даже IIIII или XXXXXX вместо V и LX. Остатки этого написания можно увидеть на часах, где четыре часто отмечается именно с помощью четырех единиц. В старых книгах также нередки случаи двойных вычитаний – XIIX или IIXX вместо стандартных в наши дни XVIII.
Также в Средневековье появилась новая римская цифра – ноль, который обозначался буквой N (от латинского nulla, ноль). Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.
Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.
Происхождение
На данный момент не существует единой теории происхождения римских цифр. Одна из самых популярных гипотез гласит, что этрусско-римские цифры произошли от системы счета, которая использует вместо цифры штрихи-зарубки.
Таким образом, цифра «I» — это не латинская или более древняя буква «и», а насечка, напоминающая форму этой буквы. Каждую пятую насечку обозначали скосом – V, а десятую перечеркивали – Х. Число 10 выглядело в этом счете следующим образом: IIIIΛIIIIX.
Именно благодаря такой записи цифр подряд мы обязаны особой системе сложения римских цифр: со временем запись числа 8 (IIIIΛIII) могла сократиться до ΛIII, что убедительно демонстрирует, каким образом римская система счета получила свою специфику. Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность.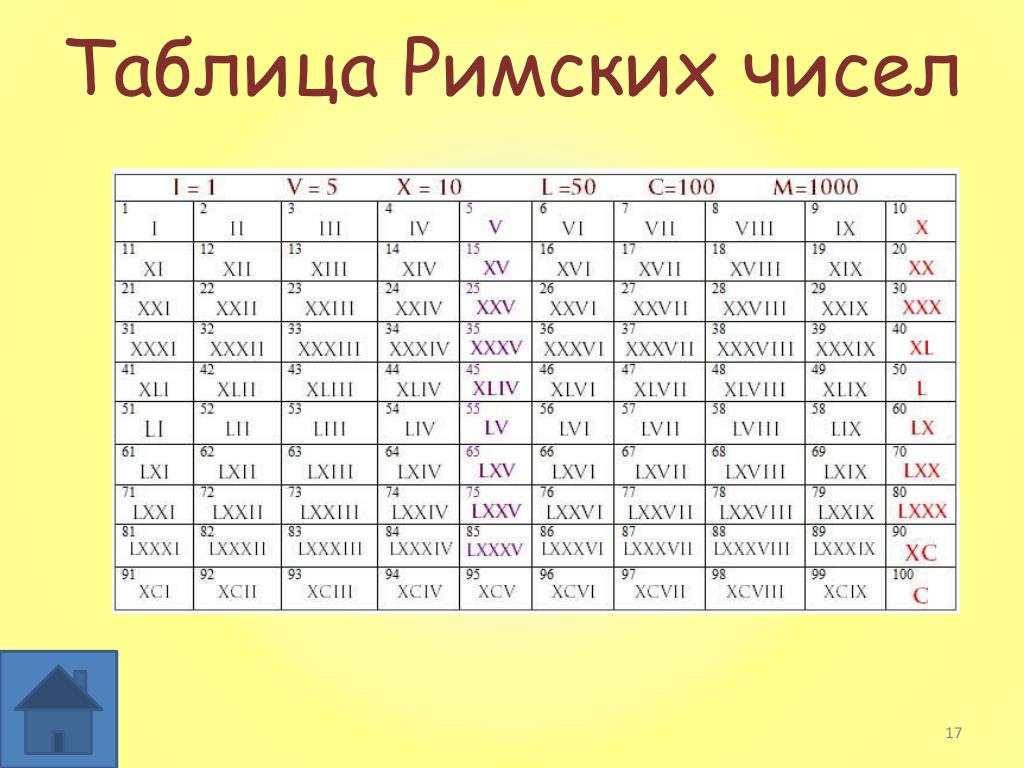 Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
Альтернативная теория принадлежит Альфреду Куперу, который предположил рассмотреть римскую систему счета с точки зрения физиологии. Купер считает, что I, II, III, IIII – это графическое представление количества пальцев правой руки, выкидываемых торговцем при назывании цены. V – это отставленный большой палец, образующий вместе с ладонью подобную букве V фигуру.
Именно поэтому римские цифры суммируют не только единицы, но и складывают их с пятерками – VI, VII и т.п. – это откинутый большой палец и другие выставленные пальцы руки. Число 10 выражали с помощью перекрещивания рук или пальцев, отсюда пошел символ X. Еще один вариант – цифру V попросту удвоили, получив X. Большие числа передавали с помощью левой ладони, которая считала десятки. Так постепенно знаки древнего пальцевого счета стали пиктограммами, которые затем начали отождествлять с буквами латинского алфавита.
Современное применение
Сегодня в России римские цифры нужны, в первую очередь, для записи номера века или тысячелетия. Римские цифры удобно ставить рядом с арабскими – если написать век римскими цифрами, а затем год – арабскими, то в глазах не будет рябить от обилия одинаковых знаков. Римские цифры имеют некоторый оттенок архаичности. С их помощью также традиционно обозначают порядковый номер монарха (Петр I), номер тома многотомного издания, иногда – главы книги. Также римские цифры используются в циферблатах часов под старину. Важные числа, такие, как год олимпиады или номер научного закона, могут также фиксироваться при помощи римских цифр: II мировая, V постулат Евклида.
В разных странах римские цифры употребляются немножко по-разному: в СССР было принято указывать с помощью них месяц года (1.XI.65). На западе римскими цифрами часто пишут номер года в титрах фильмов или на фасадах зданий.
В части Европы, в особенности в Литве, нередко можно встретить обозначение римскими цифрами дней недели (I – понедельник и так далее). В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В России при письме рукой принято подчеркивать римские числа снизу и сверху одновременно. Однако часто в других странах подчеркивание сверху значило увеличение регистра числа в 1000 раз (или 10000 раз при двойном подчеркивании).
Существует распространенное заблуждение о том, что современные западные размеры одежды имеют некую связь с римскими цифрами. На самом деле обозначения XXL, S, M, L и т.п. не имеют никакой связи с ними: это аббревиатуры английских слов eXtra (очень), Small (маленький), Large (большой).
Исторически так сложилось, что в России века пишутся римскими цифрами, правда в последнее время всё чаще можно встретить использование арабских цифр для обозначения века. Происходит это из-за банальной неграмотности и незнания, как правильно писать тот или иной век римскими цифрами, также люди всё чаще задаются вопросами, какой это век XIX в цифрах?
XIX это какой век
Чтобы не просто ответить на поставленный вопрос XIX это какой век, а избавиться от подобных вопросов в будущем, нужно понять, как же читаются римские цифры. На самом деле ничего сложного здесь нет.
На самом деле ничего сложного здесь нет.
Итак, римские цифры обозначаются следующим образом:
I – 1
II – 2
III – 3
IV – 4
V – 5
VI – 6
VII – 7
VIII – 8
IX – 9
X – 10
Получается, что лишь 5 римских цифр имеют индивидуальное начертание, остальные получаются при помощи подставления I. Если I стоит перед основной цифрой – это означает минус 1, если после, то плюс 1.
Обладая этими знаниями, можно легко ответить на вопрос — XIX это какой век?
XIX какой это век
И всё же, XIX какой это век? Читая эти нехитрые цифры многие разбивают их на 3 значения – X, I, X и получают какой-то весьма странный век – 10 – 1 – 10, т. е. 10 тысяч 110 век. Безусловно это не верная раскладка. Цифра XIX состоит из 2 компонентов – X и IX и расшифровывается очень просто – 1 и 9, т. е. получается 19.
Таким образом, ответом на вопрос, XIX какой это век, будет 19 век.
Как же будут выглядеть остальные века написанные римскими цифрами?
XI – 11
XII – 12
XIII- 13
XIV – 14
XV – 15
XVI – 16
XVII – 17
XVIII – 18
XIX – 19
XX – 20
Век, в котором мы живём сейчас обозначается как XXI .
Какой это век xix
Многие задаются вопросом, почему же в России века стали обозначать римскими цифрами, ведь всем известно, что в том же английском языке века обозначаются привычными арабскими цифрами, которые всем известны и понятны, так зачем же усложнять себе жизнь?
На самом деле всё довольно просто, дело в том, что римские цифры используются далеко не исключительно в России и не только в обозначении века. Считается, что римские цифры более торжественные и значимые чем банальные арабские, известные всем. Таким образом, римские цифры веками используются для обозначения особо значимых событий или чтобы придать некую торжественность, выделить.
Убедится в том, что далеко не только век обозначается римскими цифрами довольно просто, достаточно лишь посмотреть на книжное издание сочинений в нескольких томах, где тома, наверняка, пронумерованы римскими цифрами. Во всех странах монарших особ нумеровали римскими цифрами: Пётр I, Елизавета II, Людовик XIV и т.
д.
В некоторых странах римскими цифрами обозначаются даже года, что гораздо сложнее, чем выучить какой это век XIX, ведь когда добавляются сотни и тысячи, римские цифры также увеличиваются на несколько цифр – L, C, V и M . Годы, обозначенные римскими цифрами, в отличие от веков, выглядят действительно устрашающе, так 1984 записывается как MCMLXXXIV .
Также римскими цифрами обозначаются все Олимпийские игры. Таким образом в 2014 году XXI века в Сочи прошли XXII Зимние Олимпийские игры.
Таким образом, можно сказать, что не зная какой это век XIX, человек лишает себя возможности свободно читать о различных событиях, происходящих в мире.
Скорее всего, в скором времени века в России всё же будут обозначаться традиционными арабскими цифрами и вопросы типа какой это век XIX исчезнут сами собой, ведь девятнадцатый век будет записываться понятным для всех образом – 19 век.
И всё же, знать хотя бы первую сотню римских цифр для грамотного человека просто необходимо, ведь далеко не только века обозначаются ими.
Римские цифры часто вызывают у нас затруднение.
А ведь именно их принято использовать при нумерации столетий и книжных глав, при обозначений размеров одежды и ступеней в музыке.
Римские цифры есть в нашей жизни. Так что рано отказываться от них. Проще узнать, понять и выучить. Тем более, что это несложно.
Итак, для обозначения цифр в латинском языке приняты комбинации следующих 7 знаков: I(1), V (5), X (10), L (50), C(100), D(500), M (1000).
Почему для обозначения цифр 5, 50, 100, 500 и 1000 были выбраны латинские буквы? Оказывается, это не латинские буквы, а совсем иные знаки. Дело в том, что основой для латинского алфавита, (а он, кстати, существует в нескольких вариантах — 23, 24 и 25 буквы) послужил западногреческий алфавит.
Таким образом, к западногреческому алфавиту восходят три знака L, C, и M. Здесь они обозначали придыхательные звуки, которых не было в латинском языке. Когда оформлялся латинский алфавит, именно они оказались лишними. И их приспособили для обозначения чисел в латинской графике. Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М — (1000) — на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уже стал похож на латинскую букву. Знак V (5) являлся всего-навсего верхней половиной знака Х (10).
Позднее они по написанию совпали с латинскими буквами. Так, знак С (100) стал похож на первую букву латинского слова centum (сто), а М — (1000) — на первую букву слова mille (тысяча). Что же касается знака D (500), то он представлял собой половину знака Ф (1000), а потом уже стал похож на латинскую букву. Знак V (5) являлся всего-навсего верхней половиной знака Х (10).
В связи с этим, кстати, популярная теория о том, что название церковной должности Папы Римского (Vicarius Filii Dei) при замене букв римскими цифрами в сумме дает “дьяволово число”, кажется забавной.
Итак, как же разобраться в латинских числах?
Если знак, обозначающий меньшее число, стоит справа от знака, обозначающего большее число, то меньшее прибавляют к большему; если слева — то вычитают:
VI — 6, т.е. 5+1
IV — 4, т.е. 5-1
LX — 60, т.е. 50+10
XL — 40, т.е. 50-10
CX — 110, т.е.100+10
XC — 90, т.е. 100-10
MDCCCXII — 1812, т.е. 1000+500+100+100+100+10+1+1.
Возможно различное обозначение одного и того же числа. Так, число 80 можно представить как LXXX (50+10+10+10) и как XXC(100-20).
Так, число 80 можно представить как LXXX (50+10+10+10) и как XXC(100-20).
Основные римские цифры выглядят так:
I(1) — unus (унус)
II(2) — duo (дуо)
III(3) — tres (трэс)
IV(4) — quattuor (кваттуор)
V(5) — quinque (квинквэ)
VI(6) — sex (сэкс)
VII (7) — septem (сэптэм)
VIII (8) — octo (окто)
IX (9) — novem (новэм)
X (10) — decem (дэцем) и т.д.
XX (20) — viginti (вигинти)
XXI (21) — unus et viginti или viginti unus
XXII (22) — duo et viginti или viginti duo и т.д.
XXVIII (28) — duodetriginta (дуодэтригинта)
XXIX (29) — undetriginta (ундэтригинта)
XXX (30) — triginta (тригинта)
XL (40) — quadraginta (квадрагинта)
L (50) — quinquaginta (квинквагинта)
LX (60) — sexaginta (сэксагинта)
LXX (70) — septuaginta (сэптуагинта)
LXXX (80) — octoginta (октогинтна)
XC (90) — nonaginta (нонагинта)
C (100) — centum (центум)
CC (200) — ducenti (дуценти)
CCC (300) — trecenti (трэценти)
CD (400) — quadrigenti (квадригэнти)
D (500) — quingenti (квингэнти)
DC (600) — sexcenti (сэксценти)
DCC (700) — septigenti (сэптигэнти)
DCCC(800) — octingenti (октигенти)
CM (DCCCC) (900) — nongenti (нонгэнти)
M (1000) — mille (милле)
MM (2000) — duo milia (дуо милиа)
V (5000) — quinque milia (квинквэ милиа)
X (10000) — decem milia (дэцем милиа)
XX (20000) — viginti milia (вигинти милиа)
C (1000000) — centum milia (центум милиа)
XI (1000000) — decies centena milia (дэциэс центэна милиа)»
Елена Долотова.
В современном мире арабские цифры считаются общепризнанным стандартом исчисления. Десятичная система знаков используется для подсчетов и нумерации во всех развитых странах мира. При этом от римских цифр, которые использовались в непозиционной системе счисления древних римлян, полностью не отказались. Часто можно видеть, что с их помощью нумеруются разделы в книгах, отмечаются века в исторической литературе, указывается группа крови и многие другие параметры, для которых обозначение римскими цифрами стало стандартным.
При работе за компьютером с браузером, текстовыми редакторами и другими приложениями может понадобиться ввести некоторые значения римскими цифрами. Отдельный цифровой блок с ними отсутствует на стандартном устройстве ввода, но есть сразу несколько способов, как написать римские цифры на клавиатуре быстро.
Римские цифры на клавиатуре в любом приложении
Лишь малая часть разработчиков приложений предусматривают удобные способы ввода в своих продуктах римских цифр при помощи клавиатуры. Большая часть программ не имеет специальной функциональности для работы с непозиционной системой счисления, что требует проявления смекалки от пользователя для ввода римских цифр в них. Можно выделить два удобных способа, как ввести римские цифры с клавиатуры в любой программе.
Большая часть программ не имеет специальной функциональности для работы с непозиционной системой счисления, что требует проявления смекалки от пользователя для ввода римских цифр в них. Можно выделить два удобных способа, как ввести римские цифры с клавиатуры в любой программе.
Замена римских цифр английскими буквами
На любом компьютере по умолчанию одним из доступных языков является английский. На него можно быстро переключиться за счет комбинации клавиш Alt+Shift или Windows+Пробел (в Windows 10). Английский алфавит полностью закрывает потребность в отдельной цифровой клавиатуре для ввода римских цифр, поскольку все их аналоги могут быть набраны с его помощью заглавными буквами.
Следующие буквы английского алфавита заменяют римские цифры:
- 1 – I;
- 5 – V;
- 10 – X;
- 50 – L;
- 100 – C;
- 500 – D;
- 1000 – M.
Еще в школе обучают, каким образом необходимо использовать римские цифры, чтобы вводить различные цифры. Принцип простой: до нужного числа добираются римские цифры максимально большие подходящие в данной ситуации.
Принцип простой: до нужного числа добираются римские цифры максимально большие подходящие в данной ситуации.
Например:
Чтобы ввести число 33, потребуется использовать 10+10+10+1+1+1.
Соответственно, в римской вариации число 33 будет записано следующим образом: XXXIII.
Также имеются некоторые особые правила ввода римских цифр, позволяющие укоротить написание больших чисел.
Использование ASCII-кодов для ввода римских цифр
В операционной системе Windows поддерживаются ASCII-коды, предназначенные для ввода различных символов. Они могут использоваться, в том числе, для ввода римских цифр.
ASCII – это американская таблица кодирования, в которой приведены самые популярные печатные и непечатные символы в виде цифровых комбинаций. Чтобы использовать символы из данной таблицы на стандартной клавиатуре для ввода римских цифр, необходимо применить цифровой блок NUM – расположенный в правой части клавиатуры.
Активируйте работу дополнительного цифрового блока при помощи кнопки Num Lock. После этого зажмите левый ALT на клавиатуре и вводит комбинации римских цифр на правом цифровом блоке. После ввода каждого символа, нужно отпустить ALT, чтобы символ отобразился в поле для ввода. Далее вновь ALT требуется зажать и можно вводить следующий символ.
После этого зажмите левый ALT на клавиатуре и вводит комбинации римских цифр на правом цифровом блоке. После ввода каждого символа, нужно отпустить ALT, чтобы символ отобразился в поле для ввода. Далее вновь ALT требуется зажать и можно вводить следующий символ.
Следующие комбинации дополнительного цифрового блока идентичны римским цифрам:
- ALT+73 – I;
- ALT+86 – V;
- ALT+88 – X;
- ALT+76 – L;
- ALT+67 – C;
- ALT+68 – D;
- ALT+77 – M.
Способ ввода римских цифр с использованием ASCII-кодов нельзя назвать удобным, но он может применяться, например, когда по тем или иным причинам отключена английская раскладка на клавиатуре.
Как напечатать римские цифры в Word
Компания Microsoft при разработке офисного пакета и приложения Word учла, что пользователям, которые работают с текстами, может потребоваться ввести римские цифры. Поскольку делать это с помощью английской раскладки или ASCII-кодов не особо удобно, корпорация Microsoft ввела в Word поддержку специальной команды, автоматически переводящей арабские цифры в римские.
Римские цифры, придуманные более 2500 лет тому назад, использовались европейцами на протяжении двух тысячелетий, затем были вытеснены арабскими цифрами. Римскими цифры также используются при написании порядковых номеров монархов, энциклопедических томов, валентности различных химических элементов. На циферблатах ручных часов также часто используются цифры римской системы исчисления. Римские цифры представляют собой определенные знаки, с помощью которых записывают десятичные разряды и их половины. Используют для этого всего семь заглавных букв латинского алфавита. Числу 1 соответствует римская цифра I, 5 – V, 10 – X, 50 – L, 100 – C, 500 – D, 1000 – M. При обозначении натуральных чисел эти цифры повторяются. Так 2 можно написать, используя два раза I, то есть 2 – II, 3 — три буквы I, то есть 3 – III. В случае, когда большая цифра стоит впереди меньшей, их складывают, например 6 записывается в римской системе, как VI (то есть 5+1). Если Вы привыкли записывать числа арабскими цифрами, то могут возникнуть некоторые затруднения в том случае, когда нужно записать века римскими цифрами, какое-либо число или дату. Перевести любое число из арабской системы в римскую систему исчисления и наоборот можно очень легко и очень быстро, воспользовавшись удобным конвертером на нашем сайте. На клавиатуре компьютера достаточно перейти на английский язык, чтобы без труда записать любое число римскими цифрами. По всей видимости, древние римляне отдавали предпочтение прямым линиям, поэтому все их цифры прямые и строгие. Однако, римские цифры представляют собой ни что иное, как упрощенное изображение пальцев человеческой руки. | ||||||||||||||||
| Код | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Значение | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 50 | 100 | 500 | 1 000 |
| U+2160 | Ⅰ 2160 | Ⅱ 2161 | Ⅲ 2162 | Ⅳ 2163 | Ⅴ 2164 | Ⅵ 2165 | Ⅶ 2166 | Ⅷ 2167 | Ⅸ 2168 | Ⅹ 2169 | Ⅺ 216A | Ⅻ 216B | Ⅼ 216C | Ⅽ 216D | Ⅾ 216E | Ⅿ 216F |
| U+2170 | ⅰ 2170 | ⅱ 2171 | ⅲ 2172 | ⅳ 2173 | ⅴ 2174 | ⅵ 2175 | ⅶ 2176 | ⅷ 2177 | ⅸ 2178 | ⅹ 2179 | ⅺ 217A | ⅻ 217B | ⅼ 217C | ⅽ 217D | ⅾ 217E | ⅿ 217F |
| Значение | 1 000 | 5 000 | 10 000 | — | — | 6 | 50 | 50 000 | 100 000 | |||||||
| U+2160! U+2180 | ↀ 2180 | ↁ 2181 | ↂ 2182 | Ↄ | ↄ | ↄ | ↄ | ↄ | ↄ | |||||||
Символы в диапазоне U+2160-217F присутствуют только для совместимости с другими стандартами, которыми определены эти символы. В обиходе применяются обычные буквы латинского алфавита. Отображение таких символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы.
В обиходе применяются обычные буквы латинского алфавита. Отображение таких символов требует наличия программного обеспечения, поддерживающего стандарт Юникод, и шрифта, содержащего соответствующие этим символам глифы.
Римская цифра IIII на циферблатах часов
Римские цифры – классический элемент дизайна циферблата часов. Практически все исторические модели содержали на своих циферблатах римские цифры. Однако владельцы часов с римскими цифрами могли заметить что-то необычное. В то время как цифра 4 обычно имеет вид «IV» в римской цифровой системе, большинство часов отображают на месте четверки «IIII». Как всегда, нет единого ответа на этот вопрос, но все же есть некоторые возможные объяснения этого абсурдно важного вопроса.
Римская цифровая система больше не имеет широкого применения. Большинство западных стран используют арабские цифры, азиатские страны имеют собственную цифровую систему, а арабская культура использует свою систему, отличную от классических арабских цифр. Однако в часовом деле римские цифры использовались и все еще продолжают использоваться при оформлении циферблатов.
Однако в часовом деле римские цифры использовались и все еще продолжают использоваться при оформлении циферблатов.
Владельцы антикварных карманных часов или современных часов Glashütte Original, Lange, Ulysse Nardin, Blancpain, Cartier или даже Rolex могли заметить, что 4-я цифра на циферблате, обозначающая 4 часа, не написана в традиционном римском стиле. В большинстве случаев изображен символ «IIII». Конечно, есть исключения из правила, как, например, Биг Бен в Лондоне. Однако на большинстве циферблатов 4 часа изображено с «IIII».
Интересно понять, почему мир часового искусства почти единодушно решил переключиться на число IIII вместо привычного числа IV. Обычно римские цифры записываются следующим образом: I, II, III, IV, V, VI, VII, VIII, IX, X, XI, XII и т. д. Римские цифры возникли в древнем Риме, примерно в 1000 г. до н.э., и оставались обычным способом записи цифр по всей Европе в позднем Средневековье, задолго до упадка Римской Империи. Только в 14 веке римские цифры стали заменяться современными и более удобными арабскими цифрами. Числа в римской системе представлены комбинациями букв латинского алфавита. Упадок римских цифр совпадает с упадком латыни и появлением Ренессанса.
Только в 14 веке римские цифры стали заменяться современными и более удобными арабскими цифрами. Числа в римской системе представлены комбинациями букв латинского алфавита. Упадок римских цифр совпадает с упадком латыни и появлением Ренессанса.
Однако, хотя в настоящее время широко признано, что число 4 должно быть написано в виде IV, оригинальный и самый древний образец римских цифр был не таким, каким мы знаем его сегодня. Самые ранние модели фактически использовали VIIII для 9 (вместо IX) и IIII для 4 (вместо IV). Однако эти две цифры оказались проблематичными, их легко путали с III и VIII. Вместо оригинальной добавочной нотации римская цифровая система изменилась на более привычную субтрактивную нотацию.
Первые механические часы были созданы в Европе в 13 веке в то время, когда все еще использовались римские цифры. Большинство часов были установлены на церквях, а латынь была официальным католическим языком. Таким образом, для большинства древних часов характерны римские цифры на их циферблатах. Тем не менее, причина, по которой часовые мастера решили использовать IIII вместо IV, когда это уже стало неактуальным, остается неясным.
Тем не менее, причина, по которой часовые мастера решили использовать IIII вместо IV, когда это уже стало неактуальным, остается неясным.
Пока римляне не изобрели механические часы, они использовали концепцию солнечных часов, основанных на теневых часах в древней вавилонской астрономии (около 1500 г. до н.э.). Не стоит забывать, что часовое дело – наследие астрономии. В Риме были найдены античные солнечные часы с выгравированными римскими цифрами: и с IV, и с IIII.
Одной из причин, по которым в то время использовалась IIII, является римская мифология. Тогда самым почитаемым божеством Рима был Юпитер, бог неба и грома, царь среди богов в древнеримской религии. На латыни Юпитер был записан IVPPITER. Римляне, возможно, не решались выгравировать часть имени своего высшего божества на солнечных часах или напечатать в книгах. Вот почему число IIII, хотя и неудобное, возможно, было предпочтительнее IV. Хотя солнечные часы устарели с появлением часового дела, число IIII могло быть использовано только ради традиции.
Хотя субтрактивная нотация теперь широко применяется для римских цифр, ее использование наступало постепенно, и у ранних часовщиков все еще был выбор: использовать или не использовать IV.
Как уже упоминалось, ранние часы устанавливались на башнях церквей, где каждый житель города мог узнать время. В Древние времена и Средневековье только небольшая часть населения умела писать, читать и вычислять. Поэтому использование IIII вместо IV казалось более простым к пониманию. В то время как для IV требуется математика, базовая, но все же. Цифра IIII была куда более простой и понятной для значительной части необразованного европейского населения. Кроме того, могла возникнуть путаницу между IV и VI, а также между IX и XI. Вот почему на некоторых часах число девять написано в виде VIIII.
Также можно выдвинуть гипотезу о «ленивом часовщике». В часах, где применялся способ отливки цифр, IIII вместо IV и VIIII вместо IX могло бы существенно облегчить задачу мастеру. Таким образом, получаются цифры: I, II, III, IIII, V, VI, VII, VIII, VIIII, X, XI, XII. Это означает, что можно создать меньше форм, так как будет использоваться одна и та же основная форма для четырех первых цифр и одна и та же основная форма для чисел от VI до VIIII. Требуется только три формы: первая форма в виде IIII, которая была частично заполнена для создания чисел I, II, III и IIII, вторая — в форме VIIII, используемая для создания чисел V, VI, VII, VIII и VIIII и последняя, в виде XII, используемая для обозначения числа X, XI и XII. Хотя это не самая убедительная теория.
Таким образом, получаются цифры: I, II, III, IIII, V, VI, VII, VIII, VIIII, X, XI, XII. Это означает, что можно создать меньше форм, так как будет использоваться одна и та же основная форма для четырех первых цифр и одна и та же основная форма для чисел от VI до VIIII. Требуется только три формы: первая форма в виде IIII, которая была частично заполнена для создания чисел I, II, III и IIII, вторая — в форме VIIII, используемая для создания чисел V, VI, VII, VIII и VIIII и последняя, в виде XII, используемая для обозначения числа X, XI и XII. Хотя это не самая убедительная теория.
Более современная теория описывает французского короля Луи XIV. Этот французский монарх получил прозвище Луи Ле Гранд (Луи Великий) или Ле Рой Солейль (Солнечный король). Один из самых могущественных французских монархов, он объединил систему абсолютного монархического правления во Франции со всей политической и религиозной системой, вращающейся вокруг его фигуры — концепции божественного права королей, создающей централизованное государство, которое позже приведет к французской революция (при Людовике XVI). По тем же причинам, что и латинское написание имени Юпитер включало IV, король Людовик XIV предпочел IIII в оформлении часов. Будучи представителем Бога на Земле, часть его имени не могла быть напечатана на циферблате простых часов. Однако эта теория кажется весьма неправдоподобной. Использование IIII существовало в других землях с разными монархами, чьи имена не содержали букв IV. Это, по-видимому, не является достаточным объяснением, чтобы отказаться от субтрактивной нотации.
По тем же причинам, что и латинское написание имени Юпитер включало IV, король Людовик XIV предпочел IIII в оформлении часов. Будучи представителем Бога на Земле, часть его имени не могла быть напечатана на циферблате простых часов. Однако эта теория кажется весьма неправдоподобной. Использование IIII существовало в других землях с разными монархами, чьи имена не содержали букв IV. Это, по-видимому, не является достаточным объяснением, чтобы отказаться от субтрактивной нотации.
Последнее возможное объяснение является наиболее рациональным из всех и наиболее правдоподобным. Одной из причин использования IIII вместо IV может быть установление большего визуального баланса. IIII может обеспечить лучший визуальный баланс для цифры VIII, находящейся на другой стороне циферблата. Как в современных, так и в старинных часах присутствует как аддитивная, так и субтрактивная нотация (где 4 — IIII, а 9 — IX). Таким образом, циферблат имеет следующие цифры: I, II, III, IIII, V, VI, VII, VIII, IX, X, XI, XII. С помощью этой комбинации вы получаете три области на циферблате, в каждой из которых используются одинаковые цифры. Первая треть использует только I, вторая — использует V, и, наконец, последняя третья, которая показывает цифры с X. Таким образом, происходит балансировка циферблата с тремя отдельными областями. Современные часовые мануфактуры также используют IIII и IV на свое усмотрение и в наши дни.
С помощью этой комбинации вы получаете три области на циферблате, в каждой из которых используются одинаковые цифры. Первая треть использует только I, вторая — использует V, и, наконец, последняя третья, которая показывает цифры с X. Таким образом, происходит балансировка циферблата с тремя отдельными областями. Современные часовые мануфактуры также используют IIII и IV на свое усмотрение и в наши дни.
3000 до н.э. — 12 век
3000 лет до н.э.
В древнем Вавилоне были изобретены первые счёты – абак.
1680-1620 до н.э.
Египет. Ахмес.
Ахмес был писцом, составившим так наз. «Папирус Ринда». Этот документ, найденный шотландским египтологом Генри Риндом (Henry Rhind) в 1858 г., остается основным источником информации по математике древнего Египта. Он содержит чертежи треугольников с указаниями углов и формулами нахождения площадей, а также показывает деление числа 2 на нечётные числа от 3 до 101 в дробях и деление чисел от 1 до 9 на 10.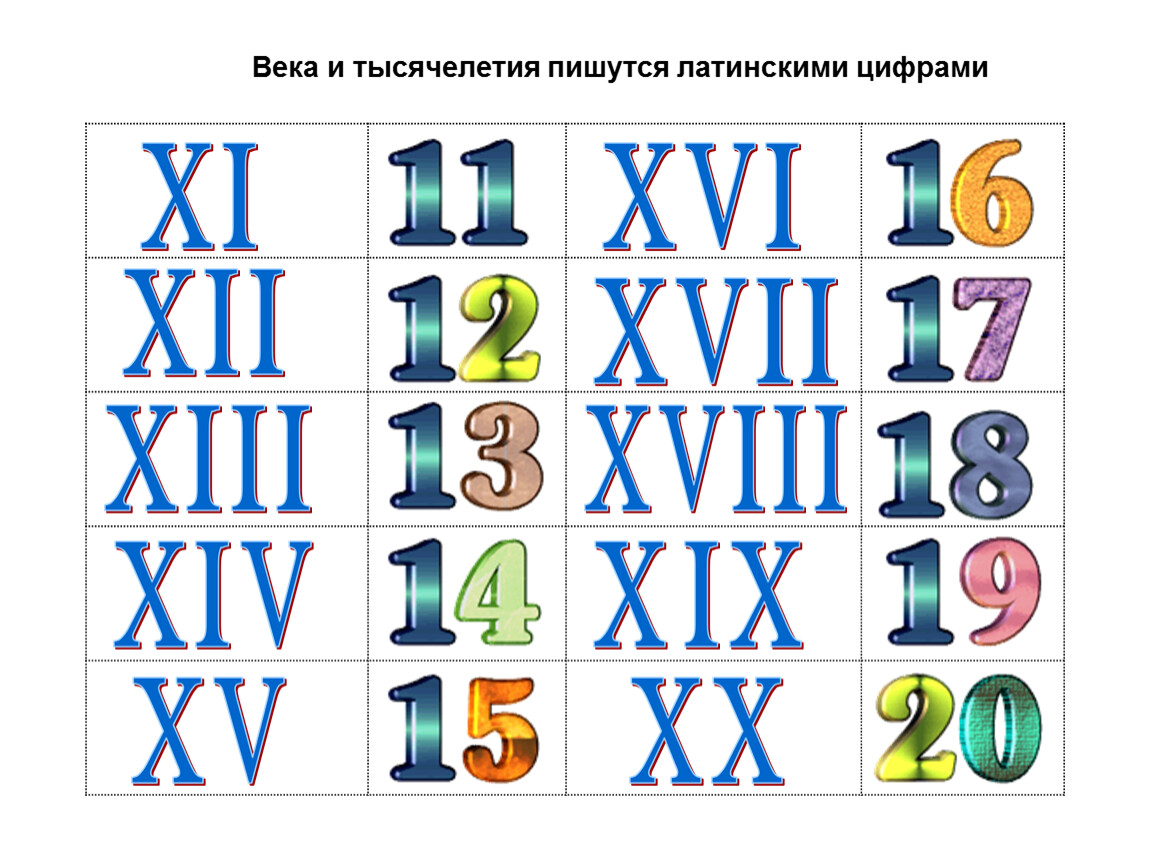 В нём также имеется 87 задач на четыре действия арифметики, решение уравнений, прогрессии, вычисление объемов зернохранилищ, правило двух третей и т. д. В честь Ахмеса этот документ также называют « Папирус Ахмеса », однако сам он указывал, что записи составлены по более ранним материалам, относящимся примерно к 2000 до н. э.
В нём также имеется 87 задач на четыре действия арифметики, решение уравнений, прогрессии, вычисление объемов зернохранилищ, правило двух третей и т. д. В честь Ахмеса этот документ также называют « Папирус Ахмеса », однако сам он указывал, что записи составлены по более ранним материалам, относящимся примерно к 2000 до н. э.
639-548 гг. до н.э.
Греческий философ Талий, изучив в Александрии достижения египетской науки (в основном геометрии), начал их распространение в Греции.
500 лет до н.э.
Появился абак, напоминающий современные счеты с косточками на проволоке.
409-325 гг. до н.э.
Диофант ввёл в употребление знак равенства и впервые использовал символический язык алгебры.
4 век до н.э.
Аристотель заложил основы математической логики. Он ввел понятие переменной в логике, применил буквы для обозначения понятий. После его работ, считавшихся верхом совершенства, в логике почти два тысячелетия наблюдался застой.
После его работ, считавшихся верхом совершенства, в логике почти два тысячелетия наблюдался застой.
300 лет до н.э.
Евклид в одной из древнейших математических книг «Элементы» привел систематическое построение теории чисел.
276-195 гг. до н.э.
Эратосфен предложил метод нахождения простых чисел, названный впоследствии «решетом Эратосфена».
262-190 гг. до н. э.
Греция. Аполлоний из Пегры
Греческий математик, известный как «Великий геометр», оказавший большое влияние на развитие математики. В его известной книге «Конусы» введены термины парабола, гипербола и эллипс .
85 -165 н. э.
Александрия (Египет в составе Римской империи).
Клавдий Птолемей (Claudius Ptolemey)
Наиболее влиятельный греческий астроном и географ своего времени. Птолемей выдвинул геоцентрическую теорию строения вселенной, принимавшуюся в течение почти 1400 лет. В ней он приводит математическую часть, содержащую тригонометрические методы, основанные на функции, родственной синусу, и их варианты [аналоги sin(a+b), sin(a-b), sin a/2], описывает 360-угольную аппроксимацию круга, приближенное число «Pi» (3,14166), квадратный корень из числа 3 (=1,73205) и т. д. Его работы в дальнейшеи оказали огромное влияние арабских и европейских математиков.
В ней он приводит математическую часть, содержащую тригонометрические методы, основанные на функции, родственной синусу, и их варианты [аналоги sin(a+b), sin(a-b), sin a/2], описывает 360-угольную аппроксимацию круга, приближенное число «Pi» (3,14166), квадратный корень из числа 3 (=1,73205) и т. д. Его работы в дальнейшеи оказали огромное влияние арабских и европейских математиков.
500 г. н. э
Индия. Первое из известных применений десятичной системы исчисления.
Ариабата Старший (первый)
Основной письменный труд Ариабаты – «Ариабатья» – суммирует математические познания Индии вплоть до 6 в. н. э. Он указывает, что написал книгу в 499 г . в возрасте 23 лет. Книга состоит из 118 стихов на астрономические темы (индийская традиция – писать в стихотворной форме) , включая 66 математических правил, модели планет и определение времени, описание небесной сферы и затмений. Ариабата писал о вращении Земли вокруг своей оси, что создает видимость движения небесных тел. Его математическая часть включает арифметику, алгебру, геометрию, в том числе и тригонометрию. Она также содержит суммы степенных рядов, дроби, квадратные уравнения и таблицу синусов. Он писал о нахождении наименьшего общего кратного и определил число «Pi» как 3,1416 (с высокой точностью). Спецификой его трактатов было обозначение цифр (от 1 до 9 и количества десятков —20, 30 и тд.) 33 согласными индийского алфавита, а для обозначения сотен и кратных им добавлялись гласные. Такая буквенная запись позволяла представить числа до 10 в 18 степени, но была более громоздкой чем десятичная. Впрочем, Ариабата почти наверняка был знаком с понятием нуля и позиционной системой обозначения разрядов. Длину земной окружности он определил как 24 835 англ. миль (современные данные — 24 902 англ. миль) и длину года 365 дней 6 ч 12 мин и 30 с (на самом деле 365 дней и менее 6 ч).
Его математическая часть включает арифметику, алгебру, геометрию, в том числе и тригонометрию. Она также содержит суммы степенных рядов, дроби, квадратные уравнения и таблицу синусов. Он писал о нахождении наименьшего общего кратного и определил число «Pi» как 3,1416 (с высокой точностью). Спецификой его трактатов было обозначение цифр (от 1 до 9 и количества десятков —20, 30 и тд.) 33 согласными индийского алфавита, а для обозначения сотен и кратных им добавлялись гласные. Такая буквенная запись позволяла представить числа до 10 в 18 степени, но была более громоздкой чем десятичная. Впрочем, Ариабата почти наверняка был знаком с понятием нуля и позиционной системой обозначения разрядов. Длину земной окружности он определил как 24 835 англ. миль (современные данные — 24 902 англ. миль) и длину года 365 дней 6 ч 12 мин и 30 с (на самом деле 365 дней и менее 6 ч).
Ариабата трудился неподалеку от города Пталипутра – тогдашней столицы империи Гупта в северной части Индии. Это был оживленный центр международных торговых путей что облегчало общение исламского мира с индийской научной школой. Его работы тщательно изучались такими известными исламскими учеными, как Бируни и др. В ХХ веке его именем был назван первый Индийский искусственный спутник земли «Ariabhata».
Его работы тщательно изучались такими известными исламскими учеными, как Бируни и др. В ХХ веке его именем был назван первый Индийский искусственный спутник земли «Ariabhata».
598—670 гг.
Индия. Брахмагупта
Брахмагупта был самым выдающимся индийским математиком своего времени. Он сделал открытия в астрономии, но самый главный вклад он внес в систему исчисления, включая алгоритмы извлечения квадратных корней и решения квадратных уравнений
735—804 гг.
Англия – Германия – Франция. Алкуин из Йорка (Alcuin of York)
Алкуин — английский математик (один из немногих образованных людей средневековой Европы) написавший простейшие тексты по основам арифметики, геометрии и астрономии. Он происходил из знатной семьи и учился в школе архиепископа Эгберта (Ecgberht) при кафедральном соборе Йорка. По окончании остался её учителем, а с 778 г . директором, собрав там одну из лучших библиотек и сделав саму школу одним из важнейших учебных центров Европы. В 781 г. он переехал в Германию, в Аахен — столицу короля франков Карла Великого, создателя Священной Римской Империи, стремившегося возродить Европу после эпохи варварства и продолжить триумф Римской цивилизации. Карл очень заботился не только о военных успехах, но и о просвещении, сам занимался улучшением алфавита и старался привлечь в Аахен ведущие научные силы. Алкуин прибыл на организованную Карлом в Аахене встречу европейских ученых и в 782 г. был назначен там главой придворной Аахенской школы. Он развил идею Карла, составив так называемый шрифт Каролингов с ясным, удобным написанием букв, легший в основу современного европейского (латинского) алфавита.
В 781 г. он переехал в Германию, в Аахен — столицу короля франков Карла Великого, создателя Священной Римской Империи, стремившегося возродить Европу после эпохи варварства и продолжить триумф Римской цивилизации. Карл очень заботился не только о военных успехах, но и о просвещении, сам занимался улучшением алфавита и старался привлечь в Аахен ведущие научные силы. Алкуин прибыл на организованную Карлом в Аахене встречу европейских ученых и в 782 г. был назначен там главой придворной Аахенской школы. Он развил идею Карла, составив так называемый шрифт Каролингов с ясным, удобным написанием букв, легший в основу современного европейского (латинского) алфавита.
Эта работа имела почти решающее значение для сохранения уцелевших греческих трудов по математике, поскольку в IX в. их начали переписывать для удобства чтения. Большинство из дошедших до нас античных математических документов сохранилось именно в «Аахенском варианте». Алкуин стал другом Карла и учителем его детей, однако в 796 г . он уехал во Францию, в Тур, где и работал до конца жизни. Для большей доходчивости он оформлял свои научные трактаты в виде диалогов (вопросов и ответов) — классический приём, использовавшийся ещё Сократом, Платоном и др. Алкуин дал импульс к развитию математики, написав элементарные тексты по арифметике, геометрии и астрономии «…на заре Возрождения, одной из движущих сил которого стал он сам».
он уехал во Францию, в Тур, где и работал до конца жизни. Для большей доходчивости он оформлял свои научные трактаты в виде диалогов (вопросов и ответов) — классический приём, использовавшийся ещё Сократом, Платоном и др. Алкуин дал импульс к развитию математики, написав элементарные тексты по арифметике, геометрии и астрономии «…на заре Возрождения, одной из движущих сил которого стал он сам».
VIII — XII вв.
Несмотря на некоторое оживление в Европе основное развитие математики и вычислений переносится на Исламский Восток, где изучается греческое и индийское наследие и делаются новые открытия.
Около 800 г.
В Китае, вероятно под влиянием Индии, используется 0.
790—840 гг.
Персия (Иран). Абу Джафар Мухаммад ибн Муса Аль-Хорезми.
Аль-Хорезми — персидский математик, предположительно происходивший из Хорезма (сам либо родители). Автор многочисленных, весьма важных исследований по индоарабской десятичной нумерации. Считается что Аль-Хорезми и предложил десятичную систему счисления в арабском мире. Он же стал одним из первых математиков, предложивших использовать знак «ноль» для обозначения десятичного разряда при записи. От имени Аль-Хорезми происходит и слово (понятие) алгоритм.
Считается что Аль-Хорезми и предложил десятичную систему счисления в арабском мире. Он же стал одним из первых математиков, предложивших использовать знак «ноль» для обозначения десятичного разряда при записи. От имени Аль-Хорезми происходит и слово (понятие) алгоритм.
Его фундаментальное исследование «Хисаб Аль-Джебр валь-Мукабала» подарило миру слово Алгебра и может считаться первым письменным трудом по алгебре.
800—860 гг.
Ирак (Багдад). Аль-Аббас ибн Саид Аль-Джавари
Основная работа Аль-Джавари состоит в написании комментариев к «Элементам» Евклида. Имя Аль-Джавари тесно связано с Домом Мудрости в Багдаде. Знаменитый халиф Гарун Аль — Рашид (правил в 786—809) стремился к развитию культуры и привлекал ко двору ученых. Его сын халиф Аль-Мамун продолжил дело отца и основал академию названную Домом Мудрости . В ней изучали работы греческих философов и собирали библиотеку манускриптов (первую после Александрийской), приобретая их в Византии. Среди работавших там ученых математиков были Аль-Хорезми, Аль-Кинди, Хунаин ибн Ишаг, Тхабит ибн Кура и братья Бану. Аль-Мамун также построил ряд обсерваторий
В ней изучали работы греческих философов и собирали библиотеку манускриптов (первую после Александрийской), приобретая их в Византии. Среди работавших там ученых математиков были Аль-Хорезми, Аль-Кинди, Хунаин ибн Ишаг, Тхабит ибн Кура и братья Бану. Аль-Мамун также построил ряд обсерваторий
805—873 гг.
Ирак (Багдад). Абу Юсуф Якуб ибн Ишаг Аль-Саббах Аль-Кинди
Аль-Кинди изучал и комментировал индийскую математику и писал о её системе исчисления, геометрии и оптике.
800—870 гг.
Ирак (Багдад). Братья Бану Мусса
Три брата-математика, вместе работавшие в «Доме Мудрости» — Багдадской академии. Их труды производят впечатление частей одного целого.
— Джафар Мухаммад Бану Мусса (800 — после 873). Лучший математик из братьев. Он внес заметный вклада в геометрию и написал трактат о конусах — критический анализ работы Аполлония «Конусы» («Conics»).
— Ахмад Бану Мусса (805—873) — писал о механике.
— Аль-Хасан Бану Мусса (810 — ок. 873) — писал об эллипсах.
808—873 гг.
Ирак (Багдад). Абу Заид Хунаин ибн Ишаг аль Ибади
Его наиболее важные математические работы — переводы трудов греческих математиков, сделавшие их доступными исламским учёным
820—880 гг.
Персия — Ирак. Абу Абд-Алла Мухаммад ибн Иса Аль-Махани
Аль-Махани известен своими работами по решению задач Архимеда, связанных с сечением сфер
830—890 гг.
Индия. Пртудакасвами (Prthudakasvami)
Известен серьезными работами по решению уравнений
835—912 гг.
Ирак — Египет. Ахмед ибн Юсуф аль Мизри
Ахмед ибн Юсуф — математик, написавший комментарии к Евклидовым «Элементам». Его работа оказала значительное влияние на последующее развитие математики в Европе
836—901 гг.
Ирак. Аль-Сабри Т(х)абит ибн Кура Аль-Харрани
Математик, внёсший вклад в теорию чисел, астрономию и статистику.
850—929 гг.
Ирак. Аль Батани ( Al-Battani, также известен как Albategnius, Albategni)
Аль Батани — исламский астроном и математик. Известен точными измерениями при изучении звезд, луны и планет. Его математические методы были использованы последующими астрономами
870—930 гг.
Индия (Бенгалия). Шридхара (Sridhara)
Шридхара много занимался практическими применениям алгебры и одним из первых вывел и доказал формулу решения квадратных уравнений
875—940 гг.
Иран — Ирак. Абуль Аббас Аль-Фадль ибн Хатим Аль-Найризи
Аль-Найризи — исламский математик, составивший объемные комментарии к работам Птолемея и Евклида
908—946 гг.
Ирак (Багдад). Ибрагим ибн Синан ибн Табит ибн Курра
Математик и астроном, изучавший геометрию, в особенности тангенсы углов в окружностях. Он внес вклад в развитие теории расчёта площадей.
920—980 гг.
Сирия (Дамаск). Абуль Хасан Ахмад ибн Ибрагим Аль-Уклидиши
Мусульманский математик, написавший две работы по арифметике. Он (предположительно) предвосхитил введение десятичных дробей.
920—1000 гг.
Индия. Ариабата (второй)
Ариабата был математиком и астрономом. Он первым составил таблицы синусов углов с точностью до пятого знака.
940—1000 гг.
Персия (Иран). Абу Саль Вайджан ибн Рустам Аль-Куи
Ведущий исламский математик, возрождавший и развивавший греческую геометрию.
9-10 век
В Европе ширится распространение арабских цифр, а также понятий нуль и позиционность. Постепенно арабские цифры вытесняют римские, но окончательно это произойдет лишь в XVII веке.
Постепенно арабские цифры вытесняют римские, но окончательно это произойдет лишь в XVII веке.
953—1029 гг.
Ирак (Багдад). Абу Бекр ибн Мухаммад ибн Аль-Хуссайн Аль-Караджи
Аль-Караджи — подробно писал о работах предшествовавших математиков. Он считается первым ученым, освободившим алгебру от геометрических операций, заменив их действиями, составляющими основу современной алгебры
973—1048 гг.
Персия (Иран). Абу Арраян Мухаммад ибн Ахмад Аль-Бируни
Бируни – одна из самых выдающихся фигур в исламской математике. Он внёс значительный вклад в астрономию, математику, физику, медицину и историю.
980—1037 гг.
Ирак. Абу Мансур ибн Тахир Аль-Багдади
Исламский математик, составивший описание различных систем арифметики в работе, имевшей принципиально важное значение в истории математики.
989—1079 гг.
Испания. Абу Абдалла Мухаммад ибн Аль-Джайани
Абу Абдалла Мухаммад ибн Аль-Джайани
Испанский (исламский) математик. Считается что Аль-Джайани родился в Кордове. В 1012-1017 он находился в Каире (Египет), а большую часть жизни провел в Хаене (Андалузия).
Аль-Джайани составил трактат «О соотношениях /пропорциях/» ( On ratio ) – важные комментарии к «Элементам» Евклида (к разделу называемому «книга V »). Это считается его важнейшей работой. Для определения понятия пропорция /соотношение/ он писал что основными понятиями геометрии являются число, линия, поверхность, угол и сплошная среда (твердое тело). Этот подход (число как геометрическая величина), необычный для предшествовавшей ему греческой мысли, понадобился Аль-Джайани определявшему понятие «пропорция» путем развития Арабской трактовки понятия «число». Он также написал первое исследование по сферической тригонометрии: «Книга о неизвестных дугах сферы».
Аль-Джайани явно испытывал большое уважение к астрономическим трудам Аль-Хорезми, свободно пользуясь данными его таблиц, но не соглашался с его астрологией, для которой он сам привлекал индийские источники.
Влияние трудов Аль-Джайани на европейских ученых весьма велико. Например многие детали его «Книги о неизвестных дугах сферы» можно найти в трудах по тригонометрии немецкого ученого Иоганна Мюллера Региомонтануса (1436-1476). С его трактовкой Евклида сходна трактовка предложенная английским математиком Исааком Барроу (1630 -1677), считавшимся первым европейским математиком правильно понявшим Евклида. Испанское влияние также сказалось и на интересах современника Аль-Джайани, ученого монаха Герберта д’Ауриллак (Папы Сильвестра II ) как и к наукам так и к астрологии (см. ниже).
Около 1000 г.
Зап. Европа — Ватикан
Архаичный абак модернизируется Гербертом (Gerbert d’Aurillac, 940 — 1003 г.) .
Герберт – французский монах, один из известнейших учёных средневековья, впоследствии римский Папа – Сильвестр II.
В 967 — 70 г. Герберт обучался в Барселоне под руководством местного епископа; знакомился с (индо- ) арабскими десятичными числами.
Герберт обучался в Барселоне под руководством местного епископа; знакомился с (индо- ) арабскими десятичными числами.
Эпоха «темного средневековья», наступившая после разорения Европы варварами, когда знание нескольких правил арифметики считалось признаком необыкновенной учёности, двигалась к своему завершению. Хозяйственная деятельность и торговля расширялись, приобретали большую организованность и выдвигали новые требования к искусству счёта.
Герберт разработал абак с 27 колонками костей (а также вспомогательными – дробными). Неизвестно, что было прототипом, египетский или римский абак (12 колонок), однако Герберт имел копию книги «Геометрия» Боэция – философа эпохи заката Рима. В любом случае абак Герберта был намного совершеннее: он имел «прогрессивную» конструкцию, обозначения латинскими буквами (цифрами) и позволял представлять десятичные числа до 10 в 27-й степени.
Хотя Герберт был искренним христианином, он не чуждался и астрологии. Он также писал работу в которой пытался доказать появление и деятельность Христа чисто научными методами.
Он также писал работу в которой пытался доказать появление и деятельность Христа чисто научными методами.
Став Папой, Герберт сохранил живой интерес к науке, что принесло немало затруднений: противники обвиняли его в связях с нечистой силой, поскольку Герберт умел делить слишком большие числа.
10 век
В Китае появляются счёты «Суань-Пан». Их поле разделено на две части: одна в пять костей, другая в две.
В России. Вместе с христианством здесь вводится письменность «Кириллица», разработанная, византийскими болгарами, братьями-монахами Кириллом и Мефодием. Согласно греческой традиции цифры в ней также обозначались буквами, что создавало большие неудобства при сложных математических расчетах.
| Календарь событий | 13 век — 16 век
Конвертер римских цифр— Число / Дата / Год
Поиск инструмента
Преобразование римских цифр
Инструмент для преобразования из / в римские цифры: система счисления с семью буквами (I, V, X, L, C, D и M), позволяющая записывать целые числа и используемая в Античном Риме и выполнять преобразования.
Результаты
Преобразование римских цифр— dCode
Тег (ы): Система счисления, История
Поделиться
dCode и другие
dCode является бесплатным, а его инструменты являются ценным подспорьем в играх, математике, геокэшинге, головоломках и задачах, которые нужно решать каждый день!
Предложение? обратная связь? Жук ? идея ? Запись в dCode !
Преобразование из / в римские цифры
Число римским шрифтом (II, IV, XIII ,…) или арабскими цифрами (2,4,13, …)MCMXCVIII 2021 06 04
Конвертировать
Ответы на вопросы (FAQ)
Какие буквы писать римскими цифрами?
В римской нумерации 7 букв соответствуют 7 цифрам. Таблица римских цифр от 1 до 1000:
За пределами нескольких тысяч букв для обозначения этих чисел нет.
Однако в некоторых архаичных сценариях (реже) использовалось 4 других символа
| Ɔ | 500 |
| ↀ | 1000 |
| ↁ | 5000 |
| ↂ | 10000 |
Как читать / писать римскими цифрами?
Римская цифра система использует два правила:
(1) — Любая буква $ L_2 $, помещенная справа от другой буквы $ L_1 $, добавляется, если $ L_2 \ leq L_1 $
Пример: VI = 5 + 1 = 6
XX = 10 + 10 = 20
(2) — Любая буква единицы $ L_1 = \ rm {I} $, помещенная непосредственно слева от другой буквы $ L_2 \ neq \ rm {I} $, вычитается.
Пример: IV = 5 — 1 = 4 IX = 10 — 1 = 9
Правило (2) иногда расширяется до: Любая буква $ L_1 $, помещенная непосредственно слева от другой буквы $ L_2> L_1 $, вычитается.
Пример: XC = 100 — 10 = 90
Пример:
| 1980, римскими цифрами | MCMLXXX | 1981, римскими цифрами | MCMLXXXI | ||
|---|---|---|---|---|---|
| 1982 in римскими цифрами | MCMLXXXII цифры | MCMLXXXIII | |||
| 1984 римскими цифрами | MCMLXXXIV | 1985 римскими цифрами | MCMLXXXV | ||
| 1986 римскими цифрами | MC41XX97 1987XVI | MCMLXXXVII | |||
| 1988, римские цифры | MCMLXXXVIII | 1989, римские цифры | MCMLXXXIX | ||
| 1990 дюймов римские цифры | MCMXC | ||||
| 1992 в римских цифрах | MCMXCII | 1993 в римских цифрах | MCMXCIII | ||
| 1994 в римских цифрах | MCMXCIV | 1995 в римских цифрах | CMC41 | ||
| 1996 в римских цифрах | MCMXCVI | 1997 в римских цифрах | MCMXCVII | ||
| 1998 в римских цифрах | MCMXCVIII | 1999 в римских цифрах | IXMCM | ||
| MM | 2001 римскими цифрами | MMI | |||
| 2002 римскими цифрами | MMII | 2003 римскими цифрами | MMIII | ||
| 2004 дюйм римские цифры | MMIV | 2005 римскими цифрами | MMV | ||
| 2006 римскими цифрами | MMVI | 2007 римскими цифрами | MMVII | ||
| 2008 римскими цифрами | MMVIII | 2009 римскими цифрами | MMIX | ||
| 2010 римскими цифрами | MMX | 2011 римскими цифрами | MMXI | ||
| 2012 римскими цифрами | MMXII | 2013 римскими цифрами | MMXIII | ||
| 2014 римскими цифрами | MMXIV | 2015 римскими цифрами | MMXV | ||
| 2016 римскими цифрами | MMXVI | 2017 римские цифры | MMXVII | 2018 римскими цифрами | MMXVIII | 2019 римскими цифрами | MMXIX |
| 2020 римскими цифрами | MMXX | 2021 римскими цифрами | MMXXI | ||
| MMXXII | 2023 римскими цифрами | MMXXIII | |||
| 2024 римскими цифрами | MMXXIV | 2025 римскими цифрами | MMXXV | 2044MMXXVI | 2027 римскими цифрами | MMXXVII |
| 2028 римскими цифрами | MMXXVIII | 2029 римскими цифрами | MMXXIX | 2029 цифрыMMXXX | 9009 7 2031 римскими цифрамиMMXXXI |
| 2032 римскими цифрами | MMXXXII | 2033 римскими цифрами | MMXXXIII |
Как работает преобразователь римских цифр в / в?
Программа автоматически определяет, является ли число арабским или римскими цифрами и выполняет преобразование / перевод.
Римская нумерация не позволяет писать большие числа, после 9999 программа будет отображать тысячи отдельно. Это письмо не стандартизировано, но остается понятным.
Программа очень разрешающая и разрешает плохо сформированные римские числа, не соответствующие правилу (2).
Пример: IVX переводится как 6
Как написать ноль (0) римскими цифрами?
Римляне не использовали ноль, для них это была не цифра, а состояние пустоты, поэтому они не писали его.
dCode записывает либо ??, либо 0.
Как написать четыре (4) римскими цифрами?
Четыре написано как IV, однако это программное обеспечение показало, что IIII = 4, необычно, IIII — это вариант IV, который допустим. Его можно найти сегодня (обычно в часах или часах).
Как написать дату римскими цифрами?
Нет специального способа записать дату (или дату рождения), за исключением записи числа дня, месяца и года отдельно.
Пример: 12.06.2008 = XII / VI / MMVIII
dCode имеет инструмент для записи даты на латыни.
Какое наибольшее число римскими цифрами?
Числа выше 10 000 невозможно представить без каких-либо инструментов расчета, они бесполезны. Если вы хотите записать значение в сотни тысяч, можно представить, что в начале числа написаны сотни М.
Пример: 9999 = MMMMMMMMMCMXCIX (немного смешно)
Как записать отрицательное число римскими цифрами?
Негативная запись не распознается, вероятно, ее не было.Понятие положительного или отрицательного числа связано с понятием нуля (которое не было известно римлянам).
Однако сегодня добавление — может помочь понять.
Пример: -XXV = -25
Как записать десятичное число римскими цифрами?
Использование десятичных чисел очень мало задокументировано в учебниках истории, однако вполне вероятно, что они использовали дроби, в том числе двенадцатеричную денежную систему (основание 12), которая позволяла делить числа на 2, 3, 4, 6 и 12 без десятичных знаков.
Когда были изобретены римские цифры?
Римские цифры родились с Античным Римом, начиная с 7 века до нашей эры. Например, они использовались с латынью.
Как писать римские цифры в Юникоде?
Римские цифры были добавлены в стандарт Unicode, они кодируют одним символом каждое число от 1 до 12 (используется в часах и часах) и 8 других чисел:
| Символ Unicode | Значение | Символ Unicode | Значение | Символ Unicode | Значение |
|---|---|---|---|---|---|
| Ⅰ | 1 | Ⅱ | 2 | Ⅲ | 3 |
| Ⅳ | 4 | Ⅴ | 5 | Ⅵ | 6 |
| Ⅶ | 7 | Ⅷ | 8 | Ⅸ | 9 |
| Ⅹ | 10 | Ⅺ | 11 | Ⅻ | 12 |
| Ⅼ | 50 | Ⅽ | 100 | Ɔ | 500 |
| Ⅾ | 500 | ↀ | 1000 | Ⅿ | 1000 9004 1 |
| ↁ | 5000 | ↂ | 10000 |
Когда использовать римские цифры?
Римские цифры изучаются в начальной школе, но используются редко, за исключением математики или истории. Сегодняшнее использование ограничено часами, датами, но также и татуировками, многие татуировки используют римские цифры .
Сегодняшнее использование ограничено часами, датами, но также и татуировками, многие татуировки используют римские цифры .
Исходный код
dCode сохраняет за собой право собственности на исходный код онлайн-инструмента «Преобразование римских цифр». За исключением явной лицензии с открытым исходным кодом (обозначенной CC / Creative Commons / free), любой алгоритм, апплет или фрагмент «преобразования римских цифр» (конвертер, решатель, шифрование / дешифрование, кодирование / декодирование, шифрование / дешифрование, переводчик) или любые «римские цифры». Функция преобразования чисел (вычисление, преобразование, решение, дешифрование / шифрование, дешифрование / шифрование, декодирование / кодирование, перевод), написанная на любом информационном языке (Python, Java, PHP, C #, Javascript, Matlab и т. Д.)), и никакая загрузка данных, скрипт, копирование и доступ к API для «Преобразования римских цифр» не будут бесплатными, то же самое для автономного использования на ПК, планшете, iPhone или Android! dCode распространяется бесплатно и онлайн.
Нужна помощь?
Пожалуйста, посетите наше сообщество dCode Discord для получения помощи!
NB: для зашифрованных сообщений проверьте наш автоматический идентификатор шифра!
Вопросы / комментарии
Сводка
Похожие страницы
Поддержка
Форум / Справка
Ключевые слова
римская цифра, преобразовать, античный, век, арабский, рим, число, год, латынь
Ссылки
Источник: https: // www.dcode.fr/roman-numerals
© 2021 dCode — Идеальный «инструментарий» для решения любых игр / загадок / геокэшинга / CTF.Как средневековая Европа наконец отказалась от римских цифр
Есть такая шутка: римские цифры. Чем они хороши IV?
Это приятный каламбур с числами, но, честно говоря, римские цифры не годятся — просто попробуйте уплатить с них налоги. К шестому веку нашей эры (и, возможно, даже раньше) в Индии была разработана гораздо лучшая система, которая теперь называется индуистско-арабской системой счисления. Он использует только 10 цифр: от одного до девяти плюс ноль — и только эти цифры. Для 50, 100, тысячи или любого другого числа не нужен специальный символ — просто комбинации этих 10 цифр.
Он использует только 10 цифр: от одного до девяти плюс ноль — и только эти цифры. Для 50, 100, тысячи или любого другого числа не нужен специальный символ — просто комбинации этих 10 цифр.
Индо-арабская система — это система с указанием места, то есть положение цифры указывает ее значение. Итак, в числе 459 четверка представляет 400; пятерка означает 50. Построение чисел в столбцы позволяет быстро выполнять сложение и вычитание. Немного неся и заимствуя, и вы также хорошо разбираетесь в умножении и делении.
Это может показаться нам ослепляюще очевидным, поскольку это числовая система, которую мы используем сейчас, но она была не так понятна средневековым европейцам. Вплоть до 13 века им приходилось довольствоваться римскими цифрами. Римская система была хороша для записи количества вещей, но не очень полезна для манипулирования этими суммами. Счеты — или счетная рамка — были полезны, но ограничены. А для более сложных расчетов римские цифры были безнадежны. Это наложило серьезные ограничения на торговлю, коммерцию и особенно науку.
(Источник: FabrikaSimf / Shutterstock)
Между тем, культурам, которые использовали индуистско-арабскую систему, не только было легче справляться с базовой арифметикой, но они также могли выполнять более сложную математику. Это позволило им добиться больших успехов в алгебре и геометрии, в то время как европейцы усердно трудились с римскими цифрами.
Путешествие из Индии
Когда торговцы из Индии продвигались в Северную Африку, они взяли с собой свою систему счисления. К XII веку индуистско-арабская система была распространена в портах Средиземного моря.Арабские поселенцы принесли эту систему в Испанию, и несколько итальянских ученых открыли ее и использовали в своей научной работе. Но многие узнали об этом только в 1202 году, когда итальянский математик Леонардо Пизанский, которого мы знаем сегодня как Фибоначчи, известный своей теорией чисел и рядами Фибоначчи, написал книгу по математике под названием Liber Abbaci (Книга вычислений). ). В нем он призвал людей положить счет и использовать для расчетов индуистско-арабскую систему. И он показал им, как это сделать.Фибоначчи изучил систему в детстве, когда жил в Алжире. Будучи гением, он сразу увидел потенциал.
И он показал им, как это сделать.Фибоначчи изучил систему в детстве, когда жил в Алжире. Будучи гением, он сразу увидел потенциал.
Однако новая система прижилась не быстро. В течение многих лет книгу Фибоначчи читали и понимали в основном ученые, которые постепенно включали его учение в свои собственные книги. И даже тогда старая римская система — неуклюжая и ограниченная — работала достаточно хорошо для того, для чего она использовалась. Мало кто мог представить себе возможности, которые откроет новая система, а привычки трудно изменить.В конце концов, однако, индуистско-арабская система закрепилась в Европе.
Хотя для понимания и принятия индуистско-арабской системы потребовалось некоторое время, вызванные ею изменения были далеко идущими, изменив не только торговлю и науку, но и повседневную жизнь. Когда это стало стандартным методом обучения расчетам, оно дало обычным людям возможность осваивать и использовать возможности математики. В своей книге о Фибоначчи «Человек чисел: арифметическая революция Фибоначчи» математик Кейт Девлин писал: «То, что сделал [Фибоначчи], было не менее революционным, чем пионеры персональных компьютеров, которые в 1980-х годах взяли вычисления у небольшой группы« компьютерных типов ». ‘и сделали компьютеры доступными и доступными для всех.
‘и сделали компьютеры доступными и доступными для всех.
У нас есть индийские и арабские математики через Фибоначчи, которых мы должны благодарить за современную науку — и за то, что нам не нужно платить налоги римскими цифрами.
Римские цифры [Таблица и преобразователь]
Хотите узнать, как читать или писать любые числа, используя римские цифры? Или, может быть, вы просто хотите перевести какое-то конкретное число, которое вам интересно?
Здесь вы можете получить и то, и другое! Переведите любое число с помощью этого интерактивного конвертера или узнайте все, что нужно знать о римских цифрах, в статье ниже.Читать дальше.
Преобразователь
Диаграмма
| 1 | I |
| 2 | II |
| 3 | III |
| 4 | IV |
| 5 | V |
| 6 | VI |
| 7 | VII |
| 8 | VIII |
| 9 | IX |
| 10 | X |
| 11 | XI |
| 12 | XII |
| 13 | XIII |
| 14 | XIV |
| 15 | XV |
| 16 | XVI |
| 17 | XVII |
| 18 | XVIII |
| 19 | XIX |
| 20 | XX |
| 21 | XXI |
| 22 | XXII |
| 23 | XXIII |
| 24 | XXIV |
| 25 | XXV |
| 26 | XXVI |
| 27 | XXVII |
| 28 | XXVIII |
| 29 | XXIX |
| 30 | XXX |
| 50 | L |
| 100 | C |
| 500 | D |
| 1000 | M |
| 1 — 50… | |
| 1 — 100… | |
| 1 — 1000… | |
| 1 — 10000… | |
Как работают римские цифры
В отличие от современной (индуистско-арабской) системы счисления, у римлян не было цифр (0–9) для обозначения чисел, поэтому они использовали буквы для их кодирования. Это семь букв, используемых для написания римских цифр, и их соответствующее значение арабскими цифрами:
Это семь букв, используемых для написания римских цифр, и их соответствующее значение арабскими цифрами:
- I
- 1
- V
- 5
- Х
- 10
- L
- 50
- С
- 100
- D
- 500
- M
- 1000
Читать и писать римские цифры несложно. Вам просто нужно знать значение каждой буквы и пару простых правил.
Основное правило таково: чтобы прочитать римское число, просто сложите значения его букв:
- III
- 1 + 1 + 1 = 3
- VI
- 5 + 1 = 6
- XVII
- 10 + 5 + 1 + 1 = 17
- XX
- 10 + 10 = 20
Вычитающая нотация : В качестве исключения из приведенного выше правила, когда буква предшествует другой, имеющей большее значение, то это не сложение, а вычитание. Некоторые примеры:
- IV
- 5 — 1 = 4
- IX
- 10 — 1 = 9
- XIX
- 10 + (10 — 1) = 19
- XL
- 50-10 = 40
- СМ
- 1000–100 = 900
Чтобы записать любое число, просто переводите каждый десятичный знак отдельно слева направо: тысячи, сотни, десятки и единицы.
- 39
- 30 + 9 → XXX + IX → XXXIX
- 140
- 100 + 40 → C + XL → CXL
- 2018
- 2000 + 10 + 8 → MM + X + VIII → MMXVIII
Принцип краткости : Вы всегда должны использовать минимальное количество букв, необходимое для каждого десятичного разряда отдельно (но не для всего числа). Например:
- 5
-
IIIII→ V - 9
-
VIIII→ IX - 44
-
XXXXIIII→ XLIV - 95
-
ВК→ XCV - 999
-
IM→ CMXCIX
Теперь вы готовы пройти любую из наших викторин по римским цифрам.Вы можете выбрать один из трех уровней сложности:
Альтернативные формы
Хотя приведенные выше правила являются «стандартными» в настоящее время, в прошлом они не применялись последовательно. Например, можно найти древние документы и надписи с использованием нестандартных римских цифр, таких как IIII (4), IC (99), IIXX (18) или MDCCCCX (1910).
Например, можно найти древние документы и надписи с использованием нестандартных римских цифр, таких как IIII (4), IC (99), IIXX (18) или MDCCCCX (1910).
Миллионы римскими цифрами
Хотя римляне обычно не нуждались в большом количестве людей, они приняли для этого множество соглашений.Одной из самых популярных (по крайней мере, в средние века) была горизонтальная линия, или vinculum , умноженная на тысячу.
- В
- 5000
- Х
- 10 000
- L
- 50 000
- С
- 100 000
- D
- 500 000
- M
- 1 000 000
Некоторые авторы предполагают, что двойная линия, таким образом, представляет собой умножение на один миллион, хотя нет никаких свидетельств того, что она когда-либо использовалась на практике.Однако для удобства наш конвертер римских цифр следует этому соглашению (на случай, если вам действительно нужно переводить такие большие числа!).
А как насчет нуля?
В римской системе счисления не было конкретной римской цифры для нуля. Для этого они просто использовали слово nulla (нет), nihil (ничего) или просто букву N .
Как сегодня используются римские цифры?
Римские цифры использовались до высокого и позднего средневековья, когда арабские цифры постепенно были введены в западном мире.
В настоящее время римские цифры используются только в определенных контекстах, например:
- В череде одноименных пап, императоров или монархов ( Елизавета II, ). Они называются regnal номерами .
- Для обозначения династий в определенных культурах ( г., XVIII династия Египта г.).
- На памятниках или мемориальных досках для обозначения года.
- Для отметки часов на циферблатах.
- Для перечисления книг, томов, глав и т. Д., в литературных произведениях.

- Для нумерации страниц в предварительных главах книг (например, в прологе).
- Для повторяющихся мероприятий, таких как конгрессы, фестивали или чемпионаты ( Super Bowl LIII ).
- Несколько серий названий продуктов или названий фильмов ( Mac OS X , Rocky IV ).
- В качестве суффиксов поколений (например, Patrick II вместо Patrick Jr. ).
- За год в авторских правах на некоторые фильмы или телешоу (напр.г., © mmxviii).
В испанском языке есть два дополнительных использования:
- Столетия всегда записываются римскими цифрами ( 21 век → siglo xxi ).
- В коротких датах месяц можно записать римскими цифрами ( 25.12.2018 → 25 / XII / 2018 ).
Список литературы
римских цифр — история и использование
римских цифр — история и использованиеКак они работают
Использование букв для чисел
Римляне изображали числа, используя семь букв алфавита в качестве цифр I = 1
V = 5
X = 10
L = 50
C = 100
D = 500
M = 1000
В средневековых текстах и некоторых старопечатных книгах цифры написаны строчными буквами, и v часто заменяли u. В последней позиции числа вместо i можно использовать j. Таким образом, 18 могло быть написано xuiij, а не XVIII.
Эти замены особенно часто встречаются в курсивных шрифтах.
В последней позиции числа вместо i можно использовать j. Таким образом, 18 могло быть написано xuiij, а не XVIII.
Эти замены особенно часто встречаются в курсивных шрифтах.
Иногда M и D были написаны с использованием того, что я называю выше «глубоких скобок». Трудно показать эти используя шрифты, доступные на компьютере, но они были похожи на C и зеркальное отображение или перевернутое изображение C. Наборщики неправильно использовали шрифт вверх изобразить это.Я буду использовать обычные скобки, чтобы показать их. В некоторых примерах римская цифра M представлена буквой I. круглые скобки, таким образом, ( I ) . Вы можете видеть, как это быстро может привести вас к написанию М. Точно так же D иногда обозначается буквой I, за которой следует назад C, таким образом, я ) . Кажется, это используется, потому что оно представляет половину буквы М или 500. Опять же, если написать быстро, это будет D.
Эта надпись, найденная в Риме, читается как M D LXXXIII или
1583. |
| Здесь наборщик использовал перевернутый шрифт C для изображения дата в книге. В него вручную внесены поправки: M D CCC XX III или 1823. Под ним, похоже, написано M D CC XC или 1790. |
Использование ( I ) для M или 1000 происходит от того, как римляне изображены большие числа, объясненные ниже..
Формовочные номера
В простейшем случае числа формируются путем соединения букв вместе, чтобы в сумме получить необходимое число. Вот так
- II = 2
XXX = 30
XII = 12
CXXIII = 123
Правило состоит в том, чтобы использовать максимально возможное число на каждом этапе, поэтому 15 обозначается XV, а не VVV или XIIIII. Из этого правила следует, что цифры всегда идут слева направо в порядке убывания. Это все еще может привести к очень длинным строкам.Например, при использовании этого правила 99 будет LXXXXVIIII. Итак, в какой-то момент было изобретено новое правило. Буква меньшего значения слева от буквы большего значения вычитается. Таким образом, 4 становится IV — что составляет 5 минус 1 —
а не IIII.
Это все еще может привести к очень длинным строкам.Например, при использовании этого правила 99 будет LXXXXVIIII. Итак, в какой-то момент было изобретено новое правило. Буква меньшего значения слева от буквы большего значения вычитается. Таким образом, 4 становится IV — что составляет 5 минус 1 —
а не IIII.
Есть три правила относительно этих меньших чисел, которые помещаются слева от большего числа и вычитаются.
- Вычитающая цифра слева должна быть I, X или C. ‘Пять’
цифры V, L и D использовать нельзя.M нельзя использовать, потому что это самая большая цифра.
- Вычитаемое число должно быть не менее десятой части значения числа, из которого оно вычитается. Таким образом, X можно разместить слева от C или L, но не слева от M или D. Правильный взгляд на это правило состоит в том, что каждая степень десяти рассматривается отдельно. Итак, 49 — это XL IX (без пробелов), а не IL
- Обычно слева можно разместить только одно меньшее число.
 Итак, 19 можно изобразить XIX, а 17 нельзя написать XIIIX.
или IIIXX.Однако это правило иногда нарушается для номеров, содержащих
восемь. На некоторых римских памятниках и гробницах встречается IIXX за 18 лет. А в последнее время
Times Times, статуя Хамо Торникрофта под названием Сеятель в Лондоне
На Kew Gardens есть надпись с датой MCMXXIIX, означающая 1928 год.
использование не является «правильным», но встречается очень редко.
Итак, 19 можно изобразить XIX, а 17 нельзя написать XIIIX.
или IIIXX.Однако это правило иногда нарушается для номеров, содержащих
восемь. На некоторых римских памятниках и гробницах встречается IIXX за 18 лет. А в последнее время
Times Times, статуя Хамо Торникрофта под названием Сеятель в Лондоне
На Kew Gardens есть надпись с датой MCMXXIIX, означающая 1928 год.
использование не является «правильным», но встречается очень редко.
Эта надпись за 1928 год нарушает одно из правил о вычитающие числа. |
Эти три правила ограничивают полезность правила вычитания для уменьшения длины римских цифр. Хотя 2000 год для ММ довольно хорош,
1999 год для MCMXCIX еще довольно длинный. MIM будет короче, но не допускается
Правило 2 выше. См. Вопрос 1999 года для обсуждения. о том, почему. Надпись за 1928 год, правильно написанная, будет MCMXXVIII, что
длиннее используемой формы.
о том, почему. Надпись за 1928 год, правильно написанная, будет MCMXXVIII, что
длиннее используемой формы.
Пакет электронных таблиц Microsoft Excel имеет функцию отображения чисел в римской форме.Чтобы получить классические римские числа, соответствующие правилам на этих страницах, используйте = ROMAN (n), где n — ваше число. Есть еще четыре версии функции, использующие все более странные версии «римских» чисел. Четвертый, ROMAN (n, 4), обозначает то, что Microsoft называет «упрощенной» версией. Ни один из этих четырех не имеет никакого отношения к тому, что действительно используют римские цифры. когда-либо, и кажется, что они были придуманы программистами в Гейтсвилле. Для преобразования действительных чисел в настоящие римские цифры в реальном времени используйте ROMAN (xy), где xy — ссылка на ячейку, содержащую число, которое вы хотите преобразовать.
Excel не будет отображать числа в римском формате без их преобразования в текст. Но другой программный пакет, Fireworkz для Windows, сделает это, позволяя работать с электронными таблицами в реальном времени с римскими цифрами! Я использовал Fireworkz для создания списков римских цифр на соседних страницах. Для получения дополнительной информации о
о цене и доступности этого превосходного и мощного программного обеспечения обращайтесь к Джеральду Фиттону из Abacus Training.
Для получения дополнительной информации о
о цене и доступности этого превосходного и мощного программного обеспечения обращайтесь к Джеральду Фиттону из Abacus Training.
Принцип вычитания был знаком римлянам, поскольку он использовался в их календаре.Дни считались числом до определенных фиксированных точек в месяце. Например, 9 марта было VII Id.
Это означает, что за седьмой день до ид 15-й день (обратите внимание, что римляне считали иды первым днем, поэтому 9-й — седьмой день.
накануне, НЕ шестой, как можно было ожидать). Мы также используем принцип вычитания в
представляет время, когда мы говорим «без четверти восемь» или «пять» и «с двадцати до девяти».
Строгие правила относительно римских цифр стали использоваться относительно недавно.В более ранние периоды, хотя использовался принцип вычитания, он был альтернативой, а не обязательной и другими формами, такими как VIIII для 9 и
СССК для 500 использовались. В любой момент можно найти исключения, как показывают эти четыре примера из разных периодов и все в самом Риме.
- Колизей, построенный между 70 и 80 годами нашей эры и известный как Амфитеатр Флавиев, вмещал 55 000 человек. Публика проходила через 80 арок, пронумерованных от 1 до 76 — четыре главных входа были ненумерованы.У каждого зрителя был билет с одним
этих номеров и вводятся через соответствующую арку. Говорят, что все они могут войти в течение десяти минут.
Сохранилось всего 33 дверных проема, пронумерованных от 23 до 54 с одним ненумерованным входом. В числах не используется сокращение IV или IX. Таким образом, арка 29 — это XXVIIII, а арка 54 — это LIIII. Однако используется сокращение для 40 — XL, поэтому дверь 44 — это XLIIII, как показано на рисунке ниже.
- Церковь Сант-Аньезе фуори-ле-Мура была построена в 7 веке нашей эры, а часть ее датируется триста лет назад.На стенах широкой мраморной лестницы, датируемой концом 16 века, есть надписи на могилах, взятые из катакомб под ними. Одна из них датирована 1256 годом — M.CC.LVI, за ней следует XIIII за номером 14.

Церковь также примечательна резным и позолоченным кессонным деревянным потолком, датируемым 1606 годом. Она обозначена MCCCCCCVI вместо более обычного MDCVI. , иллюстрируя, что даже тогда стандартные правила не всегда соблюдались.
- Замок Святого Ангела украшен резной каменной доской
АЛЕКСАНДР.VI.PONT.MAX
ИНСТАВИТ
AN.SAL.MCCCCLXXXXVЭта мемориальная доска находится на одной из четырех башен, которые Папа Александр VI, бывший понтификом в 1492–1503 годах, приказал реконструировать. Считается, что он современный, но, возможно, был вырезан при более поздней реставрации. Какой бы ни была дата, она демонстрирует полное пренебрежение принципом вычитания.
- В музее Ватикана Залы Борджиа содержат коллекцию современного религиозного искусства.
 Они пронумерованы римскими цифрами, но после комнаты 39 идет комната XXXX, затем XXXXI, затем XXXXIV, а затем еще XXXXIX, затем L.
вероятно середина 20 века.
Они пронумерованы римскими цифрами, но после комнаты 39 идет комната XXXX, затем XXXXI, затем XXXXIV, а затем еще XXXXIX, затем L.
вероятно середина 20 века.
При составлении «правильных» римских цифр необходимо использовать буквы в правильный порядок и может использовать принцип вычитания, пока вы придерживаетесь три правила вычитания.
Большие числа
Когда число становится больше нескольких тысяч, римские цифры становятся громоздкими.Нет
«большие» символы для 5000, 10 000 или миллиона. У римлян было два пути
написание больших чисел. Они использовали то, что я назвал выше «глубокими скобками», чтобы
умножьте число на 1000. Они были C
и зеркальное отображение или перевернутый C, и я использую обычные круглые скобки, чтобы показать их. Таким образом, ( I ) составляет 1000 и ( X ) составляет 10 000. ( XXIII ) есть
23000. Если вы хотите изобразить миллион
можно использовать ( M ) . В качестве альтернативы круглые скобки могут быть вложены так, что ( I ) — 1000 и (( I )) — 1000000.
Цифры могут стать немного громоздкими по мере их увеличения.
больше.
В качестве альтернативы круглые скобки могут быть вложены так, что ( I ) — 1000 и (( I )) — 1000000.
Цифры могут стать немного громоздкими по мере их увеличения.
больше.
Альтернативный способ изображения больших чисел заключался в том, чтобы поставить горизонтальную черту над цифрой, которая умножила ее на 1000. Таким образом,
| _ | _ |
| V = 5000 и | X = 10 000. |
В более крупном масштабе 3 852 429 можно представить как
| ____________ | |
| MMMDCCCL | MMCDXXIX |
Однако в некоторых случаях в предложении, содержащем слова и числа, будет использоваться горизонтальная полоса, чтобы просто показать буквы, которые использовались как числа. В другие случаи, обозначенные маленьким знаком в виде двух круглых скобок () размещены над числами.
Для изображения еще большего числа можно добавить боковые панели к строке,
умножив общую сумму еще на 100, чтобы заключенная цифра была
умножить на 100000. Таким образом,
Таким образом,
___
XII означало 12000, но
____
| XII | означало 1,200,000. Если написать воск на планшете, эти боковые панели могут
выглядят как изогнутые линии и создают неопределенность в отношении числа. Было ли это
кривая прямая или линия с короткими боковыми полосами? Говорят, что такой спор
произошли, когда римский император Тиберий унаследовал
имущество. Она выписала ему наследство, которое он должен заплатить разным людям, и один
Сульпицию Гальбе было написано как
________
| CCCCC | или 50 000 000 сестерциев.Но боковые панели были короткими, изогнутыми и
Тиберий утверждал, что это просто изогнутая линия, а истинное наследие —
год.
_______
CCCCC или 500000 сестерциев. Поскольку Тиберий был императором, бедняга Гальба получил только один
сотая часть наследства, задуманного Ливией. Сестерция хватило, чтобы купить два
буханки хлеба, поэтому современный эквивалент составляет около 1,50 или 2,50 доллара, возможно, немного
более.
Первоисточником этой истории является Светоний Транквилл. Жизни Двенадцать Цезарей , где говорится о Гальбе
«Он проявил особое уважение к Ливии Августе, благосклонности которой он многим обязан. влияние при ее жизни и по последней воле которой он почти стал богатым человек; потому что у него было самое крупное наследство среди ее наследников, одно из пятидесяти миллионов сестерциев.Но поскольку сумма была обозначена цифрами, а не записана слова, Тиберий, который был ее наследником, уменьшил наследство до пятисот тысяч, и Гальба никогда не получал даже этой суммы ». (Светоний, Гальба 5, перевел Леба Классическая библиотека 1914 г.)
Подробная информация о боковых панелях была добавлена в Жорж Ифра, Универсальная история Числа, Harvill Press, Лондон, 1998 г., стр. 200. Он ошибочно цитирует Сенеку (Гальба, 5) как его источник.
Дроби
Буква S использовалась для изображения половинки.Остальные фракции обозначены тире,
каждый рывок стоит одну двенадцатую. Итак — означает 1/12, = означает две двенадцатые, которые
одна шестая и так далее.
Итак — означает 1/12, = означает две двенадцатые, которые
одна шестая и так далее.
| – | 1/12 |
| = | 2/12 или 1/6 |
| — = | 3/12 или 1/4 |
| = = | 4/12 или 1/3 |
| — = = | 5/12 |
| S | 1/2 |
| S — | 1/2 плюс 1/12 или 7/12 часть |
| S = | 1/2 плюс 2/12 или 2/3 |
| S — = | 1/2 плюс 3/12 или 3/4 |
| S = = | 1/2 плюс 4/12 или 5/6 |
| S — = = | 1/2 плюс 5/12 или 11/12 долей |
Таким образом, двадцать три с половиной будут записаны как XXIIIS, а двенадцать с четвертью — это
XII- =. Буква S и тире никогда не использовались в качестве вычитания. Другой
дроби не могли быть изображены римскими цифрами.
Буква S и тире никогда не использовались в качестве вычитания. Другой
дроби не могли быть изображены римскими цифрами.
Ноль
Римская система счисления не включала ноль, и римляне понятия не имели о нем
в их арифметике. Это одна из причин, почему римские цифры так неуклюжи для вычислений,
хотя возможно. Они были склонны использовать счеты для арифметики, и это
В устройстве есть встроенная концепция нуля — она представлена пустой строкой.Но это был
Индийские и арабские математики после распада Римской империи изобрели
наша нынешняя система, в которой у нас есть понятие «место» и есть отчетливые
символ для представления нуля или пустого столбца. Так, например, когда мы пишем «10», ноль говорит
нам, что «1» стоит в десять раз больше, чем если бы число было просто
1. Значение этой системы для арифметики и вычислений и для изображения
числа любого размера настолько велики, что индо-арабский способ написания чисел
теперь почти универсальные, а римские цифры используются исключительно как «счет»
числами, а не вычислением чисел.
Краткое
История римских цифр
Современное использование римских цифр
Как работают римские цифры
Версия 3.11, 4 октября 2005 г.
Все материалы на этих страницах принадлежат Полу Льюису 1997-2005 гг.
Почему учить числа в средневековой Европе было так сложно
Индо-арабская система счисления была изобретена в Индии около 500 года нашей эры, а в раннем средневековье распространилась по арабоязычным странам.Он распространился в Западную Европу к концу 10 века и начал получать более широкое распространение в 13 веке. Большинство учебников по истории замалчивают введение чисел, но в недавней статье объясняется, что «освоение новых числительных было медленным, проблематичным и скачкообразным».
В своей статье «Старомодность против новомодных: чтение и запись чисел, 1200-1500» историк математики Джон Кроссли объясняет, что даже к концу Средневековья многим писателям было трудно понять, как работают числа. и предпочитал использовать старую систему римских цифр.
и предпочитал использовать старую систему римских цифр.
Когда кто-то использует римские цифры, они знают, что различные символы имеют фиксированное количество. Если бы они увидели букву V, то было бы пять, X — десять, а M — тысячу. Кроссли пишет:
, за небольшими исключениями, римские цифры не меняют своего значения, когда меняют свое место. С другой стороны, индуистско-арабские цифры меняют свое значение, когда меняют свое место. Задумайтесь над этим вопросом, что означает «3»? Когда мы встречаем 3 из 437 или 3145872, это означает две разные вещи.Это не «просто тройка!» В первом значении «тридцать», во втором «три миллиона».
Более яркий пример — это появление числа 3 из 1 234 537, где оно имеет два разных значения! Это иллюстрирует отличительную особенность использования индуистско-арабского языка в представлении чисел: их обозначение места. Это не зависит от формы цифр 0,1,… 9, поскольку, с одной стороны, вместо этих цифр могут использоваться другие символы, а с другой стороны, может использоваться другое обозначение места.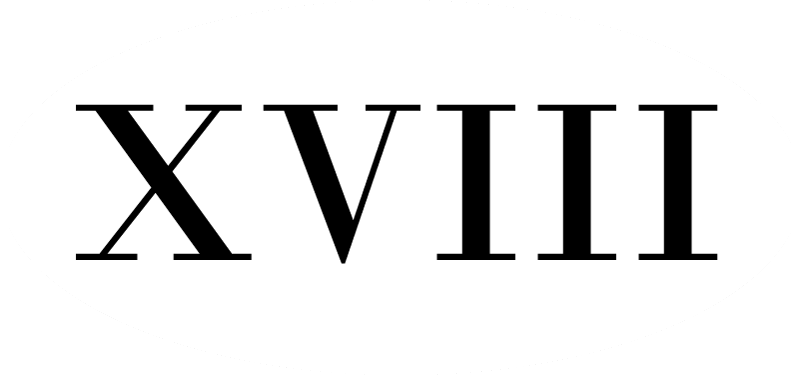
Таким образом, наша система записывает сначала число, начинающееся с наибольшего числа: «123» означает «сто двадцать три». По иронии судьбы, наименьшее число идет первым в письменном арабском языке, потому что направление арабского письма противоположно индуистскому, которое сохранилось в цифрах.
Эта концепция обозначения мест оказалась очень сложной для понимания средневековыми европейцами, особенно с учетом того, как они традиционно вычисляли суммы.В сочетании с тем фактом, что символы для чисел также были совершенно новыми для европейцев, неудивительно, что процесс перехода на новую систему был медленным.
Кроссли исследовал 1398 рукописей, созданных между 1200 и 1500 годами, чтобы увидеть, насколько широко используются индо-арабские цифры, и обнаружил, что на протяжении всего этого периода римские цифры по-прежнему в значительной степени предпочитались. В 13 веке только 7% рукописей имели новые номера, увеличившись до 17% в 14 веке и 47% в 15 веке.Он также обнаружил, что во многих случаях, когда писатели смешивали две системы, иногда в пределах одного и того же числа — например, иногда находили M (для 1000), за которым следовали арабские цифры.
В 13 веке только 7% рукописей имели новые номера, увеличившись до 17% в 14 веке и 47% в 15 веке.Он также обнаружил, что во многих случаях, когда писатели смешивали две системы, иногда в пределах одного и того же числа — например, иногда находили M (для 1000), за которым следовали арабские цифры.
Похоже, что импульс к переходу на индуистско-арабские числа в средневековой Европе исходил от бизнесменов. Кроссли пишет:
Существовало также четкое различие в доменах, в которых использовались эти два вида цифр. Римские цифры использовались в академических кругах, где в университетах преподавали абстрактные свойства: квадратные числа, треугольные числа и т. Д.Индусско-арабские цифры использовались в практической торговле. Это происходило в специальных, так называемых школах счётов, где торговцев и их служащих обучали новым индуистско-арабским числам. Такие школы были распространены в Италии. Поскольку они были тесно связаны с иногда довольно сложными вычислениями, коммерческое использование в конечном итоге привело к развитию алгебры. Только в шестнадцатом веке эти два владения соединились. В то время академические круги наконец занялись изучением методов вычисления, в частности алгебры, сохранив при этом теоретическую озабоченность абстрактными свойствами чисел.
Только в шестнадцатом веке эти два владения соединились. В то время академические круги наконец занялись изучением методов вычисления, в частности алгебры, сохранив при этом теоретическую озабоченность абстрактными свойствами чисел.
Статья «Старомодные и новомодные: чтение и запись чисел, 1200-1500» опубликована в журнале « Исследования по истории средневековья и Возрождения» , третья серия, том 10 (2013). Джон Кроссли — почетный профессор Университета Монаша в Австралии — Щелкните здесь, чтобы перейти на его веб-сайт .
См. Также Средневековые математические задачи
Верхнее изображение: страница немецкого рукописи, обучающая использованию арабских цифр — г-жа Тотт 290.2º_150v
Когда римские цифры перестали использоваться и были заменены арабскими цифрами, чтобы стать стандартной системой счисления в Европе? : AskHistorians
Система счисления, которую мы сейчас используем, была введена в Европе примерно в 12 веке и в последующие столетия почти полностью заменила римские цифры, которые использовались раньше.
Важно подчеркнуть, что не только символы новой системы отличались от римских цифр. Это была совсем другая система обозначений.В римской системе счисления каждый символ имеет только одно значение. I всегда 1, V всегда 5, X всегда 10 и так далее. Для большого или определенного числа вы просто складываете необходимые символы вместе. Например, 17 — это XVII или X (10) + V (5) + I (1) + I (1).
С индо-арабскими цифрами дело обстоит иначе. Всего 10 различных символов (от 1 до 9 и 0), и значение символа зависит от его положения. 1 может быть просто 1, но с одной другой цифрой после нее получается 10, две другие, 100 и так далее.
Индо-арабские цифры имели долгую историю, прежде чем они достигли христианской Европы. В западном мире мы называем их арабскими, но на самом деле они индийского происхождения. Цифры были введены в Европу арабскими учеными.
Первые символы, напоминающие знаменитые цифры, датируются более 2000 лет. Однако эти символы, вероятно, еще не использовали позиционную систему счисления с нулем.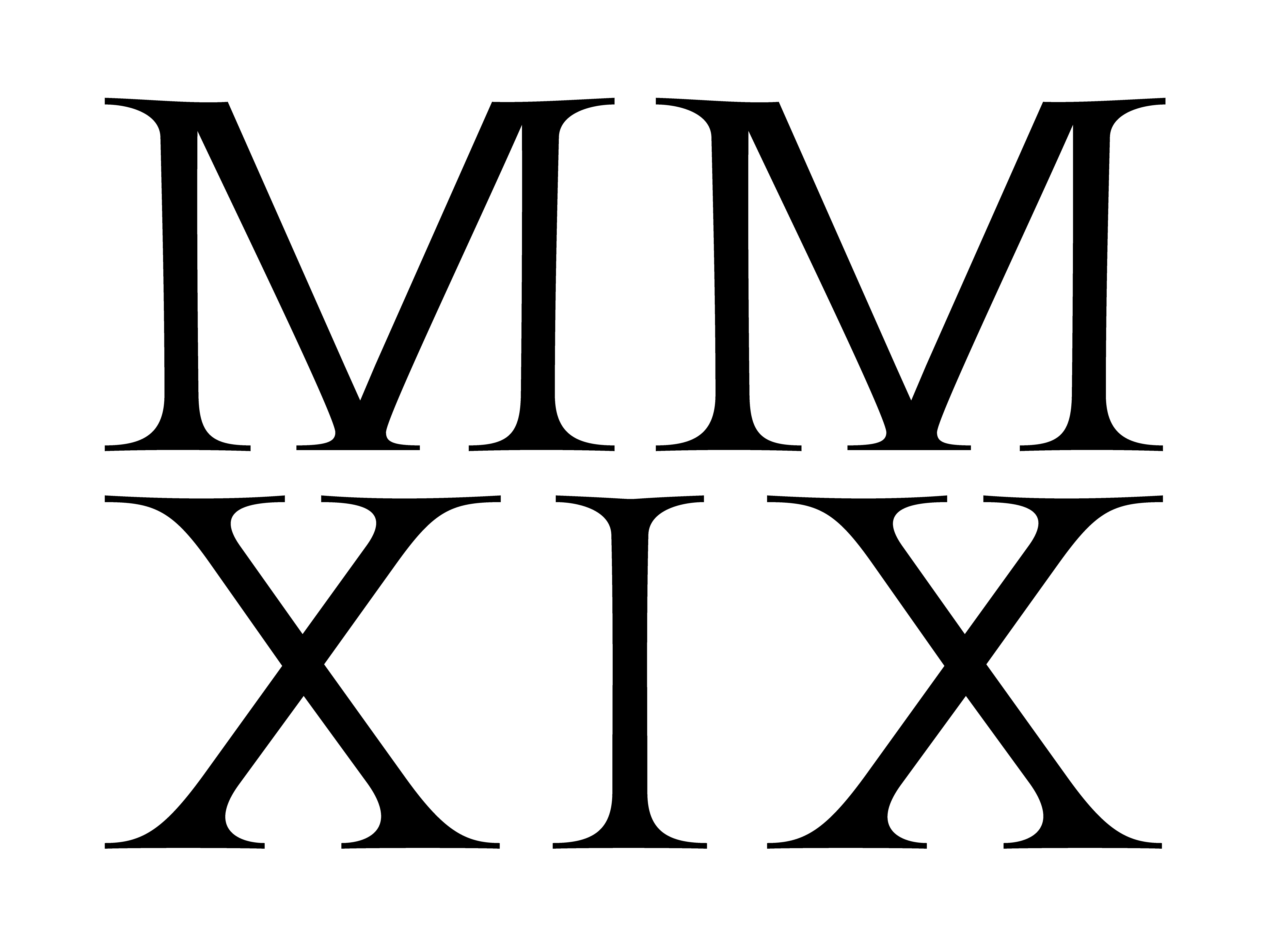 Перенесемся на пару столетий в 8 век, и так называемые цифры Деванагари вполне узнаваемы для наших нынешних цифр.Вероятно, примерно в это же время арабы вошли в контакт с индийской системой счисления во время и после завоевания Персидской империи.
Перенесемся на пару столетий в 8 век, и так называемые цифры Деванагари вполне узнаваемы для наших нынешних цифр.Вероятно, примерно в это же время арабы вошли в контакт с индийской системой счисления во время и после завоевания Персидской империи.
В начале 9 века эта система была определенно известна в арабском мире. Ученый аль-Хорезми написал трактат по алгебре, объясняющий эту систему. Именно это произведение позже было переведено и ввело числительные в Европе. Первый перевод был сделан Аделардом из Бата, английским монахом, который много путешествовал по Европе и Ближнему Востоку.
Но в основном эта система была представлена в Европе Liber Abaci (1228) Леонардо Пизанского, более известного как Фибоначчи. Он был знаком со многими различными методами бухгалтерского учета и математической записи, используемыми трейдерами в Средиземноморье, и быстро осознал потенциал этой новой системы.
Тем не менее, потребовалось несколько десятилетий и даже столетий, прежде чем система стала нормой (и даже сейчас мы все еще используем римские цифры, например, для имен монархов или в теории музыки).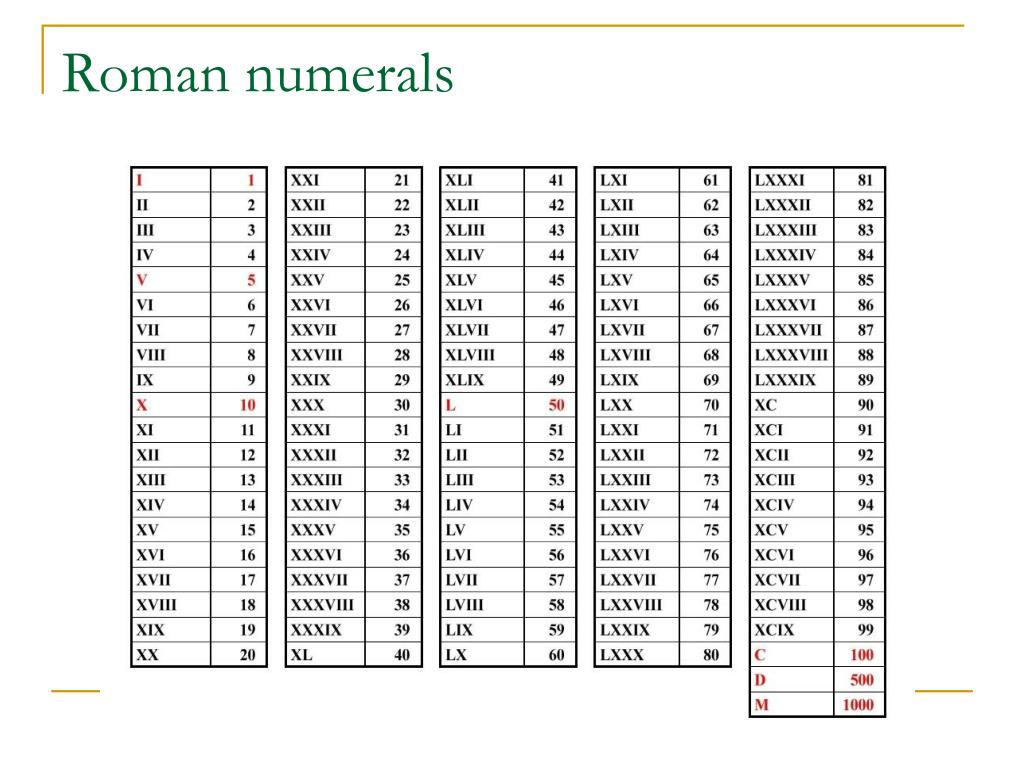 Сначала люди думали, что эти числа не подходят для ведения учета, так как их якобы было легче подделать (простое добавление нуля в конце увеличивает значение в десять раз). Тем не менее, индо-арабская система счисления была стандартной системой счисления в Европе ко времени появления печатного станка в 15 веке.
Сначала люди думали, что эти числа не подходят для ведения учета, так как их якобы было легче подделать (простое добавление нуля в конце увеличивает значение в десять раз). Тем не менее, индо-арабская система счисления была стандартной системой счисления в Европе ко времени появления печатного станка в 15 веке.
φ Вычисления в средневековой Европе ★ Фибоначчи
До того, как человек начал использовать письменные символы в математике, он использовал изображения для представления чисел и математических операций.Пальцевые знаки были особенно удобны и популярны для расчетов, но для успешного их использования требовалось много практики, чтобы развить навыки и ловкость. Тем не менее, поскольку это был надежный метод расчета, умение считать пальцами сохранялось в различных обществах, передавалось из поколения в поколение («Расчет»). Пальцевые вычисления на протяжении веков способствовали общению, преодолевая языковые барьеры. Всегда желая просвещать массы, ученые записали в книги изображения с помощью пальцевых вычислений; Самая ранняя известная транскрипция была написана преподобным Беде (около 673–735 гг. ), английским монахом-бенедиктинцем.В своей книге De Ratione Temporum он дает «полное объяснение счета пальцами и правил этого метода счета». Рисунки в его тексте показывают, что человек, используя обе руки, может представить все числа от 1 до 9 999 («Расчет»). Расчет пальцами оставался популярным даже после введения индо-арабских цифр, потому что он позволял выполнять более сложные вычисления, а также считать, сложение и вычитание. Ученые считали счет пальцев настолько важным, что руководство по расчетам считалось неполным, если оно не содержало рисунков, показывающих различные положения пальцев («Расчет»).
), английским монахом-бенедиктинцем.В своей книге De Ratione Temporum он дает «полное объяснение счета пальцами и правил этого метода счета». Рисунки в его тексте показывают, что человек, используя обе руки, может представить все числа от 1 до 9 999 («Расчет»). Расчет пальцами оставался популярным даже после введения индо-арабских цифр, потому что он позволял выполнять более сложные вычисления, а также считать, сложение и вычитание. Ученые считали счет пальцев настолько важным, что руководство по расчетам считалось неполным, если оно не содержало рисунков, показывающих различные положения пальцев («Расчет»).
ВЫЧИСЛЕНИЕ: ПАЛЬЦЕВ И ИНДУ-АРАБСКИЕ ЦИФРЫ
Достопочтенный Беде, De Temporum Ratione (725), Париж BN, MS Lat. 7418, ф. 3v Этот последний факт объясняет, почему первая книга Леонардо Пизано, Liber Abaci , включает инструкцию о том, «как числа нужно держать в руках» (Devlin, Finding 89). В конце первой главы он включает сложную систему подсчета пальцев в качестве вспомогательного средства для расчетов в «новой» системе ценностей. Древний метод счета по пальцам не был отвергнут абаком и не был полностью отодвинут на задний план в Центральной Европе до триумфа письменных вычислений с индо-арабскими цифрами в тринадцатом веке («Расчет»).
Древний метод счета по пальцам не был отвергнут абаком и не был полностью отодвинут на задний план в Центральной Европе до триумфа письменных вычислений с индо-арабскими цифрами в тринадцатом веке («Расчет»).
Проблема с вычислениями на счетах или пальцах состоит в том, что эти методы требуют значительной практики для достижения точности и скорости. Кроме того, нет возможности исправить ошибки или проверить точность, потому что «ни один метод не оставляет записи о расчетах.«При торговле необходимо иметь возможность регулярно проверять записи и проверять транзакции, — объясняет Кейт Девлин, математический историк, автор книги В поисках Фибоначчи: поиски заново забытого математического гения, изменившего мир (31). Крайне нужен был лучший метод. В Багдаде среди арабских ученых, которые изучали и переводили греческие и индуистские математические тексты, был выдающийся математик по имени Абу Абдаллах Мухаммад ибн Муса аль-Хваризмий (ок. 780 — ок.850). К середине XII века обе книги Аль-Хваризмийи были переведены учеными на латынь. Это стало важным ресурсом для европейцев, которые хотели изучать новую математику. Но подход Аль-Хваризмини не позволял людям исправлять ошибки, потому что он «требовал отмены и перезаписи, что делало невозможным отслеживание хода вычислений после их завершения» (Devlin, Finding 76-80). Хотя Аль-Хвияризми писал об индо-арабских цифрах в девятом веке, переводы его работ не появлялись в Европе до двенадцатого века.Тем не менее, даже тогда индуистско-арабские цифры не полностью заменили повседневное и коммерческое использование римских цифр до пятнадцатого века. Когда в регионе были приняты индо-арабские числа, они часто использовались только математиками, геодезистами и учеными; так было даже в арабских странах (Девлин, человек, 42).
Это стало важным ресурсом для европейцев, которые хотели изучать новую математику. Но подход Аль-Хваризмини не позволял людям исправлять ошибки, потому что он «требовал отмены и перезаписи, что делало невозможным отслеживание хода вычислений после их завершения» (Devlin, Finding 76-80). Хотя Аль-Хвияризми писал об индо-арабских цифрах в девятом веке, переводы его работ не появлялись в Европе до двенадцатого века.Тем не менее, даже тогда индуистско-арабские цифры не полностью заменили повседневное и коммерческое использование римских цифр до пятнадцатого века. Когда в регионе были приняты индо-арабские числа, они часто использовались только математиками, геодезистами и учеными; так было даже в арабских странах (Девлин, человек, 42).
Вычисления с индуистско-арабскими цифрами сосуществовали с использованием абака до начала тринадцатого века.В самом деле, одна из причин, по которой люди, возможно, неохотно отказывались от римских цифр вообще, заключается в том, что они «хорошо подходят для использования на счетах». Прежде чем стать папой Сильвестром II в X веке, Герберт Орийакский был ученым и учителем, который изобрел новые счеты, известные как гербертианские счеты. Счетчики его абака были отмечены индо-арабскими цифрами («Переход»). В некоторых переводах двенадцатого века арабских трактатов по алгоритму — искусству вычисления с помощью девяти цифр и нуля (Merriam-Webster) — представлены вычисления, проводимые с римскими цифрами, в то время как в других используются индо-арабские цифры.В начале тринадцатого века появилось несколько «очень влиятельных трактатов по алгоритму», которые «показывают большее знакомство с новой системой счисления, чем переводы из 12 века» («Переход»). Тем не менее, числовые формы широко варьировались от региона к региону, и нигде в Европе не использовались исключительно индо-арабские цифры. Вскоре после Аль-Хваризмий, великий египетский математик Абу Камил (ок. 850 — ок. 930), автор книги «Книга алгебры », иногда работал над проблемами, пока не находил все возможные решения; для одной задачи он рассчитал и записал 2676 решений! (Сезиано).
Прежде чем стать папой Сильвестром II в X веке, Герберт Орийакский был ученым и учителем, который изобрел новые счеты, известные как гербертианские счеты. Счетчики его абака были отмечены индо-арабскими цифрами («Переход»). В некоторых переводах двенадцатого века арабских трактатов по алгоритму — искусству вычисления с помощью девяти цифр и нуля (Merriam-Webster) — представлены вычисления, проводимые с римскими цифрами, в то время как в других используются индо-арабские цифры.В начале тринадцатого века появилось несколько «очень влиятельных трактатов по алгоритму», которые «показывают большее знакомство с новой системой счисления, чем переводы из 12 века» («Переход»). Тем не менее, числовые формы широко варьировались от региона к региону, и нигде в Европе не использовались исключительно индо-арабские цифры. Вскоре после Аль-Хваризмий, великий египетский математик Абу Камил (ок. 850 — ок. 930), автор книги «Книга алгебры », иногда работал над проблемами, пока не находил все возможные решения; для одной задачи он рассчитал и записал 2676 решений! (Сезиано).

 Если день недели опускается, он считается равным 1 (понедельнику).
Если день недели опускается, он считается равным 1 (понедельнику).
 )
)
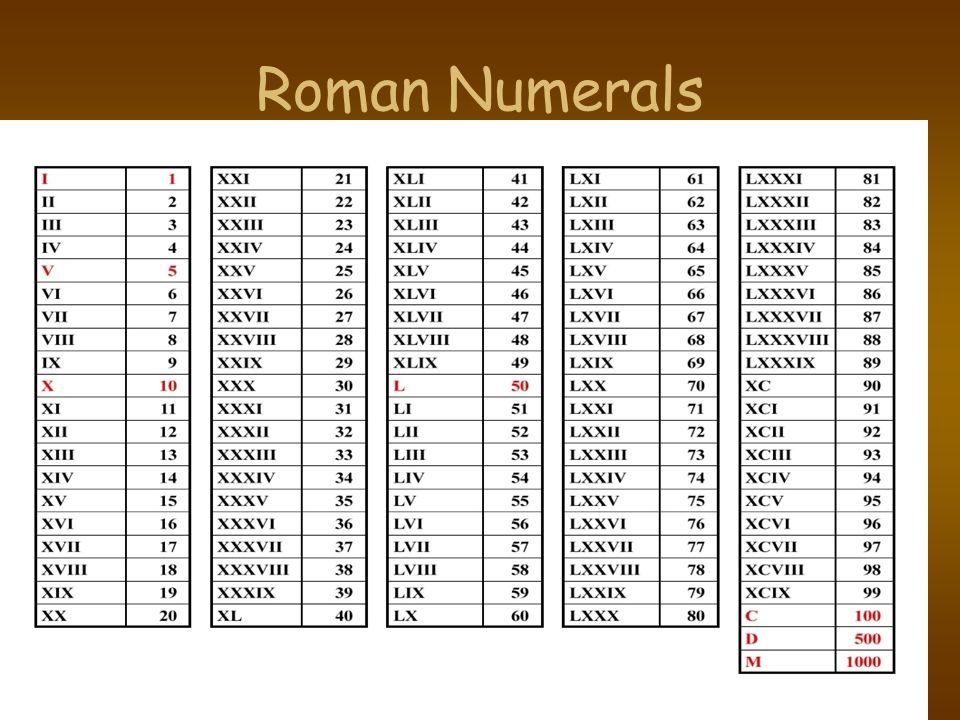 д.
д. Примерно с 14 столетия римские числа постепенно заменяются более удобными арабскими числами, использование которых стало превалирующим в наши дни. При этом римские цифры до сих пор активно используются в некоторых областях, довольно успешно сопротивляясь их переводу на арабские аналоги.
Примерно с 14 столетия римские числа постепенно заменяются более удобными арабскими числами, использование которых стало превалирующим в наши дни. При этом римские цифры до сих пор активно используются в некоторых областях, довольно успешно сопротивляясь их переводу на арабские аналоги. Римские цифры от 1 до 20 выглядят следующим образом:
Римские цифры от 1 до 20 выглядят следующим образом:
 Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам.
Чтобы образовать числа больше трех, складываются или вычитаются большая и меньшая цифры, для вычета меньшая цифра ставится перед большей, для прибавления — после, (4 = IV), та же логика действует и с другими цифрами (90 = XC). Порядок расположения тысяч, сотен, десятков и единиц тот же, что и привычный нам. Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::.
Большие числа отмечались специальными знаками: 1000 — ↀ (или C|Ɔ),5000 – ↁ(или |Ɔ),10000 – ↂ (или CC|ƆƆ). Миллионы получаются при двойном подчеркивании стандартных цифр. Дроби римскими цифрами тоже писали: с помощью значков отмечались унции – 1/12, половина отмечалась символом S, а все, что больше 6/12 – прибавлением: S = 10\12. Еще один вариант – S::. Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
Постепенно зарубки превратились в графические символы I, V и X, и приобрели самостоятельность. Позже они стали идентифицироваться с римскими буквами – так как были на них внешне похожи.
 В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр.
В Голландии римскими цифрами иногда обозначают этажи. А в Италии ими отмечают 100-метровые отрезки пути, отмечая, в то же время, арабскими цифрами каждый километр. Это произошло потому, что римские цифры записать достаточно сложно, да и любые арифметические действия в римской системе выполнять гораздо сложнее, чем в арабской системе исчисления. Не смотря на то, что сегодня римская система не часто используется, это вовсе не значит, что она стала неактуальна. В большинстве случаев века римскими цифрами обозначают, а вот годы или точные даты принято писать арабскими цифрами.
Это произошло потому, что римские цифры записать достаточно сложно, да и любые арифметические действия в римской системе выполнять гораздо сложнее, чем в арабской системе исчисления. Не смотря на то, что сегодня римская система не часто используется, это вовсе не значит, что она стала неактуальна. В большинстве случаев века римскими цифрами обозначают, а вот годы или точные даты принято писать арабскими цифрами. Если меньшая цифра стоит перед большей, то используется принцип вычитания (меньшая цифра вычитается из большей).
Так, цифра 4 изображается как IV (то есть 5-1).
Если меньшая цифра стоит перед большей, то используется принцип вычитания (меньшая цифра вычитается из большей).
Так, цифра 4 изображается как IV (то есть 5-1). Цифры с одного до четырех напоминают вытянутые пальцы, цифру пять можно сравнить с раскрытой ладонью, где большой палец оттопырен. А цифра десять напоминает две скрещенные руки. В европейских странах при счете принято разгибать пальцы, а вот в России, наоборот, загибать.
Цифры с одного до четырех напоминают вытянутые пальцы, цифру пять можно сравнить с раскрытой ладонью, где большой палец оттопырен. А цифра десять напоминает две скрещенные руки. В европейских странах при счете принято разгибать пальцы, а вот в России, наоборот, загибать.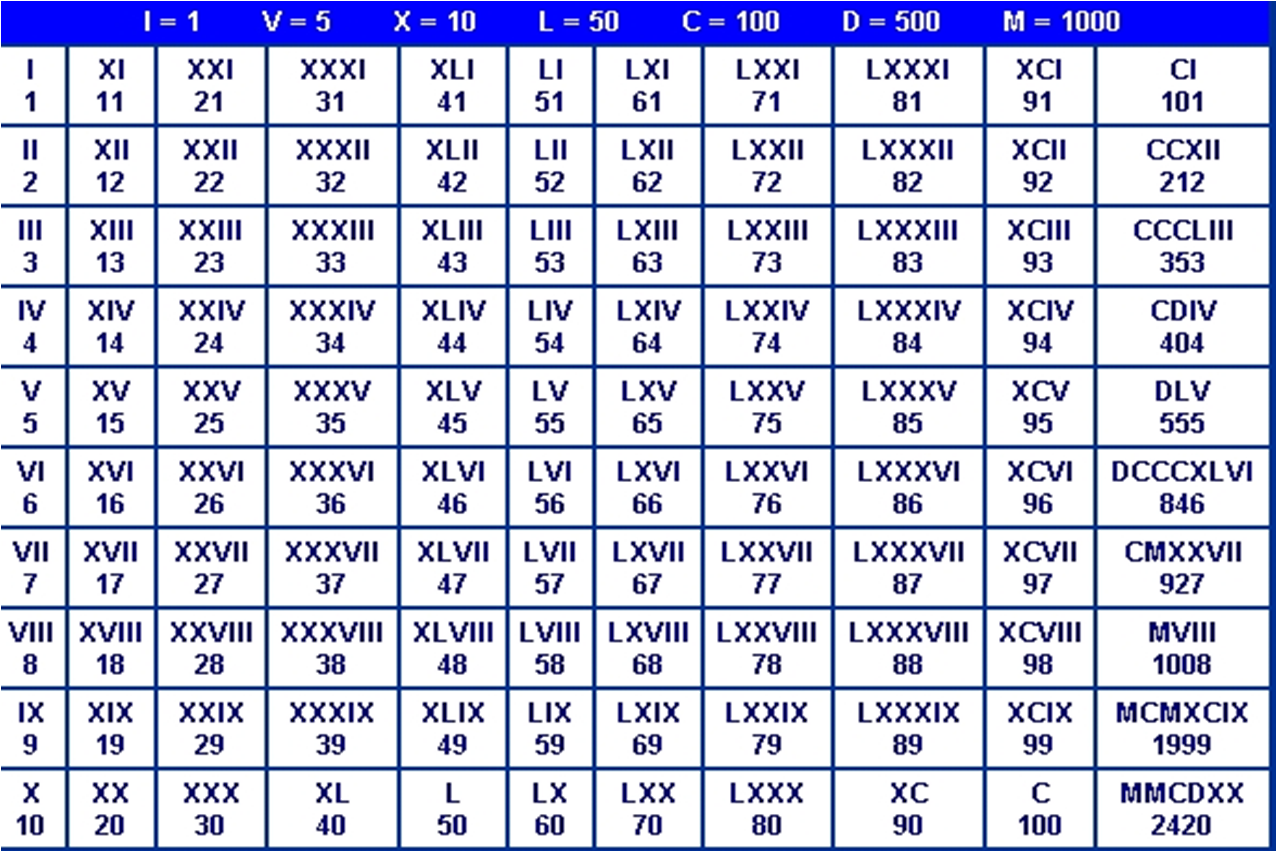
 е. 5+1
е. 5+1
 Он не рекомендуется, но иногда используется для упрощения. Отличие состоит в том, что для уменьшения цифры слева от неё может писаться любая цифра:
Он не рекомендуется, но иногда используется для упрощения. Отличие состоит в том, что для уменьшения цифры слева от неё может писаться любая цифра: э.
э. Комбинированные глифы используются для представления чисел, которые ранее составлялись из отдельных символов (например, Ⅻ
вместо его представления как Ⅹ
и Ⅱ
). В дополнение к этому, глифы существуют для архаичных форм записи чисел 1000, 5000, 10 000, большой обратной C (Ɔ
), поздней формы записи 6 (ↅ
, похожей на греческую стигму: Ϛ
), ранней формы записи числа 50 (ↆ
, похожей на стрелку, указывающую вниз ↓⫝⊥
), 50 000, и 100 000. Следует отметить, что маленькая обратная c, ↄ
не включена в символы римских цифр, но включена в стандарт Юникод как прописная клавдиева буква Ↄ
.
Комбинированные глифы используются для представления чисел, которые ранее составлялись из отдельных символов (например, Ⅻ
вместо его представления как Ⅹ
и Ⅱ
). В дополнение к этому, глифы существуют для архаичных форм записи чисел 1000, 5000, 10 000, большой обратной C (Ɔ
), поздней формы записи 6 (ↅ
, похожей на греческую стигму: Ϛ
), ранней формы записи числа 50 (ↆ
, похожей на стрелку, указывающую вниз ↓⫝⊥
), 50 000, и 100 000. Следует отметить, что маленькая обратная c, ↄ
не включена в символы римских цифр, но включена в стандарт Юникод как прописная клавдиева буква Ↄ
.
 Использование глубоких скобок — C и обратных C — очень понятно.
Использование глубоких скобок — C и обратных C — очень понятно.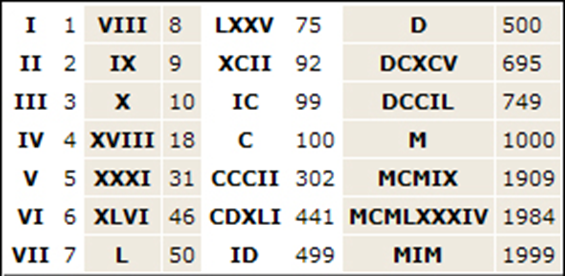 Итак, 19 можно изобразить XIX, а 17 нельзя написать XIIIX.
или IIIXX.Однако это правило иногда нарушается для номеров, содержащих
восемь. На некоторых римских памятниках и гробницах встречается IIXX за 18 лет. А в последнее время
Times Times, статуя Хамо Торникрофта под названием Сеятель в Лондоне
На Kew Gardens есть надпись с датой MCMXXIIX, означающая 1928 год.
использование не является «правильным», но встречается очень редко.
Итак, 19 можно изобразить XIX, а 17 нельзя написать XIIIX.
или IIIXX.Однако это правило иногда нарушается для номеров, содержащих
восемь. На некоторых римских памятниках и гробницах встречается IIXX за 18 лет. А в последнее время
Times Times, статуя Хамо Торникрофта под названием Сеятель в Лондоне
На Kew Gardens есть надпись с датой MCMXXIIX, означающая 1928 год.
использование не является «правильным», но встречается очень редко.
 Они пронумерованы римскими цифрами, но после комнаты 39 идет комната XXXX, затем XXXXI, затем XXXXIV, а затем еще XXXXIX, затем L.
вероятно середина 20 века.
Они пронумерованы римскими цифрами, но после комнаты 39 идет комната XXXX, затем XXXXI, затем XXXXIV, а затем еще XXXXIX, затем L.
вероятно середина 20 века.