Синус, ко синус, тангенс угла 120 градусов (sin 120 cos 120 tg 120)
Напомним себе, что 2π/3 в градусах — это 120 градусов. ( 2 * 180 / 3 = 120 ). Таким образом, найти значение тригонометрической функции для угла 2π/3 и для ула 120 градусов — это одно и то же.
Как найти значения тригонометрических функций для угла 120 градусов
Найдем значения синуса, косинуса и тангенса для угла 120 градусов аналитическим способом.На первый взгляд, нахождение значений синуса, косинуса и тангенса для угла 120 градусов — задача сложная. Однако, это не совсем так.
Прежде всего, мы должны обратить внимание, что для углов, значения которых превышают 90 градусов, у нас есть формулы приведения к углу, меньшему 90 градусов.
Поэтому, для начала, представим себе угол в 120 градусов как (90 + 30)
Тогда
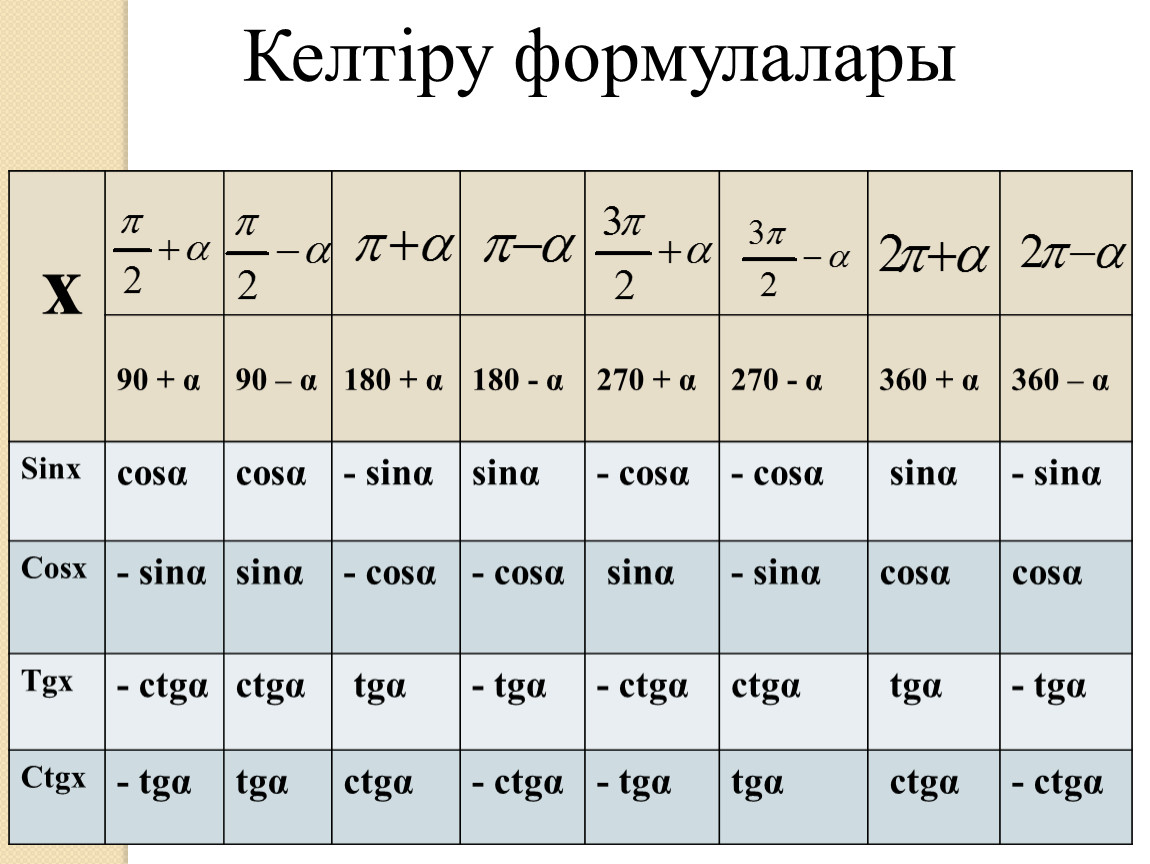
sin ( 90 + α ) = cos α
sin 120 = sin( 90 + 30 ) = cos 30
cos ( 90 + α ) = — sin α
cos 120 = cos( 90 + 30 ) = -sin 30
tg ( 90 + α ) = -ctg α
tg 120 = tg( 90 + 30 ) = -ctg 30
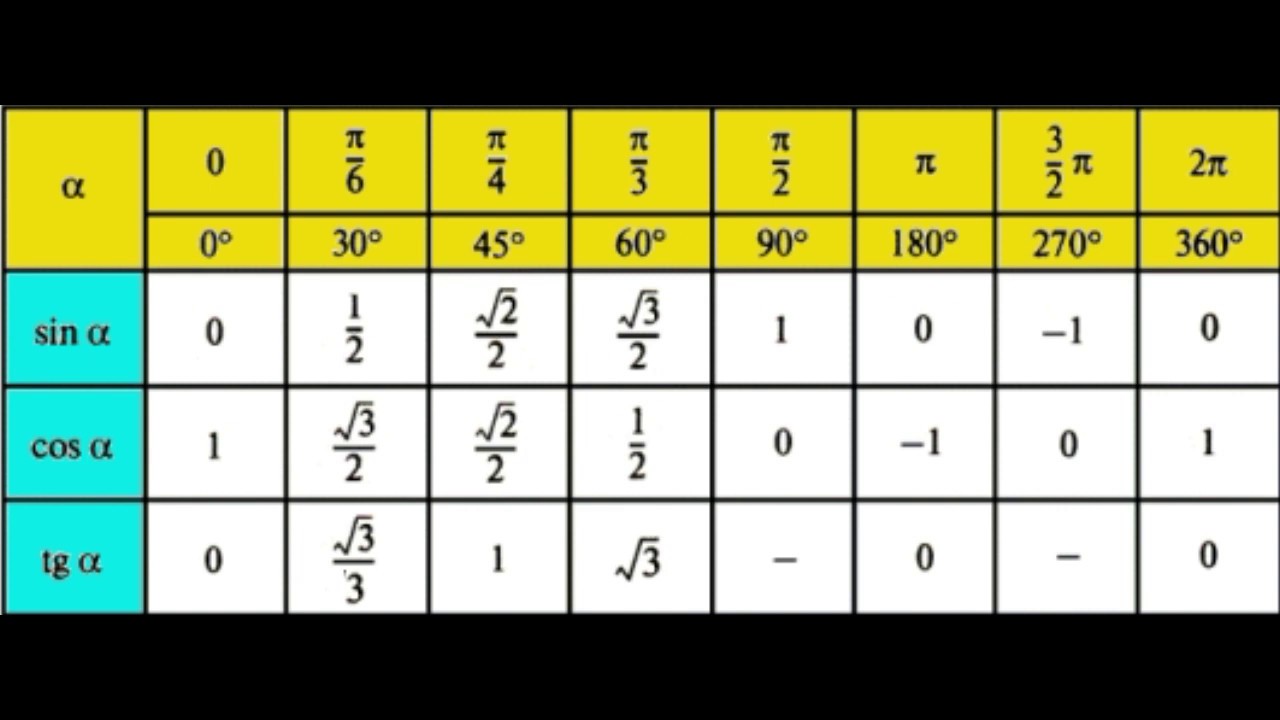
Теперь можно посмотреть значения в таблицах синуса, косинуса и тангенса 120 градусов, который преобразован в значения тригонометрических функций синуса, косинуса и тангенса угла 30 градусов.
В уроке по ссылке можно посмотреть как вычислить значения тригонометрических функций для угла 30 градусов.
В итоге получаем:
Как видно из примера, значения тригонометрических функций углов синуса, косинуса и тангенса 120 градусов могут быть получены путем несложных тригонометрических преобразований с использованием тригонометрических тождеств.
См. также полную таблицу значений тригонометрических функций (таблицу синусов, косинусов и тангенсов).
Ниже приведены также значения тригонометрических функций для угла 120 градусов в виде десятичной дроби с четырьмя знаками после запятой.
|
2π/3 |
синус 120 sin 120 |
косинус 120 cos 120 |
тангенс 120 tg 120 |
котангенс 120 ctg 120 |
| Значение | 0,8660 | -0,5000 | -1,7321 | -0,5774 |
Измерение углов: градусы и радианы
Анна Малкова
Почему полный круг составляет 360 градусов? Что такое радиан и как перевести градусы в радианы? И при чем здесь число ? Статья для тех, кто сдает ЕГЭ или просто интересуется математикой.
Для измерения углов принято использовать две основные единицы: градусы и радианы.
Начнем с привычных градусов.
Полный круг составляет 360 градусов – это мы все знаем.
Да, но почему 360?
В метре 100 сантиметров. В рубле 100 копеек, в килограмме 1000 грамм. Мы привыкли к десятичной системе, и возникла она оттого, что на каждой руке у нас по 5 пальцев, а на двух руках — по 10.
А вот в часе 60 минут, в круге 360 градусов. И в сутках 24 часа. Древние шумеры умудрились придумать двенадцатеричную систему счисления! И при этом они тоже считали по пальцам. Нет, у них не было по 6 пальцев на каждой руке. Просто считали не пальцы, а фаланги четырех пальцев (кроме большого).
Кстати, круг легко делится именно на 6 частей (умеете?). А число 12 (дюжина) делится на 2, 3, 4, 6 и, собственно, 12.
И это не все. Древние шумерские астрономы обнаружили, что в день равноденствия Солнце встает почти точно на Востоке и заходит почти точно на Западе, причем от восхода до заката проходит по небу путь, в 360 раз больший, чем видимый с Земли диаметр Солнца.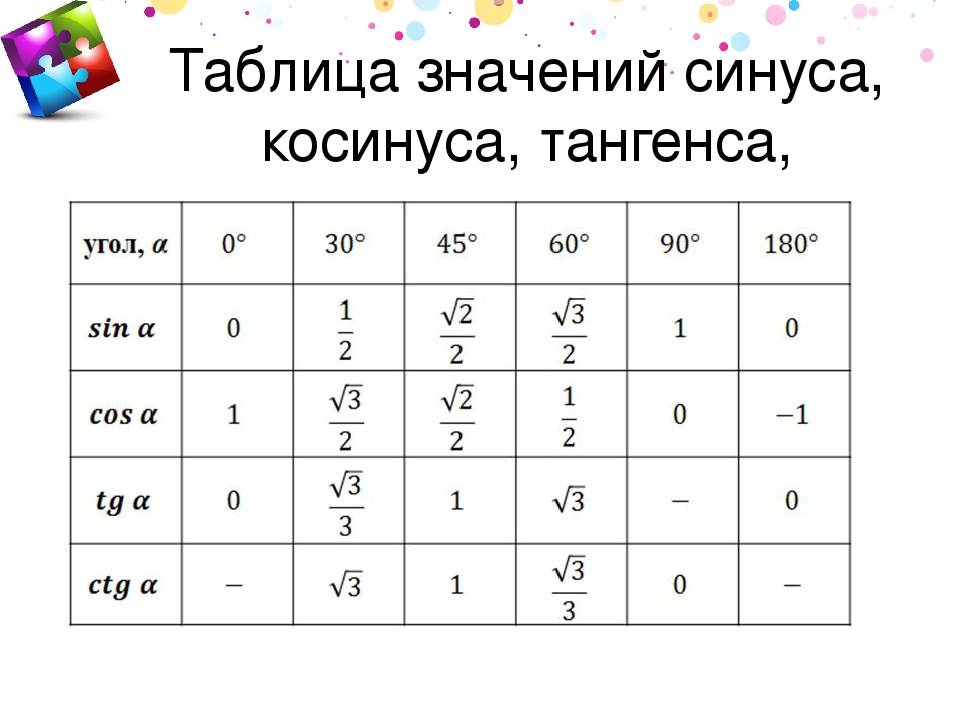
Небесную полуокружность разделили на 180 градусов.
Точнее, угловой диаметр Солнца равен примерно 32 угловых минуты, то есть чуть больше 0,5 градуса. Он еще и немного меняется в течение года из-за того, что орбита Земли не круговая, а эллиптическая.
Так что утверждение о том, что в День равноденствия Солнце проходит по небу путь, равный 360 своим «шагам» (то есть 360 видимым диаметрам солнца) – верно с некоторой точностью.
Конечно, древние астрономы наблюдали не только за движением Солнца. Они заметили, что яркая планета Юпитер совершает полный оборот вокруг Солнца за 12 лет. Точнее, не 12, а 11,86 лет, но уж очень им хотелось округлить до своего любимого числа.
Да что там Юпитер! Посмотрим на Луну. Юпитер на небе еще и не каждый найдет (а вы сможете?) – зато Луну, особенно полную, трудно не заметить! Месяц – промежуток от полнолуния до полнолуния – равен примерно 29,5 суток. Почти 30, верно?
Наша Земля совершает полный оборот вокруг Солнца за 365 дней (точнее, за 365,242 суток), и это – солнечный год.
И тогда лунный год – это 12 месяцев, в каждом месяце 30 дней (округлили), вот и получается 360 дней в году, почти столько же, сколько в солнечном, в котором 365 дней.
«Может быть, боги хотели сделать в году ровно 360 дней, но им кто-нибудь помешал, вот и получилось 365». Возможно, так и рассуждали древние астрономы, деля круг на 360 частей, 360 градусов. Тем более, что 360 – число, имеющее целых 24 делителя.
Число 360 делится на 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20, 24, 30, 36, 40, 45, 60, 72, 90, 120, 180 и 360. Очень удобно делить 360 градусов на части!
Обозначается: 360°. Этот кружок вверху – специальный символ для обозначения градуса.
Есть и другая мера измерения углов – радианная.
1 радиан – центральный угол, опирающийся на дугу, равную радиусу окружности.
Как перевести градусы в радианы и наоборот?
Полный круг – это 360 градусов. Отношение длины окружности к ее диаметру равно числу , приближенно Значит, длина окружности равна где – радиус.
Составим пропорцию. Длина окружности так относится к длине дуги на нашем рисунке, как – к величине угла, опирающегося на эту дугу, то есть к углу в 1 радиан.
Слева в нашей пропорции углы, справа – длина полной окружности и длина отмеченной на рисунке дуги.
Из этой пропорции получаем, что радиан. Значит, полный круг – это радиан. Тогда полкруга – это радиан, четверть круга (то есть ) – это радиан.
Любой угол, выраженный в градусах, можно перевести в радианы. И наоборот, 1 радиан приблизительно равен 57 градусам.
Функция COS — Служба поддержки Office
В этой статье описаны синтаксис формулы и использование функции COS в Microsoft Excel.
Описание
Возвращает косинус заданного угла.
Синтаксис
COS(число)Аргументы функции COS описаны ниже.
Замечания
Если угол задан в градусах, умножьте его на ПИ()/180 или воспользуйтесь функцией РАДИАНЫ, чтобы преобразовать его в радианы.
Пример
Скопируйте образец данных из следующей таблицы и вставьте их в ячейку A1 нового листа Excel. Чтобы отобразить результаты формул, выделите их и нажмите клавишу F2, а затем — клавишу ВВОД.
Формула | Описание | Результат |
|---|---|---|
|
=COS(1,047) |
Косинус 1,047 радиан |
0,5001711 |
|
=COS(60*ПИ()/180) |
Косинус 60 градусов |
0,5 |
|
=COS(РАДИАНЫ(60)) |
Косинус 60 градусов |
0,5 |
Градусная мера углов
Наверное, при изучении курса геометрии вы не раз задавались вопросом, что же такое эти градусы, радианы и с чем их едят? Попробуем разобраться.
Само понятие «градус» появилось еще в Древнем Вавилоне около 40 веков назад. Придумали его очень просто – взяли и разбили окружность на 360 частей, поэтому так и вышло, что 1/360 окружности и есть 1 градус. В это же время в Древнем Египте пытались измерить, во сколько же раз окружность больше, чем диаметр этой самой окружности. Установить это смогли лишь через 35 веков, и то, получили неровное число, а 3,141592, в общем, бесконечное иррациональное. Для удобства его округлили до 3,14 и получили не что иное, как всем известное число Пи.
Однако вернемся к градусам. Градусная мера угла, конечно же, хорошо, но для высшей математики не подходит. Поэтому и придумали радиан.
Что же это за зверь такой? На самом деле ничего сложного, просто чуть-чуть запутанно на первый взгляд. В основе определения радиана лежит все та же старая и добрая окружность, с которой так долго мучились египтяне. Угол величиной в 1 радиан – это угол, который вырезает в окружности такую дугу, длина которой равна радиусу окружности.
Не вдаваясь в подробности, скажем лишь одно – радиан в несколько раз больше градуса. Но давайте определим все-таки приблизительное соотношение градуса и радиана. На самом-то деле доказано, что в 180 градусов вмещается 3 радиана с хвостиком. А что же за хвостик? Его величина составляет 0,141592, то есть в 180 градусов вмещается 3,141592 радиан (число Пи). Не зря в начале статьи мы заговорили о древних египтянах, которые так долго с ним мучились.
Но все же самым главным в теме градусов и радиан остается умение переводить их друг в друга, то есть радианы в градусы и наоборот, градусы в радианы.
Градусная и радианная мера углов | ||||||||||||||||||||||||||||||||||
| π ≈ 3,1415926535897932384626433832795 | ||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||
|
Радиан, Углы больше 360 градусов, Положительные и отрицательные углы
Когда прямые пересекаются, то получается четыре разные области по отношению к точке пересечения.
Эти новые области называют углами.
На картинке видны 4 разных угла, образованных пересечением прямых AB и CD
Обычно углы измеряются в градусах, что обозначается как °.
Когда объект совершает полный круг, то есть движется из точки D через B, C, A, а затем обратно к D, то говорят что он повернулся на 360 градусов (360°).
Таким образом, градус — это $\frac{1}{360}$ круга.
Мы говорили о том, что когда объект делает полный круг вокруг точки, то он проходит 360°, однако, когда объект делает более одного круга, то он делает угол более 360 градусов. Это обычное явление в повседневной жизни. Колесо проходит многие круги, когда автомобиль движется, то есть оно образует угол больше 360°.
Для того, чтобы узнать количество циклов (пройденных кругов) при вращении объекта, мы считаем количество раз, которое нужно прибавить 360 к самому себе, чтобы получить число равное или меньшее, чем данный угол. Точно так же мы находим число, которое мы умножаем на 360, чтобы получить число меньшее, но наиболее близкое к данному углу.
{\circ} = \frac{260}{360} = \frac{7}{9}$ кругов
Объект описал $2\frac{7}{9}$ кругов
Когда объект вращается по часовой стрелки, то он образует отрицательный угол вращения, а когда вращается против часовой стрелке — положительный угол. До этого момента мы рассматривали только положительные углы.
В форме диаграммы отрицательный угол может быть изображен так, как это показано ниже.
Рисунок ниже показывает знак угла, который измеряется от общей прямой, 0 оси (оси абсцисс — х оси)
Это означает, что при наличии отрицательного угла, мы можем получить соответствующий ему положительный угол.
Например, нижняя часть вертикальной прямой это 270°. Когда измеряется в негативную сторону, то получим -90°. Мы просто вычитаем 270 из 360.
Имея отрицательный угол, мы прибавляем 360, для того чтобы получить соотвествующий положительный угол.
Когда угол равен -360°, это означает, что объект совершил более одного круга по часовой стрелке.
Пример 3
1.
Найти соответствующий положительный угол
a) -35°
b) -60°
c) -180°
d) — 670°
2. Найти соответствующий отрицательный угол 80°, 167°, 330°и 1300°.
Решение
1. Для того, чтобы найти соответствующий положительный угол мы прибавляем 360 к значению угла.
a) -35°= 360 + (-35) = 360 — 35 = 325°
b) -60°= 360 + (-60) = 360 — 60 = 300°
c) -180°= 360 + (-180) = 360 — 180 = 180°
d) -670°= 360 + (-670) = -310
Это означает один круг по часовой стрелке (360)
360 + (-310) = 50°
Угол равен 360 + 50 = 410°
2. Для того, чтобы получить соответсвующий отрицательный угол мы вычитаем 360 от значения угла.
80° = 80 — 360 = — 280°
167° = 167 — 360 = -193°
330° = 330 — 360 = -30°
1300° = 1300 — 360 = 940 (пройден один круг)
940 — 360 = 580 (пройден второй круг)
580 — 360 = 220 (пройден третий круг)
220 — 360 = -140°
Угол равен -360 — 360 — 360 — 140 = -1220°
Таким образом 1300° = -1220°
Радиан — это угол из центра круга, в который заключена дуга, длина которой равна радиусу данного круга.
{\circ}$
c) 1 рад = 57,3°
$2,4 = \frac{2,4 \times 57,3}{1} = 137,52$
Отрицаетльные углы и углы больше, чем $2\pi$ радиан
Для того чтобы преобразовать отрицательный угол в положительный, мы складываем его с $2\pi$.
Для того чтобы преобразовать положительный угол в отрицательный, мы вычитаем из него $2\pi$.
Пример 5
1. Преобразовать $-\frac{3}{4}\pi$ и $-\frac{5}{7}\pi$ в позитивные углы в радианах.
Решение
Прибавляем к углу $2\pi$
$-\frac{3}{4}\pi = -\frac{3}{4}\pi + 2\pi = \frac{5}{4}\pi = 1\frac{1}{4}\pi$
$-\frac{5}{7}\pi = -\frac{5}{7}\pi + 2\pi = \frac{9}{7}\pi = 1\frac{2}{7}\pi$
Когда объект вращается на угол больший, чем $2\pi$;, то он делает больше одного круга.
Для того, чтобы определить количество оборотов (кругов или циклов) в таком угле, мы находим такое число, умножая которое на $2\pi$, результат равен или меньше, но как можно ближе к данному числу.
Пример 6
1.
Найти количество кругов пройденных объектом при данных углах
a) $-10\pi$
b) $9\pi$
c) $\frac{7}{2}\pi$
Решение
a) $-10\pi = 5(-2\pi)$;
$-2\pi$ подразумевает один цикл в направлении по часовой стрелке, то это означает, что
объект сделал 5 циклов по часовой стрелке.
b) $9\pi = 4(2\pi) + \pi$, $\pi =$ пол цикла
объект сделал четыре с половиной цикла против часовой стрелки
c) $\frac{7}{2}\pi=3,5\pi=2\pi+1,5\pi$, $1,5\pi$ равно три четверти цикла $(\frac{1,5\pi}{2\pi}=\frac{3}{4})$
объект прошел один и три четверти цикла против часовой стрелки
Всё о трёхфазной системе электроснабжения
Трёхфазная система электроснабжения — частный случай многофазных систем электрических цепей переменного тока, в которых действуют созданные общим источником синусоидальные ЭДС одинаковой частоты, сдвинутые друг относительно друга во времени на определённый фазовый угол.
Один из вариантов многофазной системы электроснабжения — трехфазная система переменного тока.
В ней действуют три гармонические ЭДС одной частоты, создаваемые одним общим источником напряжения. Данные ЭДС сдвинуты по отношению друг к другу во времени (по фазе) на один и тот же фазовый угол, равный 120 градусов или 2*пи/3 радиан.
Первым изобретателем шестипроводной трехфазной системы был Никола Тесла, однако немалый вклад в ее развитие внес и российский физик-изобретатель Михаил Осипович Доливо-Добровольский, предложивший использовать всего три или четыре провода, что дало значительные преимущества, и было наглядно продемонстрировано в экспериментах с асинхронными электродвигателями.
В трехфазной системе переменного тока каждая синусоидальная ЭДС находится в собственной фазе, участвуя в непрерывном периодическом процессе электризации сети, поэтому данные ЭДС иногда именуют просто «фазами», как и передающие данные ЭДС проводники: первая фаза, вторая фаза, третья фаза. Фазы сдвинуты друг относительно друга на 120 градусов, а соответствующие проводники принято обозначать латинскими буквами L1, L2, L3 или A, B, C.
Такая система очень экономична, когда речь идет о передаче электрической энергии по проводам на большие расстояния. Трехфазные трансформаторы менее материалоемки.
Силовые кабели требуют меньше проводящего металла (как правило используется медь), поскольку токи в фазных проводниках, по сравнению с однофазными, имеют меньшие действующие величины, если сравнивать с однофазными цепями аналогичной передаваемой мощности.
Трехфазная система очень уравновешена, и оказывает равномерную механическую нагрузку на энергогенерирующую установку (генератор электростанции), чем продлевает срок ее службы.
При помощи трехфазных токов, пропускаемых через обмотки электрических потребителей — различных установок и двигателей, легко получить вращающееся вихревое магнитное поле, необходимое для работы двигателей и других электроприборов.
Синхронные и асинхронные трехфазные двигатели переменного тока имеют простое устройство, и гораздо экономичнее однофазных и двухфазных, а тем более — классических двигателей постоянного тока.
С трехфазной сетью в одной установке можно получить сразу два рабочих напряжения — линейное и фазное, что позволяет иметь два уровня мощности в зависимости от схемы соединения обмоток — «треугольник» (англоязычный вариант «дельта») или «звезда».
Что касается питания систем освещения, то присоединив три группы ламп — к различным фазам сети каждую, — можно значительно снизить мерцание и избавиться от вредного стробоскопического эффекта.
Перечисленные преимущества как раз и обуславливают широкое применение именно трехфазной системы электроснабжения в большой мировой электроэнергетике сегодняшнего дня.
Звезда
Соединение по схеме «звезда» предполагает соединение концов фазных обмоток генератора в одну общую «нейтральную» точку (нейтраль — N), как и концов фазных выводов потребителя.
Провода, соединяющие фазы потребителя с соответствующими фазами генератора называются в трехфазной сети линейными проводами. А провод, соединяющий между собой нейтрали генератора и потребителя — нейтральным проводом (обознаяается «N»).
При наличии нейтрали, трехфазная сеть получается четырехпроводной, а если нейтраль отсутствует — трехпроводной. В условиях, когда сопротивления в трех фазах потребителя равны друг другу, то есть при условии что Za = Zb = Zc, нагрузка будет симметричной. Это идеальный режим работы для трехфазной сети.
При наличии нейтрали, фазными называются напряжения между любым фазным проводом и нейтральным проводом. А напряжения между любыми двумя фазными проводами именуются линейными напряжениями.
Если сеть имеет схему соединения «звезда», то в условиях симметричной нагрузки соотношения между фазными и линейными токами и напряжениями могут быть описаны следующими соотношениями:
Видно, что линейные напряжения сдвинуты по отношению к соответствующим фазным на угол в 30 градусов (пи/6 радиан):
Мощность при соединении «звезда» в условиях симметричной нагрузки, с учетом известных фазных напряжений можно определить по формуле:
О важности нейтрали и «перекосе фаз»
Хотя при абсолютно симметричной нагрузке питание потребителей возможно по трем проводам линейными напряжениями даже в отсутствие нейтрали, тем не менее если нагрузки на фазах не строго симметричны, нейтраль всегда обязательна.
Если же при несимметричной нагрузке нейтральный провод оборвется, либо его сопротивление по какой-то причине значительно возрастет, произойдет «перекос фаз», и тогда нагрузки на трех фазах могут оказаться под разными напряжениями — от нуля до линейного — в зависимости от распределения сопротивлений нагрузок по фазам в момент обрыва нейтрали.
А ведь нагрузки номинально рассчитаны строго на фазные напряжения, значит что-то может выйти из строя. Особенно перекос фаз опасен для бытовой техники и электроники, поскольку из-за этого может не просто перегореть какой-нибудь прибор, но и случиться пожар.
Проблема гармоник кратных третьей
Наиболее часто бытовая и другая техника оснащается сегодня импульсными блоками питания, причем без встроенной схемы коррекции коэффициента мощности. Это значит, что моменты потребления ограничиваются тонкими импульсными пиками тока вблизи вершины сетевой синусоиды, когда конденсатор выходного фильтра, установленный после выпрямителя, резко и быстро подзаряжается.
Когда таких потребителей к сети подключено много, возникает высокий ток третьей гармоники основной частоты питающего напряжения. Данные токи гармоник (кратных третьей) суммируются в нейтральном проводнике и способны перегрузить его, несмотря на то, что на каждой из фаз потребляемая мощность не превышает допустимой.
Проблема особенно актуальна в офисных зданиях, где размещено на небольшом пространстве много разной оргтехники. Если бы во всех встроенных импульсных блоках питания имелись схемы коррекции коэффициента мощности, это бы решило проблему.
Треугольник
Соединение по схеме «треугольник» предполагает со стороны генератора соединение конца проводника первой фазы с началом проводника второй фазы, конца проводника второй фазы с началом проводника третьей фазы, конца проводника третьей фазы с началом проводника первой фазы — получается замкнутая фигура — треугольник.
Линейные и фазные напряжения и токи при симметричной нагрузке, применительно к соединению «треугольник», соотносятся следующим образом:
Мощность в трехфазной цепи при соединении треугольником, в условиях симметричной нагрузки, определяется следующим образом:
В нижеприведенной таблице отражены стандарты фазных и линейных напряжений для разных стран:
Проводники разных фаз трехфазной сети, а также нейтральные и защитные проводники традиционно маркируют собственными цветами.
Так поступают для того, чтобы предотвратить поражение электрическим током и обеспечить удобство обслуживания сетей, облегчить их монтаж и ремонт, а также сделать стандартизированной маркировку фазировки оборудования: порядок чередования фаз порой очень важен, например для задания направления вращения асинхронного двигателя, режима работы управляемого трехфазного выпрямителя и т. д. В разных странах цветовая маркировка различна, в некоторых совпадает.
Ранее ЭлектроВести писали, что немецкая энергетическая компания E.ON подписала контракт с производителем автомобилей BMW на установку и эксплуатацию одной из крупнейших сетей зарядки электромобилей в Германии, которая будет включать более 4,1 тыс. новых зарядных станций.
По материалам: electrik.info.
|
|
Онлайн калькуляторы> Преобразование> 120 градусов в радианы 120 градусов в радианы Калькулятор преобразования конвертирует 120 градусов в радианы и наоборот. Чтобы вычислить, сколько радианов в 120 градусах, разделите на 57,296.
Сколько радианов в 120 градусах?Есть 2.0944 радиана в 120 градусах, или 120 градусов = 2,0 | 04273 радиана.|
| Степень | Радиан |
|---|---|
| 120 | 2,09439 |
| 120.01 | 2,09456 |
| 120,02 | 2,09474 |
| 120,03 | 2,09491 |
| 120.04 | 2,09509 |
| 120,05 | 2,09526 |
| 120,06 | 2,09543 |
| 120,07 | 2,09561 |
| 120,08 | 2,09578 |
| 120,09 | 2,09596 |
| 120,1 | 2,09613 |
| 120.11 | 2,09631 |
| 120,12 | 2,09648 |
| 120,13 | 2,09666 |
| 120,14 | 2,09683 |
| 120,15 | 2,09701 |
| 120,16 | 2,09718 |
| 120,17 | 2,09735 |
| 120.18 | 2,09753 |
| 120,19 | 2,09770 |
| 120,2 | 2,09788 |
| 120,21 | 2,09805 |
| 120,22 | 2,09823 |
| 120,23 | 2,09840 |
| 120,24 | 2,09858 |
| 120.25 | 2,09875 |
| 120,26 | 2,09892 |
| 120,27 | 2,09910 |
| 120,28 | 2,09927 |
| 120,29 | 2,09945 |
| 120,3 | 2,09962 |
| 120,31 | 2,09980 |
| 120.32 | 2,09997 |
| 120,33 | 2,10015 |
| 120,34 | 2,10032 |
| 120,35 | 2,10050 |
| 120,36 | 2,10067 |
| 120,37 | 2,10084 |
| 120,38 | 2,10102 |
| 120.39 | 2,10119 |
| 120,4 | 2,10137 |
| 120,41 | 2,10154 |
| 120,42 | 2,10172 |
| 120,43 | 2,10189 |
| 120,44 | 2,10207 |
| 120,45 | 2.10224 |
| 120.46 | 2,10242 |
| 120,47 | 2,10259 |
| 120,48 | 2,10276 |
| 120,49 | 2,10294 |
| 120,5 | 2.10311 |
| 120,51 | 2,10329 |
| 120,52 | 2,10346 |
| 120.53 | 2.10364 |
| 120,54 | 2,10381 |
| 120,55 | 2.10399 |
| 120,56 | 2,10416 |
| 120,57 | 2.10434 |
| 120,58 | 2,10451 |
| 120,59 | 2,10468 |
| 120.6 | 2,10486 |
| 120,61 | 2,10503 |
| 120,62 | 2,10521 |
| 120,63 | 2,10538 |
| 120,64 | 2,10556 |
| 120,65 | 2,10573 |
| 120,66 | 2,10591 |
| 120.67 | 2,10608 |
| 120,68 | 2,10626 |
| 120,69 | 2,10643 |
| 120,7 | 2.10660 |
| 120,71 | 2,10678 |
| 120,72 | 2,10695 |
| 120,73 | 2,10713 |
| 120.74 | 2,10730 |
| 120,75 | 2,10748 |
| 120,76 | 2,10765 |
| 120,77 | 2,10783 |
| 120,78 | 2,10800 |
| 120,79 | 2,10818 |
| 120,8 | 2,10835 |
| 120.81 | 2,10852 |
| 120,82 | 2,10870 |
| 120,83 | 2,10887 |
| 120,84 | 2,10905 |
| 120,85 | 2,10922 |
| 120,86 | 2,10940 |
| 120,87 | 2,10957 |
| 120.88 | 2,10975 |
| 120,89 | 2,10992 |
| 120,9 | 2.11009 |
| 120,91 | 2,11027 |
| 120,92 | 2,11044 |
| 120,93 | 2,11062 |
| 120,94 | 2,11079 |
| 120.95 | 2,11097 |
| 120,96 | 2,11114 |
| 120,97 | 2,11132 |
| 120,98 | 2,11149 |
| 120,99 | 2,11167 |
125 градусов в радиан
Калькуляторы недвижимости
Бухгалтерские калькуляторы
Бизнес-калькуляторы
Строительные калькуляторы
Спортивные калькуляторы
Финансовые калькуляторы
Калькулятор сложных процентов
Ипотечный калькулятор
Сколько дома я могу себе позволить
Кредитный калькулятор
Акционный калькулятор
Инвестиционный калькулятор
Пенсионный калькулятор
Пенсионный калькулятор
Калькулятор комиссий eBay
Калькулятор комиссий PayPal
Калькулятор комиссий Etsy
Калькулятор надбавки
Калькулятор TVM
Калькулятор LTV
Калькулятор аннуитета
Сколько я заработаю в году
Математические калькуляторы
Калькулятор смешанного числа в десятичный000
Калькулятор ИМТ
Калькулятор потери веса
Преобразование
CM в футы и дюймы
MM в дюймы
Другое
Сколько мне лет
Выбор случайных имен
Генератор случайных чисел
Градус и радианы — объяснение и примеры
Как и любая другая величина, у углов также есть единицы измерения. Радианы и Градусы — две основные единицы измерения углов . Существуют и другие единицы измерения углов (например, градусов и MRAD), но в старшей школе вы увидите только эти две единицы.
Что такое градусы и радианы?
Самая популярная единица измерения углов, с которой знакомо большинство людей, — это письменный градус ( ° ). Единицы градуса — минуты и секунды. Есть 360 градусов, 180 градусов для полукруга (полукруга) и 90 градусов для четверти круга (прямоугольный треугольник) в полном круге или одном полном вращении.
Градусы в основном указывают направление и размер угла . Лицом к северу означает, что вы смотрите в направлении 0 градусов. Если вы повернете на юг, вы окажетесь лицом к лицу в направлении 90 градусов. Если вы вернетесь на север после полного поворота, вы повернетесь на 360 градусов. Обычно положительным считается направление против часовой стрелки. Если повернуть на запад с севера, угол будет либо -90 градусов, либо +270 градусов.
В геометрии есть еще одна единица измерения углов, известная как радиан ( рад ).
Итак, зачем нам радианы, если мы уже привыкли к углам?
В большинстве математических вычислений используются числа. Поскольку градусы на самом деле не являются числами, предпочтительнее использовать радианы, которые часто требуются для решения проблем.
Хороший пример , который похож на эту концепцию, использует десятичные дроби, когда у нас есть проценты . Хотя процент может быть показан с помощью числа, за которым следует знак%, мы преобразуем его в десятичную дробь (или дробь).
Концепция нахождения угла по длине дуги использовалась давно. Радиан был введен значительно позже. Роджер Котес дал понятие радиан в 1714 году, но не дал ему такого названия, а просто назвал его круговой мерой угла.
Термин « радиан, » впервые был использован в 1873 году. Позднее это название привлекло всеобщее внимание и получило разрешение.
Из этой статьи вы узнаете, как преобразовать градусы в радианы и наоборот (радианы в градусы).Давайте взглянем.
Как преобразовать градусы в радианы?
Чтобы преобразовать градусы в радианы, мы умножаем заданный угол (в градусах) на π / 180.
Угол в градусах (°) x π / 180 = Угол в радианах (Рад)
Где π = 22/7 или 3,14
Пример 1
Преобразование следующих углов из градусов в радианы
- 0 °
- 30 °
- 45 °
- 60 °
- 90 °
- 120 °
- 150 °
- 180 °
- 210 °
- 240 °
- 360 °
Решение
Угол в градусах (°) x π / 180 = Угол в радианах (Рад)
1.0 ° х π / 180
= 0 рад
2. 30 ° x π / 180
= π / 6
= 0,5 рад
3. 45 ° x π / 180
= π / 4
= 0,785 рад
4. 60 ° x π / 180
= π / 3
= 1,047 рад
5. 90 ° x π / 180
= π / 2
= 1,571рад
6. 120 ° x π / 180
= 2π / 3
= 2,094 рад
7. 150 ° x π / 180
= 5π / 6
= 2,618 рад
8.180 ° x π / 180
= π
= 3,14 рад
9. 210 ° x π / 180
= 7π / 6
= 3,665 рад
10. 240 ° x π / 180
= 3π / 2
= 4,189 рад
11. 360 ° x π / 180
= 2π
= 6,283 рад
Пример 2
Преобразование 700 градусов в радианы.
Решение
Угол в градусах (°) x π / 180 = Угол в радианах (Рад)
Путем замены,
Угол в радианах (рад) = 700 x π / 180.
= 35 π / 9
= 12,21 рад.
Пример 3
Преобразовать — 300 ° в радианы.
Решение
Угол в радианах = -300 ° x π / 180.
= — 5π / 3
= — 5,23 рад
Пример 4
Преобразовать — 270 ° в радианы.
Решение
Угол в радианах = -270 ° x π / 180.
= — 3π / 2
= -4,71 Рад.
Пример 5
Преобразует 43 градуса, 6 минут и 9 секунд в радианы.
Решение
Первый экспресс 43 градуса, 6 минут и 9 секунд только до градусов.
43 ° 6 ′ 9 ″ = 43,1025 °
43,1025 ° x π / 180 = угол в радианах
= 0,752 рад.
Пример 6
Перевести 102 ° 45 ′ 54 ″ в радианы.
Решение
102 ° 45 ′ 54 ″ равно 102.765 °
Угол в радианах = 102,765 ° x π / 180.
= 1,793 рад.
Как преобразовать радианы в градусы?
Чтобы преобразовать радианы в градусы, умножьте радиан на 180 / π. Итак, формула имеет вид,
Угол в радианах x 180 / π = Угол в градусах.
Пример 7
Преобразует каждый из следующих углов в радианах в градусы.
- 1,46
- 11π / 6
- π / 12
- 3.491
- 7,854
- -8,14
- π / 180
Решение
Угол в радианах x 180 / π = Угол в градусах.
- 46 x 180 / π
= 83,69 градуса.
- 11π / 6 x 180 / π
= 330 градусов.
- π / 12 x 180 / π
= 15 градусов.
- 491 x 180 / π
= 200,1 градуса
- 854 x 180 / π
= 450.2 градуса.
- -8,14 x 180 / π
= — 466,6 градуса.
- π / 180 x 180 / π
= 1 градус.
Пример 8
Преобразует угол π /5 радиан в градусы.
Решение
Угол в радианах x 180 / π = Угол в градусах.
Путем замены,
π /5 x 180 / π = 36 градусов.
Пример 9
Преобразование угла — π /8 радиан в градусы
Решение
-π /8 x 180 / π = — 22.5 градусов.
Пример 10
Радиус куска пиццы 9 см. Если периметр куска составляет 36,850 см, найдите угол куска пиццы в радианах и градусах.
Решение
Пусть длина дуги куска = x
Периметр = 9 + 9 + x
36,850 см = 18 + х
Вычтем 18 с обеих сторон.
18,85 = х
Итак, длина дуги детали 18,85 см.
А, длина дуги = θr
Где θ = угол в радианах, а r = радиус.
18,85 см = 9 θ
Разделите обе стороны на 9
θ = 2,09 рад
θ в градусах:
Угол в радианах x 180 / π = Угол в градусах.
= 2,09 х 180 / π
= 120 градусов.
Пример 11
Радиус сектора 3 м, а его площадь 3π / 4 м 2 . Найдите центральный угол сектора в градусах и радианах.
Решение
Учитывая это,
Площадь сектора = (r 2 θ) / 2
Где θ = центральный угол в радианах.
Запасной.
3π / 4 = (3 2 θ) / 2
3π / 4 = 9θ / 2
Перекрестное умножение.
6 π = 36 θ
Разделите обе стороны на 36, чтобы получить,
θ = 0,52 рад.
Преобразует угол в градусы.
= 0,52 х 180 / π
= 29,8 градуса.
Пример 12
Найдите центральный угол сектора с радиусом 56 см и площадью 144 см 2 .
Решение
A = (θ / 360) πr 2
144 = (θ / 360) x 3.14 х 56 х 56.
144 = 27,353 θ
Разделим обе части на θ.
θ = 5,26
Таким образом, центральный угол составляет 5,26 градуса.
Пример 13
Площадь сектора 625 мм 2 . Если радиус сектора равен 18 мм, найдите центральный угол сектора в радианах.
Решение
Площадь сектора = (θ r 2 ) / 2
625 = 18 x 18 x θ / 2
625 = 162 θ
Разделите обе стороны на 162.
θ = 3,86 радиана.
Практические вопросы
- Преобразование 330 ° в радианы.
- Преобразовать -750 ° в радианы
- Преобразует каждый из следующих углов в радианах в градусы:
а. 21π / 5
г. -15π / 2
120 градусов в радианах — learn.lif.co.id
120 градусов в край.Используя преобразователь градусов в радианы выше, вы можете найти точное значение 120 градусов в радианах в единицах пи или значение любого угла в радианах с шагом.
Единичный круг, помеченный особыми углами и значениями Клипарт и т. Д. Как запоминать математические формулы Тригонометрия
120 град. До гон.
120 градусов в радианах . Например, для преобразования 120 градусов у вас будет 120 x π180 120π180. 120 градусов по зеттарадианам. Rad 120 x 001745 209 Если вы студент, имеющий склонность и интерес к математике и геометрии, то вам наверняка будут интересны следующие несколько строк.
120 градусов в гекторадиан. 360 градусов 2 пи радиана. 120 π 180 120 π 180 радиан Сократить общий множитель 60 60.
В персидском календарном году также 360 дней, и многие предполагают, что ранние астрономы использовали 1 градус в день. Градус — это единица измерения угла в системе СИ, используемая в метрической системе. 2π3 рад можно выразить десятичной дробью, а не дробью 066666666666667π рад 201023932 радиан.
Конвертер градусов в радианы Следующий калькулятор конвертирует углы между градусами и радианами.Как перевести градусы в радианы. 120 градусов в нанорадиан.
Преобразуем градусы в радианы умножением на π 180 120 π 180 2 3 π. α радиан α градусов π 180 или. Радианы 53 x 31416 180 Вычисленное, это дает угол 925 радиан.
Пи радиан равняется 180 градусам. Это видео недоступно. Таблица перевода градусов в радианы.
Следующий факт иллюстрирует соотношение между градусами и радианами. Таким образом, 1 градус 2 пи360 радианов примерно 0175 рад или 1 радиан 3602 пи примерно 573 градуса. Чтобы преобразовать радианы в градусы, вы должны умножить на 180pi.Этот урок определяет радианы, как преобразовать 120 градусов в радианы, а также дает вам другие общие углы, измеряемые в радианах.
При работе в радианах за один оборот приходится два пи2 умножить на пи радиана. На этой странице мы добавляем 120 градусов в нашу формулу для вычисления радианов. Получив ответ, упростите радианы.
Конвертер градусов в радианы Как преобразовать радианы в градусы. 120 120 Чтобы преобразовать градусы в радианы, умножьте на π 180 π 180, так как полный круг равен 360 360 или 2π 2 π радиан.Преобразуйте 120 градусов в радианы.
120 градусов — это величина угла. Угол α в радианах равен углу α в градусах, умноженному на постоянную пи, деленному на 180 градусов. α радиан α градусов π 180 30 314159 180 05236 рад.
См. Полный ответ ниже. 1 рад 180π 57295779513 Угол α в градусах равен углу α в радианах, умноженному на 180 градусов, деленному на константу пи. 120 градусов в минуту, 120 градусов в зепторадиане.
Хотя градус не является единицей Международной системы единиц СИ, он является принятой единицей в брошюре СИ.Окончательная формула для преобразования 120 градусов в рад: Радианы градусов π 180 Пример.
Преобразует 120 градусов в радианы. Поскольку полный оборот равен 2π радианам, один градус эквивалентен π180 радианам. Радианы — это отношение длины дуги к радиусу окружности.
Единица измерения угла, определяемая полным поворотом на 360 градусов. 120 градусов к атторадиану. Переход от градусов к радианам может сбивать с толку.
В геометрии градус и радиан представляют меру угла.Вы можете рассчитать это, переведя оба числа в дроби. Калькулятор сгенерирует пошаговые пояснения.
120 2π3 2094 Рад. 120 градусов в петарадиан. Округлено до ближайшей тысячи дополнительных ресурсов.
Радианы Градусы x Пи 180 Пример. Преобразуйте угол 30 градусов в радианы. Если мы оглянемся на наши школьные и студенческие годы, мы наверняка встретили бы такие термины, как угол и градусы.
Один полный оборот против часовой стрелки может быть представлен как 2π в радианах или 360 в градусах.Градус — это угол, равный 1360-й части оборота или окружности. π rad 180 Один радиан равен 57295779513 градусам.
Следовательно, градус и радиан можно приравнять. При угле в 53 градуса радианы этого угла будут равны. Чтобы преобразовать градусы в радианы, возьмите число градусов, которое нужно преобразовать, и умножьте его на π180.
Для преобразования используйте эту формулу угловых градусов в радианы. Один оборот в градусах равен 360 градусам. π радиан 180 Это.
120 градусов до ок. α градусов α радиан 180 π. 120 равно 2π 3 радиан.
Пропустить навигацию Войти. Число 360 имеет 24 делителя, поэтому с ним довольно легко работать.
Pin Автор: Сальвадор Тимотео Валентин В Formulario De Ciencias Intelectum Тригонометрия Математические формулы Лист математических формул
Тригонометрия в прямоугольном треугольнике Тригонометрия в радианах Единичная окружность в прямоугольном треугольнике
Рабочие листы по математике в единичном круге Тригонометрия Математика и геометрия
Единица Круг Радианы Градусы Квадратные Куртаи Сочленяемыми пикселями Кафе-пресс Математические методы Единица Круг Радианы Математические модели
Graph Polar Graph Paper Radians Mandala Design Art Mandala Урок рисования мандалы для печати
Опорный угол 30 градусов Измерение радиана за один оборот Математические методы Изучение математики Обучение математике в 2021 году Математические методы Изучение математики Обучение математике
Pin De Mohammadazad Em Electronico Ensino De Matematica Formulas Matematica Truques De Matematica
Единичный круг Радианы Градусы Квадратные куртки Душ по четким пикселям Cafepress Преподавание алгебры Обучение математике Физика и математика
Круг с отметками в градусах Поиск в Google Обучение деревообработке Деревообработка Советы по деревообработке
Рабочий листрадиан в градусах Рабочий лист для вдохновляющей викторины Как преобразовать 120 градусов в радианы в 2020 г. Рабочие листы для заданий по алгебре Вдохновляющая викторина
Как преобразовать радианы в градусы 21 удивительный пример Тригонометрические науки Mathematiques Lecons De Mathematiques
Единичный круг с радианами Баннер с четкими пикселями Cafepress Тригонометрия Единичные радианы
радианов Градусы по кругу Наука Технологии Инженерия Математическая диаграмма Радианы
1 3 Круглая юбка 120 градусов Radian Is 2 P в 2020 году Выкройка для шитья круглая юбка Выкройка своими руками
График окружности с углами 0 30 45 60
Как преобразовать градусы в радианы Радианы Градусы по математике
Тан Единица Круг Единица Круг Радианы Математические формулы Единица
Шаблон под углом 30 градусов Поиск в Google Математические методы Изучение математики Математическое образование
Диаграмма тригонометрии с преобразованием в градусы и радианыМатематические диаграммы Математические методы Таблица математических формул
Преобразование градусов в радианы (° в рад)
Введите угол в градусах ниже, чтобы преобразовать значение в радианы.
Как преобразовать градусы в радианы
Чтобы преобразовать градус в радиан, умножьте угол на коэффициент преобразования.
Поскольку один градус равен 0,017453 радиана, вы можете использовать эту простую формулу для преобразования:
радианы = градусы × 0,017453
Угол в радианах равен градусам, умноженным на 0.017453.
Например, вот как преобразовать 5 градусов в радианы, используя формулу выше.5 ° = (5 × 0,017453) = 0,087266 рад
Поскольку пи радиан равен 180 °, эта формула преобразования предпочтительнее, поскольку она более точна и удобна в продвинутой математике.
радианы = градусы × π180
Другими словами, угол в радианах равен градусам, умноженным на пи, деленным на 180.
Чтобы использовать эту формулу, начните с добавления градусов к формуле. Затем переместите градусы в верхнюю часть дроби. Затем упростите дробь.
Например, преобразует 5 градусов в радианы, используя предпочтительную формулу. радианы = 5 ° × π180
радиан = 5 ° × π180
радиан = 1 × π36
радиан = 136π
Для измерения угла используются градусы и радианы. Продолжайте читать, чтобы узнать больше о каждой единице измерения.
Градус — это угол, равный 1/360 оборота или окружности. [1] Число 360 имеет 24 делителя, поэтому с ним довольно легко работать. В персидском календарном году также 360 дней, и многие предполагают, что ранние астрономы использовали 1 градус в день.
Градус — это единица измерения угла в системе СИ, используемая в метрической системе.Градус иногда также называют градусом дуги, градусом дуги или градусом дуги. Градусы могут быть сокращены как ° , а также иногда сокращены как ° . Например, 1 градус можно записать как 1 ° или 1 градус.
В качестве альтернативы десятичной форме градусы также могут быть выражены с помощью минут и секунд. Минуты и секунды выражаются с помощью штрихов (‘) и двойных штрихов (″), хотя для удобства часто используются одинарные и двойные кавычки.
Одна минута равна 1/60 градуса, а одна секунда равна 1/60 минуты.
Транспортиры обычно используются для измерения углов в градусах. Это полукруглые или полукруглые устройства со степенью маркировка, позволяющая пользователю измерить угол в градусах. Узнайте больше о том, как использовать транспортир или загрузите транспортир для печати.
Радиан — это угол, равный величине от начала до конца дуги, деленной на радиус окружности или дуги. [2] 1 радиан равен 180 / π, или примерно 57,29578 °. В круге около 6,28318 радиан.
Радиан — это производная единица измерения угла в системе СИ в метрической системе. Радианы могут быть сокращены как рад , а также иногда сокращены как c , r или R . Например, 1 радиан можно записать как 1 рад, 1 c , 1 r или 1 R .
Радианы часто выражаются с использованием их определения. Формула для нахождения радианов: θ = s / r, где угол в радианах θ равен длине дуги s, деленной на радиус r. Таким образом, радианы можно также выразить как формулу длины дуги по радиусу.
Градусы в радианы Преобразование
Преобразовать градусов в радианы .
1 ° = 0,01745329 рад
1 ° = 0,00555556 π рад
градуса в радианы.
- 90 ° = (1/2) π рад
- 90 ° = 1,5 7079633 рад
- 180 ° = π рад
- 180 ° = 3,14159265 рад
- 360 ° = 2 π рад
- 360 ° = 6.28318531 рад
Вы можете преобразовать градус в радиан и вычислить радиан двумя типами. Первое значение в радианах — это приблизительно рассчитанное с помощью пи (π), а второе значение в радианах — это точное значение в радианах, выраженное в единицах пи (π).
Как вычислить градусы в радианах
Мы знаем, что один оборот окружности равен 360 ° ( градусов ), поэтому мы можем использовать 2π = 360 °.Уравнение радиан равно 2 π рад = 360 °. Наконец, радиан равен 180 / π.
1 оборот = 360 ° 2 π рад = 360 ° рад = 180 ° / π радианы = градусы × 180 / π где π = 3.14159 радианы = градусы × 180 / 3,14159; радианы = 57,2958 градусов 1 градус = (1 / 57,2958) радиан 1 градус = 0,01745329 рад (приблизительно) через π радианы = градусы × 180 / π 1 градус = (π / 180) рад
Градусы в радианы Значения
| градусов | радиан (точно) | радиан (приблизительно) |
|---|---|---|
| 15 ° | π ⁄ 12 рад | 0.26179939 рад |
| 30 ° | π ⁄ 6 рад | 0,52359878 рад |
| 36 ° | π ⁄ 5 рад | 0,62831853 рад | π ⁄ 4 рад | 0,78539816 рад |
| 60 ° | π ⁄ 3 рад | 1.04719755 рад |
| 90 ° | π 21850 π ⁄1 915 рад 1.57079633 рад | |
| 180 ° | π рад | 3,14159265 рад |
| 360 ° | 2 π рад | 6,28318531 рад |
Таблица преобразования градусов в радианы
| Градусы | Радианы (приблизительно) | Радианы (точно) | |
|---|---|---|---|
| 0 ° | 0 рад | 0 π рад | |
| 1 ° | 0,017453 рад | 0,01 π рад | |
| 2 ° | 0.034907 рад | 0,01 π рад | |
| 3 ° | 0,05236 рад | 0,02 π рад | |
| 4 ° | 0,069813 рад | 0,02 π рад | |
| 5 ° | 0,087266 рад | 0,03 π рад | |
| 6 ° | 0,10472 рад | 0,03 π рад | |
| 7 ° | 0,122173 рад | 0,04 π рад | |
| 8 ° | 0,139626 рад | 0.04 π рад | |
| 9 ° | 0,15708 рад | 0,05 π рад | |
| 10 ° | 0,174533 рад | 0,06 π рад | |
| 11 ° | 0,1 | 0,06 π рад | |
| 12 ° | 0,20944 рад | 0,07 π рад | |
| 13 ° | 0,226893 рад | 0,07 π рад | |
| 14 ° | 0,244346 рад | 0,08 π рад | |
| 15 ° | 0.261799 рад | 0,08 π рад | |
| 16 ° | 0,279253 рад | 0,09 π рад | |
| 17 ° | 0,296706 рад | 0,09 π рад | |
| 18 ° | 0,314159 рад | 0,1 π рад | |
| 19 ° | 0,331613 рад | 0,11 π рад | |
| 20 ° | 0,349066 рад | 0,11 π рад | |
| 21 ° | 0,366519 рад | 0.12 π рад | |
| 22 ° | 0,383972 рад | 0,12 π рад | |
| 23 ° | 0,401426 рад | 0,13 π рад | |
| 24 ° | 0,418879 рад | 0,13 π рад | |
| 25 ° | 0,436332 рад | 0,14 π рад | |
| 26 ° | 0,453786 рад | 0,14 π рад | |
| 27 ° | 0,471239 рад | 0,15 π рад | |
| 28 ° | 0.488692 рад | 0,16 π рад | |
| 29 ° | 0,506145 рад | 0,16 π рад | |
| 30 ° | 0,523599 рад | 0,17 π рад | |
| 31 ° | 0,541052 рад | 0,17 π рад | |
| 32 ° | 0,558505 рад | 0,18 π рад | |
| 33 ° | 0,575959 рад | 0,18 π рад | |
| 34 ° | 0,5 | 0.19 π рад | |
| 35 ° | 0,610865 рад | 0,19 π рад | |
| 36 ° | 0,628319 рад | 0,2 π рад | |
| 37 ° | 0,645772 рад | 0,21 π рад | |
| 38 ° | 0,663225 рад | 0,21 π рад | |
| 39 ° | 0,680678 рад | 0,22 π рад | |
| 40 ° | 0,698132 рад | 0,22 π рад | |
| 41 ° | 0.715585 рад | 0,23 π рад | |
| 42 ° | 0,733038 рад | 0,23 π рад | |
| 43 ° | 0,750492 рад | 0,24 π рад | |
| 44 ° | 0,767945 рад | 0,24 π рад | |
| 45 ° | 0,785398 рад | 0,25 π рад | |
| 46 ° | 0,802851 рад | 0,26 π рад | |
| 47 ° | 0,820305 рад | 0.26 π рад | |
| 48 ° | 0,837758 рад | 0,27 π рад | |
| 49 ° | 0,855211 рад | 0,27 π рад | |
| 50 ° | 0,872665 рад | 0,28 π рад | |
| 51 ° | 0,8 | 0,28 π рад | |
| 52 ° | 0, 1 рад | 0,29 π рад | |
| 53 ° | 0, | 5 рад | 0,29 π рад |
| 54 ° | 0. | ||
| 0,3 π рад | |||
| 55 ° | 0,959931 рад | 0,31 π рад | |
| 56 ° | 0,977384 рад | 0,31 π рад | |
| 57 ° | 0,994838 рад | 0,32 π рад | |
| 58 ° | 1.012291 рад | 0,32 π рад | |
| 59 ° | 1,029744 рад | 0,33 π рад | |
| 60 ° | 1.047198 рад | 0.33 π рад | |
| 61 ° | 1.064651 рад | 0,34 π рад | |
| 62 ° | 1,082104 рад | 0,34 π рад | |
| 63 ° | 1.099557 рад | 0,35 π рад | |
| 64 ° | 1.117011 рад | 0,36 π рад | |
| 65 ° | 1,134464 рад | 0,36 π рад | |
| 66 ° | 1,151917 рад | 0,37 π рад | |
| 67 ° | 1.169371 рад | 0,37 π рад | |
| 68 ° | 1,186824 рад | 0,38 π рад | |
| 69 ° | 1,204277 рад | 0,38 π рад | |
| 70 ° | 1,22173 рад | 0,39 π рад | |
| 71 ° | 1,239184 рад | 0,39 π рад | |
| 72 ° | 1,256637 рад | 0,4 π рад | |
| 73 ° | 1,27409 рад | 0.41 π рад | |
| 74 ° | 1,2 | рад0,41 π рад | |
| 75 ° | 1,308997 рад | 0,42 π рад | |
| 76 ° | 1,32645 рад | 0,42 π рад | |
| 77 ° | 1,343904 рад | 0,43 π рад | |
| 78 ° | 1,361357 рад | 0,43 π рад | |
| 79 ° | 1,37881 рад | 0,44 π рад | |
| 80 ° | 1.396263 рад | 0,44 π рад | |
| 81 ° | 1,413717 рад | 0,45 π рад | |
| 82 ° | 1,43117 рад | 0,46 π рад | |
| 83 ° | 1,448623 рад | 0,46 π рад | |
| 84 ° | 1.466077 рад | 0,47 π рад | |
| 85 ° | 1,48353 рад | 0,47 π рад | |
| 86 ° | 1.500983 рад | 0.48 π рад | |
| 87 ° | 1,518436 рад | 0,48 π рад | |
| 88 ° | 1,53589 рад | 0,49 π рад | |
| 89 ° | 1,553343 рад | 0,49 π рад | |
| 90 ° | 1,570796 рад | 0,5 π рад | |
| 91 ° | 1,58825 рад | 0,51 π рад | |
| 92 ° | 1,605703 рад | 0,51 π рад | |
| 93 ° | 1.623156 рад | 0,52 π рад | |
| 94 ° | 1,640609 рад | 0,52 π рад | |
| 95 ° | 1,658063 рад | 0,53 π рад | |
| 96 ° | 1,675516 рад | 0,53 π рад | |
| 97 ° | 1,6 | рад0,54 π рад | |
| 98 ° | 1,710423 рад | 0,54 π рад | |
| 99 ° | 1,727876 рад | 0.55 π рад | |
| 100 ° | 1,745329 рад | 0,56 π рад | |
| 101 ° | 1,762783 рад | 0,56 π рад | |
| 102 ° | 1,780236 рад | 0,57 π рад | |
| 103 ° | 1,797689 рад | 0,57 π рад | |
| 104 ° | 1,815142 рад | 0,58 π рад | |
| 105 ° | 1,832596 рад | 0,58 π рад | |
| 106 ° | 1.850049 рад | 0,59 π рад | |
| 107 ° | 1,867502 рад | 0,59 π рад | |
| 108 ° | 1,884956 рад | 0,6 π рад | |
| 109 ° | 1, | 9 рад | 0,61 π рад |
| 110 ° | 1, | 0,61 π рад | |
| 111 ° | 1, | 5 рад0,62 π рад | |
| 112 ° | 1.954769 рад | 0.62 π рад | |
| 113 ° | 1.972222 рад | 0,63 π рад | |
| 114 ° | 1.989675 рад | 0,63 π рад | |
| 115 ° | 2,007129 рад | 0,64 π рад | |
| 116 ° | 2,024582 рад | 0,64 π рад | |
| 117 ° | 2,042035 рад | 0,65 π рад | |
| 118 ° | 2,059489 рад | 0,66 π рад | |
| 119 ° | 2.076942 рад | 0,66 π рад | |
| 120 ° | 2,0 | рад0,67 π рад |
| Градусы | Радианы (приблизительно) | Радианы (точно) | |
|---|---|---|---|
| 120 ° | 2,0 | рад0,67 π рад | |
| 121 ° | 2,111848 рад | 0,67 π рад | |
| 122 ° | 2,129302 рад | 0,68 π рад | |
| 123 ° | 2.146755 рад | 0,68 π рад | |
| 124 ° | 2,164208 рад | 0,69 π рад | |
| 125 ° | 2,181662 рад | 0,69 π рад | |
| 126 ° | 2,199115 рад | 0,7 π рад | |
| 127 ° | 2,216568 рад | 0,71 π рад | |
| 128 ° | 2,234021 рад | 0,71 π рад | |
| 129 ° | 2,251475 рад | 0.72 π рад | |
| 130 ° | 2,268928 рад | 0,72 π рад | |
| 131 ° | 2,286381 рад | 0,73 π рад | |
| 132 ° | 2,303835 рад | 0,73 π рад | |
| 133 ° | 2,321288 рад | 0,74 π рад | |
| 134 ° | 2,338741 рад | 0,74 π рад | |
| 135 ° | 2,356194 рад | 0,75 π рад | |
| 136 ° | 2.373648 рад | 0,76 π рад | |
| 137 ° | 2,3 рад | 0,76 π рад | |
| 138 ° | 2,408554 рад | 0,77 π рад | |
| 139 ° | 2,426008 рад | 0,77 π рад | |
| 140 ° | 2.443461 рад | 0,78 π рад | |
| 141 ° | 2,460914 рад | 0,78 π рад | |
| 142 ° | 2,478368 рад | 0.79 π рад | |
| 143 ° | 2.495821 рад | 0,79 π рад | |
| 144 ° | 2,513274 рад | 0,8 π рад | |
| 145 ° | 2,530727 рад | 0,81 π рад | |
| 146 ° | 2,548181 рад | 0,81 π рад | |
| 147 ° | 2,565634 рад | 0,82 π рад | |
| 148 ° | 2,583087 рад | 0,82 π рад | |
| 149 ° | 2.600541 рад | 0,83 π рад | |
| 150 ° | 2,617994 рад | 0,83 π рад | |
| 151 ° | 2,635447 рад | 0,84 π рад | |
| 152 ° | 2,6529 рад | 0,84 π рад | |
| 153 ° | 2,670354 рад | 0,85 π рад | |
| 154 ° | 2,687807 рад | 0,86 π рад | |
| 155 ° | 2,70526 рад | 0.86 π рад | |
| 156 ° | 2,722714 рад | 0,87 π рад | |
| 157 ° | 2,740167 рад | 0,87 π рад | |
| 158 ° | 2,75762 рад | 0,88 π рад | |
| 159 ° | 2,775074 рад | 0,88 π рад | |
| 160 ° | 2,7 | рад0,89 π рад | |
| 161 ° | 2,80998 рад | 0,89 π рад | |
| 162 ° | 2.827433 рад | 0,9 π рад | |
| 163 ° | 2,844887 рад | 0,91 π рад | |
| 164 ° | 2,86234 рад | 0,91 π рад | |
| 165 ° | 2,879793 рад | 0,92 π рад | |
| 166 ° | 2,897247 рад | 0,92 π рад | |
| 167 ° | 2,9147 рад | 0,93 π рад | |
| 168 ° | 2, | 3 рад0.93 π рад | |
| 169 ° | 2,949606 рад | 0,94 π рад | |
| 170 ° | 2,96706 рад | 0,94 π рад | |
| 171 ° | 2,984513 рад | 0,95 π рад | |
| 172 ° | 3,001966 рад | 0,96 π рад | |
| 173 ° | 3,01942 рад | 0,96 π рад | |
| 174 ° | 3,036873 рад | 0,97 π рад | |
| 175 ° | 3.054326 рад | 0,97 π рад | |
| 176 ° | 3,071779 рад | 0,98 π рад | |
| 177 ° | 3,089233 рад | 0,98 π рад | |
| 178 ° | 3,106686 рад | 3,106686 рад | π рад |
| 179 ° | 3,124139 рад | 0,99 π рад | |
| 180 ° | 3,141593 рад | 1 π рад | |
| 181 ° | 3,159046 рад | 1.01 π рад | |
| 182 ° | 3,176499 рад | 1,01 π рад | |
| 183 ° | 3,1 | рад1,02 π рад | |
| 184 ° | 3,211406 рад | 1,02 π рад | |
| 185 ° | 3,228859 рад | 1,03 π рад | |
| 186 ° | 3,246312 рад | 1,03 π рад | |
| 187 ° | 3,263766 рад | 1,04 π рад | |
| 188 ° | 3.281219 рад | 1,04 π рад | |
| 189 ° | 3,298672 рад | 1,05 π рад | |
| 190 ° | 3,316126 рад | 1,06 π рад | |
| 191 ° | 3,333579 рад | 1,06 π рад | |
| 192 ° | 3,351032 рад | 1,07 π рад | |
| 193 ° | 3,368485 рад | 1,07 π рад | |
| 194 ° | 3,385939 рад | 1.08 π рад | |
| 195 ° | 3,403392 рад | 1,08 π рад | |
| 196 ° | 3,420845 рад | 1,09 π рад | |
| 197 ° | 3,438299 рад | 1,09 π рад | |
| 198 ° | 3,455752 рад | 1,1 π рад | |
| 199 ° | 3,473205 рад | 1,11 π рад | |
| 200 ° | 3,4 | ||
| 1,11 π рад | |||
| 201 ° | 3.508112 рад | 1,12 π рад | |
| 202 ° | 3,525565 рад | 1,12 π рад | |
| 203 ° | 3,543018 рад | 1,13 π рад | |
| 204 ° | 3,560473 рад | 1,1 π рад | |
| 205 ° | 3,577925 рад | 1,14 π рад | |
| 206 ° | 3,595378 рад | 1,14 π рад | |
| 207 ° | 3,612832 рад | 1.15 π рад | |
| 208 ° | 3,630285 рад | 1,16 π рад | |
| 209 ° | 3,647738 рад | 1,16 π рад | |
| 210 ° | 3,665191 рад | 1,17 π рад | |
| 211 ° | 3,682645 рад | 1,17 π рад | |
| 212 ° | 3,700098 рад | 1,18 π рад | |
| 213 ° | 3,717551 рад | 1,18 π рад | |
| 214 ° | 3.735005 рад | 1,19 π рад | |
| 215 ° | 3,752458 рад | 1,19 π рад | |
| 216 ° | 3,769911 рад | 1,2 π рад | |
| 217 ° | 3,787364 рад | 1,287364 рад π рад | |
| 218 ° | 3,804818 рад | 1,21 π рад | |
| 219 ° | 3,822271 рад | 1,22 π рад | |
| 220 ° | 3,839724 рад | 1.22 π рад | |
| 221 ° | 3.857178 рад | 1,23 π рад | |
| 222 ° | 3,874631 рад | 1,23 π рад | |
| 223 ° | 3,8 | рад | 1,24 π рад |
| 224 ° | 3, 8 рад | 1,24 π рад | |
| 225 ° | 3, | 1 рад1,25 π рад | |
| 226 ° | 3, | 4 рад | 1,26 π рад |
| 227 ° | 3.961897 рад | 1,26 π рад | |
| 228 ° | 3.979351 рад | 1,27 π рад | |
| 229 ° | 3,996804 рад | 1,27 π рад | |
| 230 ° | 4,014257 рад | π рад | |
| 231 ° | 4,031711 рад | 1,28 π рад | |
| 232 ° | 4,049164 рад | 1,29 π рад | |
| 233 ° | 4,066617 рад | 1.29 π рад | |
| 234 ° | 4,08407 рад | 1,3 π рад | |
| 235 ° | 4,101524 рад | 1,31 π рад | |
| 236 ° | 4,118977 рад | 1,31 π рад | |
| 237 ° | 4,13643 рад | 1,32 π рад | |
| 238 ° | 4,153884 рад | 1,32 π рад | |
| 239 ° | 4,171337 рад | 1,33 π рад | |
| 240 ° | 4.18879 рад | 1,33 π рад |
| градусов | радиан (приблизительно) | радиан (точно) | |
|---|---|---|---|
| 240 ° | 4.18879 рад | 1,33 π рад | |
| 241 ° | 4.206243 рад | 1,34 π рад | |
| 242 ° | 4,223697 рад | 1,34 π рад | |
| 243 ° | 4,24115 рад | 1,35 π рад | |
| 244 ° | 4.258603 рад | 1,36 π рад | |
| 245 ° | 4,276057 рад | 1,36 π рад | |
| 246 ° | 4,29351 рад | 1,37 π рад | |
| 247 ° | 4,3109637 рад | π рад | |
| 248 ° | 4,328417 рад | 1,38 π рад | |
| 249 ° | 4,34587 рад | 1,38 π рад | |
| 250 ° | 4,363323 рад | 1.39 π рад | |
| 251 ° | 4,380776 рад | 1,39 π рад | |
| 252 ° | 4,39823 рад | 1,4 π рад | |
| 253 ° | 4,415683 рад | 1,41 π рад | |
| 254 ° | 4,433136 рад | 1,41 π рад | |
| 255 ° | 4,45059 рад | 1,42 π рад | |
| 256 ° | 4,468043 рад | 1,42 π рад | |
| 257 ° | 4.485496 рад | 1,43 π рад | |
| 258 ° | 4,502949 рад | 1,43 π рад | |
| 259 ° | 4,520403 рад | 1,44 π рад | |
| 260 ° | 4,537856 рад | 1,43 π рад | |
| 261 ° | 4,555309 рад | 1,45 π рад | |
| 262 ° | 4,572763 рад | 1,46 π рад | |
| 263 ° | 4,5 | рад | 1.46 π рад |
| 264 ° | 4.607669 рад | 1,47 π рад | |
| 265 ° | 4,625123 рад | 1,47 π рад | |
| 266 ° | 4,642576 рад | 1,48 π рад | |
| 267 ° | 4,660029 рад | 1,48 π рад | |
| 268 ° | 4,677482 рад | 1,49 π рад | |
| 269 ° | 4,694936 рад | 1,49 π рад | |
| 270 ° | 4.712389 рад | 1,5 π рад | |
| 271 ° | 4,729842 рад | 1,51 π рад | |
| 272 ° | 4,747296 рад | 1,51 π рад | |
| 273 ° | 4,764749 рад | 1,5 π рад | |
| 274 ° | 4,782202 рад | 1,52 π рад | |
| 275 ° | 4,799655 рад | 1,53 π рад | |
| 276 ° | 4,817109 рад | 1.53 π рад | |
| 277 ° | 4,834562 рад | 1,54 π рад | |
| 278 ° | 4,852015 рад | 1,54 π рад | |
| 279 ° | 4,869469 рад | 1,55 π рад | |
| 280 ° | 4,886922 рад | 1,56 π рад | |
| 281 ° | 4, | ||
| 1,56 π рад | |||
| 282 ° | 4, | 8 рад | 1,57 π рад |
| 283 ° | 4. | 2 рад | 1,57 π рад |
| 284 ° | 4,956735 рад | 1,58 π рад | |
| 285 ° | 4,974188 рад | 1,58 π рад | |
| 286 ° 1,5 | 4,9 | 4,9 рад | π рад |
| 287 ° | 5.009095 рад | 1,59 π рад | |
| 288 ° | 5,026548 рад | 1,6 π рад | |
| 289 ° | 5,044002 рад | 1.61 π рад | |
| 290 ° | 5.061455 рад | 1,61 π рад | |
| 291 ° | 5.078908 рад | 1,62 π рад | |
| 292 ° | 5,096361 рад | 1,62 π рад | |
| 293 ° | 5,113815 рад | 1,63 π рад | |
| 294 ° | 5,131268 рад | 1,63 π рад | |
| 295 ° | 5,148721 рад | 1,64 π рад | |
| 296 ° | 5.166175 рад | 1,64 π рад | |
| 297 ° | 5,183628 рад | 1,65 π рад | |
| 298 ° | 5.201081 рад | 1,66 π рад | |
299 °15 | 5,218534 рад | 1,65 π рад | |
| 300 ° | 5.235988 рад | 1,67 π рад | |
| 301 ° | 5,253441 рад | 1,67 π рад | |
| 302 ° | 5,270894 рад | 1.68 π рад | |
| 303 ° | 5.288348 рад | 1,68 π рад | |
| 304 ° | 5,305801 рад | 1,69 π рад | |
| 305 ° | 5,323254 рад | 1,69 π рад | |
| 306 ° | 5,340708 рад | 1,7 π рад | |
| 307 ° | 5,358161 рад | 1,71 π рад | |
| 308 ° | 5,375614 рад | 1,71 π рад | |
| 309 ° | 5.3 | рад1,72 π рад | |
| 310 ° | 5,410521 рад | 1,72 π рад | |
| 311 ° | 5,427974 рад | 1,73 π рад | |
| 312 ° | 5,445427 рад | 1,73 π рад | |
| 313 ° | 5,462881 рад | 1,74 π рад | |
| 314 ° | 5,480334 рад | 1,74 π рад | |
| 315 ° | 5,497787 рад | 1.75 π рад | |
| 316 ° | 5,51524 рад | 1,76 π рад | |
| 317 ° | 5,532694 рад | 1,76 π рад | |
| 318 ° | 5,550147 рад | 1,77 π рад | |
| 319 ° | 5,5676 рад | 1,77 π рад | |
| 320 ° | 5,585054 рад | 1,78 π рад | |
| 321 ° | 5,602507 рад | 1,78 π рад | |
| 322 ° | 5.61996 рад | 1,79 π рад | |
| 323 ° | 5,637413 рад | 1,79 π рад | |
| 324 ° | 5,654867 рад | 1,8 π рад | |
| 325 ° | 5,67232 рад | 1,81 π рад | |
| 326 ° | 5,689773 рад | 1,81 π рад | |
| 327 ° | 5,707227 рад | 1,82 π рад | |
| 328 ° | 5,72468 рад | 1.82 π рад | |
| 329 ° | 5,742133 рад | 1,83 π рад | |
| 330 ° | 5,759587 рад | 1,83 π рад | |
| 331 ° | 5,77704 рад | 1,84 π рад | |
| 332 ° | 5,7 | рад1,84 π рад | |
| 333 ° | 5,811946 рад | 1,85 π рад | |
| 334 ° | 5,8294 рад | 1,86 π рад | |
| 335 ° | 5.846853 рад | 1,86 π рад | |
| 336 ° | 5,864306 рад | 1,87 π рад | |
| 337 ° | 5,88176 рад | 1,87 π рад | |
| 338 ° | 5,899288 рад | 1.87 π рад | |
| 339 ° | 5. | 1,88 π рад | |
| 340 ° | 5, | 9 рад1,89 π рад | |
| 341 ° | 5,951573 рад | 1.89 π рад | |
| 342 ° | 5.969026 рад | 1,9 π рад | |
| 343 ° | 5,986479 рад | 1,91 π рад | |
| 344 ° | 6,003933 рад | 1,91 π рад | |
| 345 ° | 6,021386 рад | 1,92 π рад | |
| 346 ° | 6.038839 рад | 1,92 π рад | |
| 347 ° | 6.056292 рад | 1,93 π рад | |
| 348 ° | 6.073746 рад | 1,93 π рад | |
| 349 ° | 6,0 рад | 1,94 π рад | |
| 350 ° | 6,108652 рад | 1,94 π рад | |
| 351 ° | 6,126106 рад | 6,126106 рад | π рад |
| 352 ° | 6,143559 рад | 1,96 π рад | |
| 353 ° | 6,161012 рад | 1,96 π рад | |
| 354 ° | 6,178466 рад | 1.97 π рад | |
| 355 ° | 6,195919 рад | 1,97 π рад | |
| 356 ° | 6,213372 рад | 1,98 π рад | |
| 357 ° | 6,230825 рад | 1,98 π рад | |
| 358 ° | 6,248279 рад | 1,99 π рад | |
| 359 ° | 6,265732 рад | 1,99 π рад | |
| 360 ° | 6,283185 рад | 2 π рад |
Мы просто вычисляем градус в радиан , чтобы вычислить радианы в градусы, перейдите на страницу конвертера радианов в градусы.
Преобразование градусов в радианы Формула
Прежде чем переходить к изучению формулы преобразования градусов в радианы, давайте вспомним, что такое градусы и радианы. «Градусы» и «радианы» — это две разные единицы измерения углов.
- 1 градус записывается как 1 °.
- 1 радиан записывается как 1 (или) 1 c .
то есть, если после меры угла нет единицы измерения, это означает, что она выражена в радианах.
Мы знаем, что один полный оборот (против часовой стрелки) равен 360 °, что эквивалентно 2π в радианах.т.е. 360 ° = 2π. Отсюда получаем π = 180 °. Давайте выучим формулу преобразования градусов в радианы с несколькими решенными примерами в конце.
Разбивайте сложные концепции с помощью простых изображений.
Математика больше не будет сложным предметом, особенно если вы понимаете концепции посредством визуализации с помощью Cuemath.
Забронируйте бесплатную пробную версию Класс
Что такое формула преобразования градусов в радианы?
Используя приведенное выше уравнение, мы можем сказать, что для преобразования градусов в радианы мы умножаем угол (в градусах) на π / 180.Таким образом, формула преобразования градусов в радианы:
Радианы = Градусы × π / 180Примечание. С другой стороны, формула для преобразования радианов в градусы:
Градусов = Радианы × 180 / πЗдесь вы можете увидеть некоторые углы как в градусах, так и в радианах.
Давайте посмотрим на применение формулы преобразования градусов в радианы в следующем разделе.
- Пример 1: Преобразование 120 ° в радианы.
Решение:
Найти: эквивалент 120 ° в радианах.
Использование формулы преобразования градусов в радианы:
Радианы = Градусы × π / 180
Радианы = 120 × π / 180 = 2π / 3
Ответ: 120 ° = 2π / 3.
- Пример 2:
Преобразование 900 ° в радианы.
Решение:
Найти: эквивалент 900 ° в радианах.
Использование формулы преобразования градусов в радианы:
Радианы = Градусы × π / 180
Радианы = 900 × π / 180 = 5π
Ответ: 900 ° = 5π.
перейти к слайду
Тригонометрия: градусы и радианы — Magoosh Math
Мы продолжим наши уроки тригонометрии, рассмотрев градусы и радианы.
Теперь мы можем ввести очень важную идею радианов. И я начну с того, что вы когда-нибудь задумывались, почему прямой угол определяется как 90 градусов? Почему это число 90? Откуда взялась идея ученых степеней? Система восходит к древней вавилонской религии, более 3000 лет назад.
Итак, вот изображение вавилонского бога Мардука и его домашнего дракона. Эти древние вавилоняне считали 60 и 360 священными числами. Они верили во все виды вещей, они верили в сонм странных богов, они приносили в жертву скотных животных для различных целей.Это очень старая религия, которая давно вымерла. Но мы по-прежнему держимся за эти два числа.
Оказывается, вавилоняне считали, что весь круг должен делиться на 360 частей, так что отсюда и возникла система степеней. Эти вавилонские ценности также являются причиной того, что в часе 60 минут, а в минуте — 60 секунд. Итак, оказывается, что, хотя эта религия мертва уже тысячелетие, оказывается, что их ценности по-прежнему сильно влияют на то, как мы смотрим на мир.
Восстановленный Древний Вавилон
Автор: Юкка Палм
Тот факт, что вавилоняне решили измерять углы таким способом, основываясь на ценностях своей древней языческой религии, не обязательно означает, что с математической точки зрения это лучший способ измерения углов . Градусы знакомы и широко используются, но с математической точки зрения это не лучший способ измерения углов. Итак, предположим, мы начали с нуля и хотели найти лучший способ измерения углов.
Лучший способ измерения углов, самый естественный способ измерения углов, основан не на каком-то произвольном выборе, основанном на языческой религии.Но это будет происходить из качеств самого круга. Так думает математик, каковы качества самого круга? Подумайте о круге.
Image By kabzarchyk
Какая самая основная длина, связанная с кругом, по которой можно вычислить все, что есть в круге? Очевидно радиус. Мы можем вычислить площадь по радиусу, мы можем вычислить длину окружности по радиусу. Все, что нам нужно, мы можем рассчитать по радиусу.
Если бы мы могли использовать радиус окружности для определения углового измерения, это могло бы стать основой новой системы измерения углов. И именно это мы и будем делать. Эта система известна как радианы. Так что помните, что дуги окружностей имеют длину. Предположим, мы сделали дугу, длина которой равна радиусу.
Итак, у нас есть небольшой сектор. И, конечно же, из центра круга выходят два радиуса. И длина дуги тоже, хоть она и изогнута, но такая же длина.Итак, все три стороны этого маленького сектора имеют одинаковую длину. Это определило бы угол в один радиан. И мы могли бы использовать это как единицу угла.
Итак, мы могли бы измерить радианы по окружности, и это было бы то же самое, что измерить количество радиусов по окружности. Фактически, мы уже измеряем всю окружность, используя значения радиуса. Мы знаем, что длина окружности равна 2 пи р. Это означает, что по окружности имеется 2 радиуса Пи.Длина радиуса 2 пи по всей окружности.
Это означает, что по всему периметру круга есть 2 пи радиана. Итак, по всему кругу, то, что мы раньше называли 360 градусами, теперь мы будем называть это 2 пи радианами. Итак, если 360 градусов = 2 пи радиана, обратите внимание, что для градусов мы должны использовать символ градуса. Радианы настолько особенные, что нам не нужен специальный символ для них.
Нам не нужно писать r, радианы или что-то в этом роде. Мы можем просто написать 2 пи, и это означает, что это 2 пи радиана.И это позволяет нам понять, как связать всю систему градусов со всей радианной системой. Разделите это уравнение на 2, мы получим 180 = пи, что очень важно. Угол 180 градусов равен углу радиана пи.
Разделите это снова, прямой угол, который мы называем 90 градусами, теперь мы можем назвать это углом пи / 2. Это мера прямого угла в радианах, пи / 2. Теперь начнем с этого прямого угла, если мы разделим его на 2, мы получим угол в 45 градусов, и это будет пи / 4.Снова вернитесь к пи / 2, вместо этого разделите его на 3.
Мы получим 30 градусов = пи / 6, если мы умножим обе стороны на 2, мы получим 60 градусов = пи / 3. Это значения углов всех специальных треугольников в радианах. Итак, два особых треугольника, один из них — это треугольник пи / 4, пи / 4, пи / 2. Другой — треугольник пи / 6, пи / 3, пи / 2. Уравнение 180 градусов = пи часто является хорошим началом, потому что 180 имеет очень много факторов.
Предположим, нам нужно найти, скажем, 20 градусов в радианах. Конечно, 180 = 20 x 9, и это, конечно, равно Пи.Просто разделите обе стороны на 9, и мы получим 20 градусов = пи / 9. Это может быть очень быстрым способом, если количество градусов является очевидным множителем 180. Мы также можем изменить уравнение 180 градусов = пи на дробь, равную 1.
Итак, 1 = пи / 180, мы можем умножить любой градус измерение этой дроби можно изменить с градусов на радианы. Например, 270 градусов умноженные на пи / 180, мы получим 270 пи / 180, что составляет 27/18. Разделите верхнюю и нижнюю части на 9, мы получим 3 пи / 2, так что 3 пи / 2 равно 270 градусам.
Фактически, мы можем определить четыре квадранта в терминах или радианах.Первый квадрант от 0 до пи / 2, от 0 до прямого угла. Второй квадрант от пи / 2 до пи. Под прямым углом к полному полукругу. Третий квадрант от пи до 3pi / 2. Первый квадрант — от 3pi / 2 до 2pi.
Идентификация
Часто именно так тест определяет конкретный квадрант. Они не скажут третий квадрант, они скажут, что тета находится между пи и 3pi / 2. Какое из перечисленного ниже значение 240 градусов в радианах? Поставьте видео на паузу, а потом мы поговорим об этом.
Метод 1
Хорошо, метод 1, это более наглядный метод.Обратите внимание, что 240 градусов — это вдвое больше 120 градусов, а 120 градусов — это треть круга.
Это означает, что 240 градусов составляют 2/3 окружности. Полный круг равен 2 пи, поэтому 2/3 из 2 пи будут 4/3 пи. Вот что такое 240 градусов в радианах. Это метод первый.
Второй метод
Второй метод — более методичный метод, позволяющий взять это число и умножить его на пи / 180.
При умножении мы отменяем нули, затем сокращаем множитель 6 и получаем 4 пи / 3.Итак, оказывается, что ответ — вариант ответа D. Позвольте мне отметить, что очень методично просто умножать на число пи / 180. Я собираюсь отговорить вас от того, чтобы 100% времени уделять методу преобразования в радианы.
Гораздо эффективнее думать о пропорциях и думать о проблеме визуально. Вы поймете радианы гораздо глубже, если не будете просто каждый раз полагаться на умножение на это соотношение. Значения пи в радианах легко соотнести с визуальным пониманием.Угол 3pi / 4 равен 3/4 пи, то есть 3/4 полукруга.
Это очень легко представить. Возьмите полукруг, разделите его на части, 3 из которых составляют угол 3 пи / 4. Чтобы глубоко понять радианы, когда вы можете думать о них как визуально, так и численно. На этом уровне все преимущества радианов не обязательно очевидны.
Они становятся намного более очевидными в исчислении, когда мы начинаем проводить исчисление с тригонометрическими функциями. Вот где радианы действительно доказывают свою ценность.Очевидно, это выводит нас далеко за рамки всего, что связано с ACT, поэтому нам не нужно беспокоиться об этом для ACT. Это всего лишь предварительный обзор того, почему радианы так важны.