125 умножить на 5 в степени n: Mathway | Популярные задачи

2

§ Стандартный вид числа. Записать число в стандартном виде

В задачах по физике часто приходится работать с очень большими и очень малыми величинами.

Как вести вычисления в атомной физике? Или записать радиус электрона? Если потребуется сравнить массу электрона и массу планеты Земля, как произвести вычисления с числами, которые несопоставимы друг с другом в обычном виде?

Физики и математики, столкнувшись с такими задачами, поняли, что для решения подобных задач требуется привести числа к единому стандартному виду. Так появилось понятие стандартный вид числа.

---

Прежде чем переходить к объяснению, как записать число в стандартном виде, нужно вспомнить определение степени. Особенно хорошо нужно помнить, чему равняется число «10» в различных степенях.

• 10⁻² = = = 0,01 (более подробно об отрицательной степени можно прочитать в уроке 9 класса «Отрицательная степень»)
• 10⁻¹ = = = 0,1
• 10⁰ = 1
• 10¹ = 10
• 10² = 100
• 10³ = 1000
• …

Вспомним, что при умножении целого числа на 10, 100, 1000 и т. д. мы просто добавляли тоже количество нулей, что и в 10, 100, 1000 и т.д..

• 5 · 10 = 50
• 27 · 100 = 2 700
• 18 · 1000 = 18 000

Теперь запишем тоже самое, используя определение степени.

• 5 · 10 = 5 · 10¹ = 50
• 27 · 100 = 27 · 10² = 2 700
• 18 · 1000 = 18 · 10³ = 18 000

При делении целого числа на 10, 100, 1000 и т.д. мы убирали нули.

• 13 000 : 100 =

  13 000

  100

  = 130
• 50 : 10 = = 5

Для десятичных дробей действует схожее правило умножения на 10, 100, 1000. При умножении десятичной дроби на 10, 100, 1000 и т.д. мы перемещаем запятую вправо на количество нулей, что и в 10, 100, 1000 и т.д…

• 5,7 · 100 = 570
• 7,013 · 10 = 70,13
• 68,3 · 1000 = 68 300

С помощью степени можно записать вычисления выше следующим образом:

• 5,7 · 100 = 5,7 · 10² = 570
• 7,013 · 10 = 7,013 · 10¹ = 70,13
• 68,3 · 1000 = 68,3 · 10³ = 68 300

При делении на 10, 100, 1000 и т. д. перемещаем запятую влево.

• 6,7 : 10 = = 0,67
• 0,15 : 100 =

  0,15

  100

  = 0,0015

С помощью определения отрицательной степени можно записать вычисления выше следующим образом:

• 6,7 : 10 = = 6,7 · 10 ⁻¹ = 0,67
• 0,15 : 100 =

  0,15

  100

  = 0,15 · 10⁻² = 0,0015

Стандартный вид числа

Вначале обратимся к строгому математическому определению стандартного вида числа. Затем по традиции разберемся на примерах.

Запомните!

Любое натуральное число или конечную положительную десятичную дробь можно записать в виде:

a · 10ⁿ,
где 1 ≤ a < 10 и n — натуральное число.

Такая запись называется — стандартный вид числа.
При этом число «n» называют порядком числа «a».

Из определения выше важно понять, что степень, в которой стоит «10», в стандартном виде числа называется порядком.

Теперь к примеру. Пусть нам дано число «5 600» и требуется записать его в стандартном виде.

По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от «1» до «9».

В числе «5 600» первая цифра справа — «5». Поставим справа от нее запятую и посчитаем, сколько знаков у нас осталось справа от запятой.

Значит, чтобы из «5,600» получить «5600» нам нужно умножить «5,600» на «1000». Запишем полученное преобразование.

5 600 = 5,600 · 1000

Теперь запишем «1000» с использованием степени.

5 600 = 5,600 · 1000 = 5,600 · 10³

Завершающим штрихом будет отбрасывание незначащих нулей в десятичной дроби.

5 600 = 5,600 · 1000 = 5,600 · 10³
= 5,6 · 10³

Таким образом «5 600» в стандартном виде будет выглядеть следующим образом:

5 600 = 5,6 · 10³

Чтобы проверить, что мы не ошиблись в вычислениях, произведем вычисления обратно.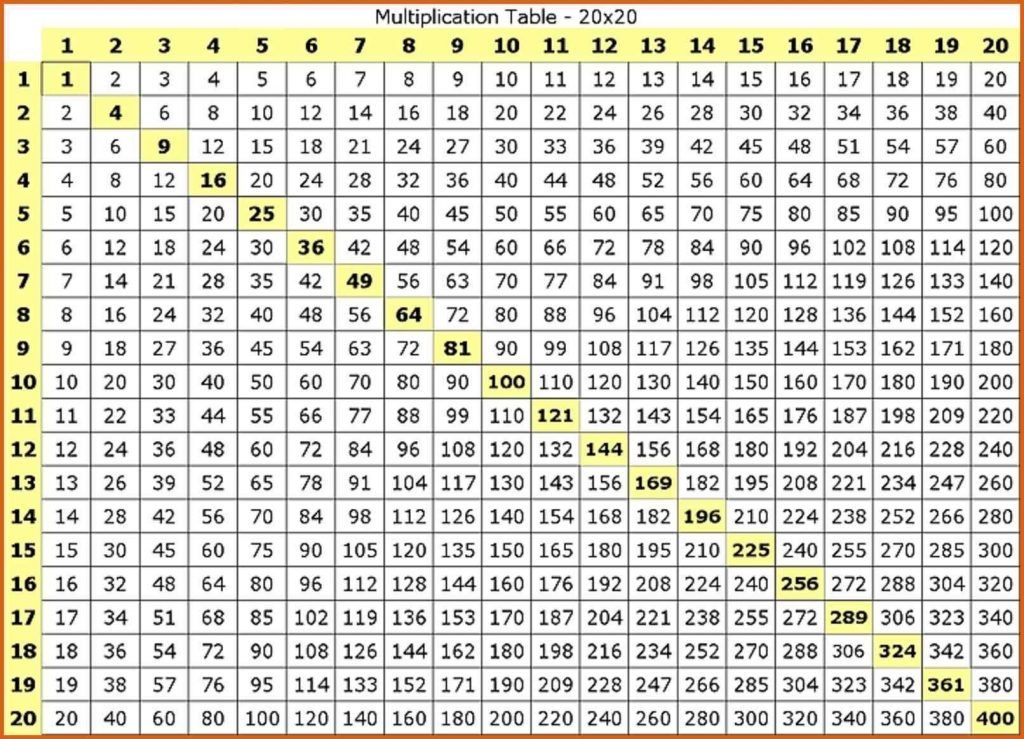

Если все выполнено корректно, мы должны получить изначальное число. Убедимся в этом.

5,6 · 10³ = 5 600

---

Рассмотрим другой пример, когда нужно представить десятичную дробь в стандартном виде. Например, десятичную дробь «0,017».

Согласно определению стандартного вида числа необходимо, чтобы первой цифрой перед запятой стояла только одна цифра от «1» до «9».

В десятичной дроби «0,017» вначале идет «0». Нам это не подходит, поэтому двигаемся слева направо, чтобы найти первую цифру отличную от «0».

Это цифра «1». Посчитаем сколько знаков (цифр) стояло от запятой до цифры «1», включая саму цифру «1».

Получается два знака. Начнем записывать «0,017» в стандартном виде. Перенесем запятую и поставим ее справа от «1».

0,017 = 1,7 · 10…

Ответим себе на вопрос: «На что нужно умножить или разделить «1,7», чтобы получить изначальное число «0,017» ?». Напоминаем, что при делении на 10, 100, 1000 и т.

д. запятая переносится Напоминаем, что при делении на 10, 100, 1000 и т.д. запятая переносится влево.

Выходит, чтобы из «1,7» сделать 0,017», нужно «1,7 разделить на «100» (чтобы перенести запятую на два знака влево).

0,017 = 1,7 : 100

Запишем это деление на «100», используя обыкновенную дробь.

0,017 = 1,7 : 100 = 1,7 ·

С помощью отрицательной степени запишем окончательный вид числа «0,017» в стандартном виде.

0,017 = 1,7 : 100 = 1,7 · =
1,7 · 10⁻²

Примеры решения задач

на запись числа в стандартном виде

Разбор примера

Определить порядок числа, выражающего значение физической константы:

1) масса покоя электрона
m_e = 9,1093897 · 10⁻³¹

---

Напоминаем, что порядком числа, которое приведено в стандартный вид, называют степень, в которой стоит «10». В данном примере «10» стоит в

степени «−31». Значит, порядком массы покоя электрона является «−31».

Разбор примера

Записать в стандартном виде и определить порядок числа k, выражающего физического константу:

2) постоянная Фарадея
F = 96485,309 Кл/моль;

---

По определению стандартного вида числа необходимо, чтобы перед запятой стояла только одна цифра от «1» до «9».

Начнем записывать постоянную Фарадея в стандартном виде. Перенесем запятую после первой цифры отличной от нуля. Это цифра «9».

96485,309 = 9,6485309 · 10…

Зададим себе вопрос: «На что нужно умножить «9,6485309», чтобы получить «96485,309» ?» Посчитаем количество знаков (цифр), на которое требуется перенести запятую в «96485,309», чтобы получить «96485309».

Получается «4» знака. Значит постоянная Фарадея в стандартном виде будет выглядеть следующим образом:

96485,309 = 9,6485309 · 10⁴

Порядком числа «9,6485309 · 10⁴» является степень, в которой стоит «10». Следовательно, порядок «k = 4».

---

3) Постоянная Лошмидта
n₀ = 2686763 · 10 ²⁶

Начнем записывать постоянную Лошмидта в стандартном виде, т.е. как:

2686763 · 10 ²⁶ =
2,686763 · 10 ²⁶ · 10…

Рассчитаем, на какое количество знаков (цифр) требуется перенести запятую, чтобы из «2,686763» получить «2686763».

Значит, чтобы получить из «2,686763» нужно изначальное число «2686763» умножить на «10⁶».

2686763 =
2,686763 · 10 ²⁶ · 10⁶

Завершим решение и запишем окончательный ответ, используя свойство «Произведение степеней».

2686763 = 2,686763 · 10 ²⁶ · 10⁶ = 2,686763 · 10 ^{26 + 6} = 2,686763 · 10 ³²

Другие примеры записи чисел в стандартном виде

• 0,52 = 5,2 · 10 ⁻¹
• 401 = 4,01 · 10 ²
• 60,756 = 6,0756 · 10¹
• 0,00123 = 1,23 · 10⁻³

Страница 40 №153-171 ГДЗ к учебнику «Математика» 5 класс Никольский, Потапов, Решетников

ГДЗ 1 класс

ГДЗ 10 класс

  

Категория: ГДЗ Математика учебник 5 класс Никольский, Потапов, Решетников

Задание № 153. Что называют степенью числа a с натуральным показателем n (n > 1)?

Решение

Степенью числа a с натуральным показателем n(n > 1) называют произведение n множителей, каждый из которых равен a.

Задание № 154

. Чему равна первая степень любого числа?

Решение

Первая степень любого числа равна самому числу.

Задание № 155. Что называют:
а) квадратом числа;
б) кубом числа?

Решение

а) Квадратом числа называют вторую степень числа.
б) Кубом числа называют третью степень числа.

Задание № 156. Запишите сумму в виде произведения:
а) 5 + 5;
б) 8 + 8 + 8 + 8;
в) а + а + а.

Решение

а) 5 + 5 = 5 * 2
б) 8 + 8 + 8 + 8 = 8 * 4
в) a + a + a = a * 3

Задание № 157. Запишите произведение в виде степени:
а) 5 * 5;
б) 8 * 8 * 8 * 8;
в) a * a * a.

Решение

а) 5*5=5²
б) 8*8*8*8=8⁴
в) a*a*a=a³

Задание № 158. Используя специальные названия второй и третьей степени, прочитайте степени
2²;2³;3²;3³;4³;5².

Решение

2² − два в квадрате.
2³ − два в кубе.
3² − три в квадрате.
3³ − три в кубе.
4³ − четыре в кубе.
5² − пять в квадрате.

Задание № 159. Вычислите:
а) 3²;
б) 3 * 2;
в) 5²;
г) 5 * 2;
д) 9²;
е) 9 * 2;
ж) 2³;
з) 2 * 3.

Решение

а) 3²=9
б) 3 * 2 = 6
в) 5²=25
г) 5 * 2 = 10
д) 9²=81
е) 9 * 2 = 18
ж) 2³=8
з) 2 * 3 = 6

Задание № 160. Вычислите:
а) 2²;
б) 4²;
в) 6²;
г) 7²;
д) 8²;
е) 9²;
ж) 10²;
з) 1².

Решение

а) 2²=4
б) 4²=16
в) 6²=36
г) 7²=49
д) 8²=64
е) 9²=81
ж) 10²=100
з) 1²=1

Задание № 161. Вычислите:
а) 3³;
б) 4³;
в) 5³;
г) 1³;
д) 0³;
е) 10³;
ж) 6³;
з) 7³.

Решение

а) 3³=27
б) 4³=64
в) 5³=125
г) 1³=1
д) 0³=0
е) 10³=1000
ж) 6³=216
з) 7³=343

Задание № 162. Вычислите:
а) 3⁴;
б) 3⁵;
в) 1⁸;
г) 0⁴;
д) 100¹;
е) 1¹;
ж) 11²;
з) 12².

Решение

а) 3⁴=81
б) 3⁵=243
в) 1⁸=1
г) 0⁴=0
д) 100¹=100
е) 1¹=1
ж) 11²=121
з) 12²=144

Задание № 163. Составьте таблицу квадратов чисел от 0 до 15.

Решение

Задание № 164. Составьте таблицу кубов чисел от 0 до 10.

Решение

Задание № 165. Вычислите степени числа 2 с показателями от 1 до 10.

Решение

2¹=2
2²=4
2³=8
2⁴=16
2⁵=32
2⁶=64
2⁷=128
2⁸=256
2⁹=512
2¹0=1024

Задание № 166.Запишите в виде квадрата натурального числа:
а) 9;
б) 25;
в) 100;
г) 16;
д) 49;
е) 81;
ж) 64;
з) 36.

Решение

а) 9=3²
б) 25=5²
в) 100=10²
г) 16=8²
д) 49=7²
е) 81=9²
ж) 64=8²
з) 36=6²

Задание № 167. Вычислите степени числа 10 с показателями от 1 до 7.

Решение

10¹=10
10²=100
10³=1000
10⁴=10000
10⁵=100000
10⁶=1000000
10⁷=10000000

Задание № 168.Запишите в виде степени с основанием 10 число:
а) 100;
б) 1000;
в) 10000;
г) 10;
д) 100000;
е) 1000000.

Решение

а) 100=10²
б) 1000=10³
в) 10000=10⁴
г) 10=10¹
д) 100000=10⁵
е) 1000000=10⁶

Задание № 169. Запишите число в виде произведения одинаковых чисел:
а) 4;
б) 1;
в) 27;
г) 256.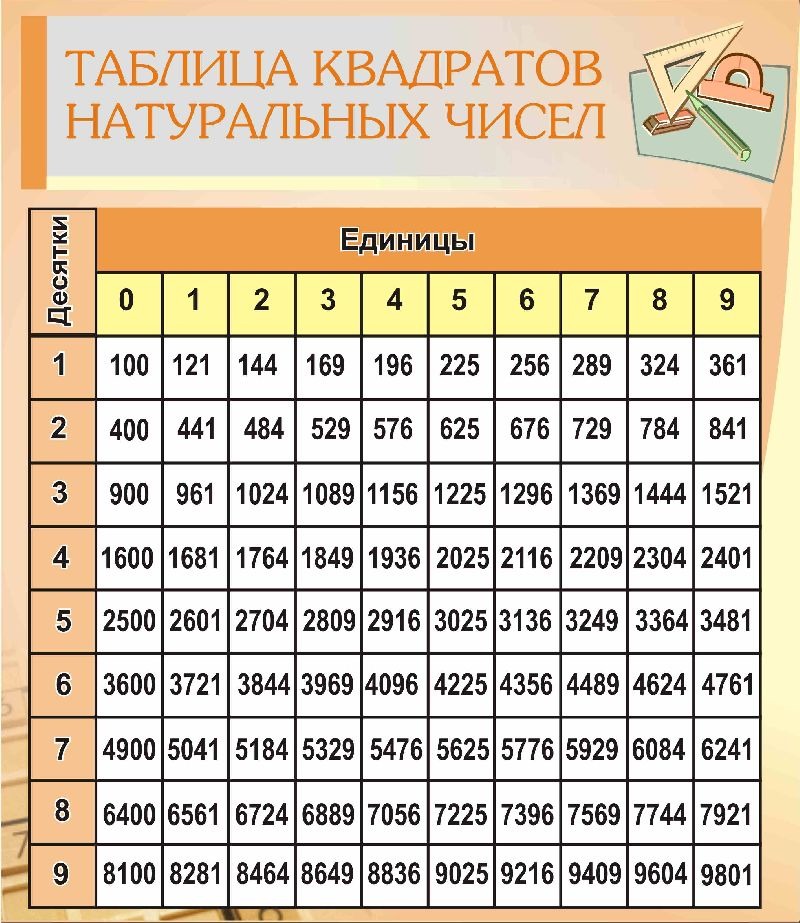

Решение

а) 4 = 2 * 2
б) 1 = 1 * 1
в) 27 = 3 * 3 * 3
г) 256 = 16 * 16
   256 = 4 * 4 * 4 * 4
   256 = 2 * 2 * 2 * 2 * 2 * 2 * 2 * 2

Задание № 170. Запишите каждое число в виде степени: 8; 125; 64; 243.

Решение

8=2³
125=5³
64=8²
64=4³
64=2⁶
243=3⁵

Задание № 171. Среди первых пяти натуральных чисел имеются два неравных числа m и n такие, что
n^m=mⁿ. Найдите эти числа.

Решение

Методом подбора получаем, что эти числа 2 и 4.
2⁴=2*2*2*2=16
4²=4*4=16
2⁴=4²
Ответ: эти числа 2 и 4.

 

• Назад
• Вперед

 
умножить наподелить на

 

org/BreadcrumbList»>
• ГДЗ
• ГДЗ по математике
• ГДЗ Математика учебник 5 класс Никольский, Потапов, Решетников

Вам может пригодиться:

3-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 93-8 9 Оценить квадратный корень из 12 10 Оценить квадратный корень из 20 11 Оценить квадратный корень из 50 94 18 Оценить квадратный корень из 45 19 Оценить квадратный корень из 32 20 Оценить квадратный корень из 18 92

3.

8 Фи-функция Эйлера

Когда что-то известно о $\Z_n$, часто полезно спросить применимо ли что-то сопоставимое к $\U_n$. Здесь мы смотрим на $\U_n$ в контексте предыдущего раздела. В помощь расследованию мы ввести новую величину, фи-функцию Эйлера , записанную $\phi (n)$, для натуральных чисел $n$.

Определение 3.8.1 $\phi (n)$ — это количество неотрицательные целые числа меньше $n$, относительно просто до $n$. Другими словами, если $n>1$, то $\phi (n)$ — это количество элементы в $\U_n$ и $\phi(1)=1$. $\квадрат$

Пример 3.8.2. Легко проверить, что $\phi (2)=1$, $\phi (4)=2$, $\phi (12)=4$ и $\phi (15)=8$. $\квадрат$

Пример 3.8.3. Если $p$ — простое число, то $\phi (p)=p-1$, поскольку $1$, $2$, …, $p-1$ взаимно просты с $p$, а $0$ — нет. $\квадрат$

Для любого числа $n$ $\phi(n)$ оказывается удивительно простым форма; то есть существует простая формула, которая дает значение $\фи(п)$. Мы уже видели, насколько это просто для простых чисел. Как есть типичных для многих результатов в теории чисел, мы будем работать по-своему постепенно до любого $n$, глядя затем на степени одного простого числа. 9{a-1}$.$\qed$

Пример 3.8.5 $\phi (32)=32-16=16$, $\phi (125)=125-25=100$. $\квадрат$

Теперь мы хотим расширить нашу формулу, чтобы обрабатывать любые натуральное число $n$. Сначала рассмотрим пример:

Пример 3.8.6 С $$ \eqalign{ \U_{20}&=\{[1],[3],[7],[9],[11],[13],[17], [19]\},\кр \U_{4}& =\{[1],[3]\},\cr \U_{5}& =\{[1],[2],[3],[4]\},\cr} $$ и $\U_{20}$, и $\U_4\times \U_5$ имеют по 8 элементов. Фактически, переписка, обсуждаемая в китайском остатке Теорема между $\Z_{20}$ и $\Z_{4}\times \Z_5$ также является соответствием 1-1 между $\U_{20}$ и $\U_4\раз \U_5$: $$ \матрица{ [1]&\стрелка влево&([1],[1])&\quad&[11]&\стрелка влево& ([3],[1])\cr [3]&\стрелка влево&([3],[3])&\quad&[13]&\стрелка влево& ([1],[3])\cr [7]&\стрелка влево&([3],[2])&\quad&[17]&\стрелка влево& ([1],[2])\cr [9]&\стрелка влево&([1],[4])&\quad&[19]&\стрелка влево& ([3],[4])\cr} $$ $\квадрат$

Использование китайского остатка Теорема, мы можем доказать, что это правда в общем.

Теорема 3.8.7. Если $a$ и $b$ относительно простое и $n=ab$, то $\phi (n)=\phi (a)\phi (b)$.

Доказательство. Мы хотим доказать, что $|\U_n|=|\U_a|\cdot|\U_b|$. Как указано в примере мы на самом деле докажем больше, выставив единицу за одно соответствие между элементами $\U_n$ и $\U_a\раз\U_b$. У нас уже есть переписка один на один между элементы $\Z_n$ и $\Z_a\times\Z_b$. Опять же, как указывает например, нам просто нужно доказать, что это же соответствие работает для $\U_n$ и $\U_a\times\U_b$. То есть мы уже умеем связывать любой $[x]$ с парой $([x],[x])$; нам просто нужно знать, что $[x]\in \U_n$ тогда и только тогда, когда $([x],[x])\in\U_a\times\U_b$. После долгого построить, вот доказательство: $[x]$ находится в $\U_n$ тогда и только тогда, когда $(х,n)=1$ тогда и только тогда, когда $(x,a)=1$ и $(x,b)=1$ тогда и только тогда, когда $([x],[x])\in \U_a\times \U_b$.$\qed$

Следствие 3.8.8. Предположим, что $n=ab$, где $a$ и $b$ взаимно просты. Для $x=0,1,…, n-1$, если $[x]\in \U_{n}$, свяжите $[x]$ с $([x], [x])\in \Z_a\times \Z_b$. Это дает один к одному соответствие между $\U_n$ и $\U_a\times \U_b$.

Доказательство. Мы доказали это уже в доказательстве предыдущего теорема, но она заслуживает отдельного утверждения.$\qed$

Теперь мы знаем достаточно, чтобы вычислить $\phi(n)$ для любого $n$.

Пример 3.8.9 $\phi (200)=\phi(25)\phi(8)=(25-5)(8-4)=80.$ $\квадрат$ 9{e_k-1}). $$

Доказательство. Доказательство по индукции оставляем в качестве упражнения.$\qed$

Леонард Эйлер. Эйлер (произносится как «майлер») родился в Базеле. в 1707 году и умер в 1783 году, после потрясающе плодовитой жизни. математическая работа. Его полная библиография насчитывает около 900 записи; его исследования составили около 800 страниц в год в течение всего его карьеры. Он продолжал заниматься исследованиями вплоть до своего внезапного смерть во время отдыха с чашкой чая. Почти все последние 17 лет своей жизни он был полностью слеп.

Широта знаний Эйлера может быть столь же впечатляющей, как и глубина его его математическая работа. У него были большие способности к языкам, и изучал теологию, медицину, астрономию и физику. Его первый назначение было в медицине при недавно созданном Санкт-Петербургском Академия. В день приезда в Россию покровитель академии, Екатерина I умерла, а сама академия едва пережила переход власти к новому режиму. В результате Эйлер оказался в кафедра натурфилософии вместо медицины.

Эйлера лучше всего помнят за его вклад в анализ и числа. теории, особенно за использование им бесконечных процессов различных виды (бесконечные суммы и произведения, цепные дроби), а для установив большую часть современной нотации математики. Эйлер положил начало использованию $e$ для основания натуральных логарифмов и $i$ для $\sqrt{-1}$; символ $\pi$ был найден в книге, изданной в 1706 г., но принятие этого символа Эйлером в 1737 г. сделало это стандарт. Он также отвечал за использование $\sum$ для представляют собой сумму, а в современных обозначениях функции $f(x)$. 92/6$. Некритическое применение Эйлером обычной алгебры к бесконечным рядам время от времени приводил его к неприятностям, но его результаты были в подавляющем большинстве правильны, а позже были оправданы более тщательной техникой, поскольку потребность в повышенной строгости математических аргументов стала очевидной. Мы еще не раз встретимся с именем Эйлера в оставшейся части главы.

Информация здесь взята из A History of Mathematics , автор Карл Бойер, Нью-Йорк: John Wiley & Sons, 1968.

9{-1}$ соответствуют?

Пример 3.8.5 Делителями числа $6$ являются $1$, $2$, $3$, $6$. Обратите внимание, что $$ \фи (1)+\фи (2)+\фи (3)+\фи (6)= 1 + 1 + 2 + 2 = 6. $$ Выполните аналогичные вычисления, заменив 6$ на 10$.

Пример 3.8.6 Найдите все $a$ такие, что $\phi (a)=6$.

Пример 3.8.7 Если $a|b$, докажите $\phi (a)|\phi (b)$.

Пример 3.8.8 Какие простые числа можно представить в виде $\phi (n)$ для какие-то $n$?

Пример 3.8.9 Докажи это $\displaystyle\phi(n)=n\prod_{p|n}\big(1-{1\over p}\big)$; продукт над всеми простыми числами $p$, которые делят $n$.

Пример 3.8.10 Докажите теорему 3.8.11.

Пример 3.8.11 Найдите все $n$, для которых $\phi(n)$ нечетно, и докажите что вы нашли все такие $n$.

No related posts.