делители, простота, двоичный вид, куб, квадрат
Укажите число, чтобы получить всю информацию о нем:
Случайное число
| Четность: |
Число 1681 является нечетным. |
| Сумма цифр: | 16 |
| Произведение цифр: | 48 |
| Количество цифр: | 4 |
| Все делители числа | 1 41 1681 |
| Количество делителей | |
| Сумма делителей | 1723 |
| Простое число |
Составное число |
| Квадратный корень | 41 |
| Кубический корень | 11,8902021368727 |
| Квадрат | 2825761 |
| Куб | 4750104241 |
| Обратное число | 0,000594883997620464 |
| Предыдущее число: 1680 | Следующее число: 1682 |
Целое положительное число 1681
является четырехзначным. 2
2
Что такое квадратный корень из 1681?
LearnPracticeDownload
Квадратный корень из числа — это значение, которое при умножении само на себя дает исходное число. например 10 × 10 = 100; квадратный корень из 100 равен 10. Точно так же 1681 – это число в совершенной квадратной форме. Квадратный корень из 1 681 будет числом, произведение которого на себя даст 1 681. Математическая операция квадратный корень является обратной квадрату. Квадратный корень числа может быть положительным или отрицательным, рациональным или иррациональным, действительным или мнимым. В этом мини-уроке мы вычислим квадратный корень из 1681 разными методами и рассмотрим некоторые интересные задачи, связанные с ним. 1681 – это число в совершенной квадратной форме, которое можно получить путем возведения в квадрат числа 41. Следовательно, квадратный корень из 1681 – рациональное число. В этом мини-уроке мы научимся находить квадратный корень из 1681 вместе с решенными примерами.
- Квадратный корень из 1681 : √1681 = 41
- Квадрат 1681: 1681 ² = 28,25,761
| 1. | Что такое квадратный корень из 1681? |
| 2. | Является ли квадратный корень из 1681 рациональным или иррациональным? |
| 3. | Как найти квадратный корень из 1681? |
| 4. | Часто задаваемые вопросы о квадратном корне из 1681 |
| 5. | Важные примечания |
Что такое квадратный корень из 1681?
Квадратный корень из числа n записывается как √n. Это число, возведенное в квадрат или умноженное само на себя, дает исходное число n. Мы знаем, что у сложения есть обратная операция — вычитание, а у умножения есть обратная операция — деление. Точно так же вычисление квадратного корня числа является операцией, обратной возведению этого числа в квадрат. Квадратный корень из 1 681 – это число, которое при умножении на себя даст в результате число 1 681. Таким образом, нам нужно придумать число, квадрат которого равен 1681.
Точно так же вычисление квадратного корня числа является операцией, обратной возведению этого числа в квадрат. Квадратный корень из 1 681 – это число, которое при умножении на себя даст в результате число 1 681. Таким образом, нам нужно придумать число, квадрат которого равен 1681.
- Квадратный корень из 1681 записывается как √1681 (коренная форма)
- Квадратный корень из 1681 = √1681 = √(41 × 41) = +41 и -41
- В экспоненциальной форме квадратный корень из 1681 выражается как (1681) 1/2
Квадратный корень из 1681 равен 41.
Является ли квадратный корень из 1681 рациональным или иррациональным?
Рациональное число — это число, которое может быть выражено в форме p/q. Число, не являющееся рациональным, называется иррациональным числом. Неконечные десятичные числа с повторяющимися числами после запятой являются рациональными числами. Теперь давайте посмотрим на квадратный корень из 1 681. 1 681 можно разбить на два множителя, которые при умножении дают 1 681. Его можно записать как квадрат 41, который является рациональным числом. Это показывает, что 1 681 – число в идеальном квадрате.
1 681 можно разбить на два множителя, которые при умножении дают 1 681. Его можно записать как квадрат 41, который является рациональным числом. Это показывает, что 1 681 – число в идеальном квадрате.
- 1681 — это число, являющееся полным квадратом, поскольку квадратным корнем из него является натуральное число.
- Квадратный корень из 1681 равен 41 .
- Квадратный корень из 1 681 может быть выражен как дробь формы p/q, что говорит нам о том, что квадратный корень из 1681 является рациональным числом.
- Квадратный корень из 1681 равен либо +41, либо -41.
- 41 и -41 могут быть выражены как 41/1 и -41/1. Оба числа могут быть представлены в виде рационального числа. Таким образом, квадратный корень из 1 681 является рациональным числом.
Как найти квадратный корень из 1681?
Квадратный корень из 1681 можно вычислить с помощью различных методов, таких как: разложение на простые множители и метод длинного деления . Так как 1681 — это полный квадрат, мы также можем использовать метод повторяющегося вычитания.
Так как 1681 — это полный квадрат, мы также можем использовать метод повторяющегося вычитания.
Давайте вычислим квадратный корень из 1681, используя метод деления в большую сторону.
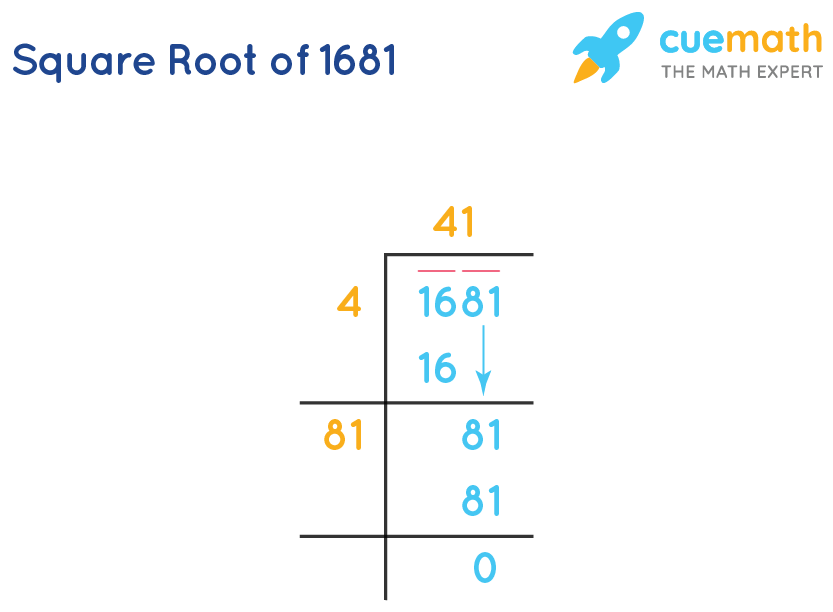
Квадратный корень из 1681 методом деления в длину
- Шаг 1. Запишите 1681, как показано на рисунке. Начните группировать числа по парам справа. 81 — первая пара справа, а следующая пара — 16.
- Шаг 2 : Найдите наибольшее число, которое при умножении само на себя даст 16 или меньшее число, ближайшее к 16. Здесь это 4 (4 × 4 = 16, остаток = 0).
- Шаг 3 : Наберите следующую пару цифр. Здесь это 81. Новый делитель равен 81, а делимое равно 81.
- Шаг 4 : Найдите наибольшее число, которое при сохранении в разряде единиц с 8 в разряде десятков, умноженном на то же число, дает 81 в качестве результата или число, ближайшее к 81.
- Шаг 5: 1 – это следующий разряд частного.
 Теперь мы получаем наш новый делитель как 81, так как 81 × 1 = 81. Завершите деление и получите остаток. Получаем 0 в качестве остатка. Таким образом, процесс деления здесь завершается.
Теперь мы получаем наш новый делитель как 81, так как 81 × 1 = 81. Завершите деление и получите остаток. Получаем 0 в качестве остатка. Таким образом, процесс деления здесь завершается.
Следовательно, квадратный корень из 1681 = 41 .
Изучение квадратных корней с помощью иллюстраций и интерактивных примеров
- Квадратный корень из 1296
- Квадратный корень из 1225
- Квадратный корень из 1000
- Квадратный корень из 24
- Квадратный корень из 16
- Квадратный корень из 144
- Квадратный корень из 81
- Квадратный корень из 288
Важные примечания:
- Квадратный корень из 1681 представлен как √1681 в подкоренной форме.
- Квадратный корень из 1681 представлен как (1681) 1/2 в экспоненциальной форме.
- В квадратном корне из четного числа, состоящего из n цифр, будет n/2 цифр.

- В квадратном корне из нечетного числа с n цифрами будет (n+2)/2 цифр.
Пример 1 : Площадь земли квадратной формы – 1681 квадрата. Вычислите длину одной стороны земли.
Решение:
Площадь земли = 1681 кв. единиц
Чтобы найти сторону квадратной земли, давайте возьмем квадратный корень из 1682 методом простой факторизации.- Шаг 1. Разложение числа 1681 на простые множители = 1 × 41 × 41
- Шаг 2. Сгруппируйте простые множители, полученные для 1681, попарно.
- Шаг 3. Выберите по одному множителю из каждой пары, и их можно записать в виде: 1681 = 41 2
- Шаг 4. Таким образом, следуя закону экспонент, мы получаем, √1681 = √(41 ² ) = 41
Таким образом, имеем √1681 = + 41 или -41
Следовательно, длина одной стороны квадрата равна 41 единице.
- Шаг 1. Разложение числа 1681 на простые множители = 1 × 41 × 41
Пример 2 : у Шерин есть квадратный коврик площадью 1681 кв.
 дюйм. Коврик украшен вышивкой по краям. Внутренняя площадь коврика составляет 1024 квадратных дюйма. Можете рассчитать ширину вышивки на коврике?
дюйм. Коврик украшен вышивкой по краям. Внутренняя площадь коврика составляет 1024 квадратных дюйма. Можете рассчитать ширину вышивки на коврике?Решение:
Мы знаем, что длина каждой стороны мата = √1681 = 41 дюйм
Длина внутренней части коврика = √1024 = 32 дюйма 90 185 Таким образом, ширина вышивки = 41 — 32 = 9 дюймов
перейти к слайдуперейти к слайду
Хотите создать прочную основу для изучения математики?
Выйдите за рамки запоминания формул и поймите «почему», стоящее за ними. Испытайте Cuemath и приступайте к работе.
Записаться на бесплатный пробный урок
перейти к слайдуперейти к слайдуперейти к слайду
Часто задаваемые вопросы о квадратном корне из 1681
Что такое квадратный корень из 1681 с помощью факторизации?
Разложение числа 1681 на простые множители = 1 × 41 × 41
Выберите один множитель из каждой пары, и они могут быть записаны как √1681 = 41
.
 Является ли 1681 идеальным квадратом?
Является ли 1681 идеальным квадратом?1681 — идеальный квадрат. 1681 – натуральное число. Поскольку существует еще одно натуральное число, которое можно возвести в квадрат и получить число 1681, то есть 41, это полный квадрат.
Чему равно √1681, умноженное на √1681?
Значение √1681 × √1681 равно 1681.
Является ли квадратный корень из 1681 рациональным числом?
Да, квадратный корень из 1681 является рациональным числом, поскольку квадратный корень из 1681 может быть представлен в виде p/q.
Можем ли мы найти квадратный корень из 1681 методом повторного вычитания?
Да, мы можем найти квадратный корень из 1681 методом повторного вычитания, так как его можно использовать только для идеальных квадратов. 1681 – идеальный квадрат.
Рабочие листы по математике и
наглядная программа
Квадратный корень из 1681 пошаговое решение
| Пожалуйста, введите реальное число: |
| Результат квадратного корня: |
Вот ответ на такие вопросы, как: Квадратный корень из 1681 пошаговое решение | √1681 или чему равен квадратный корень из 1681?
Используйте приведенный ниже калькулятор квадратного корня, чтобы найти квадратный корень любого мнимого или действительного числа.
Вавилонский метод, также известный как метод Героя
Ниже показано, как шаг за шагом вычислить квадратный корень из числа 1681 с помощью вавилонского метода , также известного как Метод Героя .
Что такое квадратный корень?
Определение квадратного корня
Квадратный корень из числа «а» — это число х, такое что х 2 = а, другими словами, число х, квадрат которого равен а. Например, 41 — это квадратный корень из 1681, потому что 41 2 = 41•41 = 1681, -41 — это квадратный корень из 1681, потому что (-41) 2 = (-41)•(-41) = 1681.
Таблица квадратных корней 1-100
Квадратные корни от 1 до 100, округленные до тысячных.
| нет | нет 2 | √ |
|---|---|---|
| 1 | 1 | 1. 000 000 |
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2.000 |
| 5 | 25 | 2.236 |
| 6 | 36 | 2.449 |
| 7 | 49 | 2.646 |
| 8 | 64 | 2.828 |
| 9 | 81 | 3.000 |
| 10 | 100 | 3.162 |
| 11 | 121 | 3.317 |
| 12 | 144 | 3.464 |
| 13 | 169 | 3.606 |
| 14 | 196 | 3.742 |
| 15 | 225 | 3.873 |
| 16 | 256 | 4.000 |
| 17 | 289 | 4.123 |
| 18 | 324 | 4. 243 243 |
| 19 | 361 | 4.359 |
| 20 | 400 | 4.472 |
| 21 | 441 | 4.583 |
| 22 | 484 | 4.690 |
| 23 | 529 | 4.796 |
| 24 | 576 | 4.899 |
| 25 | 625 | 5.000 |
| нет | нет 2 | √ |
|---|---|---|
| 26 | 676 | 5.099 |
| 27 | 729 | 5.196 |
| 28 | 784 | 5.292 |
| 29 | 841 | 5.385 |
| 30 | 900 | 5.477 |
| 31 | 961 | 5.568 |
| 32 | 1,024 | 5.657 |
| 33 | 1,089 | 5. 745 745 |
| 34 | 1,156 | 5.831 |
| 35 | 1,225 | 5.916 |
| 36 | 1,296 | 6.000 |
| 37 | 1,369 | 6.083 |
| 38 | 1,444 | 6.164 |
| 39 | 1,521 | 6.245 |
| 40 | 1,600 | 6.325 |
| 4124492333333333333333333333333333333333333333333333333333333.68 | ||
| 4124491333333333333333333333333333333333333333333333333333333333.68 | ||
| 42 | 1,764 | 6.481 |
| 43 | 1,849 | 6.557 |
| 44 | 1,936 | 6.633 |
| 45 | 2,025 | 6.708 |
| 46 | 2,116 | 6.782 |
| 47 | 2,209 | 6. 856 856 |
| 48 | 2,304 | 6.928 |
| 49 | 2 401 | 7.000 |
| 50 | 2 500 | 7.071 | 4
| нет | нет 2 | √ |
|---|---|---|
| 51 | 2,601 | 7.141 |
| 52 | 2,704 | 7.211 |
| 53 | 2,809 | 7.280 |
| 54 | 2,916 | 7.348 |
| 55 | 3,025 | 7.416 |
| 56 | 3,136 | 7.483 |
| 57 | 3,249 | 7.550 |
| 58 | 3,364 | 7.616 |
| 59 | 3,481 | 7.681 |
| 60 | 3,600 | 7.746 |
| 61 | 3,721 | 7.810 |
| 62 | 3,844 | 7.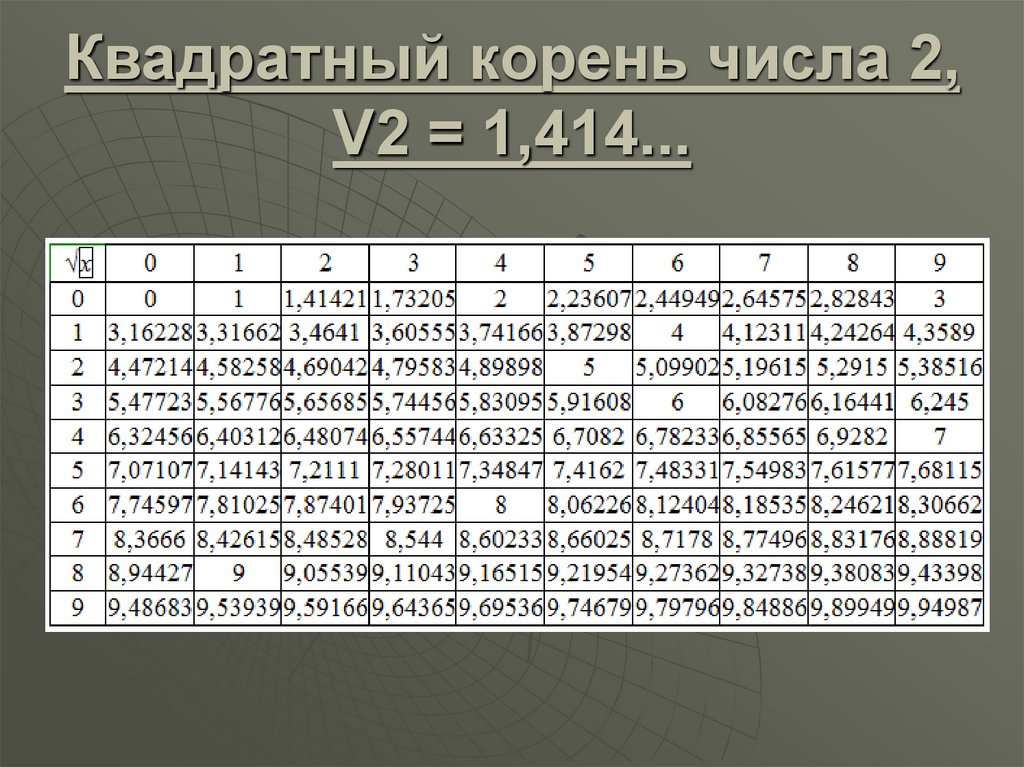 874 874 |
| 63 | 3,969 | 7.937 |
| 64 | 4,096 | 8.000 |
| 65 | 4,225 | 8.062 |
| 66 | 4,356 | 8.124 |
| 67 | 4,489 | 8.185 |
| 68 | 4,624 | 8.246 |
| 69 | 4,761 | 8.307 |
| 70 | 4,900 | 8.367 |
| 71 | 5,041 | 8.426 |
| 72 | 5,184 | 8.485 |
| 73 | 5,329 | 8.544 |
| 74 | 5476 | 8.602 |
| 75 | 5625 | 8.660 |
| нет | нет 2 | √ |
|---|---|---|
| 76 | 5,776 | 8.718 |
| 77 | 5,929 | 8. 775 775 |
| 78 | 6,084 | 8.832 |
| 79 | 6,241 | 8.888 |
| 80 | 6,400 | 8.944 |
| 81 | 6,561 | 9.000 |
| 82 | 6,724 | 9.055 |
| 83 | 6,889 | 9.110 |
| 84 | 7,056 | 9.165 |
| 85 | 7,225 | 9.220 |
| 86 | 7,396 | 9.274 |
| 87 | 7,569 | 9.327 |
| 88 | 7,744 | 9.381 |
| 89 | 7,921 | 9.434 |
| 90 | 8,100 | 9.487 |
| 91 | 8,281 | 9.539 |
| 92 | 8,464 | 9.592 |
| 93 | 8,649 | 9. |

 Теперь мы получаем наш новый делитель как 81, так как 81 × 1 = 81. Завершите деление и получите остаток. Получаем 0 в качестве остатка. Таким образом, процесс деления здесь завершается.
Теперь мы получаем наш новый делитель как 81, так как 81 × 1 = 81. Завершите деление и получите остаток. Получаем 0 в качестве остатка. Таким образом, процесс деления здесь завершается.
 дюйм. Коврик украшен вышивкой по краям. Внутренняя площадь коврика составляет 1024 квадратных дюйма. Можете рассчитать ширину вышивки на коврике?
дюйм. Коврик украшен вышивкой по краям. Внутренняя площадь коврика составляет 1024 квадратных дюйма. Можете рассчитать ширину вышивки на коврике?