9.Метрические соотношения в окружности. Свойства хорд
Окружностью называется геометрическая фигура, состоящая из всех точек плоскости, расположенных на заданном расстоянии от данной точки, называемой центром окружности. Отрезок, соединяющий центр с какой-либо точкой окружности, называется радиусом окружности.
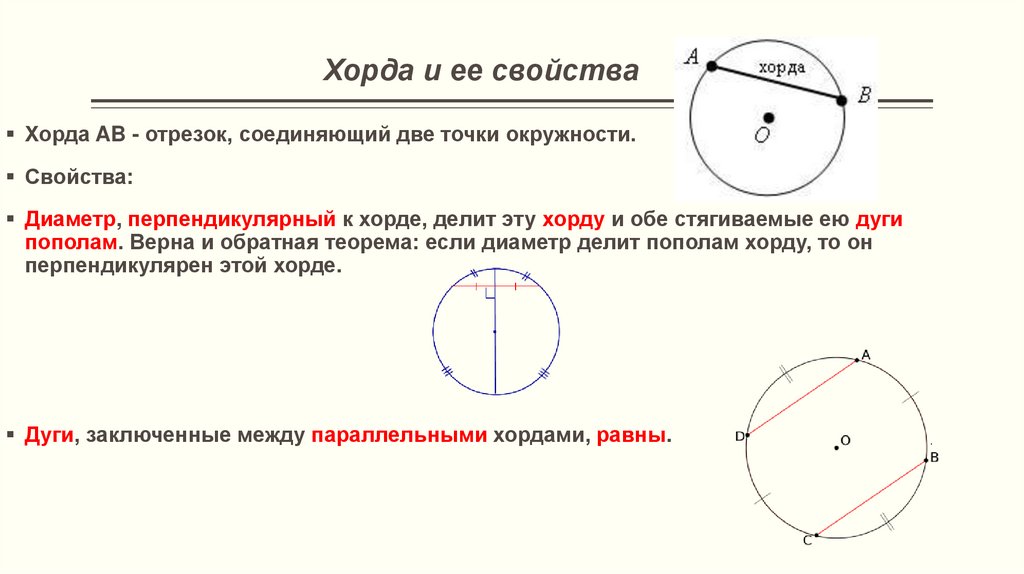
Отрезок, соединяющий две точки окружности, называется ее хордой.
Если на окружности взять две точки, то они разобьют окружность на две части, каждая из которых называется дугой окружности, а данные точки — концами этих дуг.
Дуга называется полуокружностью, если отрезок, соединяющий ее концы, является диаметром окружности. Часть плоскости, ограниченная окружностью, называется кругом.
Кругом с центром О и радиусом R называется фигура, которая состоит из всех точек плоскости, удаленных от точки О не больше, чем на расстояние
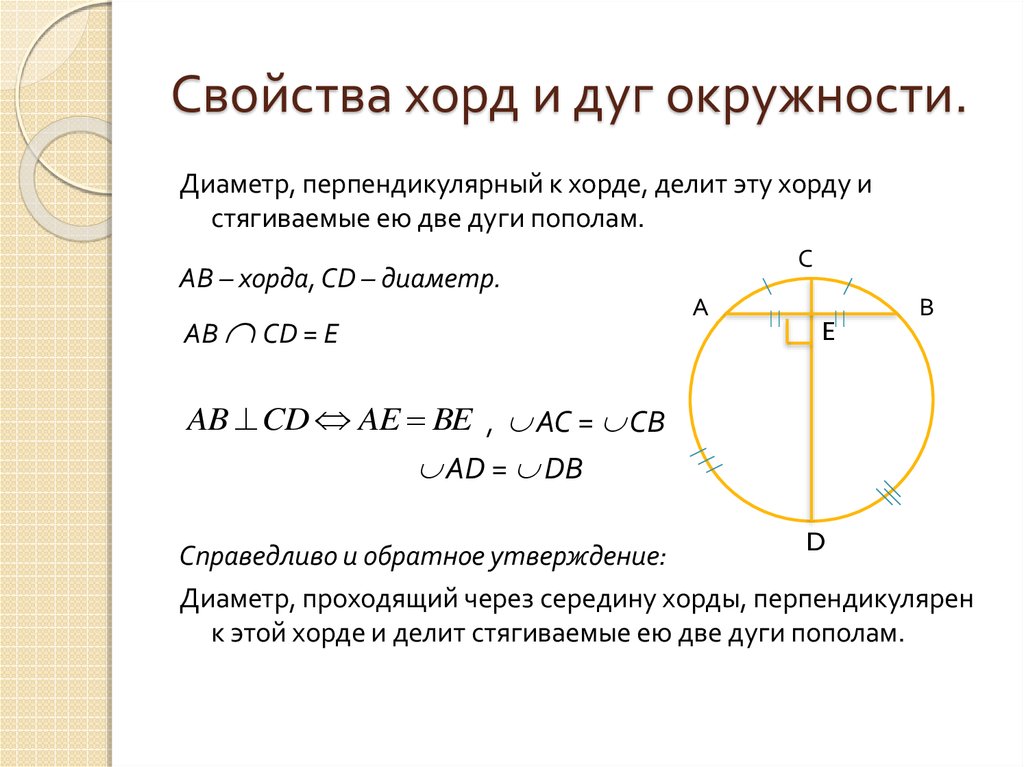
Т1. Диаметр перпендикулярен хорде, не являющейся диаметром, тогда и только тогда, когда он проходит через середину хорды. Дано: CD — диаметр окружности О, АВ — хорда окружности О. CD ∩ АВ = М , AM = MB. Доказать: CD ┴ АВ . Доказательство. Треугольник АОВ равнобедренный (OA = OB как радиусы окружности), ОМ — его медиана. Значит, ОМ — высота треугольника, т. е. ОМ ┴ АВ, или диаметр CD перпендикулярен хорде АВ. Докажем обратное.
Дано: CD — диаметр окружности О, АВ — хорда
окружности О, М = AB∩CD, CD ┴ АВ.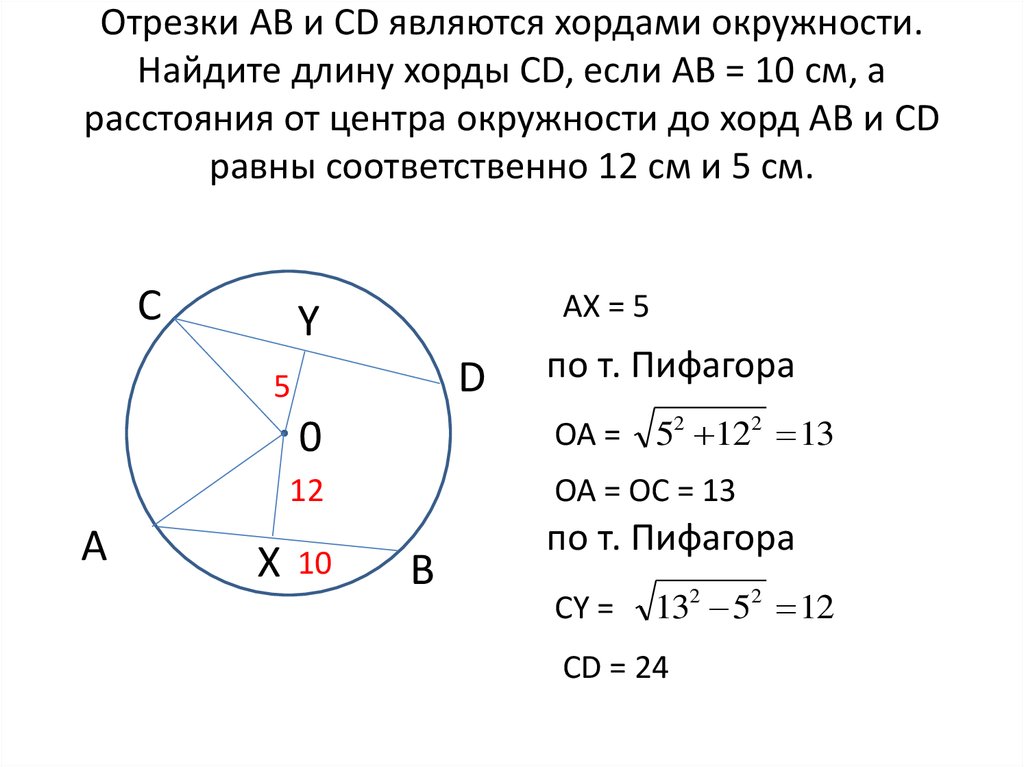
Доказать: AM = MB. Доказательство.
Треугольник АОВ равнобедренный (OA = OB) и ОМ — его высота, а значит, ОМ — медиана, т. е. AM= MB.
Следствие. Расстояние от центра окружности до хорды равно расстоянию от центра до середины хорды.
Т2. Хорды одной окружности равны тогда и только тогда, когда они равноудалены от центра. Дано: окружность
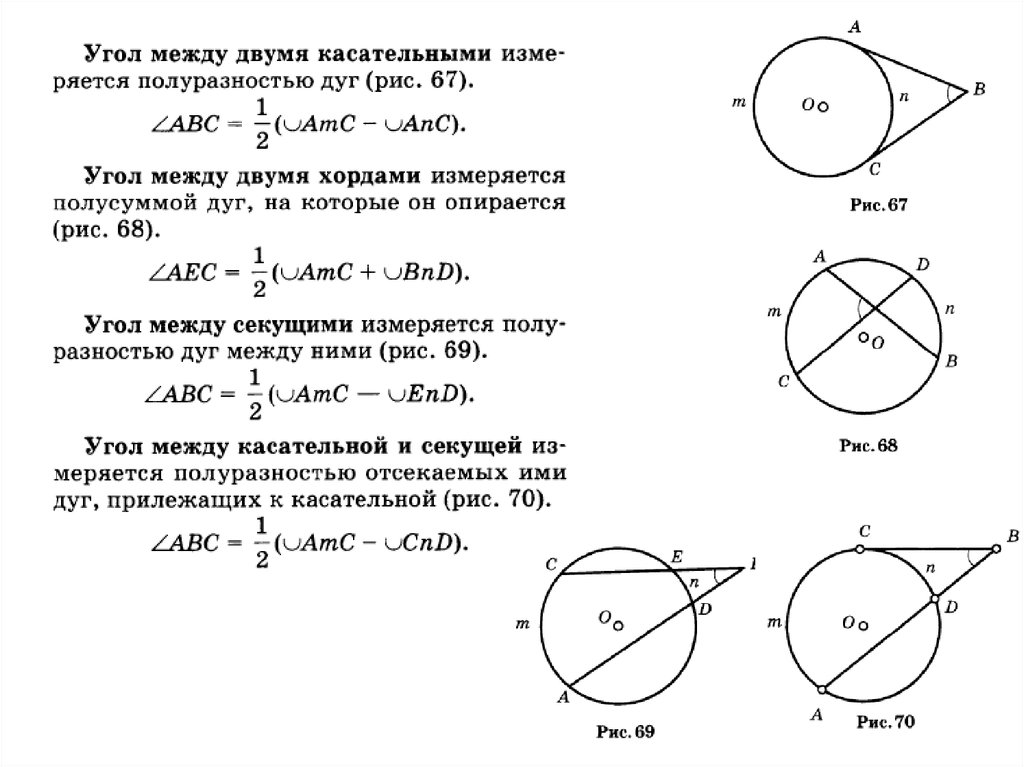Доказательство. ∆OND = ∆ОМВ,
так как они прямоугольные (ON ┴CD и ОМ┴АВ), ND= MB как половины отрезков CD и АВ, и OD = ОВ как радиусы
окружности. Из равенства треугольников OND и ОМВ следует равенство их катетов ON и ОМ. Докажем
обратное. Дано: окружность О, АВ и CD — ее хорды, ON┴CD, т. е. N—
середина CD,
М— середина АВ, т. е. ОМ ┴ АВ , ОМ= ON.
Доказать: АВ = CD. Доказательство. ∆OND = ∆OMB,
так как они прямоугольные (OND = OMB = 90°), ON = ОМ (по условию) и OD = ОВ (радиусы
окружности О).
Из равенства треугольников OND и ОМВ следует равенство их катетов NDОпр..Угол, вершина которого лежит в центре окружности, называется центральным углом.
Если две хорды АВ и KL пересекаются в точке М, то справедливо равенство: АМ*МВ=КМ*ML=R2—d2
Т3. Хорды данной окружности равны тогда и
только тогда, когда они стягивают
равные дуги. Доказательство: Равенство
хорд АВ и CD следует из равенства треугольников АОВ и COD (по двум сторонам
и углу между ними).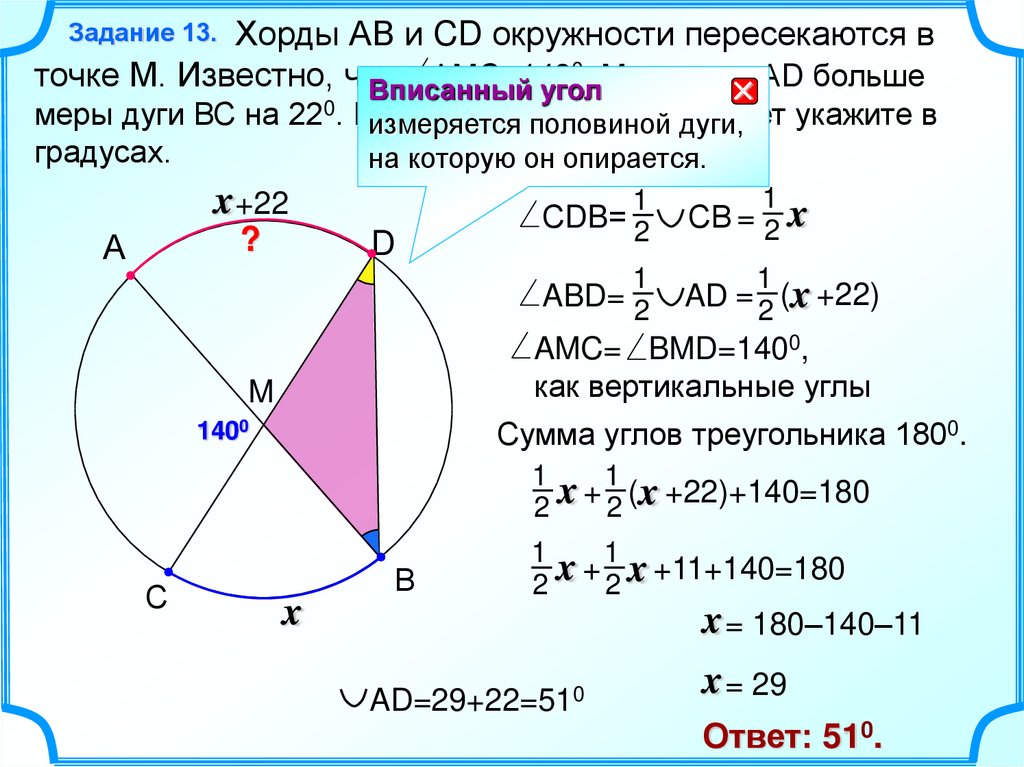
Д-во: Равенство углов АОВ и COD следует из равенства треугольников АОВ и COD (по трем сторонам).Эта теорема может
быть сформулирована и таким образом:
равные хорды видны из центра окружности
под равными углами, и наоборот, под
равными углами из центра окружности
видны равные хорды. Т4. Дуги, заключенные между параллельными
хордами окружности, равны. Док-во:
Равенство дуг АС и BD непосредственно следует из равенства
углов ABC и BCD.
(см. рис. Справа
——>——>——>——>——>——>——>)
Теория и практика окружности
Свойство касательных.
Свойства касательных и секущих.
Свойства хорд.
Углы окружности.
Площадь, сектор, длина окружности.
Задачи на окружности.
По статистике окружности никто не любит, но при этом леденец любим, солнце любим, давай и окружность полюбим!
Окружность − геометрическое место точек плоскости, равноудаленных от одной ее точки (центра). На рисунке центр − точка О.
В окружности может быть проведено 3 типа отрезка:
Отрезок, проходящий через две точки окружности, но не через центр, называют хордой (AB).
Хорда, проходящая через центр окружности, называется диаметром (самая большая хорда в окружности − диаметр (D)).
Радиус − отрезок, соединяющий центр окружности с точкой на окружности. Диаметр в два раза больше радиуса (R).
А также две прямые снаружи от окружности:
Касательная имеет одну общую точку с окружностью. Сразу стоит сказать о том, что радиус, проведенный в точку касания, будет иметь с касательной угол 90°.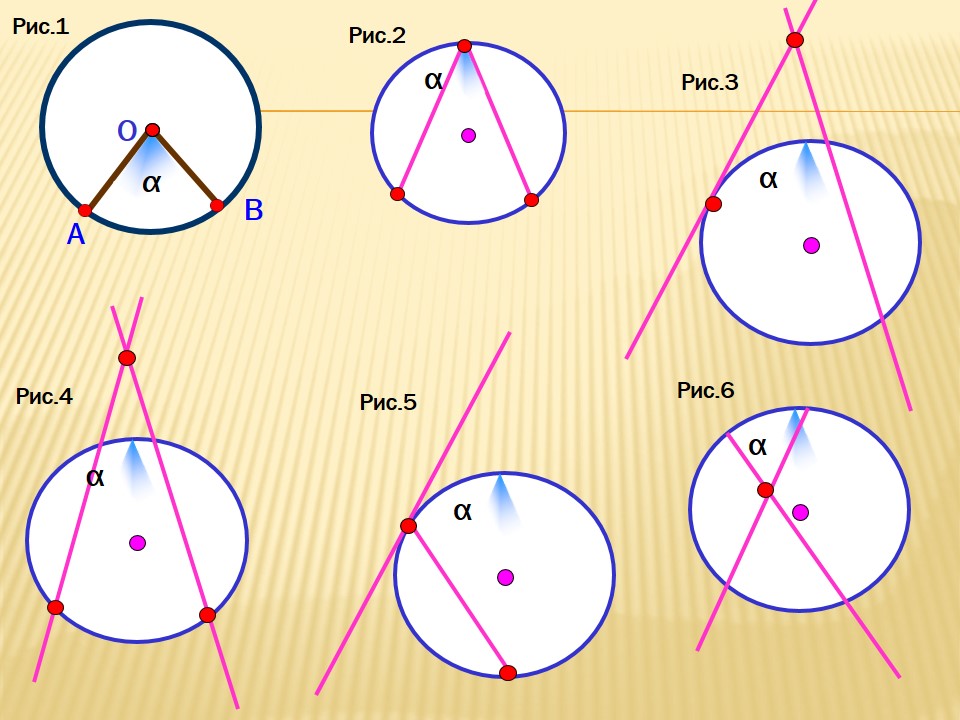
Секущая пересекает окружность в двух точках, внутри окружности получается хорда или, в частном случае, диаметр.
Теперь чуть-чуть об углах и дугах:
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают ее. Он в два раза меньше дуги, на которую опирается.
Центральный угол — это угол, вершина которого находится в центре окружности, равен дуге на которую опирается.
Вписанные углы, опирающиеся на одну дугу, равны между собой (β=β=α/2) и равны половине дуги, на которую опираются.
Градусная мера дуги – величина в °, соответствует центральному углу. Длина дуги равна α.
А вот такой угол НЕвписанный, такой угол «никто и звать никак».
Можно сделать вывод, что вписанный угол, который опирается на половину дуги окружности, будет прямым, а также будет опираться на диаметр:
Любая пара углов, опирающихся на одну и ту же хорду, вершина которых находится по разные стороны от хорды, составляет в сумме 180°.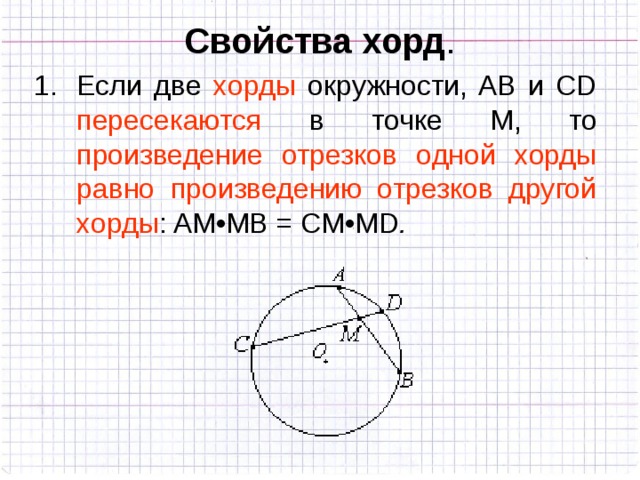
Запишем основные свойства углов в окружности:
Нашел что-то общее?
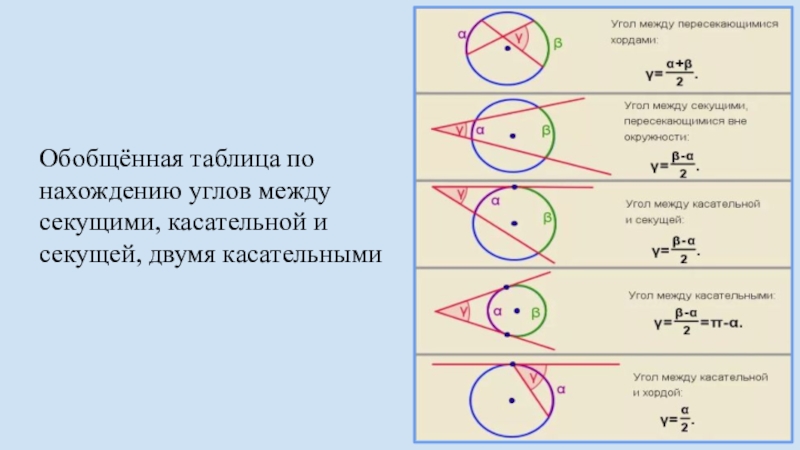
Если угол находится вне окружности, без разницы, чем он получен (касательной или секущей), то найти его можно через половину разности дуг.
Если угол находится внутри окружности, то находим его через полусумму дуг.
Если есть одна дуга, которая находится на требуемом угле, то угол равен половине этой дуги.
Отношение отрезков:
Для любых двух хорд, проходящих через некоторую точку О, выполняет равенство:
Для любых двух секущих, проходящих через некоторую точку O, выполняется равенство:
Согласен, что они похожи, особенно если не смотреть на картинки.
Как не перепутать такие равенства? В каждом отрезке должна присутствовать точка, вне окружности (О).
Если из точки, лежащей вне окружности, проведены касательная и секущая:
Аналогично в каждом отрезке присутствует точка, вне окружности (О).
Если теперь провести две касательные из точки O, то получим такие равные отрезки:
Касательные равны, как, сообственно, и радиусы!
Площадь и длина окружности находятся по формуле:
По своему определению число π показывает, во сколько раз длина окружности больше диаметра, отсюда такая формула: L = πD
Если хочешь вывести площадь круга, можешь проинтегрировать длину окружности относительно R или вывести зависимость, как сделал Архимед!
Задача №1.
Дано на рисунке:Достаточно вспомнить свойства центральных и вписанных углов.
Ответ: 39°
Задача №2. Дано на рисунке:
Найти нужно меньшую дугу BD
Ответ: 100°
Задача №3. Дано на рисунке:
Найти меньшую дугу ВС
Ответ: 114°
Задача №4. Дано на рисунке:
Найти отрезок МК
Ответ: МК = 15.
Задача №5. Дано на рисунке:
Попробуй найти подобные треугольники
Ответ: 6
Задача №5. Дано на рисунке:
Без свойства секущей и касательной здесь будет тяжело
Ответ: 12√7.
Я могу долго тебе показывать, как решать задачи, но без твоих усилий ничего не выйдет.
Попробуй эти задачи с подсказками.
О треугольниках
О четырехуголникахp.s. Не бойся ошибаться и задавать вопросы!
Если нашел опечатку, или что-то непонятно − напиши.
Свойства хорды окружности
Свойство 1 :
Равные хорды окружности образуют равные углы в центре.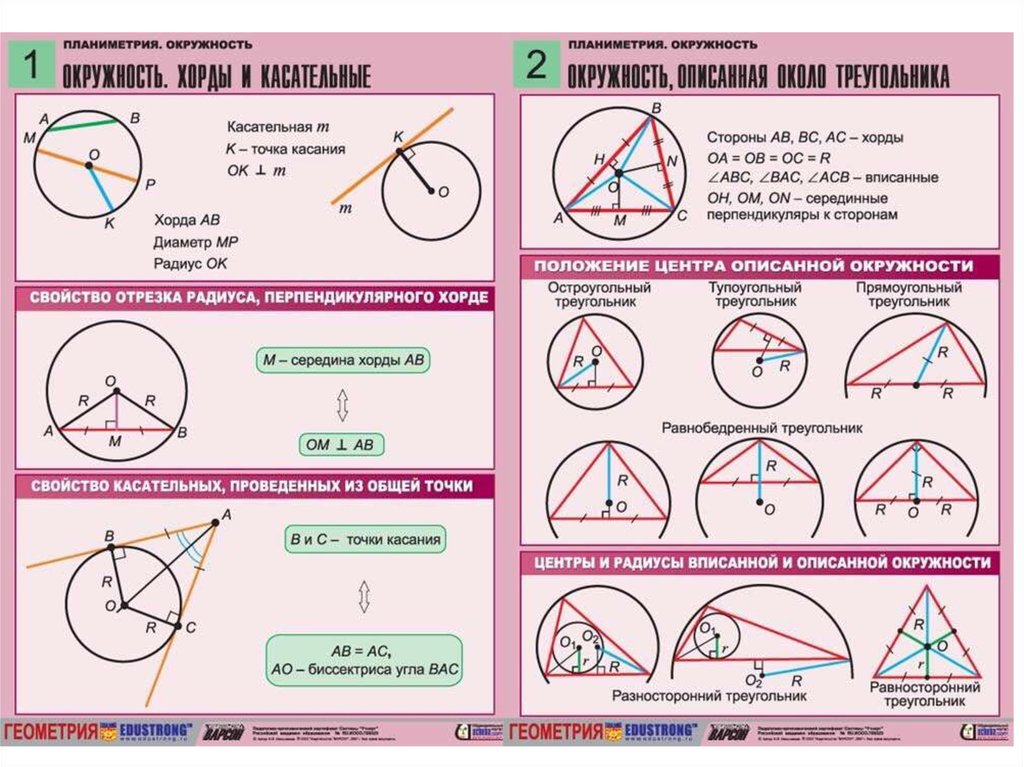
Свойство 2 : Перпендикуляр из центра окружности к хорде делит хорду пополам. AC = BC Свойство 3 : Равные хорды окружности равноудалены от центра. OM = OL Свойство 4 : Если две хорды пересекаются внутри окружности, то мера каждого образованного угла равна половине суммы мер дуг, на которые опирается угол, и его вертикального угла. м<1 = (1/2) (Измерение дуги CD + мера дуги AB) м<2 = (1/2) (Измерение дуги ВС + мера дуги CD) Свойство 5 : Если два хорды пересекаются внутри окружности, то
произведение длин отрезков
одной хорды равно произведению
длины отрезков другой хорды. EA ⋅ EB = EC ⋅ ED Равные хорды окружности стягивают равные углы в центре. хорда AB = хорда CD ( Обратное к результату: Если углы, образуемые двумя хордами в центре окружности, равны, то и хорды равны. Теорема 1 : Перпендикуляр из центра окружности к хорде делит хорду пополам. Дано: Окружность с центром O и AB является хордой окружности, отличной от диаметра и OC ⊥ AB Доказать: AC = BC Построение: соединить OA и OB Доказательство: In треугольники OAC и OBC (i) OA = OB (радиусы одной окружности) (ii) OC общий (iii) (iv) Треугольник OAC ≡ Треугольник OBC (RHS-конгруэнтность.) Следовательно, AC = BC Обратное к теореме 1 : Линия, соединяющая центр окружности и середину хорды, перпендикулярна хорде. Теорема 2 : Равные хорды окружности равноудалены от центра. Дано : Окружность с центром O и радиусом r такая, что хорда AB = хорда CD. Чтобы доказать: OL = OM Конструкция: Нарисуйте OL = AB и OM = CD. Соедините OA и OC Доказательство: (i) AL = (1/2) AB и CM = (1/2) CD (Перпендикуляр от центра окружности к хорде делит хорду пополам.) AB = CD (1/2) AB = (1/2) CD ==> AL = CM (ii) OA = OC (радиусы) (iii) (iii) Треугольник OLA ≡ Треугольник OMC (правосторонняя конгруэнтность.) OL = OM Следовательно, AB и CD равноудалены от O . Обратное к теореме 2 : Хорды окружности, равноудаленные от центра, равны. Помимо материалов, указанных выше, если вам нужны какие-либо другие материалы по математике, воспользуйтесь нашим пользовательским поиском Google здесь. Пожалуйста, отправьте ваш отзыв на [email protected] Мы всегда ценим ваши отзывы. ©Все права защищены. onlinemath5all.com 1. Перпендикуляр от центра к хорде 2. Угол, опирающийся на хорду в центре 3. Угол, опирающийся на дугу окружности 4. Угол в центре и на окружности 5. Углы на одном отрезке окружности Свойства хорд окружности В этой главе мы уже встречались с прямыми, углами, треугольниками и четырехугольниками. Недавно мы видели новый круг участников. Используя все их свойства, мы последовательно получаем некоторые стандартные результаты. Теперь мы собираемся обсудить некоторые свойства, основанные на хордах окружности. Рассматривая хорду и перпендикулярную линию из центра к хорде, мы увидим интересное свойство. 1. Перпендикуляр от центра к хорде Рассмотрим хорду AB окружности с центром O . Нарисуйте OC ⊥ AB и соедините точки OA, OB . Можем ли мы доказать, что эти треугольники равны? Теперь попробуем доказать это, используя уже изученное правило конгруэнтности треугольников. Π OCA = T OCB = 90 ° ( OC ⊥ AB ) и OA OA OA OA OA OA OA OA OA . Сторона OC общая. Критерий RHS говорит нам, что Δ AOC и Δ BOC конгруэнтны. Отсюда можно сделать вывод, что AC = BC . Это рассуждение приводит к следующему результату. Теорема 7 Перпендикуляр из центра окружности к хорде делит хорду пополам. Обратное к теореме 7 Прямая, соединяющая центр окружности и середину хорды, перпендикулярна хорде. Пример 4.5 Найдите длину хорды, которая находится на расстоянии 2√11 см от центра окружности радиусом 12см. Решение Пусть AB будет хордой, а C будет серединой AB Следовательно, OC ⊥ AB OA и 900. OA — это RADIUS , данный OC = 2√11CM и OA = 12 см в правом ΔOAC, с использованием теоремы Pythagoras, мы получаем, AC 2 = OA 2 — o. 2 = OA 2 — . = 122 −(2√11)2 = 144–44 = 100 см AC2 = 100 см AC = 10 см Следовательно, длина хорды AB = 2AC = 2 × 10 см = 20 см Примечание «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов двух других сторон». Справа Δ ABC , BC 2 = AB 2 + AC 2 . Применение этой теоремы наиболее полезно в этом разделе. Пример 4.6 В концентрических окружностях хорда AB внешней окружности пересекает внутреннюю окружность в точках C и D , как показано на диаграмме. Докажите, что AB − CD = 2 AC Решение Дано: хорды на внешних окружностях 7 разрезов AB 76 C и D. Доказать AB — CD = 2 AC Строительство BRAIN AB (By construction) Also, OM ⊥ CD Therefore, AM = MB … (1) (Perpendicular drawn from centre to chord bisect it) CM = MD … (2) Сейчас, AB — CD = 2 AM –2 CM = 2 ( AM — C 77777777777 гг. ) AB – CD =2 AC Проверка прогресса 1. Радиус окружности равен 25 см , а длина одной из ее хорд равна 40 см. Найдите расстояние от центра хорды. 2. Нарисуйте три окружности, проходящие через точки P и Q , где PQ = 4 см. Вместо одной хорды рассмотрим две равные хорды. Теперь мы собираемся обсудить другое свойство. Рассмотрим две равные хорды в окружности с центром O. Теорема 8 Равные хорды окружности опираются на равные углы в центре. Деятельность − 5 Процедура 1. Нарисуйте круг с центром O и подходящим радиусом. 2. Сделайте полукругом путем складывания. Рассмотрим на ней точки A , B . 3. Сделайте складку вдоль AB в виде полукруга и раскройте ее. 4. Получаем еще одну линию сгиба на другой части полукруга, назовем ее CD ( наблюдаем AB = CD ) 5. Соединяем радиус, чтобы получить ΔOAB и 7 6. Используя кальку, возьмите копии треугольников ΔOAB и Δ OCD . 7. Поместите эти треугольники ΔOAB и Δ OCD один на другой. Наблюдение 1. Что вы наблюдаете? Является ли Δ OAB ≡ Δ OCD ? Ответ: Да Δ OAB ≡ Δ OCD 2. Построить перпендикуляр к хордам AB 90 7 и 60177 проходя через центр O . Измерьте расстояние от O до хорд. Теперь найдем длины хорд AB и CD, , если углы, образуемые двумя хордами в центре окружности, равны. То есть ∠ AOB = ∠ COD , а две стороны, которые включают эти углы Δ AOB и Δ COD , являются радиусами и равны. По правилу SAS, Δ AOB ≡ Δ COD . Это дает хорду AB = хорду CD . Теперь запишем обратный результат следующим образом: Обратное утверждение теоремы 8 Если углы, образуемые двумя хордами в центре окружности, равны, то и хорды равны. Таким же образом будем рассуждать о расстоянии от центра, когда даны равные хорды. Проведите перпендикуляр OL ⊥ AB и OM ⊥ CD . По теореме 7 эти перпендикуляры делят хорды поровну. Таким образом, AL = CM . By comparing the Δ OAL and Δ OCM , the angles ∠ OLA = ∠ OMC = 90° and OA = OC are radii. По правилу RHS Δ OAL ≡ Δ OCM . Он дает расстояние от центра OL = OM и записывает вывод следующим образом. Теорема 9 Равные хорды окружности равноудалены от центра. Познакомимся с теоремой, обратной теореме 9, которая очень полезна при решении задач. Обратная теорема 9 Хорды окружности, равноудаленные от центра, равны. Упражнение – 6 Процедура: 1. Нарисуйте три окружности произвольного радиуса с центром O на диаграммной бумаге. 2. Из этих кругов вырежьте полукруг, малый сегмент и большой сегмент. 3. Рассмотрим три точки на этом отрезке и назовем их A , B и C . 4. (iv) Вырежьте треугольники и наклейте их на лист графика так, чтобы точка A совпадала с началом координат, как показано на рисунке. Наблюдение : (i) Угол в полуокружности равен правый угловой. (ii) Угол в большом сегменте равен острому углу. (iii) Угол на малом сегменте равен тупому углу. Теперь мы проверим соотношение между углом, образуемым дугой в центре, и углом, образуемым на окружности. Рассмотрим любую окружность с центром O. . Теперь поместите точки A , B и C на окружности. Вот малая дуга на рис.4.65, полуокружность на рис. Точка C образует разные типы углов в разных положениях (рис. 4.65–4.67). Во всех этих кругах стягивает ∠ AOB в центре и ∠ ACB в точке на окружности круга. Мы хотим доказать ∠ AOB = 2∠ ACB . Для этого удлините CO до D и соедините CD . ∠ ОСА = ОАС начиная с ОА = ОС (радиусы) Внешний угол = сумма двух внутренних противоположных углов. тий AOD = T OAC + OCA = 2om OCA …0177 = тий OBC +тий OCB = 2 В OCB …. (2) из (1) и (2), трясти AOD +№ 777 +° 7 +° 9017 77777,77 +° 777 +° 77 и (2). = 2(∠ OCA + ∠ OCB ) Наконец, мы получаем наш результат ∠ AOB = 2∠ ACB . Отсюда получаем следующий результат: Теорема 10 Проверка выполнения i. ii. Проследите данный полумесяц и завершите его как полную луну, используя линейку и циркуль. Теорема 10 Угол, образуемый дугой окружности в центре, вдвое больше угла, образуемой ею в любой точке оставшейся части окружности. Примечание • Угол, вписанный в полуокружность, является прямым. • Равные дуги окружности образуют равные углы в центре. Пример 4.7 Найдите значение x ° на следующих рисунках: Решение Используя теорему, угол, образуемый дугой окружности в центре, вдвое больше угла, образуемого ею в любой точке на оставшейся части круг. Пример 4.8 Если O является центром окружности и ∠ ABC = 30°, то найдите ∠ AOC . (см. рис. 4.73) Решение присвоил секрет ABC = 30 ° тий AOC = 2 % ABC (угол, подразделенный по дуге в центре. = 60° Теперь мы увидим еще одну интересную теорему. Мы узнали, что малая дуга стягивает тупой угол, большая дуга стягивает острый угол, а полуокружность стягивает прямой угол по окружности. Если дана хорда AB и C и D – это две разные точки на окружности, затем найдите ∠ ACB и ∠ ADB . Есть ли разница в этих углах? Рассмотрим окружность с центром O и хордой AB . C и D являются точками на окружности одного и того же отрезка. Соедините радиус OA и ОБ . 1/2 ∠AOB = ∠ACB (by theorem 10) and 1/2 ∠AOB = ∠ADB (by theorem 10) ∠ ACB = ∠ ADB Этот вывод приводит к новому результату. Теорема 11 Углы на одном отрезке окружности равны. Пример 4.9 На данном рисунке O – это центр круга. Равные хорды окружности стягивают равные углы в центре
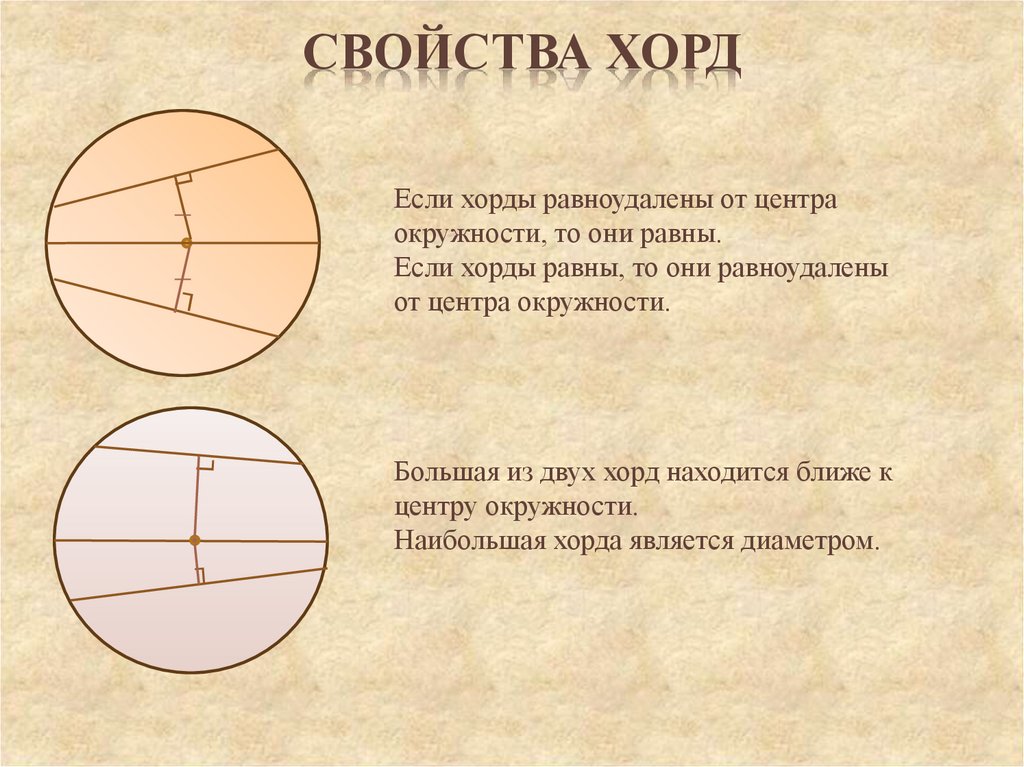
Перпендикуляр из центра окружности к хорде Делит хорду пополам
Равные хорды окружности равноудалены от центра
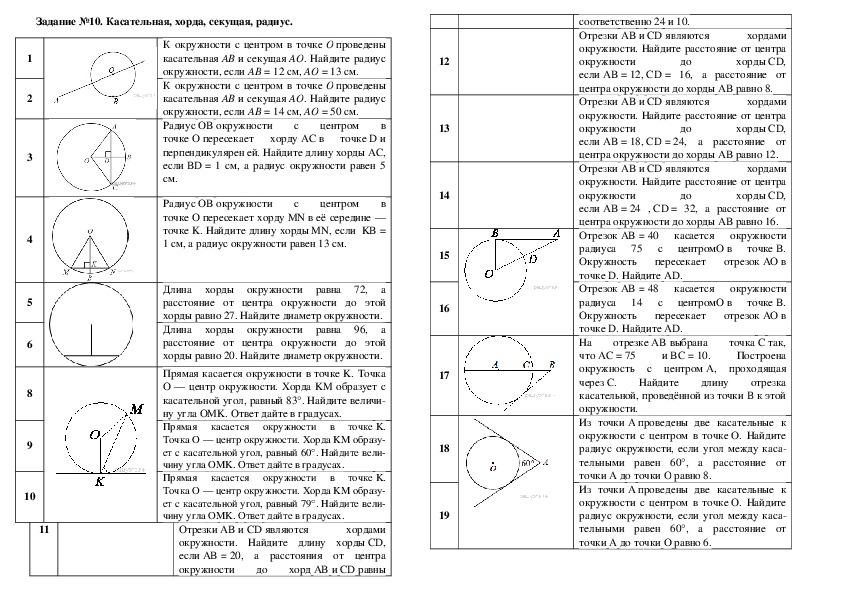
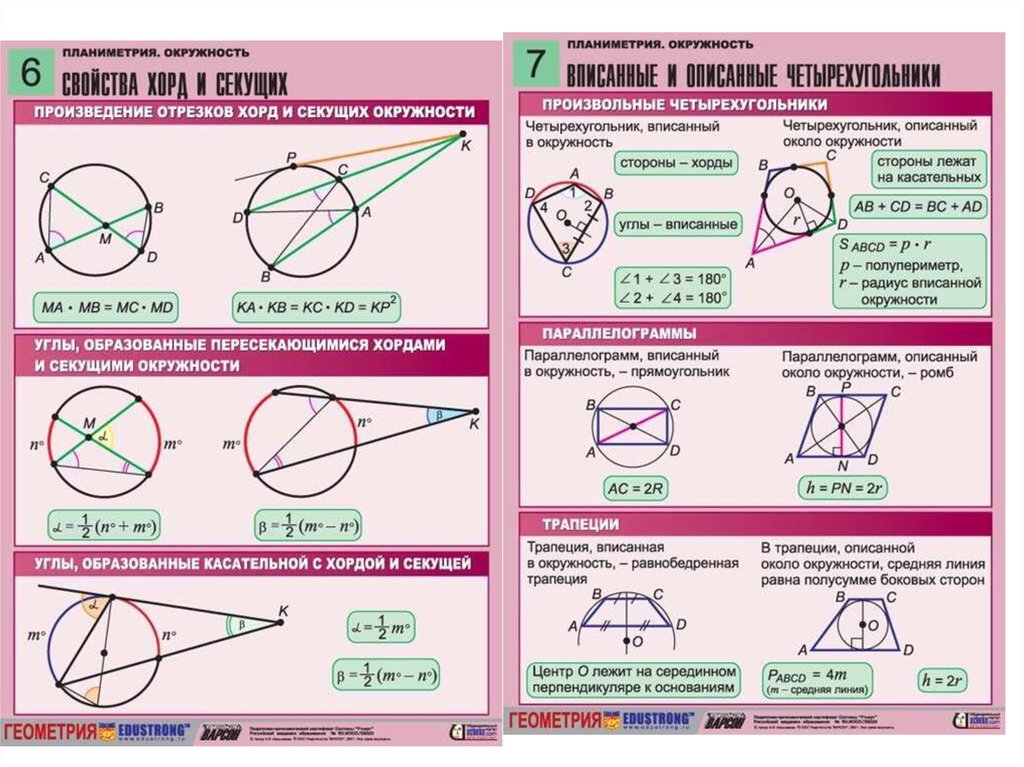
Свойства хорд окружности — Теорема с доказательством, Пример Решенные задачи | Геометрия
Здесь легко получаются два треугольника ∆ AOC и ∆ BOC (рис.4.56).
Теорема Пифагора
Соединив концы хорд с центром, получим треугольники Δ AOB и Δ OCD 907 AB 9 , 1chord CD (поскольку данные хорды равны). Другими сторонами являются радиусы, поэтому OA = OC и OB = OD . По правилу SSS треугольники конгруэнтны, то есть ΔOAB ≡ OCD . Это дает м ∠ AOB = м ∠ ХПК . Теперь это приводит к следующему результату.
4.66 и большая дуга на рис.4.67.
Нарисуйте контур браслетов разного размера и попытайтесь найти центр каждого из них, используя заданный квадрат.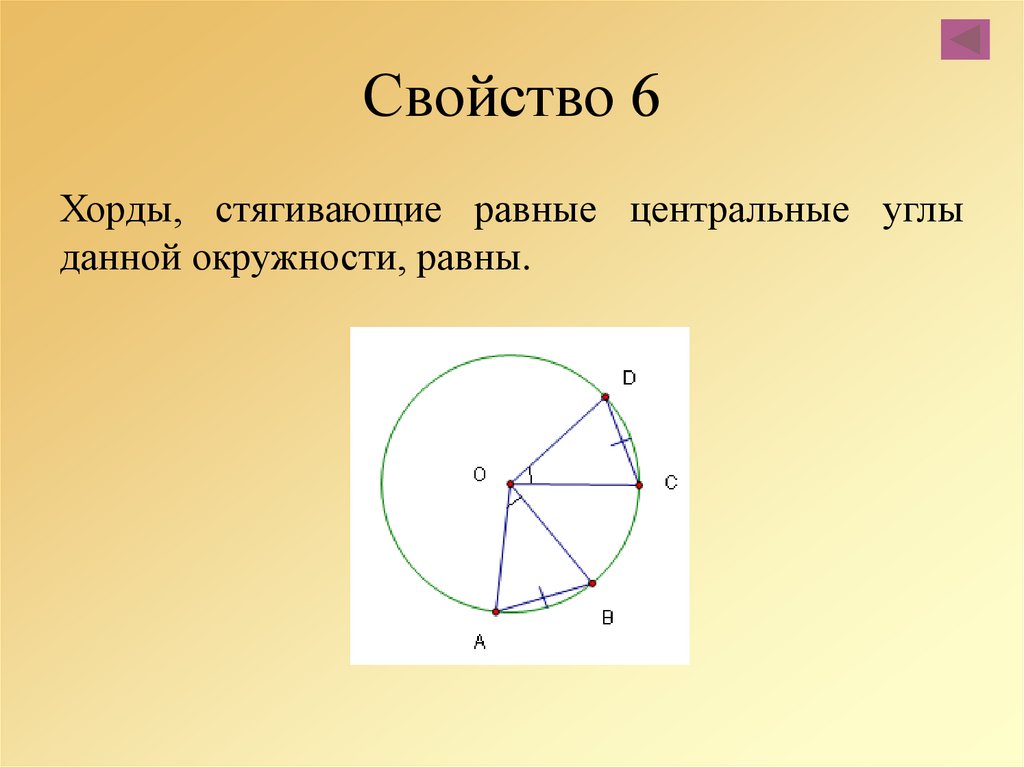
= 2×30°