2 3 матрица: Физический размер матрицы и его влияние на качество снимков

Физический размер матрицы и его влияние на качество снимков

Не все начинающие пользователи знают, что такое физический размер матрицы. Многие путают его с разрешением, но это разные вещи. При этом, физический размер матрицы — это один из важнейших параметров камеры, который влияет на качество снимков.

Прежде чем приступить к рассмотрению влияния размера матрицы на фотографии, рассмотрим сначала какие именно бывают матрицы.

Иногда бывает не просто узнать какая именно матрица стоит на том или ином фотоаппарате. Продавцы в магазинах зачастую просто не знают этого, а производители крайне редко указывают эту информацию. Почему? Этот загадка.

И всё же, что такое физический размер матрицы?

Как многие могли догадаться, физический размер матрицы — это ей длинна и ширина, измеряемые в миллиметрах.

Исторически сложилось так, что в спецификациях производители указывают физический размер матрицы в обратном количестве дюймов, а не в миллиметрах.

Это выглядит следующим образом: 1 / 3.2 — это 3.4 * 4.5 мм.

Зачастую даже в дюймах размер матрицы в спецификациях не указывается, хотя тенденция начинает изменяться. В анонсах новых камер часто можно встретить эту информацию, но не факт, что её можно будет найти в инструкции к камере. В тех случаях, когда размер неизвестен, можно воспользоваться расчетом. Облегчит это занятие таблица со стандартными значениями:

В мм.	В дюймах	KF
3.4 * 4.5	1 / 3.2 «	7. 6
4.0 * 5.4	1 / 2.7 «	6.4
4,3 * 5,8	1 / 2,5″	6.0
5,3 * 7,2	1 / 1,8″	4.9
6,6 * 8,8	2 / 3″	4. 0
15 * 23	APS-C	1.6

Первая колонка содержит значения физического размера матрицы. Вторая колонка указывает соответствующий размер в дюймах. Третья колонка содержит информацию о том, насколько диагональ кадра 35мм больше диагонали матрицы.Чтобы произвести расчет, нужны будут два значения, которые всегда указываются в спецификациях к фотоаппаратам. Это эквивалентное фокусное расстояние и фокусное расстояние. В технической документации и на объективе вся нужная информация должна быть. Если фокусное расстояние и эквивалентное фокусное расстояние известны, вычисления легко провести путем деления второго на первое. Результатом расчета будет значение коэффициента KF.

Пример: имея F = 7 – 21мм, и Feq = 35 – 105мм, можно получить две формулы. Делить можно либо 35/7, либо 105/21. Результатом обеих действий будет KF = 5. По таблице находим самое близкое значение к расчетному и получаем интересующую нас информацию. В нашем случае это физический размер 1 / 1,8″ или 5,3 * 7,2мм.

Рассмотрим матрицы по типоразмерам:

• Самые маленькие матрицы — 1 / 3.2″. Используются они чаще всего в дешевых компактных фотоаппаратах. Их соотношение сторон составляет 4:3, а физический размер — 3.4 * 4.5 мм.
• Матрицы 1 / 2.7″ с соотношением сторон 4:3 и физическим размером 4.0 * 5.4 мм применяются также в недорогих компактах.
• Матрицы 1 / 2,5″ относятся к тому же сегменту камер, что и предыдущие две позиции. Они имеют соотношение сторон 4:3, а размер — 4,3 * 5,8мм.
• Матрицы размером 1 / 1,8″ с соотношением сторон 4:3 и геометрическим размером 5,3 * 7,2 мм применяются в более дорогих компактных камерах. Их можно встретить в устройствах среднего и выше среднего ценового диапазона.
• Размер матриц 2 / 3″ имеет соотношение сторон 4:3, а физический размер 6,6 * 8,8 мм. Часто они применяются в дорогих компактах с не сменной оптикой.
• Матрицы размером 4 / 3″ — физический размер 18 * 13,5 мм и соотношение сторон 4:3 применяются в дорогих камерах.
• DX, APS-C — это формат матриц с соотношением сторон 3:2 и размером около 24 * 18 мм. Эти матрицы применяются в полупрофессиональных и профессиональных зеркальных камерах. Широкое распространение они получили благодаря относительной дешевизне и хорошем качестве снимков.
• Полнокадровая матрица имеет размер 36 * 24 мм. Её соотношение сторон 3:2, а по размеру она соответствует 35 мм кадру. Такие матрицы дорого обходятся в производстве и применяются в профессиональной фототехнике.
• Среднеформатные матрицы имеют формат 60 * 45 мм с соотношением сторон 3:2. Такие матрицы сшиваются из нескольких более простых, что непременно сказывается на стоимости такого производства. Применяются исключительно в дорогих фотоаппаратах.

Разобравшись с основными размерами, стоит поговорить о том, на что же именно они влияют.

Прежде всего, размер матрицы влияет на габариты и вес фотокамеры. Размер оптической части напрямую зависит от размера матрицы, а отсюда можно делать соответствующие выводы.

Также размер матрицы является показателем цифрового шума, который будет передаваться на снимки.

Цифровой шум существенно портит фотографии, создавая впечатление наложенной на снимок маски из точек и царапин.

Шум может возникать по многим причинам. Это может быть дефект самой матрицы, проявляющийся в утечке тока, пробивающегося на соседние пиксели. Также появление шума может быть следствием нагрева матрицы.

На показатели шума влияют как физический размер матрицы, так и размеры пикселей.

Чем размер матрицы больше, тем больше света на нее попадает. Соответственно полезной информации больше. Использование больших по размеру матриц позволяет получить более яркое изображение с естественными цветами.

При большом размере пикселей слой изоляции между ними тоже больше, а следовательно ток утечки уменьшается.

Для большего осознания понятия размера пикселя просто представьте две матрицы одинакового размера. На одной матрице 4000 пикселей (4Мп), а на второй 8000 пикселей (8Мп). Представьте теперь разницу в слое изоляции между каждым пикселем для первого и для второго случая.

Стоит заметить, что на матрицы маленького размера попадает мало света, а соответственно полезный сигнал не велик. Его нужно усиливать, а вместе с полезной информацией усиливаются и шумы.

Вывод!

Подводя итог, можно выделить тот факт, что на матрицу большого размера попадает большее количество света. Соответственно снимок будет ярче и четче.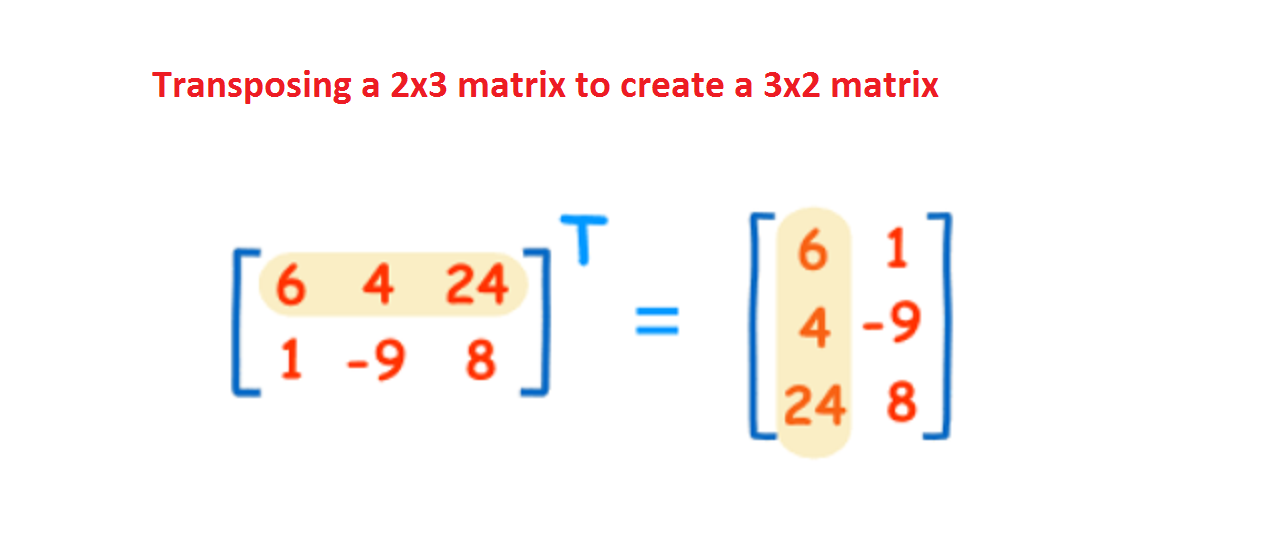

Увеличение размера матрицы увеличивает стоимость её производства, а, следовательно, фотоаппараты с матрицами большого физического размера будут стоить намного дороже своих компактных аналогов.

Copyright by TakeFoto.ru

Матрица фотоаппарата: всё что нужно знать о ней и мегапикселях | Статьи | Фото, видео, оптика

При покупке фотоаппарата одна из вещей, на которую стоит обратить внимание — матрица и её характеристики. Это самая дорогая и сложная по устройство деталь фотоаппарата. 

Разбираемся, что такое матрица, какие параметры у неё бывают, и почему количество мегапикселей при современном развитии техники не самый важный маркер качества.

pixabay.com

Что такое матрица в фотоаппарате

Матрица — это специальная светочувствительная микросхема в фотоаппарате. Она принимает попадающий в камеру свет и формирует электрический сигнал, который преобразует в цифровой. По сути, матрица «превращает» свет в изображение.

Блестящее «стёклышко» в центре микросхемы — и есть матрица / wikimedia.org

Раньше фотоаппараты фиксировали сцену в кадре с помощью светочувствительной плёнки. Матрица зеркального и цифрового фотоаппаратов — это усовершенствованный технически аналог плёнки. 

Что такое пиксели и мегапиксели в матрице

Матрица состоит из маленьких отдельных фотодиодов. Они чувствительны к свету. И именно они ловят его и преобразовывают в электрический сигнал. Один диод — это один пиксель цифровой фотографии. Получается пиксель матрицы фотоаппарата — маленький квадратик, за которым закреплены определённые цвет и яркость, которые уловила матрица фотодиодом. 

Снимок, увеличенный до 12800%. При таком приближении картинка начинает распадаться на отдельные квадратики. Каждый квадратик — пиксель / Иллюстрация автора

Все вместе пиксели составляют изображение, которое мы видит на мониторе или в экране телефона. У современной техники они настолько малы, что глаз не может различить каждый пиксель отдельно, и мы воспринимаем картинку целостно.

У современных камер количество пикселей (фотодиодов на матрице, которые ловят свет) настолько велико, что их записывают и измеряют в миллионах. То есть в мегапикселях (МП). 

Число мегапикселей — то, сколько миллионов пикселей содержит матрица. Проще всего его подсчитать, если умножить число пикселей по длине и по высоте. Например, у нас есть матрица с 5184 пикселями по длине и 3456 пикселями по высоте. 5184х3456 — это 18 мегапикселей. А, например, у Canon EOS 850D максимальное разрешение 6400х4000, что соответствует 24МП. К слову, число, указывающее количество пикселей по длине и ширине — это разрешение матрицы фотоаппарата. 

Казалось бы, всё просто — чем больше мегапикселей у матрицы, тем лучше. Но это было актуально раньше, когда технология развивалась. Гораздо важнее физический размер пикселя (фотодиода) в матрице. Чем он больше, тем больше света на него попадает и тем меньше на фотографии будет шумов. 

Именно поэтому, если вечером вы сфотографируете одну и ту же сцену на смартфон и на фотоаппарат, то у второго шумов будет меньше, а качество картинки — выше. Хотя по количеству мегапикселей смартфон может даже обгонять камеру! Дело в том, что у телефона физический размер пикселей гораздо меньше. И именно поэтому профессиональные и полупроф камеры никогда не были маленькими.

Вывод: если выбирать между фотоаппаратами, у которых одинаковый размер матрицы (о характеристиках матриц ниже), но разное разрешение, то качественнее картинка будет у того, у которого физический размер пикселя больше. То есть, у которого общее число пикселей меньше!

Как рассчитать физический размер пикселя?

• Посмотрите характеристики фотокамеры. Найдите разрешение (в пикселях) и физический размер матрицы (измеряется в миллиметрах).
• Поделите физическую длину матрицы на количество точек по длинной стороне. Полученное число — физический размер пикселя.

Например: у Canon EOS 5D Mark IV физический размер матрицы по длинной стороне — 36мм, а максимальное разрешение — 6720 пикселей. Делим 36 на 6.720 и получаем 0,005. Это и есть размер пикселя. Также у Nikon D780 делим 35.9мм на 6048 пикселей и получаем то же самое число — 0,005.

Характеристики матриц у фотоаппаратов

Рассмотрим характеристики матрицы, на которые можно опираться при выборе фотоаппарата. При этом важно, для каких целей вы берёте камеру. Если интересна ночная съемка, то следует обратить внимание на светочувствительность матрицы и то, насколько фотоаппарат «шумный». Если же нужна компактная камера для путешествий раз в год, то нет смысла переплачивать десятки тысяч за тяжёлую и громоздкую махину для профсъёмки.

Размер

Матрица — прямоугольная пластина со светочувствительными фотоэлементами на ней. Как мы выяснили выше, чем больше фотоэлемент (который потом станет пикселем), тем лучше качество снимка. 

Да, пиксели могут быть одинаковыми на матрицах разного размера. Просто в таком случае их будет меньше и, соответственно, у фотоаппарата будет меньше разрешение. Но, в теории, чем больше матрица, тем больше фотодиодов бОльшего размера на ней можно разместить.

Естественно, матрицы бывают разных форматов. Для них есть условная точка отсчёта размеров — это полный кадр (можно встретить названия фуллфрейм, полнокадровый фотоаппарат, FullFrame, FF). 

Физический размер полнокадровой матрицы фотоаппарата —  36х24мм. Почему именно 36 на 24? В плёночную эпоху это был стандартный размер фотоплёнки. И именно размер кадра в старых плёночных фотоаппаратах взяли за точку отсчёта. 

Кроп-фактор матрицы

Кроп-фактор — условный коэффициент, который обозначает, насколько матрица камеры меньше, если сравнивать с полнокадровой. Фуллфрейм — точка отсчёта, и именно поэтому в таблице ниже кроп-фактор фуллфрейма — единица. Фотоаппараты с размером матрицы меньше полнокадрового называют «кропнутыми».

Если всю картинку мы принимаем за полный кадр, то часть картинки в красном прямоугольнике — то, сколько от той же самой сцены захватит кропнутый фотоаппарат / Иллюстрация автора

На что влияет кроп-фактор?

• Фотоаппарат захватывает меньшую область, чем полнокадровая камера. Угол обзора уменьшается, так как уменьшается поле зрения кадра.

Это как смотреть сквозь свернутый в трубочку лист бумаги. Без него вы видете полную с цену, с ним — выхватываете отдельные детали. 

       – Для кропнутых камер есть своя оптика, которая не пойдет на полнокадровые фотоаппараты. У Canon такие объективы маркируют буквами EF-S, а у Nikon — DX. Например, Canon EF-S 10-18mm или Nikon 35mm f/1.8G AF-S DX. Sony отмечает оптику для полного кадра маркировкой FE вместо E для кроп-фотоаппаратов. Сравните: Sony E 18-105mm f/4 G OSS PZ и Sony FE 24mm F1.4 GM.

        – На кропнутые камеры встает оптика для полнокадровых фотоаппаратов. Но угол обзора на них будет меньше. Например, если на камеру с кроп-фактором 1,52 поставить объектив с фокусным расстоянием 50мм, то его реально фокусное расстояние будет 75мм.

         – Если надеть объектив для кропнутых камер на полноформатный фотоаппарат, по границам кадра поползет заметная чёрная виньетка. Но, например, у некоторых камер Nikon есть DX режим, который при съёмке сразу же кадрирует фотографию и тем самым обрезает виньетку.

Размер матриц фотоаппаратов. Таблица

Подразумевая размер матрицы, могут употреблять любое из этих значений: название формата или длину матрицы по диагонали, её размер в миллиметрах или кроп-фактор.

Формат или диагональ (дюймы)	Размер (мм)	Кроп-фактор
Large format	56 x 36	0.52
Medium format	44 х 33	0.78
FullFrame или 13/8″	36 × 24	1
APS-H Canon	28,1 × 18,7	1,28
APS-H Leica	27 × 18	1,33
APS-C	23,7 × 15,6	1,52
APS-C	23,7 × 15,7	1,52
APS-C	23,7 × 15,8	1,52
APS-C Canon	22,3 × 14,9	1,61
Foveon X3	20,7 × 13,8	1,74
1,5″	18,7 × 14,0	1,85
4/3″	17,3 × 13,0	2
1″	12,8 × 9,6	2,7
1″	13,2 × 8,8	2,73
1/1,33″	9,6 × 7,2	3,58
2/3″	8,8 × 6,6	3,93
1/1,63″	8,0 × 6,0	4,33
1/1,7″	7,6 × 5,7	4,55
1/1,8″	7,2 × 5,3	4,84
1/2″	6,4 × 4,8	5,41
1/2,3″	6,16 × 4,62	5,62
1/2,33″	6,08 × 4,56	5,92
1/2,5″	5,8 × 4,3	6,2
1/2,7″	5,4 × 4,0	6,7
1/2,8″	5,1 × 3,8	7,05
1/3″	4,8 × 3,6	7,5
1/3,2″	4,54 × 3,42	7,92
1/3,6″	4 × 3	9
1/4″	3,6 × 2,7	10
1/6″	2,4 × 1,8	15
1/8″	1,8 × 1,35	20

На что влияет размер матрицы

• количество шумов (зернистости) на фотографии. Чем больше матрица, тем более детализированный и чистый кадр получится. Это важный параметр, если вы снимаете в условиях плохой освещённости, вечером, ночью. Днём в яркий солнечный день разница не будет видна.
• динамический диапазон. То есть насколько широкий диапазон яркости может захватить камера, не теряя при этом качество в тенях и светах.
• глубина цвета. Чем больше матрица, тем больше оттенков и полутонов она сможет зафиксировать. Это видно на однотонных снимках. Например, зимних пейзажах. То есть, актуально достаточно редко.
• размер камеры. Чем больше матрица, тем больше и тяжелее камера.
• широта обзора. Чем больше кроп-фактор, тем уже обзор. При прочих равных визуально кажется, что объект, сфотографированный на кропнутый фотоаппарат, ближе.

Светочувствительность

Этот тот самый параметр ISO. Если перекладывать это на матрицу, то, чем выше ISO, тем более тёмные элементы может поймать фотоаппарат. Чем выше ISO, тем светлее кадр и больше шумов.

Минимальное возможное ISO — 50. Но у разных камер разные минимальные и максимальные значения. Так, у Nikon D5600 ISO колеблется в диапазоне от 100 до 25 000, а у PENTAX K-70 — от 100 до 3 200.

Тип матриц фотоаппаратов

Матрицы различаются по технологии, на основе которой они работают.

Не так давно между собой конкурировали два основных типа:

• CCD (от Charge Coupled Device или ПЗС по-русски). У таких матриц мельчайший структурный элемент — диод.
• CMOS (от Complementary Metal Oxide Semiconductor или КМОП-матрица по-русски). В основе этих матриц транзисторы с каналами разной проводимости.

Сейчас не особо актуально, так как большинство фотоаппаратов оснащают CMOS-матрицами. Они потребляют меньше энергии, выдают меньше шумов на снимке, лучше чувствуют себя в условиях плохого освещения, а также более дешёвы в производстве, если сравнивать с CCD-матрицами.

CCD-матрица компактного фотоаппарата Canon PowerShot A480 / wikimedia. org

Стабилизация матрицы

Считается, что стабилизация помогает сделать картинку менее смазанной, если вы снимаете с рук и на удлиненных значениях выдержки. Эту технологию активно используют и продвигают Sony, Panasonic, Olympus, Nikon. Например, матричная стабилизация есть у Sony Alpha A7С или Panasonic Lumix DC-GH5. 

Но, по большому счёту, это лишь маркетинговый ход. Так как никакая стабилизация не является панацеей и не изменит ситуацию кардинально. Профессионалы знают, что ничто не зафиксирует камеру лучше, чем штатив (читайте, как его выбрать). Кроме того, эта функция работает тяжело, если выдержка действительно высокая (от 1 секунды и больше). 

Если же сравнивать стабилизацию матриц и объективов, то матричная не влияет на светосилу, что однозначно плюс. При этом более эффективной и надежной всё же считается оптическая стабилизация.

матриц — Сложение матриц — можно ли сложить вместе матрицу 3×2 + матрицу 2×3?

$\begingroup$

У меня две матрицы;

$$ 1) \оставил( \begin{матрица} 3 и -2 \\ 1 и 2 \\ 0 и -3\\ \end{матрица} \Правильно) $$

А $$ 2) \оставил( \begin{матрица} -2 и 1 и 3 \\ 4 и 3 и 2 \\ \end{матрица} \Правильно) $$

Но можно ли сложить эти два вместе, возможно ли это? Я нашел из этого PDF следующую цитату:

Сумма A + B двух матриц A, B (которые должны иметь одинаковое количество строк и одинаковое количество столбцов) — это матрица (также с той же формой), полученной путем добавления соответствующие элементы A и B.

Это наводит меня на мысль, что я не могу сложить Матрицу 1 и 2, но могу сложить Матрицу 2 и третью матрицу тех же размеров, например:

$$ 3) \оставил( \begin{матрица} 2 & 1 & -1 \\ -1 & 0 & 3 \\ \end{матрица} \Правильно) $$

Я пришел к выводу, что могу сложить Матрицу 2+3, но не Матрицу 1+2 или 1+3, например. Я прав в своих предположениях здесь?

И изменится ли это каким-либо образом, если я попытаюсь перемножить матрицы?

• матрицы
• дискретная математика

$\endgroup$

$\begingroup$

Прежде всего, вы не можете сложить две матрицы, если они не имеют одинакового размера. В твоем случае, $$\слева( \begin{матрица} -2 и 1 и 3 \\ 4 и 3 и 2 \\ \end{матрица} \справа) + \слева( \begin{матрица} 2 & 1 & -1 \\ -1 & 0 & 3 \\ \end{матрица} \справа)=\слева( \begin{матрица} -2+2 и 1+1 и 3+(-1) \\ 4+(-1) и 3+0 и 2+3 \\ \end{матрица} \справа)=\слева( \begin{матрица} 0 и 2 и 2 \\ 3 и 3 и 5 \\ \end{матрица} \справа)$$

Как видите, сложение двух матриц — это то же самое, что сложение ее элементов. Если говорить об умножении, то все значительно меняется. Я рекомендую вам эту ссылку, которая очень поучительна.

$\endgroup$

1

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Умножение матриц с использованием цикла For

[Эта статья была впервые опубликована в блогах на Adejumo RS и любезно предоставлена ​​R-блогерами]. (Вы можете сообщить о проблеме с содержанием на этой странице здесь)

---

Хотите поделиться своим контентом с R-блогерами? нажмите здесь, если у вас есть блог, или здесь, если у вас его нет.

«Это все данные. Подарок вчерашнего дня, который вы получите сегодня, чтобы сделать завтрашний день лучше»
— Джон Акафф

Линейная алгебра — это раздел математики, который имеет дело с векторами и матрицами, хотя некоторые находят его трудным, я все же нахожу его проще, чем старый добрый исчисление. Векторы и матрицы — очень важные структуры данных в R, поэтому знание линейной алгебры очень важно. В этом посте мы будем использовать наше понимание «циклов for», чтобы объяснить умножение матриц в R.
Во-первых, мы собираемся определить две матрицы, a , которая представляет собой матрицу (4×3), и b , которая представляет собой матрицу (3×4). Умножение двух матриц даст нам c , которая представляет собой ( 4×4) матрица.

 а <- матрица(с(9, 4, 12, 5, 0, 7, 2, 6, 8, 9, 2, 9),
            nряд = 4, byrow = ИСТИНА)
а
## [1] [2] [3]
## [1,] 9 4 12
## [2,] 5 0 7
## [3,] 2 6 8
## [4,] 9 2 9
б <- матрица(с(5, 4, 2, 5, 2, 7, 2, 1, 8, 3, 2, 6),
            nrow = 3, byrow = ИСТИНА)
б
## [1] [2] [3] [4]
## [1,] 5 4 2 5
## [2,] 2 7 2 1
## [3,] 8 3 2 6 

Следующий код представляет собой функцию для выполнения матричного умножения между a и b для получения матрицы c .

 mat_mup <- функция (а, б) {
  если (ncol(a) != nrow(b)){
    вернуть("не умножить")
  }
  еще{
    c = матрица (rep (0, nrow (a) * ncol (b)),
               ряд = ряд (а))
    для (я в 1: nrow (а)) {
      for(j в 1:ncol(b)){
        for(k в 1:nrow(b)){
          c[i,j] <- c[i,j] + a[i,k]*b[k, j]
        }
      }
    }
  }
  возврат (с)
} 

В приведенном выше коде мы создаем функцию с именем mat_mup , функция возвращает «невозможно умножить», если количество столбцов в матрице a не соответствует количеству строк в матрице b .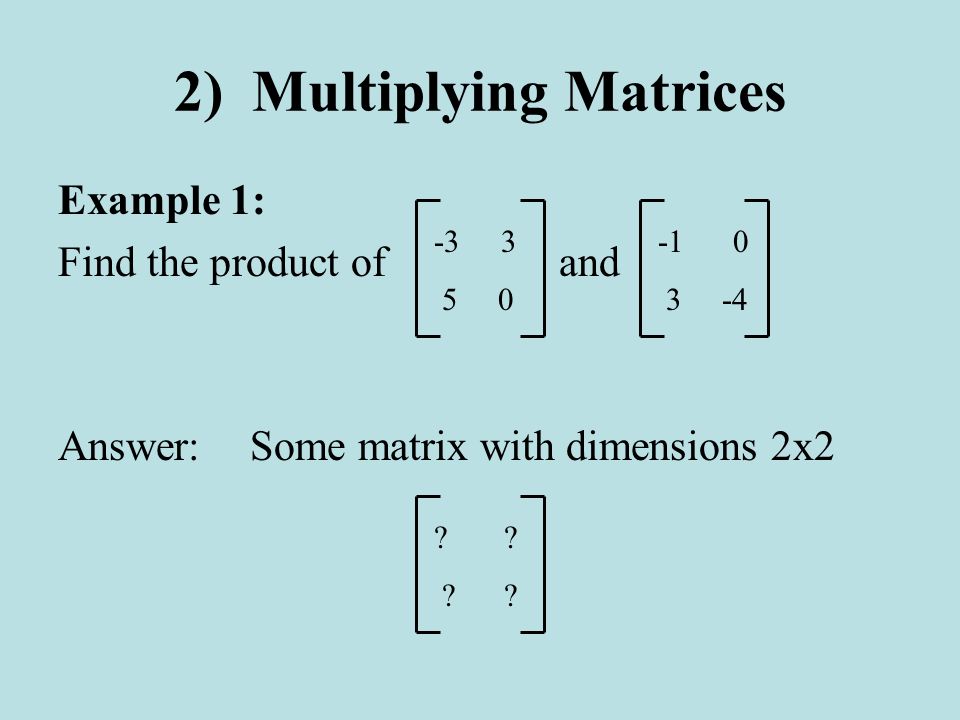 Второе условие выполняет матричную операцию с использованием трех циклов for, первый для цикла принимает i значений для количества строк в матрице a , второй для цикла принимает j для числа столбцов в матрице b и третий для цикла занимает k для количества строк в матрице b . Функция возвращает матрицу c , результат умножения на и на .

 мат_мап(а,б)
## [1] [2] [3] [4]
## [1,] 149 100 50 121
## [2,] 81 41 24 67
## [3,] 86 74 32 64
## [4,] 121 77 40 101 

Представьте, что вам нужно всегда делать то же самое только для умножения двух матриц. R имеет встроенный оператор, который обрабатывает умножение матриц. Когда-нибудь учили, почему матрица a*b возвращает ошибку в R, что ж, я оставляю это на ваше усмотрение. Оператор %*% используется для умножения матриц.

 а %*% б
## [1] [2] [3] [4]
## [1,] 149 100 50 121
## [2,] 81 41 24 67
## [3,] 86 74 32 64
## [4,] 121 77 40 101 

К оставьте комментарий для автора, перейдите по ссылке и прокомментируйте его блог: Блоги на Adejumo R.