| 1 | Найти объем | сфера (5) | |
| 2 | Найти площадь | окружность (5) | |
| 3 | Найти площадь поверхности | сфера (5) | |
| 4 | Найти площадь | окружность (7) | |
| 5 | Найти площадь | окружность (2) | |
| 6 | Найти площадь | окружность (4) | |
| 7 | Найти площадь | окружность (6) | |
| 8 | сфера (4) | | |
| 9 | Найти площадь | окружность (3) | |
| 10 | Вычислить | (5/4(424333-10220^2))^(1/2) | |
| 11 | Разложить на простые множители | 741 | |
| 12 | Найти объем | сфера (3) | |
| 13 | Вычислить | 3 квадратный корень из 8*3 квадратный корень из 10 | |
| 14 | Найти площадь | окружность (10) | |
| 15 | Найти площадь | окружность (8) | |
| 16 | Найти площадь поверхности | сфера (6) | |
| 17 | Разложить на простые множители | 1162 | |
| 18 | Найти площадь | окружность (1) | |
| 19 | Найти длину окружности | окружность (5) | |
| 20 | Найти объем | сфера (2) | |
| 21 | Найти объем | сфера (6) | |
| 22 | Найти площадь поверхности | сфера (4) | |
| 23 | Найти объем | сфера (7) | |
| 24 | Вычислить | квадратный корень из -121 | |
| 25 | Разложить на простые множители | 513 | |
| 26 | Вычислить | квадратный корень из 3/16* квадратный корень из 3/9 | |
| 27 | Найти объем | прямоугольный параллелепипед (2)(2)(2) | |
| 28 | Найти длину окружности | окружность (6) | |
| 29 | Найти длину окружности | окружность (3) | |
| 30 | Найти площадь поверхности | сфера (2) | |
| 31 | Вычислить | ||
| 32 | Найти объем | прямоугольный параллелепипед (5)(5)(5) | |
| 33 | Найти объем | прямоугольный параллелепипед (10)(10)(10) | |
| 34 | Найти длину окружности | окружность (4) | |
| 35 | Перевести в процентное соотношение | 1. 2-4*-1+2 2-4*-1+2 | |
| 45 | Разложить на простые множители | 228 | |
| 46 | Вычислить | 0+0 | |
| 47 | Найти площадь | окружность (9) | |
| 48 | Найти длину окружности | окружность (8) | |
| 49 | Найти длину окружности | окружность (7) | |
| 50 | Найти объем | сфера (10) | |
| 51 | Найти площадь поверхности | сфера (10) | |
| 52 | Найти площадь поверхности | сфера (7) | |
| 53 | Определить, простое число или составное | 5 | |
| 54 | 3/9 | ||
| 55 | Найти возможные множители | 8 | |
| 56 | Вычислить | (-2)^3*(-2)^9 | |
| 57 | Вычислить | 35÷0.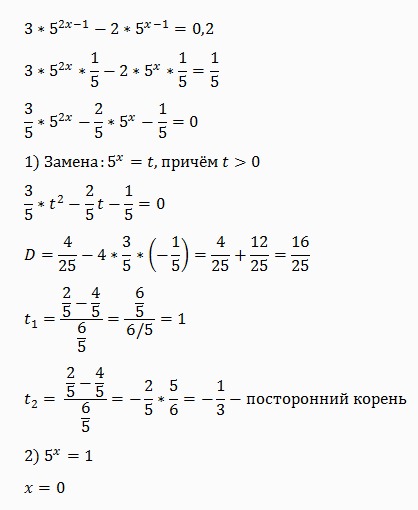 2 2 | |
| 60 | Преобразовать в упрощенную дробь | 2 1/4 | |
| 61 | Найти площадь поверхности | сфера (12) | |
| 62 | Найти объем | сфера (1) | |
| 63 | Найти длину окружности | окружность (2) | |
| 64 | Найти объем | прямоугольный параллелепипед (12)(12)(12) | |
| 65 | Сложение | 2+2= | |
| 66 | Найти площадь поверхности | прямоугольный параллелепипед (3)(3)(3) | |
| 67 | Вычислить | корень пятой степени из 6* корень шестой степени из 7 | |
| 68 | Вычислить | 7/40+17/50 | |
| 69 | Разложить на простые множители | 1617 | |
| 70 | Вычислить | 27-( квадратный корень из 89)/32 | |
| 71 | Вычислить | 9÷4 | |
| 72 | Вычислить | 2+ квадратный корень из 21 | |
| 73 | Вычислить | -2^2-9^2 | |
| 74 | Вычислить | 1-(1-15/16) | |
| 75 | Преобразовать в упрощенную дробь | 8 | |
| 76 | Оценка | 656-521 | |
| 77 | Вычислить | 3 1/2 | |
| 78 | Вычислить | -5^-2 | |
| 79 | Вычислить | 4-(6)/-5 | |
| 80 | Вычислить | 3-3*6+2 | |
| 81 | Найти площадь поверхности | прямоугольный параллелепипед (5)(5)(5) | |
| 82 | Найти площадь поверхности | сфера (8) | |
| 83 | Найти площадь | окружность (14) | |
| 84 | Преобразовать в десятичную форму | 11/5 | |
| 85 | Вычислить | 3 квадратный корень из 12*3 квадратный корень из 6 | |
| 86 | Вычислить | (11/-7)^4 | |
| 87 | Вычислить | (4/3)^-2 | |
| 88 | Вычислить | 1/2*3*9 | |
| 89 | Вычислить | 12/4-17/-4 | |
| 90 | Вычислить | 2/11+17/19 | |
| 91 | Вычислить | 3/5+3/10 | |
| 92 | Вычислить | 4/5*3/8 | |
| 93 | Вычислить | 6/(2(2+1)) | |
| 94 | Упростить | квадратный корень из 144 | |
| 95 | Преобразовать в упрощенную дробь | 725% | |
| 96 | Преобразовать в упрощенную дробь | 6 1/4 | |
| 97 | Вычислить | 7/10-2/5 | |
| 98 | Вычислить | 6÷3 | |
| 99 | Вычислить | 5+4 | |
| 100 | Вычислить | квадратный корень из 12- квадратный корень из 192 |
Степень и ее свойства.
 Определение степени
Определение степениОсновная цель
Ознакомить учащихся со свойствами степеней с натуральными показателями и научить выполнять действия со степенями.
Тема “ Степень и её свойства ” включает три вопроса:
- Определение степени с натуральным показателем.
- Умножение и деление степеней.
- Возведение в степень произведения и степени.
Контрольные вопросы
- Сформулируйте определение степени с натуральным показателем, большим 1. Приведите пример.
- Сформулируйте определение степени с показателем 1. Приведите пример.
- Каков порядок выполнения действий при вычислении значения выражения, содержащего степени?
- Сформулируйте основное свойство степени. Приведите пример.
- Сформулируйте правило умножения степеней с
одинаковыми основаниями.
 Приведите пример.
Приведите пример. - Сформулируйте правило деления степеней с одинаковыми основаниями. Приведите пример.
- Сформулируйте правило возведения в степень произведения. Приведите пример. Докажите тождество (ab)n = an•bn .
- Сформулируйте правило возведения степени в степень. Приведите пример. Докажите тождество ( аm )n = аm n .
Определение степени.
Степенью числа a с натуральным показателем n, большим 1, называется произведение n множителей, каждый из которых равен а. Степенью числа а с показателем 1 называется само число а.
Степень с основанием а и показателем n записывается так: аn . Читается “ а в степени n ”; “ n- я степень числа а ”.
По определению степени:
а1 = а
а2 = а•а
а3 = а•а•а
а4 = а• а•а•а
. . . . . . . . . . . .
. . . . . . . . . . .
аn =
Нахождение значения степени называют возведением в степень.
1. Примеры возведения в степень:
33 = 3• 3• 3 = 27
04 = 0• 0• 0• 0 = 0
( -5 )3 = ( -5 ) • ( -5 ) • ( -5 ) = -125
71 = 7
2. Представьте в виде квадрата числа: 25 ; 0,09 ;
25 = 52 ; 0,09 = ( 0,3 )2 ; .
3. Представьте в виде куба числа:
27 ; 0,001 ; 8 .
27 = 33 ; 0,001 = ( 0,1 )3 ; 8 = 23 .
4. Найти значения выражений:
а) 3• 103 = 3• 10• 10• 10 = 3• 1000 = 3000
б) -24 + ( -3 )2 = 7
24 = 16
( -3 )2 = 9
-16 + 9 = 7
Вариант 1
1. Запишите произведение в виде степени:
Запишите произведение в виде степени:
а) 0,3• 0,3• 0,3
б)
в) b• b• b• b• b• b• b
г) ( -х ) • ( -х ) • ( -х ) • ( -х )
д) ( ab ) • ( ab ) • ( ab )
2. Представьте в виде квадрата числа:
16 ; 0,25 ; .
3. Представьте в виде куба числа:
125 ; 0,027 ; .
4. Найти значения выражений :
а) 72 + 43
б) 62 + 53
в) -14 + ( -2 ) 3
г) -43 + ( -3 )2
д) 100 — 5• 24
Умножение степеней.
Для любого числа а и произвольных чисел m и n выполняется:
aman = am + n .
Доказательство:
Правило: При умножении степеней с
одинаковыми основаниями основания оставляют
прежним, а показатели степеней складывают.
amanak = am + nak = a( m + n ) + k = am + n + k
1. Представить в виде степени:
а) х5• х4 = х5 + 4 = х9
б) y• y6 = y1 • y6 = y1 + 6 = y7
в) b2 • b5 • b4 = b2 + 5 + 4 = b11г) 34 • 9 = 34•32 = 36
д) 0,01• 0,13 = 0,12 • 0,13 = 0,15
2. Представить в виде степени и найти значение по таблице:
а) 23 • 2 = 24 = 16
б) 32 • 35 = 37 = 2187
Вариант 1
1. Представить в виде степени:
а) х3 •х4 е) х2 •х3 •х4
б) а6 •а2 ж) 33•9
в) у4 •у з) 74•49
г) а• а8 и) 16• 27
д) 23•24 к) 0,33•0,09
2.
а) 22•23 в) 8• 25
б) 34•32 г) 27• 243
Деление степеней.
Для любого числа а0 и произвольных натуральных чисел m и n, таких, что m>n выполняется:
am : an = am — n
Доказательство:
am — n an = a( m — n ) + n = am — n + n = am
по определению частного:
am : an = am — n .
Правило: При делении степеней с одинаковыми основаниями основание оставляют прежним, а из показателя степени делимого вычитают показатель степени делителя.
Определение: Степень числа а, не равного нулю, с нулевым показателем равна единице
а0 = 1
т. к. аn : an = 1 при а0 .
к. аn : an = 1 при а0 .
1. Представьте в виде степени частное:
а) х4:х2 = х4 — 2 = х2
б) у8:у3 = у8 — 3 = у5
в) а7:а = а7:а1 = а7 — 1 = а6
г) с5:с0 = с5:1 = с5
2. Найдите значения выражений:
а) 57:55 = 52 = 25
б) 1020:1017 = 103 = 1000
в)
г)
д)
Вариант 1
1. Представьте в виде степени частное:
а) х5 : х2б) у9 : у4
в) b10 : b
г) с10 : с4
д) а7 : а0
2. Найдите значения выражений:
Найдите значения выражений:
а) 36 : 32
б) 715 : 713
в)
г)
д)
Возведение в степень произведения.
Для любых а и b и произвольного натурального числа n:
( ab )n = an•bn
Доказательство:
По определению степени
( ab )n =
Сгруппировав отдельно множители а и множители b, получим:
=
Доказанное свойство степени произведения распространяется на степень произведения трех и более множителей.
Например:
( a• b• c )n = an •bn •cn ;
( a• b• c• d )n = an •bn •cn •dn .
Правило: При возведении в степень
произведения возводят в эту степень каждый
множитель и результат перемножают.
1. Возвести в степень:
а) ( a• b )4 = a4 •b4
б) (2• х• у )3 =23•х3 •у3 = 8• х3 •у3
в) ( 3• а )4 = 34•а4 = 81• а4
г) ( -5• у )3 = (-5)3 •у3 = -125• у3
д) (-0,2• х• у )2 = (-0,2)2 •х2 •у2 = 0,04• х2 •у2
е) (-3• a• b• c )4 = (-3)4 •a4 •b4 •c4 = 81• a4 •b4 •c4
2. Найти значение выражения:
а) (2• 10)4 = 24•104 = 16• 1000 = 16000
б) (3• 5• 20)2= 32•1002= 9• 10000= 90000
в) 24•54 = (2• 5)4 = 104 = 10000
г) 0,2511•411 = (0,25• 4)11 = 111 = 1
д)
Вариант 1
1. Возвести в степень:
Возвести в степень:
а) ( a• b )9
б) ( 2• а• с )4
в) ( 5• а )3
г) ( -3• у )4
д) ( -0,1• х• у )3
е)
2. Найти значение выражения:
а) (3• 10)3
б) (5• 7• 20)2
в) 53•23
г)
д)
Возведение в степень степени.
Для любого числа а и произвольных натуральных чисел m и n:
( аm )n = аm n
Доказательство:
По определению степени
( аm )n =
Правило: При возведении степени в степень основание оставляют тем же, а показатели перемножают.
1. Возвести в степень:
( а3 )2 = а6 ( х5 )4 = х20
( у5 )2 = у10 ( b3 )3 = b9
2. Упростите выражения:
Упростите выражения:
а) а3 •( а2)5 = а3 •а10 = а13
б) ( b3 )2 •b7 = b6 •b7 = b13
в) ( х3 )2 •( х2 )4 = х6 •х8 = х14
г) ( у• у7 )3 = ( у8 )3 = у24
3. Найдите значение выражений:
а)
б)
Вариант 1
1. Возвести в степень:
а) ( а4 )2 б) ( х4 )5
в) ( у3 )2 г) ( b4 )4
2. Упростите выражения:
а) а4 •( а3)2
б) ( b4 )3 •b5+
в) ( х2 )4 •( х4 )3
г) ( у• у9 )2
3. Найдите значение выражений:
Найдите значение выражений:
а)
б)
Приложение
Определение степени.
Вариант 2
1ю Запишите произведение в виде степени:
а) 0,4• 0,4• 0,4
б)
в) а• а• а• а• а• а• а• а
г) ( -у ) • ( -у ) • ( -у ) • ( -у )
д) ( bс ) • ( bс ) • ( bс )
2. Представьте в виде квадрата числа:
25 ; 0,16 ; .
3. Представьте в виде куба числа:
64 ; 0,125 ; .
4. Найти значения выражений:
а) 52 + 33
б) 43 — 72
в) -13 + ( -2 )4
г) -62 + ( -3 )2
д) 4• 52 – 100
Вариант 3
1. Запишите произведение в виде степени:
Запишите произведение в виде степени:
а) 0,5• 0,5• 0,5
б)
в) с• с• с• с• с• с• с• с• с
г) ( -х ) • ( -х ) • ( -х ) • ( -х )
д) ( ab ) • ( ab ) • ( ab )
2. Представьте в виде квадрата числа: 100 ; 0,49 ; .
3. Представьте в виде куба числа:
1000 ; 0,008 ; .
4. Найти значения выражений :
а) 34 + 72
б) 63 — 92
в) -15 + ( -3 )2
г) -53 + ( -4 )2
д) 5• 42 — 100
Вариант 4
1. Запишите произведение в виде степени:
а) 0,7• 0,7• 0,7
б)
в) х• х• х• х• х• х
г) ( -а ) • ( -а ) • ( -а )
д) ( bс ) • ( bс ) • ( bс ) • ( bc )
2. Представьте в виде квадрата числа:
Представьте в виде квадрата числа:
81 ; 0,64 ;.
3. Представьте в виде куба числа:
216 ; 0,064 ; .
4. Найти значения выражений :
а) 62 + 43
б) 53 — 82
в) -14 + ( -3 )3
г) -34 + ( -5 )2
д) 100 — 3• 25
Умножение степеней.
Вариант 2
1. Представить в виде степени:
а) х4 •x5 е) х3 •х4 •х5
б) а7 •а3 ж) 23•4
в) у5 •у з) 43•16
г) а• а7 и) 4• 25
д) 22•25 к) 0,23• 0,04
2. Представить в виде степени и найти значение
по таблице:
Представить в виде степени и найти значение
по таблице:
а) 32•33 в) 16• 23
б) 24•25 г) 9• 81
Вариант 3
1. Представить в виде степени:
а) а3•а5 е) у2 •у4 •у6
б) х4•х7 ж) 35•9
в) b6•b з) 53•25
г) у• у8 и) 49• 74
д) 23•26 к) 0,34•0,27
2. Представить в виде степени и найти значение по таблице:
а) 33•34 в) 27• 34
б) 24•26 г) 16• 64
Вариант 4
1. Представить в виде степени:
а) а6•а2 е) х4 •х• х6
б) х7•х8 ж) 34•27
в) у6•у з) 43•16
г) х• х10 и) 36• 63
д) 24•25 к) 0,22•0,008
2. Представить в виде степени и найти значение
по таблице:
Представить в виде степени и найти значение
по таблице:
а) 26•23 в) 64• 24
б) 35•32 г) 81• 27
Деление степеней.
Вариант 2
1. Представьте в виде степени частное:
а) х6 : х3
б) у10 : у5
в) b9 : b
г) с12 : с7
д) а9 : а0
2. Найдите значения выражений:
а) 27 : 24
б) 610 : 68
в)
г)
д)
Вариант 3
1. Представьте в виде степени частное:
а) у7 : у4
б) а11 : а7
в) с10 : с
г) b17 : b15
д) х8 : х0
2. Найдите значения выражений:
Найдите значения выражений:
а) 38 : 35
б) 410 : 47
в)
г)
д)
Вариант 4
1. Представьте в виде степени частное:
а) х8 : х3
б) b12 : b5
в) у9 : у
г) с19 : с14
д) а10 : а0
2. Найдите значения выражений:
а) 510 : 58
б) 617 : 612
в)
г)
д)
Возведение в степень произведения.
Вариант 2
1. Возвести в степень:
а) ( х• у )7
б) (3• а• b )4
в) (2• а )5
г) (-4• у )3
д) (-0,3• a• b )2
е) ( -2• x• y• z )3
2. Найти значение выражения:
Найти значение выражения:
а) (2• 10)3
б) (7• 4• 25)2
в) 43•53
г) 49•0,259
д)
Вариант 3
1. Возвести в степень:
а) ( a• b )8
б) (2• х• у )5
в) (3• х )4
г) (-4• с )4
д) (-0,2• х• у )2
е)
2. Найти значение выражения:
а) (5• 10)3
б) (9• 4• 25)2
в) 23•33
г)
д) 0,54•44
Вариант 4
1. Возвести в степень:
а) ( х• у )9
б) (3• а• b )5
в) (2• у )6
г) (-6• b )3
д) (-0,1• a• b )2
е) ( -5• x• y• z )4
2. Найти значение выражения:
Найти значение выражения:
а) (3• 10)4
б) (8• 5• 20)2
в) 52•42
г) 0,27•57
д)
Возведение в степень степени.
Вариант 2
1. Возвести в степень:
а) ( а5 )2
б) ( х3 )5
в) ( у4 )2
г) ( b6 )6
2. Упростите выражения:
а) а4 •( а3)5
б) ( b2 )3 •b8
в) ( х3 )4 •( х2 )5
г) ( у• у10 )3
3. Найдите значение выражений:
а)
б)
Вариант 3
1. Возвести в степень:
Возвести в степень:
а) ( а7 )2
б) ( х6 )5
в) ( у10 )2
г) ( b7 )7
2. Упростите выражения:
а) а5 •( а2)3
б) ( b3 )4 •b7
в) ( х5 )2 •( х3 )4
г) ( у• у11 )2
3. Найдите значение выражений:
а)
б)
Вариант 4
1. Возвести в степень:
а) ( а6 )2
б) ( х7 )5
в) ( у8 )2
г) ( b5 )5
2. Упростите выражения:
а) а6 •( а4)2
б) ( b5 )2 •b6
в) ( х2 )5 •( х4 )3
г) ( у6 •у )3
3. Найдите значение выражений:
Найдите значение выражений:
а)
б)
Вирус папилломы человека – причина бородавок, кондилом и папиллом
Вирус папилломы человека – это семейство вирусов, вызывающих у человека бородавки, папилломы, кондиломы дисплазию или рак шейки матки и половых органов.
Общее семейство: Papillomaviridae. Латинское название: Human Papillomavirus.
Аббревиатура: ВПЧ или HPV (так пишется в анализах).
1. За 50 лет открыто более 100 типов вируса папилломы человека. Патогенные для человека — 80 типов.
2. По данным ВОЗ, 70% населения Земли инфицировано ВПЧ.
3. ВПЧ 16 и 18 типов чаще других типов приводят к раку шейки матки.
4. ВПЧ в подавляющем большинстве является причиной рака половых органов у женщин и у мужчин.
5. Самой эффективной профилактикой от рака шейки матки и половых органов во всем мире считается вакцина от 6, 11, 16 и 18 типов папилломавирусов.
Заражение.
Источник вируса клетки кожи или слизистой больного человека
Если у больного есть папиллома, даже небольшого по виду размера, именно она является непосредственным источником вируса!
При этом у больного при осмотре может еще не быть бородавки или кондиломы. Изменения могут быть еще микроскопическими, не видны глазом (субклиническая стадия заболевания). Но такой человек уже может передать вирус другому человеку.
Инфицирование обычно возникает еще в детском возрасте. Через микроповреждения кожных покровов ребенка (царапины, ссадины) папилломавирус проникает в кожу и вызывает появление бородавок.
У взрослых людей определенные типы вируса (будут рассмотрены ниже) вызывают развитие аногенитальных бородавок, или остроконечных кондилом на половых органах. Механизм передачи таких типов – преимущественно половой.
Но теоретически возможен и контактно-бытовой путь передачи — через общие гигиенические принадлежности, ободок унитаза, прием ванны, посещение бани, бассейна и т. д.
д.
Через микротравмы половых органов вирус передается от одного полового партнера к другому. При этом у больного также может не быть никаких видимых глазом изменений. Но микроскопические изменения на слизистой половых органов могут быть. И эти измененные клетки являются источниками вируса.
Далее вирус проникает в кожу или в слизистую и его встречают различные клетки иммунной системы человека. В большинстве случаев иммунные клетки уничтожают вирус. Но если иммунная система ослаблена, вирус успевает проникнуть в клетки базального слоя эпителия кожи или слизистых оболочек, встраивается в хромосомы клеток и изменяет работу этих клеток. Клетки начинают чрезмерно делиться и разрастаются на ограниченном участке, внешне превращаясь в бородавки и папилломы.
Помните:
— типы ВПЧ, вызывающие бородавки, проникают в организм еще в детстве,
— типы ВПЧ, вызывающие остроконечные кондиломы, проникают в организм преимущественно при половом контакте.
В редких случаях развитие папилломавирусной инфекции в организме человека может привести к малигнизации (то есть перерождению в рак). Поэтому все типы папилломавирусов классифицируют по степени онкогенности (то есть по степени возможного развития рака).
Классификация типов ВПЧ по онкогенности
(по данным исследований McConcl D. J., 1991; LorinczA. T., 1992; Bosch E X. et al., 2002; Козлова В. И., ПухнерА. Ф., 2003; Syrjanen S., 2003; Шахова Н. М. и др., 2006;).
1) Типы папилломавирусов, никогда не вызывающие рак: 1, 2, 3, 4, 5, 10, 28, 49
2) Типы низкого онкогенного риска (очень редко вызывают рак): 6, 11, 13, 32, 34, 40, 41, 42, 43, 44, 51, 72.
3) Типы среднего онкогенного риска (процент ракового перерождения средний): 26, 30, 35, 52, 53, 56, 58, 65.
4) Типы высокого онкогенного риска (из всех типов вируса именно эти типы чаще всего дают перерождение): 16, 18, 31, 33, 39, 45, 50, 59, 61, 62, 64, 68, 70, 73. Это особенно важно у женщин.
Это особенно важно у женщин.
Кстати, иногда классификация изменяется. Например ВПЧ 58 типа у женщин уже не является высокоонкогенным. Его стали относить к типам со средней онкогенностью.
Встречаемость при заболеваниях:
• В 73-90% случаях при раке шейки матки находят: 16, 18 и 45 тип ВПЧ
• В 77-93% случаях при раке шейки матки находят: 16, 18, 45, 31 и 59 тип ВПЧ
• В 80-94% случаях при раке шейки матки находят: 16, 18, 45, 31, 33 и 59 тип ВПЧ
• Предраковые состояния в урологии и гинекологии сочетаются часто с 61, 62, 68, 70, 73 типами ВПЧ.
Наиболее часто в анализах встречаются:
• human papillomavirus 16 (пишется HPV 16) — 50%
• human papillomavirus 18 (HPV 18) — 10%
Симптомы и клиника
Симптомы и проявления ВПЧ-инфекции — это бородавки, папилломы и
дисплазия шейки матки.
А) Бородавки.
Их вызывают следующие типы ВПЧ – 1, 2, 3, 4, 5, 10, 28, 49.
• юношеские (или плоские) бородавки — вызываются 3 и 5 типами вируса. Это мелкие плоские возвышения на коже, возникают преимущественно у детей.
• шипицы (или подошвенные бородавки) — вызываются 1 и 2 типами вируса (более подробно про них можно прочитать.
• вульгарные бородавки на пальцах рук — вызываются вирусами 2 типа.
Это плоские бородавки на лице
Это вульгарные бородавки на руке
Б) Остроконечные кондиломы.
Локализация: на половых органах, в области ануса, в полости рта и на губах (типы – 6, 11, 13, 16, 18, 31, 35).
Это остроконечные кондиломы
Основной механизм передачи этого заболевания у взрослых людей – половой. Очень редко может встречаться контактный путь передачи — через общие предметы туалета, через грязный ободок унитаза, пользование общей ванной, в бане и т. д.
д.
Если у матери, страдающей остроконечным кондиломатозом, рождается ребенок, он также инфицируется и впоследствии у него также могут появиться остроконечные кондиломы или папилломатоз гортани и дыхательных путей (рассмотрено выше). Однако частота таких симптомов у грудных детей крайне низкая. У детей достаточно высокий уровень иммунитета, который предохраняет их от подобных проявлений инфекции.
В) Папилломатоз гортани.
На голосовых связках появляются множественные наросты-папилломы. Вызывается вирусом 11 типа. Иногда появляется у детей, рожденных женщинами, имеющих остроконечные кондиломы.
Это папилломатоз гортани
Запомните:
— эрозия шейки матки и ВПЧ — ДАЛЕКО не одно и то же. Подробная статья о том, что такое эрозия шейки матки и чем она отличается от дисплазии и ВПЧ — здесь.
Современная медицина со 100% уверенностью заявляет, что рак шейки матки вызван исключительно папилломавирусами типов 16, 18, 31, 33, 35, 39, 40, 42, 43, 55, 57, 59, 61, 62, 66, 67.
На схеме — развитие ВПЧ-инфекции с годами
Е) Рак кожи полового члена (болезнь Боуэна).
Вызывается типами вируса – 16 и 18.
Ж) Сегодня некоторые зарубежные ученые считают, что вирус папилломы человека является причиной появления рака любой локализации. Поскольку рак – это злокачественная опухоль эпителия кожи или слизистой оболочки, следовательно, вирус ВПЧ, вызывающий диспластические явления как раз в эпителии, и вызывает появление рака. И с раком шейки матки это доказано на 100%.
Есть доказательства при раке молочной железы и раке гортани, правда еще не оформленные в общемировые рекомендации. И, как считают некоторые исследователи рака, не за горами тот день, когда рак другой локализации (например, кишечника) также признают результатом деятельности в организме человека вируса папилломы человека.
Помните:
— любая вирусная инфекция, постоянно находящаяся в организме человека (а ВПЧ относится именно к таким), активизируется только при снижении иммунитета.
Диагностика
1) ПЦР-анализ.
Основной способ диагностики папилломавируса – реакция ПЦР. Наиболее распространенные виды анализа на ВПЧ — 16, 18 типы вируса, а также ряд других высокоонкогенных типов.
Материал для анализа берут со слизистой влагалища и шейки матки женщины. У мужчин — со слизистой полового члена.
Реакция ПЦР может дать и ложный результат, причем как ложноположительный, так и ложноотрицательный результат, особенно если нарушены условия ее проведения (даже толчок стола, на котором проводится исследование, может привести к такому ложному результату).
Так, по данным современных исследователей на Западе, до 20% всех результатов ПЦР к папилломавирусу были ложными. И этот факт не зависел от сложности оборудования и от качества реактивов.
2) Digene-тест.
Новое исследование, набирающее популярность в медицинской среде. Этот тест используется для определения наличия клинически значимых концентраций вируса. Благодаря этому тесту, можно выявить — высокая степень онкогенности у вирусов, находящихся в организме больного, или низкая.
Благодаря этому тесту, можно выявить — высокая степень онкогенности у вирусов, находящихся в организме больного, или низкая.
Digene-тест используется в комплексе с цитологическим исследованием шейки матки, и оцениваются они также комплексно.
3) Осмотр гинекологом и/или урологом.
4) Цитологическое исследование.
Исследуется мазок, взятый при гинекологическом осмотре. Это исследование часто называют «жидкостная цитология», или просто — «цитология».
При этом врач-лаборант под микроскопом определяет наличие или отсутствие патологически измененных клеток, которых в норме быть не должно, а появляются они только при развитии заболевания. Наличие таких измененных клеток может свидетельствовать о наличии CIN (или дисплазии шейки матки) у женщины.
5) Гистологическое исследование.
Исследуется микроскопический кусочек ткани, взятый также при гинекологическом или урологическом обследовании. Другое название этого исследования — «биопсия». Под микроскопом врач оценивает степень изменения ткани, взятой на исследование.
Другое название этого исследования — «биопсия». Под микроскопом врач оценивает степень изменения ткани, взятой на исследование.
Как расшифровать анализ на ВПЧ?
Единицей измерения является количество геном-эквивалентов (если по-простому, то количество вирусов) на 100 000 клеток эпителия человека (то есть на 10 в 5 степени).
Сокращенно пишется: Lg
Градации:
1. < 3 Lg, то есть количество вирусов менее 3 на 10 в 5 степени. Это хороший показатель, вирусная нагрузка небольшая, то есть концентрация вируса малозначимая, риск развития заболевания низкий.
2. 3 – 5 Lg. Это клинически значимый показатель. Риск развития заболевания средний. Необходимо пройти обследование у врача.
3. > 5 Lg. Высокая вирусная нагрузка. Обязательно следует пройти полноценное обследование для исключения дисплазии шейки матки.
Что такое референсное значение
Это означает средние статистические показатели по данному исследованию у данной возрастной группы. То есть, по-простому, референсные значения – это норма.
То есть, по-простому, референсные значения – это норма.
По ВПЧ референсные значения – отрицательны. То есть в норме ВПЧ в анализах быть не должно.
Что такое КВМ?
КВМ – это контроль взятия материала. В норме врач должен взять соскоб таким образом, чтобы в образце материала было не менее 10 000 (или 10 в 4 степени, или 4Lg) клеток эпителия.
Если значение КВМ меньше 4Lg, это значит – мало клеток для анализа. Проведение анализа не рекомендуется, так как он будет неинформативным, и врачу рекомендуется повторить забор материала.
Лечение
В лечении вируса папилломы человека надо знать: вирус может полностью не удалиться из организма. Главная цель лечения – поднять иммунитет, стабилизировать вирус, удалить проявления вируса и снизить его концентрацию в организме, чтобы иммунитет человека сам подавлял вирус.
Обязательны 3 направления в лечении (проводится профильным специалистом- инфекционистом, иммунологом, дерматологом или гинекологом)
• прием противовирусных средств
• укрепление иммунитета
• удаление проявлений – бородавок, кондилом, дисплазии (эрозии) или рака шейки матки.
Все 3 направления эффективно проводятся современной медициной.
Самолечение имеет низкую эффективность и может привести к прогрессированию. Особенно опасно самолечение при заболеваниях половой сферы.
1) Противовирусные препараты
• Изопринозин (или гроприносин), Аллокин-альфа,
• 5% крем Алдара. Действующее вещество — имиквимод.
2) Препараты, повышающие иммунитет
Полиоксидоний, Реаферон, ронколейкин, иммунал и другие.
Основным препаратом при запущенных формах на настоящий момент является ронколейкин, который применяется по определенной схеме (назначается иммунологом или инфекционистом)
3) Удаление папиллом, бородавок, кондилом может быть
-Скальпелем –классическая хирургия, электрокоагуляцией или электрокножом-петлей, радиоволновое удаление, жидким азотом. Это устаревшие методики, которые травматичны, не всегда эффективны и могут приводить к рецидивам и постожоговым рубцам в местах удаления.
-Лазером – на сегодня это лучший способ по эффективности, безопасности, эстетичности
Не рекомендуется использовать местнонекротизирующие препараты (кислоты, щелочи):Суперчистотел, Солкодерм, Дуофилм, Колломак, Веррукацид, ферезол, Кондилин — и ряд других, так как их нанесение на кожу может способствовать распространению вируса на здоровые, непрошеные ранее участки кожи, а также приводит к ожогам кожи и последующим рубцовым изменениям
Обязательно: здоровый образ жизни, повышающий иммунитет.
Запомните: Сначала врач должен поставить верный диагноз, а это уже половина лечения!!! В том числе лечения вируса папилломы человека.
Поэтому при наличии множественных бородавок, рецидивах рекомендуется сначала провести курс противовирусной и иммуномодулирующий терапии под контролем врача инфекциониста или иммунолога!
Профилактика ВПЧ
Предупреждение – лучшее лечение. Запомните эту фразу, особенно если дело касается половой сферы.
Природа придумала для человека замечательный механизм излечения и профилактики, который потом помогает ему опять не заболеть. Это иммунная система.
Если у человека уже один раз были бородавки или папилломы, то впоследствии у него образуется иммунитет к этому типу вируса. Поэтому у взрослых очень редко появляются юношеские бородавки, шипицы и вульгарные бородавки.
Именно поэтому ТАК ВАЖНО поддерживать свой иммунитет на высоком уровне.
Перечислим основные направления профилактики папилломавирусной инфекции у человека:
• Меры личной гигиены в общественных местах
• Здоровый образ жизни, поддерживающий иммунитет на высоком уровне
• Правильный режим труда и отдыха
• Умеренная физическая культура
• Прием витаминов, фруктов, соков
• Только один половой партнер (в идеале)
• Использование презерватива при половом контакте
Предлагаем Вашему вниманию 3 видео по удалению папиллом и бородавок в клинике Аврора!!!
Узнать подробнее об услуге и стоимости удаления новообразований
Полином 5-ой степени : Высшая алгебра
Правила форума
В этом разделе нельзя создавать новые темы.
Если Вы хотите задать новый вопрос, то не дописывайте его в существующую тему, а создайте новую в корневом разделе «Помогите решить/разобраться (М)».
Если Вы зададите новый вопрос в существующей теме, то в случае нарушения оформления или других правил форума Ваше сообщение и все ответы на него могут быть удалены без предупреждения.
Не ищите на этом форуме халяву, правила запрещают участникам публиковать готовые решения стандартных учебных задач. Автор вопроса обязан привести свои попытки решения и указать конкретные затруднения.
Обязательно просмотрите тему Правила данного раздела, иначе Ваша тема может быть удалена или перемещена в Карантин, а Вы так и не узнаете, почему.
| SokolovArt |
| ||
07/01/12 |
| ||
| |||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| Praded |
| |||
21/05/11 |
| |||
| ||||
| SokolovArt |
| ||
07/01/12 |
| ||
| |||
| Tanechka |
| ||
26/05/12 |
| ||
| |||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| SokolovArt |
| ||
07/01/12 |
| ||
| |||
| Sonic86 |
| |||
08/04/08 |
| |||
| ||||
| SokolovArt |
| ||
07/01/12 |
| ||
| |||
| Joker_vD |
| |||
09/09/10 |
| |||
| ||||
| SokolovArt |
| ||
07/01/12 |
| ||
| |||
| AV_77 |
| |||
11/11/07 |
| |||
| ||||
| SokolovArt |
| ||
07/01/12 |
| ||
| |||
| verywell |
| ||
26/11/13 |
| ||
| |||
| Показать сообщения за: Все сообщения1 день7 дней2 недели1 месяц3 месяца6 месяцев1 год Поле сортировки АвторВремя размещенияЗаголовокпо возрастаниюпо убыванию |
| Страница 1 из 1 | [ Сообщений: 14 ] |
Модераторы: Модераторы Математики, Супермодераторы
Untitled-1
%PDF-1. 5
%
1 0 obj
>/OCGs[8 0 R 878 0 R]>>/Pages 3 0 R/Type/Catalog>>
endobj
2 0 obj
>stream
2018-02-07T10:13:32+03:00Adobe Illustrator CC (Macintosh)2018-02-07T10:13:49+03:002018-02-07T10:13:49+03:00
5
%
1 0 obj
>/OCGs[8 0 R 878 0 R]>>/Pages 3 0 R/Type/Catalog>>
endobj
2 0 obj
>stream
2018-02-07T10:13:32+03:00Adobe Illustrator CC (Macintosh)2018-02-07T10:13:49+03:002018-02-07T10:13:49+03:00
 3.0.1114application/pdf
3.0.1114application/pdf did:4f0ac00a-8dc4-40d4-a8bb-4406cb66fc31uuid:7c085fee-ed39-3b4c-8796-c19e27d531a1xmp.did:7522bfa4-97e0-4cd5-a60f-e84474223c63proof:pdfuuid:c1a45d90-2395-3648-9968-205825bbdf0bxmp.did:7522bfa4-97e0-4cd5-a60f-e84474223c63xmp.did:7522bfa4-97e0-4cd5-a60f-e84474223c63proof:pdf
did:4f0ac00a-8dc4-40d4-a8bb-4406cb66fc31uuid:7c085fee-ed39-3b4c-8796-c19e27d531a1xmp.did:7522bfa4-97e0-4cd5-a60f-e84474223c63proof:pdfuuid:c1a45d90-2395-3648-9968-205825bbdf0bxmp.did:7522bfa4-97e0-4cd5-a60f-e84474223c63xmp.did:7522bfa4-97e0-4cd5-a60f-e84474223c63proof:pdf 66928 5.66928 303.307 425.197]/Type/Page>>
endobj
11 0 obj
>/Resources>/ExtGState>/ProcSet[/PDF/ImageC]/Properties>/XObject>>>/Thumb 905 0 R/TrimBox[5.66928 5.66928 303.307 425.197]/Type/Page>>
endobj
897 0 obj
>stream
H|n$
z:zd«xKV`2$A_=t5Q:o?~e-3y{q2[:sG-̃OXC
66928 5.66928 303.307 425.197]/Type/Page>>
endobj
11 0 obj
>/Resources>/ExtGState>/ProcSet[/PDF/ImageC]/Properties>/XObject>>>/Thumb 905 0 R/TrimBox[5.66928 5.66928 303.307 425.197]/Type/Page>>
endobj
897 0 obj
>stream
H|n$
z:zd«xKV`2$A_=t5Q:o?~e-3y{q2[:sG-̃OXCГипертония: степени, симптомы, лечение в Красноярске
Малоподвижный образ жизни, постоянные сильные стрессы, вредные привычки могут привести к появлению патологий сердца. Гипертония – одно из частых заболеваний современного человека. Эта патология характеризуется повышенным артериальным давлением в спокойном состоянии и в течение длительного времени.
Чем опасна гипертония?
Сердце продвигает кровь по кровеносным сосудам, обеспечивая все клетки организма кислородом и питательными веществами. В случае, когда кровеносные сосуды закупориваются или теряют свою эластичность, сердце начинает работать сильнее и увеличивает давление внутри сосудов.
На фоне болезни при несвоевременном лечении могут возникнуть такие серьезные патологии, как острая сердечная недостаточность, гипертонический криз, инсульт, инфаркт миокарда.
Сложность гипертонии в том, что часто она годами протекает практически бессимптомно и человек не знает о существовании у него болезни. Часто наблюдаются симптомы – головная боль, усталость, снижение памяти, головокружение, повышенное давление, на которые человек просто не обращает внимания. Это может говорить о начале развития заболевания.
Симптомы гипертонии
- продолжающиеся мигрени;
- онемение конечностей;
- покраснение лица;
- повышенная потливость;
- «мошки» перед глазами;
- озноб;
- учащенное сердцебиение.
Причины развития гипертонии
- Лишний вес. Люди со склонностью к ожирению в несколько раз чаще страдают заболеванием сердца. Также лишний вес является причиной повышенного содержания кальция и натрия в крови, нарушения нормальной деятельности почек и заболеваний внутренних органов.
 Это, в свою очередь, дополнительных фактор для развития гипертонии.
Это, в свою очередь, дополнительных фактор для развития гипертонии. - Склероз артерий. Из-за наличия атеросклеротических бляшек на стенках сосудов, прекращается нормальная циркуляция крови. Сердцу приходится работать более усиленно, чтобы повысить давление в сосудах.
- Стрессовые ситуации. Во время стрессов повышается артериальное давление из-за выброса гормона адреналина в кровь. Воздействуя на сердце, адреналин заставляет его чаще биться, выбрасывая в сосуды больше крови.
- Вредные привычки. Курение, употребление алкоголя, жирной и тяжелой пищи увеличивают давление в кровеносных сосудах, образуют спазмы сосудов и приводят к их повреждению.
- Возраст. С годами сердце человека изнашивается. Риск развития гипертонической болезни с возрастом увеличивается, если не предавать своему здоровью должного внимания. Необходимо проходить профилактические обследования и отказаться от вредных привычек, если они есть. Повышенное давление часто развивается у лиц старше 35 лет.

- Генетическая предрасположенность. Если родственники первого звена (отец, мать, родные браться, сестры, бабушки или дедушки) страдают от гипертонии, риск развития болезни повышается.
- Малоподвижный образ жизни. При низком уровне нагрузок замедляется обмен веществ, нервная система и другие системы организма ослаблены, понижен иммунитет. Риск развития гипертонии увеличивается на 50%.
Гипертония и гипертензия: в чем разница?
Гипертония – хроническое заболевание, которое характеризуется стойким повышением артериального давления и общего тонуса мышц.
Гипертензия – состояние организма человека при повышенном давлении. В отличие от гипертонии, которая является самостоятельным заболеванием, гипертензия – симптом патологического состояния.
Виды гипертонии сердца
Существует множество классификаций заболевания, которые основываются на внешнем виде пациента, уровне давления, причинам повышения артериального давления, характеру протекания заболевания. Однако, повсеместно врачи используют классификацию по степени протекания недуга.
Однако, повсеместно врачи используют классификацию по степени протекания недуга.
Гипертония 1 степени – называется еще доклинической стадией. Это наиболее мягкая форма гипертонии, при которой артериальное давление достигает значения 140/90 мм. ртутного столба. Наблюдаются легкие головные боли, снижение работоспособности, общая утомляемость. Во время пребывания больного в спокойном состоянии давление нормализуется.
Гипертония 2 степени – умеренная стадия, при которой давление увеличивается до отметки 180/110 мм. рт. ст. наблюдается образование атеросклеротических бляшек, гипертрофии левого желудочка сердца, повышенная концентрация креатинина.
Гипертония 3 степени – давление повышается до 220/115 мм. рт. ст. в этом случае высок риск развития осложнений. При такой степени развития патологии нарушено кровоснабжение внутренних органов. Заболевание 3 степени может проявлять себя почечной недостаточностью, кровоизлиянием из глаз, слепотой.
Как диагностировать болезнь?
При появлении первых симптомов гипертонии, обратитесь на консультацию к кардиологу. Он проведет осмотр и направит на анализы:
- общий анализ крови и мочи;
- анализ крови на гемоглобин;
- анализ мочи на белок и глюкозу;
- электрокардиография;
- эхокардиография;
- рентгенография грудной клетки;
- биохимический анализ крови для выявления уровня холестерина, мочевины, глюкозы и кальция;
- фосфаты и мочевая кислота;
- компьютерная томография;
- ультразвуковое исследование.
По результатам анализов лечащий врач определит имеет ли место гипертоническая болезнь, стабильность повышения давления, степень развития патологических изменений внутренних органов, причину повышенного давления.
Лечение гипертонии
Метод лечебной терапии зависит от степени развития заболевания. При первой доклинической стадии можно поддерживать нормальный уровень артериального давления без применения медикаментов. Пациенту нужно сбалансировать питание, отказаться от вредных привычек, вести активный образ жизни и нормализовать режим сна и работы.
При первой доклинической стадии можно поддерживать нормальный уровень артериального давления без применения медикаментов. Пациенту нужно сбалансировать питание, отказаться от вредных привычек, вести активный образ жизни и нормализовать режим сна и работы.
При лечении 2 степени гипертонии врач назначает медикаментозное средство для длительного применения и с минимальным количеством противопоказаний в совокупности с умеренной активностью и отказом от вредных привычек. Лекарственный препарат выписывается врачом – кардиологом после обследования пациента. Препараты должны приниматься непрерывно, так как это может вызвать инсульт или инфаркт.
Терапия 3 степени гипертонии проводится при помощи 1-2 лекарственных из разных лекарственных групп в совокупности с активным образом жизни и стабилизацией питания и режима сна.
- диуретики с мочегонным эффектом выписывается при задержке соли и воды в организме;
- для нормализации кровообращения – ингибиторы АПФ;
- антагонисты кальция – для уменьшения потребности сердечной мышцы в кислороде;
- бета – адреноблокаторы при фибрилляции предсердий или других сопутствующих патологиях.

Поэтому при определении лечебной терапии врач должен знать всю историю болезни пациента, учитывать противопоказания, образ жизни и физические характеристики (массу тела, рост).
Лечением гипертонии в Красноярске занимаются в медицинском центре «Медюнион». У нас работают опытные кардиологи, которые проведут полный осмотр и обследование, дружелюбный медицинский персонал и качественное оборудование. Чтобы записаться на консультацию к специалисту или узнать более подробную информацию, оставьте заявку на сайте или по телефону клиники 201-03-03.
Таблицы экспонент и шаблоны
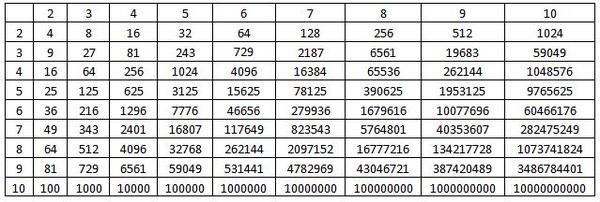
Горячая математикаВ таблицах степеней целых чисел можно найти много интересных закономерностей.
Полномочия 2 | Полномочия 3 | Полномочия 4 |
| 2 1 знак равно 2 | 3 1 знак равно 3 | 4 1 знак равно 4 |
| 2 2 знак равно 4 | 3 2 знак равно 9 | 4 2 знак равно 16 |
| 2 3 знак равно 8 | 3 3 знак равно 27 | 4 3 знак равно 64 |
| 2 4 знак равно 16 | 3 4 знак равно 81 | 4 4 знак равно 256 |
| 2 5 знак равно 32 | 3 5 знак равно 243 | 4 5 знак равно 1024 |
| 2 6 знак равно 64 | 3 6 знак равно 729 | 4 6 знак равно 4096 |
| 2 7 знак равно 128 | 3 7 знак равно 2187 | 4 7 знак равно 16384 |
| 2 8 знак равно 256 | 3 8 знак равно 6561 | 4 8 знак равно 65536 |
| 2 9 знак равно 512 | 3 9 знак равно 19683 | 4 9 знак равно 262144 |
| 2 10 знак равно 1024 | 3 10 знак равно 59049 | 4 10 знак равно 1048576 |
Одна вещь, которую вы можете заметить, это закономерности в цифрах. В полномочиях
2
таблица, единичные цифры образуют повторяющийся шаблон
2
,
4
,
8
,
6
,
2
,
4
,
8
,
6
,
…
. В полномочиях
3
таблица, единичные цифры образуют повторяющийся шаблон
3
,
9,
7
,
1
,
3
,
9
,
7
,
1
,
…
. Мы оставляем это вам, чтобы выяснить, почему это происходит!
В полномочиях
2
таблица, единичные цифры образуют повторяющийся шаблон
2
,
4
,
8
,
6
,
2
,
4
,
8
,
6
,
…
. В полномочиях
3
таблица, единичные цифры образуют повторяющийся шаблон
3
,
9,
7
,
1
,
3
,
9
,
7
,
1
,
…
. Мы оставляем это вам, чтобы выяснить, почему это происходит!
В полномочиях 4 таблица, чередуются единичные цифры: 4 , 6 , 4 , 6 . На самом деле, вы можете видеть, что силы 4 совпадают с четными степенями 2 :
4
1
знак равно
2
2
4
2
знак равно
2
4
4
3
знак равно
2
6
и т. п.
п.
Такие же отношения существуют между силы 3 и силы 9 :
Полномочия 3 | Полномочия 9 |
| 3 1 знак равно 3 | 91 знак равно 9 |
| 3 2 знак равно 9 | 9 2 знак равно 81 |
| 3 3 знак равно 27 | 9 3 знак равно 729 |
| 3 4 знак равно 81 | 9 4 знак равно 6561 |
| 3 5 знак равно 243 | 9 5 знак равно 59 049 |
| 3 6 знак равно 729 | 9 6 знак равно 531 441 |
| 3 7 знак равно 2187 | 9 7 знак равно 4 782 969 |
| 3 8 знак равно 6561 | 9 8 знак равно 43 046 721 |
| 3 9 знак равно 19,683 | 9 9 знак равно 387 420 489 |
| 3 10 знак равно 59 049 | 9 10 знак равно 3 486 784 401 |
силы
10 легко, потому что мы используем
база
10
: за
10
н
просто напишите »
1
» с
н
нули после него. За
отрицательные силы
10
−
н
, записывать »
0.
» с последующим
н
−
1
нули, а затем
1
. Полномочия
10
широко используются в
научная нотация
, так что это хорошая идея, чтобы освоиться с ними.
За
отрицательные силы
10
−
н
, записывать »
0.
» с последующим
н
−
1
нули, а затем
1
. Полномочия
10
широко используются в
научная нотация
, так что это хорошая идея, чтобы освоиться с ними.
Полномочия 10 | |
| 10 1 знак равно 10 | 10 0 знак равно 1 |
| 10 2 знак равно 100 | 10 − 1 знак равно 0,1 |
| 10 3 знак равно 1000 | 10 − 2 знак равно 0,01 |
| 10 4 знак равно 10 000 | 10 − 3 знак равно 0,001 |
10 5 знак равно 100 000 (сто тысяч) | 10 − 4 знак равно 0,0001 (одна десятитысячная) |
10 6 знак равно 1 000 000 (один миллион) | 10 − 5 знак равно 0,00001 (стотысячный) |
10 7 знак равно 10 000 000 (десять миллионов) | 10 − 6 знак равно 0,000001 (одна миллионная) |
10 8 знак равно 100 000 000 (сто миллионов) | 10 − 7 знак равно 0,0000001 (одна десятимиллионная) |
10 9 знак равно 1 000 000 000 (один миллиард) | 10 − 8 знак равно 0,00000001 (стомиллионный) |
10 10 знак равно 10 000 000 000 (десять миллиардов) | 10 − 9 знак равно 0,000000001 (одна миллиардная) |
Нажмите
здесь
для большего количества имен для
очень большие и очень маленькие числа
.
Еще одно следствие нашего использования база 10 хороший образец между отрицательными степенями 2 и полномочия 5 .
Полномочия 2 | Полномочия 5 | ||||||||||||||||||
| 2 − 5 знак равно 1 32 знак равно 0,03125 | 5 − 5 знак равно 1 3125 знак равно 0,00032 | ||||||||||||||||||
| 2 − 4 знак равно 1 16 знак равно 0,0625 | 5 − 4 знак равно 1 625 знак равно 0,0016 | ||||||||||||||||||
| 2 − 3 знак равно 1 8 знак равно 0,125 | 5 − 3 знак равно 1 125 знак равно 0,008 | ||||||||||||||||||
| 2 − 2 знак равно 1 4 знак равно 0,25 | 5 − 2 знак равно 1 25 знак равно 0,04 | ||||||||||||||||||
| 2 − 1 знак равно 1 2 знак равно 0,5 | 5 − 1 знак равно 1 5 знак равно 0,2 | ||||||||||||||||||
| 2 0 знак равно 1 | 5
0
знак равно
1
9n = \underbrace{x \times x \times \cdots \times x}_{n \text{times}}. а.
\конец{выравнивание*}
9b$, где $b$ — рациональные числа, приближающиеся к $a$.) а.
\конец{выравнивание*}
9b$, где $b$ — рациональные числа, приближающиеся к $a$.)Правила экспоненты: 7 законов экспоненты для решения сложных уравненийпоказатели в них. Но есть несколько различных типов экспоненциальных уравнений и экспоненциальных выражений, которые могут показаться сложными… поначалу. Овладение этими основными правилами экспоненты вместе с основными правилами логарифмирования (также известными как «логарифмические правила») сделает ваше изучение алгебры очень продуктивным и приятным. Имейте в виду, что во время этого процесса по-прежнему будет применяться порядок операций. Как и большинство математических приемов, существуют стратегии обучения, которые можно использовать для упрощения выполнения правил экспоненты. Чтобы помочь вам в обучении этим понятиям, у нас есть бесплатный рабочий лист правил экспоненты , который вы можете загрузить и использовать в своем классе! Что такое показатели? Показатель степени, также известный как степень, представляет собой величину, показывающую, сколько раз нужно умножить базовое число само на себя. 43= 4 × 4 × 4 = 64 Число, возводимое в степень, известно как по основанию , а надстрочное число над ним — это показатель степени или степень . Авторы и права: To The Square Inch Вышеприведенное уравнение звучит как «четыре в степени три». Степень двойки также может быть выражена как « в квадрате », а степень числа три — как « в кубе ». Эти термины часто используются при нахождении площади или объема различных фигур. Запись числа в экспоненциальной форме означает его упрощение до основания со степенью. Например, преобразование 5 × 5 × 5 в экспоненциальную форму выглядит как 53 . Экспоненты — это способ упростить уравнения, чтобы их было легче читать. Это становится особенно важным, когда вы имеете дело с такими переменными, как «𝒙» и «𝑦» — как 𝒙7× 𝑦5= ? легче читать, чем Правила экспоненты в быту Понимание свойств экспоненты не только поможет вам решать различные алгебраические задачи, экспоненты также используются на практике в повседневной жизни при расчете квадратных футов, квадратных метров и даже кубических сантиметров. Экспоненциальные правила также упрощают вычисление очень больших или очень малых величин. Они также используются в мире компьютеров и технологий при описании мегабайтов, гигабайтов и терабайтов. Каковы различные правила экспоненты?Существуют семь правил экспоненты, или законы экспоненты, которые необходимо изучить вашим ученикам. Каждое правило показывает, как решать различные типы математических уравнений и как складывать, вычитать, умножать и делить степени. Тщательно изучите каждое правило экспоненты в классе, так как каждое из них играет важную роль в решении уравнений на основе экспоненты. 1. Правило произведения степенейПри умножении двух оснований одного и того же числа оставьте основания одинаковыми, а затем сложите их показатели, чтобы получить решение. 42× 45 = ? Поскольку оба базовых значения равны четырем, оставьте их одинаковыми, а затем сложите вместе показатели степени (2 + 5). 42 × 45= 47 Затем умножьте четыре на себя семь раз, чтобы получить ответ. 47 = 4 × 4 × 4 × 4 × 4 × 4 × 4 = 16 384 Давайте расширим приведенное выше уравнение, чтобы увидеть, как работает это правило: ответ. Попробуйте задать более сложный вопрос: (4𝒙2)(2𝒙3) = ? Перемножьте коэффициенты вместе (четыре и два), так как они не являются одним и тем же основанием. Затем оставьте «𝒙» таким же и добавьте показатели степени. (4𝒙2)(2𝒙3) = 8𝒙5 2. Правило отношения степенейУмножение и деление противоположны друг другу — во многом то же самое, правило частного действует как противоположность правилу произведения. При делении двух оснований одного и того же значения оставьте основание одинаковым, а затем вычтите значения степени. 55 ÷ 53 = ? Оба основания в этом уравнении равны пяти, что означает, что они остаются прежними. Затем возьмите показатели и вычтите делитель из делимого. 55÷ 53 = 52 Наконец, упростим уравнение, если это необходимо: 52= 5 × 5 = 25 Еще раз, расширение уравнения показывает нам, что это сокращение дает правильный ответ: Взгляните на этот более сложный пример: 5𝒙4 / 10𝒙2 = ? Одинаковые переменные в знаменателе отменяют переменные в числителе. Вы можете показать это своим ученикам, зачеркнув равное количество 𝒙 сверху и снизу дроби. 5𝒙4 / 10𝒙2 = 5𝒙/10 Затем упростите, где это возможно, так же, как и с любой дробью. Пять можно превратить в десять, пять раз превратив дробь в ½ с оставшимися 𝒙 переменными. 5𝒙4/10𝒙2= 1𝒙2/2 = 𝒙2/2 3. Степень правила степениЭто правило показывает, как решать уравнения, в которых степень возводится в другой степенью. (𝒙3)3 = ? В уравнениях, подобных приведенному выше, умножьте показатели степени и оставьте основание одинаковым. (𝒙3)3 = 𝒙9 Посмотрите на расширенное уравнение, чтобы увидеть, как это работает: 4. Степень правила произведения Степень правила произведения показатель степени каждой части основания. (𝒙𝑦)3 = ? В этом уравнении степень числа три должна быть распределена как по 𝒙, так и по 𝑦 переменным. (𝒙𝑦)3 = 𝒙3𝑦3 Это правило применяется, если к основанию также присоединены экспоненты. (𝒙2𝑦2)3 = 𝒙6𝑦6 В расширенном виде уравнение будет выглядеть так: Обе переменные в этом уравнении равны в квадрате и представляют собой , возведенное в степень 3. Это означает, что три умножаются на показатели степени в обеих переменных, превращая их в переменные, которые возводятся в степень шесть. 5. Степень правила частного Частное просто означает, что вы делите две величины. В этом правиле тебе возведение частного в степень. Подобно силе правила произведения, показатель степени должен распространяться на все значения в скобках, к которым он присоединен. (𝒙/𝑦)4 = ? Здесь обе переменные в квадратных скобках увеличьте в четыре степени. Взгляните на это более сложное уравнение: (4𝒙3/5𝑦4)2 = ? Не забудьте распределить показатель степени, на который вы умножаете, на как на коэффициент, так и на переменную. Затем упростите, где это возможно. (4𝒙3/5𝑦4)2= 42𝒙6/52𝑦8 = 16𝒙6/25𝑦8 6. Правило нулевой степениЛюбое основание, возведенное в нулевую степень, равно единице. Самый простой способ объяснить это правило — использовать правило отношения степеней. 43/43 = ? Следуя правилу отношения степеней, вычтите показатели степени друг из друга, что аннулирует их, оставив только основание. Любое число, деленное само на себя, равно единице. 43/43= 4/4 = 1 Независимо от длины уравнения, все, что возведено в нулевую степень, становится единицей. (82𝒙4𝑦6)0 = ? Как правило, внешний показатель степени должен быть умножен на каждое число и переменную в скобках. (82𝒙4𝑦6) 0 = 1 Полное расширенное уравнение будет выглядеть следующим образом: (82𝒙4𝑦6) 0 = 80𝒙0𝑦0 = (1) (1) (1) = 1 7. Правило отрицательного показателяКогда есть число, возводимое в отрицательную степень, превратите его в обратную, чтобы превратить степень в положительную. Не используйте отрицательную степень для превращения основания в отрицательное. Авторы и права: Thinglink Мы уже говорили об обратных величинах в нашей статье « Как делить дроби за 3 простых шага ». По сути, обратные числа — это то, на что вы умножаете число, чтобы получить значение единицы. Например, чтобы превратить два в один, умножьте его на ½. Теперь посмотрите на этот пример с показателем степени: 𝒙-2 = ? Чтобы сделать число обратным:
Цель уравнений с отрицательными показателями заключается в том, чтобы сделать их положительными. Теперь взгляните на более сложное уравнение: 4𝒙-3𝑦2/20𝒙𝑧-3 = ? В этом уравнении есть два показателя степени с отрицательными степенями. Упростите то, что можете, а затем преобразуйте отрицательные показатели в их обратную форму. В решении 𝒙-3 перемещается в знаменатель, а 𝑧-3 перемещается в числитель. Поскольку в знаменателе уже есть значение 𝒙, к этому значению добавляется 𝒙3. 4𝒙-3𝑦2/20𝒙z-3 = 𝑦2𝑧3/5𝒙4 Имея эти семь правил в задних карманах ваших учеников, они смогут ответить на большинство экспоненциальных вопросов, с которыми они столкнутся! Таблица правил экспоненты Как Prodigy может помочь вам обучать правилам экспонентыProdigy — это математическая игра, адаптированная к учебной программе, которую вы можете использовать для постановки вопросов, отслеживания прогресса и выявления проблем в обучении ваших учеников . И вы можете бесплатно создавать учетные записи учителей и учеников! С таким количеством различных правил экспоненты, которым нужно следовать, и нескольким ученикам, которых нужно отслеживать, может быть трудно понять, кому и в чем нужна помощь. Статистика отслеживается в режиме реального времени, когда ученики играют в игру, и обратная связь доступна мгновенно. В большинстве случаев ваши ученики даже не осознают, что они участвуют в уроках математики. Все это часть их персонализированного игрового опыта! На панели управления учителя вы можете создавать планы уроков, просматривать статистику в реальном времени, вводить пользовательские задания и готовить своих учеников к предстоящим тестам. Вот как вы можете использовать Prodigy для :
Рабочие листы по математике — это удобные инструменты, которые могут показать, как учащиеся понимают ключевые понятия. С помощью нашей команды учителей мы составили рабочий лист правил экспоненты, чтобы помочь вам с уроками экспоненты. Щелкните здесь , чтобы загрузить нашу таблицу правил экспоненты с ключом ответа! Заключение: практика правил экспонентыЭкспоненты используются, чтобы показать, сколько раз базовое значение умножается само на себя. Это упрощает уравнения до более удобного для чтения формата. (𝒙𝒙𝒙𝒙𝒙𝒙𝒙𝒙𝒙)(𝑦𝑦𝑦𝑦𝑦𝑦)(𝑧𝑧𝑧𝑧𝑧) = 𝒙9𝑦6𝑧5 Напомним, что есть семь основных правил, которые включают в себя решение большинства математических уравнений. Правила экспоненты:
, когда полиномиал имеет четыре термина (такие как 5x 6 , когда полиномиал имеет четыре термина (такие как 5x 6 . — 17x 2 + 97 + 24x), его иногда называют четырехчленом. Однако более крупные многочлены обычно известны как многочлены с четырьмя членами, многочлены с пятью членами и так далее. Степени мономов и многочленов Степень монома или многочлена — это наивысшая степень переменной в этом многочлене, если имеется только одна переменная. Если имеется более одной переменной, вы складываете показатели степени для всех переменных, чтобы найти степень. Если многочлен имеет более одной переменной, то вы можете найти степень, взглянув на каждый моном. Например: 14x 4 + 27x 2 y — y имеет степень 4. Глядя на каждый отдельный термин, вы обнаружите, что показатели степени равны 4, 3 (2 + неявная 1) и 1). 4 является наивысшим, поэтому степень равна 4. Например:
Реклама Степени многочленовМногочлен второй степени (например, 6x 2 + 13x + c) также называется «квадратичным». Вы можете задаться вопросом, откуда взялось слово «квадратный», ведь приставка «квадратный» обычно означает «четыре». Слово происходит от латинского слова «делать квадратным». Итак, в данном случае «квадрат» относится к четырем углам квадрата. Многочлен третьей степени называется «кубическим», четвертой степени — «квартикой», а многочлен пятой степени — «квинтикой». Полиномы шестой степени являются секстическими, а полиномы седьмой степени — септическими. Алгебра означает восстановление Алгебра, что в переводе с арабского означает «восстановление», является разделом чистой математики. Чистая математика отличается от других дисциплин тем, что она не обязательно применяется к какой-либо конкретной ситуации, но исследует концепции и красоту самой математики. История алгебры также обогащает; от древних математических табличек Вавилона до классических дней Диофанта, греческого математика и писателя г. Штатный писатель Заказ математических операций, БОДМАС | SkillsYouNeedДля расчета, который имеет только одну математическую операцию с двумя числами, это простой случай сложения, вычитания, умножения или деления, чтобы найти ответ. А как быть, когда есть несколько номеров и разные операции? Может быть, вам нужно делить и умножать или складывать и делить. Что вы делаете тогда? К счастью, математика основана на логике. Как это часто бывает, есть несколько простых правил, которые помогут вам определить порядок выполнения вычислений. Они известны как «Порядок операций» . Правила упорядочения в математике — BODMAS BODMAS — полезная аббревиатура, указывающая порядок решения математических задач. Аббревиатура BODMAS означает:
BODMAS, BIDMAS или PEMDAS? Часто можно встретить BIDMAS вместо БОДМАС. Они точно такие же. В BIDMAS «I» относится к индексам, которые аналогичны ордерам. Для получения дополнительной информации см. нашу страницу, посвященную специальным номерам и понятиям. PEMDAS PEMDAS широко используется в США и работает так же, как BODMAS. Акроним PEMDAS: P aretheses, E xponents (степени и корни), M умножение и D A 9008 9003 90Добавление 0009 и удаление S . Дополнительная литература по необходимым навыкам Руководство по необходимым навыкам счета Это руководство, состоящее из четырех частей, знакомит вас с основами счета от арифметики до алгебры с остановками на дробях, десятичных дробях, геометрия и статистика. Если вы хотите освежить свои знания или помочь своим детям в обучении, эта книга для вас. Использование BODMASСкобкиНачните с чего-нибудь внутри скобок , двигаясь слева направо. ПриказыЗатем выполните все, что связано со степенью или квадратным корнем (они также известны как приказы ), снова работая слева направо, если их больше одного. Деление и умножениеПосле того, как вы сделали какие-либо части вычислений с использованием скобок или степеней, следующим шагом будет деление и умножение . Умножение и деление имеют одинаковый ранг, поэтому вы работаете слева направо в сумме, выполняя каждую операцию в том порядке, в котором она указана. См. наши страницы: Умножение и Деление , чтобы узнать больше. Сложение и вычитаниеПоследним шагом является вычисление любого сложения или вычитания . Опять же, вычитание и сложение имеют одинаковый ранг, и вы просто работаете слева направо. См. наши страницы: Сложение и Вычитание , чтобы узнать больше. Собираем все вместеЭтот окончательный рабочий пример включает в себя все элементы BODMAS. Тестовые вопросы по БОДМАСПравила БОДМАС легче понять после некоторой практики и примеров. Попробуйте эти расчеты самостоятельно, а затем откройте окно (щелкните символ + слева), чтобы увидеть работу и ответы. В этом расчете нет скобок или порядков.
Таким образом, ответ будет 63 .
Таким образом, ответ равен 24 .
Таким образом, ответ будет 76 . Когда нет такого знака, как в этом вычислении, оператор является умножением, таким же, как запись 5 × (3 + 2) + 5 2 .
Ответ: 50 . В этом есть все! Но не паникуйте. BODMAS по-прежнему применяется, и все, что вам нужно сделать, это отменить расчет.
Ответ: 299 . Подобные проблемы часто циркулируют в социальных сетях с надписями типа «90% людей понимают это неправильно». Просто следуйте правилам BODMAS, чтобы получить правильный ответ. |

 Приведите пример.
Приведите пример.