Что такое алкогольное опьянение и его степени?
Mуниципальные районы Новошешминский муниципальный район Защита прав потребителей Памятки и полезные советы Что такое алкогольное опьянение и его степени?
Алкогольное опьянение представляет собой сочетание расстройств в различных сферах жизнедеятельности человека, возникающих в результате приема спиртосодержащих веществ.
Принимая алкоголь, человек снимает напряжение, поднимает настроение, у него появляется ощущение свободы и веселья. Однако с увеличением дозы алкоголя, эти проявления сменяются другими, более отрицательными характеристиками. Появляется состояние возбуждения с утратой самоконтроля, агрессивность, может меняться настроение вплоть до его угнетения и подавленности.
Степень или «стадия» опьянения определяется количеством принятого алкоголя в перерасчёте на 1 кг веса, индивидуальной его переносимостью, а также состоянием организма во время приема спиртного.
Среди многих медицинских источников, в большей степени принято выделять три стадии (степени) алкогольного опьянения:
- Это легкое алкогольное опьянение (содержание алкоголя в крови примерно 0,5 – 1,5 промилле). Оно сопровождается своеобразным подъемом настроения с примесью благодушия, возникает ощущение некоего комфорта, человек начинает стремиться к общению. При этом рассеивается внимание, суждения выпившего становятся поверхностными, снижается самоконтроль, появляется ощущение собственного превосходства. На этом этапе память не нарушается.
- Это опьянение средней степени (содержания алкоголя в крови примерно 1,5 – 2,5 промилле). При этом у человека появляется раздражительность, недовольство, злоба, неудовлетворение собой и окружающей ситуацией.
Часто возникает агрессивное поведение. Всё это сопровождается нарушением координации движений, могут развиваться вялость и сонливость. На этом этапе есть возможность частичной потери памяти. - И это сильная степень опьянения (содержание алкоголя в крови примерно 2,5 – 3 промилле). Она сопровождается потерей ориентировки в окружающем пространстве, во времени и нередко в собственной личности, речь выпившего человека замедляется, мимика становится однообразной или вовсе утрачивается. Также возникают вестибулярные расстройства: головокружение, тошнота, рвота. Может нарушаться сознание, вплоть до развития коматозного состояния, замедляться дыхание, понижаться тонус сердечно-сосудистой системы, развиваться снижение двигательной активности вследствие расслабления мышц. Иногда у человека употребившего столь высокую дозу алкоголя развиваются судорожные припадки. В тяжелых случаях может возникнуть паралич дыхательного или сосудодвигательного центра, в результате чего нередко наступает смерть.
Часто возникает агрессивное поведение. Всё это сопровождается нарушением координации движений, могут развиваться вялость и сонливость. На этом этапе есть возможность частичной потери памяти.
При увеличении содержания алкоголя в крови до критических цифр 3 – 5 промилле развивается тяжелое отравление с возможным летальным исходом, требующее неотложной токсикологической помощи.
Чистопольский территориальный орган Госалкогольинспекции Республики Татарстан
Последнее обновление: 30 июля 2019 г., 14:09
Все материалы сайта доступны по лицензии:
Creative Commons Attribution 4.0 International
Обнаружили ошибку? Выделите слово или предложение и нажмите CTRL+ENTER
Калькулятор степени 3
Калькулятор степени 3 помогает вычислить степень 3 числа
Что такое возведение в степень?
Возведение в степень — это математическая операция, записываемая как b n , включающая два числа: основание b и показатель степени или степень n.
Когда n — натуральное число, возведение в степень соответствует многократному умножению основания: то есть b n — это произведение числа b n раз умноженного.
Калькулятор степени 3
Что такое номер
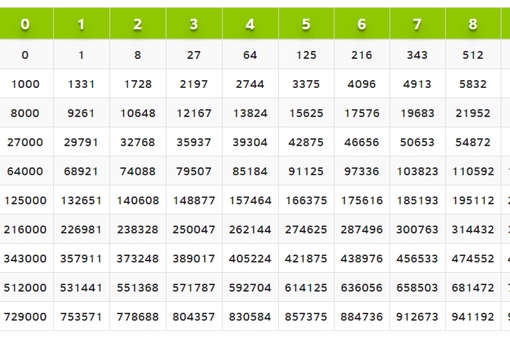
Экспонента 3 Таблица значений
Показатель степени 3 от 1 равен 1 (= 1 3 )
Показатель степени 3 от 2 равен 8 (= 2
Показатель степени 3 от 3 равен 27 (= 3 3 )
Показатель степени 3 от 4 равно 64 ( = 4 3 )
Показатель степени 3 из 5 равен 125 ( = 5 3 )
Показатель степени 3 от 6 равен 216 ( = 6 3 )
Показатель степени 3 от 7 равен 343 ( = 7 3 )
Показатель степени 3 от 8 равен 512 ( = 8 3 )
Показатель степени 3 от 9 равен 729 ( = 9 1 3 90) Показатель степени 3 из 10 равен 1,000 (= 10 3 )
Показатель степени 3 из 11 равен 1,331 (= 11 3 )
Показатель степени 3 из 12 равен 1,728 (= 12 3 0) Показатель степени 3 900 3 2,197 ( = 13
3 )
Показатель степени 3 из 14 равен 2,744 ( = 14 3 )
Показатель степени 3 из 15 равен 3,375 ( = 15 3 )
Экспонент 3 из 16 составляет 4,096 (= 16 3 )
.
Показатель 3 из 17 составляет 4913 (= 17 3 )
Экспонент 3 из 18 составляет 5,832 (= 18 3 )
. Показатель степени 3 из 19 равен 6 859 (= 19 3 )
Показатель степени 3 из 20 равен 8 000 (= 20 3 )
Показатель степени 3 из 21 равен 9 261 (= 21 3 0) Показатель степени 3 10 648 (= 22
3 )
Показатель степени 3 числа 23 равен 12 167 (= 23 3 )
Показатель степени 3 числа 24 равен 13 824 (= 24 3 )
Экспонент 3 из 25 составляет 15 625 (= 25 3 )
Экспонент 3 из 26 составляет 17 576 (= 26 3 )
Экспонент 3 из 27 составляет 19 683 (= 27 3 )
. Показатель степени 3 из 28 равен 21 952 ( = 28 3 )
Показатель степени 3 из 29 равен 24 389 ( = 29 3 )
Показатель степени 3 из 30 равен 27 000 ( = 30 3 ) 29 791 ( = 31
3 )
Показатель 3 из 32 равен 32 768 ( = 32 3 )
Показатель 3 из 33 равен 35,937 ( = 33 3 )
Показатель степени 3 от 34 равен 39 304 ( = 34 3 )
Показатель степени 3 от 35 равен 42 875 ( = 35 3 )
Показатель степени 4 от 36 3 )
Экспонент 3 из 37 составляет 50 653 (= 37 3 )
Опонент 3 из 38 составляет 54 872 (= 38 3 )
Экспонент 3 из 39 — 59,319 (= 39 3 )
— 59,319 (= 39 3 )
— 59 319 (= 39 3 )
Показатель степени 3 из 40 равен 64 000 (= 40 3 )
Показатель степени 3 из 41 равен 68 921 (= 41 3 )
Показатель степени 3 от 42 равен 74 088 (= 42 3 )
Показатель степени 3 от 43 равен 79 507 (= 43 3 ) 45 равно 91 125 (= 45 3 )
Показатель 3 числа 46 равен 97 336 (= 46 3 )
Показатель степени 3 числа 47 равен 103 823 (= 47 3 = 1,5 4) Показатель степени 4
48 3 )
Показатель степени 3 из 49 равен 117 649 ( = 49 3 )
Показатель степени 3 из 50 равен 125 000 ( = 50 3 )
Экспонент 3 из 51 составляет 132 651 (= 51 3 )
Экспонент 3 из 52 составляет 140 608 (= 52 3 )
Эффект 3 из 53 — 148,877 (= 53 3 )
.
. Показатель степени 3 из 54 составляет 157 464 (= 54 3 )
Показатель степени 3 из 55 составляет 166 375 (= 55 3 )
Показатель степени 3 из 56 равен 175 616 (= 57 3
Показатель степени 3 из 58 равен 195 112 (= 58 3 )
Показатель степени 3 из 59 равен 205 379 (= 59 3 )
Показатель степени 3 от 60 равен 216 000 (= 60 3 ) 62 IS 238,328 (= 62 3 )
Экспонент 3 из 63 равен 250,047 (= 63 3 )
Экспонент 3 из 64 равен 262 144 (= 64 3 )
. Экспонент 3 — 274 625 (= = = 625 (= = 625 (= = 625 (= = 625 (= = 625 (= = = 625 (= = = 625 65 3 )
Показатель степени 3 числа 66 равен 287 496 ( = 66 3 )
Показатель степени 3 числа 67 равен 300 763 ( = 67 3 )
Упонент 3 из 68 составляет 314 432 (= 68 3 )
Эпохание 3 из 69 — 328 509 (= 69 3 )
.
Действие 3 из 70 — 343 000 (= 70 3 ) . Показатель 3 числа 71 равен 357 911 (= 71 3 )
Показатель степени 3 числа 72 равен 373 248 (= 72 3 )
Показатель степени 3 числа 73 равен 389 017 (= 73 35) 405 224 (= 74 3 )
Показатель степени 3 от 75 равен 421 875 (= 75 3 )
Показатель степени 3 от 76 равен 438 976 (= 76 3 )
Показатель степени 3 от числа 77 равен 456 533 (= 77 3 ) 79 IS 493,039 (= 79 3 )
Экспонент 3 из 80 составляет 512 000 (= 80 3 )
Экспонент 3 из 81 составляет 531 441 (= 81 3 )
ЭКОНЕР 3 из 82 — 551 368 (= = = = = = = = = = = = = = = = = = = = 82 3 )
Показатель степени 3 от 83 равен 571 787 ( = 83 3 )
Показатель степени 3 от 84 равен 592 704 (= 84 3 )
Экспонент 3 из 85 равен 614,125 (= 85 3 )
Экспонент 3 из 86 — 636,056 (= 86 3 )
Экономический 3 -й из 87 — 658 503 (= 87 )
.
Опонент 3 — 658 503 (= 87 ) . Экономик 3 — 658 503 (= 87 ). 3 )
Экспонент 3 из 88 составляет 681 472 (= 88 3 )
Экспонент 3 из 89 составляет 704 969 (= 89 3 )
Экспонент 3 из 90 — 729 000 (= 90 3 )
90 — 729 000 (= 90 3 )
. Показатель степени 3 числа 91 равен 753 571 (= 91 3 )
Показатель степени 3 числа 92 равен 778 688 (= 92 3 )
Экспонент 3 из 93 равен 804 357 (= 93 3 )
Экспонент 3 из 94 равен 830 584 (= 94 3 )
Эффект 3 из 95 — 857,375 (= 95 3 )
101010101010101010101010101010101010101010101015101010101015101010151010151015101015101015101015)
10151015)
1010101510151510
1510151015)
101015)
101015)
101015). Показатель степени 3 числа 96 равен 884 736 (= 96 3 )
Показатель степени 3 числа 97 равен 912 673 (= 97 3 )
Показатель степени 3 числа 98 равен 941 192 (= 98 3) 970 299 (= 99 3 )
Показатель степени 3 от 100 равен 1 000 000 (= 100 3 )
Что такое восходящий порядок? Значение, решенные примеры, факты
Что такое по возрастанию?
Восходящий порядок означает расположение чисел в порядке возрастания, то есть от меньшего к большему.
Чтобы расположить числа в любом порядке, нам сначала нужно их сравнить.
Сначала Сравните , затем Закажите
Расположите числа в порядке возрастания:
- Подсчитайте количество цифр в каждом числе. Число с наименьшим количеством цифр является наименьшим. Напишите это первым. Продолжайте до тех пор, пока все числа, оставшиеся для сравнения, не будут иметь одинаковое количество цифр.
- Для чисел с одинаковым количеством цифр начните со сравнения чисел с самой левой цифры. Запишите число с наименьшей цифрой.
- Если крайние левые цифры совпадают, перейдите к цифрам справа и сравните их. Напишите число с меньшей цифрой.
- Продолжайте делать это с оставшимися числами, пока мы не упорядочим все числа.
Пример : Расположите 22554, 231, 22, 245, 22354 в порядке возрастания.
Число 22 имеет наименьшее количество цифр.
Далее, 231 и 245 — трехзначные числа. У обоих по 2 на сотне. Итак, переходим к цифре справа. Сравните 2 3 1 и 2 4 5 Поскольку, $3 \lt 4;\;$ Итак, $231 \lt 245$
Затем сравните 22554 и 22354, так как оба имеют 5 цифр. Сравнивая 22 5 54 и 22 3 54, находим $3 \lt 5$
Итак, $22354 \lt 22554$
Затем мы также можем расположить числа на числовой прямой, как показано на рисунке:
Родственные игры
Упорядочивание дробей в порядке возрастания
- Упорядочивание дробей с одинаковыми знаменателями
Для дробей с одинаковым знаменателем наименьшей является дробь с наименьшим числителем.
Пример : Упорядочить $\frac{3}{7},\; \фракция{2}{7},\; \фракция{5}{7},\; \frac{1}{7}$ в порядке возрастания.
Сравнивая числители, получаем $1 \lt 2 \lt 3 \lt 5$
Следовательно, $\frac{1}{7} \lt \frac{2}{7} \lt \frac{3}{7} \lt \frac{5}{7}$
- Упорядочивание дробей с одинаковыми числителями
Если дроби имеют одинаковый числитель, то дробь с наибольшим знаменателем является наименьшей.
Пример : Расположите $\frac{3}{7},\; \фракция{3}{8},\; \фракция{3}{5},\; \frac{3}{4}$ в порядке возрастания.
Здесь числитель равен 3 во всех дробях. Итак, сравним знаменатель.
Сравнив знаменатели, получим: $4 \lt 5 \lt 7 \lt 8$
Следовательно, $\frac{3}{8} \lt \frac{3}{7} \lt \frac{3 }{5} \lt \frac{3}{4}$
- Упорядочивание дробей с разными числителями и знаменателями
Приведите дроби к одинаковым знаменателям (или числителям), а затем сравните и упорядочите их.
Пример : Упорядочить $\frac{2}{5},\; \ гидроразрыв {4} {6}, \; \frac{3}{5}$ и $\frac{1}{3}$ в порядке возрастания.
Знаменатели 5, 6 и 3.
Связанные листы
Упорядочивание десятичных знаков по возрастанию- Сначала сравните целую часть числа в каждом десятичном разряде. Число с наименьшим целым числом является наименьшим.
- Если целые части числа одинаковы, сравните десятичные части так же, как мы сравниваем целые числа.
Пример : Расположите 22.44, 22.04, 22.40 и 2.45 в порядке возрастания.
Сначала сравним целые числа:
22.44, 22.04, 22.40 и 2.45
2 — самое маленькое, пишем его первым.
| 2,45 |
22,44, 22,04, 22.40 All Have 22.
22,44, 22,04, 22.40 All Have 22.
SO.
0,04 $ \lt 0,40 \lt 0,44 $
Следовательно, 22,04 $ \lt 22,40 \lt 22,44 $
The ascending order is:
| 2.45 | 22.04 | 22.40 | 22.44 |
| Fun Facts – To remember ascending order, remember the flight of an “airplane”, от низкого к высокому. |
Практические задачи по возрастанию
1
Расположите следующие десятичные числа в порядке возрастания — 4,3, 1,24, 2,4, 1,2
$1,2 \lt 2,4 \lt 9,240003
$4,3 \lt 2,4 \lt 1,24 \lt 1,2$
$1,24 \lt 1,2 \lt 2,4 \lt 4,3$
$1,2 \lt 1,24 \lt 2,4 \lt 4,3$
4 \lt 1,2 $1.
2 lt 2.4 \lt 4.3$ Десятичные числа сравниваются так же, как и многозначные числа, сохраняя количество цифр одинаковым с помощью завершающих нулей.
2
Расположите следующие дроби в порядке возрастания — $\frac{3}{7},\; \фракция{3}{5},\; \фракция{3}{9},\; \frac{3}{11}$
$\frac{3}{5} \lt \frac{3}{7} \lt \frac{3}{9} \lt \frac{3}{11}$
$\frac{3}{11} \lt \frac{3}{7} \lt \frac{3}{5} \lt \frac{3} {9}$
$\frac{3}{11} \lt \frac{3}{9} \lt \frac{3}{7} \lt \frac{3}{5}$
$\ frac{3}{7} \lt \frac{3}{11} \lt \frac{3}{9} \lt \frac{3}{7}$
Правильный ответ: $\frac{3} {11} \lt \frac{3}{9} \lt \frac{3}{7} \lt \frac{3}{5}$
Для дробей с одинаковыми числителями дробь с наименьшим знаменателем является наибольшая дробь, а дробь с наибольшим числителем является наименьшей дробью.
3
Расположите следующие дроби в порядке возрастания — $\frac{2}{9},\; \фракция{3}{9},\; \фракция{7}{9},\; \frac{5}{9}$
$\frac{2}{9} \lt \frac{3}{9} \lt \frac{5}{9} \lt \frac{7}{9} $
$\frac{7}{9} \lt \frac{5}{9} \lt \frac{3}{9} \lt \frac{2}{9}$
$\frac{2 }{9} \lt \frac{7}{9} \lt \frac{5}{9} \lt \frac{3}{9}$
$\frac{7}{9} \lt \frac {5}{9} \lt \frac{2}{9} \lt \frac{3}{9}$
Правильный ответ: $\frac{2}{9} \lt \frac{3}{ 9} \lt \frac{5}{9} \lt \frac{7}{9}$
Для дробей с одинаковыми знаменателями дробь с наименьшим числителем является наименьшей дробью, а дробь с наибольшим числителем – наибольшей дробью.
4
Расположите следующие числа в порядке возрастания — 22, 2322, 2222, 222
$22 \lt 222 \lt 2322 \lt 2222$
$22 \lt 222 \lt 2222 \lt 2 9002 $ lt 2222 \lt 222 \lt 2322$
$2322 \lt 2222 \lt 222 \lt 224$
Правильный ответ: $22 \lt 222 \lt 2222 \lt 2322$
При сравнении многозначных чисел первыми идут числа с наименьшим количеством цифр. Для многозначных чисел с одинаковым количеством цифр мы сравниваем цифры слева направо.
Часто задаваемые вопросы по возрастанию
В порядке убывания от меньшего к большему?
Нет. В порядке убывания от большего к меньшему. Наибольшее количество или число помещается первым, а наименьшее количество или число помещается в последнюю позицию.
Можно ли расположить дроби в порядке возрастания или убывания?
Да. Как и целые числа, дроби можно расположить в порядке возрастания или убывания.
Какие символы используются при расположении чисел в порядке возрастания и убывания?
Символы $\lt$ (меньше) и $\gt$ (больше) используются при упорядочении чисел в порядке возрастания и убывания.