Основные темы математики / Четные и нечетные числа
Почему? Зачем ? Как? Отчего? С незапамятных времен эти простые детские вопросы заставляли человека искать, изучать, находить ответы и постигать истину. Наука стала основным средством для объяснения явлений окружающей действительности. Неведение пугает, поэтому человек испокон веков стремился найти и объяснить все непонятное, проникнуть в суть предмета или явления.
Задолго до нашей эры древнегреческий ученый, занимаясь музыкой установил связь между длинной струны музыкального инструмента и издаваемым звуком. Это наблюдение позволило Пифагору сделать вывод, что не только законы музыки, но и все на свете можно выразить с помощью чисел. «Числа правят миром!» — провозгласил великий ученый.
Числа стали для Пифагора всем. Именно он впервые разделил все числа на четные и нечетные. Исследования Пифагора и его учеников положили начало важнейшей области математики — теории чисел.
Современные ученые доказали важность этой теории.
Разделение всех чисел на четные и нечетные нашло свое подтверждение в структуре вирусов и ДНК, в знаменитых опытах Пастера с поляризацией винной кислоты, в нарушении четности элементарных частиц и других теориях.
Пифагорейцы приписывали числам магические свойства. Поэтому их учение о числа носит мистический характер. Пифагор и его последователи считали шестерку совершенным и божественным числом. Справедливость и равенство, по Пифагору, символизировал квадрат числа. Олицетворением постоянства в Древней Греции было число девять, поскольку все кратные девяти числа имеют в сумме цифр — девятку. Числа восемь символизировало смерть, так как все кратные восьми числа имеют уменьшающуюся сумму цифр.
Кстати сказать, что четные числа пифагорейцы считали женскими, а нечетные — мужскими. Символом брака у древних греков было число пять, которая состоит из суммы нечетной тройки и четной двойки.
Кроме математики Пифагор страстно любил музыку. Пифагор связал науку и искусство с помощью чисел.
Первые четыре числа задают все известные консонантные интервалы в музыке: октаву (1:2), квинту (2:3) и кварту (3:4).
Четные и нечетные числа стали неотъемлемой частью нашей жизни. В теории числе четность определяется как характеристика целого числа, определяющая его способность делиться на два без остатка. То есть, если целое число делится без остатка на два, оно является чётным (2, 28, −8, 40), если нет — нечётным (1, 3, 75, −19).
Интересно узнать, что нуль считается чётным числом.
К основным признакам четности относятся следующие:
В том случае, если в десятичной форме записи числа последняя цифра является чётным числом (0, 2, 4, 6 или 8), то всё число является чётным, в противном случае — нечётным.
Например, 42, 104, 11110, 9115817342 — чётные числа.
31, 703, 78527, 2356895125 — нечётные числа.
Так же были выделены закономерности получения четных и нечетные чисел при выполнении основным арифметический действий:
При сложении и вычитании:
Чётное ± Чётное = Чётное
Чётное ± Нечётное = Нечётное
Нечётное ± Чётное = Нечётное
Нечётное ± Нечётное = Чётное
При умножение:
Чётное × Чётное = Чётное
Чётное × Нечётное = Чётное
Нечётное × Нечётное = Нечётное
При делении:
Чётное / Чётное — не дает однозначного ответа о чётности результата, поскольку, если результат целое число, то оно может быть как чётным, так и нечётным;
Чётное / Нечётное = четное, если результат целое число;
Нечётное / Чётное — результат не может быть целым числом, следовательно у него отсутствуют показатели четности;
Нечётное / Нечётное = нечетное, если результат целое число.
Поделиться ссылкой
Четные и нечетные числа
Во вселенной существуют пары противоположностей, которые являются важным фактором ее устройства. Основные свойства, которые нумерологи приписывают четным (1, 3, 5, 7, 9) и нечетным (2, 4, 6, 8) числам, как парам противоположностей, следующие:
1 — активный, целеустремленный, властный, черствый, руководящий, инициативный;
2 — пассивный, восприимчивый, слабый, сочувствующий, подчиненный;
3 — яркий, веселый, артистичный, удачливый, легко добивающийся успеха;
4 — трудолюбивый, скучный, безынициативный, несчастный, тяжелый труд и частое поражение;
5 — подвижный, предприимчивый, нервный, неуверенный, сексуальный;
6 — простой, спокойный, домашний, устроенный; материнская любовь;
7 — уход от мира, мистика, тайны;
8 — мирская жизнь; материальная удача или поражение;
9 — интеллектуальное и духовное совершенство.
Нечетные числа обладают гораздо более яркими свойствами.
Рядом с энергией «1», блеском и удачливостью «3», авантюрной подвижностью и многогранностью «5», мудростью «7» и совершенством «9» четные числа выглядят не столь ярко. Насчитывается 10 основных пар противоположностей, существующих во Вселенной. Среди этих пар: четное — нечетное, один — много, правое — левое, мужское — женское, добро — зло. Один, правое, мужское и доброе ассоциировалось с нечетными числами; много, левое, женское и злое — с четными.
Нечетные числа обладают некой производящей серединой, в то время как в любом четном числе есть воспринимающее отверстие как бы лакуна внутри себя. Мужские свойства фаллических нечетных чисел вытекают из того факта, что они сильнее четных. Если четное число расщепить пополам, то, кроме пустоты, посередине ничего не останется. Нечетное число разбить непросто, потому что посередине остается точка. Если же соединить вместе четное и нечетное числа, то победит нечетное, так как результат всегда будет нечетным. Именно поэтому нечетные числа обладают мужскими свойствами, властными и резкими, а четные — женскими, пассивными и воспринимающими.
Нечетных чисел нечетное число: их пять. Четных чисел четное число — четыре.
Нечетные числа — солнечные, электрические, кислотные и динамичные. Они являются слагаемыми; их с чем либо складывают. Четные числа — лунные, магнетические, щелочные и статичные. Они являются вычитаемыми, их уменьшают. Они остаются без движения, потому что имеют четные группы пар (2 и 4; 6 и 8).
Если мы сгруппируем нечетные числа, одно число всегда останется без своей пары (1 и 3; 5 и 7; 9). Это делает их динамичными. Два подобных числа (два нечетных числа или два четных) не являются благоприятными.
четное + четное = четное (статичное) 2+2=4
четное + нечетное = нечетное (динамичное) 3+2=5
нечетное + нечетное = четное (статичное) 3+3=6
Некоторые числа дружественны, другие — противостоят друг другу. Взаимоотношения чисел определяются отношениями между планетами, которые ими управляют (подробности в разделе «Совместимость чисел»). Когда два дружественных числа соприкасаются, их сотрудничество не очень продуктивно.
Подобно друзьям, они расслабляются — и ничего не происходит. Но когда в одной комбинации находятся враждебные числа, они заставляют друг друга быть настороже и побуждают к активным действиям; таким образом, эти два человека работают намного больше. В таком случае, враждебные числа оказываются на самом деле друзьями, а друзья — настоящими врагами, тормозящими прогресс. Нейтральные числа остаются неактивными. Они не дают поддержки, не вызывают и не подавляют активность.
Сумма двух нечетных чисел четна
ПоискМы хотим показать, что если мы сложим два нечетных числа , то сумма всегда будет четным числом .
Прежде чем мы даже напишем фактическое доказательство, нам нужно убедиться, что в данном утверждении есть доля правды. Мы можем проверить утверждение на нескольких примерах.
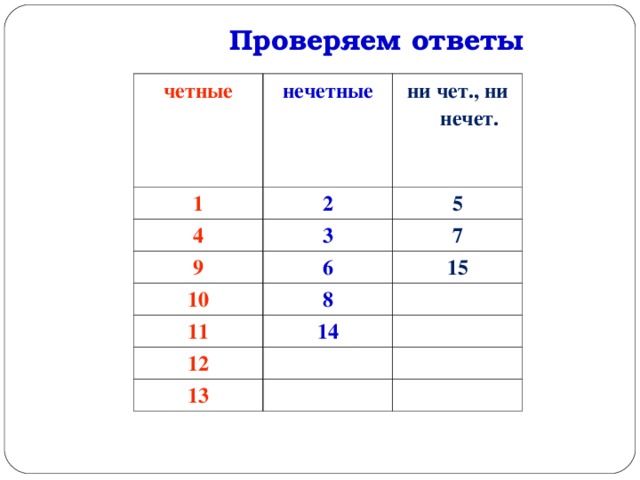
Я подготовил таблицу ниже, чтобы собрать результаты некоторых чисел, которые я использовал для проверки утверждения.
Похоже, что утверждение, что сумма двух нечетных чисел четна, верно.
Однако простое приведение бесконечного множества примеров не является доказательством. Невозможно перечислить все возможные случаи.
Вместо этого нам нужно показать, что утверждение справедливо для ВСЕХ возможных случаев. Единственный способ добиться этого — выразить нечетное число в его общей форме. Затем мы складываем два нечетных числа, записанных в общей форме, чтобы получить сумму четного числа, также выраженную в общей форме.
Чтобы написать доказательство этой теоремы, вы уже должны иметь четкое представление об общих формах как четных, так и нечетных чисел.
- Четные числа
Число n равно , даже , если его можно выразить как
п=2к
, где k — целое число.
- Нечетные числа
С другой стороны, число n равно нечетному , если его можно записать как
п=2к+1
такое, что k — некоторое целое число.
Примечание: Цель мозгового штурма при письменном доказательстве состоит в том, чтобы мы поняли, что пытается передать теорема; и соберите достаточно информации, чтобы соединить точки, которые будут использоваться для соединения гипотезы и заключения.
Возьмем два произвольных нечетных числа 2a + 1 и 2b + 1, где a и b — целые числа.
Поскольку нам нужна сумма, мы хотим добавить 2a + 1 и 2b + 1.
\влево( {2a + 1} \вправо) + \влево( {2b + 1} \вправо)
, что дает нам
\left( {2a + 1} \right) + \left( {2b + 1} \right) = 2a + 2b + 2.
Обратите внимание, что мы не можем объединить 2a и 2b, потому что это не похожие термины. Однако нам удалось объединить константы, таким образом, 1 + 1 = 2,
Что нам делать дальше? Если подумать, то в 2a + 2b + 2 есть общий делитель 2. Если вычесть 2, мы получим 2\left( {a + b + 1} \right).
Что дальше? Что ж, если мы заглянем внутрь скобок, станет очевидно, что перед нами просто целое число.
Сначала оно может не отображаться как целое число, потому что мы видим, как складываются несколько целых чисел.
Вызов свойства замыкания сложения для набора целых чисел.
Предположим, что a и b принадлежат множеству целых чисел. Сумма a и b, равная {a+b}, также является целым числом.
На самом деле, вы можете расширить это свойство замыкания сложения до более чем двух целых чисел. Например, сумма целых чисел -7, -1, 0, 4 и 10 равна 6, что также является целым числом. Таким образом,
(-7)+(-1)+0+4+10=6.
Возвращаясь к тому месту, где мы остановились, в 2\left( {a + b + 1} \right) выражение внутри круглых скобок является просто целым числом, поскольку сумма целых чисел a, b и 1 является просто другим целым числом . Для простоты назовем его целым числом k.
Итак,
а+б+1=к
Это означает, что 2\left( {a + b + 1} \right) может быть выражено как
2\влево( {а + б + 1} \вправо) =2k
, где 2k — это общая форма четного числа.
НАПИШИТЕ ДОКАЗАТЕЛЬСТВО
ТЕОРЕМА: Сумма двух нечетных чисел является четным числом.
ДОКАЗАТЕЛЬСТВО: Предположим, что 2a+1 и 2b+1 — любые два нечетных числа, где a и b — целые числа. Сумма этих двух нечетных чисел равна \left( {2a + 1} \right) + \left( {2b + 1} \right). Это можно упростить как {2a + 2b + 2}, объединив аналогичные термины. Вынесите из {2a+2b+2} наибольший общий делитель (GCF) \bold{2}, чтобы получить 2\left({a + b + 1} \right). Поскольку сумма целых чисел — это просто еще одно целое число, скажем, целое число k, тогда {k=a+b+1}. Подстановкой мы имеем 2\left( {a + b + 1} \right) = 2k, где 2k, очевидно, является общей формой четного числа. Следовательно, сумма двух нечетных чисел является четным числом. ◾️
Доказательство: сумма двух четных чисел является четным числом
Логика— Между любыми двумя четными числами есть нечетное число
$\begingroup$
Напишите полное математическое логическое выражение следующего выражения: между любыми двумя четными числами есть нечетное число.
Моя попытка:
$E(x): x$ четно.
$O(x): x$ нечетно.
$$∀m∀n∃k[(E(m) ∧ E(n) ∧ O(k)) ∧ (m < k < n)]$$
По-английски это выглядит так: я говорю: для всех m и для всех n существует k, где m — четное, n — четное, k — нечетное и m меньше, чем k меньше n, что означает, что существует некоторое нечетное число между любыми двумя четными числами.
Или мне нужно указать, что n также может быть меньше m?
РЕДАКТИРОВАТЬ: Попытка 2:
$$∀m∀n∃k[(E(m) ∧ E(n) ∧ O(k)) ∧ ((m < k < n) v (n < k < m))]$$
- логика
- логика предикатов 92,\;\exists k{\in}\mathbb O\,\Big(\text{$k$ находится между $m$ и $n$}\Big)$$ Но подождите, эта формализация допускает такие пары, как $( 2,2),(16,16),$ и т.д.! Предполагая, что автор на самом деле имеет в виду «два различных четных чисел» (в этом случае данное утверждение верно), мы должны уточнить его (приняв обычное соглашение о приоритете, чтобы минимизировать мое количество скобок): $$∀m∀n \;\bigg(Em ∧ En ∧ m\ne n \to ∃k\: \Big(Ok ∧ (m < k < n \;\lor\; n < k < m)\Big)\bigg).
$ $ Обратите внимание, что я не настаивал на том, чтобы все кванторы были сведены вместе впереди; легче понять смысл перевода, когда они размещены на своих естественных местах. Наконец, если предварительная форма предпочтительна: $$∀m∀n∃k\; \bigg(Em ∧ En ∧ m\ne n \to Ok ∧ \big(m < k < n \;\lor\; n < k < m\big)\bigg).$$ Обратите внимание, хотя кажется, что Я просто вытащил квантификаторы вперед, фактический алгоритм преобразования логической формулы в предваряющую форму немного менее прямолинеен, чем этот.В качестве альтернативы предыдущую формулу можно переписать без условного оператора: $$∀m∀n∃k\; \bigg(¬Em ∨ ¬En ∨ m=n ∨ \Big( Ok ∧ \big(m < k < n \;\lor\; n < k < m\big)\Big)\bigg).$$
При оформлении изложения (аналогично написанию эссе в черновиках) не обязательно делать это за один шаг, и предварительные шаги не обязательно должны быть полностью правильными.
Попытка 2: $$∀m∀n∃k[(E(m) ∧ E(n) ∧ O(k)) ∧ ((m < k < n) \;\lor\; (n < k < m ))]$$
Это предложение неверно: для $(m,n)=(1,2),$ не существует $k$, для которых $$E(m) ∧ E(n) ∧ O(k) ∧ ( m < k < n \;\lor\; n < k < m)$$ верно.