| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |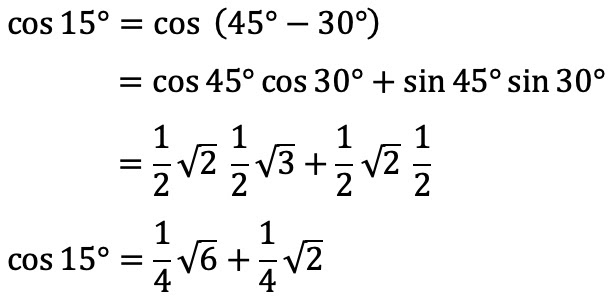
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | ||
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
Чему равен косинус 15° градусов
математика тригонометрия решение косинус
Только в сентябре: получи кредитку по акции с бонусом 2000р. и годом без % Получить карту
Как определить точное значение косинуса 15° градусов cos (15°)? Чему он равен?
Похвалить 0 Пожаловаться
3 ответа
Попробуем найти косинус 15 градусов путем решения задачи.
Допустим, у нас есть треугольник ACB, поделенные на равнобедренный тр. ADE, треугольник с 30, 60 и 90 градусов (BDE) и тр. BCD, у которого есть угол 15 градусов.
И нам известно, что равнобедренная сторона AE равна 1 сантиметру. Чтобы вычислить косинус 15 градусов, нам нужно найти размер сторон треугольника BCD.
ADE — равнобедренный треугольник, потому сторона DE равна AE = 1 см. AD легко найти по теореме Пифагора (прибавляем квадраты сторон AE и AD, вычитаем корень суммы) — длина стороны — это √2. Стороны треугольника BDE находим при помощи известного градуса:
- ∠DBE = 30 гр.;
- соотношение сторон BE и BD — это cos 30 гр.
- табличное значение cos 30 — √3 поделить на 2;
- делаем вывод: BD = 2, BE = √3.
Поскольку углы CAE, CBA равны 45 гр., самый большой треугольник ABC тоже равнобедренный (стороны AC и BC одинаковые по размеру), можно применить теорему Пифагора:
Стороны большого треугольника найдены — осталось отыскать длину самой маленькой фигуры, в которой и есть нужный градус для вычисления косинуса.
Принимаем CD за икс(это указано на иллюстрации выше). Находим значение переменной с помощью теоремы Пифагора. Для этого предположим, что икс плюс √2 равен квадратному корню из суммы квадратов двух других катетов, минус √2. Считаем:
Осталось совсем чуть-чуть! Делаем заключительное соотношение для вычисления косинуса:
Получается табличное значение cos 15:
Точное значение косинуса 15 гр. дуги
В нешкольных задачах используют точные цифры по таблице Брадиса. Если довести уравнение до конца получится следующее число:
Смотрите также способы определить косинус 60 градусов и как найти cos 75.
Похвалить 3 Пожаловаться
Что такое косинус угла
Косинусом угла в прямоугольном треугольнике называется отношение длины противолежащего катета к длине гипотенузы.
На приведенном ниже рисунке для угла ‘х’ противолежащим катетом будет сторона ‘а’, а гипотенузой – сторона ‘с’.
Таким образом, cos(х)=а/с.
Как вычислить значение cos(15°)
Рассмотрим несколько способов вычисления этого значения.
Первый способ – по математическим таблицам
По таблицам Брадиса или с помощью калькулятора: cos(15°)=0,9659.
Второй способ – используя тригонометрические выражения
1) Так как угол 15° равен половине 30°, то его косинус можно рассчитать по формуле половинного угла:
Известно, что косинус угла 30° определяется простым выражением:
Подставляя значение cos(30°) в предыдущую формулу получим:
2) Угол 15° также можно представить как разность между 60° и 45°. Тогда косинус 15° можно рассчитать по тригонометрической формуле:
Значения косинусов и синусов углов 60° и 45° определяются простыми выражениями, подставляя которые в предыдущую формулу получим:
Третий способ – графически
Это наименее точный способ. Используя транспортир и линейку следует начертить прямоугольный треугольник произвольного размера, аналогичный показанному на рисунке.
Затем с помощью линейки измерить длину сторон ‘а’ и ‘с’ треугольника и рассчитать их математическое отношение.
Похвалить 2 Пожаловаться
Определяем значение косинуса угла, равного 15 градусов, чтобы определить, рассмотрим треугольник.
Итак, косинус угла в прямоугольном треугольнике — отношение длины противолежащего катета к длине гипотенузы.
На нашем рисунке:
- неизвестный угол «α»;
- противолежащий катет сторона «а»;
- гипотенуза — «с».
Таким образом, cos(α)=а/с, определяем косинус угла в 15 градусов согласно таблице Брадиса: cos(15)=0,9659.
Таблица Брадиса — это таблица, которая поможет при вычислениях в решении задач как в школе (на математике, алгебре, геометрии и физике в старших классах), так и в вузах. На этой странице четырехзначные математические онлайн таблички для синусов, косинусов, тангенсов и котангенсов.
Итак, cos (15°)=0,966
Ознакомьтесь также:
- Чему равен косинус 90° градусов — cos(90°)?
- Чему равен косинус 180° градусов — cos(180°)?
- Чему равен косинус 330° градусов — cos(330°)?
Похвалить 0 Пожаловаться
Дать ответ и заработать:
Cимволов:
| 1 | Найти производную — d/dx | бревно натуральное х | |
| 2 | Оценить интеграл | интеграл натурального логарифма x относительно x | |
| 3 | Найти производную — d/dx | 92)||
| 21 | Оценить интеграл | интеграл от 0 до 1 кубического корня из 1+7x относительно x | |
| 22 | Найти производную — d/dx | грех(2x) | |
| 23 | Найти производную — d/dx | 9(3x) по отношению к x||
| 41 | Оценить интеграл | интеграл от cos(2x) относительно x | |
| 42 | Найти производную — d/dx | 1/(корень квадратный из х) | |
| 43 | Оценка интеграла 9бесконечность | ||
| 45 | Найти производную — d/dx | х/2 | |
| 46 | Найти производную — d/dx | -cos(x) | |
| 47 | Найти производную — d/dx | грех(3x) | 92+1|
| 68 | Оценить интеграл | интеграл от sin(x) по x | |
| 69 | Найти производную — d/dx | угловой синус(х) | |
| 70 | Оценить предел | ограничение, когда x приближается к 0 из (sin(x))/x 92 по отношению к х | |
| 85 | Найти производную — d/dx | лог х | |
| 86 | Найти производную — d/dx | арктан(х) | |
| 87 | Найти производную — d/dx | бревно натуральное 5х92 |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус (-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. |