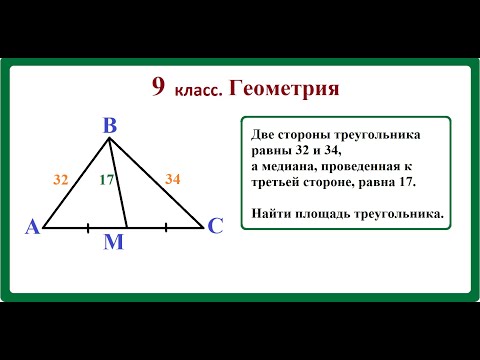
3.Медиана треугольника. Теоремы связанные с медианами треугольника. Формулы для нахождения медиан
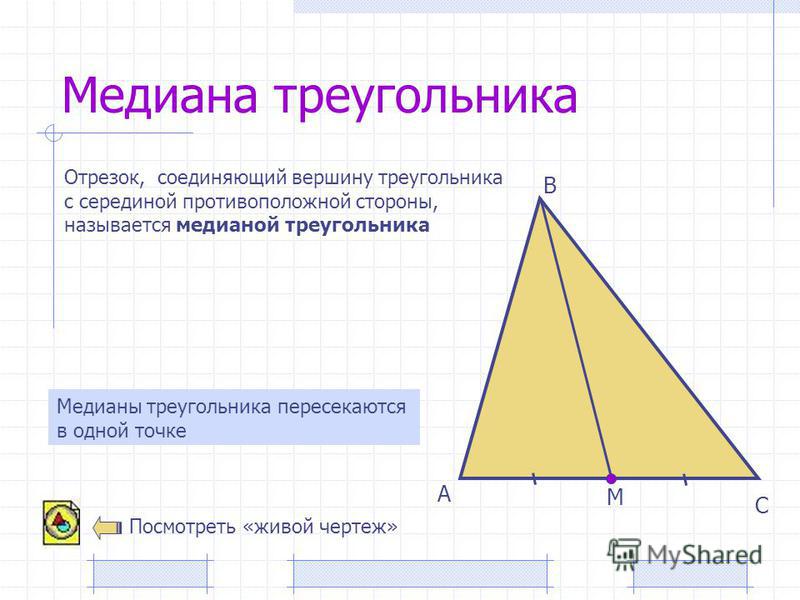
Медиана треугольника — это отрезок, соединяющий верщину треугольника с серединой противолежащей стороны этого треугольника.
Свойства медиан треугольника
Медиана разбивает треугольник на два треугольника одинаковой площади.
Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника (центроидом).
Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
Длина медианы проведенной к стороне: (док-во достроением до параллелограмма и использованием равенства в параллелограмме удвоенной суммы квадратов сторон и суммы квадратов диагоналей )
Т1.
. Д-во: Пусть М — точка пересечения медиан СС1, АА1 треугольника ABC. Отметим A2 — середину отрезка AM и С2 — середину отрезка СМ. Тогда A2C2 — средняя линия треугольника АМС. Значит, А2 С2 || АС
и A2C2 = 0,5*АС. С1А1 — средняя линия треугольника ABC. Значит, А1С1 || АС и А1С1 = 0,5*АС.
Четырехугольник А2С1А 1С2 — параллелограмм, так как его
противоположные стороны А1С1 и А2С2 равны и параллельны.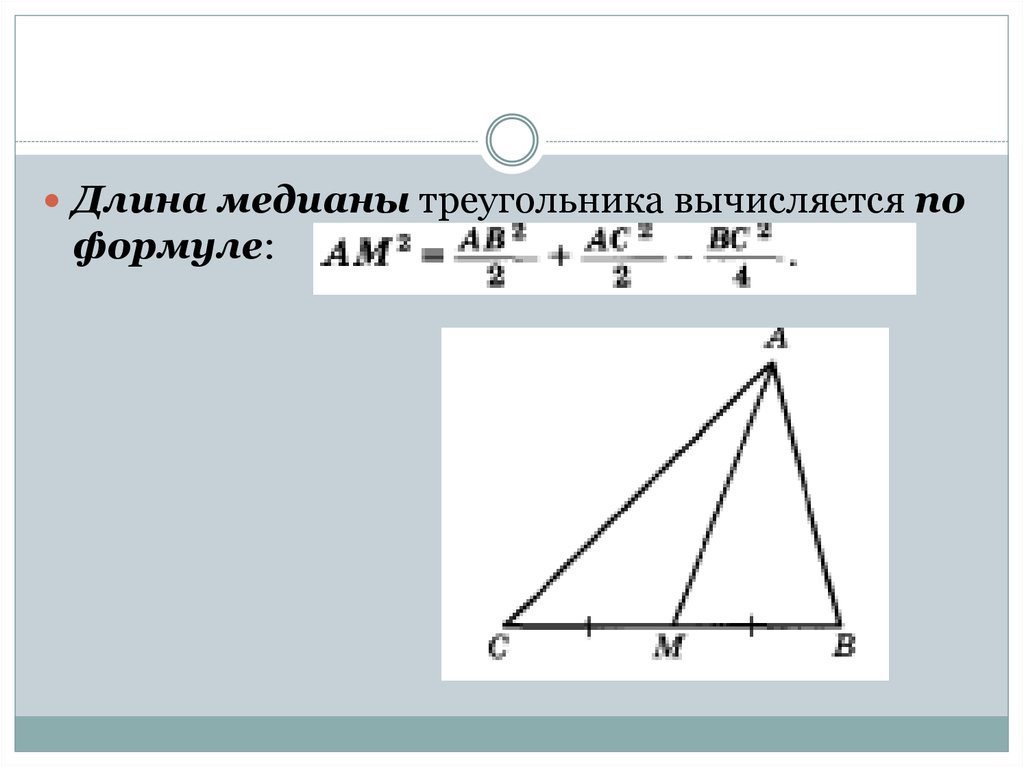 Следовательно, А2М
= МА1 и С2М
= МC1. Это означает, что
точки А2 и M делят медиану АА2 на три равные части, т. е. AM
= 2МА2 . Аналогично СМ = 2MC1.
Итак, точка М пересечения двух медиан АА2 и CC2 треугольника ABC
делит каждую из них в отношении 2:1,
считая от вершин треугольника.
Совершенно аналогично доказывается,
что точка пересечения медиан АА1 и BB1 делит каждую из них в отношении 2:1,
считая от вершин треугольника.
Следовательно, А2М
= МА1 и С2М
= МC1. Это означает, что
точки А2 и M делят медиану АА2 на три равные части, т. е. AM
= 2МА2 . Аналогично СМ = 2MC1.
Итак, точка М пересечения двух медиан АА2 и CC2 треугольника ABC
делит каждую из них в отношении 2:1,
считая от вершин треугольника.
Совершенно аналогично доказывается,
что точка пересечения медиан АА1 и BB1 делит каждую из них в отношении 2:1,
считая от вершин треугольника.
На медиане АА1 такой точкой является точка М, следовательно, точка М и есть точка пересечения медиан АА1 и BB1.
Таким образом,
T2. Докажите, что отрезки, которые соединяют
центроид с вершинами треугольника,
делят его на три равновеликие части.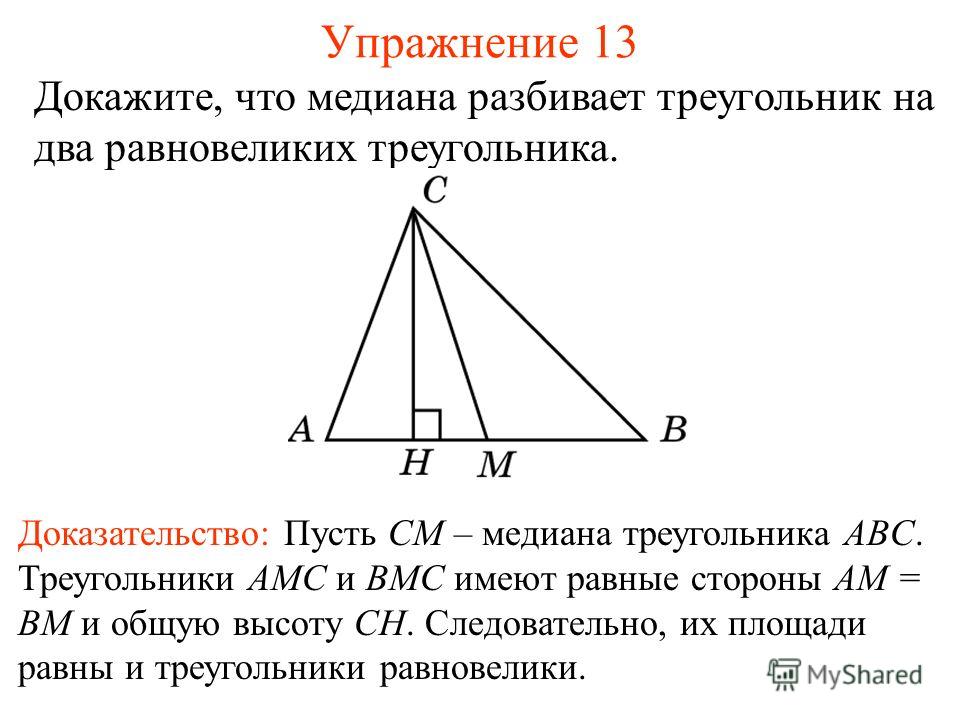 Дано: ∆ABC
,
— его медианы.
Дано: ∆ABC
,
— его медианы.
Доказать: SAMB = SBMC = SAMC. Доказательство. и высота, проведенная из вершины В, у них общая. т.к. равны их основания и высота, проведенная из вершины М, у них общая. Тогда
Аналогичным образом доказывается, что S
AMB = SAMC. Таким образом, SAMB = SAMC = SCMB . 4.Биссектриса треугольника. Теоремы связанные с биссектрисами треугольника. Формулы для нахождения биссектрис
Биссектриса угла — луч с началом в вершине угла, делящий угол на два равных угла.
Биссектриса
угла есть геометрическое место точек
внутри угла, равноудалённых от сторон
угла.
Свойства
Теорема о биссектрисе: Биссектриса внутреннего угла треугольника делит противоположную сторону в отношении, равном отношению двух прилежащих сторон
Биссектрисы внутренних углов треугольника пересекаются в одной точке — инцентре — центре вписанной в этот треугольник окружности.
Если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера — Лемуса).
Вычисление длины биссектрисы
где:
lc — длина биссектрисы, проведённой к стороне c,
a,b,c — стороны треугольника против вершин A,B,C соответственно,
p — полупериметр треугольника,
al,bl — длины отрезков, на которые биссектриса lc делит сторону c,
α,β,γ — внутренние углы треугольника при вершинах A,B,C соответственно,
hc — высота треугольника, опущенная на
сторону c.
Квадрат длины медианы в произвольном треугольнике
Автор: Магомедов Саид Абдурахманович
Научный руководитель: Акопов Вачакан Ваграмович
Рубрика: Математика: алгебра и начала анализа, геометрия
Опубликовано в Юный учёный №5 (57) май 2022 г.
Дата публикации: 02.05.2022 2022-05-02
Статья просмотрена: 101 раз
Скачать электронную версию
Библиографическое описание: Магомедов, С.
В данной статье рассматривается вывод формулы длины медианы в произвольном треугольнике. Вывод формулы разными способами даёт возможность учащимся повторить широкий спектр геометрических фактов, совершенствовать навыки применения разных методов и приёмов решения задач, способствует более глубокому и прочному пониманию и запоминанию материала.
Ключевые слова: медиана, длина, полупериметр, произвольный треугольник.
Математика — это искусство называть разные вещи одним и тем же именем.
А. Пуанкаре
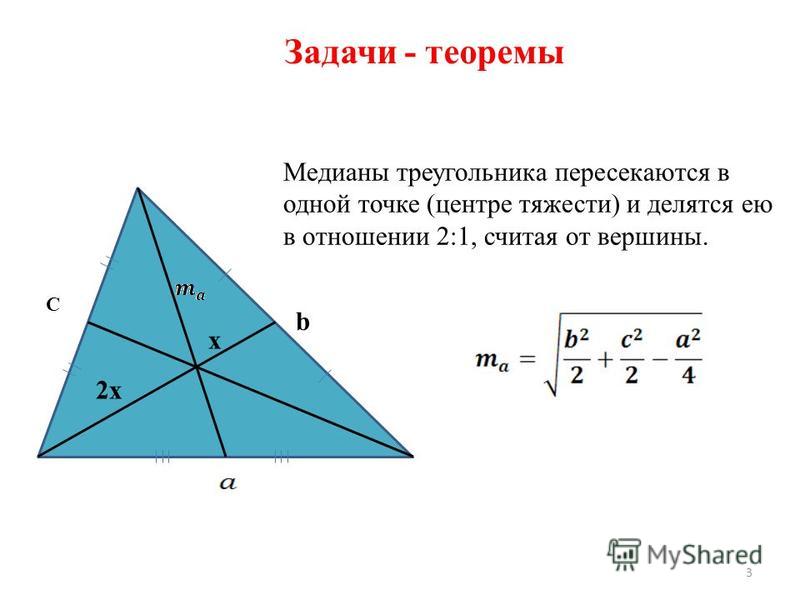
Медианой треугольника называется отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны (рис.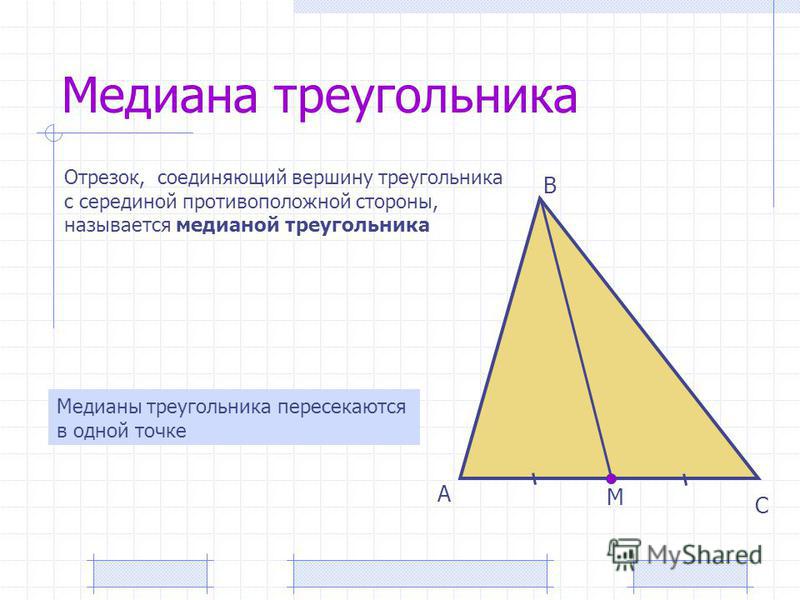 1). Медиана, соединяющая вершину A треугольника с серединой стороны a , обозначается m a .
1). Медиана, соединяющая вершину A треугольника с серединой стороны a , обозначается m a .
Рис. 1
На сегодня известны две формулы квадрата длины медианы в произвольном треугольнике:
- Через стороны треугольника:
, (1).
где a, b, c — стороны треугольника, x , y — отрезки основания медианы, A, B, C — углы треугольника.
Докажем эту формулу, для чего воспользуемся теоремой Стюарта: Если точка D лежит на стороне BC треугольника
или , тогда, учитывая, что , будем иметь: , что и требовалось доказать.
Задача. В треугольнике АВС (рис.1) проведена медиана АD . Известно, что b=8 , c=10 и m a =7.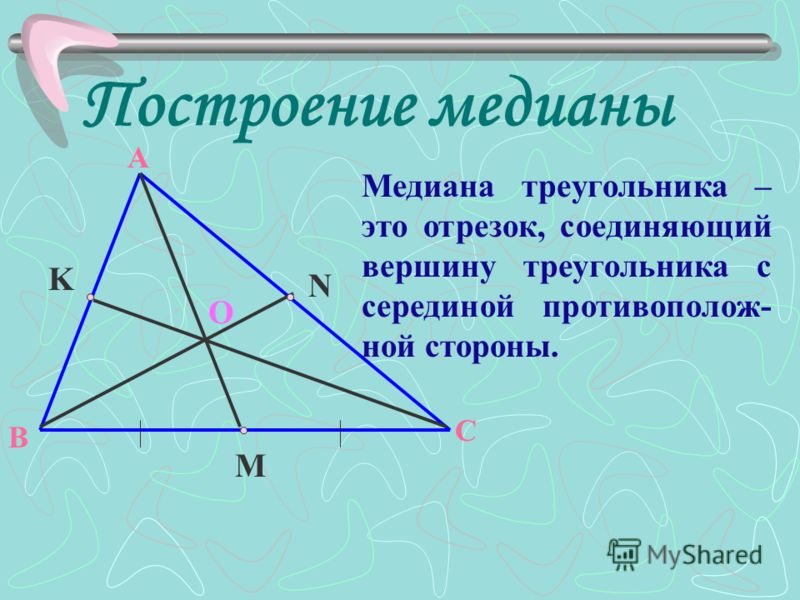 Найти a .
Найти a .
- Через две стороны и угол: , (2).
Докажем эту формулу, для чего рассмотрим треугольник АВС (рис.1) со сторонами a, b и c . Из вершины А на сторону СВ=a опустим медиану АD=m a . Из треугольника АВС по теореме косинусов, имеем: . С другой стороны воспользуемся выражением (1): Используя эти два выражения, получим: , отсюда или , что и требовалось доказать.
Задача. В треугольнике АВС (рис.1) проведена медиана АD . Известно, что b=8 , c=10 и m a =7. Найти угол А .
Рассмотрим зависимость квадрата длины медианы в произвольном треугольнике через полупериметр и стороны.
Используя формулу двойного угла
с учётом, что
и
, будем иметь:
, отсюда
, (3). Из треугольника АВС по теореме косинусов имеем:
, отсюда
, (4). Используя выражения (3) и (4), получим:
, отсюда
, (5). Используя выражения (1) и (5), будем иметь:
, отсюда
, (6).
Из треугольника АВС по теореме косинусов имеем:
, отсюда
, (4). Используя выражения (3) и (4), получим:
, отсюда
, (5). Используя выражения (1) и (5), будем иметь:
, отсюда
, (6).
Таким образом, квадрат длины медианы произвольного треугольника равен одной четвёртой квадрата разности периметра и одной из сторон треугольника без произведения разностей полупериметра и каждой из двух других его сторон.
Задача. В треугольнике АВС (рис.1) с полупериметром 21см и сторонами b=14см и c=12см из вершины А проведена медиана m a . Найти квадрат медианы.
Литература:
- Выгодский М. Я. Справочник по элементарной математике. Москва. «Наука». 1986.
- Некрасов В. Б. Школьная математика. Санкт-Петербург. «Авалон». 2006.
длина, медиана, произвольный треугольник, полупериметр
медиана, длина, полупериметр, произвольный треугольник
- Как издать спецвыпуск?
- Правила оформления статей
- Оплата и скидки
Медиана треугольника (формулы, примеры и видео)
Написано
Малкольм МакКинси
Череплен фактом
Пол Маццола
Медиана Triangle (определение, формала, формала, формала, формала, формала, формала, формала, формала, формала & Примеры)
Математическое слово «медиана» имеет разные значения при различных операциях.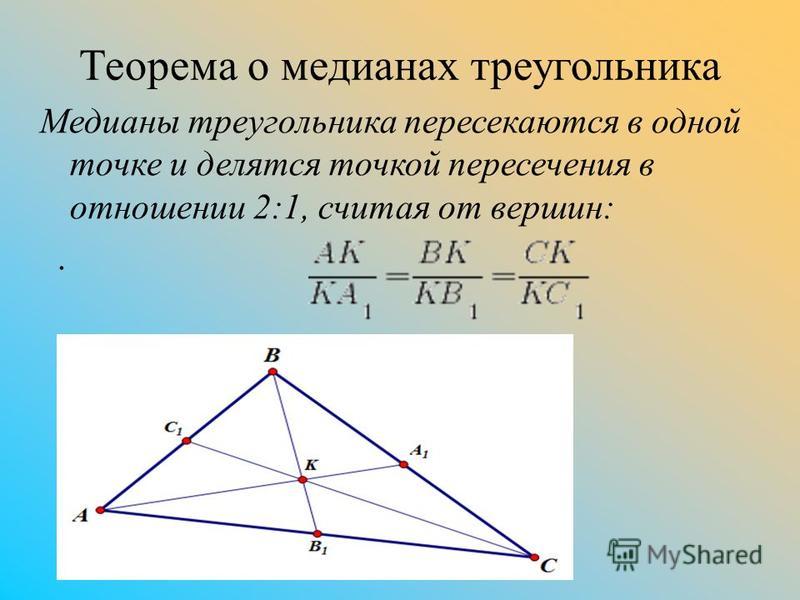 В статистике это значение, лежащее в середине набора данных.
В статистике это значение, лежащее в середине набора данных.
Итак, для набора данных {3, 5, 7, 9, 11} , 7 — медиана. В геометрии медиана — это отрезок прямой от внутреннего угла треугольника до середины противоположной стороны.
Изучение геометрической медианы может облегчить вашу жизнь в геометрии и, возможно, на кухне.
Треугольник
Любой треугольник является многоугольником с тремя прямыми сторонами, ограничивающими пространство. Треугольники, названные по их углам, могут быть остроугольными или тупоугольными (которые группируются как косоугольные треугольники) или прямоугольными треугольниками. Треугольники, названные по их сторонам, могут быть разносторонними, равнобедренными или равносторонними.
Площадь
Площадь – это пространство, занимаемое многоугольником в двух измерениях. Каждый треугольник имеет внутреннее пространство, которое является площадью треугольника. Эта площадь всегда измеряется в квадратных единицах, независимо от того, какую форму вы измеряете.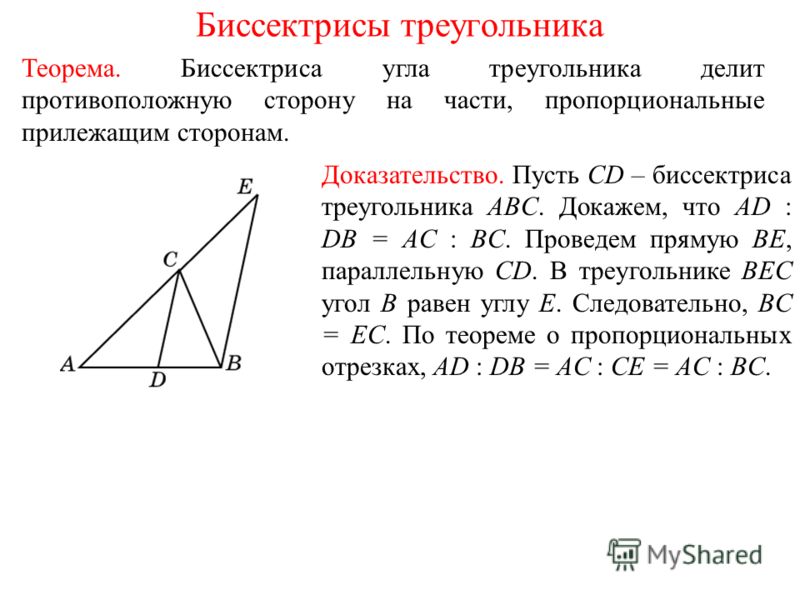
Вот формула площади треугольника:
Что такое медиана треугольника?
Если вы нашли середину любой стороны треугольника, вы нашли его середину. От этой средней точки можно построить отрезок к противоположному внутреннему углу. Эта построенная линия от середины стороны до противоположного внутреннего угла представляет собой медиана .
Поскольку у треугольника всегда три стороны, у него всегда три медианы.
Центроид треугольника
Там, где медианы пересекаются, точка, общая для всех трех медиан, называется центроидом . Центроид – это точка параллелизма . всегда будет внутри треугольника, в отличие от других точек параллелизма, таких как ортоцентр.
Медианы, сходящиеся в центроиде, обладают особым свойством. Центроид всегда находится на расстоянии двух третей пути вдоль каждой медианы от внутреннего угла этой медианы. Это означает, что он устанавливает 2:1 соотношение для каждой из трех медиан:
Центр масс
Центроид треугольника не только теоретический. Это центр масс или центр тяжести треугольника. Нарисовав все три медианы, вы сможете найти точное место, где физически существующий треугольник будет идеально сбалансирован!
Это центр масс или центр тяжести треугольника. Нарисовав все три медианы, вы сможете найти точное место, где физически существующий треугольник будет идеально сбалансирован!
Это может иметь для вас практическое применение, если вы имеете дело с треугольниками, вырезанными из картона или дерева. Вы можете найти центр тяжести и сбалансировать треугольник кончиком карандаша или кончиком пальца.
Как найти медиану треугольника
Теорема, называемая Теорема Аполлония , может дать вам длину медианы треугольника. Это немного многословно, но может быть переведено в формулу. Во-первых, теорема:
Теорема Аполлония утверждает, что в любом треугольнике сумма квадратов любых двух сторон равна удвоенному квадрату половины третьей стороны вместе с удвоенным квадратом медианы, которая делит третью сторону пополам.
В виде формулы это выглядит так, где a , b и c — длины сторон, а м — медиана от внутреннего угла A до стороны a :
Медиана треугольника пример
A 900 900 линия, разделяющая исходный треугольник на два меньших треугольника равной площади. Эта особенность медианы может пригодиться.
Эта особенность медианы может пригодиться. Здесь у нас есть △EAT , пицца с разносторонними треугольниками, приготовленная в начале науки о семье и потреблении. Форма не на что смотреть, но вы приготовили свою первую пиццу и гордитесь ею. Вы предлагаете поделиться им с другом. Как вы разделите свою пиццу, чтобы каждый получил одинаковое количество?
Использовать медиану. С любого внутреннего угла режьте до середины противоположной стороны. Теперь у вас и вашего друга поровну порций пиццы.
Предположим, к вам присоединятся еще двое друзей и захотят попробовать вашу пиццу необычной формы. Разрежьте по другой медиане от любого внутреннего угла до середины противоположной стороны! Кусочки меньше и определенно странной формы, но все они одинаковой площади.
О-о! Еще двое друзей хотят войти. Пицца может выглядеть странно, но пахнет чудесно. Так что отрежьте третью срединную линию, и все шестеро из вас получат одинаковое количество пиццы, даже если все формы будут немного… разными.
Итоги урока
Проработав этот урок, вы теперь можете вспомнить, что у каждого треугольника есть три медианы, нарисовать или определить медианы в треугольниках, определить центр тяжести треугольника, используя его медианы, вычислить длину медианы , и свяжите площадь с медианами треугольников.
Медиана треугольника | Что такое медиана треугольника
Содержание
Этот пост также доступен в:
हिन्दी (хинди)
Треугольник — одна из самых важных двумерных фигур в геометрии. Треугольники обладают определенными свойствами, которые используются для решения задач. Одним из таких свойств является медиана треугольника.
Давайте разберемся, что такое медиана треугольника и ее свойства.
Что такое медиана треугольника?
Отрезок, соединяющий вершину с серединой стороны, противоположной этой вершине, называется медианой треугольника. Треугольник может иметь три медианы, соединяющие каждую из вершин с серединой противоположной стороны.
На приведенном выше рисунке в $\triangle \text{ABC}$ точка $\text{D}$ является серединой стороны $\text{BC}$. $\text{AD}$ — это отрезок, соединяющий вершину $\text{A}$ с $\text{D}$ и, таким образом, являющийся одной из медиан $\треугольника \text{ABC}$.
СКАЧАТЬ БЕСПЛАТНО КАРТОЧКИ ПО МАТЕМАТИКЕ:
Красиво оформленные карточки для печати, которые помогут вам запомнить все важные математические понятия и формулы.
Свойства медианы треугольника
Ниже приведены свойства медианы треугольника, которые помогут вам ее идентифицировать.
- Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой его противоположной стороны.
- Он делит противоположную сторону пополам, разделяя ее на две равные части.
- Медиана треугольника далее делит треугольник на два треугольника, имеющих одинаковую площадь.
- Независимо от формы или размера треугольника, три его медианы сходятся в одной точке.

- Каждый треугольник имеет три медианы, по одной из каждой вершины. Точка пересечения трех медиан образует центр тяжести треугольника.
- Каждая медиана треугольника делит его на два меньших треугольника с равными площадями. Три медианы делят треугольник на шесть меньших треугольников равной площади. 92}{4}$.
Как найти медиану треугольника с заданными координатами?
Когда известны координаты трех вершин треугольника, используются следующие шаги для нахождения длины медианы треугольника.
Шаг 1: Используя координаты вершин треугольника, найдите координаты середины отрезка, на котором образована медиана. Это можно сделать с помощью формулы средней точки. Формула для средней точки: $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$, где $\left(x_1, y_1 \right)$ и $ \left(x_2, y_2 \right)$ — координаты концов отрезка. 92}$ где $\left(x_1, y_1 \right)$ и $\left(x_2, y_2 \right)$ — координаты медианы.
Разница между медианой и высотой треугольника
Ниже приведены различия между медианой и высотой треугольника.
Медиана треугольника Высота треугольника Медиана треугольника — это отрезок, проведенный от вершины к противоположной стороне. Высота треугольника — это расстояние по перпендикуляру от основания до противоположной вершины. Он всегда лежит внутри треугольника. Может быть как снаружи, так и внутри треугольника в зависимости от типа треугольника. Делит треугольник на две равные части. Не делит треугольник на две равные части. Делит основание треугольника пополам на две равные части. Не делит основание треугольника пополам. Точка, где сходятся три медианы треугольника, называется центром тяжести треугольника. Точка, где встречаются три высоты треугольника, называется ортоцентром этого треугольника.
Ключевые выводы
- Каждая медиана делит треугольник на два меньших треугольника одинаковой площади.

- Центроид (точка, где они встречаются) является центром тяжести треугольника.
- Периметр треугольника больше суммы трех его медиан.
- Если два треугольника конгруэнтны, медианы конгруэнтных треугольников равны, так как соответствующие части конгруэнтных треугольников конгруэнтны.
Типы систем координат Практические задачи
- Что такое медиана треугольника?
- Сколько медиан может быть у треугольника?
- Точка пересечения всех медиан треугольника называется _________.
- Найдите длину медианы AD, если координаты треугольника ABC заданы как A (4, 10), B (8, 2), C (-8, 4).
Часто задаваемые вопросы
Что такое медиана треугольника?
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны, таким образом делящий эту сторону пополам.

Как найти медиану треугольника с заданными координатами?
Когда известны координаты трех вершин треугольника, используются следующие шаги для нахождения длины медианы треугольника.
Шаг 1: Используя координаты вершин треугольника, найдите координаты середины отрезка, на котором образована медиана. Это можно сделать с помощью формулы средней точки. Формула для средней точки: $\left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right)$, где $\left(x_1, y_1 \right)$ и $ \left(x_2, y_2 \right)$ — координаты концов отрезка. 92}$ где $\left(x_1, y_1 \right)$ и $\left(x_2, y_2 \right)$ — координаты медианы.
Разница между медианой и высотой треугольника
Ниже приведены различия между медианой и высотой треугольника.
| Медиана треугольника | Высота треугольника |
| Медиана треугольника — это отрезок, проведенный от вершины к противоположной стороне. | Высота треугольника — это расстояние по перпендикуляру от основания до противоположной вершины. |
| Он всегда лежит внутри треугольника. | Может быть как снаружи, так и внутри треугольника в зависимости от типа треугольника. |
| Делит треугольник на две равные части. | Не делит треугольник на две равные части. |
| Делит основание треугольника пополам на две равные части. | Не делит основание треугольника пополам. |
| Точка, где сходятся три медианы треугольника, называется центром тяжести треугольника. | Точка, где встречаются три высоты треугольника, называется ортоцентром этого треугольника. |
Ключевые выводы
- Каждая медиана делит треугольник на два меньших треугольника одинаковой площади.

- Центроид (точка, где они встречаются) является центром тяжести треугольника.
- Периметр треугольника больше суммы трех его медиан.
- Если два треугольника конгруэнтны, медианы конгруэнтных треугольников равны, так как соответствующие части конгруэнтных треугольников конгруэнтны.
Практические задачи
- Что такое медиана треугольника?
- Сколько медиан может быть у треугольника?
- Точка пересечения всех медиан треугольника называется _________.
- Найдите длину медианы AD, если координаты треугольника ABC заданы как A (4, 10), B (8, 2), C (-8, 4).
Часто задаваемые вопросы
Что такое медиана треугольника?
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противоположной стороны, таким образом делящий эту сторону пополам.

 Эта особенность медианы может пригодиться.
Эта особенность медианы может пригодиться.