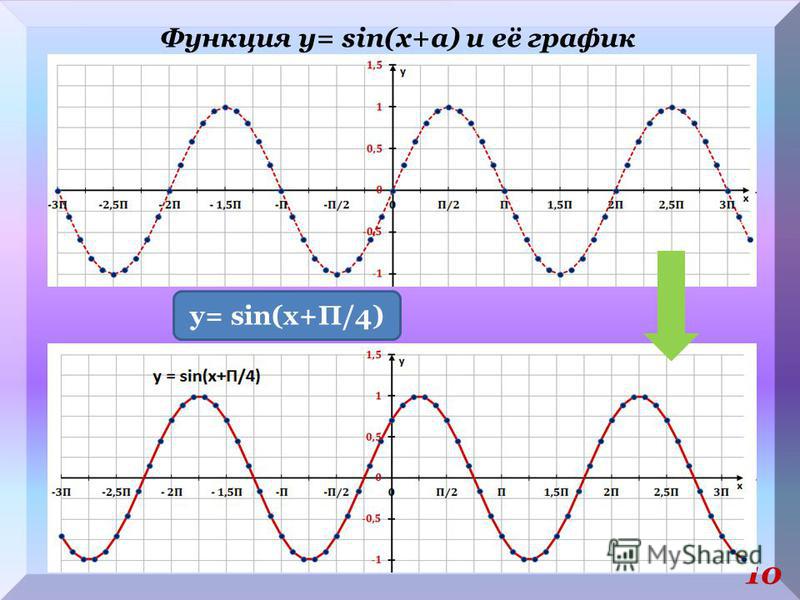
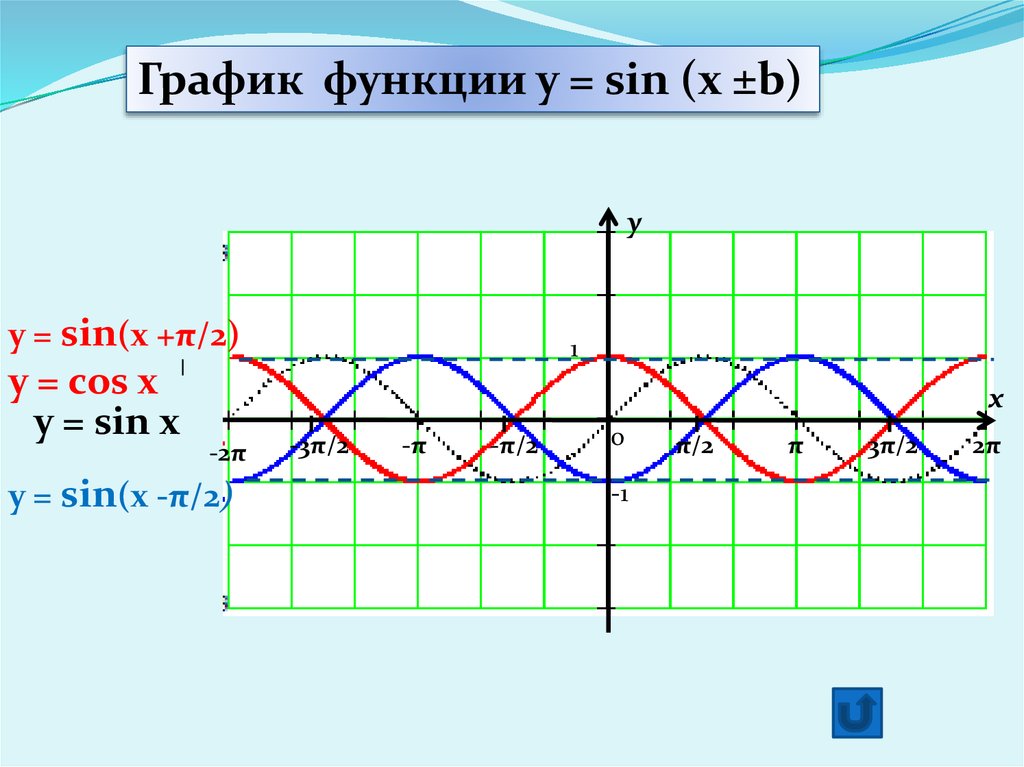
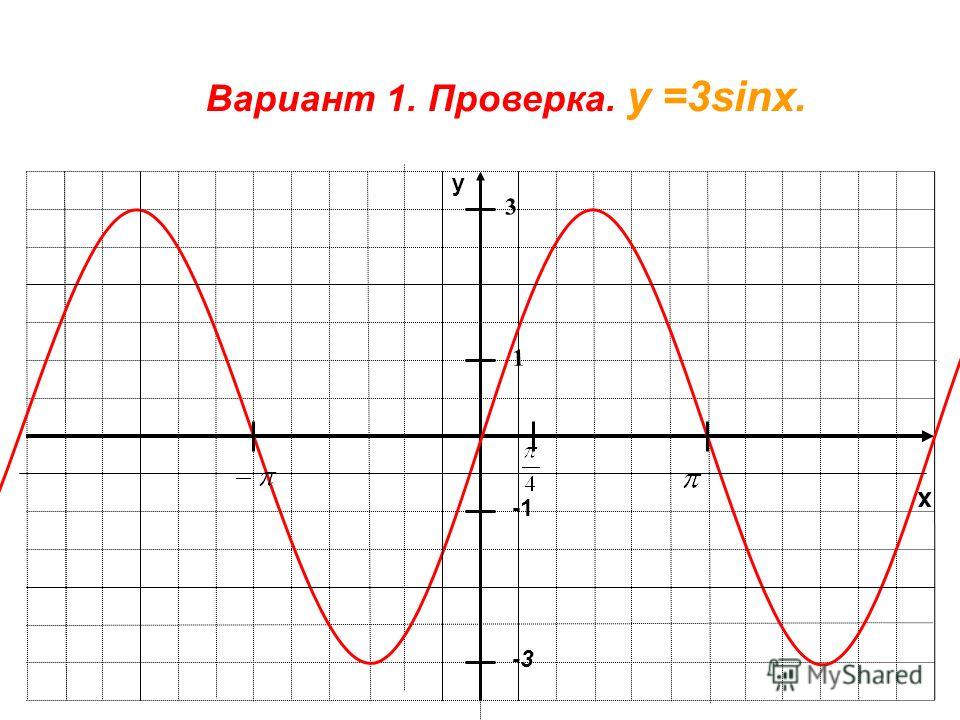
Решить график синуса y sin x 3. Графики функций
На этом уроке мы подробно рассмотрим функцию у = sin х, ее основные свойства и график. В начале урока дадим определение тригонометрической функции у = sin t на координатной окружности и рассмотрим график функции на окружности и прямой. Покажем периодичность этой функции на графике и рассмотрим основные свойства функции. В конце урока решим несколько простейших задач с использованием графика функции и ее свойств.
Тема: Тригонометрические функции
Урок: Функция y=sinx, её основные свойства и график
При рассмотрении функции важно каждому значению аргумента поставить в соответствие единственное значение функции. Этот закон соответствия и называется функцией.
Определим закон соответствия для .
Любому действительному числу соответствует единственная точка на единичной окружности У точки есть единственная ордината, которая и называется синусом числа (рис. 1).
Каждому значению аргумента ставится в соответствие единственное значение функции.
Из определения синуса вытекают очевидные свойства.
На рисунке видно, что т.к. это ордината точки единичной окружности.
Рассмотрим график функции . Вспомним геометрическую интерпретацию аргумента. Аргумент — это центральный угол, измеряемый в радианах. По оси мы будем откладывать действительные числа или углы в радианах, по оси соответствующие значения функции.
Например, угол на единичной окружности соответствует точке на графике (рис. 2)
Мы получили график функции на участке Но зная период синуса мы можем изобразить график функции на всей области определения (рис. 3).
Основным периодом функции является Это значит, что график можно получить на отрезке а затем продолжить на всю область определения.
Рассмотрим свойства функции :
1) Область определения:
2) Область значений:
3) Функция нечетная:
4) Наименьший положительный период:
5) Координаты точек пересечения графика с осью абсцисс:
6) Координаты точки пересечения графика с осью ординат:
7) Промежутки, на которых функция принимает положительные значения:
8) Промежутки, на которых функция принимает отрицательные значения:
9) Промежутки возрастания:
10) Промежутки убывания:
11) Точки минимума:
12) Минимум функции:
13) Точки максимума:
14) Максимум функции:
Мы рассмотрели свойства функции и её график.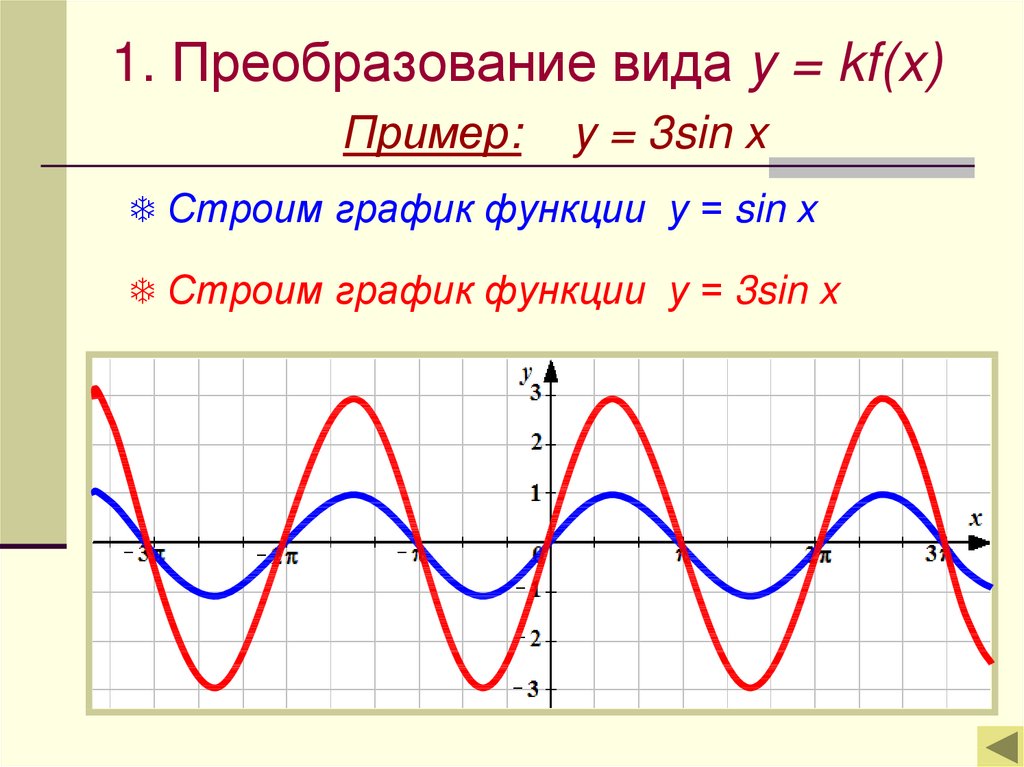 Свойства неоднократно будут использоваться при решении задач.
Свойства неоднократно будут использоваться при решении задач.
Список литературы
1. Алгебра и начала анализа, 10 класс (в двух частях). Учебник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2009.
2. Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред. А. Г. Мордковича. -М.: Мнемозина, 2007.
3. Виленкин Н.Я., Ивашев-Мусатов О.С., Шварцбурд С.И. Алгебра и математический анализ для 10 класса (учебное пособие для учащихся школ и классов с углубленным изучением математики).-М.: Просвещение, 1996.
4. Галицкий М.Л., Мошкович М.М., Шварцбурд С.И. Углубленное изучение алгебры и математического анализа.-М.: Просвещение, 1997.
5. Сборник задач по математике для поступающих во ВТУЗы (под ред. М.И.Сканави).-М.:Высшая школа, 1992.
6. Мерзляк А.Г., Полонский В.Б., Якир М.С. Алгебраический тренажер.-К.: А.С.К., 1997.
7. Саакян С.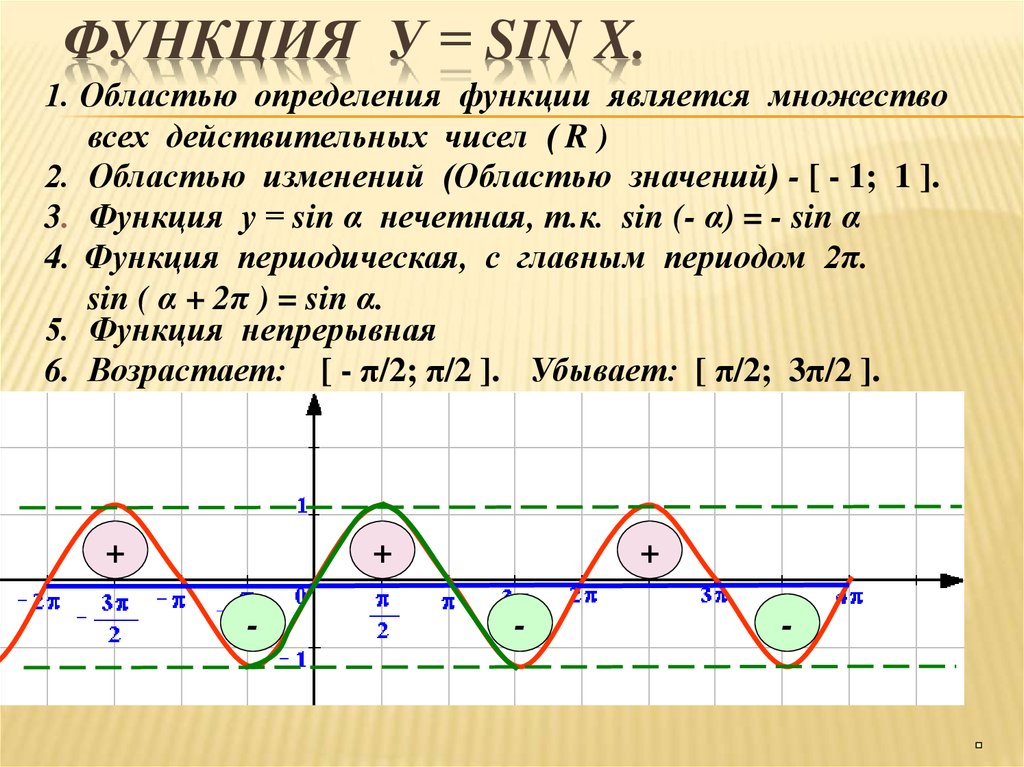 М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
М., Гольдман А.М., Денисов Д.В. Задачи по алгебре и началам анализа (пособие для учащихся 10-11 классов общеобразов. учреждений).-М.: Просвещение, 2003.
8. Карп А.П. Сборник задач по алгебре и началам анализа: учеб. пособие для 10-11 кл. с углубл. изуч. математики.-М.: Просвещение, 2006.
Домашнее задание
Алгебра и начала анализа, 10 класс (в двух частях). Задачник для общеобразовательных учреждений (профильный уровень) под ред.
А. Г. Мордковича. -М.: Мнемозина, 2007.
№№ 16.4, 16.5, 16.8.
Дополнительные веб-ресурсы
3. Образовательный портал для подготовки к экзаменам ().
Х y O Единичная тригонометрическая окружность
3 =180 3,14 рад R R О Р М R Рассмотрим окружность радиуса R. Построим MOP: МР = R 1 радиан Величина МОР равна 1 радиан МР =1рад МОР 57 17= 1рад Радианная мера угла
4 Длина окружности выражается формулой C=2 R, где R – радиус окружности. 3, Окружность, радиус которой равен 1, называется … Точки М,Р,К,N – назовем узловыми. Отметим точки А,В,С. Длину единичной окружности удобно измерять в радианах. Если R=1, то С=2 рад! Наименование радиан обычно опускают. y х К Р С В А Длина дуги половины окружности равна рад. М N рад – четверть длины окружности рад – три четверти длины окружности О 1 единичной Радианная мера угла
uk-badge uk-margin-small-right»>
5 Градусная мера Радианная мера0 Итак, величину угла поворота точки, а также величину дуги единичной окружности, можно задавать: I четверть II четверть III четверть IV четверть О в градусной мере в радианной мере Радианная мера угла 0 2 I четверть II четверть III четверть IV четверть О 2
Отметим точки А,В,С. Длину единичной окружности удобно измерять в радианах. Если R=1, то С=2 рад! Наименование радиан обычно опускают. y х К Р С В А Длина дуги половины окружности равна рад. М N рад – четверть длины окружности рад – три четверти длины окружности О 1 единичной Радианная мера угла
uk-badge uk-margin-small-right»>
5 Градусная мера Радианная мера0 Итак, величину угла поворота точки, а также величину дуги единичной окружности, можно задавать: I четверть II четверть III четверть IV четверть О в градусной мере в радианной мере Радианная мера угла 0 2 I четверть II четверть III четверть IV четверть О 2
6 «Размотаем» окружность как нить на координатный луч с началом в точке 0 Установим соответствие между множеством действительных чисел на числовой прямой и точками единичной окружности. Такое «разматывание» можно продолжать бесконечно. 3,14 0 Построение графика х y=sin x
13 Преобразование графиков Функция Преобразование 1 y= f (x) + mПараллельный перенос вдоль оси OY на m единиц 2 y= f (x – n)Параллельный перенос вдоль оси OX на n единиц 3 y=А f (x) Растяжение вдоль оси OY относительно оси OX в А раз 4 y= f (k x)Сжатие вдоль оси OX относительно оси OY в k раз 5 y= – f (x) Симметричное отражение относительно оси OX 6 y= f (– x) Симметричное отражение относительно оси OY y = f (x)
20 Построим график функции y= 3 sin(2x+ /3)–2 Этапы построения: 1. y= sin x – синусоида 3. y= sin(2x+ /3) – перенос на /3 единиц влево 4. y= 3 sin(2x+ /3) – растяжение в 3 раза вдоль оси Oy 2. y= sin 2x – сжатие в 2 раза вдоль оси Ох 5. y= 3 sin(2x+ /3)–2 – перенос на 2 единицы вниз
y= sin x – синусоида 3. y= sin(2x+ /3) – перенос на /3 единиц влево 4. y= 3 sin(2x+ /3) – растяжение в 3 раза вдоль оси Oy 2. y= sin 2x – сжатие в 2 раза вдоль оси Ох 5. y= 3 sin(2x+ /3)–2 – перенос на 2 единицы вниз
26 Преобразование графиков Функция Преобразование 1 y=sin(kx)Сжатие вдоль оси OX относительно оси OY в k раз 2 y=sin(x–m)Параллельный перенос вдоль оси OX на m единиц 3 y=А sin x Растяжение вдоль оси OY относительно оси OX в А раз 4 y=sin x+nПараллельный перенос вдоль оси OY на n единиц 5 y= – sin x Симметричное отражение относительно оси OX 6 y= sin (–x) Симметричное отражение относительно оси OY y = Asin(kx–n)+m
 Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если
Нули функции (точки пересечения графика функции с осью абсцисс): sinx=0, если x= n. (n Z) Некоторые свойства функции y=sinx sin x= – 1, если sin x=1, если |BD| — длина дуги окружности с центром в точке A .
α — угол, выраженный в радианах.
Синус (sin
α
) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |BC| к длине гипотенузы |AC|.
Косинус (cos
α
) — это тригонометрическая функция, зависящая от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |AB| к длине гипотенузы |AC|.
Принятые обозначения
;
;
.
;
;
.
График функции синус, y = sin x
График функции косинус, y = cos x
Свойства синуса и косинуса
Периодичность
Функции y = sin x и y = cos x периодичны с периодом 2 π .
Четность
Функция синус — нечетная. Функция косинус — четная.
Функция косинус — четная.
Область определения и значений, экстремумы, возрастание, убывание
Функции синус и косинус непрерывны на своей области определения, то есть для всех x (см. доказательство непрерывности). Их основные свойства представлены в таблице (n — целое).
| y = sin x | y = cos x | |
| Область определения и непрерывность | — ∞ | — ∞ |
| Область значений | -1 ≤ y ≤ 1 | |
| Возрастание | ||
| Убывание | ||
| Максимумы, y = 1 | ||
| Минимумы, y = -1 | ||
| Нули, y = 0 | ||
| Точки пересечения с осью ординат, x = 0 | y = 0 | y = 1 |
Основные формулы
Сумма квадратов синуса и косинуса
Формулы синуса и косинуса от суммы и разности
;
;
Формулы произведения синусов и косинусов
Формулы суммы и разности
Выражение синуса через косинус
;
;
;
.
Выражение косинуса через синус
;
;
;
.
Выражение через тангенс
; .
При ,
имеем:
;
.
При :
;
.
Таблица синусов и косинусов, тангенсов и котангенсов
В данной таблице представлены значения синусов и косинусов при некоторых значениях аргумента.
Выражения через комплексные переменные
;
Формула Эйлера
Выражения через гиперболические функции
;
;
Производные
; . Вывод формул > > >
Производные n-го порядка:
{ -∞
Секанс, косеканс
Обратные функции
Обратными функциями к синусу и косинусу являются арксинус и арккосинус , соответственно.
Арксинус, arcsin
Арккосинус, arccos
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
См. также:
ГРАФИКИ ФУНКЦИЙ
Функция синус
— множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. синус функция — ограниченная .
Функция нечетная: sin(−x)=−sin x для всех х ∈ R .
Функция периодическая
sin(x+2π· k) = sin x, где k ∈ Z для всех х ∈ R .
sin x = 0 при x = π·k , k ∈ Z .
sin x > 0 (положительная) для всех x ∈ (2π·k , π+2π·k ), k ∈ Z .
sin x (отрицательная) для всех x ∈ (π+2π·k , 2π+2π·k ), k ∈ Z .
Функция косинус
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок [-1; 1], т.е. косинус функция — ограниченная .
Функция четная:
Функция периодическая с наименьшим положительным периодом 2π :
cos(x+2π· k ) = cos x, где k ∈ Z для всех х ∈ R .
| cos x = 0 при | |
| cos x > 0 для всех | |
| cos x для всех | |
| Функция возрастает от −1 до 1 на промежутках: | |
| Функция убывает от −1 до 1 на промежутках: | |
| Наибольшее значение функции sin x = 1 в точках: | |
| Наименьшее значение функции sin x = −1 в точках: |
Множество значений функции — вся числовая прямая, т.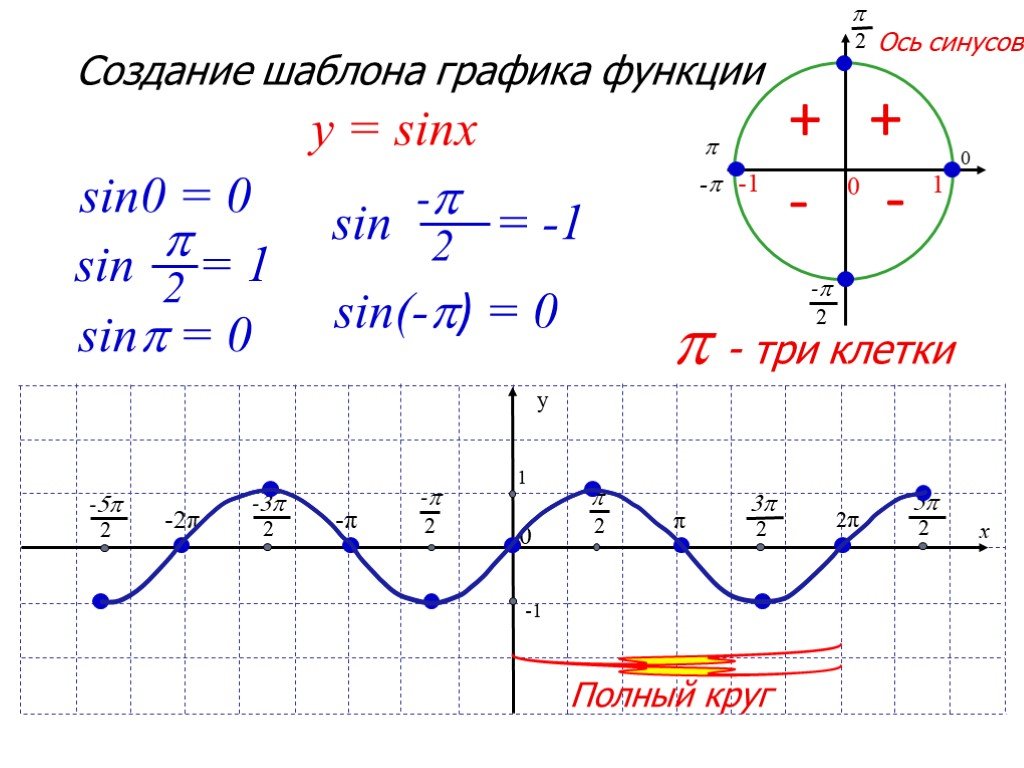 е. тангенс — функция неограниченная .
е. тангенс — функция неограниченная .
Функция нечетная: tg(−x)=−tg x
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом π , т.е. tg(x+π· k ) = tg x, k ∈ Z для всех х из области определения.
Функция котангенс
Множество значений функции — вся числовая прямая, т.е. котангенс — функция неограниченная .
Функция нечетная: ctg(−x)=−ctg x для всех х из области определения.
График функции симметричен относительно оси OY.
Функция периодическая с наименьшим положительным периодом π , т.е. ctg(x+π· k )=ctg x, k ∈ Z для всех х из области определения.
Функция арксинус
Область определения функции — отрезок [-1; 1]
Множество значений функции — отрезок -π
/2 arcsin x π
/2, т.е. арксинус — функция ограниченная .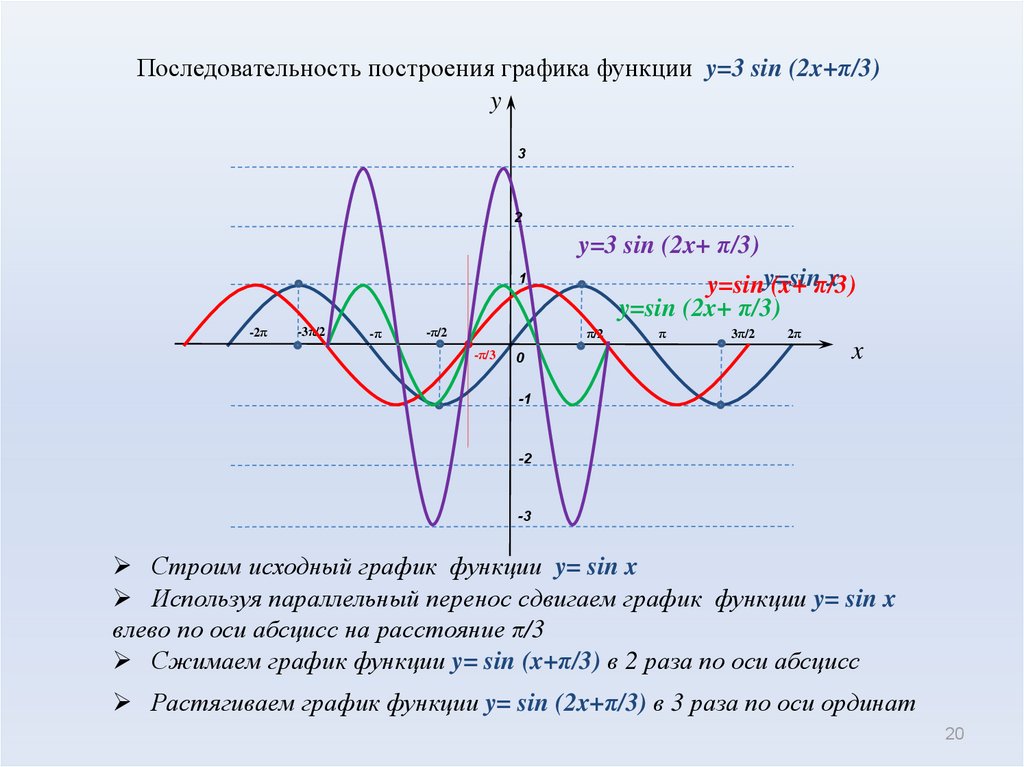
Функция нечетная: arcsin(−x)=−arcsin x для всех х ∈ R .
График функции симметричен относительно начала координат.
На всей области определения.
Функция арккосинус
Область определения функции — отрезок [-1; 1]
Множество значений функции — отрезок 0 arccos x π , т.е. арккосинус — функция ограниченная .
Функция является возрастающей на всей области определения.
Функция арктангенс
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок 0 π, т.е. арктангенс — функция ограниченная .
Функция нечетная: arctg(−x)=−arctg x для всех х ∈ R .
График функции симметричен относительно начала координат.
Функция является возрастающей на всей области определения.
Функция арккотангенс
Область определения функции — множество R всех действительных чисел.
Множество значений функции — отрезок 0 π, т.е. арккотангенс — функция ограниченная .
Функция не является ни четной, ни нечетной.
График функции несимметричен ни относительно начала координат, ни относительно оси Оy.
Функция является убывающей на всей области определения.
, Конкурс «Презентация к уроку»
Презентация к уроку
Назад
Вперёд
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Железо ржавеет, не находя себе применения,
стоячая вода гниет или на холоде замерзает,
а ум человека, не находя себе применения, чахнет.
Леонардо да Винчи
Используемые технологии: проблемного
обучения, критического мышления,
коммуникативного общения.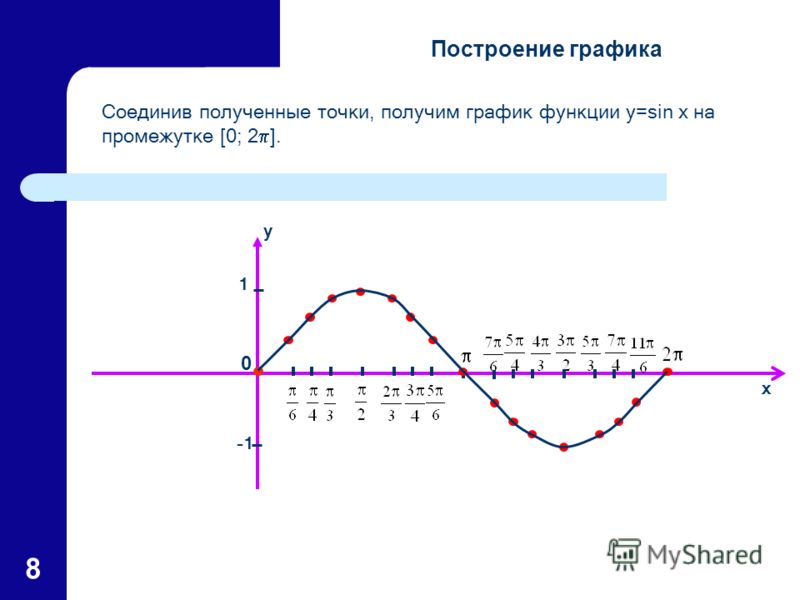
Цели:
- Развитие познавательного интереса к обучению.
- Изучение свойств функции у = sin x.
- Формирование практических навыков построения графика функции у = sin x на основе изученного теоретического материала.
Задачи:
1. Использовать имеющийся потенциал знаний о свойствах функции у = sin x в конкретных ситуациях.
2. Применять осознанное установление связей между аналитической и геометрической моделями функции у = sin x.
Развивать инициативу, определенную готовность и интерес к поиску решения; умение принимать решения, не останавливаться на достигнутом, отстаивать свою точку зрения.
Воспитывать у учащихся познавательную активность, чувство ответственности, уважения друг к другу, взаимопонимания, взаимоподдержки, уверенности в себе; культуру общения.
Ход урока
1 этап. Актуализация опорных знаний, мотивация изучения нового материала
«Вход в урок».
На доске написаны 3 утверждения:
- Тригонометрическое уравнение sin t = a всегда
имеет решения.

- График нечетной функции можно построить с помощью преобразования симметрии относительно оси Оу.
- График тригонометрической функции можно построить, используя одну главную полуволну.
Учащиеся обсуждают в парах: верны ли утверждения? (1 минута). Затем результаты первоначального обсуждения (да, нет) вносятся в таблицу в столбец «До».
Учитель ставит цели и задачи урока.
2. Актуализация знаний (фронтально на модели тригонометрического круга ).
Мы уже познакомились с функцией s = sin t.
1) Какие значения может принимать переменная t. Какова область определения этой функции?
2) В каком промежутке заключены значения выражения sin t. Найти наибольшее и наименьшее значения функции s = sin t.
3) Решите уравнение sin t = 0.
4) Что происходит с ординатой точки при ее
движении по первой четверти? (ордината
увеличивается). Что происходит с ординатой точки
при ее движении по второй четверти? (ордината
постепенно уменьшается).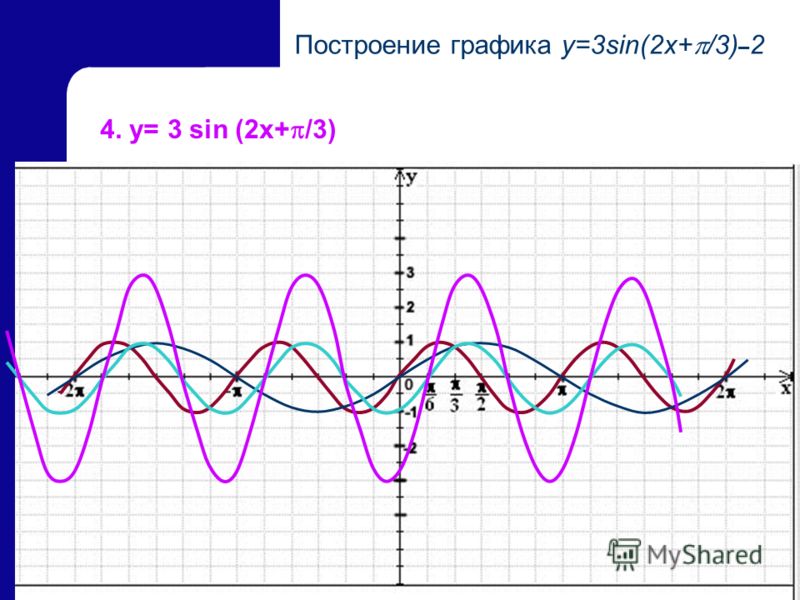 Как это связано с
монотонностью функции? (функция s = sin t возрастает
на отрезке и
убывает на отрезке ).
Как это связано с
монотонностью функции? (функция s = sin t возрастает
на отрезке и
убывает на отрезке ).
5) Запишем функцию s = sin t в привычном для нас виде у = sin x (строить будем в привычной системе координат хОу) и составим таблицу значений этой функции.
| х | 0 | ||||||
| у | 0 | 1 | 0 |
2 этап. Восприятие, осмысление, первичное закрепление, непроизвольное запоминание
4 этап. Первичная систематизация знаний и способов деятельности, их перенос и применение в новых ситуациях
6. № 10.18 (б,в)
№ 10.18 (б,в)
5 этап. Итоговый контроль, коррекция, оценка и самооценка
7. Возвращаемся к утверждениям (начало урока), обсуждаем, используя свойства тригонометрической функции у = sin x, и заполняем в таблице столбец «После».
8. Д/з: п.10, №№ 10.7(а), 10.8(б), 10.11(б), 10.16(а)
Ответы | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
Алла на 6 лет моложе Веры. Сейчас папа в 11 раз старше Аллы и на 24 года старше Веры. Через сколько лет папа будет в 3 раза старше Веры?
Сейчас папа в 11 раз старше Аллы и на 24 года старше Веры. Через сколько лет папа будет в 3 раза старше Веры?
Медиана равностороннего треугольника равна 13√3.Найдите его сторону. Решение плиз
Решено
Помогите пожалуйста решить задачу 4-го класса. Если около каждого дома посадить по 9 саженцев, то не зватит 100 саженцев, а если по 5 саженцев, то 20 саженцев останется. Сколько домов? Сколько
Какое количество теплоты выделится при кристаллизации и охлаждении 1,5 кг цынка до температуры 20с?
Решено
Во дворе бегали кошки и циплята. всего 14 голов и 38 лапок. сколько бегало кошек и сколько циплят?
Пользуйтесь нашим приложением
преобразований sin-графа
Мы собираемся изучить графики
y = a sin(bx + c) для различных значений a, b и c и изучить влияние каждого из этих параметров.
Прежде чем я попрошу студентов изучить преобразования синусоидального графика, я попрошу их изучить преобразования функции для обзора.
Обзор: Нарисуйте график следующих функций и запишите свои наблюдения для каждой из них.
Для этого исследования я бы порекомендовал учащимся использовать какую-либо программу графического калькулятора. Я буду использовать программное обеспечение Graphing Calculator 4.0. Студенты могут использовать графические калькуляторы, но эти преобразования гораздо легче увидеть на экране компьютера. Function Flyer — это бесплатный апплет от Shodor, который также могут использовать студенты. Этот апплет доступен по адресу http://www.shodor.org/interactivate/activities/FunctionFlyer/
. Кроме того, этот апплет называется Math Flyer в App Store и доступен по цене 0,9 доллара США.9. Преподаватель потенциально может предложить своим ученикам выполнить это исследование с помощью своих смартфонов.
Мы хотим изучить графики
y = a sin(bx + c) и влияние параметров a, b и c.К этому моменту учащиеся должны знать, как выглядит график y = sin(x).
Фиолетовая кривая — это график синусоиды.
Красная кривая — трансформация.у = 2 sin(x)
у = ½ sin(x)
Обратите внимание, что минимальное и максимальное значения функции увеличились с -1 и 1 до -2 и 2.
Обратите внимание, что минимальное и максимальное значения функции уменьшились с -1 и 1 до -1/2 и 1/2.
Эти графики представляют изменения амплитуды.Абсолютное значение параметра a представляет собой амплитуду графика.
= Амплитуда
Для дальнейшего исследования попросите учащихся изучить преобразования, когда a
< 0.
Из наших знаний об единичной окружности мы знаем, что период y = sin(x) равен 2π. Функция синуса начинает повторяться каждые 2π единиц. Таким образом, он завершает один цикл от 0 до 2π, другой от 2π до 4π и т. д.
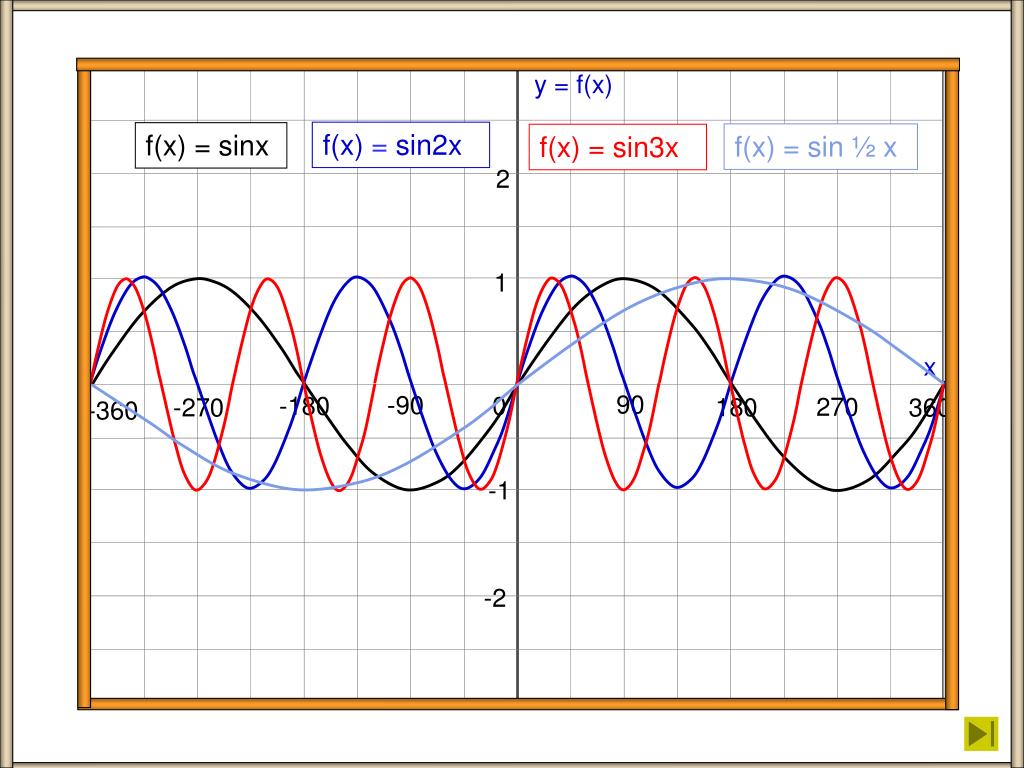
у = грех(2х)
График y = sin(2x) выглядит так, будто его сжали с боков, как пружину.
Мы можем видеть, что y=sin(2x) совершает два цикла в интервале от 0 до 2π вместо одного.у = sin(½x)
График y = sin(½x) выглядит так, как будто он растянут с боков.
Мы видим, что y = sin(½x) завершает половину цикла в интервале от 0 до 2π вместо одного.Параметр b относится к периоду синусоиды. Итак, период синусоиды равен (2π/b)
Обратите внимание на приведенную выше анимацию: по мере увеличения значения b от 0 до 5 график сжимается, а период синусоиды уменьшается.
Обратите внимание на приведенную выше анимацию: по мере уменьшения значения b от 0 до -5 график растягивается, а период синусоиды увеличивается.Что происходит с периодом функции, когда b
< 0? Как вы думаете, как будут выглядеть графики функции y = sin(5x) и y = sin(-5x)?
у = грех(х + 2)
y = sin(x — 2)
Обратите внимание, что на графике y = sin(x + 2) синусоида сдвинута на две единицы влево.На графике y = sin(x — 2) синусоида сместилась вправо на две единицы.
Эти преобразования часто называют горизонтальными или фазовыми сдвигами.
Параметр c представляет фазовый сдвиг (также называемый сдвигом средней линии).
Я считаю, что проще сначала изменить период, но нет определенного порядка, в котором эти преобразования должны выполняться.
b = 4, поэтому период функции равен (2π/4) = (1/2π). у = грех(4х)
Теперь давайте возьмем график выше и выполним фазовый сдвиг.c = -1, поэтому график сместился вправо на 1. y = sin(4x -1)
Наконец, давайте учтем изменение амплитуды.
a = 3, поэтому минимальное и максимальное значения равны -3 и 3. y = 3 sin(4x -1)
Следовательно, мы изобразили y = 3 sin(4x -1).
Для дальнейшего исследования попросите учащихся сделать еще один шаг и предсказать влияние параметра d на графике y = a sin(bx + c) + d
Нажмите здесь, чтобы вернуться на домашнюю страницу Лейси
Математическая сцена — Правила тригонометрии
Математическая сцена — Правила тригонометрии — Урок 3| 2008 Расмус Эф и Джанн Сак | Триггерные правила |
Урок 3
Уравнения типа a sin x + b cos x = c
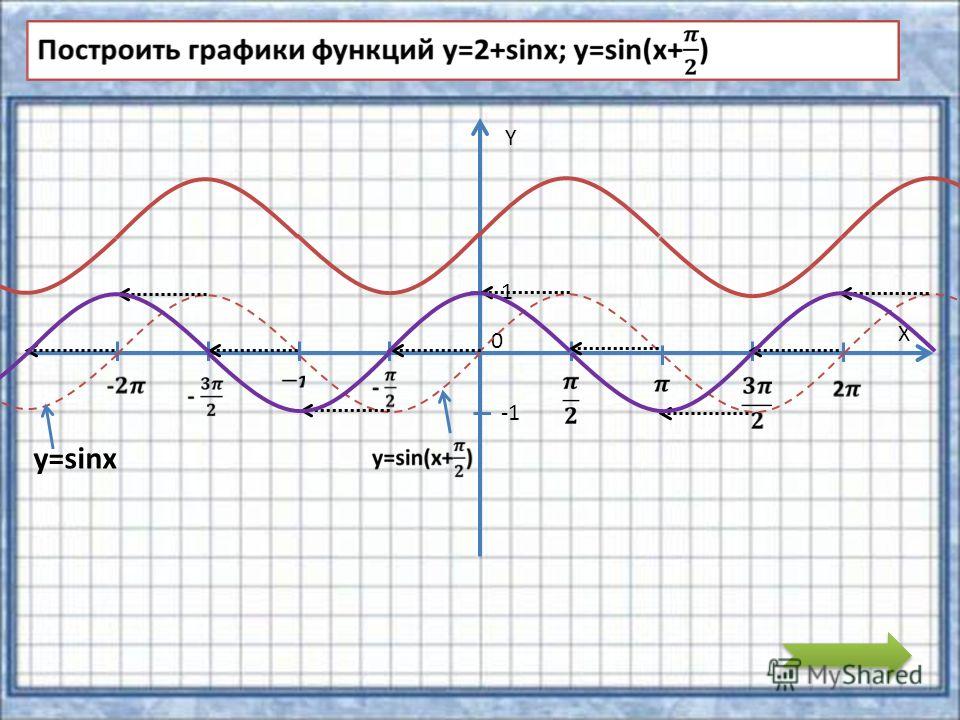
На диаграмме показан график функции f(x) = грех х + 2 потому что х.
Удивительно похоже на обычную синусоиду
который был переведен в одну сторону и с амплитудой, превышающей
что основной волны. Мы уже видели, что влияет на амплитуду
и как можно увеличить амплитуду от значения 1 путем умножения на a
константа больше 1.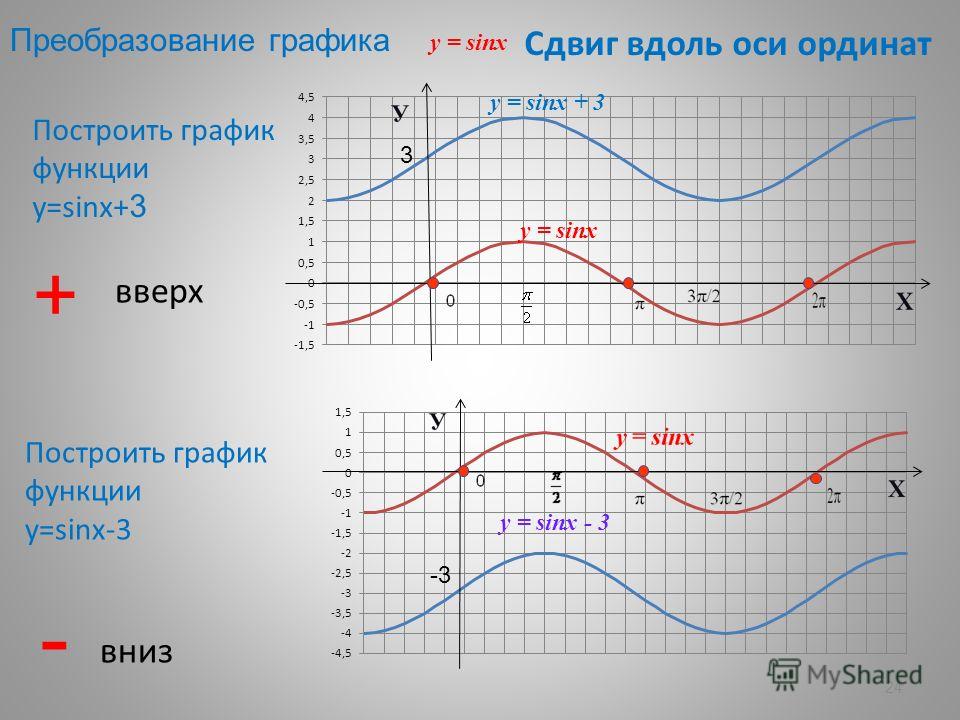 (см. триггерные функции, урок 3). Мы также видели, что график основного
функцию можно перевести по горизонтали, добавив константу к углу. С
это разум, мы должны быть в состоянии переписать наше уравнение в форме m sin (x +
v), такой, что
(см. триггерные функции, урок 3). Мы также видели, что график основного
функцию можно перевести по горизонтали, добавив константу к углу. С
это разум, мы должны быть в состоянии переписать наше уравнение в форме m sin (x +
v), такой, что
м грех (х + v) = грех х + 2 cos х
Теперь посмотрите на график g(x) = sin x − 2 потому что х.
Очевидно, это та же самая кривая, за исключением тот факт, что перевод теперь в направлении, противоположном предыдущему, сдвинута вправо на ту же длину, на которую была сдвинута предыдущая кривая Слева. В этом случае мы должны быть в состоянии составить эквивалентное уравнение.
м грех (х — v) = грех х — 2 потому что х
Теперь перепишем эти выражения, используя формула сложения:
грех (x + v) = sin x cos v + cos x sin v
грех (x — v) = sin x cos v — cos x sin v
Умножая на m получаем:
м sin (x + v) = m sin x cos v + m cos x sin v
м грех (x — v) = m sin x cos v — m cos x sin v
Сравните результат с исходным уравнением.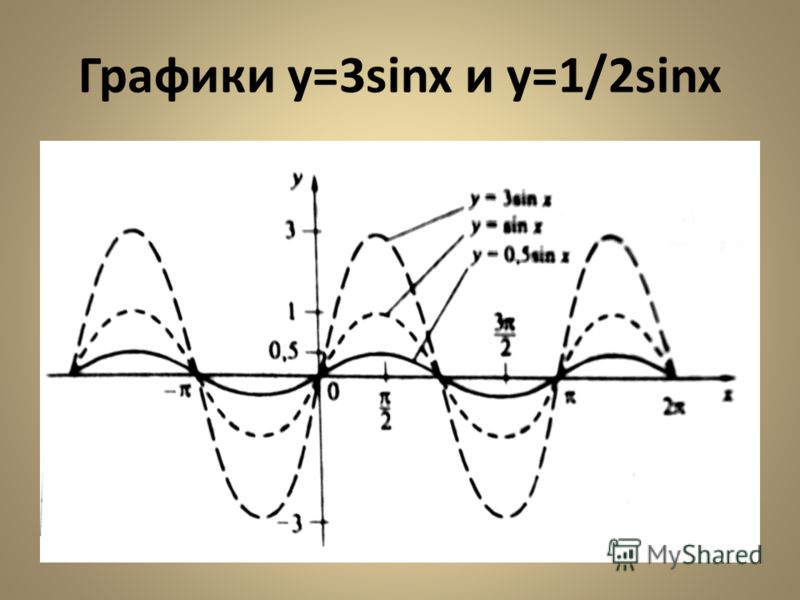
м sin (x + v) = 1 sin x + 2 cos x
= m cos v sin x + m sin v cos x
м грех (х — v) = 1 грех х — 2 потому что х
= m cos v sin x − m sin v cos x
Мы видим, что в обоих случаях должно быть правда:
м потому что v = 1
м sin v = 2
Если мы разделим нижнее уравнение на верхнее, мы получить следующее:
желтовато-коричневый v = 2 / 1
Что дает угол v = tan −1 (2) ≈ 63,4°.
Если мы нарисуем прямоугольный треугольник с более короткие стороны1 и 2, те же значения, что и в уравнении, то мы можем вычислить длину гипотенузы и увидеть, что:
cos v = 1 / и sin v = 2 /.
Использование уравнений
м потому что v = 1
m sin v = 2,
Дает нам это:
м1 / = 1
м =
Другими словами, мы можем переписать уравнение как:
Мы видим, что амплитуда волны в
функции
f (x) = sin x + 2, потому что x и g (x) = sin x — 2, потому что x есть .
Обобщение и использование a и b для констант
получаем следующее правило:
Угол v можно найти с помощью:
| тангенс v = б / а где а > 0, b > 0 и 0° < v°< 90° |
Пример 1
Найдите амплитуду функция f(x) = 3 sin x + 4 cos x.
Начнем с перезаписи функция.
Амплитуда 5.
Пример 2
График функции f(x) = 3 sin x + 4 cos x — преобразованная синусоида. Рассчитать по на сколько градусов и в каком направлении была переведена волна.
f(x) = 3 sin x + 4 cos x
= 5 sin (x + v)
v = tan −1 ( 4 / 3 ) ≈ 53,1°
Волна переведена
на 53,1° влево
(f(x) ≈ 5 sin (x + 53,1°).
Пример 3
Учитывая функцию f(x) = 5
sin x + 12 cos x + 3.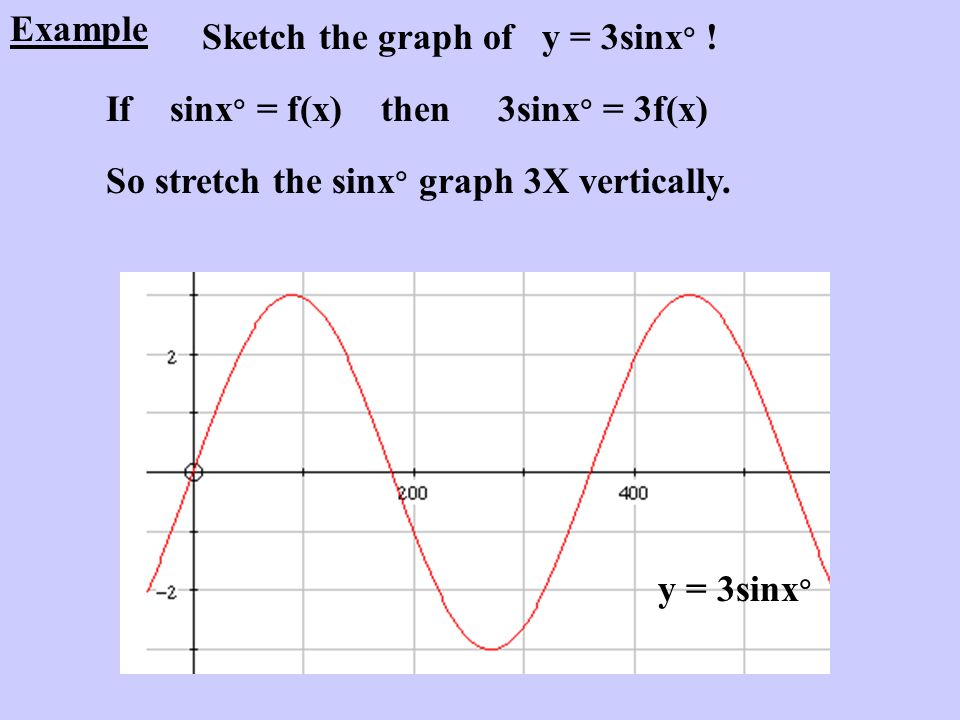 Найдите амплитуду, максимальную высоту и перевод
волны.
Найдите амплитуду, максимальную высоту и перевод
волны.
Переписать f(x).
тангенс −1 (12/5) ≈ 67,4°
f(x) = 13 sin (x + 67,4°) + 3
Амплитуда равна 13 , поэтому максимальная высота 13 + 3 = 16. Посмотрите на график.
Пример 4
Решите уравнение 3 sin x + 4 cos x = 5 на
интервал
0° x < 360°.
3 sin x + 4 cos x = 5
= 5 sin (x + 53,1°)
sin (x + 53,1°) = 5 / 5 = 1
x + 53,1° = sin −1 1 = 90 + k360°
x = −53,1 + 90 + k360°
х = 36,9°
Это дает одно решение 36,9° в первом квадранте.
Интересно посмотреть на график. Мы видим другого решения на искомом интервале нет.
Пример 5
Найти все решения
уравнение грех х — 3 потому что х знак равно 1 .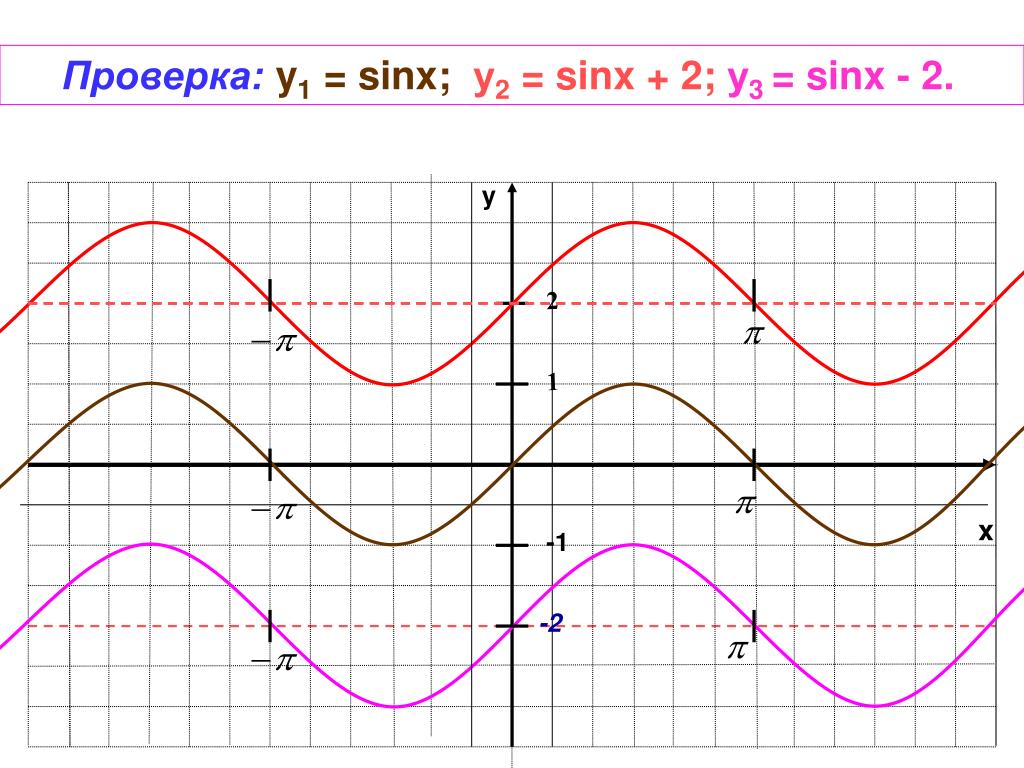

 12.17
12.17