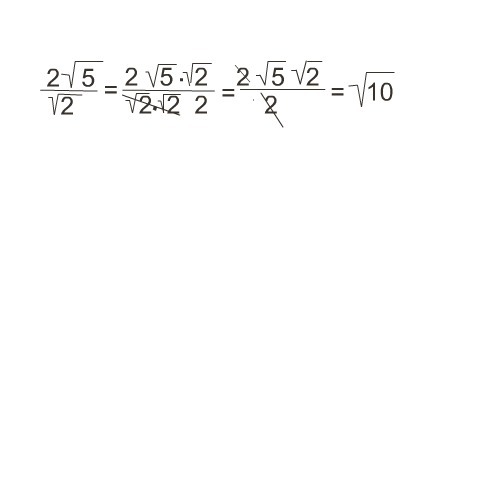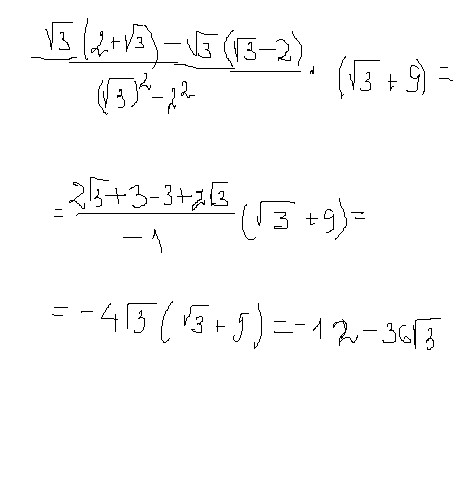2 корня из 3 делить на корень из 3 — Знания.site
Последние вопросы
Алгебра
7 минут назад
После приведения подобных слагаемых 9,9m +g+g-29,06м получаем + (выбери правильный ответ): -19,16m² + 2g2 + другой ответ -19,16m + 2g 2 -19,16m + g O -19,16m² + g2Алгебра
1 час назад
\х-5\ в квадр+5\2х-1\=0 розвьязати ривнянняАлгебра
1 час назад
Знайти значення аргументу, при якому функція у=0,5х-1 дорівнюватиме 7Алгебра
1 час назад
Обчисліть значення функції у = -7x +10 для значення аргументу, що дорівнює — 1.
Алгебра
1 час назад
Чому дорівнює неповний квадрат різниці виразів х і Зy?СРОЧНО!!!!!!!!!!!! 30 БАЛОВ Алгебра
1 час назад
7, спростити вираз:(√7+√5)²-12=Алгебра
1 час назад
3. [5 баллов) Дана функция f(x) = x² — 8x + 12. а) Запишите уравнение оси симметрии графика данной функции. б) В какой точки график данной функции пересекает ось ОХ? в) Найдите точки пересечения графика функции с осью OY. г) Постройте график функции.-
Алгебра
1 час назад
Помогите!! Желательно показать решение, и в конце ответ. Функция задана формулой f(x) = -x2 + 4. Найти f (1).
Функция задана формулой f(x) = -x2 + 4. Найти f (1). Алгебра
1 час назад
3. Знайдіть значення виразу: A) 7a² — 7b², якщо a=101; b=99Б) 14x²-28xy+14у², якщо x=57, y=53.Алгебра
1 час назад
Представьте в виде многочленовАлгебра
2 часа назад
5, звільнитися від ірраціональності у знаменнику дробу: \frac{ \\ 48}{ \\ \sqrt{6} } Алгебра
2 часа назад
Доведіть тотожності/докажите тождества: tga/tga+ctga=sin^2 a \frac{tga}{tga+ctga}=sin^{2} aАлгебра
2 часа назад
Знайдіть двоцифрове число, яке в 4 рази більше за суму його цифр і в 2 рази більше від добутку його цифр.
Алгебра
2 часа назад
Внушают в украине учись it будеш в сша получать 10тыщ, но им необъяснили что большинство неспособны выучиться выше чем-Алгебра
2 часа назад
4. Знайти значення добутку: √27.√3 = пж
Все предметы
Выберите язык и регион
English
United States
Polski
Polska
Português
Brasil
English
India
Türkçe
Türkiye
English
Philippines
Español
España
Bahasa Indonesia
Indonesia
Русский
Россия
How much to ban the user?
1 hour 1 day 100 years
Как найти корень 2? – Обзоры Вики
Квадратный корень из 2 равен 1. 414. Следовательно, 17 √2 = 17 × 1.414 = 24.042.
414. Следовательно, 17 √2 = 17 × 1.414 = 24.042.
Следовательно, каков ответ 2 корня 2? Значение 2√2 равно 2.828. Следовательно, 2√2 = 2(1.414) = 2.828.
Где корень из 3? Квадратный корень из 3 равен 1.732.
Дополнительно Что такое значение корня? Квадратный корень из числа b является решением уравнения x2 = b . Это число, которое при умножении само на себя дает b. Каждое положительное число b имеет два квадратных корня, обозначаемых √b и −√b. Главный квадратный корень из b — это положительный квадратный корень, обозначаемый √b.
Почему √ 2 иррациональное число? В частности, греки обнаружили, что диагональ квадрата со стороной в 1 единицу имеет диагональ, длина которой не может быть рациональной. По теореме Пифагора длина диагонали равна квадратному корню из 2. Итак, квадратный корень из 2 иррационален!
Что такое 3 Корень 2 Целый квадрат?
Значение (3√2)² равно 18.
Что означает 2 Root 3? Ответ 12.
Является ли √ 2 рациональным числом? Сал доказывает, что квадратный корень из 2 равен иррациональное число, т. е. не может быть задано как отношение двух целых чисел.
е. не может быть задано как отношение двух целых чисел.
Что такое квадрат 3 2?
Ответ и объяснение: В виде дроби квадратный корень из 3/2 может быть выражен как √1.51 или просто как √1.5 .
Также Что такое квадрат 2? Список идеальных квадратов
| НОМЕР | ПЛОЩАДЬ | КВАДРАТНЫЙ КОРЕНЬ |
|---|---|---|
| 2 | 4 | 1.414 |
| 3 | 9 | 1.732 |
| 4 | 16 | 2.000 |
| 5 | 25 | 2.236 |
• 17 ноября 2021 г.
√ 3 — иррациональное число?
Квадратный корень из 3 — это положительное действительное число, которое при умножении само на себя дает число 3. … Квадратный корень из 3 это иррациональное число. Она также известна как константа Феодора в честь Феодора из Кирены, доказавшего ее иррациональность.
Я в квадрате 1? Символ i был определен как мнимое число что при возведении в квадрат дает -1. Это определение не должно нарушаться.
Это определение не должно нарушаться.
Как найти значение 1 корень 2?
Значение единицы при корне 2 равно 0.707.
Является ли ноль рациональным числом?
Почему 0 — рациональное число? Это рациональное выражение доказывает, что 0 — рациональное число, потому что любое число может быть разделено на 0 и равно 0. Дробь r / s показывает, что когда 0 делится на целое число, получается бесконечность. Бесконечность не является целым числом, потому что ее нельзя выразить в дробной форме.
Является ли корень 3 простым? √3 не простое число.
Как преобразовать 3 2 в root? Ответ: 33/2 в радикальной форме √33 = √27. Давайте решим это шаг за шагом.
Каков ответ корня 3 2?
Квадратный корень из 5. Квадратный корень из 6. Квадратный корень от 1 до 25.
…
Таблица квадратного корня.
| Число | Квадратный корень (√) |
|---|---|
| 2 | 1. 414 414 |
| 3 | 1.732 |
| 4 | 2.000 |
| 5 | 2.236 |
• 4 июня 2020 г.
Чему равен кубический корень из 54 в упрощенном виде? Простая факторизация числа 54 равна 2 × 3 × 3 × 3, следовательно, кубический корень из 54 в его низшей радикальной форме выражается как 3 ∛2 .
…
Кубический корень 54.
| 1. | Что такое кубический корень из 54? |
|---|---|
| 3. | Является ли кубический корень из 54 иррациональным? |
| 4. | Часто задаваемые вопросы о Cube Root of 54 |
Что такое 2 корень 3 упрощенный?
хотя это не может быть упрощением, 2√3 можно представить как √12 .
Каково значение 2 корня 3 корня 3? Это пример сложения двух иррациональных чисел. Следовательно, 2√3 + √3 равно 3√3.
Что такое root4?
Значение корня 4 равно равно ровно 2.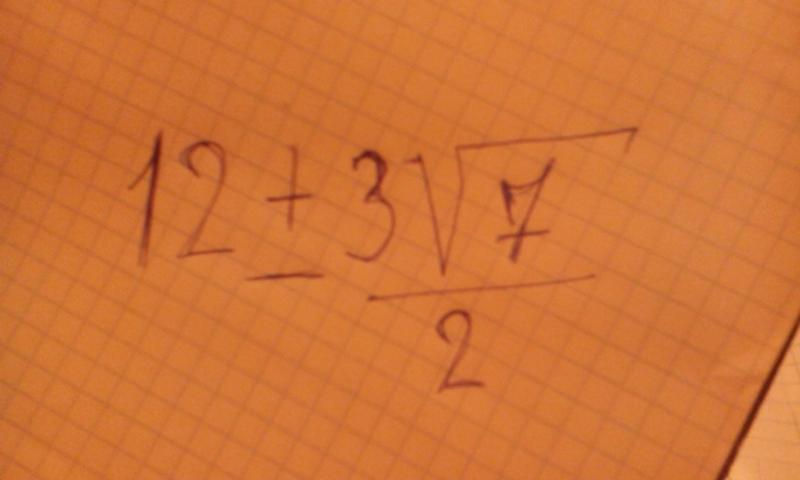 Но корни могут быть положительными или отрицательными, или мы можем сказать, что у любого заданного числа всегда есть два корня. Следовательно, корень 4 равен ±2 или +2 и -2 (положительное 2 и отрицательное 2). Вы также можете найти квадратный корень на калькуляторе.
Но корни могут быть положительными или отрицательными, или мы можем сказать, что у любого заданного числа всегда есть два корня. Следовательно, корень 4 равен ±2 или +2 и -2 (положительное 2 и отрицательное 2). Вы также можете найти квадратный корень на калькуляторе.
Является ли √ 2 иррациональным числом? √2 — это иррациональное число.
Кто доказал, что Root 2 иррационален?
Доказательство иррациональности корня 2 часто приписывают Гиппас метапонта, член пифагорейского культа. Говорят, что он был убит за свое открытие (хотя исторические свидетельства довольно туманны), поскольку пифагорейцам не нравилась идея иррациональных чисел.
Архимед и квадратный корень из 3 |
|
Один из наиболее часто
обсуждаемые вопросы истории математики — это «загадочные»
приближение , использованное Архимедом в его
расчет с. |
|
Казалось бы… у [Архимеда] было немного (в настоящее время неизвестно) метод извлечения квадратного корня из чисел примерно. |
WW Rouse Ball, Короткий Отчет об истории математики , 1908 |
|
…расчет [p] начинается от большего и меньшего предела до значения , который Архимед
принимается без замечаний как известное, а именно (265/153) < < (1351/780). Как
Архимед пришел к этому конкретному приближению? Ни одна головоломка не выполнялась
большее увлечение писателей, интересующихся историей математики...
Самое простое предположение, безусловно [см. Клайн ниже]. Другой
предположение... заключается в том, что последовательные решения в целых числах уравнений x 2 -3y 2 =1 и x 2 -3y 2 =-2 могли быть найдены. |
Т. Хит, История Греческая математика , 1921 |
|
…он же дал методы приближения к квадрату корни, которые показывают, что он предвосхитил изобретение индусами того, что представляют собой периодические цепные дроби. |
ET Bell, Мужчины Математика , 1937 |
Его метод вычисления квадратных корней был похож на которым пользовались вавилоняне. |
CB Boyer, История Математика , 1968 |
|
Он также получил отличное приближение к , а именно
(1351/780) > >
(265/153), но не объясняет, как он получил этот результат. |
М. Клайн, математический Мысль от древности до современности , 1972 |
|
Архимед приблизился к немного меньше значение 265/153… Как он ухитрился извлекать свои квадратные корни с такими точность… это одна из загадок, которые этот выдающийся человек завещал нам. |
П. Бекманн, История р , 1977 |
|
Архимед. |
Сондхеймер и Роджерсон, номеров и Инфинити , 1981 |
|
Клайн не указывает первоначальная оценка и не касается распространения значений, производимых предложенный им метод (удвоение числа верхних и нижних границ на каждом шаг). И Бойер, и Зондхеймер ссылаются на «вавилонский метод». извлечения квадратных корней, причем Бойер заявил, что метод Архимеда был похоже, в то время как Зондхеймер предполагает, что из-за примитивной системы счисления использовавшейся греками, у Архимеда возникли бы трудности со сложным дроби, задействованные в вавилонском методе. |
Оба автора описывают
«Вавилонский метод» (также называемый методом Ньютона) заключается в следующем: найти , возьми 1 как первое приближение. |
|
|
|
Однако, похоже, некоторая путаница в обсуждении Бойером приближения для , используемого вавилоняне. Значение, которое он приводит из древневавилонской таблички № 7289 от коллекция Йельского университета интерпретируется как число, выраженное в основе 60, показано ниже: |
|
|
|
|
, который записывается как
1;24,51,10. Бойер говорит, что это значение приблизительно равно 1,414222, что отличается от
от истинного по
о (8.4)10 -6 .
проблема в том, что шестидесятеричное значение 1;24;51;10 на самом деле соответствует
десятичное число 1,4142129 (как правильно указал Зондхеймер), что отличается от
правда по
(5,99)10 -7 . |
|
В любом случае вроде понятно
что какой бы точный метод ни использовался, он был связан с продолжающимся
расширение дроби , что конечно тесно
связано с уравнением Пелла x 2 —
3y 2 = 1. |
|
Один из возможных методов, который может
использовалась греками, заключается в следующем: квадратный корень из А может быть
разбить на целую часть и остаток, т. е. = N + r, где N —
наибольшее целое число такое, что N 2 меньше, чем A. |
|
|
|
Легко видеть, что значение (A-N 2 )(s n /s n+1 ) приближается к r, когда n стремится к бесконечности. Это форма так называемого «лестничная арифметика», некоторые примеры которой из древней Вавилонии выжили. Например, чтобы найти , мы имеем A = 3 и N = 1, поэтому рекуррентная формула просто s n = 2s n -1 + 2s n -2 . Если мы выберем начальные значения s 0 = 0 и s 1 = 1, последующие значения в последовательность |
|
|
|
Последовательные термины 18272
и 49920 дают r = 571/780, что дает = 1 + r = 1351/780, Архимеда
верхняя граница. |
|
|
|
Однако, если бы они использовали это метода, непонятно, почему они не выбрали нижнюю границу 989/571 на основе на 6688 и 18272. Таким образом, хотя этот метод, безусловно, был в их способность, вряд ли она была источником Архимеда. ценности. |
|
На мой взгляд, наиболее правдоподобный
источником верхней и нижней границ Архимеда является простая дробно-линейная итерация. |
|
|
|
Таким образом, ошибка сбрасывается и уменьшается почти в 52 раза на каждом шаге. Начиная с x = 5/3, последовательность итераций x → (5x+9)/(3x+5) равна |
|
|
|
что дает архимедову
нижняя и верхняя границы по мере 2-й и 3-й итераций. |
|
Для обсуждения того, как Архимед использовал его значение для оценки значения PI, см. обратите внимание на Архимеда и Годфри. |
|
Возврат в главное меню MathPages |
Как решать Surds 2: четыре основных метода Surd
Как решать surds — Упрощение surd с двойным квадратным корнем, Факторирование терминов Surd, Сравнение коэффициентов Surd, Рационализация Surd
На этом втором концептуальном занятии как решать surds, вы подробно изучите три важных метода упрощения surd и рационализация surds вкратце,
- Упрощение surd двойного квадратного корня или квадратного корня surds: Как упростить surds двойного квадратного корня, который является выражением surd под вторым квадратным корнем.
 Внутреннее сурд-выражение должно быть освобождено от внешнего квадратного корня путем преобразования его в целое квадратное сурд-выражение.
Внутреннее сурд-выражение должно быть освобождено от внешнего квадратного корня путем преобразования его в целое квадратное сурд-выражение. - Разложение исходных терминов на множители: Как упростить сурд-выражения, убрав сурд-множитель из терма в двучленном сурд-выражении. Пример: $3+\sqrt{3}=\sqrt{3}(\sqrt{3}+1)$ и,
- Сравнение коэффициентов сурда: Как решить уравнение сурда, сравнивая коэффициенты сурда и не сурда в двух частях уравнения.
- Рационализация сурдов: В сурд дроби с одним из числителя или знаменателя 92-б$.
Мы подробно объясним, как решать сурды с помощью первых трех методов, решая выбранные тестовые примеры задач на сурды.
Кроме того, будет кратко рассмотрена рационализация сурдов. Чтобы узнать больше о методе рационализации Surd, обратитесь к нашей статье
How to Solve Surds 1 — Rationalization of Surds
Если вы знаете, как использовать эти методы, , вам будет легко решить большинство проблем в ваши конкурсные тесты на сурде.
Как решить surds: Как преобразовать квадратный корень surds в целое квадратное выражение surd
Квадратный корень surds появляется в двух формах. Первые три примера первого типа проще упростить. Это
$\sqrt{10+2\sqrt{21}}$
$\sqrt{3+2\sqrt{2}}$
$\sqrt{9+4\sqrt{5}} $
Во многих задачах упрощения surd появляются такие сурды с квадратным корнем. Если вы не освободите surd выражение от окружающего его квадратного корня, вы не сможете двигаться дальше. 92$ как единственный суровый термин.
Прорыв обеспечивается средним членом формы $2ab$.
Техника: Пренебрегая коэффициентом 2, разобьем оставшуюся часть среднего члена на два множителя. По крайней мере, один из этих двух будет сурдом, так что сумма квадратов двух равна рациональному числовому члену исходного двухчленного сурд-выражения под квадратным корнем.
В этом случае средний член без учета коэффициента 2 равен $\sqrt{21}$.
У него есть два поверхностных множителя, $\sqrt{7}$ и $\sqrt{3}$, и сумма квадратов этих двух факторов, как и ожидалось, равна 10. 2}$. 92}$.
2}$. 92}$.
Примечание: Здесь следует соглашение о написании большего члена сурдового выражения первым.
Немного потренировавшись, вы без труда сможете упростить такие выражения квадратного или двойного квадратного корня.
Обратите внимание, что метод во всех трех случаях зависит от удаления коэффициента 2 из сурового среднего члена.
Что делать, если такого коэффициента 2 вообще не существует в сурд-среднем члене двухчленного сурд-выражения под квадратным корнем!
Пример задачи 4: Средний член квадратного корня из сурд-выражения без множителя 2
Возьмем очень распространенный пример двухчленного сурд-выражения $(2 + \sqrt{3})$. Это часто встречающееся сурдовое выражение. Иногда его ставят под квадратным корнем,
$\sqrt{2+\sqrt{3}}$.
Как бы вы в этом случае удалили окружающий квадратный корень?
Метод следует из двухэтапного дедуктивного рассуждения,
- Если сурд-выражение под корнем должно быть освобождено от квадратного корня, оно должно быть выражено как $a^2 +2ab +b^2$.

- Если 2 отсутствует в среднем члене сурда , мы должны искусственно ввести 2, умножив и разделив само сурд-выражение под квадратным корнем на 2, а затем попытаться выразить числитель сурд-выражения в виде целого квадрата.
Применим новый метод к четвертому примеру задачи.
Суровое выражение, которое нужно упростить,
$\sqrt{2+\sqrt{3}}$.
Умножив и разделив surd выражение под квадратным корнем на 2, вы получите 92}$
$=\displaystyle\frac{1}{\sqrt{2}}(\sqrt{3}+1)$.
Упрощение только этого типа выражения немного сложно, но с практикой и правильными методами упрощение любой формы квадратного корня из surds должно быть легким.
Теперь вы узнаете, как применяется метод факторинга Surd.
Как решать сурд: метод факторинга сурд-членов
Примеры
Любая из следующих двух форм сурд-выражений может появляться в сурд-задачах без каких-либо других действий над ними,
$2 + \sqrt{6}$
$3 + \sqrt{15}$.
Если вы посмотрите внимательно, то обнаружите, что каждое из целых чисел под квадратным корнем состоит из двух простых множителей. Если один из этих двух факторов также совпадает со вторым числовым термином, это веский случай факторизации сурд-терма.
Посмотрим как.
Первый пример,
$2+\sqrt{6}=\sqrt{2}(\sqrt{3}+\sqrt{2})$.
Вы убрали множитель $\sqrt{2}$ не только из исходного члена, но и также вне числового термина.
Часто вы обнаружите, что преобразованное сурд-выражение появляется либо в числителе, либо в знаменателе, либо в его дополнительном сурд-выражении, что значительно упрощает задачу.
Во втором примере
$3+\sqrt{15}=\sqrt{3}(\sqrt{5}+\sqrt{3})$.
В обоих этих случаях вы убрали общий множитель из обоих членов в surd выражении.
Иногда вы вынимаете множитель из одного сурдового термина. Пример, 92$.
Если вычесть множитель 4 из 24 под квадратным корнем, выражение преобразуется таким образом, что его можно выразить как квадрат выражения суммы.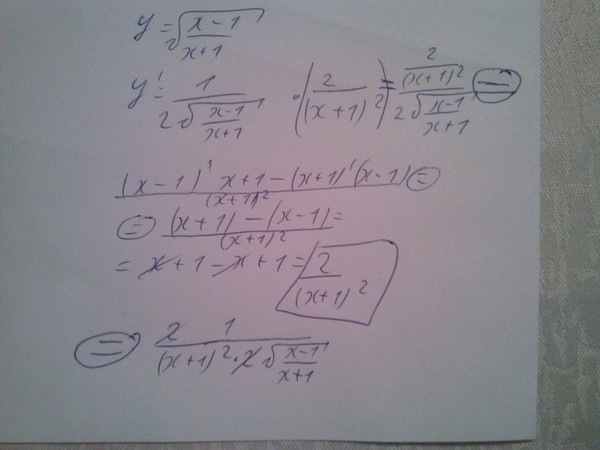
Иногда вы можете определить общий сурдовый термин, скрытый в числовом термине. Например,
$3+\sqrt{3}=\sqrt{3}(\sqrt{3}+1)$.
Как решать surds: Рационализация техники surds
Мы покажем использование техники на примере решения задачи.
Пример задачи 5. 9{-\frac{1}{2}}$ есть,
- $4$
- $3\sqrt{3}$
- 7$
- $2\sqrt{3}$
Это задача на двойное квадратное корень упрощение как взятие квадратного корня из $a$, которое уже включает квадратный корень, приведет к тому, что один квадратный корень меньше второго квадратного корня. .
Давайте сначала покажем вам, как преобразовать выражение $a$ в квадратное выражение.
9{-\frac{1}{2}}$$=(2-\sqrt{3})+\displaystyle\frac{1}{(2-\sqrt{3})}$.
Теперь только мы приведем сурд-знаменатель к числовому значению, умножив и разделив второй член выражения на $(2+\sqrt{3})$.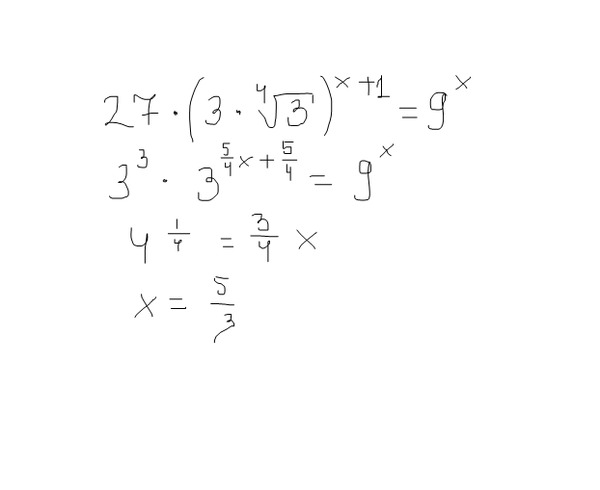 Это выражение, дополнительное к стороннему знаменателю $(2-\sqrt{3})$.
Это выражение, дополнительное к стороннему знаменателю $(2-\sqrt{3})$.
Результат действия:
$E=(2-\sqrt{3})+(2+\sqrt{3})$
$=4$.
Общий знаменатель $(2-\sqrt{3})$ рационализирован до 1,
92=4-3=1$.Ответ: Вариант а: 4.
Для решения этой задачи используются два метода решения поверхностных задач:
- Упрощение с использованием двойного квадратного корня и .
- Рационализация сурдов.
Рационализация сурдов обычно делается для рационализации сурдового знаменателя дроби. Но эта концепция 90 556 вполне может быть применена для рационализации сурдового числителя 90 557, даже если этого требует ситуация.
Рационализация сурдов более подробно описана в нашей предыдущей статье из этой серии о том, как решать сурды. Ссылка:
Как решить Surds 1 — Рационализация Surds.
На этом фоне давайте теперь решим несколько реальных тестовых задач с исходным кодом, в которых появляются выражения с квадратным корнем, а также вам нужно использовать метод факторинга с исходным термином.
В задаче четвертого тестового уровня вы узнаете, как применять метод сравнения и выравнивания коэффициентов , чтобы решить уравнение Surds.
Задачи тестового уровня: упрощение квадратного корня из surds, разложение surd-членов, рационализация surds и сравнение surds коэффициентов
Задача 1.
Значение $\sqrt{5+2\sqrt{6}} — \displaystyle\ frac{1}{\sqrt{5+2\sqrt{6}}}$ is,
- $\sqrt{5}-1$
- $1+\sqrt{5}$
- $2\sqrt{2}$
- $\sqrt{2}$
Решение задачи 1.
Сначала упростим вычитаемую сумму обратных величин, 92}}$
$=\displaystyle\frac{2(2+\sqrt{6})}{\sqrt{3}+\sqrt{2}}$.
Взяв множитель $\sqrt{2}$ из двух членов в числителе,
$E=\displaystyle\frac{2\sqrt{2}(\sqrt{3}+\sqrt{2})} {\sqrt{3}+\sqrt{2}}$
$=2\sqrt{2}$.
Ответ: Вариант c: $2\sqrt{2}$.
Вы не только извлекли сурд-выражение в знаменателе из охватывающих его квадратных корней, но также определили схему удобной возможности сурд-факторизации в числителе, взяв множитель $\sqrt{2}$ как из $2$, так и из $\sqrt{6}$.
Этот тип факторизации не сразу виден и требуется более тщательный анализ, чтобы определить возможность. Этот метод Surd факторизации значительно упрощает многократное упрощение. В этом решении вообще не использовалась рационализация сурдов.
Альтернативное решение: сначала упростить квадратный корень из сурдов, а затем применить рационализацию сурдов.2}}$, упрощая оба квадратных корня из surds,
$=(\sqrt{3}+\sqrt{2})-\displaystyle\frac{1}{(\sqrt{3}+\sqrt{2} )}$
$=(\sqrt{3}+\sqrt{2})-(\sqrt{3}-\sqrt{2})$, умножение и деление второго члена на $(\sqrt{3}- \sqrt{2})$ с применением Рационализация сурдов,
$=2\sqrt{2}$.
Это решение требует меньшего количества шагов и работает быстрее.
Сложная сурдовая проблема часто может быть решена более чем одним способом. Вы должны выбрать самый простой путь.
Задача 2.
Значение $\sqrt{\displaystyle\frac{(\sqrt{12}-\sqrt{8})(\sqrt{3}+\sqrt{2})}{5+\ sqrt{24}}}$ есть,
- $\sqrt{6}-\sqrt{2}$
- $2-\sqrt{6}$
- $\sqrt{6}-2$
- $\sqrt{6}+\sqrt{2}$
Решение задачи 2.

В первую очередь ваше внимание привлекают два множителя: $(\sqrt{12}-\sqrt{8})$ в числителе и $(5+\sqrt{24})$ в знаменателе. . Имея термины, богатые факторами, эти два поверхностных выражения нуждаются в немедленном упрощении с помощью факторизации поверхностных терминов. 92$, применяя упрощение квадрата surds.
Данное выражение упрощается до
$E=\displaystyle\frac{\sqrt{2}}{\sqrt{3}+\sqrt{2}}$.
Теперь рационализируйте знаменатель, умножив и разделив на $(\sqrt{3}-\sqrt{2})$,
$E=\sqrt{2}(\sqrt{3}-\sqrt{2}) =\sqrt{6}-2$.
Ответ. Вариант c: $\sqrt{6}-2$.
Чтобы решить эту проблему, вы применили все три техники решения сложных проблем, которые вы изучили до сих пор,
- Рационализация сурдов.
- Упрощение квадрата сурдов и
- Срочный факторинг.
Хотя третий метод кажется легковесным по сравнению с двумя другими, способность видеть возможность факторинга суровых терминов часто становится решающей для достижения решения.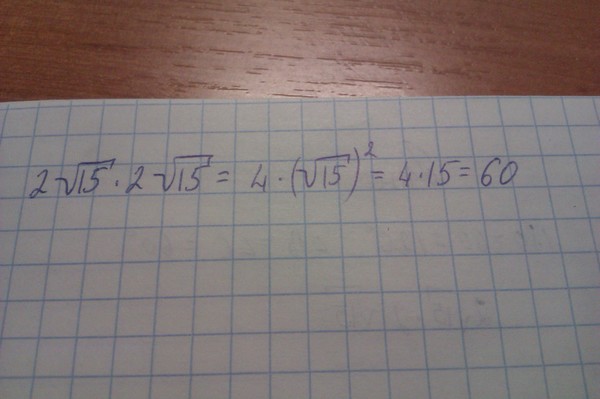
Теперь давайте решим суровую задачу третьего уровня.
Задача
3.Значение $\displaystyle\frac{1}{\sqrt{12-\sqrt{140}}}-\displaystyle\frac{1}{\sqrt{8-\sqrt{ 60}}}-\displaystyle\frac{2}{\sqrt{10+\sqrt{84}}}$ есть,
- 3
- 0
- 1
- 2
Решение 3: анализ задач и выполнение решения
Всякий раз, когда вы встречаете сурд-выражение под квадратным корнем, вы точно знаете, что сурд-выражение под квадратным корнем должно быть преобразовано в квадрат суммы. Эта задача имеет три таких выражения. В каждом случае извлеките сначала факторы из каждого из сурд-термов, применяя метод факторинга сурд-термов (и в соответствии с только что изложенной стратегией).
Сначала применяя метод факторизации исходного члена, а затем метод упрощения квадрата исходного, к трем полученным знаменателям, 92$.
Сумма сумм в скобках равна трем знаменателям (после извлечения квадратных корней).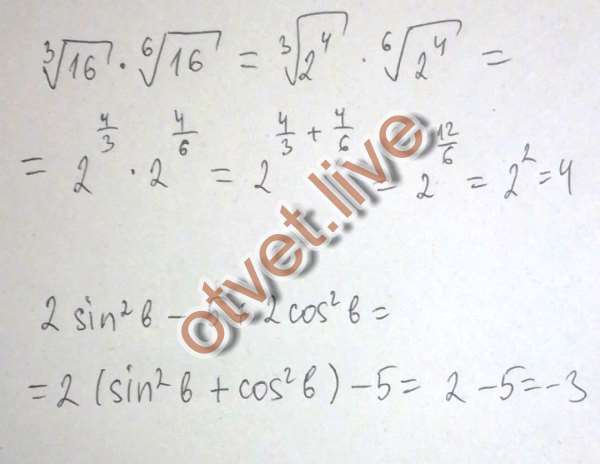
Теперь рационализируйте, чтобы сформировать упрощенное выражение, исключающее знаменатели в процессе,
$\displaystyle\frac{1}{\sqrt{12-\sqrt{140}}}-\displaystyle\frac{1}{\sqrt {8-\sqrt{60}}}-\displaystyle\frac{2}{\sqrt{10+\sqrt{84}}}$
$=\displaystyle\frac{1}{\sqrt{7}- \sqrt{5}}-\displaystyle\frac{1}{\sqrt{5}-\sqrt{3}}-\displaystyle\frac{2}{\sqrt{7}+\sqrt{3}}$
$=\displaystyle\frac{\sqrt{7}+\sqrt{5}}{2}-\displaystyle\frac{\sqrt{5}+\sqrt{3}}{2}-\displaystyle\frac {\sqrt{7}-\sqrt{3}}{2}$
$=0$, все условия отменяются.
Ответ: Вариант b: 0.
Чтобы решить эту третью задачу, вы также применили все три метода, которые вы изучили,
- Разложение на множители Surd
- Упрощение площади сурдов и
- Рационализация сурдов.
Теперь вы узнаете, как применять четвёртую технику решения сложных проблем из Сравнение коэффициентов Сурда и приравнивание сходных переменных между двумя частями уравнения.
Как решить surds: сравнение коэффициентов и выравнивание для аналогичных переменных }}}=A + \sqrt{B}$, тогда $B-A$ равно
- $-13$
- $3\sqrt{3}-7$
- $13$
- $\sqrt{13}$
Решение
4: Анализ проблемы и выполнение решения 92$.Рационализируя преобразованный знаменатель $2+\sqrt{3}$, вы получаете данное выражение как
$(4+3\sqrt{3})(2-\sqrt{3})=A + \sqrt{ B}$,
Или $-1+2\sqrt{3}=A+\sqrt{B}$.
Так как $\sqrt{B}$ является сурдовым термином, он должен быть равен ПОХОЖЕМУ иррациональному сурдовому термину в LHS. Аналогично рациональный член $A$ также должен быть равен $-1$.
Это потому, что
Неверный термин, являющийся иррациональным числом с непрерывающимся неповторяющимся десятичным компонентом, не может быть численно добавлен к рациональному числу, что дает результат, который вы можете выразить с уверенностью.
Примечание: Сурд-форма — это $\sqrt{n}$, где $n$ имеет хотя бы один целочисленный делитель, не являющийся квадратом.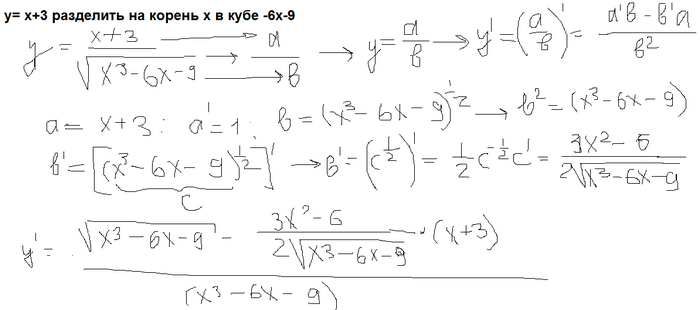 Численно он всегда имеет компонент , не завершающийся неповторяющийся десятичный компонент , и не может быть выражен в виде дроби в форме рационального числа, $\displaystyle\frac{p}{q}$, где и $p$, и $q $ — целые числа.
Численно он всегда имеет компонент , не завершающийся неповторяющийся десятичный компонент , и не может быть выражен в виде дроби в форме рационального числа, $\displaystyle\frac{p}{q}$, где и $p$, и $q $ — целые числа.
Это то, что мы называем Сравнение коэффициентов и выравнивание для подобных переменных , которые не смешиваются друг с другом. Это следует за фундаментальный алгебраический принцип,
В уравнении коэффициенты одинаковых переменных в обеих частях уравнения должны быть равны.
Таким образом,
$A=-1$ и
$2\sqrt{3}=\sqrt{B}$,
Или, $B=12$, и
$B-A=13$.
Ответ: Вариант c: 13.
Чтобы решить эту последнюю задачу, вам также понадобились три метода,
- Во-первых, преобразование в квадрат суммы исходного выражения с использованием метода упрощения квадрата суммы
- Второй, Рационализация сурдов и
- В-третьих, Сравнение коэффициентов и выравнивание для подобных переменных.

Вы можете решить большинство трудных сурд-задач с помощью этих трех методов и факторинга сурд-членов.
Вы были бы удивлены, узнав, что,
Для решения сложных задач по алгебре, а также по тригонометрии вам придется использовать эти суровые методы упрощения.
На следующем концептуальном занятии о том, как решать сурды, вы узнаете, как решать более сложные задачи Сравнение и ранжирование выражений Surd.
Пошаговая помощь по дробям, сурдам и индексам в Suresolv
Чтобы получить наилучшие результаты из обширного ассортимента статей учебных пособий , вопросов и решений по 9055 индексам и дробям, Suresolv, следуйте руководству,
Suresolv Дроби, Surds и индексы Чтение и практическое руководство для SSC CHSL, SSC CGL, SSC CGL Tier II и других конкурсных экзаменов.


 Функция задана формулой f(x) = -x2 + 4. Найти f (1).
Функция задана формулой f(x) = -x2 + 4. Найти f (1).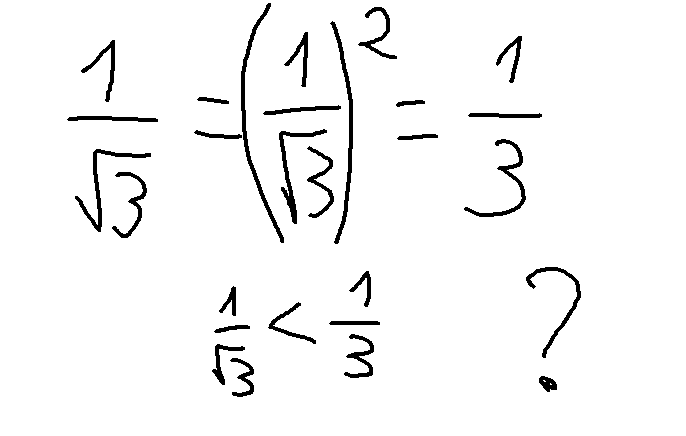
 Вот обзор
что говорится в нескольких популярных книгах по этому поводу:
Вот обзор
что говорится в нескольких популярных книгах по этому поводу: .. аналогичным образом … пифагорейцы.
остальные предложения сводятся по большей части к использованию метода
непрерывные дроби более или менее замаскированы.
.. аналогичным образом … пифагорейцы.
остальные предложения сводятся по большей части к использованию метода
непрерывные дроби более или менее замаскированы. Среди многих
предположения в исторической литературе о его происхождении
следующее очень правдоподобно. Учитывая число A, если кто-то напишет его как
Среди многих
предположения в исторической литературе о его происхождении
следующее очень правдоподобно. Учитывая число A, если кто-то напишет его как 
 Затем итеративно вычислить
Затем итеративно вычислить Бойера
десятичное значение 1,414222 на самом деле соответствует 1;24;51;12. Дело в том
еще больше сбивает с толку утверждение Бойера о том, что вавилонское значение это 3 из итерации, основанной на 1 = 3/2, что не может быть правдой,
потому что все итерации «а», начиная с 3/2, будут немного выше ,
тогда как 1;24,51,10 немного
Бойера
десятичное значение 1,414222 на самом деле соответствует 1;24;51;12. Дело в том
еще больше сбивает с толку утверждение Бойера о том, что вавилонское значение это 3 из итерации, основанной на 1 = 3/2, что не может быть правдой,
потому что все итерации «а», начиная с 3/2, будут немного выше ,
тогда как 1;24,51,10 немного  (Последнее естественно возникает, если мы ищем рациональное
квадрат (х/у) 2 чуть больше 3, что означает, что мы хотим
целое число x 2 должно быть чуть больше, чем целое число 3y 2 .
Установка этой разницы в 1 дает уравнение Пелла.) В противном случае это было бы
очень трудно объяснить, как они могли прийти к двум конвергентам
265/153 и 1351/780, каждый из которых является «наилучшим рациональным
приближение» до соответствующих знаменателей. Однако я согласен с
Sondheimer, что явный алгоритм непрерывной дроби был бы трудным
для греков, чтобы выступить из-за всех необходимых длинных делений.
(Последнее естественно возникает, если мы ищем рациональное
квадрат (х/у) 2 чуть больше 3, что означает, что мы хотим
целое число x 2 должно быть чуть больше, чем целое число 3y 2 .
Установка этой разницы в 1 дает уравнение Пелла.) В противном случае это было бы
очень трудно объяснить, как они могли прийти к двум конвергентам
265/153 и 1351/780, каждый из которых является «наилучшим рациональным
приближение» до соответствующих знаменателей. Однако я согласен с
Sondheimer, что явный алгоритм непрерывной дроби был бы трудным
для греков, чтобы выступить из-за всех необходимых длинных делений. Значение r может
быть аппроксимирован с любой желаемой степенью точности, используя только целое число
сложения и умножения на основе рекуррентной формулы
Значение r может
быть аппроксимирован с любой желаемой степенью точности, используя только целое число
сложения и умножения на основе рекуррентной формулы Точно так же последовательные члены 896 и 2448 дают меньшую
переплет, которым пользовался Архимед. Главное преимущество такого подхода в том, что он
опирается только на простые целочисленные операции. Размер целых чисел может
были сохранены небольшими за счет устранения аккумулирующих способностей 2 на каждом
этап следующим образом
Точно так же последовательные члены 896 и 2448 дают меньшую
переплет, которым пользовался Архимед. Главное преимущество такого подхода в том, что он
опирается только на простые целочисленные операции. Размер целых чисел может
были сохранены небольшими за счет устранения аккумулирующих способностей 2 на каждом
этап следующим образом Представьте, что их первая оценка квадратного корня из 3 была 5/3, возможно.
исходя из того, что 5 2 = 25 близко к 3(3 2 ) = 27.
Отсюда нетрудно увидеть, что если x является границей квадратного корня из 3,
тогда (5x+9)/(3x+5) является более близкой границей на противоположной стороне. Обозначив через e ошибку x 2 — 3 для оценки x, ошибку
следующая оценка
Представьте, что их первая оценка квадратного корня из 3 была 5/3, возможно.
исходя из того, что 5 2 = 25 близко к 3(3 2 ) = 27.
Отсюда нетрудно увидеть, что если x является границей квадратного корня из 3,
тогда (5x+9)/(3x+5) является более близкой границей на противоположной стороне. Обозначив через e ошибку x 2 — 3 для оценки x, ошибку
следующая оценка Учитывая их ограниченность
средства для численного расчета, легко понять, почему они не
перешли к вычислению 13775/7953 или любые более высокие итерации.
Учитывая их ограниченность
средства для численного расчета, легко понять, почему они не
перешли к вычислению 13775/7953 или любые более высокие итерации. Внутреннее сурд-выражение должно быть освобождено от внешнего квадратного корня путем преобразования его в целое квадратное сурд-выражение.
Внутреннее сурд-выражение должно быть освобождено от внешнего квадратного корня путем преобразования его в целое квадратное сурд-выражение.