Исследовательский проект по математике на тему: «Графики функций, аналитическое задание которых содержит знаки модуля»
Слайд 1
Исследовательский проект по математике на тему: « Графики функций, аналитическое задание которых содержит знаки модуля» Журавлёва Алеся Евгеньевна 10 класс Товменко Светлана Петровна Учитель математики МКОУ Бондаревская СОШ
Слайд 2
Цель моей исследовательской работы: 1. Провести исследование и анализ имеющихся способов построения графиков функций, содержащих переменную под знаком модуля . 2. Выбрать из найденных способов решения наиболее оптимальные. 3. Провести обобщение и систематизацию имеющего материала: а) научиться строить графики функций, содержащих переменную под знаком модуля; б) составить подборку задач по теме «Графики функций, содержащих переменную под знаком модуля «. Объект исследования : функции, содержащие переменную под знаком модуля. Предмет исследования : механизм построения графиков .
Слайд 3
Содержание Введение Историческая справка. Определение модуля ………………… 1 §1 . Построение графиков функций, содержащих модуль …..7 1.1 . Построение графика функции у=f(∣x∣ )………………….8 1.2 . Построение графика функции у=∣f(x) ∣ ………………….10 1.3. Построение графиков функций вида ∣у∣=f(x )……………12 1.4. Построение графиков функции вида ∣у∣=∣f(x) ∣ ……………13 1.5. Построение графиков функции вида у=∣f(x)∣ + ∣f1(x)∣ + ∣f2(x)∣+ …+ ∣ fn (x) ∣ ………………………………………………..14 § 2.Решение задач из КИМ ОГЭ по теме «Построение графиков функций, содержащих переменную под знаком модуля »……..16
Слайд 4
Историческая справка К началу ХVII века алгебра была уже достаточно развитой наукой. Трудами многих поколений учёных были подготовлены условия для нового большого открытия в науке, которое послужило бы толчком к её дальнейшему развитию. Таким открытием явилось введение в математику понятия переменной величины и прямоугольной системы координат. Честь введения в математику функциональной зависимости принадлежит французскому учёному Ренэ Декарту.
Ренэ Декарт придумал систему прямоугольных координат, которой пользуемся мы другое. Трудами Декарта алгебра была значительно усовершенствована. Термин «функция» впервые встречается в письме немецкого математика Лейбница В обычное употребление термина введено в начале ХVIII в. Иоганном Бернулли
Слайд 5
Историческая справка Понятие «модуль» является одним из основных понятий элементарной математики. Слово «модуль» произошло от лат. modulus — «маленькая мера»..Знак модуля, пожалуй, одно из самых интересных явлений в математике. Слово «модуль» многозначное слово, которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках. В архитектуре — это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов. В технике — это термин, применяемый в различных областях техники, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например модуль зацепления, модуль упругости и .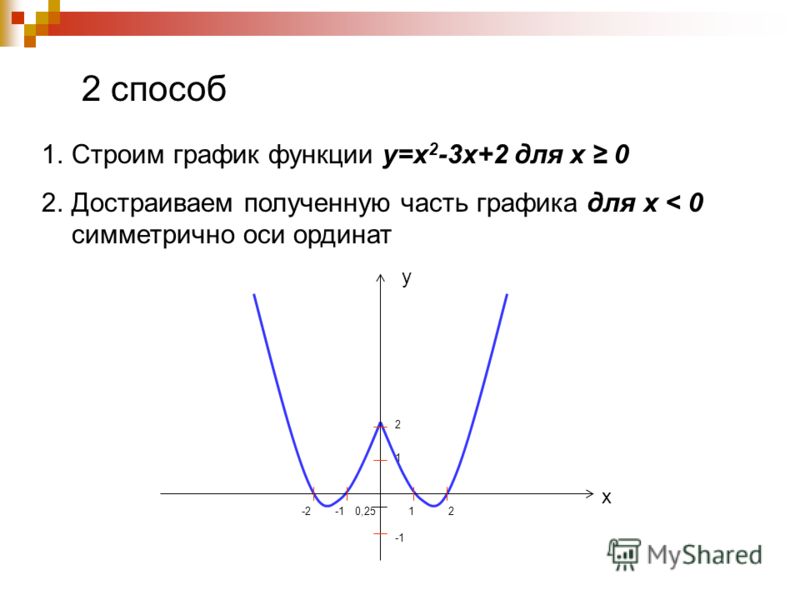
т.п. Модуль объемного сжатия( в физике)-отношение нормального напряжения в материале к относительному удлинению.
Слайд 6
О пределение модуля Определение модуля в математике: Модуль неотрицательного числа a равен самому числу a, модуль отрицательного числа a равен противоположному ему положительному числу –a.
Слайд 7
Построение графиков функций, содержащих модуль Построение графиков следует осуществлять двумя способами: 1) на основании определения модуля; 2) на основании правил (алгоритмов) геометрического преобразования графиков функций.
Слайд 8
Построить график функции у=2∣х∣-2. Построение: 1-й способ. 2-й способ. 1) Строим график функции у=2х-2 для х>0. 2) Достраиваем его левую часть для х
Слайд 9
ё Построить график функцииу =х2-2|х|-3. Решение. По свойству модуля, х2=|х|2, значит у=х2-2|х|-3 можно представить в виде у=|х|2-2|х|-3. Тогда для того чтобы построить график у=х2-2|х|-3 нужно построить график функции у=х2-2х-3. Для этого найдём х0=-b/2a=-(-2)/2=1, y0=y(1)=1-2-3=-4, ось параболы х=1, её вершина имеет координаты (1;-4), при у=0 х=3 или х=-1, при х=0 у=-3 Теперь оставим без изменений часть графика, расположенную в правой полуплоскости, и отобразим её симметрично относительно оси У(другую часть графика отбросим).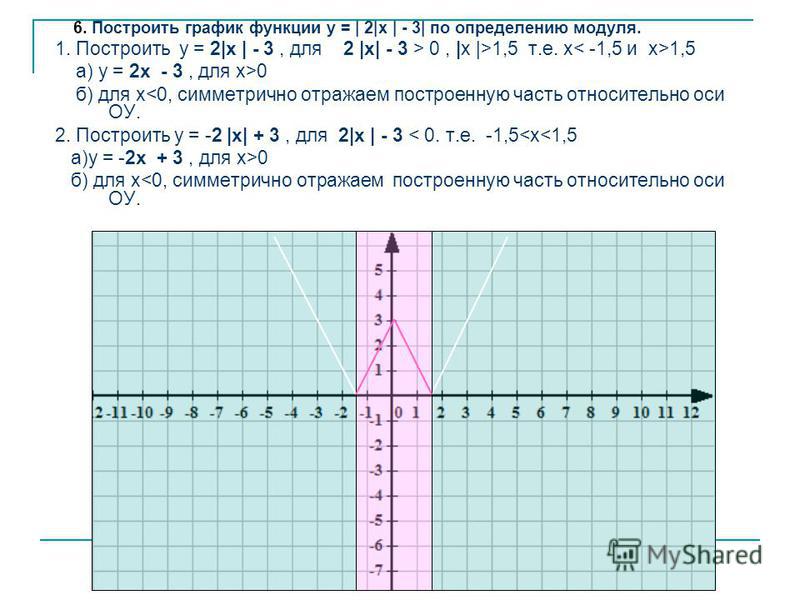
Слайд 10
1.2. Построение графика функции у=∣f(x)∣ Отсюда вытекает алгоритм построения графиков функции у=∣f(x)∣. а) Строим график функции f(x). б) Часть графика у=f(x), лежащая над осью Ох, сохраняется, часть его, лежащая под осью Ох, отображается симметрично относительно оси Ох.
Слайд 11
Построить график функции у=∣х2-2х-3∣. 1) Строим график функции у=х2-2х-3. 2) График нижней полуплоскости отображаем вверх симметрично относительно оси Ох
Слайд 12
Построить график функции ∣у∣= х2-2х-3 1 способ: 2 способ: 1) Строим график функции у=х2-2х-3; 2) Отображаем ту часть графика, которая находится выше оси абсцисс симметрично относительно оси абсцисс.
Слайд 13
Построить график функции ∣у∣=∣1-х∣ Решение: 1 способ. 2 способ. 1. Строим график функции у=1-x. 2. График у=∣1-х∣ получаем из графика у=1-x, симметрично отобразив ту часть, лежащую под осью относительно оси Ох. 3. График ∣у∣=∣1-х∣ получаем из графика у=∣1-х∣, отобразив последний симметрично относительно оси Ох.
Слайд 14
1. Построить график функции у=∣х-1∣+∣х-3∣. Решение: Точки х=1 и х=3 разбивают числовую ось на три промежутка, для каждого запишем функцию: 1) при х≤1 имеем у=4-2х; 2) при 13 имеем у=2х-4
Слайд 15
Метод вершин Графиком непрерывной кусочно-линейной функции является ломаная с двумя бесконечными крайними звеньями. Пример: Построить график функции у=∣х∣-∣х-1 ∣ Алгоритм построения: 1) Найдём нули каждого подмодульного выражения х=0 и х=1. 2) Составим таблицу, в которой кроме 0 и 1 записываем по одному целому справа и слева от этих значений. 3 ) Наносим эти точки на координатную плоскость и соединяем последовательно . Точки перелома и есть вершины ломаной х -1 0 1 2 у -1 -1 1 1
Слайд 16
§ 2.Решение задач из ЕГЭ по теме «Построение графиков функций, содержащих переменную под знаком модуля » Постройте график функции — х2-2х+2, если х ≥ — 3 у= -x-4, если x
Слайд 17
Спасибо за внимание
Решение | Можем ли мы нарисовать график y = |x| + |х-1| + |х-4|? | Думая о функциях
Рассматривая диапазоны \(x < 0\), \(0 \le x < 1\), \(1 \le x < 4\) и \(x \ge 4\), покажите, что график \[\begin{уравнение*} у = \большой|х\большой| + \большой|х-1\большой| + \большой|х-4\большой| \end{уравнение*}\]
состоит из четырех отрезков и дает уравнение каждого отрезка.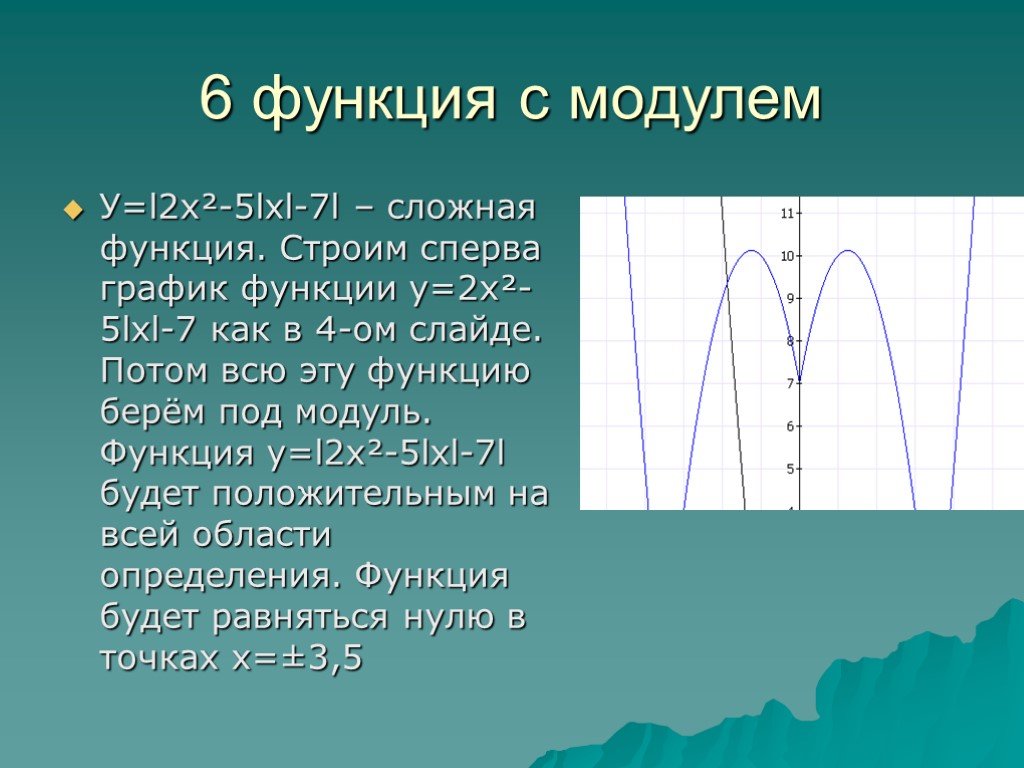
Нарисуйте график.
Давайте посмотрим на описанные четыре региона.
Район 1: \(x
< 0\)В этом случае \(x\), \(x-1\) и \(x-4\) отрицательны, поэтому \[\begin{уравнение*} у = \большой|х\большой| + \большой|х-1\большой| + \большой|х-4\большой| = -х — (х-1) — (х-4) = -3х + 5. \end{уравнение*}\]
Район 2: \(0 \le x
< 1\)Когда мы находимся в этой области, \(x\) положительно, но \(x-1\) и \(x-4\) отрицательны, поэтому \[\begin{уравнение*} у = \большой|х\большой| + \большой|х-1\большой| + \большой|х-4\большой| = х — (х-1) — (х-4) = -х + 5. \end{уравнение*}\]
Район 3: \(1 \le x
< 4\)В таком случае, \[\begin{уравнение*} у = \большой|х\большой| + \большой|х-1\большой| + \большой|х-4\большой| = х + (х-1) — (х-4) = х + 3. \end{уравнение*}\]
Район 4: \(x \ge 4\)
Наконец, в этом регионе
\[\begin{уравнение*}
у = \большой|х\большой| + \большой|х-1\большой| + \большой|х-4\большой| = х + (х-1) + (х-4) = 3х — 5.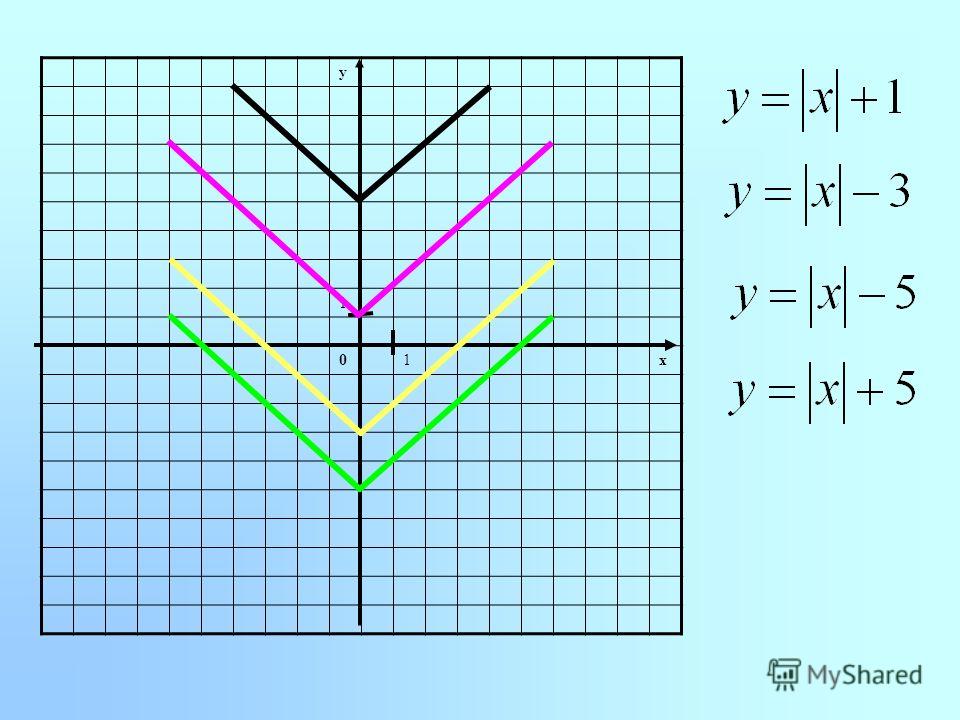
\end{уравнение*}\]
Таким образом, график \(y\) состоит из четырех отрезков. Это приводит к следующему эскизу.
Обратите внимание, что сегменты линии соединяются на концах. Почему это должно быть так для такой функции?
Вычислить корни уравнений
- \(\big|x\big| + \big|x-1\big| + \big|x-4\big| = 6 — \dfrac{1}{3 }х\),
Если мы мысленно добавим линию \(y = 6 — \dfrac{1}{3}x\) к нашему наброску, мы увидим, что ожидаем два решения, одно отрицательное, другое положительное.
Район 1: \(x
< 0\)В этой области уравнение для решения становится \[\begin{уравнение*} -3x + 5 = 6 — \frac{x}{3} \iff \frac{8x}{3} = -1 \iff x = -\frac{3}{8}. \end{уравнение*}\]
Поскольку это находится в области \(x < 0\), это верное решение.
Район 2: \(0 \le x
< 1\) Уравнение, которое нужно решить, можно записать в виде
\[\begin{уравнение*}
-x + 5 = 6 — \frac{x}{3} \iff \frac{2x}{3} = -1 \iff x = -\frac{3}{2}.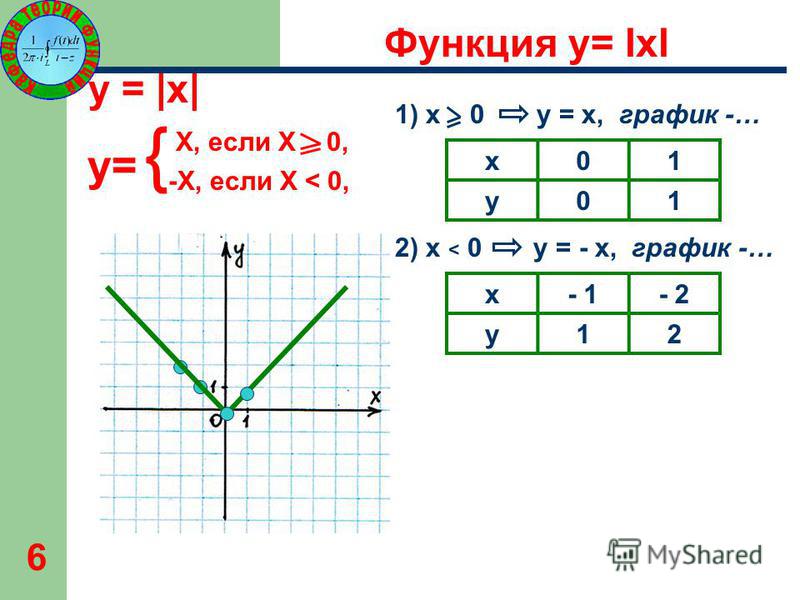
\end{уравнение*}\]
Поскольку , а не попадает в рассматриваемую область (\(0 \le x < 1\)), то решения в этой области нет.
Район 3: \(1 \le x
< 4\)В этой области уравнение для решения становится \[\begin{уравнение*} x + 3 = 6 — \frac{x}{3} \iff \frac{4x}{3} = 3 \iff x = \frac{9{4}. \end{уравнение*}\]
Поскольку это часть области \(1 \le x < 4\), это второе решение исходного уравнения.
Район 4: \(x \ge 4\)
Наконец, в этом регионе нам предстоит решить \[\begin{уравнение*} 3x — 5 = 6 — \frac{x}{3} \iff \frac{10x}{3} = 11 \iff x = \frac{33}{10}. \end{уравнение*}\]
Поскольку \(\dfrac{33}{10} < 4\), решение не попадает в рассматриваемую область и, следовательно, не является решением уравнения.
Таким образом, два решения уравнения
\[\begin{уравнение*}
x = -\frac{3}{8} \quad\text{and}\quad x = \frac{9}{4}.
\end{уравнение*}\]
Нарисовав линию \(y = 6 — \frac{1}{3}x\), мы могли бы, вероятно, увидеть, что решения должны попадать в области 1 и 3, и сэкономили себе некоторую работу.
- \(\big|x\big| + \big|x-1\big| + \big|x-4\big| = \dfrac{1}{x}\).
Еще раз, если мы представим добавление линии \(y = \dfrac{1}{x}\) к нашему эскизу, мы увидим, что ожидаем одно положительное решение этой проблемы. 92 — 4 \times (-1) \times (-1)}}{2 \times (-1)} = \frac{-5 \pm \sqrt{25 — 4}}{-2} = \frac{ 5 \mp\sqrt{21}}{2}.
\end{уравнение*}\]
Ясно, что
\[\begin{уравнение*}
\frac{5 + \sqrt{21}}{2} > \frac{5}{2} > 1
\end{уравнение*}\]
так, чтобы одно из двух решений не попало в интересующую область. Что касается другого,
\[\begin{уравнение*}
\frac{5 — \sqrt{21}}{2} \le \frac{5 — 4}{2} = \frac{1}{2} < 1
\end{уравнение*}\]
и
\[\begin{уравнение*}
\frac{5 - \sqrt{21}}{2} > \frac{5 — 5}{2} = 0
\end{уравнение*}\]
92 — 4 \times 3 \times (-1)}}{2 \times 3} = \frac{5 \pm \sqrt{25 + 12}}{6} = \frac{5 \pm \sqrt{37} {6}.
\end{уравнение*}\]
Поскольку \(\sqrt{37} > 6\), следует, что
\[\begin{уравнение*}
\frac{5 — \sqrt{37}}{6} < \frac{5 - 6}{6} < 0
\end{уравнение*}\]
так что это возможное решение выходит за пределы интересующей области. Для другого, поскольку \(\sqrt{37} < 7\),
\[\begin{уравнение*}
\frac{5 + \sqrt{37}}{6} < \frac{5 + 7}{6} = 2
\end{уравнение*}\]
решение также выходит за пределы интересующей области.
Таким образом, существует только одно решение уравнения, а именно \[\begin{уравнение*} х = \frac{5 — \sqrt{21}}{2}. \end{equation*}\]
Функции абсолютного значения
Единственная абсолютная вещь в этом мире — это абсолютное значение. Естественно, если абсолютные значения абсолютны, то абсолютны и функции абсолютных значений.
Знаете, что еще абсолютно? Гуси. Или, по крайней мере, строй, в котором летают гуси. Удобно, что они всегда летают в форме буквы V. Мы говорим удобно, потому что графики абсолютных значений тоже выглядят как V.
Кто знал, что гуси знают такую продвинутую математику?
График y = | х | это простейший график абсолютного значения, с которым мы можем столкнуться.
Этот график не выглядит знакомым? Она выглядит точно так же, как и кусочная функция, о которой мы говорили в предыдущем разделе. Так и должно быть, потому что это точно так же.
В этой кусочной функции f ( x ) положительно, когда x отрицательно, и f ( x ) положительно, когда x — положительный. У этого f ( x ) просто позитивный взгляд на жизнь, как и у y =| х |.
Чтобы мы снова встретились здесь, должно быть, судьба; это или математика. На самом деле мы склоняемся к математике.
Играем на AbsoLute
Функции абсолютного значения могут делать намного больше, чем мы уже видели. Например, сыграть сокрушительную песню на их лютнях.
Пример задачи
График y = -2| х |
Функция — это хорошо, но чтобы построить график, нужна конкретика.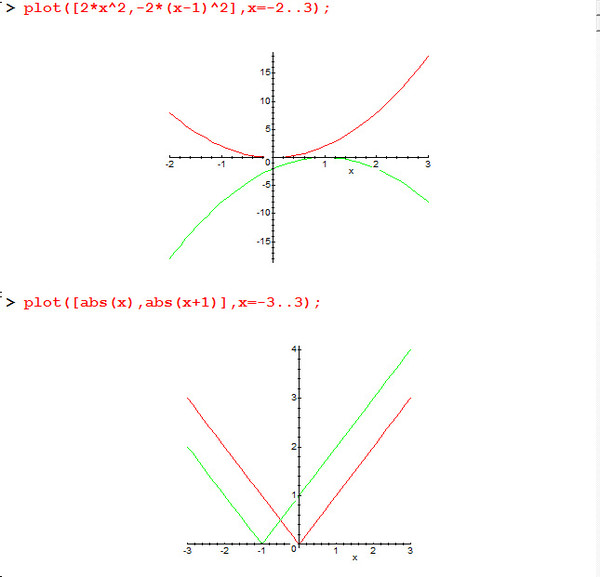
Ценности. Что-то конкретное, во что можно вонзить зубы и оставить след на странице.
Для этого давайте составим таблицу из пары значений и посмотрим, что получится. Надеюсь, не змея или клоун.
Теперь мы можем построить наш график.
Две половины графика сходятся в точке (0, 0). Это называется вершиной функции абсолютного значения. Весь мир вращается вокруг вершины… или, по крайней мере, вся функция.
Мы также видим, что весь граф симметричен относительно вершины, т. е. x = 0. Если мы найдем точку на одной половине графа, мы можем использовать ее для поиска ее близнеца на другой половине. Может быть, мы получим пожизненный контракт на фильм о воссоединении этих потерянных братьев и сестер.
Чем этот график отличается от y = | х |? Знак минус за пределами столбцов абсолютного значения перевернул весь график вверх дном. Затем 2 снаружи сделали V-образную форму более узкой, что облегчило хранение в нашем шкафу.
Число меньше 1 имело бы противоположный эффект, расширяя график и занимая все место в шкафу.
Пример задачи
График y = | х + 1| + 2
Из последней задачи мы знаем, что эта функция будет указывать вверх, но дальше этого мы в темноте.
Ой, мы только что наткнулись на кофейный столик? Где этот выключатель, бормотание ворчание. Подождите, мы думаем, что это была таблица значений, на которую мы натолкнулись.
А, намного лучше. При включенном свете мы можем построить график этой функции.
По сравнению с обычным, ванильный г = | x |, этот график имеет серьезную окраску: он был перемещен на 2 вверх и на 1 влево. Как правило, числа, добавленные или вычтенные за пределами столбцов, перемещают график вверх или вниз. Номера, добавленные или вычтенные внутри баров, должны заказать газировку, если они планируют водить машину. Они также заставляют график двигаться влево и вправо, но в направлении, противоположном их знаку.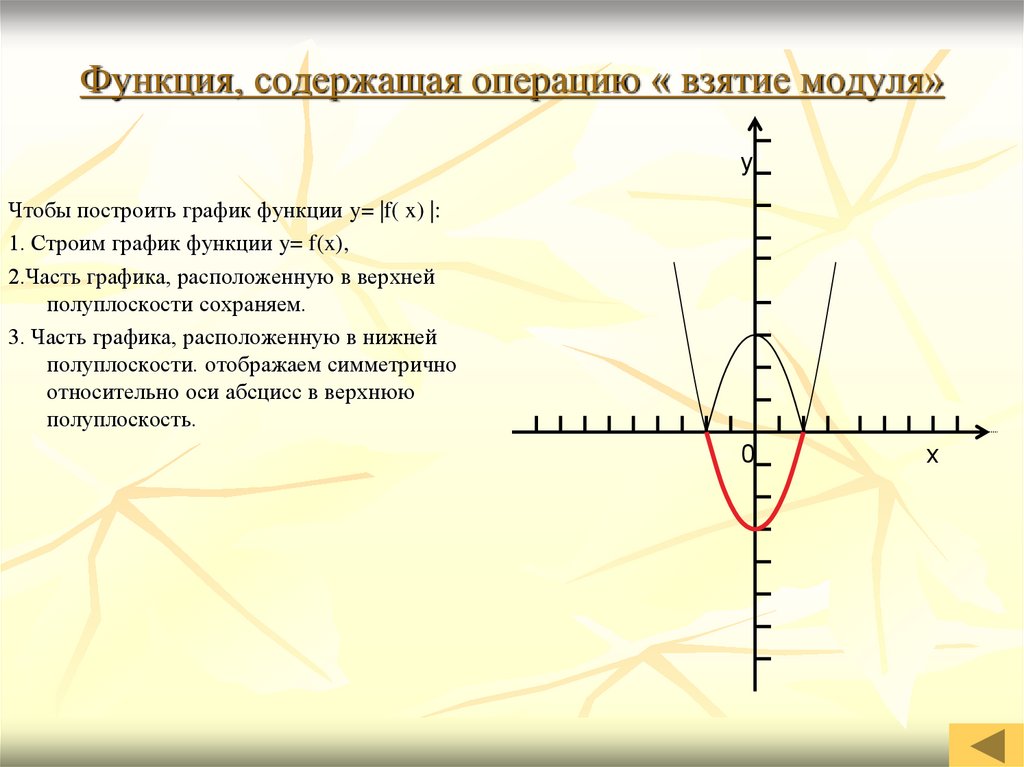
Симметрия графа сместилась вместе с вершиной; теперь он симметричен примерно x = -1.
V-образный для Victory
Мы можем взять все, чему мы научились, и связать это воедино настоящим математическим способом.
Уравнение для функции абсолютного значения имеет общий вид:
y = a | x – ч | + k
Было бы довольно страшно, если бы мы просто бросили вам это уравнение с кучей букв, сидящих там без контекста. Однако мы уже работали с каждой частью этого уравнения, так что это еще не все.
- Вершина графа находится в точке ( h , k ).
- Симметрично относительно прямой х = ч .
- График V-образный.
- Он открывается вверх, если a > 0. Он открывается вниз, если a < 0.
- Он шире графика y = | х | если | и | < 1.
