| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | sin(pi/6) | |
| 8 | cos(pi/4) | ||
| 9 | Найти точное значение | sin(45 град. ) ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град.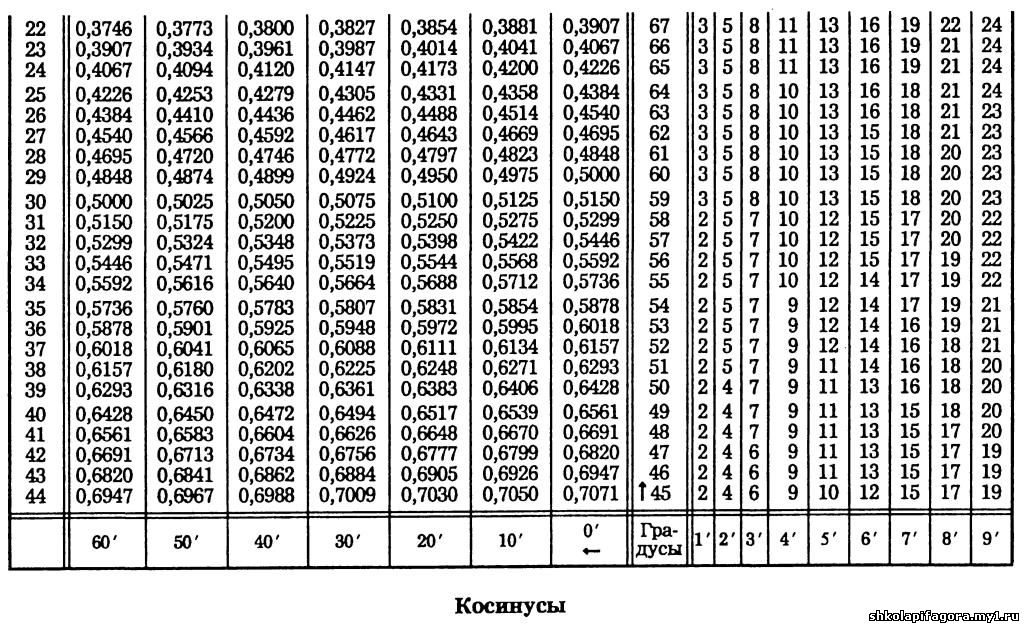 ) ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | ||
| 22 | Найти точное значение | tan(45 град. ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град. ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
| 1 | Найти точное значение | sin(30) | |
| 2 | Найти точное значение | sin(45) | |
| 3 | Найти точное значение | sin(30 град. ) ) | |
| 4 | Найти точное значение | sin(60 град. ) | |
| 5 | Найти точное значение | tan(30 град. ) | |
| 6 | Найти точное значение | arcsin(-1) | |
| 7 | Найти точное значение | ||
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | sin(45 град. ) | |
| 10 | Найти точное значение | sin(pi/3) | |
| 11 | Найти точное значение | arctan(-1) | |
| 12 | Найти точное значение | cos(45 град. ) ) | |
| 13 | Найти точное значение | cos(30 град. ) | |
| 14 | Найти точное значение | tan(60) | |
| 15 | Найти точное значение | csc(45 град. ) | |
| 16 | Найти точное значение | tan(60 град. ) | |
| 17 | Найти точное значение | sec(30 град. ) | |
| 18 | Найти точное значение | cos(60 град. ) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | sin(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | tan(45 град. ) ) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 град. ) | |
| 25 | Найти точное значение | sec(45 град. ) | |
| 26 | Найти точное значение | csc(30 град. ) | |
| 27 | Найти точное значение | sin(0) | |
| 28 | Найти точное значение | sin(120) | |
| 29 | Найти точное значение | cos(90) | |
| 30 | Преобразовать из радианов в градусы | pi/3 | |
| 31 | Найти точное значение | tan(30) | |
| 32 | Преобразовать из градусов в радианы | 45 | |
| 33 | Найти точное значение | cos(45) | |
| 34 | Упростить | sin(theta)^2+cos(theta)^2 | |
| 35 | Преобразовать из радианов в градусы | pi/6 | |
| 36 | Найти точное значение | cot(30 град.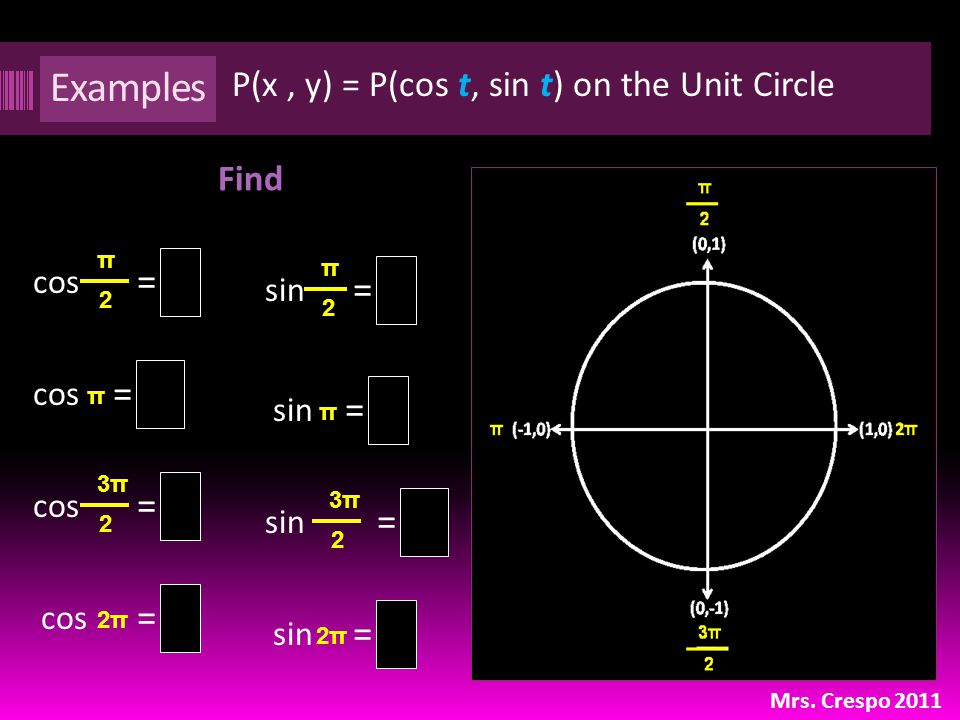 ) ) | |
| 37 | Найти точное значение | arccos(-1) | |
| 38 | Найти точное значение | arctan(0) | |
| 39 | Найти точное значение | cot(60 град. ) | |
| 40 | Преобразовать из градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2pi)/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | tan(pi/2) | |
| 45 | Найти точное значение | sin(300) | |
| 46 | Найти точное значение | cos(30) | |
| 47 | Найти точное значение | cos(60) | |
| 48 | Найти точное значение | cos(0) | |
| 49 | Найти точное значение | cos(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | sec(60 град. ) ) | |
| 53 | Найти точное значение | sin(300 град. ) | |
| 54 | Преобразовать из градусов в радианы | 135 | |
| 55 | Преобразовать из градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5pi)/6 | |
| 57 | Преобразовать из радианов в градусы | (5pi)/3 | |
| 58 | Преобразовать из градусов в радианы | 89 град. | |
| 59 | Преобразовать из градусов в радианы | 60 | |
| 60 | Найти точное значение | sin(135 град. ) ) | |
| 61 | Найти точное значение | sin(150) | |
| 62 | Найти точное значение | sin(240 град. ) | |
| 63 | Найти точное значение | cot(45 град. ) | |
| 64 | Преобразовать из радианов в градусы | (5pi)/4 | |
| 65 | Найти точное значение | sin(225) | |
| 66 | Найти точное значение | sin(240) | |
| 67 | Найти точное значение | cos(150 град. ) | |
| 68 | Найти точное значение | tan(45) | |
| 69 | Вычислить | sin(30 град. ) ) | |
| 70 | Найти точное значение | sec(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | csc(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | tan((5pi)/3) | |
| 75 | Найти точное значение | tan(0) | |
| 76 | Вычислить | sin(60 град. ) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3pi)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | arcsin(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | csc(45) | |
| 83 | Упростить | arctan( квадратный корень из 3) | |
| 84 | Найти точное значение | sin(135) | |
| 85 | Найти точное значение | sin(105) | |
| 86 | Найти точное значение | sin(150 град. ) ) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | tan((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | pi/4 | |
| 90 | Найти точное значение | sin(pi/2) | |
| 91 | Найти точное значение | sec(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | arcsin(0) | |
| 95 | Найти точное значение | sin(120 град. ) ) | |
| 96 | Найти точное значение | tan((7pi)/6) | |
| 97 | Найти точное значение | cos(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразовать из градусов в радианы | 88 град. |
XYZ — Таблица синусов. Синусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов углов.
Проект Карла III Ребане и хорошей компании | Раздел недели: Перевод единиц измерения величин. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Техническая информация тут Поиск на сайте DPVA Полезные ссылки О проекте Обратная связь Оглавление | Адрес этой страницы (вложенность) в справочнике DPVA.xyz: главная страница / / Техническая информация/ / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица синусов. Синусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов углов.
 Введите свой запрос: Введите свой запрос: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Коды баннеров проекта DPVA.xyz Консультации и техническая | Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.DPVA.xyz не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
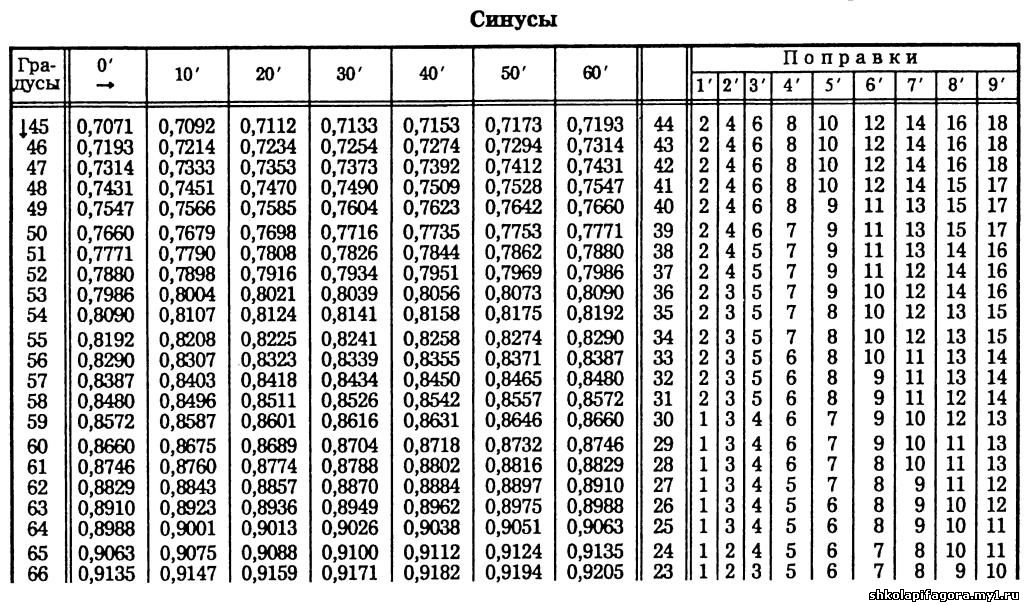
Таблица синусов. Синусы углов от 0°
Таблица синусов. Синусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов углов. Адрес этой страницы (вложенность) в справочнике dpva. ru: главная страница / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица синусов. Синусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов углов. ru: главная страница / / Математический справочник / / Таблицы численных значений. (Таблица квадратов, кубов, синусов ….) + Таблицы Брадиса / / Таблица синусов. Синусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов углов.Поделиться: | |
Вы сейчас находитесь в каталоге: Таблица синусов. Синусы углов от 0° — 360°. Углы с шагом в 1°. Таблица значений синусов углов. |
sin(0°)=sin(360°)=0; точная, но чуть более сложная таблица ( с точностью до 1″) здесь.
|
Углы |
Углы |
Углы |
Углы |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Синус
Примеры:
\(\sin{30^°}=\)\(\frac{1}{2}\)
\(\sin\)\(\frac{π}{3}\)\(=\)\(\frac{\sqrt{3}}{2}\)
\(\sin2=0,909…\)
Содержание:
- Аргумент и значение
- Синус острого угла
- Синус числа
- Синус любого угла
- Связь с другими функциями
- Функция
Аргумент и значение
Синус острого угла
Синус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению противолежащего катета к гипотенузе.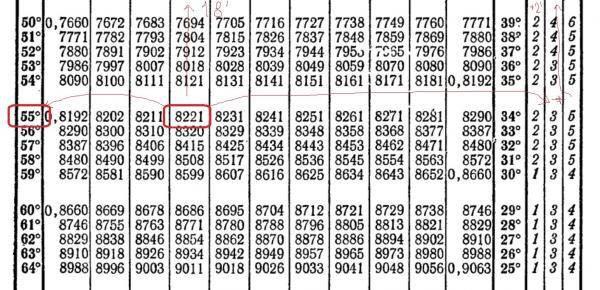
Пример:
1) Пусть дан угол и нужно определить синус этого угла.
2) Достроим на этом угле любой прямоугольный треугольник.
3) Измерив, нужные стороны, можем вычислить \(sinA\).
Синус числа
Синус числа можно определить с помощью числовой окружности – синус числа равен ординате соответствующей точки на ней.
Числовая окружность позволяет определить синус любого числа, но обычно находят синус чисел как-то связанных с Пи: \(\frac{π}{2}\), \(\frac{3π}{4}\), \(-2π\).
Например, для числа \(\frac{π}{6}\) — синус будет равен \(0,5\). А для числа \(-\)\(\frac{3π}{4}\) он будет равен \(-\)\(\frac{\sqrt{2}}{2}\) (приблизительно \(-0,71\)).
Подробнее как вычисляется синус разных чисел можно прочитать в этой статье.
Значение синуса всегда лежит в пределах от \(-1\) до \(1\).
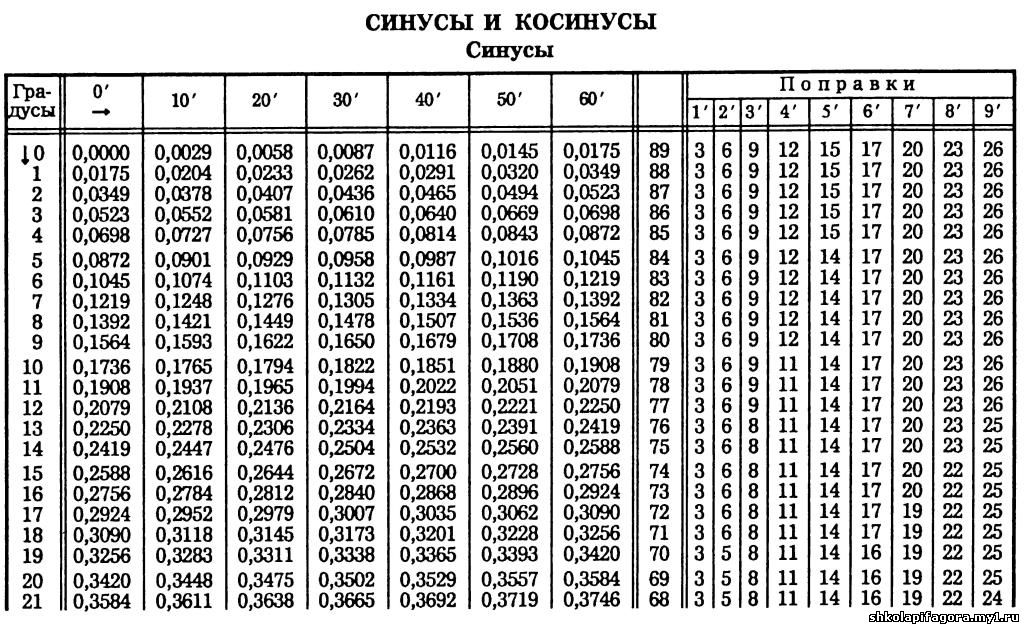 При этом вычислен он может быть для абсолютно любого угла и числа.
При этом вычислен он может быть для абсолютно любого угла и числа.
Синус любого угла
Благодаря единичному кругу можно определять тригонометрические функции не только острого угла, но и тупого, отрицательного, и даже большего, чем \(360°\) (полный оборот). Как это делать — проще один раз увидеть, чем \(100\) раз услышать, поэтому смотрите картинку.
Теперь пояснение: пусть нужно определить \(sin∠КОА\) с градусной мерой в \(150°\). Совмещаем точку О с центром окружности, а сторону ОК – с осью \(x\). После этого откладываем \(150°\) против часовой стрелки. Тогда ордината точки А покажет нам \(\sin∠KOA\).
Если же нас интересует угол с градусной мерой, например, в \(-60°\) (угол КОВ), делаем также, но \(60°\) откладываем по часовой стрелке.
И, наконец, угол больше \(360°\) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов».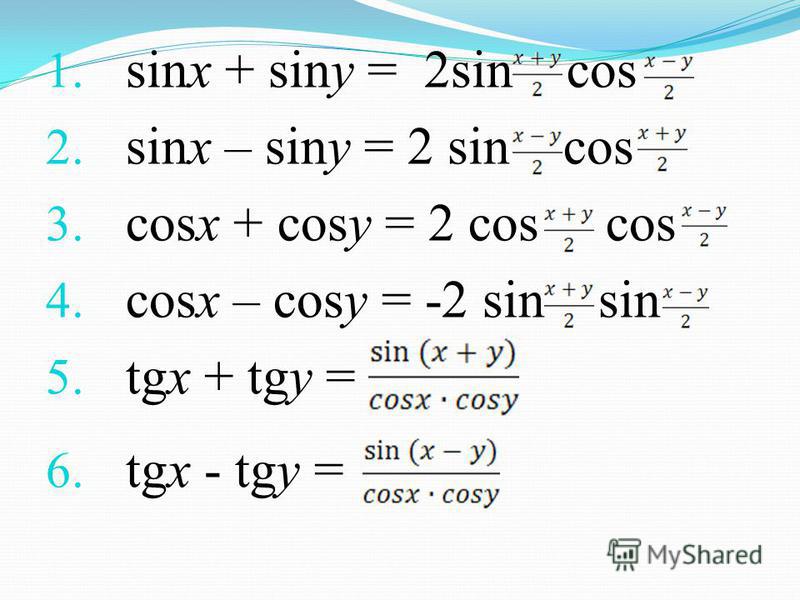 2x}\)
2x}\)
Другие наиболее часто применяемые формулы смотри здесь.
Функция \(y=\sinx\)
Если отложить по оси \(x\) углы в радианах, а по оси \(y\) — соответствующие этим углам значения синуса, мы получим следующий график:
График данной функции называется синусоида и обладает следующими свойствами:
— область определения – любое значение икса: \(D(\sinx )=R\)
— область значений – от \(-1\) до \(1\) включительно: \(E(\sinx )=[-1;1]\)
— нечетная: \(\sin(-x)=-\sinx\)
— периодическая с периодом \(2π\): \(\sin(x+2π)=\sinx\)
— точки пересечения с осями координат:
ось абсцисс: \((πn;0)\), где \(n ϵ Z\)
ось ординат: \((0;0)\)
— промежутки знакопостоянства:
функция положительна на интервалах: \((2πn;π+2πn)\), где \(n ϵ Z\)
функция отрицательна на интервалах: \((π+2πn;2π+2πn)\), где \(n ϵ Z\)
— промежутки возрастания и убывания:
функция возрастает на интервалах: \((-\)\(\frac{π}{2}\)\(+2πn;\) \(\frac{π}{2}\)\(+2πn)\), где \(n ϵ Z\)
функция убывает на интервалах: \((\)\(\frac{π}{2}\)\(+2πn;\)\(\frac{3π}{2}\)\(+2πn)\), где \(n ϵ Z\)
— максимумы и минимумы функции:
функция имеет максимальное значение \(y=1\) в точках \(x=\)\(\frac{π}{2}\)\(+2πn\), где \(n ϵ Z\)
функция имеет минимальное значение \(y=-1\) в точках \(x=-\)\(\frac{π}{2}\)\(+2πn\), где \(n ϵ Z\).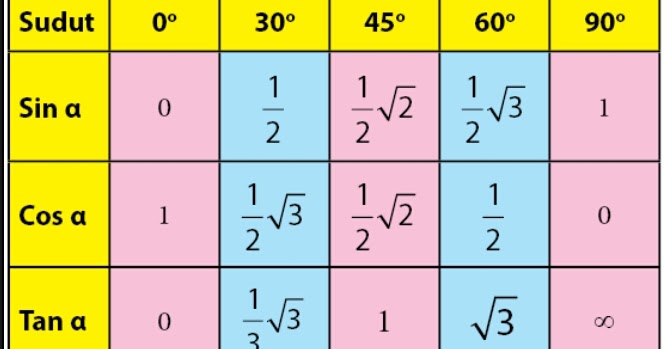
Смотрите также:
Косинус
Тангенс
Котангенс
Решение уравнения \(\sinx=a\)
заказ решений на аукционе за минимальную цену с максимальным качеством
Предлагаю идею сайта-аукциона по выполнению домашних заданий. Он будет включать:
- решение задач по математике (сейчас доступен решебник Филиппова), физике, химии, экономике
- написание лабораторных, рефератов и курсовых
- выполнение заданий по литературе, русскому или иностранному языку.
Основное отличие от большинства сайтов, предлагающих выполнение работ на заказ – сайт рассчитан на две категории пользователей: заказчиков и решающих задания. Причем, по желанию (чтобы заработать, увеличить свой рейтинг, получить решение сложной задачи) пользователи могут играть любую из этих ролей.
Объединение сервисов в одну систему
Основой для идеи послужили несколько работающих систем, объединение которых позволит сделать сервис для решения задач на заказ. Эти системы:
Эти системы:
- Форум, где посетители обмениваются идеями и помогают друг другу
- Система bugtracking, где обнаруженные проблемы проходят путь от публикации до принятия в исполнение и решения
- Аукцион, где цена за товар или услугу определяется в результате торгов
- Система рейтингов, где участники могут оценивать ответы друг друга. Причем, чем больше рейтинг пользователя, тем более значимым становится его голос
Принцип работы
Для удобства и проведения аналогий с реальной жизнью назовем заказчиков студентами, а решающих задания – репетиторами.
Итак, студенту необходимо решить несколько задач. Он заходит на сайт, выбирает раздел с соответствующей дисциплиной и создает новую тему (аналогия с форумом). Но при создании темы он также указывает стартовую (максимальную) цену, которую он готов заплатить за решение задач и крайний срок исполнения задания.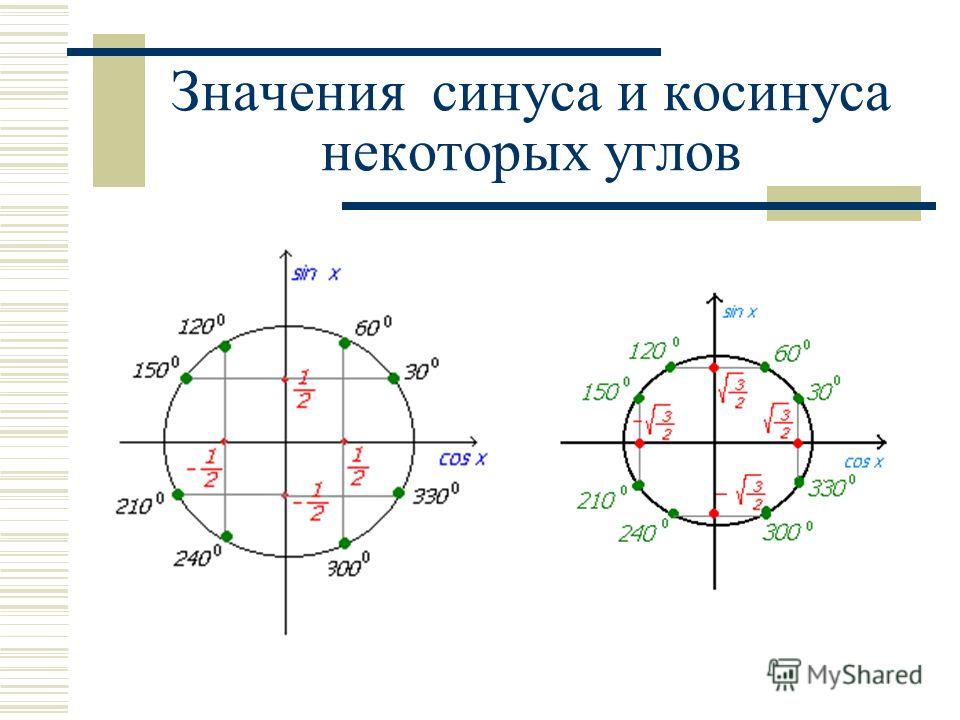 Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Можно будет назначить и нулевую цену – если студенту нужно только бесплатное решение.
Как только тема создана, все пожелавшие подписаться на раздел репетиторы получают уведомление. Причем, условие получения уведомлений можно настроить. Например, уведомлять только о заказах со стартовой ценой более 500 р. и сроком решения не менее недели.
Заинтересовавшиеся репетиторы делают ставки. Причем студент (автор темы) видит ставки и может посмотреть информацию по каждому репетитору (его решения, рейтинг, дату начала участия в проекте). Когда студент посчитает нужным, он может остановить аукцион и назначить задание одному из репетиторов, сделавшему ставку (не обязательно самую низкую, т.к. можно учитывать и другие факторы – см. выше).
Деньги блокируются на счете студента, и репетитор начинает решать задание. Он должен представить его к сроку, заданному изначально. Выполненное решение публикуется в свободном доступе и его может оценить как заказчик, так и другие репетиторы. На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
На этих оценках и строится рейтинг. Если к решению нет претензий – деньги окончательно переводятся со счета студента на счет репетитора.
За счет чего будет развиваться сервис
Первое – положительная обратная связь. Чем больше условий задач и решений будет опубликовано на сайте, тем чаще его будут находить пользователи через поисковики, будет больше ссылок на готовые решения. Именно поэтому важно размещать решенные задачи в свободном доступе. Знаю это по опыту своего сайта exir.ru (ex irodov.nm.ru) – большая ссылочная база получена исключительно за счет благодарных пользователей.
Второе – удобный сервис для заказчиков и для желающих заработать на решениях.
Преимущества для заказчиков
Студентам и школьникам не нужно перебирать десятки сайтов для сравнения цен, а потом надеяться, что после оплаты они получат качественное решение (и, вообще, все не закончится перечислением денег). Заказчики создают аукцион на понижение цены и могут смотреть на рейтинги желающих решить задачи и ранее выполненные ими решения.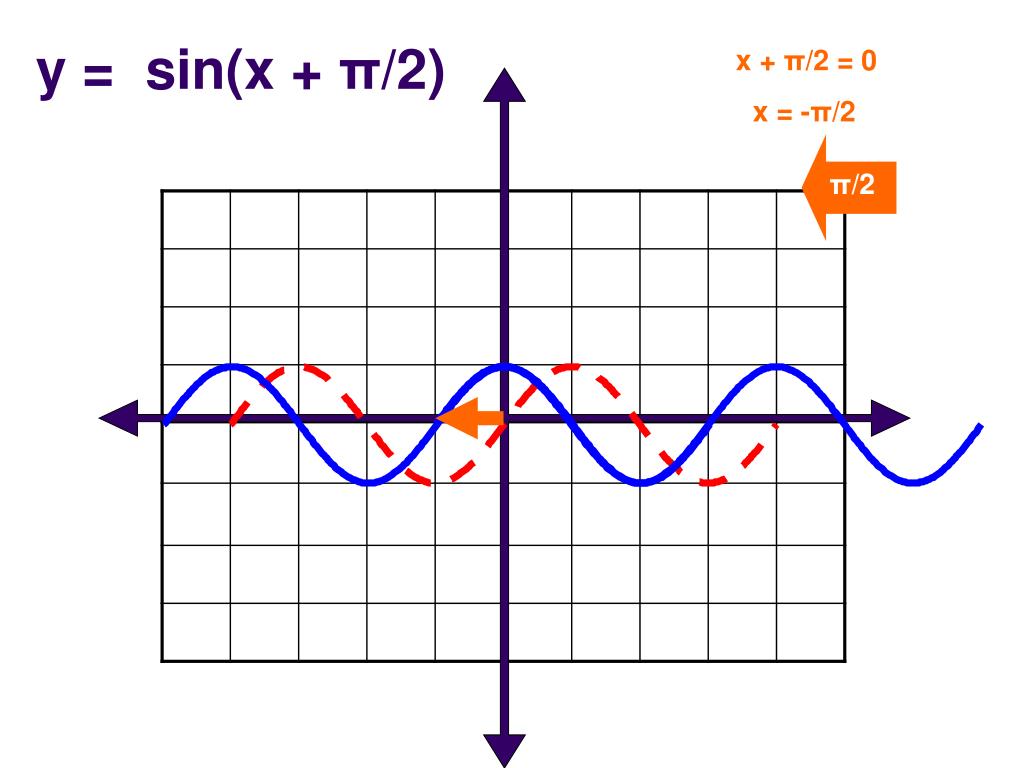 Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Кроме того, деньги окончательно перечисляются исполнителю только после полного решения.
Преимущества для решающих задания
Не нужно создавать и продвигать свой сайт, размещать множество объявлений во всех доступных источниках информации. Заказчики сами придут к вам. Не нужно решать все присланные задания с целью поддержания репутации – можно выбирать те, которые будут интересны по уровню сложности, цене и срокам решения.
Преимущества для владельца сервиса
Если вы не понимаете, какую выгоду получит делающий вам какое-нибудь предложение – будьте осторожны! 🙂 У меня уже есть большой опыт работы с сайтом, предоставляющим бесплатные решения по физике. И вариант с получением прибыли от размещения рекламы подходит и для нового сервиса. Кроме того, мне нравится помогать людям и довольно тяжело смотреть, как множество вопросов по задачам остаются на форуме без ответа. Предложенный аукцион решений сможет значительно сократить число вопросов без ответов.
В будущем возможен вариант и с получением некоторого небольшого процента от оплаты заказов. Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Но процент этот должен быть минимален и на начальном этапе он взиматься точно не будет.
Что необходимо для создания сервиса
- Самым важное сейчас – собрать команду, готовую принять участие в выполнении заданий. Если покупатели заходят в пустой магазин – они надолго забывают в него дорогу.
Поэтому я собираю предварительные заявки от посетителей, готовых заниматься решениями. Не нужно подписания никаких договоров о намерениях. Просто сообщите, на какие темы вы готовы решать задания, какой у вас опыт подобной работы (e-mail: [email protected]). Когда сервис заработает – я пришлю приглашение на регистрацию.
- Выбрать платежную систему.
- Сделать подходящий движок для сайта. Нужно решить – создавать его с нуля или изменить какой-нибудь существующий движок (например, форумный) с открытой лицензией.
- Привлечь посетителей. Учитывая посещаемость exir.ru и число публикуемых на форуме вопросов, думаю, это не будет большой проблемой.
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | cos(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | 92|||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
| 1 | Найти точное значение | грех(30) | |
| 2 | Найти точное значение | грех(45) | |
| 3 | Найти точное значение | грех(30 градусов) | |
| 4 | Найти точное значение | грех(60 градусов) | |
| 5 | Найти точное значение | загар (30 градусов) | |
| 6 | Найти точное значение | угловой синус(-1) | |
| 7 | Найти точное значение | грех(пи/6) | |
| 8 | Найти точное значение | cos(pi/4) | |
| 9 | Найти точное значение | грех(45 градусов) | |
| 10 | Найти точное значение | грех(пи/3) | |
| 11 | Найти точное значение | арктан(-1) | |
| 12 | Найти точное значение | cos(45 градусов) | |
| 13 | Найти точное значение | cos(30 градусов) | |
| 14 | Найти точное значение | желтовато-коричневый(60) | |
| 15 | Найти точное значение | csc(45 градусов) | |
| 16 | Найти точное значение | загар (60 градусов) | |
| 17 | Найти точное значение | сек(30 градусов) | |
| 18 | Найти точное значение | cos(60 градусов) | |
| 19 | Найти точное значение | соз(150) | |
| 20 | Найти точное значение | грех(60) | |
| 21 | Найти точное значение | cos(pi/2) | |
| 22 | Найти точное значение | загар (45 градусов) | |
| 23 | Найти точное значение | arctan(- квадратный корень из 3) | |
| 24 | Найти точное значение | csc(60 градусов) | |
| 25 | Найти точное значение | сек(45 градусов) | |
| 26 | Найти точное значение | csc(30 градусов) | |
| 27 | Найти точное значение | грех(0) | |
| 28 | Найти точное значение | грех(120) | |
| 29 | Найти точное значение | соз(90) | |
| 30 | Преобразовать из радианов в градусы | пи/3 | |
| 31 | Найти точное значение | желтовато-коричневый(30) | |
| 32 | Преобразование градусов в радианы 92 | ||
| 35 | Преобразовать из радианов в градусы | пи/6 | |
| 36 | Найти точное значение | детская кроватка(30 градусов) | |
| 37 | Найти точное значение | арккос(-1) | |
| 38 | Найти точное значение | арктан(0) | |
| 39 | Найти точное значение | детская кроватка(60 градусов) | |
| 40 | Преобразование градусов в радианы | 30 | |
| 41 | Преобразовать из радианов в градусы | (2 шт. )/3 )/3 | |
| 42 | Найти точное значение | sin((5pi)/3) | |
| 43 | Найти точное значение | sin((3pi)/4) | |
| 44 | Найти точное значение | тан(пи/2) | |
| 45 | Найти точное значение | грех(300) | |
| 46 | Найти точное значение | соз(30) | |
| 47 | Найти точное значение | соз(60) | |
| 48 | Найти точное значение | соз(0) | |
| 49 | Найти точное значение | соз(135) | |
| 50 | Найти точное значение | cos((5pi)/3) | |
| 51 | Найти точное значение | cos(210) | |
| 52 | Найти точное значение | сек(60 градусов) | |
| 53 | Найти точное значение | грех(300 градусов) | |
| 54 | Преобразование градусов в радианы | 135 | |
| 55 | Преобразование градусов в радианы | 150 | |
| 56 | Преобразовать из радианов в градусы | (5 дюймов)/6 | |
| 57 | Преобразовать из радианов в градусы | (5 дюймов)/3 | |
| 58 | Преобразование градусов в радианы | 89 градусов | |
| 59 | Преобразование градусов в радианы | 60 | |
| 60 | Найти точное значение | грех(135 градусов) | |
| 61 | Найти точное значение | грех(150) | |
| 62 | Найти точное значение | грех(240 градусов) | |
| 63 | Найти точное значение | детская кроватка(45 градусов) | |
| 64 | Преобразовать из радианов в градусы | (5 дюймов)/4 | |
| 65 | Найти точное значение | грех(225) | |
| 66 | Найти точное значение | грех(240) | |
| 67 | Найти точное значение | cos(150 градусов) | |
| 68 | Найти точное значение | желтовато-коричневый(45) | |
| 69 | Оценить | грех(30 градусов) | |
| 70 | Найти точное значение | сек(0) | |
| 71 | Найти точное значение | cos((5pi)/6) | |
| 72 | Найти точное значение | КСК(30) | |
| 73 | Найти точное значение | arcsin(( квадратный корень из 2)/2) | |
| 74 | Найти точное значение | загар((5pi)/3) | |
| 75 | Найти точное значение | желтовато-коричневый(0) | |
| 76 | Оценить | грех(60 градусов) | |
| 77 | Найти точное значение | arctan(-( квадратный корень из 3)/3) | |
| 78 | Преобразовать из радианов в градусы | (3 пи)/4 | |
| 79 | Найти точное значение | sin((7pi)/4) | |
| 80 | Найти точное значение | угловой синус(-1/2) | |
| 81 | Найти точное значение | sin((4pi)/3) | |
| 82 | Найти точное значение | КСК(45) | |
| 83 | Упростить | арктан(квадратный корень из 3) | |
| 84 | Найти точное значение | грех(135) | |
| 85 | Найти точное значение | грех(105) | |
| 86 | Найти точное значение | грех(150 градусов) | |
| 87 | Найти точное значение | sin((2pi)/3) | |
| 88 | Найти точное значение | загар((2pi)/3) | |
| 89 | Преобразовать из радианов в градусы | пи/4 | |
| 90 | Найти точное значение | грех(пи/2) | |
| 91 | Найти точное значение | сек(45) | |
| 92 | Найти точное значение | cos((5pi)/4) | |
| 93 | Найти точное значение | cos((7pi)/6) | |
| 94 | Найти точное значение | угловой синус(0) | |
| 95 | Найти точное значение | грех(120 градусов) | |
| 96 | Найти точное значение | желтовато-коричневый ((7pi)/6) | |
| 97 | Найти точное значение | соз(270) | |
| 98 | Найти точное значение | sin((7pi)/6) | |
| 99 | Найти точное значение | arcsin(-( квадратный корень из 2)/2) | |
| 100 | Преобразование градусов в радианы | 88 градусов |
тригонометрия — Решить уравнение $ \cos x+\sin x=0$
спросил
Изменено 1 год, 9 месяцев назад
Просмотрено 14 тысяч раз
$\begingroup$
Я пытаюсь решить здесь уравнение, но, к сожалению, не могу. 2), t=\tan x/2, \ $, но я не могу найти правильное решение.
Также я пробовал квадратировать обе стороны, но все равно ничего.
2), t=\tan x/2, \ $, но я не могу найти правильное решение.
Также я пробовал квадратировать обе стороны, но все равно ничего.
Кто-нибудь может мне помочь?
- тригонометрия
$\endgroup$
1
$\begingroup$
Обратите внимание, что $\cos x + \sin x = 0 \iff \cos x = -\sin x$$
Теперь $\cos x$ не может равняться нулю, так как в противном случае $\sin x = -1$ или $\sin x = 1$, в этом случае данное уравнение не выполняется.
Итак, мы можем разделить на $\cos x$, чтобы получить $$1 = \dfrac{-\sin x}{\cos x} = -\tan x \iff \tan x = -1$$ 92x+2\sin x \cos x=0 \Rightarrow 1+\sin2x=0$$
Используя $\sin 2x = 2\sin x \cos x$.
Это означает, что
$$\sin 2x = -1$$ и, следовательно, $$2x = \frac {3\pi}{2}+2k\pi \Rightarrow x=\frac {3\pi}{4 }+k\pi$$
$\endgroup$
$\begingroup$
Я собираюсь пройти через это, предполагая, что вы ищете решения в пределах $[0,2\pi]$.
$\cos х+\sin х=0$ $\implies \cos x=-\sin x$
С помощью этого мы можем вытащить нашу верную старую единичную окружность:
Затем нам нужно найти любые углы на окружности, где $\cos x = -\sin x$
Извините за низкое разрешение на втором изображении. Но, как видите, у нас есть свои углы. Решениями $\sin x+\cos x=0$ между $[0,2\pi]$ являются $\frac{3\pi}{4}$ и $\frac{7\pi}{4}$.
Надеюсь, это поможет!
$\endgroup$
1
$\begingroup$
Так как $$\cos x+\sin x=\sqrt 2\sin(x+(\pi/4)),$$ ты можешь решить $$\sin(x+(\pi/4))=0.$$
Следовательно, у вас будет $$x+(\pi/4)=n\pi\ \ \ (n\in\mathbb Z).$$
$\endgroup$
$\begingroup$
Подсказка :
$\cos x=-\sin x=\cos\left(\frac{1}{2}\pi+x\right)$
$\cos x=\cos\alpha $ дает $x=\pm\alpha+2k\pi$ для $k\in\mathbb{Z}$
$\endgroup$
$\begingroup$
У вас уже есть несколько хороших ответов, но просто для удовольствия есть еще один способ:
$$\cos x+\sin x=\cos x+\cos(π/2-x)=2\cos(π/4)\cos(x-π/4)=0,$$ откуда следует $$ \cos(x-π/4)=0,$$, так что имеем $$x-\fracπ4=\fracπ2+πk,$$, где $k$ — любое целое число. Наконец, это дает $$x=\frac{3π}{4}+πk,k\in\mathrm Z.$$
Наконец, это дает $$x=\frac{3π}{4}+πk,k\in\mathrm Z.$$
$\endgroup$
$\begingroup$
$$\cos x + \sin x = 0$$
Умножить $\dfrac{\sqrt2}{2}$ в обе стороны:
$$\dfrac{\sqrt2}{2}\cos x + \dfrac{\sqrt2}{2}\sin x = 0$$
Или:
$$\cos\dfrac{\pi}{4}\cos x + \sin\dfrac{\pi}{4}\sin x = 0$$
Тогда:
$$\cos\left( x — \dfrac{\pi}{4}\right) = 0$$
Итак:
$$x — \dfrac{\pi}{4} = \dfrac{\pi}{2} + k\ pi$$
Следовательно:
$$x = \dfrac{3\pi}{4} + k\pi\qquad (k \in \Bbb Z)$$
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Обязательно, но не отображается
Опубликовать как гость
г.
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.Если sin θ = 12/13, найдите значение sin² θ- cos² θ/2 sin θ.cos θ x 1/tan² θ
Тригонометрия — это, в основном, изучение отношений между углами и сторонами треугольника. Это одна из широко используемых тем математики, которая используется в повседневной жизни. Он включает в себя операции над прямоугольным треугольником, т.е. треугольником, один из углов которого равен 90 ° . Есть некоторые термины, которые мы должны знать, прежде чем идти дальше. Эти термины,
- Гипотенуза — это сторона, противоположная прямому углу в прямоугольном треугольнике.
 Это самая длинная сторона прямоугольного треугольника. На рисунке 1 сторона AC является гипотенузой.
Это самая длинная сторона прямоугольного треугольника. На рисунке 1 сторона AC является гипотенузой. - Перпендикуляр – перпендикуляр треугольника, соответствующий особо острому углу θ, является стороной, противоположной углу θ. На рисунке 1 сторона AB — это перпендикуляр, соответствующий углу θ.
- Основание – это сторона, примыкающая к особо острому углу θ. На рис. 1 сторона ВС является основанием, соответствующим углу θ.
Рисунок 1
Как было сказано ранее, тригонометрия отображает соотношение между углами и сторонами прямоугольного треугольника. Эти отношения представлены стандартными отношениями и даны следующим образом,
- Синус (sin) Синусом угла θ называется отношение длины перпендикуляра, соответствующего углу θ, к длине гипотенузы треугольника.
sin θ = перпендикуляр/гипотенуза = p/h
- Косинус (cos) Косинус угла θ – это отношение длины основания, соответствующего углу θ, к длине гипотенузы треугольника.

cos θ = основание/гипотенуза = b/h
- Тангенс (tan) Тангенс угла θ – это отношение длины перпендикуляра, соответствующего углу θ, к длине основания для данного угла треугольника.
tan θ = перпендикуляр/основание = p/b
- Котангенс (котангенс) Это обратная величина касательной.
cot θ = 1/tan θ=основание/перпендикуляр = b/p
- Секанс (сек) Это величина, обратная косинусу.
сек θ = 1/cos θ = гипотенуза/основание = h/b
- Косеканс (косек) Это величина, обратная синусу.
cosec θ = 1/sin θ = гипотенуза/перпендикуляр = h/p
Также существуют соотношения между каждым из этих отношений, и некоторые из них, которые мы будем использовать, следующие:
- tan θ = sin θ/cos θ
- cot θ = cos θ/ sin θ
- sin² θ + cos² θ =1
Если sin θ = 12/13, 0°
< θ < 90°, найдите значение sin² θ – cos² θ /2 sin θ × cos θ × 1/tan² θРешение:
Дано,
SIN θ = 12/13
SIN² θ = 144/169
Это известно,
SIN² θ + Cos² θ = 1
,
SIN² θ + Cos² θ = 1
SIN² θ + Cos² θ = 1
.
cos θ = √(1 – sin² θ)
Здесь sin θ = 12/13
Следовательно,
cos θ = √(1 – (12/13) 2 )
co √(1 – 144/169)
cos θ = √((169 – 144)/169)
cos θ = √(25/169)
cos θ = 5/13
/ и cos² θ = 169
тангенс θ = sin θ/cos θ
тангенс θ = (12/13)/(5/13)
тангенс θ = (12/13) × (13/5)
тангенс θ = 12/5
тангенс 2 θ = 144/25
Имея все это в наших руках, теперь найдите значение нашего уравнения
= (144/169 – 25/169)/(2 × 12/13 × 5/13) × 1/(144/25)
= (119/169) / (120/169) × (25/ 144)
= (119/169) × (169/120) × (25/144)
= 0,172
Следовательно, искомый ответ данного уравнения равен 0,172.
Аналогичные задачи
Вопрос 1. Если sin θ = 1/2 и cos ϕ = √3/2, то найдите значение (tan θ + tan ϕ)/(1- tan θ × tan ϕ).
Решение:
sin θ = 1/2
sin² θ + cos² θ = 1
cos² θ = 1 — sin² θ
cos θ = √ (1— sin θ θ
1810 cos θ = √ (1— sin θ θ θ10cos = √ (1— sin θ θ θ
10cos = √ (1— sin)
10 cos = in)
.
= √(1 – 1/4)
cos θ = √3/2
тангенс θ = sin θ / cos θ
= (1/2)/(√3/2)
= 1/√3
Аналогично,
sin ϕ = √(1 – cos 2 ϕ)
= √(1 – 3/ 4)
= 1/2
tan ϕ = sin ϕ / cos ϕ
= (1/2)/(√3/2)
= 1/√3
Следовательно,
+(tan θ tan ϕ) /(1- tan θ × tan ϕ) = (1/√3 + 1/√3)/( 1 -1/√3 × 1/√3)
= (2/√3)/( 1 – 1/3)
= (2/√3)/(2/3)
= (2/√3) × (3/2)
= √3
Вопрос 2: Если 5 cos x – 12 sin x = 0, затем найдите значение (sin x + cos x)/(2 cos x – sin x).
Решение:
5 COS X — 12 SIN X = 0
5 COS X = 12 SIN X
5 = 12 × SINX/COS X
5 = 12 TANX
13TAN X = 5. /12
(sin x + cos x)/(2 cos x – sin x)
деление числителя и знаменателя на cos x,
(tan x + 1)/(2 – tan x)
= ( 5/12 + 1)/(2 – 5/12)
= (17/12)/(19/12)
= 17/19
Вопрос 3: Если a cos x + b sin x= t и a sin x – b cos x = u, затем найдите sin x и cos x.
Решение:
Дано,
a cos x + b sin x = t ⇢ (i)
a sin x – b cos x = u ⇢ (ii)
3, 91 × i ) + a × (ii),
ab cos x + b 2 sin x + a 2 sin x – ab cos x = bt + a
sin x (a 2 + b 2 ) = bt + au
sin x = (bt + au)/(a 2 + b 2 )
Аналогично,
. 2 cos x + ab sin x – ab sin x + b 2 cos x = at – bu
cos x (a 2 + b 2 ) = at – bu
cos x = (at – bu)/(a 2 + b 2 )
Вопрос 4: В прямоугольном треугольнике ABC угол B = 90 ° и tg C = 1/2. Если AC = 5, найдите длины сторон AB и BC.
Решение:
Дано, тангенс C = 1/2
тангенс C = p/b = AB/BC
Следовательно,
tan C = AB/BC =1/2
Пусть AB и BC равны k и 2k соответственно.
By Pythagoras’ theorem,
AB 2 + BC 2 = AC 2
k 2 + (2k) 2 = 52
5 k 2 = 25
k 2 = 5
k = √5
Следовательно,
AB = k = √5 и
BC = 2k = 2√51810 LearnPracticeDownload
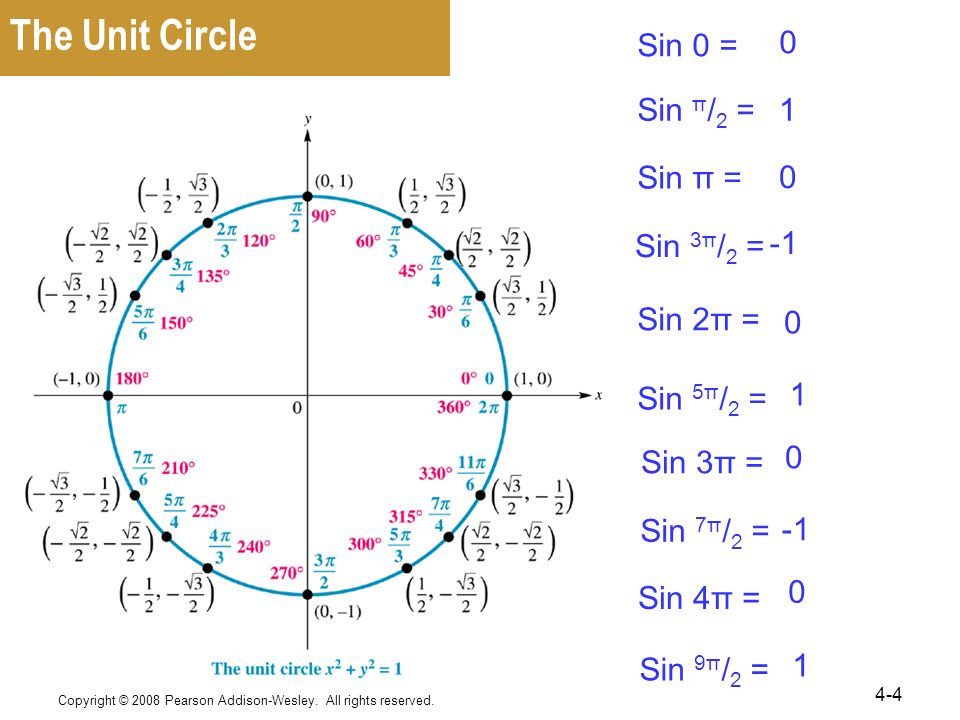
Значение sin pi/2 равно 1 . Sin пи/2 радиан в градусах записывается как sin ((π/2) × 180°/π), т. е. sin (90°). В этой статье мы обсудим методы определения значения sin pi/2 на примерах.
- Синус пи/2: 1
- Sin (-pi/2): -1
- Sin pi/2 в градусах: sin (90°)
Каково значение Sin pi/2?
Значение sin pi/2 равно 1. Sin pi/2 также можно выразить с помощью эквивалента заданного угла (pi/2) в градусах (90°).
Мы знаем, используя преобразование радиан в градусы, θ в градусах = θ в радианах × (180°/pi)
⇒ пи/2 радиан = пи/2 × (180°/пи) = 90° или 90 градусов
∴ sin pi/2 = sin π/2 = sin(90°) = 1Пояснение:
Для sin pi/2 угол pi/2 лежит на положительной оси y.
Таким образом, значение sin pi/2 = 1
Поскольку функция синуса является периодической функцией, мы можем представить sin pi/2 как sin pi/2 = sin(pi/2 + n × 2pi), n ∈ Z.
⇒ грех пи/2 = грех 5пи/2 = грех 9пи/2 и так далее.
Примечание: Поскольку синус является нечетной функцией, значение sin(-pi/2) = -sin(pi/2).Методы нахождения значения sin pi/2
Значение sin pi/2 задается как 1. Мы можем найти значение sin pi/2 по:
- Используя тригонометрические функции
- Использование единичного круга
Sin pi/2 в терминах тригонометрических функций
Используя формулы тригонометрии, мы можем представить sin pi/2 как:
- ± √(1-cos²(pi/2))
г.- ± тангенс(пи/2)/√(1 + тангенс²(пи/2))
- ± 1/√(1 + кроватка²(пи/2))
- ± √(сек²(пи/2) — 1)/сек(пи/2)
- 1/косек(пи/2)
Примечание: Поскольку число pi/2 лежит на положительной оси ординат, окончательное значение sin pi/2 равно 1.
Мы можем использовать тригонометрические тождества для представления sin pi/2 в виде — пи/2) = sin пи/2
-sin(pi + pi/2) = -sin 3pi/2 cos(pi/2 — pi/2) = cos 0 г.-cos(pi/2 + pi/2) = -cos pi Sin pi/2 с помощью единичной окружности
Чтобы найти значение sin π/2 с помощью единичной окружности:
- Поверните ‘r’ против часовой стрелки, чтобы образовать угол pi/2 с положительной осью x.
- Синус pi/2 равен координате y(1) точки пересечения (0, 1) единичной окружности и r.
Отсюда значение sin pi/2 = y = 1
☛ Также проверьте:
- tan pi
г.- потому что 11pi/6
- желтовато-коричневый 11pi/12
- потому что 2pi/8
- грех 4pi/3
- потому что 7pi/6
Примеры использования Sinpi/2
Пример 1. Найдите значение sin(pi/2), если cosec(pi/2) равно 1.
Решение:
Так как sin pi/2 = 1/csc(pi/2)
⇒ sin пи/2 = 1/1 = 1Пример 2.
Найдите значение 5 sin(pi/2)/7 cos(0).
Решение:
Используя тригонометрические тождества, мы знаем, что sin(pi/2) = cos(pi/2 — pi/2) = cos(0).
⇒ sin(pi/2) = cos(0)
⇒ Значение 5 sin(pi/2)/7 cos(0) = 5/7Пример 3. Используя значение sin pi/2, найдите: (1-cos²(pi/2)).
Решение:
Мы знаем, (1-cos²(pi/2)) = (sin²(pi/2)) = 1
⇒ (1-cos²(pi/2)) = 1перейти к слайдуперейти к слайдуперейти к слайду
Готовы увидеть мир глазами математика?
Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.
Забронируйте бесплатный пробный урок
Часто задаваемые вопросы о Sin pi/2
Что такое Sin pi/2?
Sin pi/2 — значение тригонометрической функции синуса для угла, равного pi/2 радианам.
Значение sin pi/2 равно 1.
Каково значение Sin pi/2 в пересчете на Cot pi/2?
Мы можем представить функцию синуса в терминах функции котангенса, используя тригонометрические тождества, sin pi/2 можно записать как 1/√(1 + cot²(pi/2)). Здесь значение cot pi/2 равно 0.
Как найти значение Sin pi/2?
Значение sin pi/2 можно вычислить, построив угол π/2 радиан с осью x, а затем найдя координаты соответствующей точки (0, 1) на единичной окружности. Значение sin pi/2 равно координате y (1). ∴ sin пи/2 = 1,
Каково значение Sin pi/2 в пересчете на Cosec pi/2?
Поскольку функция косеканса является обратной величиной функции синуса, мы можем записать sin pi/2 как 1/cosec(pi/2). Значение cosec pi/2 равно 1.
Как найти Sin pi/2 в терминах других тригонометрических функций?
Используя формулу тригонометрии, значение sin π/2 можно выразить через другие тригонометрические функции следующим образом:
- ± √(1-cos²(pi/2))
- ± тангенс(пи/2)/√(1 + тангенс²(пи/2))
г.- ± 1/√(1 + кроватка²(пи/2))
- ± √(сек²(пи/2) — 1)/сек(пи/2)
- 1/косек(пи/2)
☛ Также проверьте: Тригонометрическая таблица
Скачать БЕСПЛАТНЫЕ учебные материалы
Тригонометрия
Рабочие листы по математике и
наглядная программаПроизводные тригонометрических функций
Три наиболее полезных производных в тригонометрии:
d dx sin(x) = cos(x)
г.d dx cos(x) = −sin(x)
d dx tan(x) = sec 2 (x)
Они просто упали с неба? Можем ли мы их как-то доказать?Доказательство производной синуса
Нам нужно вернуться, прямо к первым принципам, основной формуле для производных:
dy dx = lim Δx→0 f(x+Δx)−f(x) Δx
Поп в sin(x):
г.d dx sin(x) = lim Δx→0 sin(x+Δx)−sin(x) Δx
Затем мы можем использовать это тригонометрическое тождество: sin(A+B) = sin(A)cos(B) + cos(A)sin(B), чтобы получить:
lim Δx→0 sin(x)cos(Δx) + cos(x)sin(Δx) − sin(x) Δx
Перегруппировка:
lim Δx→0 sin(x)(cos(Δx)−1) + cos(x)sin(Δx) Δx
Разделить на два лимита:
LIM ΔX → 0 SIN (x) (COS (Δx) −1) Δx + LIM Δx → 0 COS (x Ар (xbre x) x Cos (xbr Δx → 0 Cos (x.
X ).
И мы можем вывести sin(x) и cos(x) за пределы, потому что они являются функциями x, а не Δx
sin(x) lim Δx→0 cos(Δx)−1 Δx + cos(x) lim Δx→0
19×539 sin2(Δ4)7 Δx
Теперь все, что нам нужно сделать, это оценить эти два маленьких предела. Легко, верно? Ха!
Предел
sin(θ) θНачиная с
lim θ→0 sin(θ) θ
с помощью некоторой геометрии:
Можем посмотреть области:
Площадь треугольника AOB < Площадь сектора AOB < Площадь треугольника AOC
г.1 2 R 2 SIN (θ) < 1 2 R 2 θ < 99999999970 θ < 9999999970 θ < 99 θ .
Разделить все члены на 1 2 r 2 sin(θ)
1 < θ sin(θ) < 1 cos(θ)
Возьми обратку:
1 > sin(θ) θ > cos(θ)
г.Теперь, когда θ→0, тогда cos(θ)→1
Итак, sin(θ) θ лежит между 1 и чем-то, что стремится к 1
Так как θ→0, то sin(θ) θ →1 и так:
lim θ→0 sin(θ) θ = 1
(Примечание: мы также должны доказать, что это верно с отрицательной стороны, как насчет того, чтобы попробовать с отрицательными значениями θ ?)
Предел
cos(θ)−1 θИтак, далее мы хотим узнать вот это:
lim θ→0 cos(θ)−1 θ
Когда мы умножаем верх и низ на cos(θ)+1, получаем:
(cos(θ)−1)(cos(θ)+1) θ(cos(θ)+1) = cos 2 (θ)−1 θ(cos(θ)+ 1)
Теперь мы используем это тригонометрическое тождество, основанное на теореме Пифагора:
cos 2 (х) + sin 2 (х) = 1
г.Преобразовано в эту форму:
cos 2 (x) − 1 = −sin 2 (x)
И предел, с которого мы начали, может стать:
lim θ→0 −sin 2 (θ) θ(cos(θ)+1)
Выглядит хуже! Но на самом деле лучше, потому что мы можем превратить его в два предела, умноженных вместе:
lim θ→0 sin(θ) θ × lim θ→0 −sin(θ) cos(θ)+1
Мы знаем первый предел (мы вычислили его выше), а второй предел не требует особых усилий, потому что при θ=0 мы непосредственно знаем, что −sin(0) cos(0)+1 = 0, значит:
lim θ→0 sin(θ) θ × lim θ→0 −sin(θ) cos(θ)+1 = 1 × 0 = 0
Собираем вместе
Так что же мы опять пытались сделать? О, верно, мы очень хотели это проработать:
г.d dx sin(x) = sin(x) lim Δx→0 cos(Δx)−1 Δx + cos(x) lim Δx→0 sin (Δx) Δx
Теперь мы можем подставить значения, которые мы только что вычислили, и получить:
d dx sin(x) = sin(x) × 0 + cos(x) × 1
И так (та да!):
d dx sin(x) = cos(x)
Производная косинуса
г.Теперь косинус!
d dx cos(x) = lim Δx→0 cos(x+Δx)−cos(x) Δx
На этот раз мы будем использовать формулу угла cos(A+B) = cos(A)cos(B) − sin(A)sin(B) :
lim Δx→0 cos(x)cos(Δx) − sin(x)sin(Δx) − cos(x) Δx
Изменить на:
lim Δx→0 cos(x)(cos(Δx)−1) − sin(x)sin(Δx) Δx
Разделить на два лимита:
LIM Δx → 0 COS (x) (COS (Δx) −1) Δx — Lim Δx → 0 (x Δx → 0 (x Δx → 0 (x Δx → 0 (x .
Мы можем вывести cos(x) и sin(x) за пределы, потому что они являются функциями x, а не Δx
cos(x) lim Δx→0 cos(Δx)−1 Δx − sin(x) lim Δx→0 sin(Δx2540 Δx
И используя наши знания свыше:
d dx cos(x) = cos(x) × 0 − sin(x) × 1
И так:
d dx cos(x) = −sin(x)
Производная касательной
Чтобы найти производную от tan(x), мы можем использовать это тождество:
tan(x) = sin(x) cos(x)
Начнем с:
г дх tan(x) = d dx ( sin(x) cos(x) )
Теперь мы можем воспользоваться правилом частных производных:
( f g )’ = gf’ − fg’ g 2
И получаем:
d dx tan(x) = cos(x) × cos(x) − sin(x) × −sin(x) cos 2 (x)
d dx tan(x) = cos 2 (x) + sin 2 (х) cos 2 (х)
Тогда используйте этот идентификатор:
cos 2 (х) + sin 2 (х) = 1
Чтобы получить
d dx tan(x) = 1 cos 2 (x)
Готово!
Но большинству людей нравится использовать тот факт, что cos = 1 сек , чтобы получить:
d dx tan(x) = sec 2 (x)
Примечание: мы также можем сделать это:
d dx tan(x) = cos 2 (x) + sin 2 (x) cos 2 (x)
d dx tan(x) = 1 + sin 2 (x) cos 2 (x) = 1 + tan 2 х (1x )
(И, да, 1 + загар 2 (x) = sec 2 (x) в любом случае, см.

 Перевод единиц измерения физических величин. Таблицы перевода единиц величин. Перевод химических и технических единиц измерения величин. Величины измерения. Таблицы соответствия величин.
Перевод единиц измерения физических величин. Таблицы перевода единиц величин. Перевод химических и технических единиц измерения величин. Величины измерения. Таблицы соответствия величин.
 0872
0872 2756
2756 454
454 6157
6157 7547
7547 866
866 9455
9455 9903
9903 9998
9998 9781
9781 9205
9205 829
829 7071
7071 5592
5592 3907
3907 2079
2079 0175
0175 1219
1219 2924
2924 454
454 6018
6018 7314
7314 8387
8387 9205
9205 9744
9744 9986
9986 9962
9962 9659
9659 9063
9063 8192
8192 7071
7071 5736
5736 4226
4226 2588
2588 0872
0872 Углы с шагом в 1°. Таблица значений синусов.
Углы с шагом в 1°. Таблица значений синусов. 0175
0175 2079
2079 3907
3907 5592
5592 7071
7071 829
829 9205
9205 9781
9781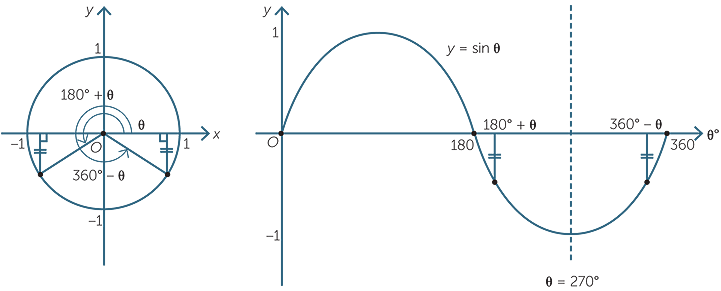 9998
9998 9925
9925 9511
9511 8746
8746 766
766 6293
6293 4695
4695 2924
2924 1045
1045 0349
0349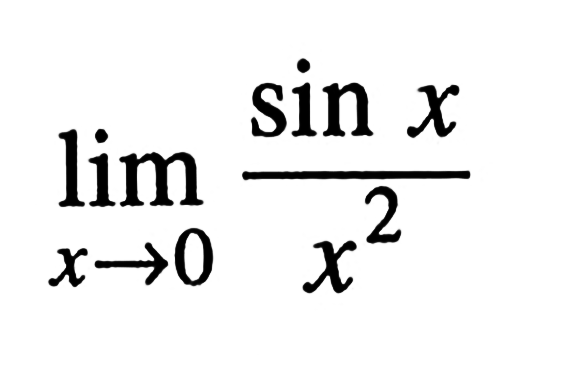 2079
2079 3746
3746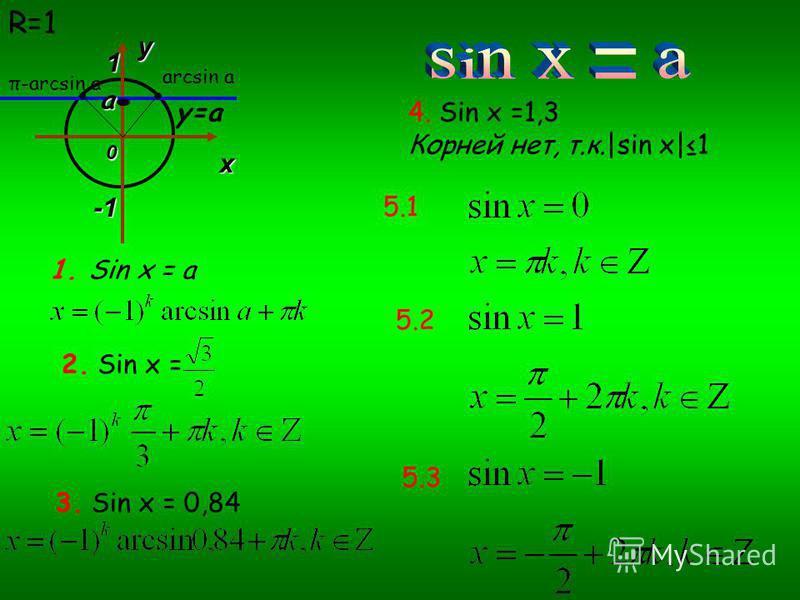 5299
5299 6691
6691 788
788 8829
8829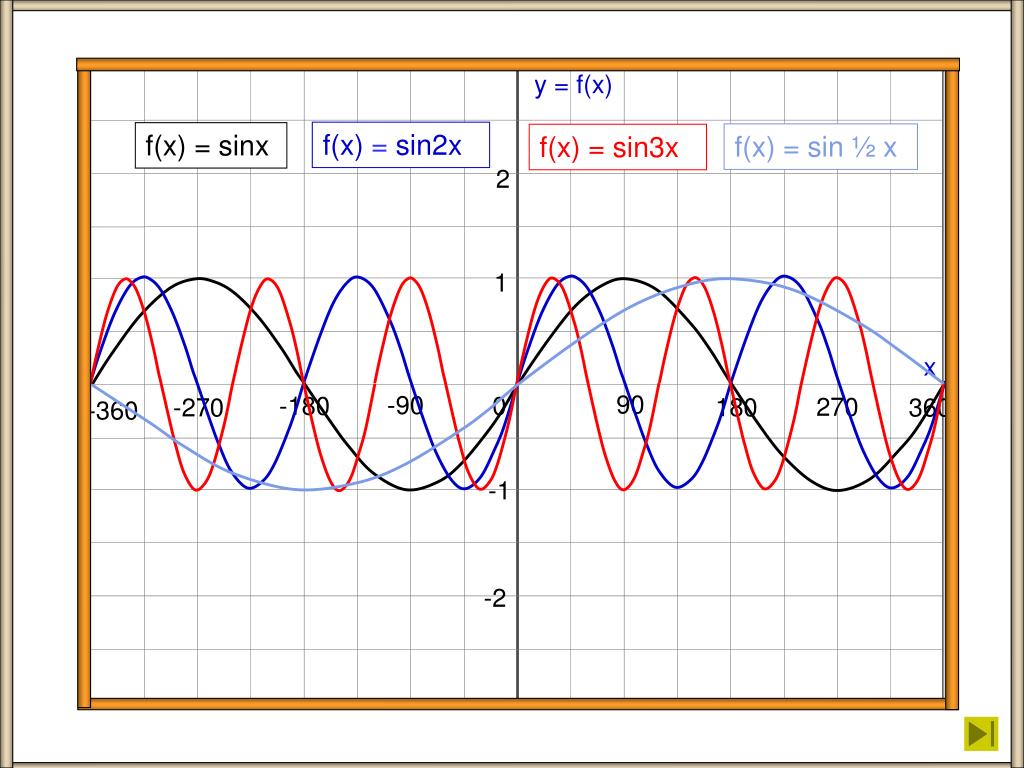 9511
9511 9903
9903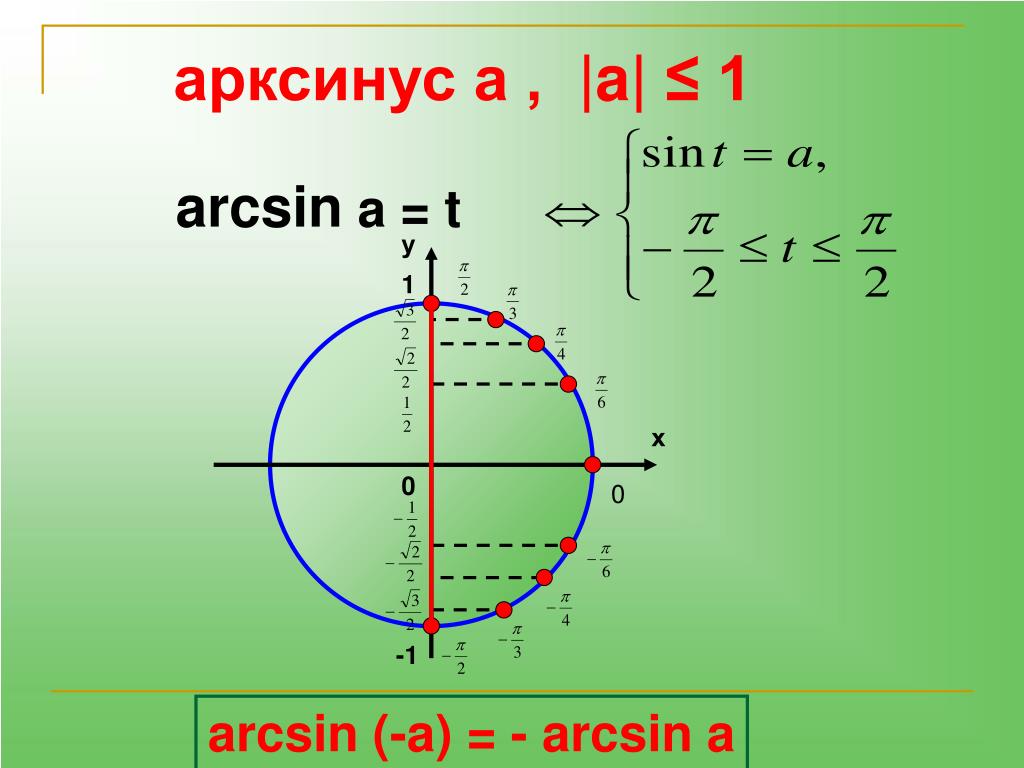 9998
9998 9816
9816 9336
9336 8572
8572 7547
7547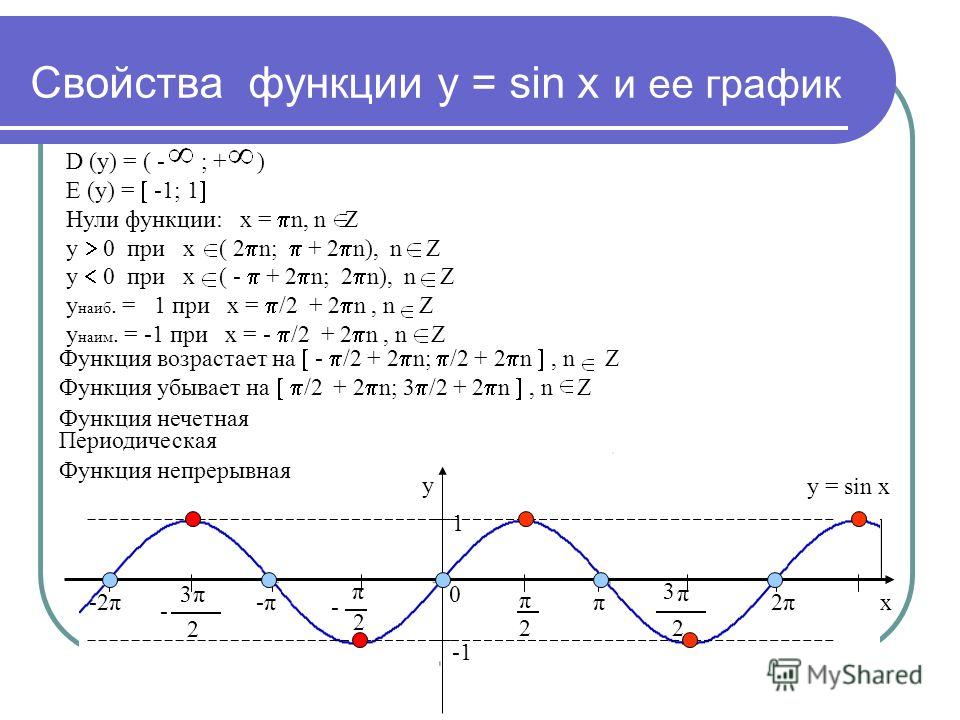 6293
6293 4848
4848 3256
3256 1564
1564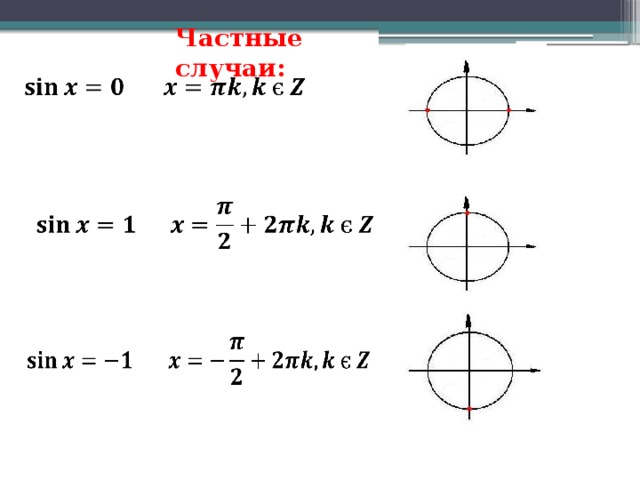 Это самая длинная сторона прямоугольного треугольника. На рисунке 1 сторона AC является гипотенузой.
Это самая длинная сторона прямоугольного треугольника. На рисунке 1 сторона AC является гипотенузой.

 = √(1 – 1/4)
= √(1 – 1/4)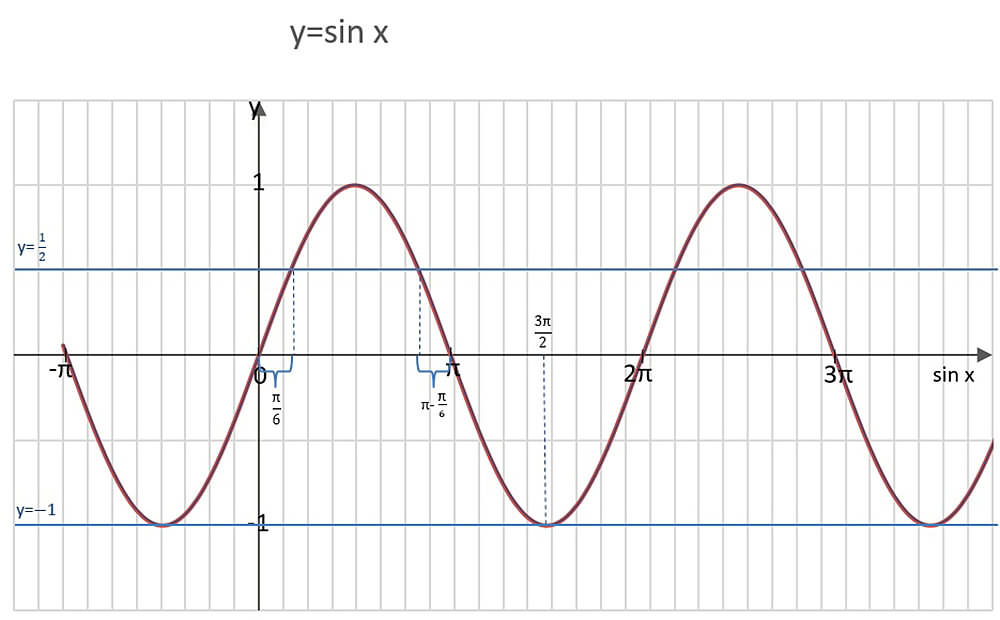
 Таким образом, значение sin pi/2 = 1
Таким образом, значение sin pi/2 = 1 
 Найдите значение 5 sin(pi/2)/7 cos(0).
Найдите значение 5 sin(pi/2)/7 cos(0). 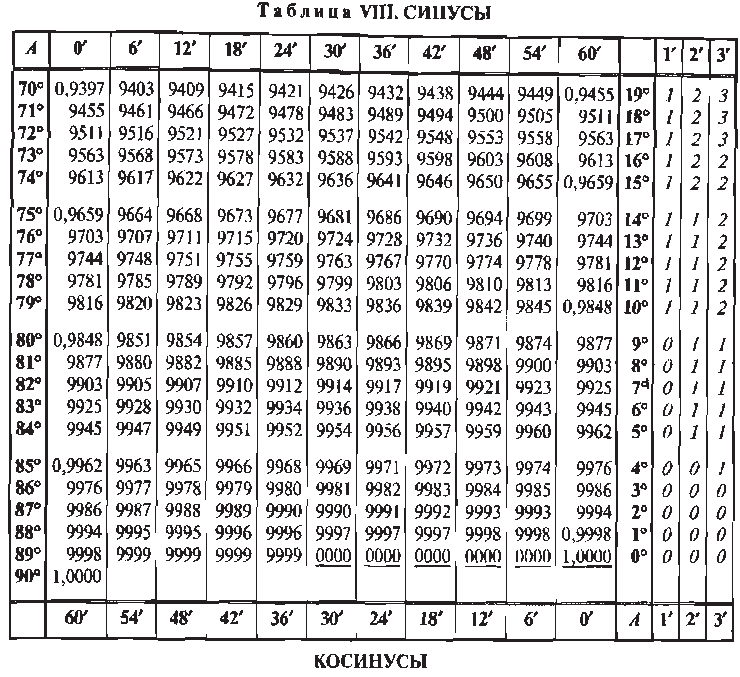 Значение sin pi/2 равно 1.
Значение sin pi/2 равно 1. 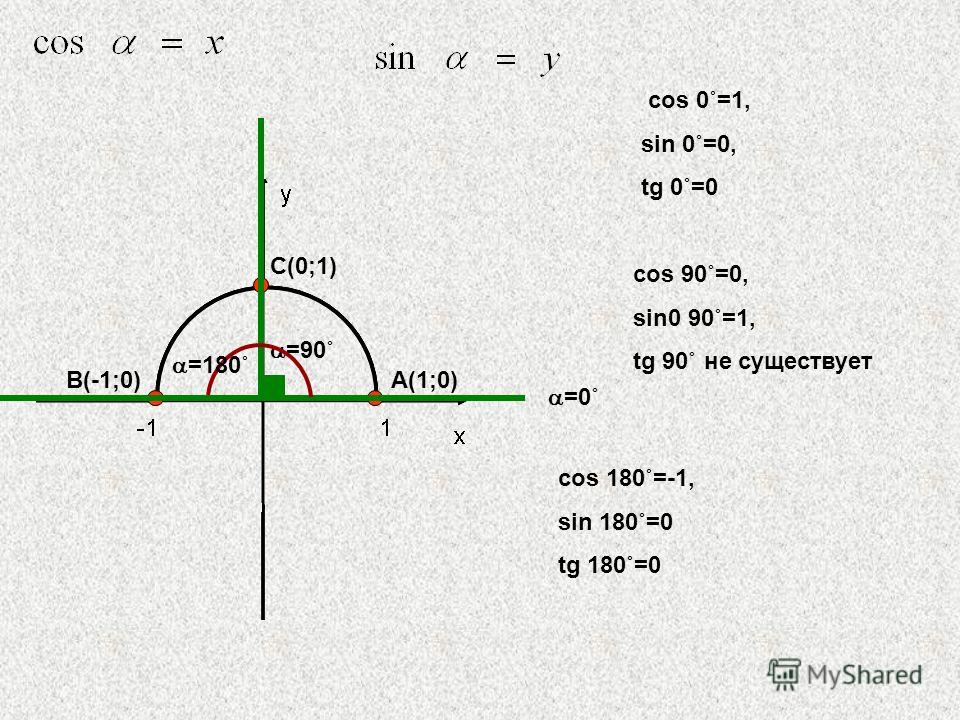
 X ).
X ).