Лучший ответ по мнению автора | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
| |||||||||||||||||
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||
Посмотреть всех экспертов из раздела Учеба и наука
| Похожие вопросы |
решите уравнение ((tgx+корень из 3)*log_13 (2sin^2 x))/log_31 (корень из 2 *Cosx)
Решено
Радиус вписанной в квадрат окружности равен 4√2 найти радиус окружности описанной около этого квадрата
На экзамене 20 билетов, Андрей не выучил 1 из них.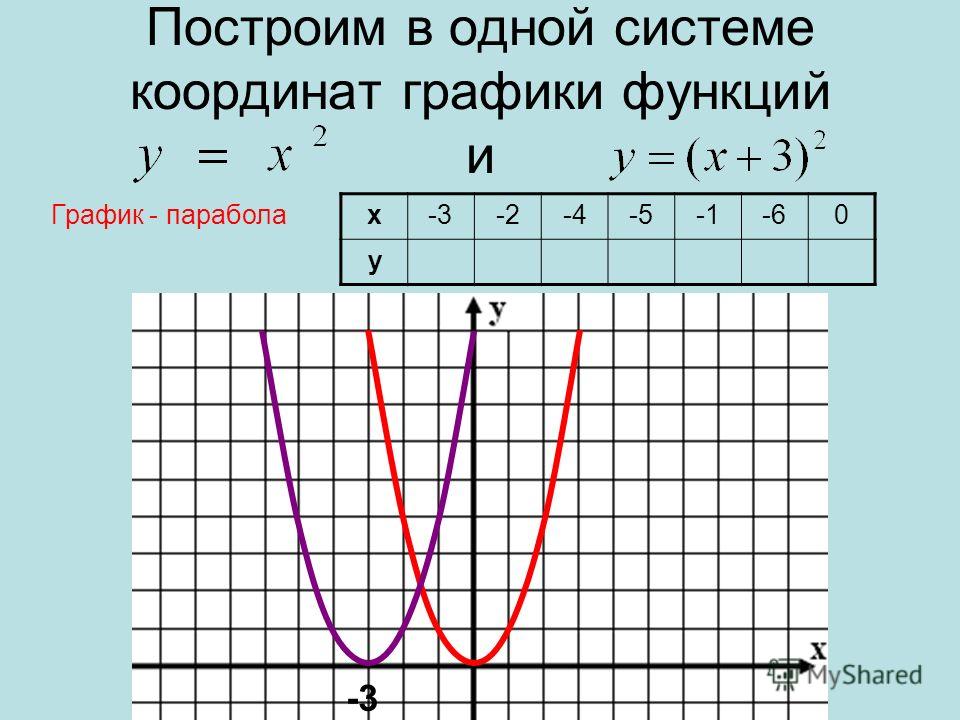 Найдите вероятность того, что ему попадется выученный билет
Найдите вероятность того, что ему попадется выученный билет
Na2SO3 h3SO4 Na2S=S Na2SO4 h3O…
Геометрическая прогрессия (bn) задана условиями:b1=-6,bn+1=3bn.Найдите сумма первых пяти членов.
Пользуйтесь нашим приложением
График 2x 2. Функции. Основные виды, графики, способы задания. Теперь попробуем найти область значений функции
Построение графиков онлайн весьма полезный способ графически отобразить то, что не в силах передать словами.
Информация – это будущее электронного маркетинга, при этом правильно преподнесенные зрительные образы являются мощным инструментом для привлечения целевой аудитории.
Тут на помощь приходит инфографика, позволяющая в простой и выразительной форме преподносить различного рода информацию.
Однако построение инфографических изображений требует определенного аналитического мышления и богатства фантазии.
Спешим вас обрадовать – в интернете достаточно ресурсов, предоставляющих построение графиков онлайн.
Yotx.ru
Замечательный русскоязычный сервис, осуществляющий построение графиков онлайн по точкам (по значениям) и графиков функций (обычных и параметрических).
Этот сайт обладает интуитивно понятным интерфейсом и легок в использовании. Не требует регистрации, что существенно экономит время пользователя.
Позволяет быстро сохранять готовые графики на компьютере, а также генерирует код для размещения на блоге или сайте.
На Yotx.ru есть учебник и примеры графиков, которые были созданы пользователями.
Возможно, для людей, углубленно изучающих математику или физику, этого сервиса будет мало (например, нельзя построить график в полярных координатах, так как на сервисе нет логарифмической шкалы), но для выполнения самых простых лабораторных работ вполне достаточно.
Преимуществом сервиса является то, что он не заставляет как многие другие программы, искать полученный результат по всей двумерной плоскости.
Размер графика и интервалы по осям координат автоматически генерируются так, чтобы график оказался удобным для просматривания.
Одновременно на одной плоскости есть возможность построить несколько графиков.
Дополнительно на сайте можно использовать калькулятор матриц, с помощью которого легко производить различные действия и преобразования.
ChartGo
Англоязычный сервис для разработки многофункциональных и разноцветных гистограмм, линейных графиков, круговых диаграмм.
Для обучения пользователям представляется подробное руководство и деморолики.
ChartGo будет полезен для тех, кто нуждается в регулярно. Среди подобных ресурсов отличается простотой «Create a graph online quickly».
Построение графиков онлайн осуществляется по таблице.
В начале работы необходимо выбрать одну из разновидностей диаграмм.
Приложение обеспечивает пользователям ряд простых вариантов настройки построения графиков различных функций в двумерных и трехмерных координатах.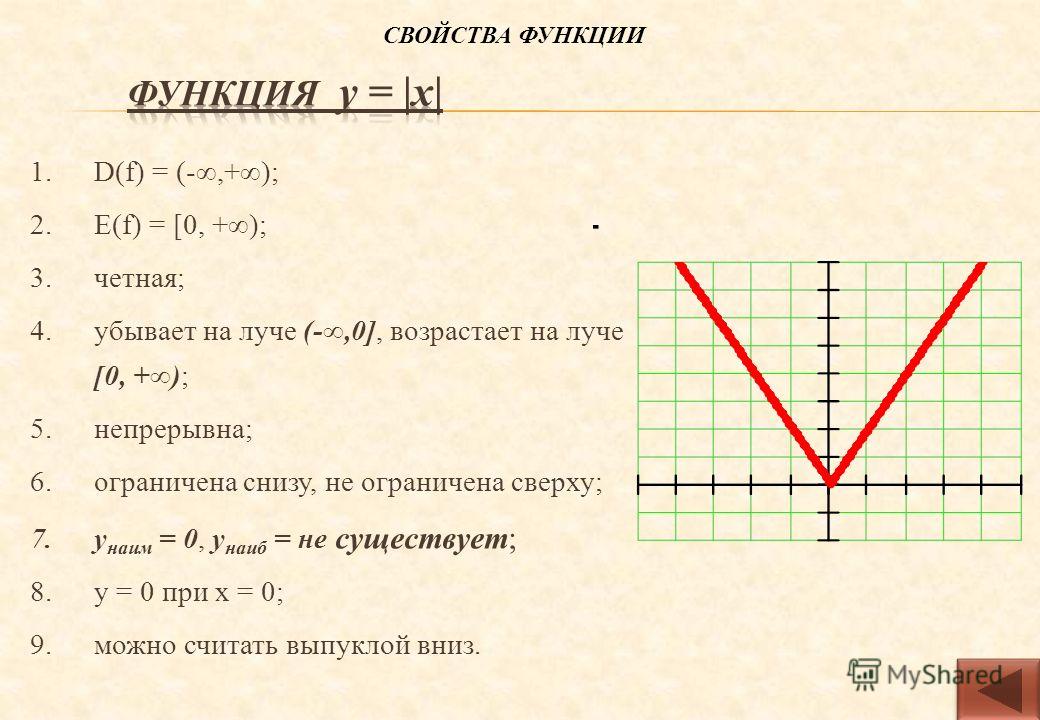
Можно выбрать одну из разновидностей диаграмм и переключаться между 2D и 3D.
Настройки размера обеспечивают максимальный контроль между вертикальной и горизонтальной ориентацией.
Пользователи могут настраивать свои диаграммы с уникальным названием, а также присваивать названия для X и Y элементов.
Для построения графиков онлайн xyz в разделе «Example» доступно множество макетов, которые можно изменять на свое усмотрение.
Обратите внимание! В ChartGo в одной прямоугольной системе может быть построено множество графиков. При этом каждый график составлен с помощью точек и линий. Функции действительного переменного (аналитические) задаются пользователем в параметрическом виде.
Разработан и дополнительный функционал, который включает мониторинг и вывод координат на плоскости или в трехмерной системе, импорт и экспорт числовых данных в определенных форматах.
Программа имеет гибко настраиваемый интерфейс.
После создания диаграммы, пользователь может воспользоваться функцией печати результата и сохранения графика в виде статичного рисунка.
OnlineCharts.ru
Еще одно отличное приложение для эффектного представления информации вы можете найти на сайте OnlineCharts.ru, где можно построить график функции онлайн бесплатно.
Сервис способен работать с множеством видов диаграмм, включая линейные, пузырьковые, круговые, столбчатые и радиальные.
Система обладает очень простым и наглядным интерфейсом. Все доступные функции разделены вкладками в виде горизонтального меню.
Чтобы начать работу необходимо выбрать тип диаграммы, которую вы хотите построить.
После этого можно настроить некоторые дополнительные параметры внешнего вида, в зависимости от выбранного типа графика.
Во вкладке «Добавить данные» пользователю предлагается задать количество строк и если необходимо количество групп.
Также можно определить цвет.
Обратите внимание! Вкладка «Подписи и шрифты» предлагает задать свойства подписей (нужно ли их выводить вообще, если да, то каким цветом и размером шрифта). Также предоставляется возможность выбора типа шрифта и его размера для основного текста диаграммы.
Также предоставляется возможность выбора типа шрифта и его размера для основного текста диаграммы.
Все предельно просто.
Aiportal.ru
Самый простой и наименее функциональный из всех, представленных здесь онлайн-сервисов. Создать трехмерный график онлайн на этом сайте не удастся.
Он предназначен для построения графиков сложных функций в системе координат на определенном интервале значений.
Для удобства пользователей сервис предоставляет справочные данные по синтаксису различных математических операций , а также по перечню поддерживаемых функций и константных значений.
Все необходимые для составления графика данные вводятся в окно «Функции». Одновременно на одной плоскости пользователь может построить несколько графиков.
Поэтому разрешается вносить подряд несколько функций, но после каждой функции необходимо вставлять точку с запятой. Также задается и область построения.
Предусмотрена возможность построения графиков онлайн по таблице или без нее.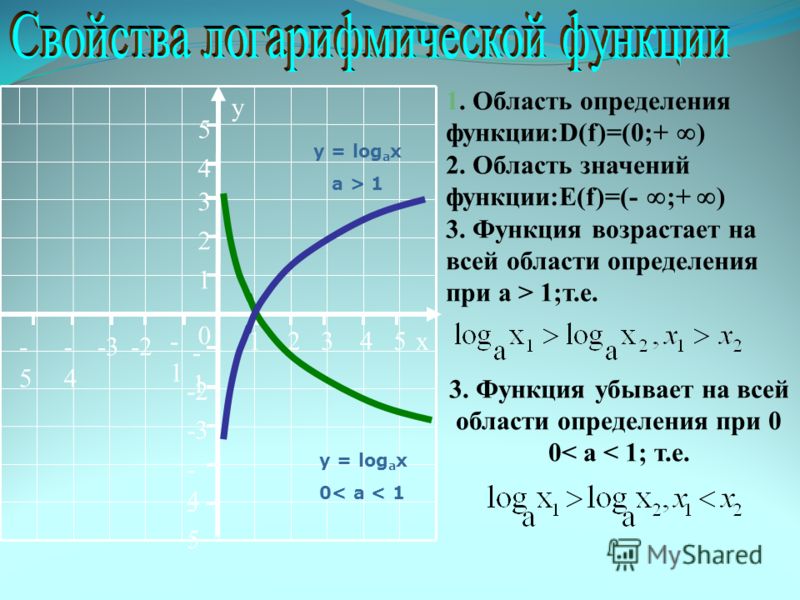 Поддерживается цветовая легенда.
Поддерживается цветовая легенда.
Несмотря на небогатый функционал, все же это онлайн-сервис, поэтому вам не придется долго искать, скачивать и устанавливать какое-либо программное обеспечение.
Для построения графика достаточно лишь иметь с любого имеющегося устройства: ПК, ноутбука, планшета или смартфона.
Построение графика функции онлайн
ТОП-4 лучших сервиса для построения графиков онлайн
Построение графиков функций — одна из возможностей Excel. В этой статье мы рассмотрим процесс построение графиков некоторых математических функций: линейной, квадратичной и обратной пропорциональности.
Функция, это множество точек (x, y), удовлетворяющее выражению y=f(x). Поэтому, нам необходимо заполнить массив таких точек, а Excel построит нам на их основе график функции.
1) Рассмотрим пример построения графика линейной функции: y=5x-2
Графиком линейной функции является прямая, которую можно построить по двум точкам. Создадим табличку
В нашем случае y=5x-2. В ячейку с первым значением y введем формулу: =5*D4-2 . В другую ячейку формулу можно ввести аналогично (изменив D4 на D5 ) или использовать маркер автозаполнения.
В ячейку с первым значением y введем формулу: =5*D4-2 . В другую ячейку формулу можно ввести аналогично (изменив D4 на D5 ) или использовать маркер автозаполнения.
В итоге мы получим табличку:
Теперь можно приступать к созданию графика.
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ (рекомендую использовать именно этот тип диаграммы)
Появиться пустая область диаграмм. Нажимаем кнопку ВЫБРАТЬ ДАННЫЕ
Выберем данные: диапазон ячеек оси абсцисс (х) и оси ординат (у). В качестве имени ряда можем ввести саму функцию в кавычках «y=5x-2» или что-то другое. Вот что получилось:
Нажимаем ОК. Перед нами график линейной функции.
2) Рассмотрим процесс построения графика квадратичной функции — параболы y=2x 2 -2
Параболу по двум точкам уже не построить, в отличии от прямой.
Зададим интервал на оси x , на котором будет строиться наша парабола. 2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х .
2-2. Используя маркер автозаполнения, рассчитываем значения у для остальных х .
Выбираем: ВСТАВКА — > ТОЧЕЧНАЯ -> ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ И МАРКЕРАМИ и действуем аналогично построению графика линейной функции.
Чтобы не было точек на графике, поменяйте тип диаграммы на ТОЧЕЧНАЯ С ГЛАДКИМИ КРИВЫМИ.
Любые другие графики непрерывных функций строятся аналогично.
3) Если функция кусочная, то необходимо каждый «кусочек» графика объединить в одной области диаграмм.
Рассмотрим это на примере функции у=1/х .
Функция определена на интервалах (- беск;0) и (0; +беск)
Создадим график функции на интервалах: [-4;0) и (0; 4].
Подготовим две таблички, где х изменяется с шагом 0,2 :
Находим значения функции от каждого аргумента х аналогично примерам выше.
На диаграмму вы должны добавить два ряда — для первой и второй таблички соответственно
Получаем график функции y=1/x
В дополнение привожу видео — где показан порядок действий, описанный выше.
В следующей статье расскажу как создать 3-мерные графики в Excel.
Спасибо за внимание!
К сожалению, не все студенты и школьники знают и любят алгебру, но готовить домашние задания, решать контрольные и сдавать экзамены приходится каждому. Особенно трудно многим даются задачи на построение графиков функций: если где-то что-то не понял, не доучил, упустил — ошибки неизбежны. Но кому же хочется получать плохие оценки?
Не желаете пополнить когорту хвостистов и двоечников? Для этого у вас есть 2 пути: засесть за учебники и восполнить пробелы знаний либо воспользоваться виртуальным помощником — сервисом автоматического построения графиков функций по заданным условиям. С решением или без. Сегодня мы познакомим вас с несколькими из них.
Лучшее, что есть в Desmos.com, это гибко настраиваемый интерфейс, интерактивность, возможность разносить результаты по таблицам и бесплатно хранить свои работы в базе ресурса без ограничений по времени. А недостаток — в том, что сервис не полностью переведен на русский язык.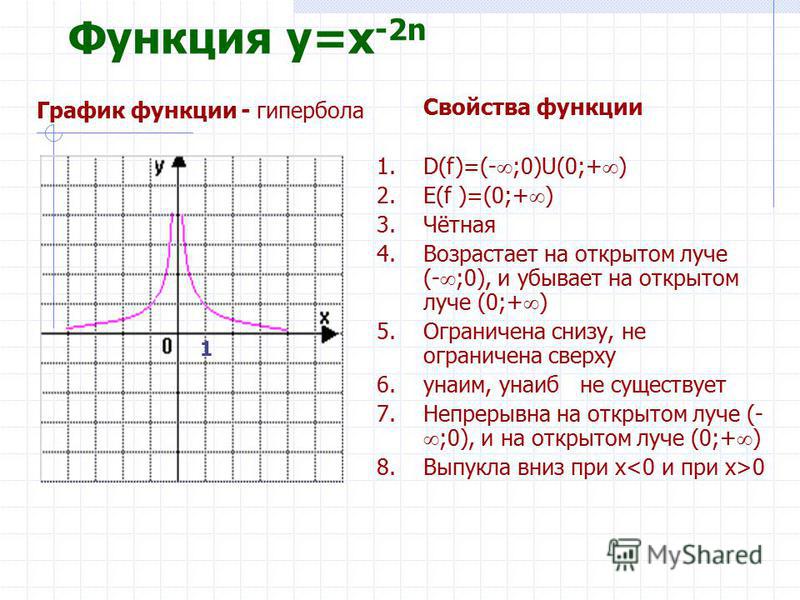
Grafikus.ru
Grafikus.ru — еще один достойный внимания русскоязычный калькулятор для построения графиков. Причем он строит их не только в двухмерном, но и в трехмерном пространстве.
Вот неполный перечень заданий, с которыми этот сервис успешно справляется:
- Черчение 2D-графиков простых функций: прямых, парабол, гипербол, тригонометрических, логарифмических и т. д.
- Черчение 2D-графиков параметрических функций: окружностей, спиралей, фигур Лиссажу и прочих.
- Черчение 2D-графиков в полярных координатах.
- Построение 3D-поверхностей простых функций.
- Построение 3D-поверхностей параметрических функций.
Готовый результат открывается в отдельном окне. Пользователю доступны опции скачивания, печати и копирования ссылки на него. Для последнего придется авторизоваться на сервисе через кнопки соцсетей.
Координатная плоскость Grafikus.ru поддерживает изменение границ осей, подписей к ним, шага сетки, а также — ширины и высоты самой плоскости и размера шрифта.
Самая сильная сторона Grafikus.ru — возможность построения 3D-графиков. В остальном он работает не хуже и не лучше, чем ресурсы-аналоги.
Onlinecharts.ru
Онлайн-помощник Onlinecharts.ru строит не графики, а диаграммы практически всех существующих видов. В том числе:
- Линейные.
- Столбчатые.
- Круговые.
- С областями.
- Радиальные.
- XY-графики.
- Пузырьковые.
- Точечные.
- Полярные бульки.
- Пирамиды.
- Спидометры.
- Столбчато-линейные.
Пользоваться ресурсом очень просто. Внешний вид диаграммы (цвет фона, сетки, линий, указателей, форма углов, шрифты, прозрачность, спецэффекты и т. д.) полностью определяется пользователем. Данные для построения можно ввести как вручную, так и импортировать из таблицы CSV-файла, хранимого на компьютере. Готовый результат доступен для скачивания на ПК в виде картинки, PDF-, CSV- или SVG-файлов, а также для сохранения онлайн на фотохостинге ImageShack.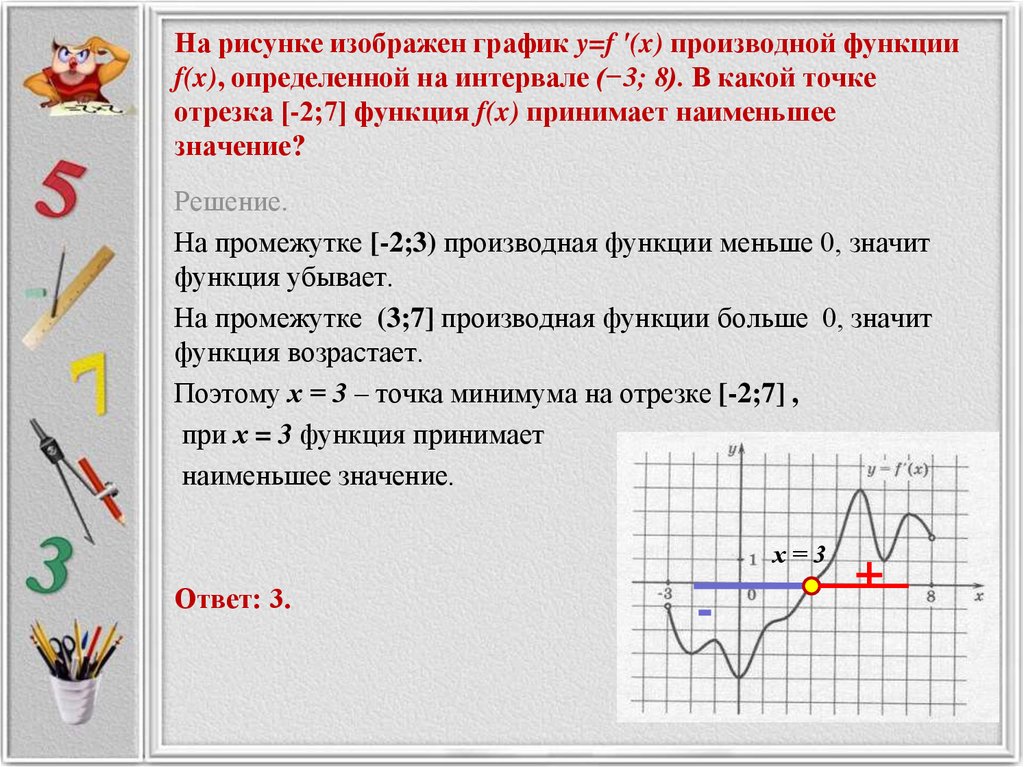
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x).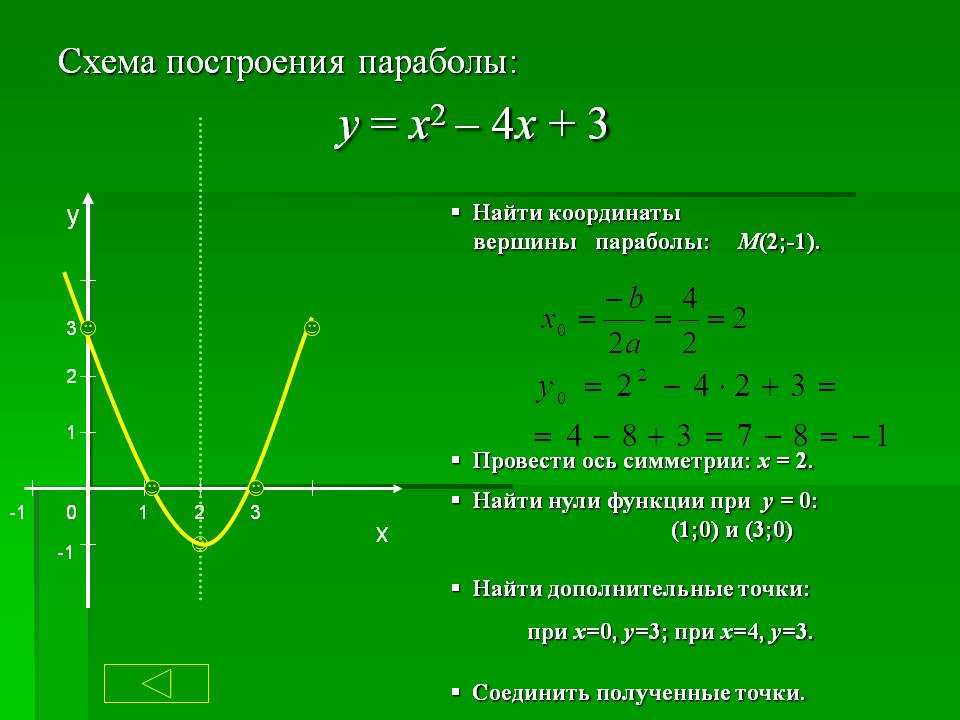 Значит, графики таких функций симметричны относительно оси 0y.
Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.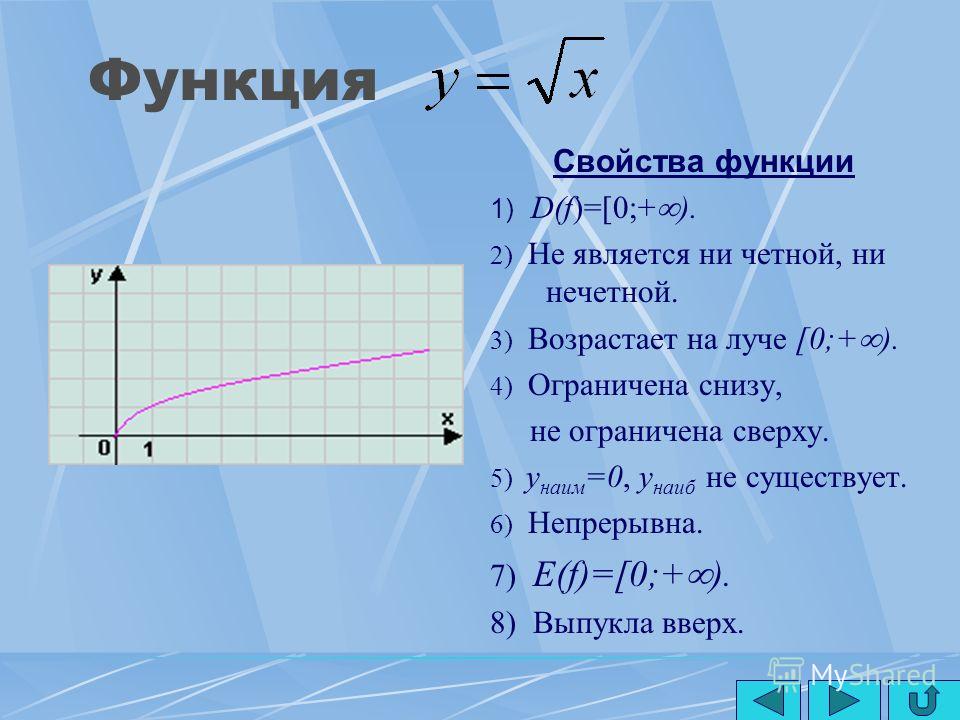
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y. Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.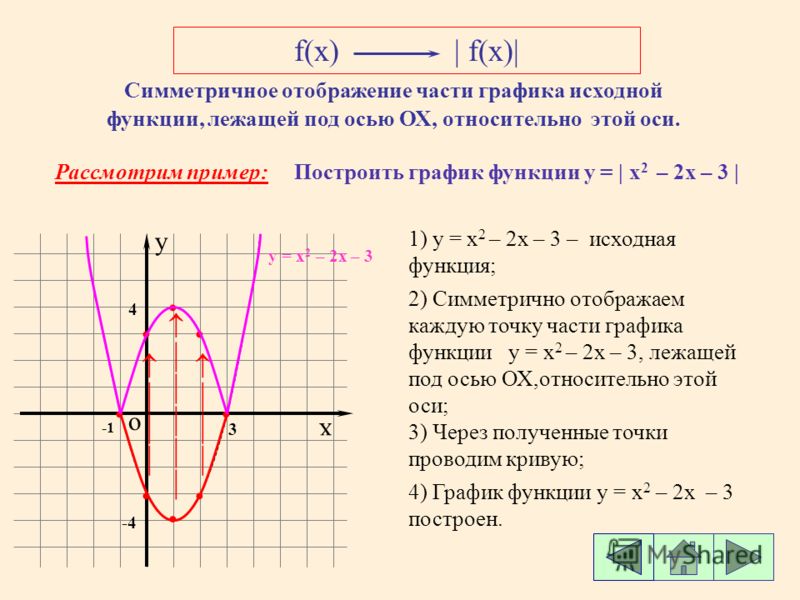
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.
3) Часть графика, расположенную ниже оси 0x, отобразим симметрично относительно 0x.
4) Окончательный график изображен на рисунке (рис. 11) .
сайт, при полном или частичном копировании материала ссылка на первоисточник обязательна.
График функции y 2x 2 4x 6. Постройте график функции y=
Построение графиков функций, содержащих модули, обычно вызывает немалые затруднения у школьников. Однако, все не так плохо. Достаточно запомнить несколько алгоритмов решения таких задач, и вы сможете без труда построить график даже самой на вид сложной функции. Давайте разберемся, что же это за алгоритмы.
Давайте разберемся, что же это за алгоритмы.
1. Построение графика функции y = |f(x)|
Заметим, что множество значений функций y = |f(x)| : y ≥ 0. Таким образом, графики таких функций всегда расположены полностью в верхней полуплоскости.
Построение графика функции y = |f(x)| состоит из следующих простых четырех этапов.
1) Построить аккуратно и внимательно график функции y = f(x).
2) Оставить без изменения все точки графика, которые находятся выше оси 0x или на ней.
3) Часть графика, которая лежит ниже оси 0x, отобразить симметрично относительно оси 0x.
Пример 1. Изобразить график функции y = |x 2 – 4x + 3|
1) Строим график функции y = x 2 – 4x + 3. Очевидно, что график данной функции – парабола. Найдем координаты всех точек пересечения параболы с осями координат и координаты вершины параболы.
x 2 – 4x + 3 = 0.
x 1 = 3, x 2 = 1.
Следовательно, парабола пересекает ось 0x в точках (3, 0) и (1, 0).
y = 0 2 – 4 · 0 + 3 = 3.
Следовательно, парабола пересекает ось 0y в точке (0, 3).
Координаты вершины параболы:
x в = -(-4/2) = 2, y в = 2 2 – 4 · 2 + 3 = -1.
Следовательно, точка (2, -1) является вершиной данной параболы.
Рисуем параболу, используя полученные данные (рис. 1)
2) Часть графика, лежащую ниже оси 0x, отображаем симметрично относительно оси 0x.
3) Получаем график исходной функции (рис. 2 , изображен пунктиром).
2. Построение графика функции y = f(|x|)
Заметим, что функции вида y = f(|x|) являются четными:
y(-x) = f(|-x|) = f(|x|) = y(x). Значит, графики таких функций симметричны относительно оси 0y.
Построение графика функции y = f(|x|) состоит из следующей несложной цепочки действий.
1) Построить график функции y = f(x).
2) Оставить ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отобразить указанную в пункте (2) часть графика симметрично оси 0y.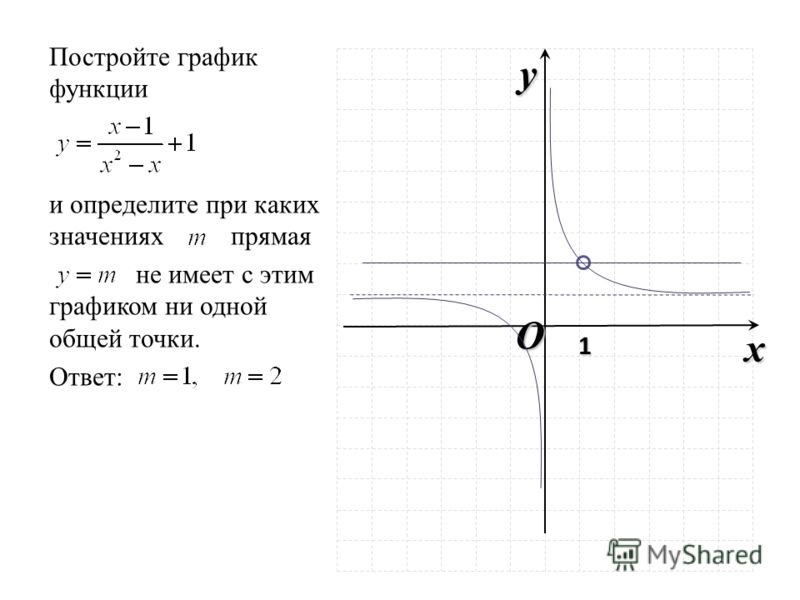
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 2. Изобразить график функции y = x 2 – 4 · |x| + 3
Так как x 2 = |x| 2 , то исходную функцию можно переписать в следующем виде: y = |x| 2 – 4 · |x| + 3. А теперь можем применять предложенный выше алгоритм.
1) Строим аккуратно и внимательно график функции y = x 2 – 4 · x + 3 (см. также рис. 1 ).
2) Оставляем ту часть графика, для которой x ≥ 0, то есть часть графика, расположенную в правой полуплоскости.
3) Отображаем правую часть графика симметрично оси 0y.
(рис. 3) .
Пример 3. Изобразить график функции y = log 2 |x|
Применяем схему, данную выше.
1) Строим график функции y = log 2 x (рис. 4) .
3. Построение графика функции y = |f(|x|)|
Заметим, что функции вида y = |f(|x|)| тоже являются четными. Действительно, y(-x) = y = |f(|-x|)| = y = |f(|x|)| = y(x), и поэтому, их графики симметричны относительно оси 0y.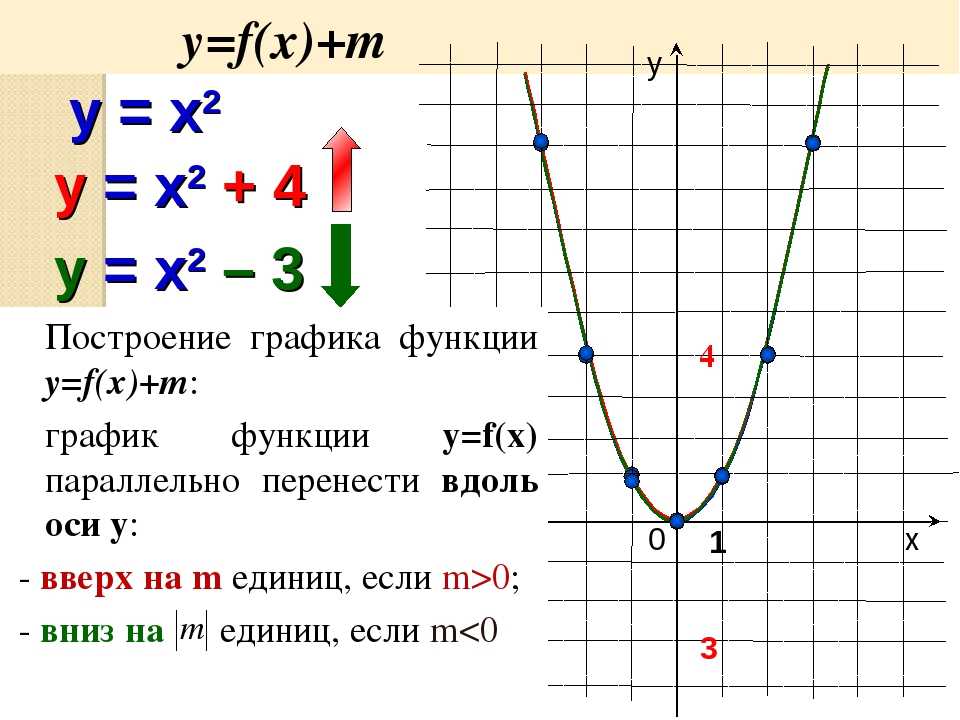 Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Множество значений таких функций: y ≥ 0. Значит, графики таких функций расположены полностью в верхней полуплоскости.
Чтобы построить график функции y = |f(|x|)|, необходимо:
1) Построить аккуратно график функции y = f(|x|).
2) Оставить без изменений ту часть графика, которая находится выше оси 0x или на ней.
3) Часть графика, расположенную ниже оси 0x, отобразить симметрично относительно оси 0x.
4) В качестве окончательного графика выделить объединение кривых, полученных в пунктах (2) и (3).
Пример 4. Изобразить график функции y = |-x 2 + 2|x| – 1|.
1) Заметим, что x 2 = |x| 2 . Значит, вместо исходной функции y = -x 2 + 2|x| – 1
можно использовать функцию y = -|x| 2 + 2|x| – 1, так как их графики совпадают.
Строим график y = -|x| 2 + 2|x| – 1. Для этого применяем алгоритм 2.
a) Строим график функции y = -x 2 + 2x – 1 (рис. 6) .
b) Оставляем ту часть графика, которая расположена в правой полуплоскости.
c) Отображаем полученную часть графика симметрично оси 0y.
d) Полученный график изображен на рисунке пунктиром (рис. 7) .
2) Выше оси 0х точек нет, точки на оси 0х оставляем без изменения.
3) Часть графика, расположенную ниже оси 0x, отображаем симметрично относительно 0x.
4) Полученный график изображен на рисунке пунктиром (рис. 8) .
Пример 5. Построить график функции y = |(2|x| – 4) / (|x| + 3)|
1) Сначала необходимо построить график функции y = (2|x| – 4) / (|x| + 3). Для этого возвращаемся к алгоритму 2.
a) Аккуратно строим график функции y = (2x – 4) / (x + 3) (рис. 9) .
Заметим, что данная функция является дробно-линейной и ее график есть гипербола. Для построения кривой сначала необходимо найти асимптоты графика. Горизонтальная – y = 2/1 (отношение коэффициентов при x в числителе и знаменателе дроби), вертикальная – x = -3.
2) Ту часть графика, которая находится выше оси 0x или на ней, оставим без изменений.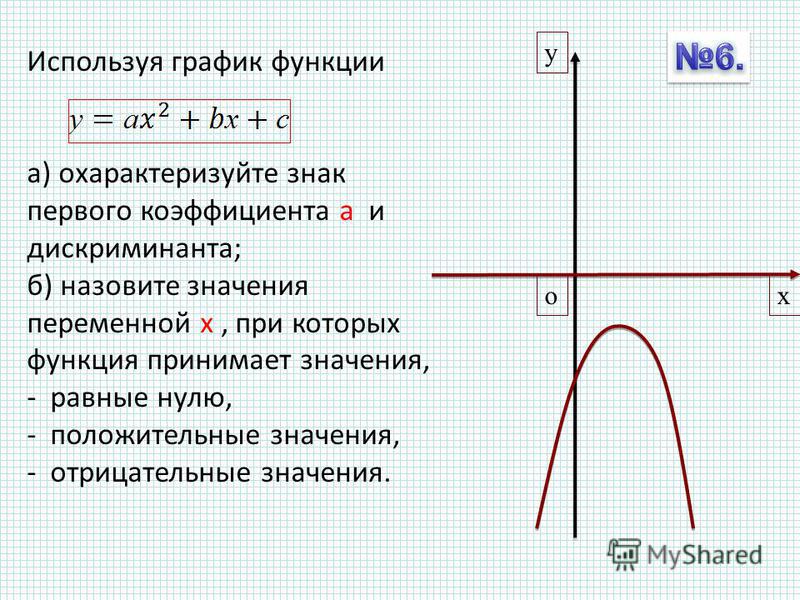 3$.
3$.
2. Найдем точку А, координата x, которой равна 1,5. Мы видим, что координата функции находится между значениями 3 и 4 (см. рис. 2). Значит надо заказать 4 куба.
Разберем как строить график с модулем.
Найдем точки при переходе которых знак модулей меняется.
Каждое выражения, которое под модулем приравниваем к 0. У нас их два x-3 и x+3.
x-3=0 и x+3=0
x=3 и x=-3
У нас числовая прямая разделится на три интервала (-∞;-3)U(-3;3)U(3;+∞). На каждом интервале нужно определить знак под модульных выражений.
1. Это сделать очень просто, рассмотрим первый интервал (-∞;-3). Возьмем с этого отрезка любое значение, например, -4 и подставим в каждое под модульное уравнение вместо значения х.
х=-4
x-3=-4-3=-7 и x+3=-4+3=-1
У обоих выражений знаки отрицательный, значит перед знаком модуля в уравнении ставим минус, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (-∞;-3).
y=— (x-3)-(— (x+3))=-х+3+х+3=6
На интервале (-∞;-3) получился график линейной функции (прямой) у=6
2. Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
Рассмотрим второй интервал (-3;3). Найдем как будет выглядеть уравнение графика на этом отрезке. Возьмем любое число от -3 до 3, например, 0. Подставим вместо значения х значение 0.
х=0
x-3=0-3=-3 и x+3=0+3=3
У первого выражения x-3 знак отрицательный получился, а у второго выражения x+3 положительный. Следовательно, перед выражением x-3 запишем знак минус, а перед вторым выражением знак плюс.
y=— (x-3)-(+ (x+3))=-х+3-х-3=-2x
На интервале (-3;3) получился график линейной функции (прямой) у=-2х
3.Рассмотрим третий интервал (3;+∞). Возьмем с этого отрезка любое значение, например 5, и подставим в каждое под модульное уравнение вместо значения х.
х=5
x-3=5-3=2 и x+3=5+3=8
У обоих выражений знаки получились положительными, значит перед знаком модуля в уравнении ставим плюс, а вместо знака модуля ставим скобки и получим искомое уравнение на интервале (3;+∞).
y=+ (x-3)-(+ (x+3))=х-3-х-3=-6
На интервале (3;+∞) получился график линейной функции (прямой) у=-6
4.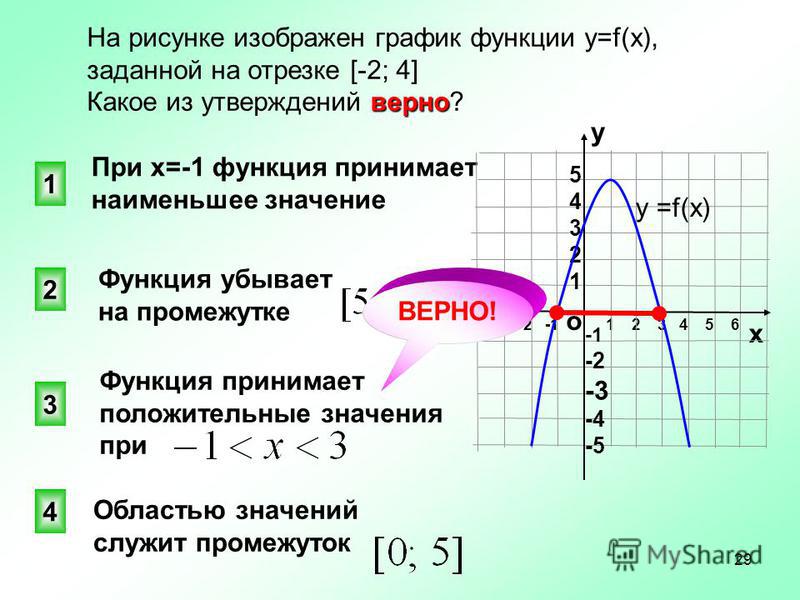 Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
Теперь подведем итог.Постоим график y=|x-3|-|x+3|.
На интервале (-∞;-3) строим график линейной функции (прямой) у=6.
На интервале (-3;3) строим график линейной функции (прямой) у=-2х.
Чтобы построить график у=-2х подберем несколько точек.
x=-3 y=-2*(-3)=6 получилась точка (-3;6)
x=0 y=-2*0=0 получилась точка (0;0)
x=3 y=-2*(3)=-6 получилась точка (3;-6)
На интервале (3;+∞) строим график линейной функции (прямой) у=-6.
5. Теперь проанализируем результат и ответим на вопрос задания найдем значение k, при которых прямая y=kx имеет с графиком y=|x-3|-|x+3| данной функции ровно одну общую точку.
Прямая y=kx при любом значении k всегда будет проходить через точку (0;0). Поэтому мы можем изменить только наклон данной прямой y=kx, а за наклон у нас отвечает коэффициент k.
Если k будет любое положительное число, то будет одно пересечение прямой y=kx с графиком y=|x-3|-|x+3|. Этот вариант нам подходит.
Если k будет принимать значение (-2;0), то пересечений прямой y=kx с графиком y=|x-3|-|x+3| будет три. Этот вариант нам не подходит.
Этот вариант нам не подходит.
Если k=-2, решений будет множество [-2;2], потому что прямая y=kx будет совпадать с графиком y=|x-3|-|x+3| на данном участке. Этот вариант нам не подходит.
Если k будет меньше -2, то прямая y=kx с графиком y=|x-3|-|x+3| будет иметь одно пересечение.Этот вариант нам подходит.
Если k=0, то пересечений прямой y=kx с графиком y=|x-3|-|x+3| также будет одно.Этот вариант нам подходит.
Ответ: при k принадлежащей интервалу (-∞;-2)U и возрастает на промежутке }
MacBook Pro 14 дюймов и MacBook Pro 16 дюймов – Apple (RU)
Суперсила профессионалов.
Мы создали самый мощный MacBook Pro в истории. И это монстр. Супербыстрые M1 Pro и M1 Max — первые чипы Apple, разработанные специально для профессионалов. Они дают феноменальную производительность и обеспечивают удивительно долгое время работы без подзарядки. Прибавьте к этому потрясающий дисплей Liquid Retina XDR, превосходную камеру и звук, а также больше портов для профессиональной работы. С этим ноутбуком всё становится возможным.
С этим ноутбуком всё становится возможным.
- Смотрите презентацию
- Смотрите видео
До
3,7x
выше
производительность
процессора1
До
13x
быстрее
обработка
графики2
машинное
обучение3
До
21
часа работы
без подзарядки4
Теперь держитесь.
Теперь держитесь.
Дико
быстро.

Процессор до 10 ядер
Графический процессор до 16 ядер
Объединённая память до 32 ГБ
Пропускная способность
памяти до 200 ГБ/с
Дико
быстрее.
Процессор 10 ядер
Графический процессор до 32 ядер
Объединённая память до 64 ГБ
Пропускная способность
памяти до 400 ГБ/с
Чипы M1 Pro и M1 Max — это совершенно новый масштаб архитектуры М1. И впервые мы разработали систему на чипе специально для профессиональных ноутбуков. У обоих чипов больше ядер в центральном и графическом процессорах и больше объединённой памяти, чем в чипе M1. А ещё мощная система Neural Engine для высокой скорости машинного обучения и обновлённые медиапроцессоры с поддержкой ProRes. M1 Pro и M1 Max позволяют профессионалам создавать то, что раньше казалось невозможным.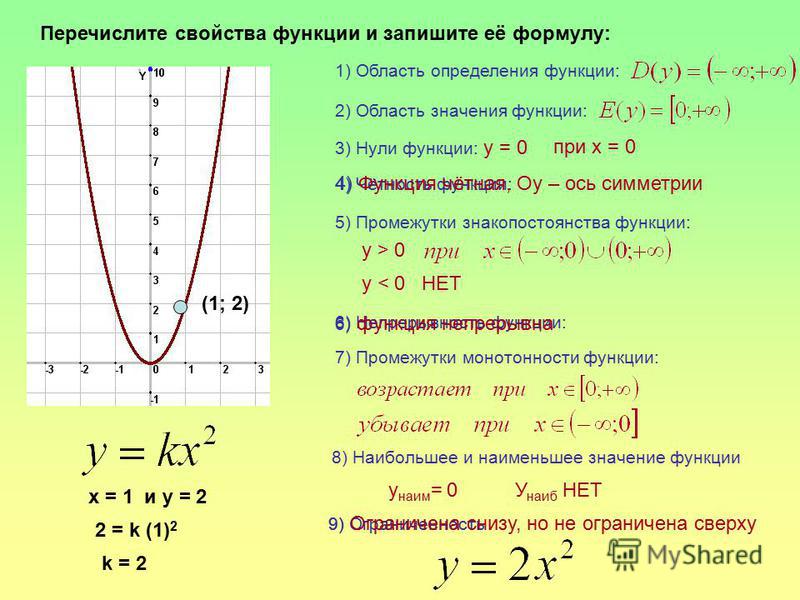
M1 Pro
Дико быстро.
M1 Pro выводит архитектуру M1 на новый уровень производительности, открывая невероятные возможности для профессиональной работы. До 10 ядер в центральном процессоре и до 16 в графическом, 16‑ядерная система Neural Engine, выделенные медиапроцессоры для кодирования и декодирования файлов с поддержкой кодеков H.264, HEVC и ProRes — такой ноутбук легко справится с самыми амбициозными проектами.
M1 Max
Дико быстрее.
M1 Max — невероятно мощный чип для ноутбуков профессионального уровня. Он оснащается 10‑ядерным процессором, графическим процессором до 32 ядер и 16‑ядерной системой Neural Engine. Скорость обработки графики и пропускная способность памяти у этого чипа вдвое больше, чем у M1 Pro. Кодирование видео происходит до 2 раз быстрее, поскольку в M1 Max установлено два медиапроцессора для кодирования и отдельный медиапроцессор для декодирования, а два ускорителя ProRes помогают при работе с несколькими потоками видео.
Выберите размер. Выберите чип.
И полетели.
Final Cut ProLogic Pro
Новый MacBook Pro представлен двумя моделями: 14 дюймов и 16 дюймов. Для каждой из них можно выбрать чип M1 Pro или M1 Max, и любая конфигурация обеспечит беспрецедентный уровень производительности. Вы сможете работать с миллионами полигонов в Cinema 4D, монтировать до семи потоков видео 8K в формате ProRes в Final Cut Pro, выполнять грейдинг в HDR, работая с видео 8K ProRes 4444, — и всё это на ноутбуке, а не в оборудованной монтажной комнате.
Производительность процессора
- Xcode /
- NASA TetrUSS /
- Logic Pro /
- Vectorworks /
- Affinity Photo
Выше скорость сборки проектов7
Модель 14 дюймов
M1 Max с 10‑ядерным процессором
M1 Pro с 10‑ядерным процессором
MacBook Pro 13 дюймов c 4‑ядерным
процессором Intel Core i7
Модель 16 дюймов
M1 Max с 10‑ядерным процессором
M1 Pro с 10‑ядерным процессором
MacBook Pro 16 дюймов c 8‑ядерным
процессором Intel Core i9
Выше скорость расчёта
динамики текучих сред8
Модель 14 дюймов
M1 Max с 10‑ядерным процессором
M1 Pro с 10‑ядерным процессором
MacBook Pro 13 дюймов c 4‑ядерным
процессором Intel Core i7
Модель 16 дюймов
M1 Max с 10‑ядерным процессором
M1 Pro с 10‑ядерным процессором
MacBook Pro 16 дюймов c 8‑ядерным
процессором Intel Core i9
Больше плагинов Amp Designer9
Модель 14 дюймов
M1 Max с 10‑ядерным процессором
M1 Pro с 10‑ядерным процессором
MacBook Pro 13 дюймов c 4‑ядерным
процессором Intel Core i7
Модель 16 дюймов
M1 Max с 10‑ядерным процессором
M1 Pro с 10‑ядерным процессором
MacBook Pro 16 дюймов c 8‑ядерным
процессором Intel Core i9
Выше скорость публикации10
Модель 14 дюймов
M1 Max с 10‑ядерным процессором
M1 Pro с 10‑ядерным процессором
MacBook Pro 13 дюймов c 4‑ядерным
процессором Intel Core i7
Модель 16 дюймов
M1 Max с 10‑ядерным процессором
M1 Pro с 10‑ядерным процессором
MacBook Pro 16 дюймов c 8‑ядерным
процессором Intel Core i9
Выше скорость обработки векторной графики
при задействовании нескольких ядер11
Модель 14 дюймов
M1 Max с 10‑ядерным процессором
M1 Pro с 10‑ядерным процессором
MacBook Pro 13 дюймов c 4‑ядерным
процессором Intel Core i7
Модель 16 дюймов
M1 Max с 10‑ядерным процессором
M1 Pro с 10‑ядерным процессором
MacBook Pro 16 дюймов c 8‑ядерным
процессором Intel Core i9
Производительность графического процессора
- Final Cut Pro /
- Maxon Cinema 4D /
- Blackmagic DaVinci Resolve Studio /
- Adobe Photoshop /
- Affinity Photo
Выше скорость рендеринга в 4K12
Модель 14 дюймов
M1 Max с 32‑ядерным
графическим процессором
13,4 x
M1 Pro с 16‑ядерным
графическим процессором
MacBook Pro 13 дюймов с графическим
процессором Intel Iris Plus
Выше скорость рендеринга в 8K13
Модель 16 дюймов
M1 Max с 32‑ядерным
графическим процессором
M1 Pro с 16‑ядерным
графическим процессором
MacBook Pro с графическим
процессором
Radeon Pro 5600M и 8 ГБ памяти HBM2
Выше скорость обработки 3D
в реальном времени14
Модель 14 дюймов
M1 Max с 32‑ядерным
графическим процессором
M1 Pro с 16‑ядерным
графическим процессором
MacBook Pro 13 дюймов с графическим
процессором Intel Iris Plus
Выше скорость рендеринга
в Redshift15
Модель 16 дюймов
M1 Max с 32‑ядерным
графическим процессором
M1 Pro с 16‑ядерным
графическим процессором
MacBook Pro с графическим
процессором
Radeon Pro 5600M и 8 ГБ памяти HBM2
Выше скорость рендеринга эффектов16
Модель 14 дюймов
M1 Max с 32‑ядерным
графическим процессором
M1 Pro с 16‑ядерным
графическим процессором
MacBook Pro 13 дюймов с графическим
процессором Intel Iris Plus
Модель 16 дюймов
M1 Max с 32‑ядерным
графическим процессором
M1 Pro с 16‑ядерным
графическим процессором
MacBook Pro с графическим
процессором
Radeon Pro 5600M и 8 ГБ памяти HBM2
Выше скорость работы фильтров и функций,
использующих ускорение графического процессора17
Модель 14 дюймов
M1 Max с 32‑ядерным
графическим процессором
M1 Pro с 16‑ядерным
графическим процессором
MacBook Pro 13 дюймов с графическим
процессором Intel Iris Plus
Модель 16 дюймов
M1 Max с 32‑ядерным
графическим процессором
M1 Pro с 16‑ядерным
графическим процессором
MacBook Pro с графическим
процессором
Radeon Pro 5600M и 8 ГБ памяти HBM2
Выше скорость обработки объектов,
сочетающих в себе векторную
и растровую графику18
Модель 14 дюймов
M1 Max с 32‑ядерным
графическим процессором
M1 Pro с 16‑ядерным
графическим процессором
MacBook Pro 13 дюймов с графическим
процессором Intel Iris Plus
Модель 16 дюймов
M1 Max с 32‑ядерным
графическим процессором
M1 Pro с 16‑ядерным
графическим процессором
MacBook Pro с графическим
процессором
Radeon Pro 5600M и 8 ГБ памяти HBM2
День напролёт.
 Adobe Photoshop Lightroom Classic
Adobe Photoshop Lightroom ClassicНеукротимая мощь и невероятное время работы от аккумулятора — вот она, настоящая магия чипов Apple. С ними вы можете скомпилировать до четырёх раз больше кода в Xcode19 и до двух раз дольше заниматься обработкой изображений в Lightroom Classic20, прежде чем аккумулятор разрядится полностью. Причём MacBook Pro сохраняет высокий уровень производительности, даже если выключить его из розетки.
Модель 14 дюймов
До17часоввоспроизведения видео21
До11часовработы в интернете по беспроводной сети21
Модель 16 дюймов
До21часавоспроизведения видео22
До14часовработы в интернете по беспроводной сети22
Охлаждение что надо. Передовые компоненты систем охлаждения подают на 50 процентов больше воздуха даже при низкой скорости вращения вентиляторов. А при выполнении многих повседневных задач они вообще не включаются — настолько эффективно работают чипы Apple.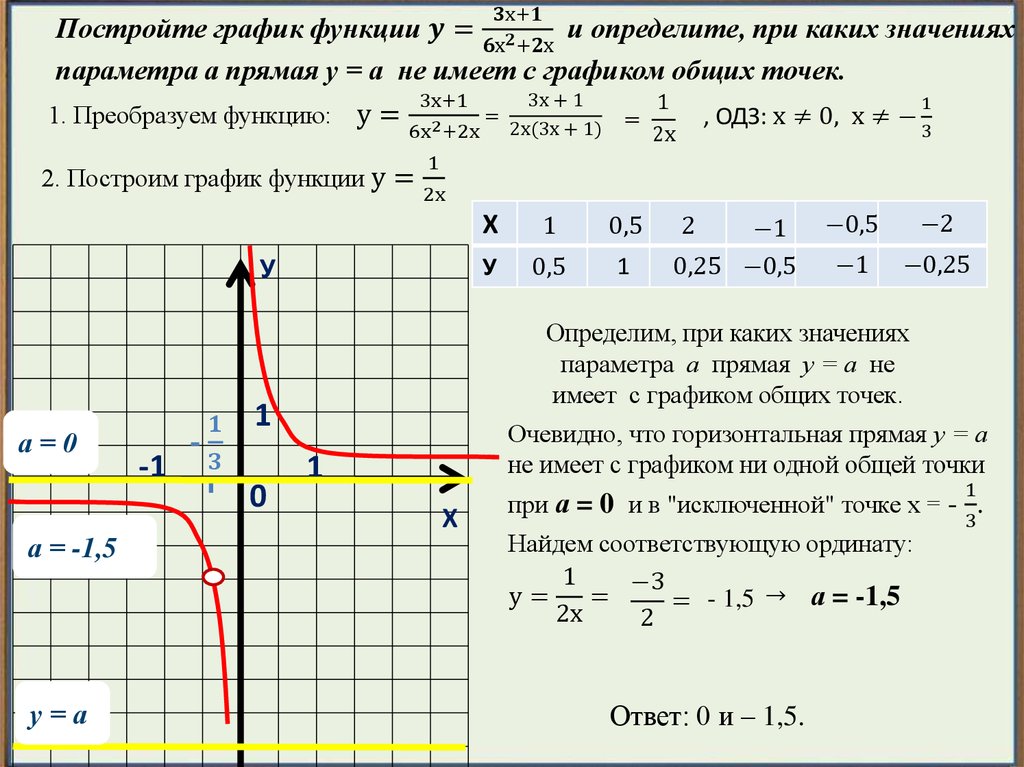
Объёмы на скорости. В новые MacBook Pro устанавливаются SSD‑накопители ёмкостью до 8 ТБ с невероятной скоростью чтения данных 7,4 ГБ/с23 — более чем в 2 раза выше по сравнению с моделями предыдущего поколения.24 С таким диском вы сможете мгновенно открывать видео в формате 8K и хранить сотни тысяч фото в формате RAW.
Мощная перестройка.
Новый MacBook Pro первым получил систему на чипе, созданном специально для ноутбуков профессионального уровня. В таких ноутбуках часто используются процессоры, потребляющие много энергии, дискретные графические процессоры и множество отдельных специализированных чипов. Здесь же центральный и графический процессор, контроллеры ввода-вывода и система Neural Engine являются частью одной системы на чипе с объединённой памятью. В результате M1 Pro и M1 Max не только легко справляются с ресурсоёмкими задачами, прежде недоступными для ноутбуков, но ещё и позволяют невероятно долго работать без подзарядки.
Связанные одним чипом. Многие компьютеры копируют одни и те же данные по несколько раз через медленные интерфейсы. Но только не новый MacBook Pro. Его центральный и графический процессоры используют объединённую память. Это значит, что все компоненты чипа напрямую обращаются к памяти и хранящимся в ней данным, не копируя их, и поэтому всё работает быстрее и эффективнее.
M1 Pro
До 32 ГБ объединённой памяти
До 200 ГБ/с пропускная способность памяти
M1 Max
До 64 ГБ объединённой памяти
До 400 ГБ/с пропускная способность памяти
Центральные процессоры в чипах M1 Pro и M1 Max
содержат до восьми ядер производительности и два ядра эффективности, что позволяет им быстрее обрабатывать данные и расходовать при этом в десять раз меньше энергии. А графические процессоры обращаются к данным с меньшей задержкой и при улучшенной энергоэффективности имеют превосходный показатель производительности на ватт.
Процессор
до 10 ядер
Графический
процессор до 16 ядер
Система
Neural Engine 16 ядер
Процессор
10 ядер
Графический
процессор до 32 ядер
Система
Neural Engine 16 ядер
Максимальная производительность.
Минимум энергозатрат.
Соотношение производительности центрального процессора и потребляемой энергии
Пиковая производительность M1 Pro и M1 Max в 1,7 раза выше, чем у некоторых 8‑ядерных процессоров для сопоставимых по мощности ноутбуков. А равную с ними производительность новые чипы обеспечивают, расходуя на 70 процентов меньше энергии. 25
25
В
1,7X
выше
производительность
На
70%
меньше
потребление энергии
Чип M1 Pro: соотношение производительности графического процессора и потребляемой энергии
При пиковой производительности M1 Pro потребляет на 70 процентов меньше энергии, чем некоторые ноутбуки PC с дискретным графическим процессором.26
На 70% меньше потребление энергии
Чип M1 Max: соотношение производительности графического процессора и потребляемой энергии
В пиковом режиме M1 Max обеспечивает более высокую производительность и потребляет на 40 процентов меньше энергии, чем некоторые компактные ноутбуки уровня Pro с мощными дискретными графическими процессорами. А если сравнивать с наиболее мощными ноутбуками с дискретной графикой, то M1 Max обеспечивает схожий уровень производительности, потребляя на 100 Вт энергии меньше. 26
26
На 100 Вт меньше потребление энергии
XDRадует.
Blackmagic Design DaVinci ResolveLiquid Retina XDR. Это первый дисплей для ноутбуков Mac с экстремальным динамическим диапазоном и контрастностью миллион к одному. На таком экране превосходно смотрятся фото, игры и видео в формате HDR. Отлично видны светлые участки, чётко передаются все детали в тёмных областях, цвета получаются яркими и естественными. Каждый дисплей проходит заводскую калибровку и поддерживает профессиональные режимы для грейдинга в HDR, работы с фотографиями, дизайна и предпечатной подготовки.
ProMotion. Это первые компьютеры Mac, для которых была реализована поддержка ProMotion. С ней всё работает быстро и гладко — от прокрутки веб-страниц до движений в компьютерных играх, — и при этом ноутбук потребляет меньше энергии. Максимальная частота обновления экрана составляет 120 Гц. Фактическое значение адаптивно меняется, подстраиваясь под скорость движения объектов на экране ноутбука.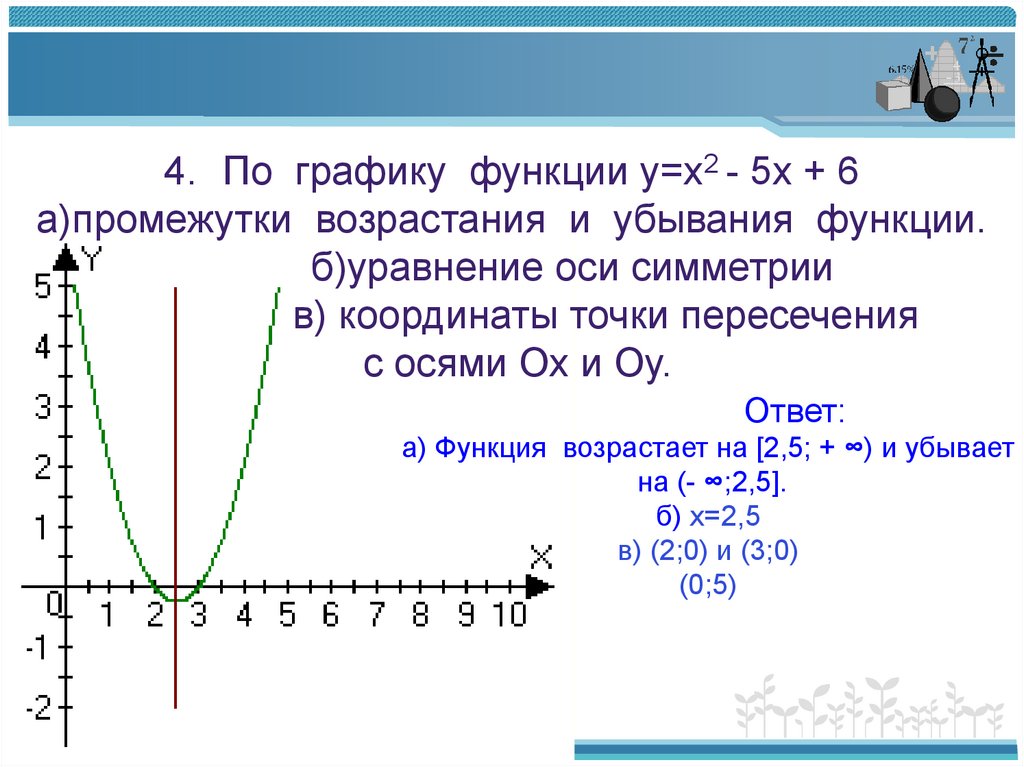 А для редактирования видео можно выбрать фиксированную частоту обновления, соответствующую параметрам записи.
А для редактирования видео можно выбрать фиксированную частоту обновления, соответствующую параметрам записи.
- корпус
- подсветка
- рассеиватели
- ЖК-панель
Корпус дисплея. Толщина корпуса составляет менее 4 мм. Этого достаточно, чтобы разместить превосходный дисплей MacBook Pro.
Диоды mini-LED. Тысячи диодов сгруппированы в независимые локальные зоны затемнения. Таким образом достигается оптимальная яркость и контрастность.
Оптические плёнки и рассеиватели. Семь плёнок и рассеивателей эффективно формируют потоки света, помогая сделать дисплей невероятно тонким.
ЖК‑панель. Активная область экрана доходит почти до самых краёв корпуса. Рамка стала до 60 процентов тоньше, а значит, появилось больше места для контента.
На секундочку — камера HD 1080p.

Быть на связи сегодня как никогда важно. Поэтому мы удвоили разрешение камеры MacBook Pro — до 1080p — и увеличили диафрагму, чтобы она пропускала больше света. Обладая при этом увеличенной матрицей с большим количеством эффективных пикселей, камера даёт в два раза более качественное изображение при слабом освещении.
Три микрофона студийного уровня. У микрофонов в этих моделях до 60 процентов ниже порог шума, поэтому MacBook Pro может воспринимать даже самые тихие звуки. А система из трёх направленных микрофонов помогает сделать так, чтобы ваш голос всегда звучал громко и отчётливо.
Система из шести динамиков. Четыре низкочастотных динамика с подавлением резонанса расширяют диапазон звучания — разница составляет до половины октавы — и воспроизводят до 80 процентов больше басов. Эффективные высокочастотные динамики более чётко и полно передают вокальные партии.
Пространственное аудио. При воспроизведении музыки и видео со звуком формате Dolby Atmos система из шести динамиков и передовые алгоритмы позволяют MacBook Pro формировать пространственное аудио, обеспечивая богатое объёмное звучание.
Всё у вас подключится.
Слот для карт SDXC позволяет переносить фото и видео. Порт HDMI — подключать телевизоры и мониторы. Выход 3,5 мм автоматически распознаёт наушники с высоким импедансом и корректирует параметры. Три порта Thunderbolt 4 служат для подключения высокоскоростных периферийных устройств. А к разъёму питания MagSafe 3 легко примагнитить кабель для быстрой зарядки.
- MagSafe 3
- Thunderbolt 4
- Наушники
- SDXC
- Thunderbolt 4
- HDMI
- MagSafe 3
- Ещё больше пикселей. К моделям с чипом M1 Max можно подключить до трёх мониторов Pro Display XDR и один телевизор с разрешением 4K. К моделям с чипом M1 Pro — до двух мониторов Pro Display XDR.
Мощь и клавиатура — парочка уровня Pro.
На клавиатуре Magic Keyboard у MacBook Pro впервые появился ряд полноразмерных механических функциональных клавиш. Такие клавиши особенно ценят профессиональные пользователи из‑за тактильных ощущений. Вы сможете быстро активировать поиск Spotlight, Диктовку и функцию «Не беспокоить». Кроме того, на клавише Touch ID теперь есть специальное рельефное кольцо, которое помогает правильно приложить палец для разблокировки Mac.
Такие клавиши особенно ценят профессиональные пользователи из‑за тактильных ощущений. Вы сможете быстро активировать поиск Spotlight, Диктовку и функцию «Не беспокоить». Кроме того, на клавише Touch ID теперь есть специальное рельефное кольцо, которое помогает правильно приложить палец для разблокировки Mac.
macOS Monterey и чип Apple.
Мощное сочетание.
В macOS Monterey можно использовать одну клавиатуру, трекпад и мышь для одновременной и непрерывной работы на Mac и iPad — с функцией «Универсальное управление».28 Автоматизировать сложные задачи с помощью Быстрых команд. Передавать изображение со своего экрана, вместе смотреть фильмы и работать над проектами через FaceTime. И просматривать веб‑сайты в Safari — браузер стал ещё лучше. А режим фокусирования поможет сосредоточиться, временно отключив лишние уведомления.
Подробнее о macOS Monterey
Профессиональные приложения.
Мощь чипов M1 Pro
и M1 Max в действии.

Более 10 000 приложений и плагинов уже оптимизированы для работы с чипами Apple. К тому же технология Rosetta 2 автоматически адаптирует приложения, созданные для компьютеров с процессорами Intel, и позволяет использовать их на новых MacBook Pro.
- Редактирование фото /
- Графический дизайн /
- 3D‑рендеринг /
- Запись и обработка аудио /
- Видеомонтаж /
- Разработка приложений /
- Точные науки
Adobe Photoshop
Octane X
Logic Pro
Adobe Premiere Pro
Xcode
NASA TetrUSS
Adobe Photoshop, Affinity Photo, Capture One, Adobe Photoshop Lightroom Classic и многое другое.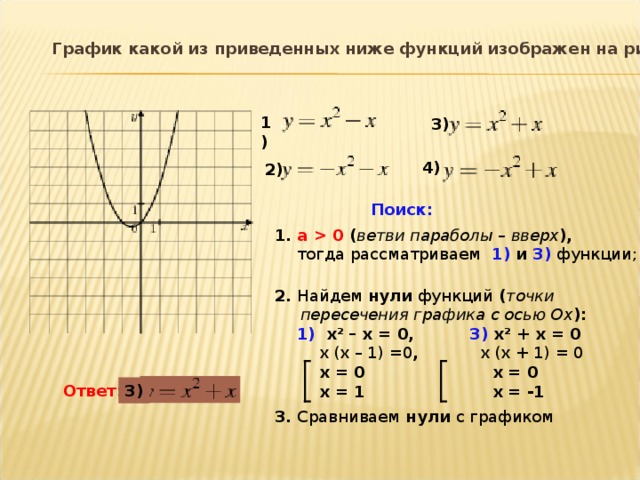
Affinity Designer, Sketch, Vectorworks, Adobe Illustrator, Pixelmator Pro и многое другое.
Octane X29, Maxon Cinema 4D, Redshift, Blender и многое другое.
Logic Pro, Ableton Live 11, Adobe Audition, FL Studio и многое другое.
Adobe Premiere Pro, Blackmagic Design DaVinci Resolve, Final Cut Pro, Motion, Compressor, Adobe Media Encoder, Blackmagic Fusion Studio, Adobe After Effects30 и многое другое.
Xcode, Unity Editor30, Create ML, TensorFlow, Visual Studio Code, NAG Fortran Compiler и многое другое.
NASA TetrUSS, Wolfram Mathematica, OsiriX MD, Shapr3D, CrystalMaker® и многое другое.
Посмотрите в дополненной реальности, как будет выглядеть MacBook Pro на вашем рабочем месте.
Откройте эту страницу в Safari на iPhone или iPad.
селектор цвета- «Серый космос»
- Серебристый
Создан с заботой об окружающей среде.

Создавая MacBook Pro, мы стремились максимально снизить его воздействие на окружающую среду. Теперь для производства корпуса используется
только переработанный алюминий. И все редкоземельные элементы в магнитах являются переработанными. В MacBook Pro нет ни одного из многочисленных вредных веществ. А первичное древесное волокно, применяемое в составе упаковки, получено исключительно из рационально управляемых лесных хозяйств.
Подробнее об Apple
и окружающей среде
Выберите аксессуары для Mac.
Выберите свой Mac.
Сравните все модели Mac
Apple в бизнесе
Мощный стимул для развития вашей компании.
Подробнее об Apple для работы
Узнайте о преимуществах Mac для бизнеса
Apple в образовании
Помогаем преподавателям и учащимся двигаться в будущее.
Подробнее об Apple в образовании
Обзор компактной портативной колонки Tronsmart Groove 2 в защищенном исполнении / Hi-Fi и цифровой звук / iXBT Live
Не секрет, что Bluetooth колонки пользуются особой популярность, как портативные колонки с хорошим звучанием и в защищенном корпусе — наиболее востребованы. Одна из лучших представителей подобных моделей — это компактная колонка Tronsmart Groove 2, в прорезиненном корпусе с защитой от воды и ударов.
Одна из лучших представителей подобных моделей — это компактная колонка Tronsmart Groove 2, в прорезиненном корпусе с защитой от воды и ударов.
- Бренд: Tronsmart
- Модель: Groove 2
- Тип: беспроводная Bluetooth колонка
- Подключение: беспроводное Bluetooth 5.3, проводное (AUX)
- Кодек: SBC
- Мощность: 10 Вт
- Защита: IPX7
- Питание: USB-C, быстрая зарядка, аккумулятор 2500 мАч
- Время работы: до 18 ч (~50% громкости)
- Особенности: защита от ударов и воды, работа в стереопаре, EQ, карабин в комплекте
- Размеры: 10 x 10 x 6 см
- Масса: около 470 г
Колонка Tronsmart Groove 2 — это хороший представитель компактных моделей, продолжение удачной линейки Groove от известного производителя. Фактически, это половинка большой Tronsmart Mega или Tronsmart Force с одним динамиком, но в специальном «брутальном» корпусе.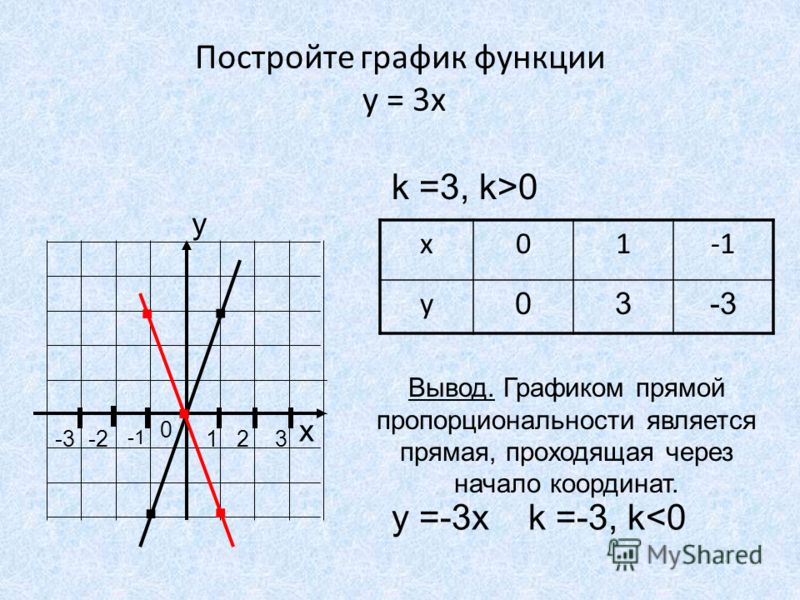
В комплекте поставки с колонкой входит краткое руководство, кабель AUX, кабель USB-C, D-образный карабин. Упаковка компактная, но такую не стыдно подарить.
Внешний вид колонки Tronsmart Groove 2 представлен на фотографии ниже. Отмечу довольно агрессивное оформление передней панели, да и корпуса в целом, наличие пассивного излучателя и защитной решетки.
Руководство довольно содержательное, есть интересные функции и описание конкретных действий. Например, для сброса колонки потребуется зажать кнопку питания на 8 сек, а тройное нажатие активирует функцию допобработки звука (SoundPulse).
Колонка не боится ударов и падений, защищена от брызг воды, вполне прилично и довольно громко играет. На верхней панели присутствует кнопочная панель для управления колонкой и воспроизведением. Есть и светодиодный индикатор режима работы.
Для того чтобы установить колонку, можно воспользоваться резьбой 1/4″ и фотоштативом или соответствующими креплениями. Усиленное «ухо» позволяет подвешивать колонку, например, на рюкзак, или на перекладину в палатке. Задняя панель разъемов защищена толстой резиновой заглушкой.
Задняя панель разъемов защищена толстой резиновой заглушкой.
Из интерфейсов доступно подключение через AUX, а также воспроизведение с карты памяти MicroSD. Для подзарядки используется USB-C (может работать на зарядке). Ну и, конечно же, bluetooth. Есть функция работы двух колонок в стереопаре.
Кнопки прорезинены, позволяют перематывать композиции, отвечать на вызовы, активировать функции, в том числе и подсветку. Вся колонка собрана на довольно массивном крепеже под внутренний шестигранник.
Одна из киллерфич данной модели — динамическая контурная подсветка, которая представляет собой тонкую светодиодную RGB полоску, расположенную вокруг сетки динамика. Цвет и оттенок свечения меняется в зависимости от громкости звука. Можно отключить данную функцию для экономии аккумулятора.
Выше я упоминал, что в комплекте с колонкой поставляется оригинальный карабин для крепления колонки. С помощью подобного карабина можно буквально в одно движение «защелкнуть» колонку на рюкзак во время перемещения по улице.
Подключается колонка точно так же, как и ее «старшие» собратья, например, Tronsmart Bang. Просто ищем в поиске Bluetooth устройств «Tronsmart Groove 2» и подтверждаем сопряжение.
Аналогичным образом подключается колонка и к мобильным гаджетам. Доступно отображение уровня заряда батареи и раздельные протоколы для голоса и звука (можно отключить входящие звонки просто деактивировав данный профиль).
Довольно неплохой и громкий звук у Groove 2, присутствуют и низы, и верхи. Так как излучатель всего один (на 10 Вт), то запредельного качества ждать не следует. Но свою стоимость колонка отрабатывает на все 100!
Технология обработки звука SoundPulse несколько выравнивает звучание и делает определенный акцент на басах. Колонка начинает звучать более ярко, но зависит от композиции в целом.
Если проверить работу пассивного излучателя, то отмечу, что его направлении громко передаются в основном только средние (от 100 Гц) частоты, то есть вокал и разговор.
За предоставленные фотографии разобранной колонки благодарность коллеге.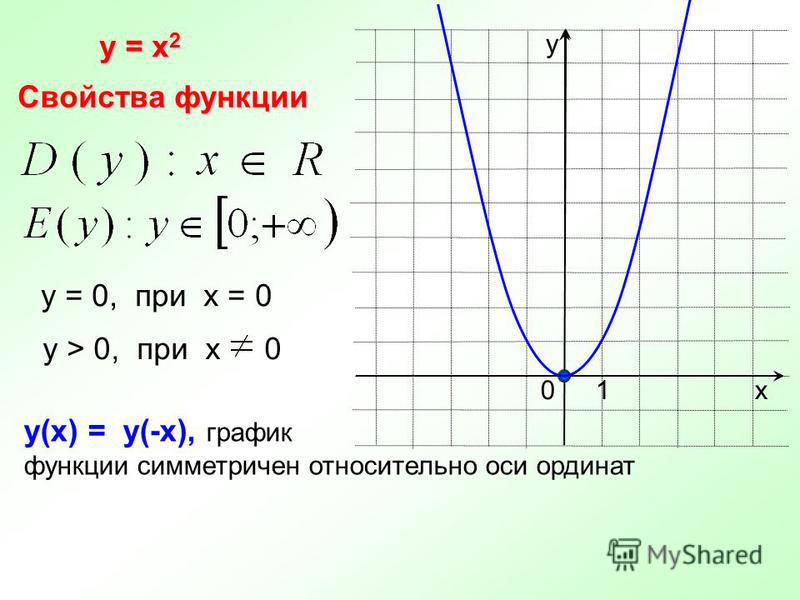 Как видно, маркировка на элементе 18650 соответствует заявленным 2500 мАч, а маркировка на динамике — заявленной мощности 10 Вт (при 4 Омах).
Как видно, маркировка на элементе 18650 соответствует заявленным 2500 мАч, а маркировка на динамике — заявленной мощности 10 Вт (при 4 Омах).
Колонка реально портативная — ей не страшны удары и падения (даже динамик защищен сеткой). Можно «забыть» колонку под дождем, ополоснуть после грязного/пыльного пляжа. Корпус с покрытием стойко переносит потертости при активной эксплуатации. Самое то для улицы, для музыкального сопровождения во время занятий на открытом воздухе, для туризма и просто для посиделок в компании.
Отдельно выделю работу пассивного излучателя. За счет подобного оснащения колонка получает объемное звучание, что особенно важно при прослушивании на природе. Да и карабин будет не лишним — удобно подвешивать колонку во время отдыха. Светодиодная подсветка не позволит забыть колонку в сумерках.
Приобрести колонку можно в официальном магазине Tronsmart, в настоящий момент со скидкой. Описание можно посмотреть в карточке товара на Яндекс.Маркете. Отмечу, что именно портативная колонка Tronsmart Groove 2 — это хороший подарок увлеченному человеку.
Дополнительно можно посмотреть рекомендательные статьи:
Подборка умных колонок с голосовым ассистентом (Алиса/Маруся).
Выбираем комфортное компьютерное кресло.
Как управлять роботом-пылесосом с помощью помощника Алисы Яндекса.
С другими тестами и обзорами смарт-гаджетов и техники, а также подборками вы можете ознакомиться по ссылкам ниже и в моем профиле.
HAVAL F7 (Хавейл Ф7) 2022 года – Официальный импортер Haval в России
ЦЕНА ОТ 2 449 000 ₽ С УЧЕТОМ ВЫГОДЫ*
Дополнительная выгода с учетом лизинга 160 000 ₽**
Запросить предложение
Запись на тест-драйв
Запись на тест-драйв
HAVAL F7 в наличии
Доплата за вариант цвета металлик составляет 20 000 ₽
Динамичный и смелый дизайн — не привилегия
Технологичный и стильный внешний вид привлекает внимание и демонстрирует ваше безупречное чувство вкуса.
Зимние опции
Подогрев задних и передних сидений, обогрев всего лобового стекла и руля станут приятным дополнением к общему комфортному нахождению внутри автомобиля.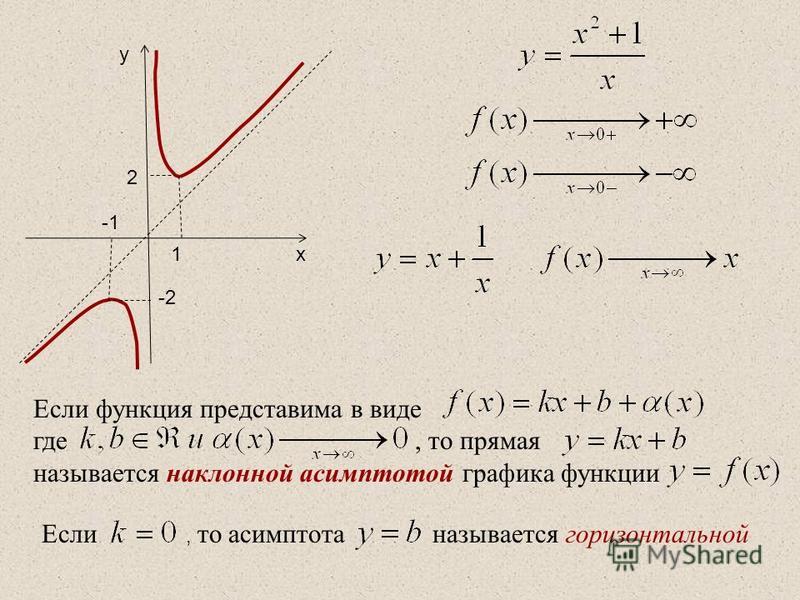
2-х зонный климат контроль
Доступна персональная настройка температуры внутри автомобиля.
Беспроводная зарядка
Беспроводная зарядка для смартфона позволит всегда оставаться на связи.
8 динамиков аудиосистемы
Качественное звучание, передающее все тонкости музыкальных композиций.
Комфорт в салоне
Салон выполнен из высококлассной эко-кожи с перфорацией в стильном сочетании синего и благородного бежевого цвета. А сиденье водителя регулируется в 8 направлениях, оснащено вентиляцией и электроприводом поясничной поддержки, что полезно для спины и позволяет ей не уставать при дальних поездках.
HAVAL F7
Функциональное мобильное приложение MY HAVAL
Дистанционно управлять центральным замком автомобиля, закрывать окна, запускать двигатель, настраивать климат-контроль и обогрев сидений, а также быстро находить автомобиль на парковке – эти и другие опции доступны в удобном мобильном приложении MY HAVAL.
Узнать больше
Система полного привода с 6-ю режимами движения
Система интеллектуального полного привода 4WD, которая предусматривает выбор из шести различных режимов работы в соответствии с условиями движения – «Экологичный», «Спорт», «Нормальный», «Снег», «Грязь», «Песок».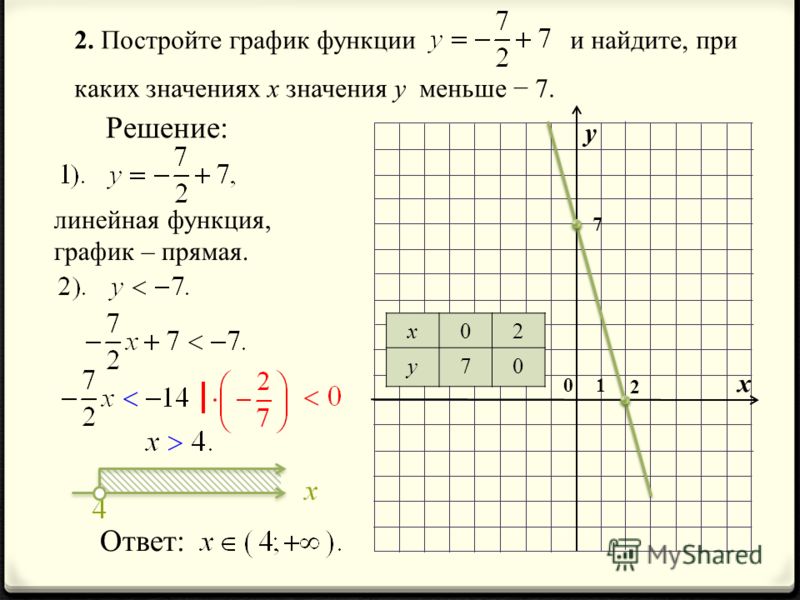
7-ступенчатая коробка передач с двойным сцеплением “мокрого” типа (7DCT)
Современная коробка передач снижает расход топлива.
Бензиновый двигатель
Доступны два двигателя 1,5Т (150 л.с., 280 Н•м) с приводом на передние колеса или системой подключаемого полного привода и двигатель 2.0Т (190 л.с., 340 Н•м) с полным приводом.
Новая 12.3” цифровая приборная панель
Цифровая приборная панель с изображением высокого качества отображает всю необходимую информацию о скорости движения и расходе топлива.
Новая мультимедиа с 12.3” сенсорным экраном
Современная мультимедийная панель позволяет легко контролировать функции автомобиля и синхронизироваться с мобильным устройством.
Поддержка Apple Carplay и Android Auto
Раскройте функционал вашего автомобиля через мультимедийную систему: отвечайте на звонки и переключайте треки с Apple Carplay и Android Auto.
Адаптивный круиз контроль c функцией движения на малых скоростях
Продвинутый адаптивный круиз-контроль поддерживает скорость автомобиля и реагирует на меняющуюся ситуацию на дорогах.
Система камер кругового обзора 360⁰
Круговые камеры с изображением высокого качества позволят избежать непредвиденных ситуаций на дорогах и в зоне парковки.
Система автоматической парковки
Система автоматической парковки распознает свободное место и принимает на себя работу рулевым управлением. Водителю, по указанию электроники, остается только следовать подсказкам, появляющимся на экране.
Система сохранения и удержания автомобиля в центре полосы
HAVAL F7 оборудован системой предупреждения о выходе из полосы движения с функциями возврата в полосу и удержания в центре полосы.
Система мониторинга перекрестков
Если при повороте на перекрестке возникнет риск столкновения, система автоматически задействует тормоз автомобиля.
Система отслеживания помех при открытой двери
Водитель будет предупрежден при возникновении транспортных средств или пешеходов при открытии водительской двери.
Распознавание дорожных знаков
Получайте информацию обо всех ограничениях скорости на дороге в реальном времени.
Система мониторинга слепых зон
Движение на дорогах может быть непредсказуемым, для повышения безопасности система радаров HAVAL F7 отслеживает слепые зоны и предупреждает о возможных помехах.
Система предупреждения/торможения при выезде с парковки задним ходом
Система подаст сигнал, если при выезде задним ходом будет препятствие.
6 подушек безопасности
Подушки безопасности расположены так, чтобы гарантировать надежную защиту при столкновении.
Конструкция кузова высокой прочности
Конструкция кузова выполнена из современных материалов, обеспечивающих долговечность.
1.5T 2WD
1.5T 2WD
1.5T 2WD
Экстерьер- Светодиодные дневные ходовые огни
- Рейлинги на крыше
- Светодиодные задние фонари
- Задний дворник
- Светодиодные передние противотуманные фары с функцией освещения поворотов
- Антенна в форме плавника
- Галогеновые фары
1.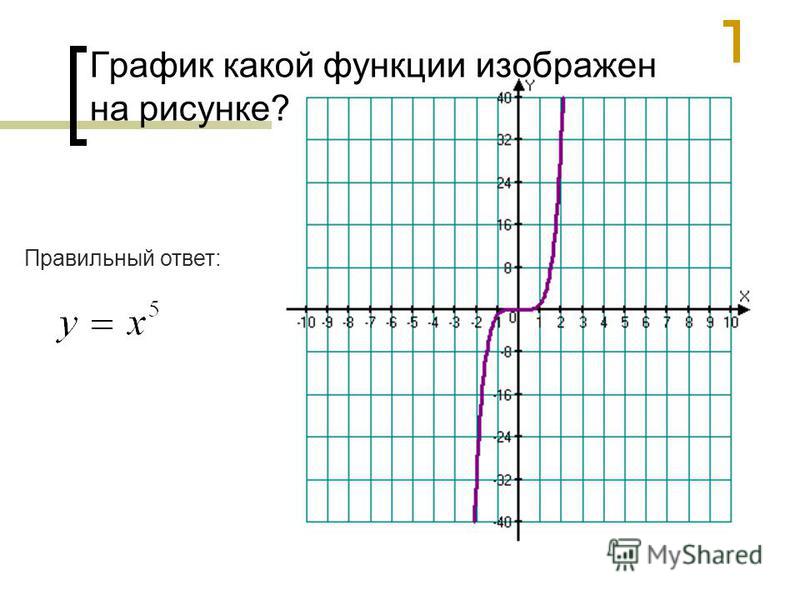 5 л. (150 л.с.) АКПП 4х21.5 л. (150 л.с.) АКПП 4х42.0 л. (190 л.с.) АКПП 4х4
5 л. (150 л.с.) АКПП 4х21.5 л. (150 л.с.) АКПП 4х42.0 л. (190 л.с.) АКПП 4х4
1.5 л. (150 л.с.) АКПП 4х2
Модификация
Основные характеристики
Тип двигателя
бензиновый, с турбонаддувом
Рабочий объем, см3
1499
Число цилиндров
4, рядное
Максимальная мощность, л.с. / при об/мин.
150 / 5000-5600
Тип привода
Передний 2WD
Коробка передач
7-ступенчатая, роботизированная, с двойным сцеплением мокрого типа
Время разгона 0 — 100 км/ч, с
11
Максимальная скорость, км/ч
180
Все характеристикиЗапись на сервис
Запись на тест-драйв
Каталог
Прайс-лист
3-8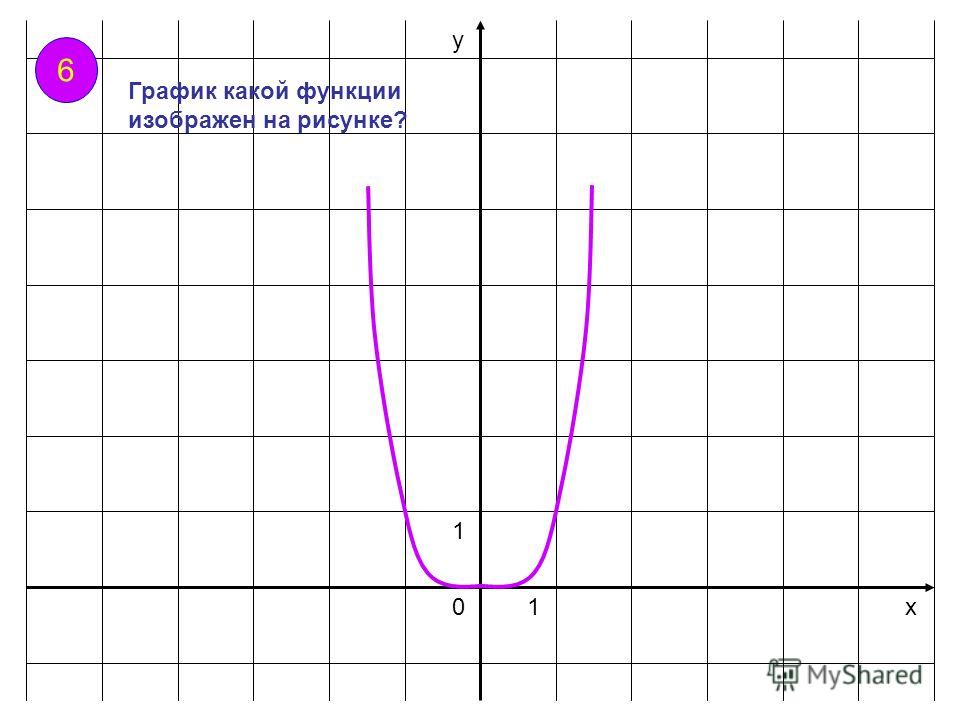 Он быстро уменьшается по мере увеличения $x$, как показано на его графике.
Он быстро уменьшается по мере увеличения $x$, как показано на его графике.При экспоненциальном росте $f(x)$ функция удваивается каждый раз, когда вы добавляете единицу к ее входу $x$. При экспоненциальном затухании $g(x)$ функция уменьшается вдвое каждый раз, когда вы добавляете единицу к ее входу $x$. Наличие этого времени удвоения или периода полураспада характерно для экспоненциальных функций, указывающих, насколько быстро они растут или затухают.
Параметры показательной функции
Как и в случае любой функции, действие экспоненциальной функции $f(x)$ можно описать с помощью метафоры функциональной машины, которая принимает входные данные $x$ и преобразует их в выходные данные $f(x)$.
Метафора функциональной машины полезна для введения параметров в функцию. Приведенные выше экспоненциальные функции $f(x)$ и $g(x)$ — это две разные функции, но они отличаются только изменением основания возведения в степень с 2 на 1/2. Мы могли бы зафиксировать обе функции, используя одну функциональную машину, но циферблаты для представления параметров, влияющих на работу машины.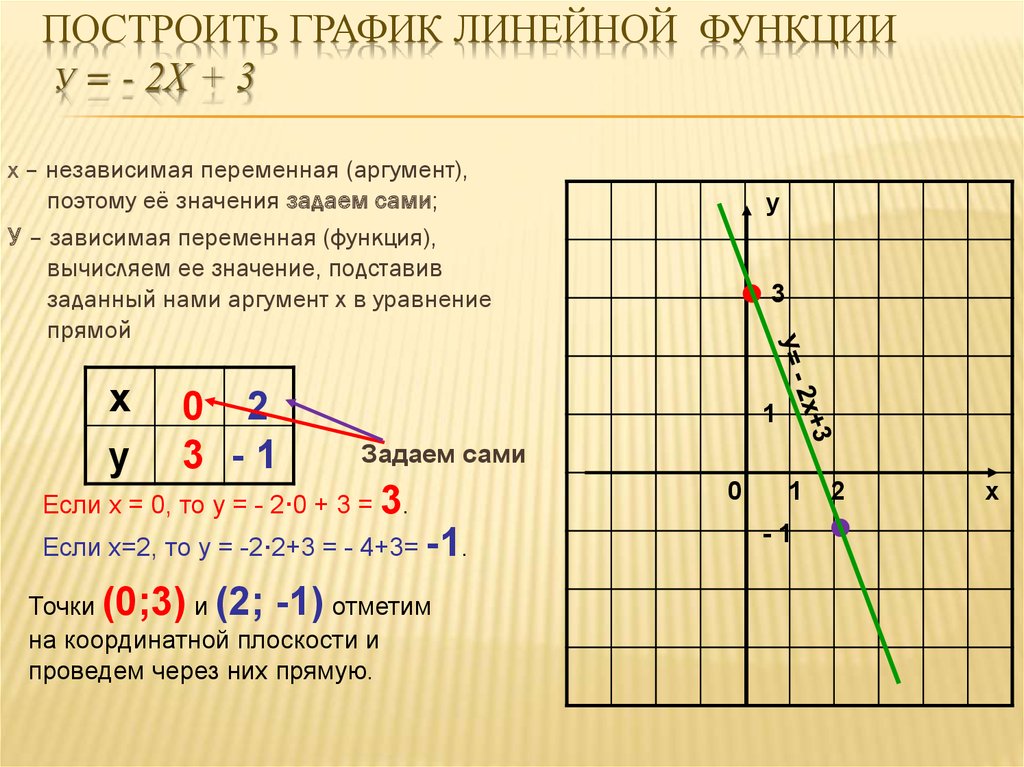 {kx}$. Согласно приведенному выше обсуждению, не должно иметь значения, используем ли мы $b=2$ или $b=10$, поскольку мы можем получить одни и те же функции в любом случае (только с разными значениями $k$). 9{кх}.$$
Вы можете добавить параметр $c$ в апплет, установив флажок «функция масштабирования».
{kx}$. Согласно приведенному выше обсуждению, не должно иметь значения, используем ли мы $b=2$ или $b=10$, поскольку мы можем получить одни и те же функции в любом случае (только с разными значениями $k$). 9{кх}.$$
Вы можете добавить параметр $c$ в апплет, установив флажок «функция масштабирования».
Что такое обозначение функций и почему меня это должно волновать?
Вычисление четных и нечетных функций в выражениях
Purplemath
Вы уже некоторое время играете с » y =» разного рода уравнениями. И вы видели, что «хорошие» уравнения (скажем, прямые линии, а не эллипсы) — это те, которые вы можете решить для « y =» и затем вставить в свой графический калькулятор. Эти « y =» уравнения — это функции. Но вопрос, с которым вы сталкиваетесь в данный момент, заключается в следующем: «Зачем мне нужна эта запись функций, особенно когда у меня есть прекрасное ‘ y =’, и как эта запись работает? »
Вспомните, когда вы учились в начальной школе. Ваш учитель давал вам рабочие листы, содержащие такие утверждения, как «[ ] + 2 = 4», и велел вам заполнить поле. Когда вы стали старше, ваш учитель начал давать вам рабочие листы, содержащие такие заявления, как « x + 2 = 4» и сказали вам «решить для x «.
Ваш учитель давал вам рабочие листы, содержащие такие утверждения, как «[ ] + 2 = 4», и велел вам заполнить поле. Когда вы стали старше, ваш учитель начал давать вам рабочие листы, содержащие такие заявления, как « x + 2 = 4» и сказали вам «решить для x «.
Содержимое продолжается ниже
MathHelp.com
Обозначение функций
Почему ваши учителя перешли от блоков к переменным? Подумайте об этом: сколько форм вам пришлось бы использовать для формул, подобных этой для площади A трапеции с верхним основанием a , нижним основанием b и высотой h ? )( a + b )
Если вы попытаетесь выразить это или что-то более сложное, используя коробки различной формы, у вас быстро закончатся формы. Кроме того, вы знаете из опыта, что « А » означает «площадь», « h » означает «высота», а « а » и « b » обозначают длины параллельных вершин и нижние стороны. Одному небу известно, что может означать квадратная коробка или треугольная коробка!
Одному небу известно, что может означать квадратная коробка или треугольная коробка!
Другими словами, они перешли от блоков к переменным, потому что хотя блоки и буквы означают одно и то же (а именно, слот, ожидающий заполнения значением), переменные лучше. Переменные более гибкие, их легче читать, и они могут дать вам больше информации.
То же самое верно для « y » и « f ( x )» (произносится как «эфф-оф-экс»). Для функций эти два обозначения означают одно и то же, но « f ( x )» дает вам больше гибкости и больше информации. Раньше вы говорили: « х = 2 х + 3; найдите х , когда х = −1». Теперь вы говорите: « f ( x ) = 2 x + 3; найдите f (−1)» (произносится как « f -из- x равно 2 x плюс три; найти f -отрицательной-единицы»). В любом случае вы делаете одно и то же: подставляете −1 вместо x , умножаете на 2, а затем прибавляете 3, упрощая, чтобы получить конечное значение +1.
Но обозначение функций дает вам большую гибкость, чем использование только « y » для каждой формулы. Например, ваш графический калькулятор будет отображать различные функции как y1, y2 и т. д., так что вы можете сказать уравнения друг от друга, когда, скажем, вы просматриваете их значения в «ТАБЛИЦЕ».0909
Точно так же в учебниках и при записи мы используем разные имена функций, такие как f ( x ), g ( x ), h ( x ), ( t ) и т. д., чтобы отслеживать и работать с более чем одной формулой в любом отдельном контексте. Благодаря нотации функций мы теперь можем использовать более одной функции одновременно, не запутываясь и не путая формулы, заставляя себя задаваться вопросом: «Хорошо, а что y ‘ is this one?» И обозначения могут быть полезными пояснениями.
Из геометрии вы знаете, что « A ( r ) = π r 2 » указывает площадь окружности, заданной в терминах значения радиуса r , в то время как « C ( r ) = 2π r » указывает на длину окружности, заданную в терминах радиуса r .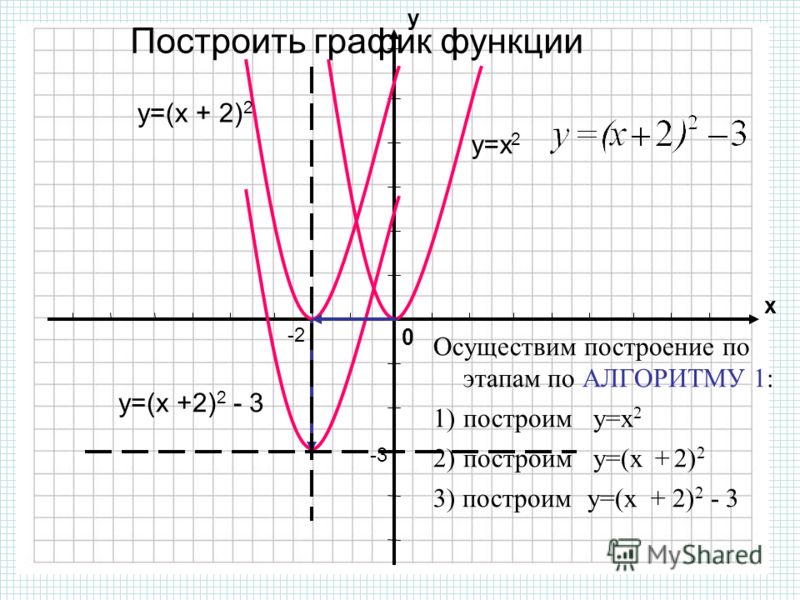 Обе функции имеют один и тот же плагин- в переменной (« r «), но « A » напоминает вам, что первая функция — это формула для «площади», а « C » напоминает вам, что вторая функция — это формула для «длины окружности». )» — это то же самое, что и « y «. Вы даже можете обозначить ось y на своих графиках как « f ( x )», если хотите.
Обе функции имеют один и тот же плагин- в переменной (« r «), но « A » напоминает вам, что первая функция — это формула для «площади», а « C » напоминает вам, что вторая функция — это формула для «длины окружности». )» — это то же самое, что и « y «. Вы даже можете обозначить ось y на своих графиках как « f ( x )», если хотите.
Пусть Я поясню еще один момент. В то время как круглые скобки до сих пор всегда обозначали умножение, это не относится к обозначению функций. Вопреки всему предыдущему опыту, скобки для обозначения функций делают , а не указывают на умножение.
Выражение « f ( x )» означает «формула с именем f имеет x в качестве входной переменной». , а не означает «умножить на и на »!
Не смущайтесь, произнося (или думая) « f ( x )» как « f x x », и никогда не пытайтесь «умножить» имя функции на ее ввод в скобках.
В обозначениях функций « x » в « f ( x )» называется «аргументом функции» или просто «аргументом». Так что, если вам дадут выражение « ф (2)» и спросят «аргумент», ответ будет просто «2».
Почему ввод функции называется «аргументом»?
Термин «аргумент» имеет долгую историю. Первоначально это был логический термин, относящийся к заявлению, которое выдвигало доказательство или, в менее формальном смысле, к утверждению, которое использовалось, чтобы попытаться кого-то в чем-то убедить. В конце концов, в раннем научном контексте этот термин стал обозначать любое математическое значение, которое было необходимо в качестве исходных данных для других вычислений, или любое значение, от которого зависели более поздние результаты.
В двадцатом веке, когда компьютерное кодирование стало популярным, кодеры приняли математический смысл для обозначения входных данных для своего кодирования. В нашем математическом контексте «аргумент» — это независимая переменная (та, для которой вы выбираете значение, обычно это значение x ), а выход функции — это зависимая переменная (та, значение которой зависит от того, что было подключено). in, обычно это значение y ).
in, обычно это значение y ).
Сначала сделаю вторую часть. Аргументом является то, что находится внутри круглых скобок, поэтому аргумент здесь равен 9.0941 с .
Имя функции — это переменная, которая стоит перед круглыми скобками. В этом случае имя функции h .
имя функции: h
аргумент: s
Аргументом является то, что подключено. В этом конкретном (необычном) случае подключаемая переменная — « y «. (В конце концов, нет правила, согласно которому и не могут быть независимой переменной.) Итак:
аргумент равен 9.0941 y
Имя функции стоит перед круглыми скобками, поэтому имя функции здесь g .
Во второй части вопроса от меня требуют аргументации. В первой части мне дали имя и аргумент функции (часть « g ( t )») и формулу (часть « t 2 + t «), аргумент был t . Но во второй части они подставили конкретное значение для 9. 0941 т . Итак, во второй части аргументом является число −1.
0941 т . Итак, во второй части аргументом является число −1.
имя функции: г
аргумент г (-1): -1
Как функция вычисляется по числу?
Вы оцениваете « f ( x )» точно так же, как вы всегда оценивали « y »; а именно, вы берете число, которое они вам дают, в качестве входной переменной, подставляете его в качестве переменной и упрощаете, чтобы получить ответ. Например:
Чтобы оценить f ( x ) при x = 2, я подставлю 2 для каждого экземпляра x в правиле функции:
f (2) = 90 (2) 2 +2(2) − 1
Чтобы все было ясно в моей голове (и ясно в моей работе), я заключил в скобки каждый экземпляр аргумента 2 в формуле для f . Теперь я могу упростить:
(2) 2 + 2(2) — 1
= 4 + 4 — 1
= 7
Тогда мой ответ:
f (2) = 7
Чтобы оценить, я делаю то, что делал всегда. Я подставлю заданное значение (−3) для указанной переменной ( x ) в данную формулу:
Я подставлю заданное значение (−3) для указанной переменной ( x ) в данную формулу:
f (−3) = (−3) 2 + 2(−3) − 1
Я снова использовал круглые скобки, чтобы четко обозначить значение, вводимое в формулу. В этом случае скобки помогают мне отслеживать знаки «минус». Теперь я могу упростить:
(−3) 2 + 2(−3) − 1
= 9 − 6 − 1
= 2
Тогда мой ответ:
f (−3) = 909 2 909 2 вы испытываете трудности при работе с негативами, попробуйте использовать круглые скобки, как я сделал выше. Это помогает отслеживать такие вещи, как, например, находится ли показатель степени на знаке «минус». И вообще это хорошая привычка, которую нужно развивать.
Важный тип функции называется «кусочной» функцией, потому что она состоит из частей. Например, следующая функция является кусочной:
Как видите, эта функция разделена на две половины: половина, предшествующая x = 1, и половина, идущая от x = 1 до бесконечности. Какую половину функции вы используете, зависит от значения x . Давайте рассмотрим это:
Какую половину функции вы используете, зависит от значения x . Давайте рассмотрим это:
. Учитывая функцию
f ( x ), как определено выше, оцените функцию при следующих значениях: x = −1, x = 3 и x = 1,
Эта функция поставляется по частям; отсюда и название «кусочная» функция. Когда я оцениваю его при различных значениях x , я должен быть осторожным, чтобы вставить аргумент в правильную часть функции.
Сначала они хотят, чтобы я оценил x = −1. Так как это меньше 1, то этот аргумент входит в первую часть функции. Для обновления функция такова:
Затем я подставлю -1 в правило ) − 1
= 2 − 1 = 1
Далее они хотят, чтобы я нашел значение f (3). Поскольку 3 больше 1, мне нужно будет подключить вторую часть функции, поэтому:
f (3) = (3) + 4 = 7
Наконец, они хотят, чтобы я вычислил f ( x ) на x = 1.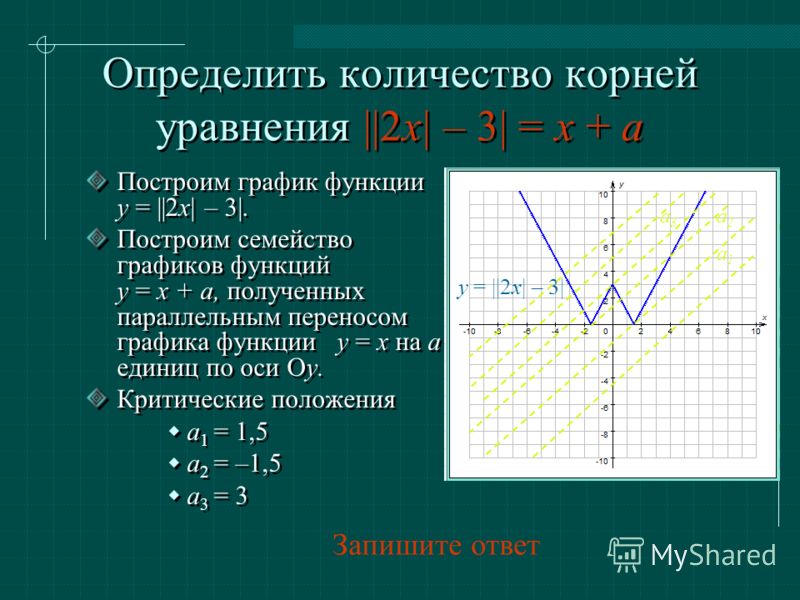 Это единственное значение x , которое немного сложно. Какую половину я использую?
Это единственное значение x , которое немного сложно. Какую половину я использую?
Внимательно изучив правила для функций, я вижу, что первая часть — это правило для x — значений, которые строго меньше 1; правило не применяется, когда x равно 1. С другой стороны, вторая часть применяется, когда x больше или равно 1. Поскольку я имею дело с x = 1, то применяется правило второй части.
е (1) = (1) + 4 = 5
Тогда мой ответ:
е (−1) = 1
е (3) = 7
2 99 9 1) = 5
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в вычислении функций с заданным числовым значением. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Оценить», чтобы сравнить свой ответ с ответом Mathway.
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Нажмите «Нажмите, чтобы просмотреть шаги», чтобы перейти непосредственно на сайт Mathway для платного обновления.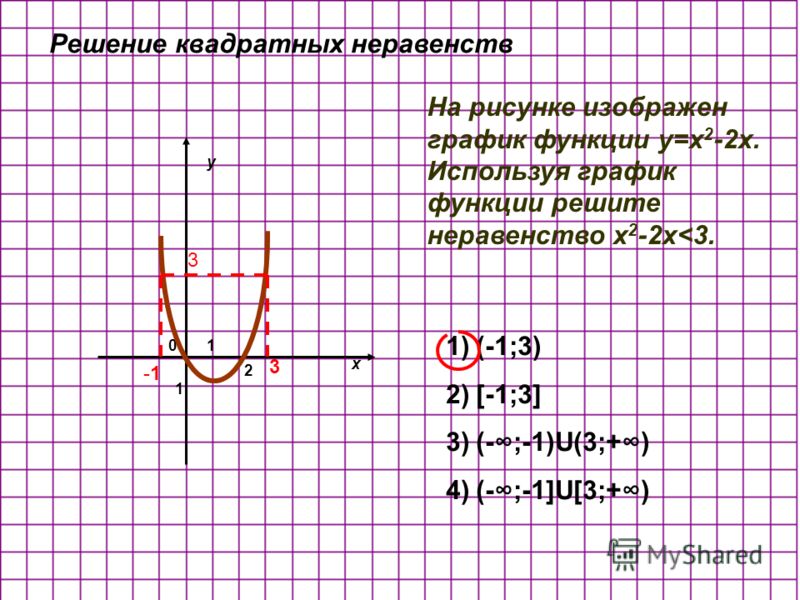 )
)
Страница 2Страница 3
Операции над функциями | Purplemath
Purplemath
Сначала вы узнали (еще в начальной школе), что можете складывать, вычитать, умножать и делить числа. Затем вы узнали, что можете складывать, вычитать, умножать и делить многочлены. Теперь вы узнаете, что вы также можете складывать, вычитать, умножать и делить функции. Выполнение этих операций над функциями не сложнее самой записи. Например, когда вам дают формулы для двух функций и просят найти сумму, все, что вам говорят, это сложить две формулы. В этой теме нет ничего большего, кроме, возможно, некоторого упрощения задействованных выражений.
Содержание продолжается ниже
MathHelp.com
дано
F ( x ) = 3 x +2 и G ( x ) = 4 — 5 x , Find ( F + x , Find ( F + x , Find ( F + x , Find ( F ). ( f — г )( x ), ( f × г )( x ) и ( f / 90 2 х 90 942 90 942 ).
( f — г )( x ), ( f × г )( x ) и ( f / 90 2 х 90 942 90 942 ).
Чтобы найти ответы, все, что мне нужно сделать, это применить операции (плюс, минус, умножить и разделить), которые они мне говорят, в том порядке, в котором они мне говорят.
( F + G ) ( x ) = F ( x ) + G ( x ) g ( x ) G ( x ) g ( x ). х ]
= 3 х + 2 + 4 — 5 х
= 3 х — 5 х + 2 + 4 —
( F — G ) ( x ) = F ( x ) — G ( x ) — G ( x ) — G ( x ) — G ( x ) — G ( x ) — G ) — ( x ) — G ( x ). — [4 — 5 x ]
— [4 — 5 x ]
= 3 x + 2 — 4 + 5 x
= 3 x + 5 x + 2 — 4
0942 + 5 x + 2 — 4004 2 + 5 x + 2 — 409094 2 + 5 x + 2 — 40942 + 5 x + 2 x + 5 x + 2 x + 5 x . ( f × г )( x ) = [ f ( x )][ г ( x )] = (3 x + 2) (4 — 5 x ) = 12 x + 8 — 15 x 2
Мой ответ — это аккуратное перечисление каждого из моих результатов, четко обозначенное, где есть что.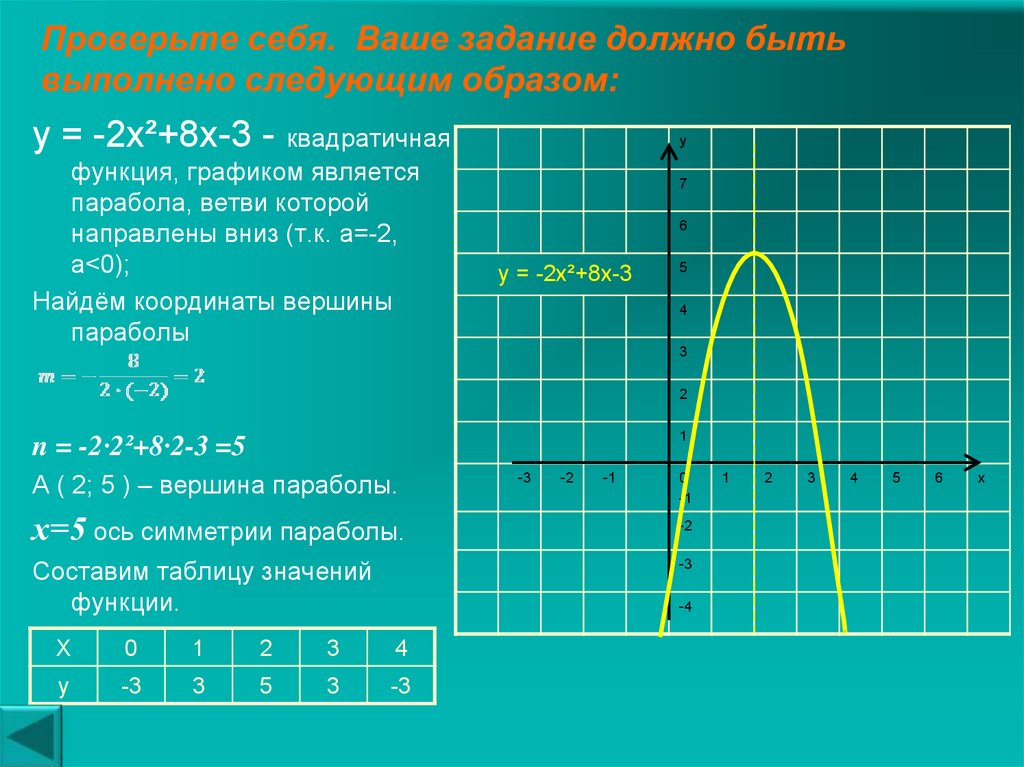
( f + g ) ( x ) = −2 x + 6
( f − g ) ( x ) = 8 x − 2
( f × g ) ( x ) = −15 x 2 + 2 x + 8
( f / г )( x ) = (3 x + 2)/(4 − 5 x )
Дано
f ( x ) = 2 x , g ( x ) = x + 4, и ч — 5 х 909 42 ( 909 4 )0941 x 3 , найти ( f + g )(2), ( h − g )(2), ( f ) и (91 × h) ч / г )(2).
Это упражнение отличается от предыдущего тем, что мне нужно не только выполнять операции с функциями, но и вычислять их при определенном значении x . Чтобы найти ответы, я могу либо работать символически (как в предыдущем примере), а затем вычислять, либо я могу найти значения функций в x = 2, а затем работайте оттуда.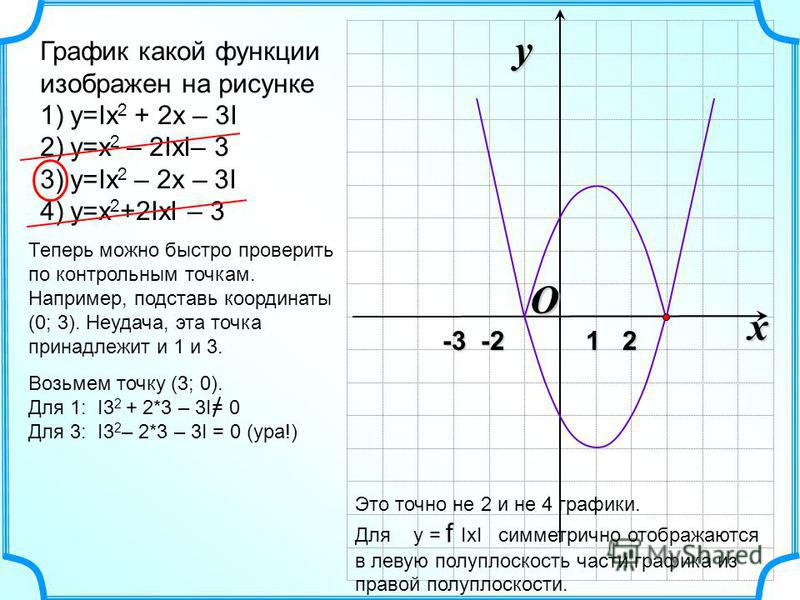 Вероятно, в этом случае проще вычислить сначала, поэтому:
Вероятно, в этом случае проще вычислить сначала, поэтому:
f (2) = 2(2) = 4
g (2) = (2) + 4 = 6
h (2 ) = 5 − (2) 3 = 5 − 8 = −3
Теперь я могу вычислить перечисленные выражения:
( f + g )(2) = f (2) + г (2)
= 4 + 6 = 10
( ч − г )(2) = ч (2) − г (2)
= −3 − 6 = −9
( f × ч )(2) = f (2) × ч (2)
= (4)(−3)= − 12
( ч / г )(2) = ч (2) ÷ г (2)
= −3 ÷ 6 = −0,5
(909 909) Тогда мой ответ: 909 909 f + г )(2) = 10, ( ч — г )(2) = -9, ( f × ч )(2) = -12, ( h / g )(2) = -0,5 Если вы сначала работаете с символами и подставляете значение x только в конце, вы все равно получите те же результаты. В любом случае будет работать. Оценить первым обычно проще, но выбор за вами.
В любом случае будет работать. Оценить первым обычно проще, но выбор за вами.
Вы можете использовать виджет Mathway ниже, чтобы попрактиковаться в работе с функциями. Попробуйте введенное упражнение или введите свое собственное упражнение. Затем нажмите кнопку и выберите «Решить», чтобы сравнить свой ответ с ответом Mathway. (Или пропустите виджет и продолжите урок.)
Пожалуйста, примите куки-файлы настроек, чтобы включить этот виджет.
(Щелкнув «Нажмите для просмотра шагов» на экране ответов виджета, вы перейдете на сайт Mathway для платного обновления .)
На самом деле это не вопрос о функциях-операциях, но что-то подобное часто возникает в контексте функций-операций. Это выглядит намного хуже, чем есть на самом деле, пока я готов не торопиться и быть осторожным.
Для меня самый простой способ продолжить это упражнение — работать по частям, упрощая по мере продвижения; тогда я соберу все вместе и упрощу в конце.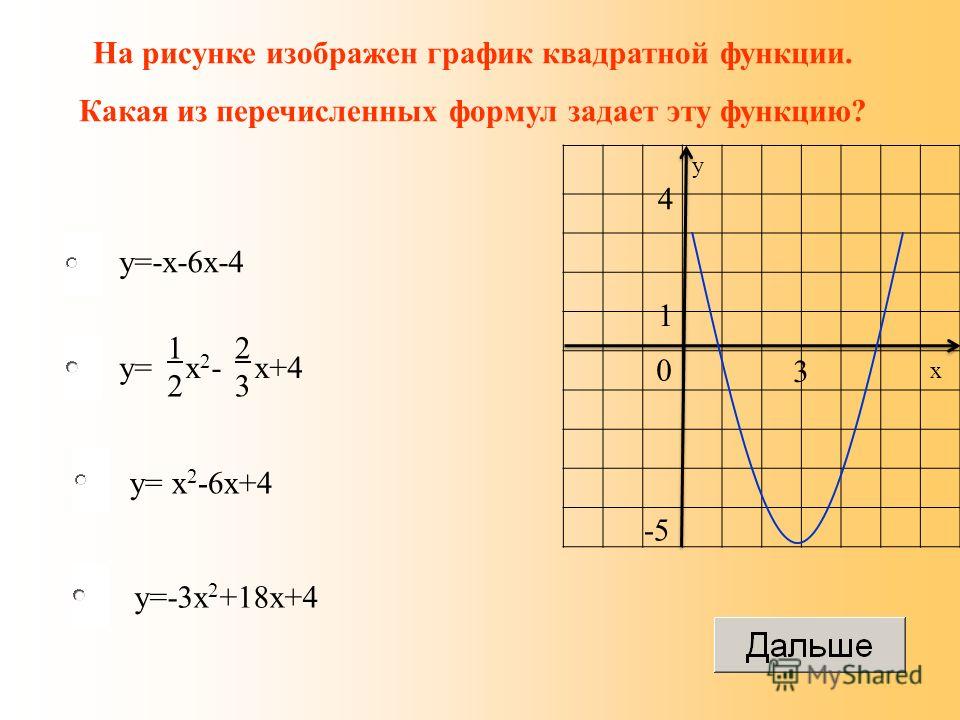
Для первой части числителя мне нужно подставить выражение » x + h » для каждого » x » в формуле функции, используя то, что я узнал о записи функции, а затем упростите:
f ( x + h )
= 3( x + H ) 2 — ( x + H ) + 4
= 3 ( x 2 + 2 x
99 2 + 2 x 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2 + 2. — H + 4= 3 x 2 + 6 XH + 3 H 2 — x 2 — x
9 2 — h 2 — . числитель — это просто сама функция:f ( x ) = 3 x 2 − x + 4
Теперь вычту и упрощу:
Осталось только разделить на знаменатель; разложение позволяет упростить:
Теперь я должен вычислить ч = 0, поэтому:
6 x + 3(0) — 1 = 6 x — 1
упрощенная форма: 6 x + 3 h — 1
значение в h = 0: 6 x — 1
Это почти все, что нужно для «операций над функциями», пока вы не доберетесь до композиции функций.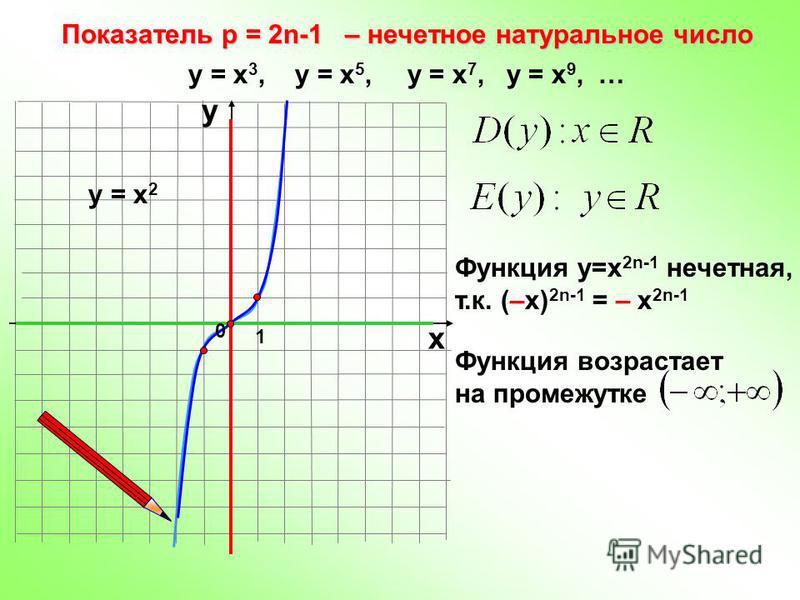 Пусть вас не беспокоит обозначение этой темы; оно означает не что иное, как именно то, что оно говорит: сложить, вычесть, умножить или разделить; затем упростите и оцените по мере необходимости. Не переусердствуйте с этим. Это действительно так просто.
Пусть вас не беспокоит обозначение этой темы; оно означает не что иное, как именно то, что оно говорит: сложить, вычесть, умножить или разделить; затем упростите и оцените по мере необходимости. Не переусердствуйте с этим. Это действительно так просто.
О, последний пример? Они поместили это туда, чтобы вы могли «попрактиковаться» в том, что вы будете делать в исчислении. Вы, скорее всего, не вспомните об этом к тому времени, когда на самом деле приступите к исчислению, но вы будете следовать очень похожему процессу для нахождения того, что называется «производными».
URL: https://www.purplemath.com/modules/fcnops.htm
Обратные функции
Обратная функция работает в обратном направлении!
Начнем с примера:
Здесь у нас есть функция f(x) = 2x+3 , записанное в виде блок-схемы:
Обратная функция работает в другом направлении:
Таким образом, обратная функция: 2x+3 равна: (y-3) /2
Обратное обычно изображается путем добавления небольшого «-1» после имени функции, например:
f -1 (y)
Мы говорим « f обратное y»
Итак, обратное выражение f(x) = 2x+3 записывается:
f -1 (y) = (y-3)/2
(я также использовал y вместо x , чтобы показать, что мы используем другое значение.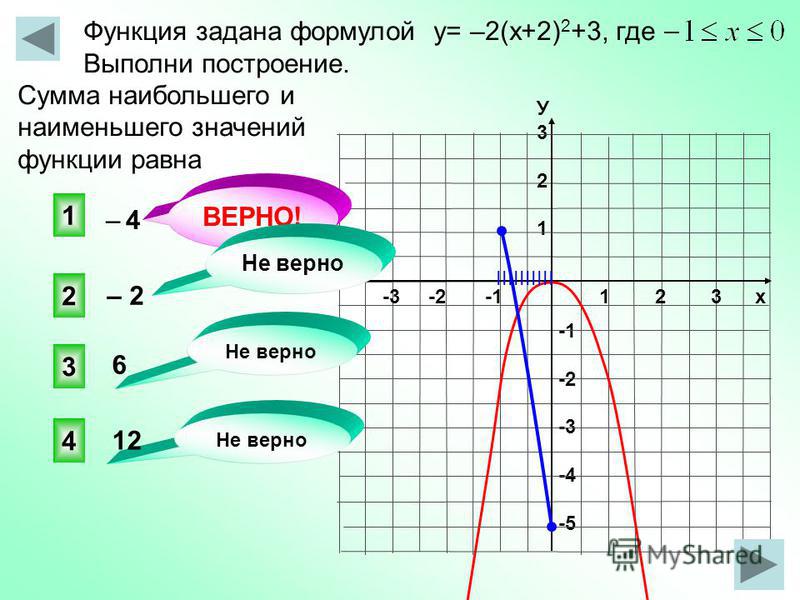 )
)
Назад к тому, с чего мы начали
наоборот, она должна вернуть нам исходное значение:
Когда функция f превращает яблоко в банан,
Тогда обратная функция f -1 превращает банан обратно в яблоко
Пример:
Используя приведенные выше формулы, мы можем начать с x=4:
f(4) = 2×4+3 = 11
Затем мы можем использовать обратное число 11:
f -1 (11) = (11-3)/2 = 4
И мы волшебным образом вернуть 4 обратно!
Мы можем записать это в одну строку:
f -1 ( f(4) ) = 4
«f обратное значение f от 4 равно 4» f -1 возвращает нам исходное значение:
f -1 ( f(x) ) = x
Мы могли бы также расположить функции в другом порядке, и это все еще работает:
f( f -1 (x)) = x
Пример:
Начните с:
f -1 ( 11) = (11-3)/2 = 4
И тогда:
f(4) = 2×4+3 = 11
Итак, мы можем сказать:
f( f -1 (11) ) = 11
«f из f, обратное 11, равно 11»
Решить с помощью алгебры
Мы можем решить обратное с помощью алгебры. Подставьте «y» вместо «f(x)» и найдите x:
Подставьте «y» вместо «f(x)» и найдите x:
| Функция: | ф(х) | = | 2x+3 | |
| Поставьте «y» вместо «f(x)»: | г | = | 2x+3 | |
| Вычесть 3 с обеих сторон: | г-3 | = | 2x | |
| Разделить обе стороны на 2: | (у-3)/2 | = | х | |
| Поменять стороны: | х | = | (у-3)/2 | |
| Решение (поместите «f -1 (y)» вместо «x»): | ф -1 (у) | = | (у-3)/2 |
Этот метод хорошо работает для более сложных инверсий.
градусов Фаренгейта в градусы Цельсия
Полезным примером является преобразование градусов Фаренгейта в градусы Цельсия:
Преобразование градусов Фаренгейта в градусы Цельсия: f(F) = (F — 32) × 5 9
Обратная функция (градусы Цельсия обратно в градусы Фаренгейта): f -1 (C) = (C × 9 916 5 ) + 32
Для вас: посмотрите, сможете ли вы выполнить шаги для создания этой инверсии!
Инверсия общих функций
До сих пор это было легко, потому что мы знаем, что инверсия к умножению — это деление, а инверсия к сложению — это вычитание, но как насчет других функций?
Вот список, который вам поможет:
| Обратные | Осторожно! | ||
| <=> | |||
| <=> | Не делить на ноль | ||
| 1 х | <=> | 1 г | x и y не равны нулю |
| x 2 | <=> | х и у ≥ 0 | |
| x нет | <=> | или | n не ноль (разные правила когда n нечетное, четное, отрицательное или положительное) |
| е х | <=> | п(у) | г > 0 |
| а х | <=> | журнал a (у) | г и а > 0 |
| грех(х) | <=> | грех -1 (у) | от -π/2 до +π/2 |
| кос(х) | <=> | соз -1 (у) | от 0 до π |
| желто-коричневый(х) | <=> | рыжевато-коричневый -1 (у) | от -π/2 до +π/2 |
(Примечание: вы можете прочитать больше об арксинусе, косинусе и тангенсе. )
)
Осторожно!
Вы видели «Осторожно!» колонка выше? Это потому, что некоторые инверсии работают только с определенными значениями .
Пример: возведение в квадрат и квадратный корень
Когда мы возводим в квадрат отрицательное число, а затем делаем обратное, получается следующее:
Возведение в квадрат:(−2) 2 = 4
Обратное (квадратный корень): √(4) = 2
Но мы не вернули исходное значение! Мы получили 2 вместо −2 . Наша вина, что мы не были осторожны!
Таким образом, функция квадрата (в ее нынешнем виде) не имеет обратной
Но мы можем это исправить!
Ограничить домен (значения, которые могут быть переданы в функцию).
Пример: (продолжение)
Только убедитесь, что мы не используем отрицательные числа.
Другими словами, ограничьте его до x ≥ 0 , и тогда мы получим обратное.
Итак, у нас есть такая ситуация:
- x 2 имеет ли , а не обратное
- но {х 2 | x ≥ 0 } (что говорит «x в квадрате, так что x больше или равен нулю», используя нотацию построителя наборов) имеет ли инверсию.

Нет обратного?
Давайте графически посмотрим, что здесь происходит:
Чтобы получить обратное значение, нам нужно уникальных значений .
Только подумайте… если есть два или более x-значений для одного y-значения , как мы узнаем, какое из них выбрать при возврате назад?
| Общие функции |
| Нет обратного |
Представьте, что мы пришли из x 1 к определенному значению y, куда мы вернемся? х 1 или х 2 ?
В этом случае у нас не может быть обратного.
Но если мы можем иметь ровно один x для каждого y, мы можем получить обратное.
Это называется «однозначным соответствием» или Биективной функцией, например,
| Биективной функцией |
| Имеет инверсию |
Функция должна быть «биективной», чтобы иметь обратную.
Таким образом, биективная функция подчиняется более строгим правилам, чем общая функция, что позволяет нам иметь обратную функцию.
Домен и диапазон
Итак, о чем все эти разговоры о « Ограничение домена «?
В своей простейшей форме домен — это все значения, которые входят в функцию (а диапазон — это все значения, которые выходят).
В нынешнем виде приведенная выше функция имеет обратную функцию , а не , потому что некоторые значения y будут иметь более одного значения x.
Но мы могли бы ограничить домен, чтобы было уникальный x для каждого y …
… и теперь мы можем иметь обратную:
Обратите также внимание:
- Функция f(x) переходит из домена в диапазон ,
- Обратная функция f -1 (y) переходит из диапазона обратно в домен.
Давайте изобразим их обоих с точки зрения x . .. так что теперь f -1 (x) , а не f -1 (y) :
.. так что теперь f -1 (x) , а не f -1 (y) :
f(x) и f -1 (x) подобны зеркальным отражениям
(перевернуто по диагонали).
Другими словами:
График f(x) и f -1 (x) симметричен относительно прямой y=x
)
Сначала , мы ограничиваем домен до x ≥ 0 :
- {x 2 | x ≥ 0 } «x в квадрате так, что x больше или равен нулю»
- {√x | x ≥ 0 } «квадратный корень из x такой, что x больше или равен нулю»
И вы можете видеть, что они «зеркальные изображения»
относительно диагонали y=x.
Примечание: когда мы ограничиваем домен до x ≤ 0 (меньше или равно 0), тогда обратное значение равно f -1 (x) = −√x :
- {x 2 | х ≤ 0 }
- {−√x | х ≥ 0 }
Которые тоже обратные.
Не всегда решаемо!
Иногда невозможно найти обратную функцию.
Пример: f(x) = x/2 + sin(x)
Мы не можем вычислить обратное, потому что мы не можем найти «x»:
y = x/2 + sin(x)
г … ? = х
Примечания к обозначениям
Несмотря на то, что мы пишем f -1 (x), «-1» — это , а не показатель степени (или степени):
| f -1 (x) | …отличается от… | ф(х) -1 |
| Обратная функция f | ф(х) -1 = 1/ф(х) (Взаимное) |
Резюме
- Обратное значение f(x) равно f -1 (y)
- Мы можем найти обратное, обратив «блок-схему»
- Или мы можем найти обратное, используя алгебру:
- Поставьте «y» вместо «f(x)» и
- Найти x
- Нам может понадобиться ограничить домен , чтобы функция имела обратную
Горизонтальные и вертикальные переносы экспоненциальных функций 9{x}[/latex] в том же окне, точки пересечения, если таковые имеются, представляют собой решения уравнения.


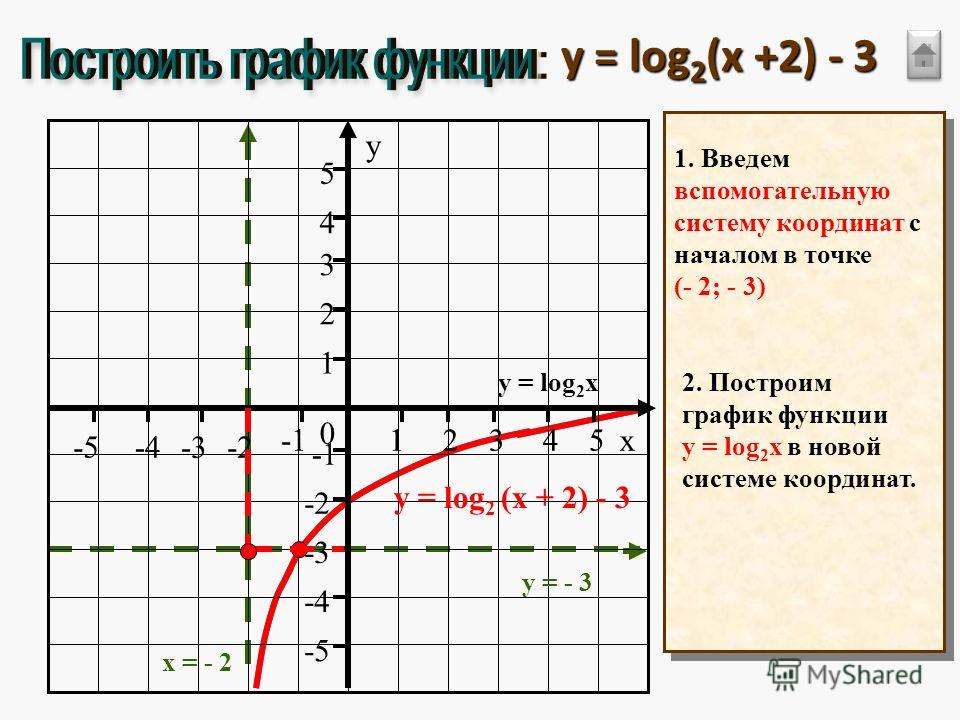 ( f — г )( x ), ( f × г )( x ) и ( f / 90 2 х 90 942 90 942 ).
( f — г )( x ), ( f × г )( x ) и ( f / 90 2 х 90 942 90 942 ).