Урок 7. десятичное разложение рациональных чисел — Алгебра — 7 класс
Алгебра
7 класс
Урок № 7
Десятичное разложение рациональных чисел
Перечень рассматриваемых вопросов:
- Множества натуральных, целых, рациональных чисел.
- Соотношение между этими множествами, сравнение чисел.
- Действия с отрицательными и положительными дробями.
Тезаурус:
Натуральные, целые отрицательные числа и число ноль образуют множество целых чисел.
Сумма, разность и произведение целых чисел всегда целое, а частное двух целых чисел не всегда целое число.
Положительные дроби, отрицательные дроби и число ноль образуют множество рациональных чисел.
Сумма, разность, произведение, частное рациональных чисел будет являться рациональным числом. На ноль делить нельзя!
Поставим перед периодической дробью знак минус, получим отрицательную периодическую дробь.
Ноль тоже может быть записан в виде нулевой периодической дроби.
Каждое рациональное число может быть представлено в виде периодической дроби, а каждая периодическая дробь – это десятичное разложение некоторого рационального числа.
Основная литература:
- Никольский С. М. Алгебра: 7 класс. // Никольский С. М., Потапов М. К., Решетников Н. Н., Шевкин А. В. – М.: Просвещение, 2017. – 287 с.
Дополнительная литература:
- Чулков П. В. Алгебра: тематические тесты 7 класс. // Чулков П. В. – М.: Просвещение, 2014 – 95 с.
- Потапов М. К. Алгебра: дидактические материалы 7 класс. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 96 с.
- Потапов М. К. Рабочая тетрадь по алгебре 7 класс: к учебнику С. М. Никольского и др. «Алгебра: 7 класс». 1, 2 ч. // Потапов М. К., Шевкин А. В. – М.: Просвещение, 2017. – 160 с.
Теоретический материал для самостоятельного изучения.
На уроке, мы рассмотрим множества натуральных, целых, рациональных чисел.
Поставим перед натуральным числом знак
« + » (плюс), получим равное ему число.
Поэтому пишут, например:
6 = + 6, + 123 = 123.
Если поставим перед натуральным числом знак « – » (минус), получится противоположное ему число, называемое целым отрицательным числом. Например:
-4, -21, 143.
Натуральные, целые отрицательные числа и число ноль образуют множество целых чисел.
Сумма, разность и произведение целых чисел всегда целое, а частное двух целых чисел не всегда целое число.
Поставим перед обыкновенной дробью (положительным рациональным числом) знак «+» (плюс), получим равную ей дробь. Значит, можем записать:
Если поставим перед обыкновенной положительной дробью знак « –» (минус), то получится противоположная ей – отрицательная дробь, называемая отрицательным рациональным числом. Например,
Знак « –» (минус), стоящий перед отрицательной дробью, можно записать или в числитель, или в знаменатель дроби.
Значит, можем записать:
Сумма, разность, произведение, частное рациональных чисел будет являться рациональным числом. На ноль делить нельзя!
На ноль делить нельзя!
На прошлом уроке мы рассмотрели, что любое положительное рациональное число преобразуется в периодическую дробь.
Поставим перед ней знак «+» (плюс), получим равную ей дробь. Тогда запишем:
Поставим перед ней знак «–» (минус), получим отрицательную периодическую дробь.
Значит, запишем:
Периодическую дробь в левой части данного равенства называют десятичным разложением числа, записанного в правой части.
Число ноль тоже может быть записано в виде нулевой периодической дроби:
0 = 0,(0) = + 0,(0) = -0,(0).
Таким образом:
Каждое рациональное число может быть представлено в виде периодической дроби, а каждая периодическая дробь – это десятичное разложение некоторого рационального числа.
Итак, на этом уроке мы:
рассмотрели множества натуральных, целых, рациональных чисел;
узнали понятие десятичного разложения рациональных чисел.
Запись периодической дроби в виде рационального числа.
Рассмотрим, как записать периодическую дробь в виде рационального числа.
Представить периодическую дробь –6,(17) в виде рационального числа.
Решение.
Нам нужно периодическую дробь, представить обыкновенной отрицательной дробью.
Пусть искомая дробь равна х.
Тогда запишем равенство.
Рассмотрим, ещё пример, как записать периодическую дробь в виде обыкновенной несократимой дроби
Представить периодическую дробь 0, 23(45) в виде обыкновенной несократимой дроби
Нам нужно периодическую дробь, представить обыкновенной отрицательной дробью.
Пусть искомая дробь равна х.
Тогда запишем равенство.
Разбор заданий тренировочного модуля.
1. Представьте периодическую десятичную дробь –5,67(0) в виде обыкновенной несократимой дроби.
Варианты ответа:
Решение.
2. Решите задачу.
За три дня было вспахано 153 га земли. В первый день было вспахано 0,(3), а во второй день – 0,(4) этой площади. Сколько гектаров земли было вспахано в третий день. Варианты ответа:
Сколько гектаров земли было вспахано в третий день. Варианты ответа:
Решение:
Запишем периодические дроби в виде обыкновенных несократимых дробей.
Ответ: 34 га вспахано в третий день.
Рациональные числа / Рациональные числа / Справочник по математике 5-9 класс
- Главная
- Справочники
- Справочник по математике 5-9 класс
- Рациональные числа
- Рациональные числа
Вместе целые и дробные числа образуют рациональные числа.
| Число, которое можно записать в виде отношения , где — целое число, а — натуральное число, называют рациональным числом. |
Нам известно, что любое целое число можно записать в виде , — целое число, 1 — это натуральное число, значит, любое целое число является рациональным числом.
Примеры:
Рассмотрим дробь: , — целое число, — натуральное число.
То есть любая отрицательная дробь является рациональным числом
Любое смешанное число и любая десятичная дробь также являются рациональными числами.
Примеры:
, 17 — целое число, 100 — натуральное число.
, 5191 — целое число, 1000 — натуральное число.
, 26 — целое число, 7 — натуральное число.
Рассмотрим разность, сумму и произведение двух рациональных чисел:
, 1 — целое число, 10 — натуральное число.
5 — целое число, 24 — натуральное число.
,
2 — целое число, 1 — натуральное число.
То есть сумма, разность и произведение рациональных чисел являются рациональными числами.
Если делитель отличен от нуля, то частное двух рациональных чисел тоже рациональное число.
Пример:
,
, 3 — целое число, 2 — натуральное число.
Нам известно, что обыкновенную дробь можно представить в виде десятичной дроби
, разделив ее числитель на знаменатель, например:, так как 13 : 50 = 0,26.
| — | 1 | 3 | 0 | 0 | 5 | 0 | |||
| 1 | 0 | 0 | 0 | 2 | 6 | ||||
| — | 3 | 0 | 0 | ||||||
| 3 | 0 | 0 | |||||||
| 0 |
Нам также известно, что не любую обыкновенную дробь можно представить в виде десятичной дроби, например, если нам дана дробь , то при делении числителя на знаменатель мы получим сначала нуль целых, потом одну десятую, семь сотых , три тысячных и дальше при делении все время будут повторятся остаток 25 и в частном цифра 3.
| — | 1 | 3 | 7 | 5 | |||||||||
| 7 | 5 | 0 | , | 1 | 7 | 3 | 3 | . | . | ||||
| — | 5 | 5 | 0 | ||||||||||
| 5 | 2 | 5 | |||||||||||
| — | 2 | 5 | 0 | ||||||||||
| 2 | 2 | 5 | |||||||||||
| — | 2 | 5 | 0 | ||||||||||
| 2 | 2 | 5 | |||||||||||
| 2 | 5 |
Данное деление никогда не кончится, то есть дробь нельзя представить в виде десятичной дроби. При этом если разрешить писать бесконечные дроби, то .
При этом если разрешить писать бесконечные дроби, то .
Рассмотрим дроби , , , в записях данных дробей одна или несколько цифр начинают повторяться бесконечно много раз. Такого вида записи называют периодическими дробями, при этом вместо 0,296296… пишут 0,(296), вместо 0,5833… пишут 0,58(3), вместо 0,1818… пишут 0,(18).
| Любое рациональное число можно записать в виде десятичной дроби (в частности целого числа), либо в виде периодической дроби. |
Для дроби число 0,173 является приближённым значением до тысячных с недостатком: 0,173 < . Число 0,174 является приближённым значением этой дроби до тысячных с избытком: < 0,174. То есть получаем, что 0,173 < < 0,174.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Положительные и отрицательные числа. Координаты на прямой
Модуль числа
Сравнение рациональных чисел
Сложение рациональных чисел
Вычитание рациональных чисел
Умножение рациональных чисел
Деление рациональных чисел
Свойства действий с рациональными числами
Раскрытие скобок
Решение уравнений
Рациональные числа
Правило встречается в следующих упражнениях:
5 класс
Задание 4, Виленкин, Жохов, Чесноков, Шварцбург, Учебник, часть 2
6 класс
Номер 982, Мерзляк, Полонский, Якир, Учебник
Номер 1026, Мерзляк, Полонский, Якир, Учебник
Номер 1037, Мерзляк, Полонский, Якир, Учебник
Номер 1038, Мерзляк, Полонский, Якир, Учебник
Номер 1039, Мерзляк, Полонский, Якир, Учебник
Номер 1042, Мерзляк, Полонский, Якир, Учебник
Номер 1175, Мерзляк, Полонский, Якир, Учебник
Номер 1293, Мерзляк, Полонский, Якир, Учебник
Номер 1294, Мерзляк, Полонский, Якир, Учебник
Задание 1184, Виленкин, Жохов, Чесноков, Шварцбург, Учебник
7 класс
Номер 3, Мерзляк, Полонский, Якир, Учебник
Номер 5, Мерзляк, Полонский, Якир, Учебник
Номер 7, Мерзляк, Полонский, Якир, Учебник
Номер 27, Мерзляк, Полонский, Якир, Учебник
Номер 117, Мерзляк, Полонский, Якир, Учебник
Номер 121, Мерзляк, Полонский, Якир, Учебник
Номер 124, Мерзляк, Полонский, Якир, Учебник
Номер 125, Мерзляк, Полонский, Якир, Учебник
Номер 126, Мерзляк, Полонский, Якир, Учебник
Номер 561, Мерзляк, Полонский, Якир, Учебник
Рациональные числа | Примеры для 10 класса
В прошлой статье преподаватель математики Дмитрий Айстраханов рассматривал целые числа и их основные характеристики. Продолжая тему, в новой статье разбираемся с рациональными числами.
Еще пару тысяч лет назад древние люди столкнулись с необходимостью
измерять части целого при вычислении веса, площади земельного участка,
длины и т.д., что привело их к понятию доли целого (дроби): половина, четверть, треть и т.п. Достоверное известно, что древние египтяне, шумеры и греки использовали дроби в вычислениях.
Рациональным является число, которое можно представить обыкновенной дробью, в которой числитель – целое число, а знаменатель – натуральное число. Так какие числа являются рациональными? Дробные. Выражение «дробное число (дробь)» является синонимом термина «рациональное число». Иногда так называют любое нецелое число. Надо помнить, что нецелые рациональные числа являются частным случаем дробных чисел. Различают правильные (модуль числителя меньше модуля знаменателя), неправильные (дробь не являющаяся правильной) и смешанные (неправильная дробь представляется в виде суммы целого числа и правильной дроби). Рациональные числа меньшие по модулю единицы, представляются правильной дробью. Большее или равное единице по модулю рациональное число соответствует неправильной дроби.
Так какие числа являются рациональными? Дробные. Выражение «дробное число (дробь)» является синонимом термина «рациональное число». Иногда так называют любое нецелое число. Надо помнить, что нецелые рациональные числа являются частным случаем дробных чисел. Различают правильные (модуль числителя меньше модуля знаменателя), неправильные (дробь не являющаяся правильной) и смешанные (неправильная дробь представляется в виде суммы целого числа и правильной дроби). Рациональные числа меньшие по модулю единицы, представляются правильной дробью. Большее или равное единице по модулю рациональное число соответствует неправильной дроби.
Дейтсвия с рациональными числами:
1. Сложение (вычитание). В случае равных знаменателей сложение (вычитание) рациональных чисел сводится к сложению (вычитанию) числителей. В случае разных знаменателей требуется приведение дробей к одинаковым знаменателям, который является наименьшим общим кратным знаменателей. Можно общий знаменатель получить перемножением заданных знаменателей.
Можно общий знаменатель получить перемножением заданных знаменателей.
2. Умножение рациональных чисел сводиться к умножению числителей и отдельно умножению знаменателей.
Деление двух дробей сводится к умножению первой дроби на обратную дробь (знаменатель идет в числитель, числитель идет в знаменатель) второй дроби. Это правило используется и при вычислении многоэтажных дробей.
3. Вычисления с рациональными числами производить следует вручную, требуется отличное знание таблицы умножения и навыков устного счета.
Автор: Дмитрий Айстраханов
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа». Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Дмитрий Владимирович Замков
Репетитор по математике
Стаж (лет)
Образование:
Самарский государственный экономический университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 7-11 классов. Использую смешанную методику преподавания. Западная методика обучения вкупе с российской, около индивидуальная форма. Отличительными особенностями моего преподавания является нестандартность, выстраивание теплой и веселой атмосферы с учеником.
Использую смешанную методику преподавания. Западная методика обучения вкупе с российской, около индивидуальная форма. Отличительными особенностями моего преподавания является нестандартность, выстраивание теплой и веселой атмосферы с учеником.
Владимир Анатольевич Смагин
Репетитор по математике
Стаж (лет)
Образование:
Центр «Биоинженерия» РАН, Москва
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по биологии 5-11 кл. Кандидат биологических наук. Биология — это наука о жизни, о нас и о мире в котором мы живём: от продуктов питания и воздуха, до противовирусных вакцин и лекарств от рака. На данный момент актуальной задачей является натаскивание ученика на ЕГЭ. Однако, я также имею возможность честно ответить на самые сложные вопросы пытливого ума. Методика обучения проста — будем сидеть и повторять за мной столько сколько нужно, отвечать на вопросы, проходить тесты, а дома — читать и смотреть материалы.
Биология — это наука о жизни, о нас и о мире в котором мы живём: от продуктов питания и воздуха, до противовирусных вакцин и лекарств от рака. На данный момент актуальной задачей является натаскивание ученика на ЕГЭ. Однако, я также имею возможность честно ответить на самые сложные вопросы пытливого ума. Методика обучения проста — будем сидеть и повторять за мной столько сколько нужно, отвечать на вопросы, проходить тесты, а дома — читать и смотреть материалы.
Эмма Акоповна Акопян
Репетитор по математике
Стаж (лет)
Образование:
Пятигорский государственный институт иностранных языков
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по английскому языку 6-11 классы. Готовлю к ОГЭ. Имею большой опыт как преподавательской, так и репетиторской деятельности, доступно объясняю темы, помогаю преодолеть языковой барьер. На занятиях применяю методику развития критического мышления, коммуникативную методику. Занятия включают упражнения на развитие всех речевых видов деятельности. Использую индивидуальный подход к каждому конкретному ученику.
Готовлю к ОГЭ. Имею большой опыт как преподавательской, так и репетиторской деятельности, доступно объясняю темы, помогаю преодолеть языковой барьер. На занятиях применяю методику развития критического мышления, коммуникативную методику. Занятия включают упражнения на развитие всех речевых видов деятельности. Использую индивидуальный подход к каждому конкретному ученику.
Похожие статьи
- Средняя линия треугольника
- Как решать иррациональные уравнения?
- МИФИ (Экономическая Безопасность): Проходной балл, учебный план
- Кафедра Химии (РУДН)
- Учимся решать текстовые задачи. ЕГЭ, базовый уровень
- Задачи на вычисление степенных выражений
- День матери: что подарить самому близкому человеку?
- Как заинтересовать ребенка читать + 20 книг для школьников всех возрастов
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
1 | Устная работа: | ||||||||||||||
Вычислите: | Вычислите: | Вычислите: | Вычислите: | ||||||||||||
2 | Объяснение новой темы: | ||||||||||||||
| Числа, которые мы используем при счете предметов, называются натуральными. | ||||||||||||||
| Дополним множество натуральных чисел, нулем и отрицательными числами(т.е. числами противоположными натуральным). Мы получим множество целых чисел. Надо заметить, что при сложении, вычитании, умножении целых чисел, всегда образуются целые числа. Однако частное двух целых чисел, не обязятельно будет целым числом. | ||||||||||||||
| Введение рациональных чисел, то есть чисел вида , где – целое число, – натуральное число, дает возможность находить частное двух рациональных чисел при условии, что делитель не равен нулю. Каждое целое число также является рациональным, так как его можно представить в виде При выполнении четырех арифметических действий (кроме деления на нуль) над рациональными числами всегда получаются рациональные числа. | ||||||||||||||
| Если рациональное число можно представить в виде дроби – целое число, – натуральное число, то его можно записать в виде конечной десятичной дроби. Например, можно записать Например, | ||||||||||||||
| Существуют рациональные числа, которые нельзя записать в виде конечной десятичной дроби, например Если, например, попытаться записать число в виде десятичной дроби, разделив числитель на знаменатель, то получится бесконечная десятичная дробь Бесконечную деятичную дробь называют периодической, а повторяющуюся цифру 3 — ее периодом. Коротко записывают так: (ноль целых три десятых в периоде) | ||||||||||||||
| Определение Периодическая дробь – это бесконечная десятичная дробь, у которой начиная с некоторого десятичного знака повторяется одна и та же цифра или несколько цифр – период дроби. | ||||||||||||||
3 | Решение ключевых задач. | Задача 1. Записать число в виде бесконечной десятичной дроби. Решение: | |||||||||||||
Задача 2. Представить бесконечную периодическую десятичную дробь в виде обыкновенной. Решение: 1.Пусть Так как в записи этого числа до периода содержится только один десятичный знак, то, умножая на 10, получаем (1) 2)Период этой дроби состоит из двух цифр. (2) 3)Вычитая из равенства (2) равенство (1), получаем | |||||||||||||||
4 | Решение тренировочных упражнений из учебника «Алгебра и начала анализа 10-11» на закрепление темы: | ||||||||||||||
№1. Записать в виде десятичной дроби: Решение: | |||||||||||||||
№2. Выполнить действия и записать результат в виде десятичной дроби: | |||||||||||||||
№4. | |||||||||||||||
| |||||||||||||||
| |||||||||||||||
№5.Вычислить: | |||||||||||||||
5 | Самостоятельная работа | ||||||||||||||
1 вариант | 2 вариант | ||||||||||||||
Закончите предложения таким образом, чтобы высказывание стало истинным | |||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
|
| ||||||||||||||
Представьте бесконечную периодическую десятичную дробь в виде десятичной | |||||||||||||||
Решение: Так как в записи нашего числа до периода содержится только один десятичный знак, то, умножая на 10, получаем Период нашей дроби состоит из одной цифры.
Вычитая из равенства (2) равенство (1), получаем | Решение: Так как в записи нашего числа до периода содержится только один десятичный знак, то, умножая на 10, получаем Период нашей дроби состоит из одной цифры. Поэтому, умножая обе части последнего равенства на находим Вычитая из равенства (2) равенство (1), получаем | ||||||||||||||
Презентация исследовательской работы по алгебре на тему Рациональные числа (8 класс) доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация исследовательской работы по алгебре на тему Рациональные числа (8 класс), предмет презентации: Алгебра. Этот материал в формате pptx (PowerPoint) содержит 11 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 11 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Выполнила:
Паршина Виктория
Ученица 8 «Г» класса
МБОУ СОШ №10 г.Ногинска
Преподаватель:
Сингатуллина Маргарита Ивановна
Рациональные
числа
«Числа не управляют миром,
но они показывают,
как управлять им».
( И. Гёте).
Цель:
Познакомиться с рациональными числами
Понять какие числа являются рациональными
Изучить свойства рациональных чисел
Рациональные числа
это числа, которые можно записать в виде положительной обыкновенной дроби m/n, отрицательной обыкновенной дроби -m/n или числа нуль.
Из озвученного определения следует, что рациональным числом является:
Любое натуральное число n (1,2,3 и т.д.). Действительно, можно представить любое натуральное число в виде обыкновенной дроби.
Например: 3=3/1.
Любое целое число, в частности, число нуль (−2,−1, 0 1, 2 и т.д.). В самом деле, любое целое число можно записать в виде либо положительной обыкновенной дроби, либо в виде отрицательной обыкновенной дроби, либо как нуль.
Например: 26=26/1, -5= -5/1
Любая обыкновенная дробь положительная или отрицательная (1/2, 1/3 -1/4, — 3/4). Это напрямую утверждается приведенным определением рациональных чисел.
Любое смешанное число ( 2 ¼, 3 ½ , -6 ¾.) Действительно, всегда можно представить смешанное число в виде неправильной обыкновенной дроби
Например: -1¼= -5/4, 6½=13/2
Любая конечная десятичная дробь (0,2, -3,6). Десятичные дроби переводятся в обыкновенные дроби.
Десятичные дроби переводятся в обыкновенные дроби.
Например: 0,2=2/10, -3,6= — 36/10
Любая бесконечная периодическая дробь (0, (3)). Переводим периодическую дробь в обыкновенную.
Например: 0,(3)=3/9
Также понятно, что любая бесконечная непериодическая десятичная дробь
НЕ является рациональным числом, так как она не может быть представлена в виде обыкновенной дроби.
Из приведенных примеров видно, что существуют и положительные и отрицательные рациональные числа, а рациональное число нуль не является ни положительным, ни отрицательным.
Озвученное выше определение рациональных чисел можно сформулировать более краткой форме.
Определение рациональных чисел можно дать и в следующей формулировке:
Рациональные числа – это числа, которые могут быть записаны в виде конечной или бесконечной периодической десятичной дроби.
Это определение также равносильно первому определению, так как всякой обыкновенной дроби соответствует конечная или периодическая десятичная дробь и обратно, а любому целому числу можно сопоставить десятичную дробь с нулями после запятой. Например, числа 5, 0, −13, 4/5, -7 2/11 представляют собой примеры рациональных чисел, так как их можно записать в виде следующих десятичных дробей 5,0, 0,0, −13,0, 0,8 и −7,(18).
Итак выведем следующие утверждения:
целые и дробные числа (положительные и отрицательные) составляют множество рациональных чисел;
каждое рациональное число может быть представлено в виде дроби с целым числителем и натуральным знаменателем, а каждая такая дробь представляет собой некоторое рациональное число;
каждое рациональное число может быть представлено в виде конечной или бесконечной периодической десятичной дроби, а каждая такая дробь представляет собой некоторое рациональное число.
Свойства рациональных чисел
СПАСИБО
ЗА
ВНИМАНИЕ!!!
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему: «6 класс Рациональные числа — это натуральные, отрицательные и дробные (обыкновенные и конечные десятичные) числа. От английского «ratio»
1 6 класс
2
Рациональные числа — это натуральные, отрицательные и дробные (обыкновенные и конечные десятичные) числа. От английского «ratio» — отношение,соотношение. Примеры рациональных чисел:
От английского «ratio» — отношение,соотношение. Примеры рациональных чисел:
3
К созданию понятия отрицательного числа китайские ученые подошли раньше математиков других народов, во II в. до н. э. Положительные количества в китайской математике называли чжен, отрицательные – фу. Их изображали разными цветами: чжен — красным, фу — черным. Такой способ изображения использовался в Китае до середины ХII столетия, пока Ли Е не предложил более удобное обозначение отрицательных чисел — цифры, которые изображали отрицательные числа перечеркивали черточкой справа налево. Введение отрицательных чисел и правил их сложения и вычитания можно считать одним из самых крупных открытий китайских ученых В Европе с сознанием уверенности в справедливости своих вычислений начал оперировать с отрицательными числами французский математик Никола Шюке. В своих трудах в 1484 г. Он рассматривает задачи, приводящие к уравнениям с отрицательными корнями. Шюке заявляет, что это вычисление, которое иные считают невозможным, правильно. Чех Ян Видман уже писал + и — для сложения и вычитания. А чуть позднее немецкий ученый Михель Штофель написал Полную Арифметику, которая была напечатана в 1544 году. В ней встречаются такие записи для чисел: 0 – 2; 0 + 2; 0 – 5; Всеобщее признание отрицательные числа получили в первой половине XIX в., когда была развита строгая теория положительных и отрицательных чисел.
Введение отрицательных чисел и правил их сложения и вычитания можно считать одним из самых крупных открытий китайских ученых В Европе с сознанием уверенности в справедливости своих вычислений начал оперировать с отрицательными числами французский математик Никола Шюке. В своих трудах в 1484 г. Он рассматривает задачи, приводящие к уравнениям с отрицательными корнями. Шюке заявляет, что это вычисление, которое иные считают невозможным, правильно. Чех Ян Видман уже писал + и — для сложения и вычитания. А чуть позднее немецкий ученый Михель Штофель написал Полную Арифметику, которая была напечатана в 1544 году. В ней встречаются такие записи для чисел: 0 – 2; 0 + 2; 0 – 5; Всеобщее признание отрицательные числа получили в первой половине XIX в., когда была развита строгая теория положительных и отрицательных чисел.
4
Множество рациональных чисел обозначаются заглавной английской буквой Q (кью). Множество Q включает в себя множество целых чисел (Z) и натуральных чисел (N).
Множество Q включает в себя множество целых чисел (Z) и натуральных чисел (N).
5 Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель — натуральным. a/b, где a Z ( a принадлежит целым числам ), b N ( b принадлежит натуральным числам ).
6
Сравнение рациональных чисел это сравнение чисел положительных и отрицательных, целых и дробных (обыкновенные дроби и десятичные дроби). Из двух рациональных чисел больше то, которому на числовой оси соответствует точка, расположенная правее. Всякое положительное число больше 0. Всякое отрицательное число меньше 0. Из двух отрицательных чисел больше то, модуль которого меньше. Любое положительное число больше любого отрицательного числа.
Из двух рациональных чисел больше то, которому на числовой оси соответствует точка, расположенная правее. Всякое положительное число больше 0. Всякое отрицательное число меньше 0. Из двух отрицательных чисел больше то, модуль которого меньше. Любое положительное число больше любого отрицательного числа.
7
Даны числа: 3; 2,5; -5,6; 0,25; — 6,89, 0. Назовите числа противоположные числам. Найдите модуль каждого из чисел. Выберите число, модуль которого наибольший; наименьший. Сравните дроби: 1) 1 и 1 ; 2) 2 и 3 ; 3) 5 и
Сравните дроби: 1) 1 и 1 ; 2) 2 и 3 ; 3) 5 и
8
Чтобы сложить рациональные числа с одинаковыми знаками, складывают их модули и перед суммой ставят их общий знак. (+19) + (+23) = 42; (-16) + (-307) = Чтобы сложить два рациональных числа с разными знаками и разными модулями, необходимо поставить знак числа с большим модулем и приписать к нему разность между большим и меньшим модулем. (+107) + (-56) = 51; (-23,6) + 7,5 = -16,1. Сумма двух противоположных чисел (то есть, с разными знаками и одинаковыми модулями) равна нулю. (-2,57) + (+2,57) = 0. При сложении любого рационального числа и нуля получаем само это число.
(-2,57) + (+2,57) = 0. При сложении любого рационального числа и нуля получаем само это число.
9
Законы сложения положительных чисел (переместительный и сочетательный) справедливы и для рациональных чисел. Применяя их, можно по-разному находить сумму нескольких чисел. Например, сложение нескольких чисел с разными знаками можно выполнять последовательно: сначала найти сумму первых двух слагаемых, к ней прибавить третье слагаемое и т. д. Но иногда удобнее сложение выполнять таким способом: сложить отдельно все положительные числа и отдельно все отрицательные числа, затем полученные два числа сложить по правилу сложения чисел с разными знаками. (+105) + (-4) + (-8) + (+21) + (-7) = (+126) + (-19) = +107.
(+105) + (-4) + (-8) + (+21) + (-7) = (+126) + (-19) = +107.
10
Вычитание рациональных чисел зависит от знаков чисел уменьшаемого и вычитаемого. Чтобы из одного числа вычесть другое, достаточно к уменьшаемому прибавить число, противоположное вычитаемому. Например: -102 (-80) = = -22. Если уменьшаемое отрицательное число, а вычитаемое положительное число, то нужно сложить модули уменьшаемого и вычитаемого и перед полученным результатом поставить знак «-». Например: = (|-839|+|-71|) = (839+71) = Если уменьшаемое положительное число н вычитаемое положительное число, то нужно найти разность модулей уменьшаемого и вычитаемого и перед полученным результатом поставить знак «-», если модуль уменьшаемого меньше модуля вычитаемого. Если модуль уменьшаемого равен модулю вычитаемого, то разность равна нулю. Примеры. 0,165 0,015 = 0,15 т. к. |0,1б5| > |0, = 0 т. к. |1 307| = |1 307|
Если модуль уменьшаемого равен модулю вычитаемого, то разность равна нулю. Примеры. 0,165 0,015 = 0,15 т. к. |0,1б5| > |0, = 0 т. к. |1 307| = |1 307|
11
При умножении двух рациональных чисел умножаются их абсолютные величины (модули чисел) и перед произведением ставится знак, зависящий от знаков множителей. Знак произведения определяется по таблице знаков. Таблица знаков Первый знак Второй знак Знак произведения Если произведение содержит более двух рациональных чисел, то результат можно определить поэтапно («шаг за шагом»), на каждом этапе вычисляя произведение двух сомножителей. А можно по особому правилу определить знак произведения для всех множителей сразу. Если в произведении все числа положительные, то модуль их произведения равен произведению модулей всех множителей, а знак произведения «+». Если в произведении есть числа положительные и отрицательные, то модуль их произведения равен произведению модулей всех множителей, а знак произведении «+» при четном количестве отрицательных множителей (минусов) и «-» при нечетном количестве отрицательных множителей (минусов) * 7 * 24 = * (-13) * (-7) * 24 = 4 368, т. к. количество минусов четное; (-2) * (-13) * (-7) * 24 = , т. к. количество минусов нечетное. Если при умножении рациональных чисел одни или несколько множителей равны 0, то все произведение равно 0. 2 * 0,71 * 172 * 0 * ( ) = 0
А можно по особому правилу определить знак произведения для всех множителей сразу. Если в произведении все числа положительные, то модуль их произведения равен произведению модулей всех множителей, а знак произведения «+». Если в произведении есть числа положительные и отрицательные, то модуль их произведения равен произведению модулей всех множителей, а знак произведении «+» при четном количестве отрицательных множителей (минусов) и «-» при нечетном количестве отрицательных множителей (минусов) * 7 * 24 = * (-13) * (-7) * 24 = 4 368, т. к. количество минусов четное; (-2) * (-13) * (-7) * 24 = , т. к. количество минусов нечетное. Если при умножении рациональных чисел одни или несколько множителей равны 0, то все произведение равно 0. 2 * 0,71 * 172 * 0 * ( ) = 0
12
Частное от деления двух отрицательных чисел есть число положительное. Модуль частного есть частное модулей делимого и делителя. Например: (-81) : (-9) = |-81|:|-9| = 81 : 9 = 9; (-0,74) : (-0,37) = |-0.74| : |0,37| = 0,74 : 0,37 = 2 Частное от деления отрицательного числа на положительное число и положительного числа на отрицательное число есть число отрицательное. Модуль частного есть частное модулей делимого и делителя. Например: (-180) : 3 = |180| : |3| = (180 : 3) = -60 Рациональные числа, как и другие, па нуль делить нельзя. Если делимое нуль, а делитель рациональное число, то при любом его значении и знаке частное равно нулю. Правила, по которым определяется знак произведения, действительны и для частного. Поэтому знак частного тоже проверяется по таблице знаков.
Модуль частного есть частное модулей делимого и делителя. Например: (-81) : (-9) = |-81|:|-9| = 81 : 9 = 9; (-0,74) : (-0,37) = |-0.74| : |0,37| = 0,74 : 0,37 = 2 Частное от деления отрицательного числа на положительное число и положительного числа на отрицательное число есть число отрицательное. Модуль частного есть частное модулей делимого и делителя. Например: (-180) : 3 = |180| : |3| = (180 : 3) = -60 Рациональные числа, как и другие, па нуль делить нельзя. Если делимое нуль, а делитель рациональное число, то при любом его значении и знаке частное равно нулю. Правила, по которым определяется знак произведения, действительны и для частного. Поэтому знак частного тоже проверяется по таблице знаков.
13
Степень любого числа это произведение одинаковых сомножителей. Количество сомножителей определяет показатель степени. Четная степень отрицательного числа число положительное. Нечетная степень отрицательного числа число отрицательное. Любая степень числа нуль равна нулю.
Количество сомножителей определяет показатель степени. Четная степень отрицательного числа число положительное. Нечетная степень отрицательного числа число отрицательное. Любая степень числа нуль равна нулю.
14
Математика, 7 класс, Работа с рациональными числами, Понимание рациональных чисел
CCSS.Math.Content.7.NS.A.2d 7 класс, Система счисления
Кластер: применение и расширение предыдущего понимания операций с дробями для сложения, вычитания, умножения и деления рациональных чисел. известно, что десятичная форма рационального числа оканчивается на 0 или со временем повторяется.
известно, что десятичная форма рационального числа оканчивается на 0 или со временем повторяется.
Степень выравнивания: Без рейтинга (0 пользователей)
CCSS.Math.Content.7.NS.A.2c 7 класс, Система счисления
Кластер: Применение и расширение предыдущего понимания операций с дробями для сложения, вычитания, умножения и деления рациональных чисел
Стандарт: Применение свойств операций в качестве стратегий для умножения и деления рациональных чисел.
Степень выравнивания: Без рейтинга (0 пользователей)
CCSS.Math.Content.7.NS.A.2a 7-й класс, Система счисления
Кластер: применить и расширить прежнее понимание операций с дробями для сложения, вычитания, умножения и деления рациональных чисел. удовлетворяют свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (–1)(–1) = 1, и правилам умножения чисел со знаком. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
Степень выравнивания: Без рейтинга (0 пользователей)
CCSS.Math.Content.7.NS.A.2 7 класс, Система счисления
Кластер: Применить и расширить предыдущие представления о действиях с дробями для сложения, вычитания, умножения и деления рациональных чисел
Стандарт: Применить и расширить предыдущие представления о действиях с дробями для и разделить рациональные числа. Применяйте и расширяйте прежнее понимание умножения и деления, а также дробей, чтобы умножать и делить рациональные числа.
Степень выравнивания: Без рейтинга (0 пользователей)
CCSS.Math.Content.7.NS.A.2b 7 класс, Система счисления
Кластер: применять и расширять предыдущие знания об операциях с дробями для сложения, вычитания, умножения и деления рациональных чисел
Стандарт: понимать, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если p и q целые числа, то –(p/q) = (–p)/q = p/(–q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
Если p и q целые числа, то –(p/q) = (–p)/q = p/(–q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
Степень выравнивания: Без рейтинга (0 пользователей)
MCCRS.Math.Content.7.NS.A.2c 7 класс
Область обучения: Система счисления
Стандарт: Применение и расширение предыдущего понимания операций с дробями для сложения, вычитания, умножения и деления рациональных чисел
Индикатор: Применение свойств операций в качестве стратегий для умножения и деления рациональных чисел .
Степень выравнивания: Без рейтинга (0 пользователей)
MCCRS.Math.Content.7.NS.A.2d 7 класс
Область обучения: Система счисления
Стандарт: Применение и расширение предыдущего понимания операций с дробями для сложения, вычитания, умножения и деления рациональных чисел
Индикатор: Преобразование рационального числа в десятичное с использованием длинного деления; известно, что десятичная форма рационального числа оканчивается на 0 или со временем повторяется.
Степень выравнивания: Без рейтинга (0 пользователей)
MCCRS.Math.Content.7.NS.A.2b 7 класс
Область обучения: Система счисления
Стандарт: Применение и расширение предыдущего понимания операций с дробями для сложения, вычитания, умножения и деления рациональных чисел
Индикатор: Понимание того, что целые числа можно разделить при условии, что делитель не ноль, и каждое частное целых чисел (с не делителем нуля) является рациональным числом. Если p и q целые числа, то -(p/q) = (-p)/q = p/(-q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
Степень выравнивания: Без рейтинга (0 пользователей)
MCCRS.Math.Content.7.NS.A.2 7 класс
Область обучения: Система счисления
Стандарт: Применение и расширение предыдущего понимания операций с дробями для сложения, вычитания, умножения и деления рациональных чисел
Индикатор: Применение и расширение предыдущего понимания операций с дробями для сложения, вычитать, умножать и делить рациональные числа. Применяйте и расширяйте прежнее понимание умножения и деления, а также дробей, чтобы умножать и делить рациональные числа.
Применяйте и расширяйте прежнее понимание умножения и деления, а также дробей, чтобы умножать и делить рациональные числа.
Степень выравнивания: Без рейтинга (0 пользователей)
MCCRS.Math.Content.7.NS.A.2a 7 класс
Область обучения: Система счисления
Стандарт: Применять и расширять прежнее понимание операций с дробями для сложения, вычитания, умножения и деления рациональных чисел что операции продолжают удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (-1)(-1) = 1, и правилам умножения чисел со знаком. Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.
Степень выравнивания: Без рейтинга (0 пользователей)
Рациональные числа — Определение | Примеры рациональных чисел, свойств, типов
Рациональные числа представлены в форме p/q, где p и q могут быть любыми целыми числами, а q ≠ 0. дроби целых чисел и десятичные дроби (завершающие десятичные дроби и повторяющиеся десятичные дроби). Давайте узнаем больше о рациональных числах и о том, как идентифицировать рациональные числа и примеров рациональных чисел в этом уроке.
дроби целых чисел и десятичные дроби (завершающие десятичные дроби и повторяющиеся десятичные дроби). Давайте узнаем больше о рациональных числах и о том, как идентифицировать рациональные числа и примеров рациональных чисел в этом уроке.
| 1. | Что такое рациональные числа? |
| 2. | Типы рациональных чисел |
| 3. | Как определить рациональные числа? |
| 4. | Рациональные и иррациональные числа |
| 5. | Часто задаваемые вопросы о рациональных числах |
Что такое рациональные числа?
Слово «рациональный» произошло от слова «рацио». Итак, рациональные числа хорошо связаны с концепцией дробей, которые представляют отношения. Другими словами, если число может быть выражено в виде дроби, где и числитель, и знаменатель являются целыми числами, число является рациональным числом.
Рациональные числа Определение
Рациональное число — это число, имеющее форму p/q, где p и q — целые числа, а q не равно 0. Множество рациональных чисел обозначается Q. Обратите внимание на следующий рисунок, на котором определяет рациональное число.
Примеры рациональных чисел
Если число может быть представлено в виде дроби, где и числитель, и знаменатель являются целыми числами, это число является рациональным числом. Ниже приведены некоторые примеры рациональных чисел.
- 56 (можно записать как 56/1)
- 0 (другая форма 0/1)
- 1/2
- √16, что равно 4
- -3/4
- 0,3 или 3/10
- -0,7 или -7/10
- 0,141414… или 14/99
Типы рациональных чисел
Различные типы рациональных чисел даны следующим образом.
- Целые числа, такие как -2, 0, 3 и т. д., являются рациональными числами.
- Дроби, числители и знаменатели которых являются целыми числами, такими как 3/7, -6/5 и т.
 д., являются рациональными числами.
д., являются рациональными числами. - Завершающие десятичные дроби, такие как 0,35, 0,7116, 0,9768 и т. д., являются рациональными числами.
- Неконечные десятичные числа с некоторыми повторяющимися шаблонами (после запятой), например 0,333…, 0,141414… и т. д., являются рациональными числами. Они широко известны как непрерывающиеся повторяющиеся десятичные дроби.
Как идентифицировать рациональные числа?
Рациональные числа легко идентифицировать с помощью следующих характеристик.
- Все целые числа, целые числа, натуральные числа и дроби с целыми числами являются рациональными числами.
- Если десятичная форма числа завершается или повторяется, как в случае 5,6 или 2,141414, мы знаем, что это рациональные числа.
- Если десятичные дроби кажутся бесконечными или неповторяющимися, то такие числа называются иррациональными. Как и в случае с √5, равным 2,236067977499789696409173… что является иррациональным числом.

- Другой способ идентифицировать рациональные числа состоит в том, чтобы посмотреть, может ли число быть выражено в форме p/q, где p и q — целые числа, а q не равно 0.
Пример: Является ли 0,
6
6
6
6
6… рациональным числом?
Решение: Данное число имеет набор десятичных знаков
6, который повторяется постоянно. Таким образом, это рациональное число.
Возьмем другой пример.
Пример: Является ли √2 рациональным числом?
Решение: Если мы запишем десятичное значение √2, мы получим √2 = 1,414213562…, которое является непрерывающимся и неповторяющимся десятичным числом. Следовательно, это не рациональное число. Это иррациональное число.
Рациональные числа в десятичной форме
Рациональные числа также могут быть представлены в десятичной форме. Вы знаете, что 1,1 — рациональное число? Да, потому что 1,1 можно записать как 1,1 = 11/10. Теперь давайте поговорим о некончающихся десятичных дробях, таких как 0,333… Поскольку 0,333… можно записать как 1/3, следовательно, это рациональное число. Следовательно, неконечные десятичные числа, имеющие повторяющиеся числа после запятой, также являются рациональными числами.
Теперь давайте поговорим о некончающихся десятичных дробях, таких как 0,333… Поскольку 0,333… можно записать как 1/3, следовательно, это рациональное число. Следовательно, неконечные десятичные числа, имеющие повторяющиеся числа после запятой, также являются рациональными числами.
Является ли 0 рациональным числом?
Да, 0 — рациональное число, поскольку его можно записать в виде дроби целых чисел, например 0/1, 0/-2,… и т. д. Другими словами, 0/5 = 0, 0/-2 = 0 , 0/1 = 0 и так далее.
Список рациональных чисел
Из приведенной выше информации становится ясно, что существует бесконечное количество рациональных чисел. Следовательно, невозможно определить весь список рациональных чисел. Однако некоторые рациональные числа могут быть перечислены как 3, 4,57, 3/4, 0, -7 и так далее. Это показывает, что все натуральные числа, целые числа, целые числа, дроби и десятичные числа (завершающие десятичные числа и повторяющиеся десятичные числа) считаются рациональными числами.
Сложение и вычитание рациональных чисел
Для сложения и вычитания рациональных чисел мы используем одни и те же правила сложения и вычитания целых чисел. Давайте разберемся в этом с помощью примера.
Пример: Решить 1/2 — (-2/3)
Решение: Решим это, используя следующие шаги:
- Шаг 1: Поскольку мы упрощаем 1/2 — (-2 /3), мы будем следовать правилу сложения и вычитания чисел, согласно которому факт вычитания может измениться на факт сложения, а знак вычитаемого изменится на противоположный. Это сделает его 1/2 + 2/3
- Шаг 2: Теперь нам нужно сложить эти дроби 1/2 + 2/3
- Шаг 3: Используя правила сложения дробей, мы преобразуем данные дроби в подобные дроби, чтобы получить общие знаменатели, чтобы их стало легче складывать. Для этого нам нужно найти НОК знаменателей 2 и 3, который равен 6. Затем мы преобразуем дроби в соответствующие им эквивалентные дроби, что сделает их 3/6 + 4/6.
 Это даст сумму 7/6, которую можно записать в виде смешанной дроби \(1\dfrac{1}{6}\)
Это даст сумму 7/6, которую можно записать в виде смешанной дроби \(1\dfrac{1}{6}\)
Умножение и деление рациональных чисел
Умножение и деление рациональных чисел можно выполнять так же, как дроби. Чтобы умножить любые два рациональных числа, мы умножаем их числители и знаменатели по отдельности и упрощаем полученную дробь. Давайте разберемся в этом с помощью примера.
Пример: Умножить 3/5 × -2/7
Решение: Решим это, выполнив следующие шаги:
- Шаг 1: Чтобы умножить 3/5 × (-2)/7, мы сначала умножим числители, а затем умножим знаменатели.
- Шаг 2: В этом случае, когда мы умножаем числители, это будет 3 × (-2) = -6.
- Шаг 3: Когда мы умножим знаменатели, получится 5 × 7 = 35. Следовательно, произведение будет -6/35.
Когда нам нужно разделить любые две дроби, мы умножаем первую дробь (которая является делимым) на величину, обратную второй дроби (которая является делителем). Давайте разберемся в этом с помощью примера.
Давайте разберемся в этом с помощью примера.
Пример: Разделить 3/5 ÷ 2/7
Решение: Решим это, используя следующие шаги:
- Шаг 1: Чтобы разделить 3/5 ÷ 2/7, мы сначала напишет обратную величину второй дроби. Это составит 3/5 × 7/2 .
- Шаг 2: Теперь мы умножим числители Это будет 3 × 7 = 21.
- Шаг 3: Затем умножим знаменатели, будет 5 × 2 = 10. Следовательно, произведение будет 21/10 или \(2\dfrac{1}{10}\)
Рациональные и иррациональные числа
Числа, которые НЕ являются рациональными числами, называются иррациональными числами. Множество иррациональных чисел представлено Q´. Разницу между рациональными и иррациональными числами можно понять из следующего рисунка и таблицы, приведенных ниже.
| Рациональные числа | Иррациональные числа |
|---|---|
Это числа, которые можно представить в виде целых чисел. Примеры: 1/2, 0,75, -31/5 и т. д. | Это числа, которые нельзя представить в виде целых чисел. Примеры: √5, π и т. д. |
| Они завершают десятичные дроби. | Они НИКОГДА не завершают десятичные дроби, которые не имеют точного значения. |
Они могут быть неконечными десятичными знаками с повторяющимися шаблонами десятичных знаков или повторяющимися десятичными знаками. Пример: 1.414, 414, 414 … содержит повторяющиеся десятичные дроби, где 414 повторяется. | Они должны быть неконечными десятичными знаками без повторяющихся шаблонов десятичных знаков. Пример: √5 = 2,236067977499789696409173…. не имеет повторяющихся десятичных знаков |
| Множество рациональных чисел содержит полностью натуральные числа, все целые числа и все целые числа. | Набор иррациональных чисел является отдельным набором и НЕ содержит никаких других наборов чисел. |
Советы и рекомендации по использованию рациональных чисел
- Рациональные числа включают дроби и любые числа, которые могут быть выражены дробями.
- Натуральные числа, целые числа, целые числа, дроби целых чисел и конечные десятичные дроби являются рациональными числами.
- Неконечные десятичные числа с повторяющимися шаблонами десятичных знаков, то есть повторяющиеся десятичные числа, также являются рациональными числами.
☛ Статьи по теме
- Простые числа
- Составные номера
- Четные числа
- Нечетные числа
- Реальные числа
- Натуральные числа
- Целые числа
- Иррациональные числа
- Подсчет чисел
- Кардинальные числа
- Четные и нечетные числа
Примеры рациональных чисел
Пример 1: Определите рациональные числа среди следующих: √4, √3, √5/2, -4/5, π, 1,41421356237309504.
 ….
….Решение:
Рациональное число, когда упрощенный должен быть либо завершающим десятичным числом, либо неконечным десятичным числом с повторяющимся шаблоном десятичных знаков. Следовательно, рациональные числа среди заданных чисел равны √4 (в результате получается 2) и -4/5.
Пример 2: Укажите истинное или ложное значение относительно рациональных чисел.
а.) Каждое целое является рациональным числом.
б.) Каждое рациональное число является целым числом.
Решение:
а.) Верно, каждое целое является рациональным числом.
б.) Неверно, каждое рациональное число не является целым числом. Это может быть часть целых чисел или десятичная дробь. К рациональным числам относятся натуральные числа, целые числа, целые числа и дроби целых чисел.
Пример 3:
Запишите следующее рациональное число в десятичной форме: 1/2
Решение:
Рациональное число 1/2 можно преобразовать в десятичное число, разделив числитель на знаменатель.
 Нам нужно разделить 1 на 2 и мы получим 0,5
Нам нужно разделить 1 на 2 и мы получим 0,5
перейти к слайдуперейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, что стоит за математикой, с нашими сертифицированными экспертами
Записаться на бесплатный пробный урок
Практические вопросы по рациональным числам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о рациональных числах
Что такое рациональное число?
Любое число в форме p/q, где p и q — целые числа, а q не равно 0, является рациональным числом. Примеры рациональных чисел: 1/2, -3/4, 0,3 или 3/10.
Как определить рациональное число?
Чтобы определить, является ли данное число рациональным или иррациональным, нам нужно преобразовать его в десятичную форму. Если десятичная дробь заканчивается или не заканчивается повторяющимися десятичными знаками, то число является рациональным. В противном случае это нерационально. Например, 1,414, 414, 414… имеет повторяющиеся шаблоны десятичных знаков, где повторяется 414. Значит, это рациональное число. С другой стороны, если мы возьмем пример √5 = 2,236067977499789696409173…., мы видим, что оно не имеет конца и не имеет повторяющихся шаблонов десятичных знаков. Значит, это иррациональное число. Другой способ определить рациональное число — проверить, является ли оно натуральным числом, целым числом, целым числом или дробью целых чисел. Если это одно из них, то это рациональное число.
В противном случае это нерационально. Например, 1,414, 414, 414… имеет повторяющиеся шаблоны десятичных знаков, где повторяется 414. Значит, это рациональное число. С другой стороны, если мы возьмем пример √5 = 2,236067977499789696409173…., мы видим, что оно не имеет конца и не имеет повторяющихся шаблонов десятичных знаков. Значит, это иррациональное число. Другой способ определить рациональное число — проверить, является ли оно натуральным числом, целым числом, целым числом или дробью целых чисел. Если это одно из них, то это рациональное число.
Что такое завершающие рациональные числа?
Завершающими рациональными числами являются те десятичные числа, которые заканчиваются после определенного количества знаков после запятой. Например, 1,5, 3,4, 0,25 и т. д. являются конечными числами. Все конечные числа являются рациональными числами, поскольку их легко записать в виде p/q.
В чем разница между рациональными и иррациональными числами?
Рациональное число — это число, десятичная форма которого является конечной или повторяющейся по своей природе. Например, 2,67 и 5,666 … Принимая во внимание, что иррациональные числа — это те числа, десятичная форма которых не заканчивается и не повторяется после определенного количества знаков после запятой. Например, √5 = 2,236067977499789696409173…. не имеет повторяющихся десятичных знаков и не заканчивается, поэтому это иррациональное число.
Например, 2,67 и 5,666 … Принимая во внимание, что иррациональные числа — это те числа, десятичная форма которых не заканчивается и не повторяется после определенного количества знаков после запятой. Например, √5 = 2,236067977499789696409173…. не имеет повторяющихся десятичных знаков и не заканчивается, поэтому это иррациональное число.
Что такое иррациональные числа?
Иррациональные числа — это те, которые не могут быть представлены целыми числами в форме p/q. Множество иррациональных чисел обозначается Q´. Несколько примеров иррациональных чисел: √2, √5 и так далее. Их десятичные формы не прекращаются и не повторяются.
Является ли 0 рациональным числом?
Да, 0 — рациональное число, так как его можно записать как 0/1, где 0 и 1 — целые числа, а знаменатель не равен 0.
Какое число нужно добавить к числу Пи, чтобы получить рациональное число?
Если мы добавим — π к π, мы получим, — π + π = 0. Эта сумма является рациональным числом. Следовательно, добавляя — π к π, мы получаем рациональное число.
Следовательно, добавляя — π к π, мы получаем рациональное число.
Как складывать рациональные числа?
Для сложения рациональных чисел мы используем те же правила сложения целых чисел. Давайте разберемся в этом с помощью примера. Если нам нужно добавить 4,53 + 2,31, мы начнем добавлять с правой стороны. Расставив числа в столбцах по разрядности, начнем с сотого места. Итак, 3 + 1 = 4. Переходя к десятому столбцу, мы добавляем 5 + 3 = 8. Затем мы добавляем цифры в столбце единиц, то есть 4 + 2 = 6. Таким образом, мы получаем сумму как 6,84
Как делить рациональные числа?
Чтобы разделить рациональные числа, мы используем обычные правила деления целых чисел, дробей или десятичных дробей, в зависимости от обстоятельств. Например, разделим дроби 7/5 ÷ 1/5. Чтобы разделить 7/5 ÷ 1/5, сначала напишем обратную величину второй дроби. Это сделает его 7/5 × 5/1. Теперь мы умножим числители. Это будет 7 × 5 = 35. Затем мы умножим знаменатели, это будет 5 × 1 = 5. Следовательно, произведение будет 35/5, что равно 7.
Следовательно, произведение будет 35/5, что равно 7.
Как умножать рациональные числа?
Рациональные числа можно умножать, используя правила умножения. Например, умножим 43 × 10, получим произведение 430.
Скачать БЕСПЛАТНО учебные материалы
Скачать бесплатно рабочие листы для 9 класса
Операции над рациональными числами — правила, методы, примеры.
Операции над рациональными числами выполняются так же, как и арифметические операции, такие как сложение, вычитание, умножение и деление над целыми числами и дробями. Арифметические операции над рациональными числами с одинаковыми знаменателями легко вычислить, но в случае с рациональными числами с разными знаменателями мы должны действовать, сделав знаменатели одинаковыми. Рациональные числа выражаются в виде дробей, но мы не называем их дробями, так как дроби включают только положительные числа, а рациональные числа включают как положительные, так и отрицательные числа. Дроби являются частью рациональных чисел, а рациональные числа — это широкая категория, включающая другие типы чисел.
На этом уроке мы изучим операции с рациональными числами, изучая сложение, вычитание, умножение и деление рациональных чисел, а также их свойства.
| 1. | Что такое операции над рациональными числами? |
| 2. | Свойства операций над рациональными числами |
| 3. | Примеры операций над рациональными числами |
| 4. | Практические вопросы по операциям над рациональными числами |
| 5. | Часто задаваемые вопросы об операциях над рациональными числами |
Что такое операции над рациональными числами?
Операции над рациональными числами относятся к математическим операциям, выполняемым над двумя или более рациональными числами. Рациональное число — это число в форме p/q, где: p и q — целые числа, q ≠ 0. Некоторые примеры рациональных чисел: 1/2, −3/4, 0,3 (или) 3/10. , −0,7 (или) −7/10 и т. д.
, −0,7 (или) −7/10 и т. д.
Мы знаем о дробях и о том, как можно использовать разные операторы для разных дробей. Все правила и принципы, применимые к дробям, применимы и к рациональным числам. Единственное, что нам нужно помнить, это то, что рациональные числа также включают отрицательные значения. Таким образом, хотя 1/5 является рациональным числом, верно и то, что −1/5 также является рациональным числом. Существует четыре основных арифметических действия с рациональными числами: сложение, вычитание, умножение и деление. Давайте узнаем о каждом подробно.
Сложение рациональных чисел
Сложение рациональных чисел можно выполнять так же, как сложение дробей. Есть два случая, связанные со сложением рациональных чисел.
- Сложение рациональных чисел с одинаковыми знаменателями
- Сложение рациональных чисел с разными знаменателями
Чтобы сложить два или более рациональных числа с одинаковыми знаменателями, мы просто складываем все числители и записываем общий знаменатель. Например, добавьте 1/8 и 3/8. Давайте поймем это с помощью числовой прямой.
Например, добавьте 1/8 и 3/8. Давайте поймем это с помощью числовой прямой.
- На числовой прямой мы начинаем с 1/8.
- Мы совершим 3 прыжка вправо, так как добавляем к нему 3/8. В итоге доходим до точки 4/8. 1/8 + 3/8 = (1 + 3)/8 = 4/8 = 1/2
- Таким образом, 1/8 + 3/8 = 1/2.
Когда рациональные числа имеют разные знаменатели, первый шаг — сделать их знаменатели эквивалентными, используя НОК знаменателей. Рассмотрим пример. Сложим числа −1/3 и 3/5
- Шаг 1: Знаменатели у данных чисел разные. Давайте найдем НОК 3 и 5, чтобы найти общий знаменатель. LCM 3 и 5 =15
- Шаг 2: Найдите эквивалентное рациональное число с общим знаменателем. Для этого умножьте −1/3 на 5 и 3/5 на 3 −1/3 × 5/5 и − 5/15 = 3/5 × 3/3 = 9/15.
- Шаг 3: Теперь знаменатели одинаковы; просто добавьте числители, а затем скопируйте общий знаменатель. Всегда сокращайте свой окончательный ответ до наименьшего термина.
 −1/3+3/5=(−1/3×5/5)+(3/5×3/3) =−5/5+9/15 =4/15
−1/3+3/5=(−1/3×5/5)+(3/5×3/3) =−5/5+9/15 =4/15
Вычитание рациональных чисел
Процесс вычитания рациональных чисел такой же, как и сложения. Вычитая два рациональных числа на числовой прямой, мы движемся влево. Давайте разберемся с этим методом на примере. Вычтите 1/2x−1/3x
- Шаг 1: Найдите НОК знаменателей. НОК (2, 3) = 6,
- Шаг 2: Преобразуйте числа в их эквиваленты с 6 в качестве общего знаменателя. 1/2x × 3/3 = 3/6x = 1/3x × 2/2 = 2/6x
- Шаг 3: Вычтите числа, полученные на шаге 2.
Умножение рациональных чисел
Умножение рациональных чисел похоже на то, как мы умножаем дроби. Чтобы умножить любые два рациональных числа, мы должны выполнить три простых шага. Перемножим следующие рациональные числа: −2/3×(−4/5). Шаги, чтобы найти решение:
- Шаг 1: Умножьте числители. (−2)×(−4)=8
- Шаг 2: Умножьте знаменатели.
 (3)×(5)=15
(3)×(5)=15 - Шаг 3: Сократите полученное число до наименьшего члена. Так как это уже самый низкий срок, мы можем оставить все как есть. (−23)×(−45) = (−2)×(−4)/(3)×(5) = 8/15
Деление рациональных чисел
Из деления целых чисел мы узнали, что делимое делится на делитель. Dividend÷Divisor=Дивиденд/Делитель. При делении любых двух чисел мы должны видеть, сколько частей делителя содержится в делимом. То же самое относится и к делению рациональных чисел. Давайте возьмем пример, чтобы понять это лучше. Шаги, которые необходимо выполнить, чтобы разделить два рациональных числа, приведены ниже:
- Шаг 1: Возьмем обратную величину делителя (второе рациональное число). 2х/9 = 9/2х
- Шаг 2: Умножьте на делимое. −4x/3 × 9/2x 90 162
- Шаг 3: Произведение этих двух чисел и будет решением. (−4x × 9) / (3 × 2x) = −6
Свойства операций над рациональными числами
Некоторые из свойств, применимых к операциям над рациональными числами, перечислены ниже:
| Заявление | Уравнение | |
| Имущество закрытия | Это свойство указывает, что при сложении, вычитании, умножении или делении любых двух рациональных чисел результатом также является рациональное число. | \(\dfrac{x}{y} \pm \dfrac{m}{n}=\dfrac{xn\pm ym}{yn}\), что является рациональным числом. \(\dfrac{x}{y} \times \dfrac{m}{n}=\dfrac{xm}{yn}\) \(\dfrac{x}{y} \div \dfrac{m}{n}=\dfrac{xn}{ym}\) |
| Ассоциативная собственность | Для сложения или умножения трех рациональных чисел их можно переставить внутри без какого-либо влияния на окончательный ответ. Это свойство не выполняется для вычитания и деления рациональных чисел. | \(\dfrac{x}{y}+(\dfrac{m}{n}+\dfrac{p}{q})\)=\((\dfrac{x}{y}+\dfrac{m {n})+\dfrac{p}{q}\) \(\dfrac{x}{y} \times (\dfrac{m}{n} \times \dfrac{p}{q})\)=\((\dfrac{x}{y}\times \ dfrac{m}{n}) \times \dfrac{p}{q}\) |
| Коммутативное имущество | Это свойство указывает, что два рациональных числа можно складывать или умножать независимо от их порядка. Это свойство не выполняется для вычитания и деления рациональных чисел. | \(\dfrac{x}{y}+\dfrac{m}{n}=\dfrac{m}{n}+\dfrac{x}{y}\) \(\dfrac{x}{y} \times \dfrac{m}{n}=\dfrac{m}{n} \times \dfrac{x}{y}\) |
| Аддитивная/мультипликативная идентичность | 0 — аддитивная идентичность любого рационального числа. Когда мы добавляем 0 к любому рациональному числу, результатом является само число. 1 является мультипликативной инверсией любого рационального числа. Когда мы умножаем 1 на любое рациональное число, результатом является само число. | \(\dfrac{x}{y}+0=\dfrac{x}{y}\) \(\dfrac{x}{y} \times 1=\dfrac{x}{y}\) |
| Аддитивное/мультипликативное обратное | Для любого рационального числа \(\dfrac{x}{y}\) существует \(-\dfrac{x}{y}\) такое, что сложение обоих чисел дает 0, \(-\dfrac{x}{y}\) является аддитивной инверсией \(\dfrac{x}{y}\). Аналогично, для любого рационального числа \(\dfrac{x}{y}\) существует \(\dfrac{y}{x}\) такое, что произведение обоих чисел равно 1. \(\dfrac{y}{x}\) является мультипликативной инверсией \(\dfrac{x}{y}\). | \(\dfrac{x}{y}+(-\dfrac{x}{y})=0\) \(\dfrac{x}{y} \times \dfrac{y}{x}=1\) |
| Распределительная собственность | Два рациональных числа в сочетании с оператором сложения или вычитания можно умножить на третье рациональное число отдельно, поставив между ними знак сложения или вычитания. | Если есть \(3\) рациональных чисел, \(\dfrac{p}{q}\), \(\dfrac{m}{n}\) и \(\dfrac{a}{b}\) , тогда \(\dfrac{p}{q} \times (\dfrac{m}{n}\pm \dfrac{a}{b})\)=\((\dfrac{p}{q} \times \ dfrac{m}{n})\pm(\dfrac{p}{q} \times \dfrac{a}{b})\) |
Статьи по теме
Ознакомьтесь с еще несколькими интересными статьями, связанными с операциями над рациональными числами.
- Десятичное представление иррациональных чисел
- Иррациональные числа
- Рационализировать знаменатель
- Является ли пи рациональным или иррациональным числом
Важные примечания
- Свойство тождества не выполняется для вычитания и деления рациональных чисел.

- Свойство замыкания верно для всех четырех операций над рациональными числами.
- Свойство коммутативности и ассоциативности справедливо для сложения и умножения рациональных чисел.
- Обратное свойство не выполняется для вычитания и деления рациональных чисел.x/y−(−x/y)≠0, x/y:y/x≠1
Часто задаваемые вопросы об операциях с рациональными числами
Каково влияние различных операций на рациональные и иррациональные числа?
- Результат сложения рационального числа и иррационального числа является иррациональным числом только потому, что он не влияет на неповторяющийся и непрерывный характер иррациональных чисел.
- Сумма двух рациональных чисел является рациональным числом.
- Сумма рационального числа и иррационального числа иррациональна.
- Сумма двух иррациональных чисел является иррациональным числом.
- Произведение двух рациональных чисел является рациональным числом.

- Произведение рационального числа на иррациональное число является иррациональным числом.
- Произведение двух иррациональных чисел является иррациональным числом.
Как вы выполняете операции над рациональными числами?
Мы выполняем операции над рациональными числами следующим образом:
- Сложение и вычитание рациональных чисел: В случае, если знаменатели совпадают, просто сложите или вычтите напрямую. В случае, если знаменатели разные, возьмите LCM, чтобы сделать знаменатели одинаковыми, а затем решите.
- Умножение рациональных чисел: умножьте числители и умножьте знаменатели. Приведите полученную таким образом дробь к низшей форме.
- Деление рациональных чисел: Умножьте обратную величину делителя на делимое.
Каковы свойства сложения рациональных чисел?
Свойства сложения рациональных чисел описаны ниже:
- Сложение двух рациональных чисел также является рациональным числом.
 (свойство закрытия)
(свойство закрытия) - Три рациональных числа можно складывать в любом порядке. (ассоциативное свойство)
- Два рациональных числа можно переставить внутри, не влияя на сложение чисел. (Переместительное свойство)
- 0 — аддитивная единица любого рационального числа.
- Аддитивная инверсия рационального числа в форме p/q равна −pq.
Сохраняется ли свойство идентичности при вычитании рациональных чисел?
Свойство тождества частично выполняется в случае вычитания рациональных чисел, поскольку x/y − 0 = x/y, но 0 − x/y ≠ x/y.
Каково правило вычитания рациональных чисел?
Чтобы вычесть любые два рациональных числа
- Шаг 1: Проверьте, совпадают ли знаменатели.
- Шаг 2: Сделайте знаменатели одинаковыми, взяв НОК знаменателей.
- Шаг 3: Вычтите заданные числа, вычитая их числители, оставив знаменатель прежним.
В чем разница между операциями над дробями и операциями над рациональными числами?
При операциях с рациональными числами необходимо использовать правила операций над целыми числами, а также операции над дробями, поскольку рациональные числа включают в себя и отрицательные числа. Для положительных рациональных чисел процесс применения операций такой же, как и для дробей.
Для положительных рациональных чисел процесс применения операций такой же, как и для дробей.
Верно ли обратное свойство деления рациональных чисел?
Нет, обратное свойство не выполняется для деления рациональных чисел, поэтому мы называем это мультипликативным обратным, а не обратным делением. Потому что если мы разделим x/y на y/x, мы не получим 1 в качестве ответа. Давай проверим. х/у ÷ у/х = х/у × х/у = х 2 /год 2 ≠16.
Как сложить два отрицательных рациональных числа?
Давайте рассмотрим пример, чтобы понять, как сложить два отрицательных рациональных числа. Добавить: −1/2+(−3/4)
- Всякий раз, когда за скобками стоит положительный знак, мы учитываем знаки отдельных членов внутри скобок. Итак, здесь мы можем записать это как −1/2 − 3/4.
- Теперь возьмем НОК знаменателей, чтобы сделать эти члены похожими. НОК (2,4)=4
- Решите числители и запишите окончательный ответ. −2/4 − 3/4 = −5/4
Вот как мы складываем два отрицательных рациональных числа.
Как вычесть два отрицательных рациональных числа?
Давайте рассмотрим пример, чтобы понять, как вычесть два отрицательных рациональных числа. Вычтите −3/7−(−4/3)
- Всякий раз, когда за скобками стоит отрицательный знак, мы меняем знак отдельных членов внутри скобки. Итак, здесь мы пишем −4/3 как +4/3.
- Теперь возьмем НОК знаменателей, чтобы сделать эти члены похожими. НОК(7,3)=21
- −12/21 + 28/21. Решите числители и запишите окончательный ответ. −12/21 + 28/21 = 16/21
Вот как мы вычитаем два отрицательных рациональных числа.
Математика 7 класс | Операции с рациональными числами
Учащиеся расширяют возможности операций сложения, вычитания, умножения и деления, включая положительные и отрицательные рациональные числа, и развивают беглость, оценивая числовые выражения.
Блок 2
7 класс
Резюме модуля
В модуле 2 учащиеся седьмого класса расширяют операции сложения, вычитания, умножения и деления, включая положительные и отрицательные рациональные числа. Стандарты 7.NS.1 и 7.NS.2 представляют собой кульминацию расширения четырех операций на все рациональные числа. В этом разделе учащиеся моделируют сложение и вычитание на числовой прямой и путем повторных рассуждений и применения свойств операций определяют эффективные правила вычисления с рациональными числами (MP.8). Учащиеся получают возможность моделировать более широкий спектр контекстов реального мира, включая ситуации, связанные с высотой над уровнем моря, изменениями температуры, долгами и кредитами, а также пропорциональными отношениями с отрицательными скоростями изменений (MP.4). Они также развивают большую беглость при оценке числовых выражений, используя свойства операций для повышения гибкости своего подхода.
Стандарты 7.NS.1 и 7.NS.2 представляют собой кульминацию расширения четырех операций на все рациональные числа. В этом разделе учащиеся моделируют сложение и вычитание на числовой прямой и путем повторных рассуждений и применения свойств операций определяют эффективные правила вычисления с рациональными числами (MP.8). Учащиеся получают возможность моделировать более широкий спектр контекстов реального мира, включая ситуации, связанные с высотой над уровнем моря, изменениями температуры, долгами и кредитами, а также пропорциональными отношениями с отрицательными скоростями изменений (MP.4). Они также развивают большую беглость при оценке числовых выражений, используя свойства операций для повышения гибкости своего подхода.
Начиная с первого класса учащиеся узнают о коммутативных и ассоциативных свойствах сложения, а также о связи между сложением и вычитанием. В третьем классе учащиеся расширяют свое понимание свойств операций, включая умножение и распределительное свойство. На протяжении многих лет студенты применяли эти свойства и отношения между операциями к целым числам, дробям и десятичным числам. В седьмом классе все эти навыки и концепции объединяются, так как ученики оперируют всеми рациональными числами, включая отрицательные числа.
В седьмом классе все эти навыки и концепции объединяются, так как ученики оперируют всеми рациональными числами, включая отрицательные числа.
В нескольких предстоящих модулях учащиеся седьмого класса будут полагаться на свое обострившееся чувство числа и способность к вычислениям с рациональными числами, в частности, в Модуле 3, Численные и алгебраические выражения, и в Модуле 4, Уравнения и неравенства. К тому времени, когда учащиеся переходят в восьмой класс, учащиеся должны хорошо разбираться в работе с рациональными числами, что будет лежать в основе многих алгебраических понятий. В восьмом классе учащиеся знакомятся с иррациональными числами, углубляя свое понимание системы действительных чисел, прежде чем изучать комплексные числа в старшей школе.
В материалы этого раздела включены некоторые задания, направленные на поддержку и улучшение навыков учащихся в области целочисленных вычислений, особенно в уме. См. наше Руководство по процессуальным навыкам и беглости для получения дополнительной информации, а также рекомендаций по стратегии и деятельности.
Темп: 22 учебных дня (18 уроков, 3 гибких дня, 1 контрольный день)
Fishtank Plus для математики
Разблокируйте функции, чтобы оптимизировать время подготовки, планировать увлекательные уроки и следить за успеваемостью учащихся.
Узнать больше
Оценка
Следующие оценки сопровождают Блок 2.
Предварительная часть
Предложите учащимся пройти предварительную оценку и самооценку перед началом модуля. Используйте Руководство по анализу предварительной оценки, чтобы определить пробелы в фундаментальном понимании и наметить план ускорения обучения на протяжении всего модуля.
Mid-Unit
Предложите учащимся выполнить Mid-Unit Assessment после урока 11.
Post-Unit
Используйте приведенные ниже ресурсы для оценки усвоения учащимися содержания модуля и плана действий для будущих модулей.
Постмодальная оценка
Ключ к ответам после модульной оценки
Руководство по анализу послемодульной оценки
92F25A3F-8529-4314-9899-6EE68694E3D0Пост-юнит самооценка
Расширенный пакет оценивания
Используйте данные учащихся для управления планированием с помощью расширенного набора модульных оценок, помогающих оценить уровень владения учащимися базовыми навыками и понятиями, а также их прогресс в изучении содержания модуля.
Загрузка образца
Подготовка блока
Интеллектуальная подготовка
Рекомендации по подготовке к изучению этого модуля
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Запуск модуля
Подготовьтесь к преподаванию этого модуля, погрузившись в стандарты, большие идеи и связи с предыдущим и будущим содержанием. Запуск модулей включает в себя серию коротких видеороликов, целевую литературу и возможности для планирования действий.
Обновление до Плюс
Интернализация стандартов посредством итоговой оценки
- Пройдите заключительную оценку. Аннотировать для:
- Стандарты, которым соответствует каждый вопрос
- Стратегии и представления, используемые на ежедневных уроках
- Связь с основными понятиями модуля
- Уроки, на которые Оценка указывает
Интернализация траектории отряда
- Прочитайте и аннотируйте сводку отряда.
- Обратите внимание на последовательность понятий в модуле с помощью схемы урока.

- Выполнить все целевые задания. Аннотируйте целевые задачи для:
- Основные понятия
- Связь с вопросами послемодульной оценки
- Определите ключевые возможности для вовлечения учащихся в академический дискурс. Прочтите наш Инструмент для учителя на Академический дискурс и ссылайтесь на него на протяжении всего модуля.
Интеллектуальная подготовка для конкретного подразделения
- Прочтите «Прогрессы для общих основных стандартов по математике, система счисления», 6–8 для соответствующих стандартов в области системы счисления.
Основные понятия
Основные математические концепции, которые учащиеся поймут в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Свойства операций сложения, вычитания, умножения и деления сохраняются для рациональных чисел.
- В уравнении $${p+q=r}$$, где $$p$$, $$q$$ и $$r$$ – рациональные числа, $$\left | q \right |$$ представляет расстояние между $$p$$ и $$r$$, а также представляется как $$\left | р-р \право |$$.

- Частное или произведение двух отрицательных или двух положительных чисел положительно.
- Частное или произведение двух чисел, в котором одно из чисел отрицательное, отрицательно.
Материалы
Материалы, изображения и инструменты, которые потребуются преподавателям и учащимся для этого раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950- Калькуляторы (по 1 на учащегося)
- Миллиметровая бумага (1 лист на учащегося)
- Дополнительно : Сухой стираемый маркер (1 на учащегося)
- Ламинированная числовая строка (1 на учащегося)
- Игровая фишка или жетон (1 на учащегося)
- Карточки с числами (по 1 на учащегося) — используются в Задаче-привязке 1 и требуют некоторой подготовки.
- Дополнительно : стандартная колода игральных карт (по 1 на учащегося или небольшую группу)
Чтобы ознакомиться со всеми материалами, необходимыми для этого курса, ознакомьтесь с нашим Обзором материалов курса для 7-го класса.
Запас слов
Terms and notation that students learn or use in the unit
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950absolute value
additive inverse
associative property
commutative property
distributive property
multiplicative inverse
opposite
рациональное число
повторяющееся десятичное число
завершающее десятичное число
Чтобы увидеть весь словарный запас для модуля 2, просмотрите наш глоссарий лексики для 7-го класса.
Карта урока
Тема A: Сложение и вычитание рациональных чисел
Представление рациональных чисел на числовой прямой. Определите противоположности и абсолютное значение.
7.NS.A.1
Сравнить и упорядочить рациональные числа. Напишите и интерпретируйте неравенства, чтобы описать порядок рациональных чисел.
7.NS.A.1
Опишите ситуации, в которых противоположные величины объединяются в ноль.
7.НС.А.1.А
Смоделируйте сложение целых чисел с помощью числовой строки.
7.НС.А.1.Б 7.НС.А.1.Д
Определите эффективные способы сложения рациональных чисел с числовой прямой и без нее.
7.НС.А.1.Б 7.НС.А.1.Д
Эффективно складывать и рассуждать о суммах рациональных чисел.
7.НС.А.1.Б 7.НС.А.1.Д
Под вычитанием понимается сложение противоположного значения (или обратная добавка).
7.NS.A.1.C 7.НС.А.1.Д
Найти и представить расстояние между двумя рациональными числами как абсолютное значение их разности.
7.NS.A.1.C
Вычитание рациональных чисел с числовой прямой и без нее.
7.NS.A.1.C 7.НС.А.1.Д
Эффективно складывать и вычитать рациональные числа, используя свойства операций.
7.НС.А.1.Д
Складывать и вычитать рациональные числа, используя различные стратегии.
7.NS.A.1 7.НС.А.1.А 7.НС.А.1.Б 7.NS.A.1.C 7.НС.А.1.Д
Тема B: Умножение и деление рациональных чисел
Определите правила умножения чисел со знаком.
7.НС.А.2.А 7.NS.A.2.C
Умножайте знаковые рациональные числа и интерпретируйте продукты в контексте реального мира.
7.НС.А.2.А 7.NS.A.2.C
Определите правила деления чисел со знаком.
7.НС.А.2.Б 7.NS.A.2.C
Деление знаковых рациональных чисел и интерпретация частных в контексте реального мира.
7.НС.А.2.Б 7.NS.A.2.C
Преобразуйте рациональные числа в десятичные, используя деление в длинную и эквивалентные дроби.
7.НС.А.2.Д
Умножать и делить рациональные числа, используя свойства операций.
7.NS.A.2 7.NS.A.2.C
Тема C: Использование всех четырех операций с рациональными числами
Решите задачи с рациональными числами и всеми четырьмя операциями.
7.NS.A.3
Общие базовые стандарты
Ключ
Основной кластер
Вспомогательный кластер
Дополнительный кластер
Основные стандарты
Стандарты содержания, рассматриваемые в этом модуле
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Система счисления
7.
 НС.А.1 — применять и расширять прежнее понимание сложения и вычитания для сложения и вычитания рациональных чисел; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями.
НС.А.1 — применять и расширять прежнее понимание сложения и вычитания для сложения и вычитания рациональных чисел; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями. 7.НС.А.1.А — Опишите ситуации, в которых противоположные величины объединяются, чтобы получить 0. Например, атом водорода имеет нулевой заряд, потому что две его составляющие заряжены противоположно.
7.НС.А.1.Б — Под p + q понимается число, расположенное на расстоянии |q| от p в положительном или отрицательном направлении в зависимости от того, является ли q положительным или отрицательным. Покажите, что число и его противоположность имеют сумму 0 (аддитивные инверсии). Интерпретируйте суммы рациональных чисел, описывая контексты реального мира.
7.НС.А.
 1.С — Понимайте вычитание рациональных чисел как сложение обратной добавки, p — q = p + (-q). Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира.
1.С — Понимайте вычитание рациональных чисел как сложение обратной добавки, p — q = p + (-q). Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира. 7.НС.А.1.Д — Применение свойств операций как стратегий сложения и вычитания рациональных чисел.
7.НС.А.2 — Применять и расширять прежнее понимание умножения и деления и дробей для умножения и деления рациональных чисел.
7.НС.А.2.А — Поймите, что умножение распространяется с дробей на рациональные числа, требуя, чтобы операции продолжали удовлетворять свойствам операций, в частности свойству распределения, что приводит к таким произведениям, как (-1)(-1) = 1, и правилам умножения чисел со знаком. . Интерпретируйте произведения рациональных чисел, описывая контексты реального мира.

7.НС.А.2.Б — Поймите, что целые числа можно делить при условии, что делитель не равен нулю, и каждое частное целых чисел (с ненулевым делителем) является рациональным числом. Если p и q целые числа, то -(p/q) = (-p)/q = p/(-q). Интерпретируйте частные рациональных чисел, описывая контексты реального мира.
7.НС.А.2.С — Применяйте свойства операций как стратегии для умножения и деления рациональных чисел.
7.НС.А.2.Д — Преобразование рационального числа в десятичное с использованием длинного деления; известно, что десятичная форма рационального числа оканчивается на 0 или со временем повторяется.
7.НС.А.3 — Решайте реальные и математические задачи, связанные с четырьмя операциями с рациональными числами.
 Вычисления с рациональными числами распространяют правила работы с дробями на сложные дроби.
Вычисления с рациональными числами распространяют правила работы с дробями на сложные дроби.
Основополагающие стандарты
Стандарты, описанные в предыдущих модулях или классах, которые являются важными фоновыми для текущего модуля
4.НБТ.Б.5
Числа и операции — дроби
4.NF.B.3
5.NF.A.1
5.NF.A.2
5.NF.B.3
Операции и алгебраическое мышление
1.ОА.Б.3
3.OA.B.5
3.OA.B.6
Система счисления
6.
 НС.А.1
НС.А.16.НС.Б.2
6.НС.Б.3
6.NS.C.5
6.NS.C.6
6.NS.C.7
6.NS.C.7.C
6.NS.C.8
Будущие стандарты
Стандарты будущих классов или разделы, связанные с содержанием данного раздела
A628D5C3-5B97-4E03-B1EC-5AD5C66D8950Средняя школа — номер и количество
Н.Р.А.1
Н.Р.А.2
Н.Р.Н.Б.3
Система счисления
8.
 НС.А.1
НС.А.18.НС.А.2
Стандарты математической практики
CCSS.MATH.PRACTICE.MP1 — Разбираться в проблемах и настойчиво решать их.
CCSS.MATH.PRACTICE.MP2 — Рассуждайте абстрактно и количественно.
CCSS.MATH.PRACTICE.MP3 — Придумывайте жизнеспособные аргументы и критикуйте рассуждения других.
CCSS.MATH.PRACTICE.MP4 — Модель с математикой.
CCSS.MATH.PRACTICE.MP5 — Стратегически используйте соответствующие инструменты.
CCSS.MATH.PRACTICE.MP6 — Следите за точностью.
CCSS.MATH.PRACTICE.MP7 — Ищите и используйте структуру.
CCSS.MATH.PRACTICE.MP8 — Ищите и выражайте закономерность в повторяющихся рассуждениях.
Блок 1
Пропорциональные отношения
значок/стрелка/вправо/большойБлок 3
Числовые и алгебраические выражения
Что такое рациональные числа? Определение, свойства, примеры
Основой овладения любым предметом является знание его лексики. То, как мы комбинируем буквы алфавита, чтобы составить слово, а затем упорядочиваем слова в предложениях, чтобы передать наши мысли, является для нас естественным инстинктом только потому, что мы знаем английский алфавит. Итак, каким должен быть 101 балл, чтобы сделать математику естественным инстинктом? Знание его рудиментарной единицы: чисел. Мы учим считать, используя целые числа, но одним из наиболее важных аспектов математической системы счисления являются рациональные числа, или, проще говоря, числа между числами.
То, как мы комбинируем буквы алфавита, чтобы составить слово, а затем упорядочиваем слова в предложениях, чтобы передать наши мысли, является для нас естественным инстинктом только потому, что мы знаем английский алфавит. Итак, каким должен быть 101 балл, чтобы сделать математику естественным инстинктом? Знание его рудиментарной единицы: чисел. Мы учим считать, используя целые числа, но одним из наиболее важных аспектов математической системы счисления являются рациональные числа, или, проще говоря, числа между числами.
Что такое рациональные числа?
Рациональные числа — это числа, которые можно записать в виде pq, где p и q — целые числа, а q≠0. Отличие рациональных чисел от дробей заключается в том, что у дробей не может быть отрицательных числителя или знаменателя. Следовательно, числитель и знаменатель дроби — целые числа (знаменатель ≠ 0), тогда как в случае рациональных чисел числитель и знаменатель — целые числа.
Примеры рациональных чисел
- $\frac{4}{5}$, $\frac{-10}{15}$, $\frac{9}{-17}$, $\frac{-2}{-7}$
- Ноль является рациональным числом, поскольку его можно записать в виде $\frac{0}{10}$, $\frac{0}{2}$, $\frac{0}{-15}$, $ \frac{0}{27}$ и т.
 д.
д.
Таким образом, ноль можно представить в виде дроби с ненулевым знаменателем.
- Каждое натуральное число является рациональным числом.
1 = $\frac{1}{1}$, 5 = $\frac{5}{1}$, 8 = $\frac{8}{1}$
Итак, каждое натуральное число может быть выражается в виде дроби с 1 в знаменателе.
- Каждое целое число является рациональным числом.
-7 = $\frac{-7}{1}$, -13 = $\frac{-13}{1}$
Итак, каждое целое число можно представить в виде дроби с 1 в знаменателе .
- Каждая дробь является рациональным числом.
$\frac{2}{3}$, $\frac{18}{7}$, $\frac{19}{11}$
Где числитель и знаменатель — целые числа, а знаменатель — нет равен нулю.
- Положительные рациональные числа
Рациональное число положительно, если его числитель и знаменатель имеют одинаковые знаки (либо оба положительные, либо оба отрицательные).
$\frac{-5}{-6}$, $\frac{7}{12}$, $\frac{-19}{-12}$, $\frac{42}{85}$
- Отрицательные рациональные числа
Рациональное число отрицательно, если его числитель и знаменатель имеют противоположные знаки (один из них положительный, а другой отрицательный).
$\frac{-32}{43}$, $\frac{27}{-63}$, $\frac{-12}{14}$, $\frac{9}{-16}$
- Десятичные числа: 0,45, 0,5446, 0,01864. Поскольку десятичные дроби можно записать в виде дробей со знаменателем 10, 100, 1000… десятичные числа также считаются рациональными числами.
Непримеры рационального числа
- Квадратный корень, кубический корень и т. д. натуральных чисел, если их точное значение не может быть определено.
$\sqrt{2}$, $\sqrt{3}$, $\sqrt[2]{8}$, $\sqrt[3]{81}$, $\sqrt[4]{27} $
- $\sqrt{3}$, – $\sqrt{5}$, 8 + $\sqrt{10}$, $\sqrt{2}$ + $\sqrt{3}$
Стандартная форма рациональных чисел
Говорят, что рациональное число $\frac{p}{q}$ находится в стандартной форме, если числитель и знаменатель (p и q) не имеют общего делителя ( или фактор), за исключением 1 и знаменатель « q » положительный.
Как преобразовать рациональное число в стандартную форму:
- Рассмотрим рациональное число $\frac{18}{–24}$;
Давайте посмотрим, как мы можем преобразовать это рациональное число в его стандартную форму.
Шаг 1: Убедитесь, что знаменатель положительный. Если нет, умножьте числитель и знаменатель на «-1», чтобы изменить знак.
Шаг 2: Найдите все общие делители числителя и знаменателя.
Здесь числа 18 и 24 имеют общие делители 1, 2, 3, 6.
Шаг 3: Разделите числитель и знаменатель на их наибольший общий делитель. Вот так:
Шаг 3 не требуется! Как видите, $\frac{–3}{4}$ – стандартное рациональное число и стандартная форма $\frac{18}{–24}$.
- Рассмотрим десятичное число 0,5
Шаг 1: Чтобы преобразовать десятичное число в стандартное рациональное число, мы сначала преобразуем его в рациональное число.
Шаг 2: Теперь выполните те же шаги для преобразования рационального числа в его стандартную форму, как определено выше, и мы получим
Операции над рациональными числами
Сложение рациональных чисел:
- числа равны:
Сложите числители и оставьте прежними знаменатели.
Например, мы можем сложить два рациональных числа 2/8 и ⅜ следующим образом:
- Когда знаменатели заданных чисел не равны:
Например, чтобы сложить рациональные числа ⅖ и ¾
Шаг 1: Найдите НОК знаменателя заданных рациональных чисел. Здесь НОК 4 и 5 равен 20.
Шаг 2: Преобразуйте каждое рациональное число в эквивалентное рациональное число с НОК в качестве нового знаменателя.
Шаг 3: Для этих новых рациональных чисел сложите числители и оставьте прежними знаменатели, и это будет окончательный ответ.
Следовательно, ⅖ + ¾ = 23/20.
Вычитание рациональных чисел:
- Когда знаменатели данных чисел равны:
Вычтите числители и оставьте знаменатель таким же.
Например:
- Когда знаменатели данных чисел не равны:
Например, чтобы вычесть ⅓ из ½
Шаг 1: Найдите НОК знаменателя заданных рациональных чисел. В этом случае НОК 2 и 3 равен 6.
Шаг 2: Преобразуйте каждое рациональное число в эквивалентное рациональное число с НОК в качестве нового знаменателя.
Шаг 3: Выполните шаги вычитания рациональных чисел с одинаковыми знаменателями.
Следовательно, ½ – ⅓ = ⅙
Умножение рациональных чисел:
Это, пожалуй, самая простая операция над рациональными числами.
Чтобы умножить два рациональных числа, просто умножьте числитель и знаменатель первого рационального числа на числитель и знаменатель второго рационального числа соответственно.
Например, чтобы умножить рациональные числа ⅖ и ¾,
Решаемые примеры
Пример 1: Выразите $\frac{25}{40}$ в стандартной форме.
Решение:
Наибольший делитель 25 и 40 = 5
Пример 2. Сложите: $\frac{2}{11}+\frac{7}{11}$ .
Решение:
$\frac{2}{11}+\frac{7}{11}= \frac{2+7}{11}=\frac{9}{11}$
Пример 3. Вычтите $\frac{5}{7}$ из $\frac{9}{7}$ .
Вычтите $\frac{5}{7}$ из $\frac{9}{7}$ .
Решение:
$\frac{9}{7}–\frac{5}{7}= \frac{9–5}{7}=\frac{2}{7}$
Практические задачи
398/1 0/398 1/398 398 не является рациональным числом. Правильный ответ: 398/1 $\frac{10}{7}$ $ \frac{7}{10}$ $\frac{0.7}{10}$ 0,7 не является рациональным числом Правильный ответ: $\frac{7}{10}$ 1 $\frac{2}{5}$ $\frac{-10}{3}$ $\frac{3 }{-10}$ Правильный ответ: $\frac{-10}{3}$ $\frac{64}{81}$ 1 $\frac{72}{81}$ Правильный ответ: 1 |
Часто задаваемые вопросы
Является ли 1 рациональным числом ?
Да, 1 является рациональным числом, поскольку его можно представить в виде дроби как $\frac{1}{1}$.
Как определить рациональное число?
Любое число, которое можно представить в виде дроби, является рациональным числом. Обратите внимание, что знаменатель рационального числа не может быть равен 0.
Как найти стандартную форму рационального числа?
Разделите числитель и знаменатель на их наибольший общий делитель.
Решения NCERT для класса 7 по математике, глава 9
- Решения НЦЭРТ
- Класс 7
- Математика
- рациональное число
Математика NCERT 7 класс, глава 9: рациональных чисел — Как следует из названия, глава посвящена рациональным числам. Подробное объяснение рациональных чисел дано в главе. Следующие ключевые моменты и темы обсуждаются в первом разделе главы рациональных чисел :
Подробное объяснение рациональных чисел дано в главе. Следующие ключевые моменты и темы обсуждаются в первом разделе главы рациональных чисел :
- Потребность в рациональных числах
- Что такое рациональные числа?
Число, которое может быть выражено в виде p / q , где p и q являются целыми числами, а q ≠ 0, называется рациональным числом 90 106 . Все целых чисел и дробей являются рациональными числами .
Примеры: -2/7, 3/8 и т.д.
- Числитель и знаменатель
В p / q целое число p является числителем , а целое число q (≠ 0) является знаменателем .
- Эквивалентные рациональные числа: Умножая числитель и знаменатель рационального числа на такое же ненулевое целое число , мы получаем другое рациональное число, эквивалентное данному рациональному числу.
- Положительные рациональные числа: Когда числитель и знаменатель положительны
- отрицательные рациональные числа: Когда числитель положительный, а знаменатель отрицательный.
- Число 0 не является ни положительным, ни отрицательным рациональным числом.
- Далее также объясняется понятие рациональных чисел на числовой прямой .
После этого, в первой половине главы, объясняются еще некоторые темы, такие как рациональных чисел в стандартной форме , сравнение рациональных чисел и рациональных чисел между двумя рациональными числами s.
- Стандартная форма рациональных чисел 9Необходимо изучить 0106, в котором говорится, что рациональное число находится в стандартной форме , если его знаменатель является положительным целым числом , а числитель и знаменатель не имеют общего делителя, кроме 1.
- Между двумя рациональными числами может быть неограниченное количество рациональных чисел.
Во второй половине главы обсуждаются операции над рациональными числами . ОПЕРАЦИИ , обсуждаемые в главе 9,0105 :
1. Сложение
2. Аддитивное обратное
3. Вычитание
4. Умножение
5. Деление
Глава Рациональные числа заканчивается кратким изложением.
Страница № 182:
Вопрос 1:
Список пять рациональные числа между:
(i) — 1 и 0 (ii) − 2 и − 1
(iii) (iv)
Ответ:
(i) −1 и 0
(ii) −2 и −1
пять рациональных чисел
(iii)
Пять рациональных чисел
(iv)
Пять рациональных чисел
Страница № 182:
Вопрос 2:
Впишите еще четыре рациональных числа в каждый из следующих шаблонов:
(i) (ii)
(iii) (iv)
Ответ:
(i)
Можно заметить, что числитель кратен 3, а знаменатель кратен 5, и по мере дальнейшего увеличения эти кратные увеличиваются. Следовательно, следующие четыре рациональных числа в этом образце — 9.0004
Следовательно, следующие четыре рациональных числа в этом образце — 9.0004
(II)
Следующие четыре рациональных числа в этой схеме
(III)
Следующие четыре рациональные номера в этой схеме
(iv)
.
Следующие четыре рациональных числа в этом шаблоне:
Видео Решение для рациональных чисел (Страница: 182 , Q.No.: 2)
NCERT Решение для 7 класса математика — рациональные числа 182 , Вопрос 2
Страница № 183:
Вопрос 3:
Дайте четыре рациональные числа, эквивалентные:
(i) (ii) (iii)
Ответ:
(i)
Четыре рациональных числа
(ii)
Четыре рациональных числа
(iii)
Четыре рациональных числа
Страница № 183:
Вопрос 4:
Нарисуйте числовую прямую и изобразите на ней следующие рациональные числа:
(i) (ii)
(iii) (iv)
Ответ:
(i)
Эта дробь представляет собой 3 части из 4 равных частей. Следовательно, каждый пробел между двумя целыми числами в числовой строке должен быть разделен на 4 равные части.
Следовательно, каждый пробел между двумя целыми числами в числовой строке должен быть разделен на 4 равные части.
можно представить как
(ii)
Эта дробь представляет собой 5 частей из 8 равных частей. Знак минус означает, что он находится на отрицательной стороне числовой прямой. Следовательно, каждый пробел между двумя целыми числами в числовой строке должен быть разделен на 8 равных частей.
можно представить как
(iii)
Эта дробь представляет собой 1 полную часть и 3 части из 4 равных частей. Знак минус означает, что он находится на отрицательной стороне числовой прямой. Следовательно, каждый пробел между двумя целыми числами в числовой строке должен быть разделен на 4 равные части.
можно представить как
(iv)
Эта дробь представляет собой 7 частей из 8 равных частей. Следовательно, каждый пробел между двумя целыми числами в числовой строке должен быть разделен на 8 равных частей.
можно представить как
Видео Решение для рациональных чисел (Страница: 183 , Q.No.: 4)
NCERT Решение для 7 класса математики — рациональные числа 183 , Вопрос 4
Страница № 183:
Вопрос 5:
Точки P, Q, R, S, T, U, A и B на числовой прямой таковы, что
TR = RS = SU и AP = PQ = QB. Назовите рациональные числа, представленные P, Q, R и S.
Ответ:
Расстояние между U и T = 1 единица
Делится на 3 равные части.
TR = RS = SU =
R =
S =
Аналогично,
AB = 1 единица
Делится на 3 равные части.
P =
Q =
Видео Решение для рациональных чисел (Страница: 183 , Q.No.: 5) 183:
Вопрос 6:
Какой из следующие пары представляют одно и то же рациональное число?
(i) (ii) (iii)
(iv) (v) (vi)
(vii)
Ответ:
(i)
В качестве,
следовательно, он не представляет одни и те же рациональные числа.
(ii)
Следовательно, он представляет собой одинаковые рациональные числа.
(iii)
Следовательно, он представляет собой одинаковые рациональные числа.
(iv)
Следовательно, он представляет собой одинаковые рациональные числа.
(в)
Следовательно, он представляет собой одинаковые рациональные числа.
(vi)
В качестве, следовательно, он не представляет одни и те же рациональные числа.
(vii)
Страница № 183:
Вопрос 7:
Переписать
(i) (ii)
(iii) (iv)
Ответ:
(i)
(ii)
(iii)
(iv)
Страница № 183:
Вопрос 8:
Заполнить коробки с правильным символом из >, < и =
(i) (ii) (iii)
(iv) (v) (vi)
(vii)
Ответ:
(i)
Поскольку −15 < 14,
Следовательно,
(ii)
Как −28 < −25
Следовательно,
(iii) Здесь,
Следовательно,
(iv)
Поскольку −32 > −35,
Следовательно,
(в)
Поскольку −4 < −3,
Следовательно,
(vi)
(vii)
Номер страницы 184:
Вопрос 9:
Что такое больше в каждом из следующих?
(i) (ii) (iii)
(iv) (v)
Ответ:
(i)
Преобразовав их в одинаковые дроби,
Поскольку 15 > 4, следовательно,
является
больше.
(ii)
(iii)
Преобразовав их в одинаковые дроби,
(iv)
(в)
Преобразовав их в одинаковые дроби,
Страница № 184:
Вопрос 10:
Запишите следующие рациональные числа в порядке возрастания:
(i) (ii) (iii)
Ответ:
(i)
As −3 < −2 < −1,
(ii)
путем преобразования в них в подобные фракции,
как -12 <-3 <-2,
(III)
, преобразуя в такие похожие фракции,
. As −42 < −21 < −12,
Видео Решение для рациональных чисел (Страница: 184 , Q.No.: 10)
NCERT Решение для 7 класса по математике — рациональные числа 184 , Вопрос 10
Страница № 190:
Вопрос 1:
Найдите сумму:
(i) (ii) (iii)
(iv) (v) (vi)
(vii)
Ответ:
(i)45+-11 4 = 45- 11 4 = 16-5520 = -39 20
(II)
L.

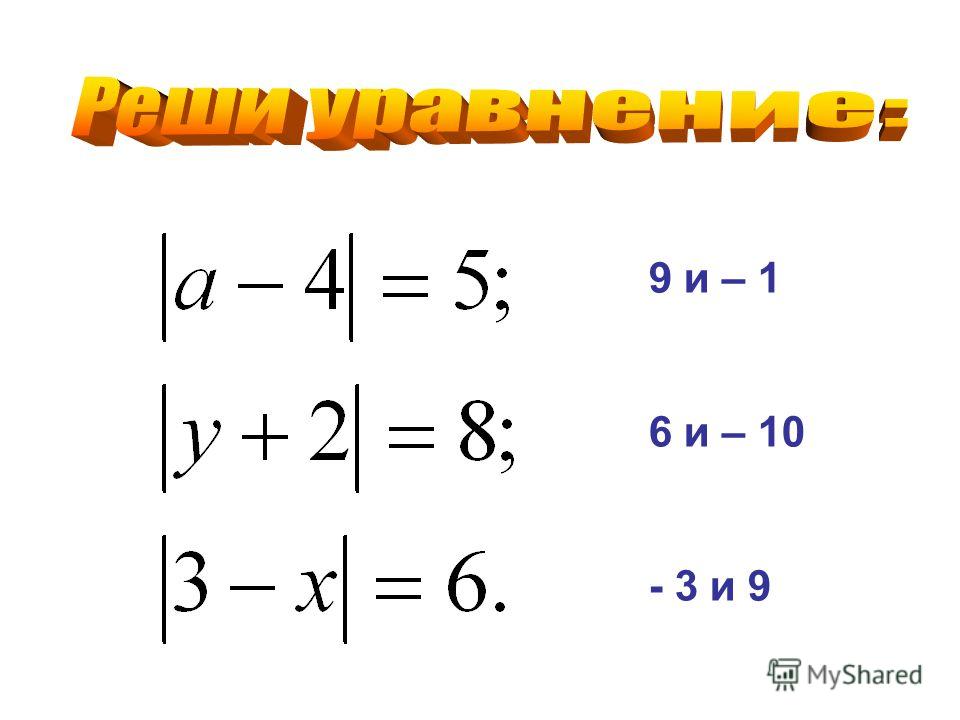 При сложении и умножении натуральных чисел всегда получаются натуральные числа. Однако разность и частное натуральных чисел не всегда являются натуральными числами.
При сложении и умножении натуральных чисел всегда получаются натуральные числа. Однако разность и частное натуральных чисел не всегда являются натуральными числами.

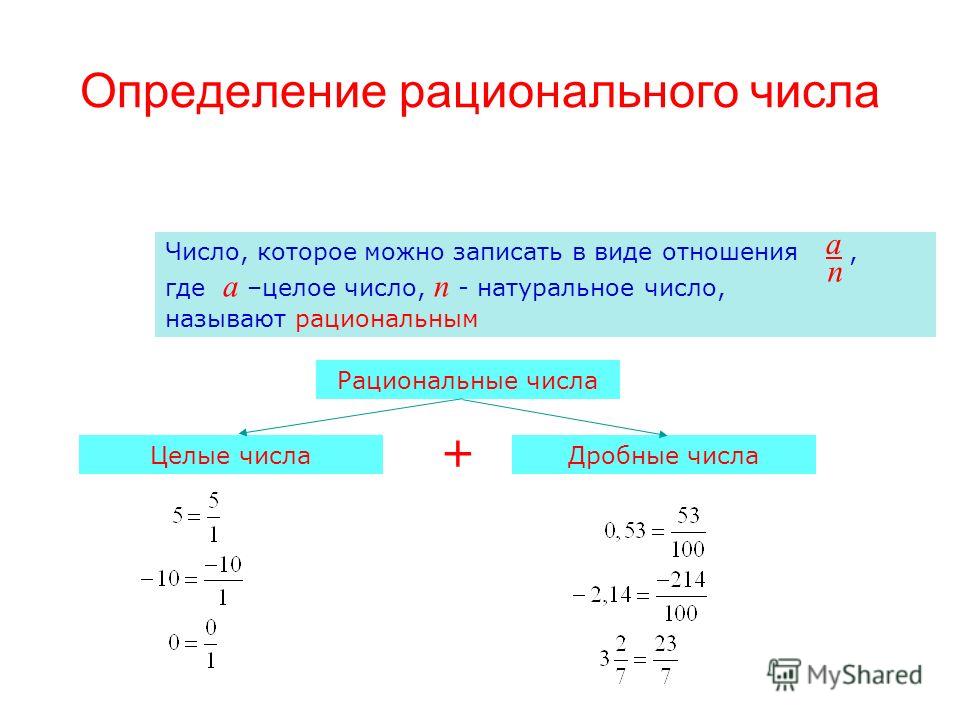 Поэтому, умножая обе части последнего равенства на находим
Поэтому, умножая обе части последнего равенства на находим Вычислить:
Вычислить: две его последние цифры нули или число, кратное 4.
две его последние цифры нули или число, кратное 4. Поэтому, умножая обе части последнего равенства на находим
Поэтому, умножая обе части последнего равенства на находим д., являются рациональными числами.
д., являются рациональными числами.
 Это даст сумму 7/6, которую можно записать в виде смешанной дроби \(1\dfrac{1}{6}\)
Это даст сумму 7/6, которую можно записать в виде смешанной дроби \(1\dfrac{1}{6}\)
 ….
…. Нам нужно разделить 1 на 2 и мы получим 0,5
Нам нужно разделить 1 на 2 и мы получим 0,5 −1/3+3/5=(−1/3×5/5)+(3/5×3/3) =−5/5+9/15 =4/15
−1/3+3/5=(−1/3×5/5)+(3/5×3/3) =−5/5+9/15 =4/15 (3)×(5)=15
(3)×(5)=15



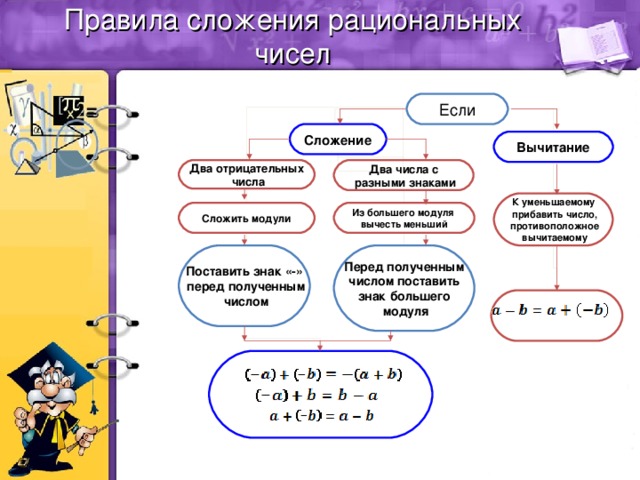
 (свойство закрытия)
(свойство закрытия)

 НС.А.1 — применять и расширять прежнее понимание сложения и вычитания для сложения и вычитания рациональных чисел; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями.
НС.А.1 — применять и расширять прежнее понимание сложения и вычитания для сложения и вычитания рациональных чисел; представляют сложение и вычитание на горизонтальной или вертикальной диаграмме с числовыми линиями.  1.С — Понимайте вычитание рациональных чисел как сложение обратной добавки, p — q = p + (-q). Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира.
1.С — Понимайте вычитание рациональных чисел как сложение обратной добавки, p — q = p + (-q). Покажите, что расстояние между двумя рациональными числами на числовой прямой равно абсолютному значению их разности, и примените этот принцип в контексте реального мира. 
 Вычисления с рациональными числами распространяют правила работы с дробями на сложные дроби.
Вычисления с рациональными числами распространяют правила работы с дробями на сложные дроби.  НС.А.1
НС.А.1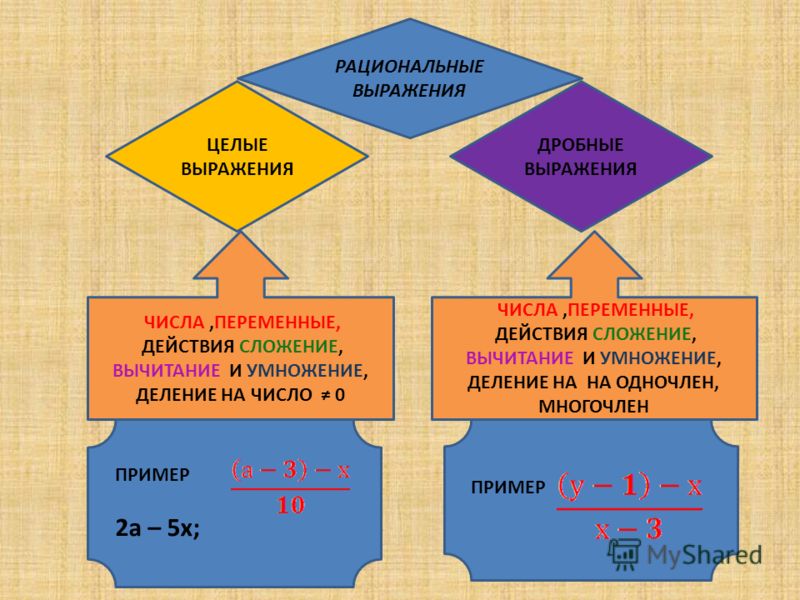 НС.А.1
НС.А.1 д.
д.