Четные и нечетные числа ✅ Блог IQsha.ru
Больше онлайн заданий по математике для детей от 2 до 11 лет. Начните прямо сейчас!
Уже в дошкольном возрасте ребята узнают, что бывают четные и нечетные числа. Определить абстрактно, четное число или нечетное, бывает непросто. Зато каждому понятно, получится ли некоторое количество разделить на двоих без остатка, или нет. Объяснить ребенку четные и нечетные числа помогут занимательные упражнения.
Что такое четные и нечетные числа
Четные числа — те, которые делятся на два без остатка. Но как же объяснить ребенку деление на два, если сложные математические операции осваивать еще рано? Самый простой способ — запомнить наизусть: на два делятся числа 2, 4, 6, 8 и все многозначные числа, которые оканчиваются на них же, а также на 0.
Нечетные числа на 2 ровно не делятся , это числа 1, 3, 5, 7, 9 и те многозначные числа, которые оканчиваются на них же.
Чтобы быстро определить, четным или нечетным является число, можно воспользоваться таблицей до 100. В ней четные и нечетные числа будут чередоваться. В нашей таблице выделены четные числа.
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
Как объяснить ребенку четные и нечетные числа
Сначала расскажите ребенку, что такое четные и нечетные числа.
Проиллюстрируйте это на примерах – раскладывайте перед ребенком разное количество карандашей и попытайтесь разделить на две равные части. Если так получилось сделать, то число карандашей является четным. Если остался лишний карандаш – число нечетное.
Наглядно показать четность или нечетность можно на любых предметах — игрушках, фишках, ложечках. Если получились две равные группы и не осталось лишних предметов, то общее количество является четным. Если остался лишний предмет – число нечетное.
Закрепляем знание о четных и нечетных числах
Запоминание приходит с практикой. Вначале пусть ребенок продолжает ряды четных или нечетных чисел, начиная с указанного вами числа. В этом упражнении пригодится навык счета через один. Следующим этапом предлагайте определить четность или нечетность любого числа. Поиграйте в игру: вы загадываете число в небольшом диапазоне и сообщаете, что оно находится между 4 и 7. А ребенок, используя вопрос: «Это четное или нечетное число?», пытается угадать задуманное число. Если ребенок угадал, то следующий вопрос задает он.
Если ребенок угадал, то следующий вопрос задает он.
Выполните развивающие упражнения от Айкьюши
Свойства четных и нечетных чисел
Даже если ребенок не умеет складывать числа в уме, он может запомнить несколько простых правил:
при сложении двух четных чисел всегда получится тоже четное число. 24+32=56 — четное
при сложении двух нечетных чисел получается четное число. 13+17=30 — четное
при сложении одного четного и одного нечетного числа всегда получится нечетное число. 43+32=65 — нечетное
Какое число 0 – четное или нечетное?
Ноль – это четное число.
Некоторые взрослые до сих пор затрудняются правильно ответить на этот вопрос. Как же это доступно объяснить детям?
Во-первых, чтобы определить четность или нечетность, нужно вспомнить какие числа называются четными – те, которые делятся на 2 без остатка. Ноль делится на 2 без остатка. Значит, ноль – четное число.
Во-вторых, мы уже знаем, что четные и нечетные числа чередуются. После ноля стоит нечетное число 1. Значит ноль – четное число.
После ноля стоит нечетное число 1. Значит ноль – четное число.
Также поможет запомнить четность ноля тот факт, что все числа, которые заканчиваются на 0 – четные. Значит и ноль тоже четное число.
Четные и нечетные числа до 20
Чётные числа до 20:
Нечётные числа до 20:
Дошкольники в силу своего возраста и опыта лучше справляются с операциями в пределах 20. Поэтому постарайтесь не выходить за это число: придумывайте бытовые задачки и акцентируйте внимание на доступных примерах. После тренировок изучать четные и нечетные числа в пределах 20 дошкольники могут, уже абстрагируясь от конкретных предметов, учась оперировать только абстрактными числами.
Можно провести занятие с таблицей Шульте, где четные и нечетные числа до 20 отличаются цветом:
Игры с четными и нечетными числами
Для того чтобы знания о четных и нечетных числах закрепились у малыша в памяти, регулярно используйте эти понятия в игре.
Например, в игре в магазин вы можете “печатать” для товаров ценники только с нечетными числами, выдумывая двузначные или трёхзначные числа из головы. Остается только вспомнить, на какие цифры должны оканчиваться эти числа.
Поиграйте в подвижную игру: если ты услышишь четное число, хлопни в ладоши. А если нечетное — топни ногой. 37, 18, 24, 53, 22, 95, 38, 14…
Еще можно играть в шпионов, которые передают друг другу информацию четными числами. Если каждое число ассоциировать с каким-то словом, то можно играть в сочинение предложений. Например, один шпион получил радиограмму: 2 8 4 6 10. А у него в ключе написано: 2 — апельсин, 4 — радость, 6 — бежит, 8 — красный, 10 — немедленно. Какое предложение можно составить, если по порядку расположить Апельсин Красный Радость Бежит Немедленно?
Напомнить знания о четных и нечетных поможет обычное русское лото. Когда вы с ребенком заполняете фишками карточки лото, проговаривайте вслух, является ли число четным.
Айкьюша поможет легко и в игровой форме познакомиться с математикой для детей 6-7 лет. Раздел включает задания и игры по арифметике для дошкольников: счет, сложение, вычитание, сравнение, умножение, деление, изучение геометрических фигур. Познавательные уроки и занятия для развития мальчиков и девочек.
Раздел включает задания и игры по арифметике для дошкольников: счет, сложение, вычитание, сравнение, умножение, деление, изучение геометрических фигур. Познавательные уроки и занятия для развития мальчиков и девочек.
Материалы для самостоятельных занятий по математике с дошкольником
| Предложите ребенку раскрасить предметы с четными числами в зеленый цвет, а с нечетными – в красный. | Распечатайте картинку и предложите ребенку продолжить последовательность четных и нечетных чисел, начиная с шеи жирафа. |
Превратите изучение четных и нечетных чисел в увлекательное занятие – и ребенок без труда освоит эту непростую тему!
Надеемся, что с нашей помощью математика для дошкольников не станет для вас сложной наукой. Рекомендуем вам также обратить внимание на раздел Задания с геометрическими фигурами для детей. Тренируйтесь в игровой форме и почаще устраивайте увлекательные занятия дома. Тогда освоить сложение и вычитание будет просто в бытовых ситуациях, а разобраться, что такое умножение и деление вам всегда поможет Айкьюша.
Тогда освоить сложение и вычитание будет просто в бытовых ситуациях, а разобраться, что такое умножение и деление вам всегда поможет Айкьюша.
Айкьюша и команда
Чётные — нечётные числа | Язык чисел
Что означают чётные и нечётные числа в духовной нумерологии? В изучении языка чисел это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?
Общеизвестно, что чётные числа — те числа, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.
А что означают чётные числа относительно духовной нумерологии? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.
У цифры 2 несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.
Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Нечётные числа
Нечётные числа — те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?
Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел, никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.
Возьмём для примера число 3 — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.
Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…
Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.
Чётные и нечётные числа в нумерологии
Подведём итоги. В чём главное отличие чётных чисел от нечётных?
Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…
Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…
Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…
Автор Статьи: Иосиф Лазарев
———————————————————————————————
Обратите внимание!
В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом, а также для заказа книги пройдите по следующей ссылке: «Духовная нумерология книга«
С теплом, автор книги и этого сайта Иосиф Лазарев
———————————————————————————————
от литературных затей до шахмат»
Сайт «Занимательные и методические материалы из книг Игоря Сухина: от литературных затей до шахмат»
Сайт «Занимательные и методические материалы из книг Игоря Сухина: от литературных затей до шахмат»
Избранные страницы из книги И. Г.Сухина «800 новых логических и математических головоломок» (часть 2)
Г.Сухина «800 новых логических и математических головоломок» (часть 2)
ЧАСТЬ 1 РАСПОЛОЖЕНА ЗДЕСЬ
И.Г. СУХИН
НАТУРАЛЬНЫЕ, ПРОСТЫЕ, СОСТАВНЫЕ, ЧЁТНЫЕ, НЕЧЁТНЫЕ, КРУГЛЫЕ
Шпаргалка
Цифры: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Однозначные числа: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
Натуральные числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13…
Простые числа: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41…
Составные числа: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 22…
Чётные числа: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26…
Нечётные числа: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25. ..
..
Круглые числа: 10, 20, 30, 40, 50, 60, 70, 80, 90, 100, 110, 120…
Примечание: в задачах на вычитание уменьшаемое не должно быть меньше вычитаемого.
И.Г. СУХИН
Задачи из тетради гнома Загадалки
ОТ НУЛЯ ДО ДЕВЯТИ
(однозначные числа)
1. Что больше: наименьшее натуральное число или наименьшее простое?
2. Что меньше: самое маленькое натуральное число или самое маленькое однозначное?
3. Что больше: наименьшее чётное число или наименьшее нечётное?
4. Какое однозначное число не является натуральным?
5. Сумма двух неких однозначных чисел равна их разности. Назови одно из них.
6. Сумма двух слагаемых равна первому слагаемому. Назови второе слагаемое.
Сумма двух слагаемых равна первому слагаемому. Назови второе слагаемое.
7. Сумма трёх одинаковых однозначных чисел равна их произведению. Что это за числа?
8. Какое из натуральных чисел наименьшее?
9. Произведение двух натуральных чисел равно частному от их деления. Назови один из сомножителей и делитель.
10. Произведение двух натуральных чисел меньше их суммы. Назови одно из чисел.
11. Если произведение двух натуральных чисел – простое число, то чему равен меньший сомножитель?
12. Сумма девяти натуральных чисел – однозначное число. Что это за числа?
13. Произведение двух неких натуральных чисел не является ни простым, ни составным числом. Что это за числа?
14. Какое натуральное число в 4 раза меньше самого маленького составного числа?
15. Сумма двух однозначных чисел в 2 раза больше их произведения. Какие это числа?
Сумма двух однозначных чисел в 2 раза больше их произведения. Какие это числа?
16. Какое чётное число является простым?
17. Чему равна наименьшая разность неодинаковых нечётных чисел?
18. Назови все чётные простые числа.
19. Сумма двух неких простых чисел есть нечётное число. Назови одно из слагаемых.
20. Произведение трёх простых чисел – однозначное число. Что это за числа?
21. Сумма четырёх чётных чисел – однозначное число. Какие это числа?
22. Произведение двух простых чисел равно их сумме. Что это за числа?
23. Сумма двух чётных чисел – однозначное число. Чему равно меньшее слагаемое?
24. Подсчитай сумму двух простых чётных чисел.
25. Вычти из наибольшего однозначного числа наименьшее простое.
26. Какое однозначное простое число больше 5?
27. Вычти из самого большого однозначного числа самое маленькое натуральное. Каков ответ?
28. Сумма двух однозначных чисел равна 1. Назови эти числа.
29. Разность двух однозначных чисел равна 9. Что это за числа?
30. Сумма двух натуральных чисел равна 3. Назови слагаемые.
31. Сумма двух чисел равна 4, а разность – в 2 раза меньше. Что это за числа?
32. Частное от деления двух однозначных чисел равно 5. Назови эти числа.
33. Произведение двух однозначных чисел равно 7. Что это за числа?
34. Сумма двух натуральных чисел равна 9, а произведение есть число однозначное. Найди эти числа.35. Разность двух неодинаковых однозначных чисел равна 8. Назови эти числа.
Назови эти числа.
36. Разность двух нечётных однозначных чисел равна 8. Какие это числа?
37. Произведение каких различных простых чисел будет числом однозначным?
38. Если сумма двух чётных чисел равна 6, то каковы слагаемые?
39. Если произведение двух неодинаковых чётных однозначных чисел – также число однозначное, то что это за числа?
40. Произведение двух однозначных чисел в 4 раза больше их разности. Вычисли эти числа.
41. Сумма каких двух простых чисел равна наибольшему однозначному простому числу?
42. Разность двух чисел равна 4, а сумма – в 2 раза больше. Что это за числа?
43. Сумма двух простых чисел равна 9. Назови эти числа.
44. Разность двух однозначных чётных чисел равна 6. Что это за числа?
45. Сумма двух простых чисел равна 8. Какие это числа?
Сумма двух простых чисел равна 8. Какие это числа?
46. Какие два соседних числа натурального ряда надо сложить, чтобы получить наибольшее однозначное число?
47. Сумма каких трёх последовательных чисел натурального ряда равна их произведению?
48. Каким натуральным числам не может равняться сумма нескольких простых чисел?
49. Какие три последовательных числа натурального ряда надо сложить, чтобы получить наибольшее однозначное число?
50. Если частное от деления двух неодинаковых однозначных чётных чисел будет числом нечётным, то чему равны частное и эти чётные числа?
И.Г. СУХИН
ОТ НУЛЯ ДО ДВАДЦАТИ
(однозначные и двузначные числа)
51. Если сумма двух неодинаковых однозначных чисел равна 16, то чему равна их разность?
52. Разность двух чётных однозначных чисел равняется 6. Вычисли их сумму.
Разность двух чётных однозначных чисел равняется 6. Вычисли их сумму.
53. Если разность двух нечётных однозначных чисел равна 8, то чему равна их сумма?
54. Подсчитай сумму самого маленького простого числа и самого большого однозначного.
55. Найди наибольшую сумму двух однозначных чисел.
56. Произведение однозначного и двузначного чисел равно 15. Найди эти числа.
57. Произведение двух неодинаковых однозначных чисел равно 16. Что это за числа?
58. Произведение двух однозначных чисел равняется 15. Каковы сомножители?
59. Сумма двух неодинаковых простых чисел равна 14. Назови слагаемые.
60. Произведение двух однозначных чисел равно 20. Что это за числа?
61. Сумма двух разных чётных однозначных чисел равна 12. Какие это числа?
Какие это числа?
62. Сумма двух простых чисел равна 12. Каковы слагаемые?
63. Сумма двух разных нечётных однозначных чисел равна 14. Назови их.
64. Сумма двух однозначных чисел равна 15, а разность – 3. Вычисли эти числа.
65. Сумма двух однозначных чисел равна 17. Что это за числа?
66. Разность двузначного и однозначного чисел равна единице. Каковы уменьшаемое и вычитаемое?
67. Даны 4 разных однозначных числа. Первое – 9. Если умножить 9 на второе, то получим столько же, сколько и при умножении третьего на четвёртое. Назови неизвестные числа.
68. Даны 4 неодинаковых однозначных числа. Известно, что первое – 2, а числа 9 среди них нет. Если умножить 2 на второе, то получим столько же, сколько и при перемножении третьего и четвёртого. Каковы неизвестные числа?
69. Какие последовательные числа натурального ряда надо сложить, чтобы получить наименьшее двузначное число?
Какие последовательные числа натурального ряда надо сложить, чтобы получить наименьшее двузначное число?
70. Сумма нескольких разных простых чисел равна 17. Назови эти числа.
71. Что меньше: сумма чётных однозначных чисел или сумма простых однозначных чисел?
И.Г. СУХИН
СЮЖЕТНЫЕ ЗАДАЧИ
156. Какую отметку впервые в жизни получил по математике Фома, если известно, что она является числом не простым, а составным?
157. Таня послала Игорю некоторое чётное число писем, а Игорь Тане – на 2 письма больше. При этом общее число писем есть число однозначное. Какое?
158. Сколько всего мячей оказалось на поле во время матча между командами «Зубило» и «Шайба», когда старик Хоттабыч наколдовал каждому футболисту по одному мячу?
159. Сколько яиц снесла за месяц курочка ряба, если известно, что число их не составное, а простое, больше 19, но меньше 29?
Сколько яиц снесла за месяц курочка ряба, если известно, что число их не составное, а простое, больше 19, но меньше 29?
160. Сколько лет сиднем просидел на печи Илья Муромец? Известно, что если бы он просидел ещё 2 раза по столько, то его возраст составил бы наибольшее двузначное число.
161. В какой известной сказке богатырей можно было бы выстроить несколькими равными рядами по 11 в каждом ряду? Каково число богатырей?
162. Барон Мюнхгаузен по секрету сообщил нам, что он пересчитал число волшебных волос в бороде старика Хоттабыча. Оно оказалось равным сумме наименьшего трёхзначного числа и наибольшего двузначного. Что это за число?
163. Если наибольшее двузначное число ты умножишь на 4 и прибавишь 4, то узнаешь, сколько муравьёв послал Артемон, чтобы перегрызть верёвку, на которой разбойники повесили за ноги главного героя сказки А.Толстого «Золотой ключик, или Приключения Буратино».
164. Раздели самое маленькое четырёхзначное число на наименьшее простое и узнаешь, сколько лет не умывалась, не чистила зубы и даже пальцем не прикасалась к воде злая волшебница Гингема из повести-сказки А.Волкова «Волшебник Изумрудного города».
165. В русской народной сказке «Притворная болезнь» у трёх чудищ было разное однозначное число голов, кратное трём. Какое?
166. В русской народной сказке «Хрустальная гора» Иван-царевич сражался по очереди с тремя змеями. У первого из них было в 2 раза меньше голов, чем у второго, а у второго – в 2 раза меньше, чем у третьего. Общее число голов у змеев – 21. Сколько голов было у каждого змея до встречи с Иваном-царевичем?
167. Сколько голов у каждого чуда-юда из русской народной сказки «Иван – коровий сын», если известно, что у второго чуда-юда на три головы больше, чем у первого, а у третьего – на 3 больше, чем у второго, причём всего голов было – 27?
И. Г. СУХИН
Г. СУХИН
ИСПРАВЛЕНИЕ, ЗАЧЁРКИВАНИЕ, ПРЕВРАЩЕНИЕ, ОТГАДЫВАНИЕ ЦИФР И ЧИСЕЛ
Задачи из тетради гнома Загадалки
1. Зачеркни одинаковые цифры. Какое число осталось?
5 3 7 1 8 3 5 8 7
2. Какую цифру надо зачеркнуть в числе 621, чтобы оставшееся число делилось на 3?
3. Это число от 2 до 10, но не 5; кроме того, оно нечётное и не делится на 3. Назови его.
4. Перед тобой однозначные числа. Вычеркни нечётные. Какая цифра осталась?
7 9 3 1 9 5 8 7
5. Зачеркни в следующем числе цифры, которые встречаются только один раз. Остальные цифры соедини. Что за число получилось?
7290342615
6. Угадай число от 1 до 28, если в его написание не входят цифры 1, 5 и 7; кроме того, оно нечётное и не делится на 3.
Угадай число от 1 до 28, если в его написание не входят цифры 1, 5 и 7; кроме того, оно нечётное и не делится на 3.
7. Отгадай число от 1 до 58, если в его написание не входят цифры 1, 2 и 3; кроме того, оно нечётное и не делится на 3, 5 и 7.
8. Угадай число от 1 до 88, если в его написание не входят цифры 1, 2, 3 и 7; кроме того, оно нечётное и не делится на 3, 5 и 7.
9. Отгадай число от 1 до 408, если в его написание не входят цифры 1, 2, 3, 5, 7; кроме того, оно нечётное и не делится на 3 и 7.
10. Перед тобой однозначные числа. Зачеркни чётные. Оставшиеся цифры соедини. Какое число осталось?
4 2 6 4 8 2 9 6 5
11. Преврати в числе 123 одну цифру в пятёрку так, чтобы получившееся число делилось на 9. Каково оно?
Каково оно?
12. Исправь в числе 982 одну цифру на четвёрку так, чтобы получившееся число делилось на 3. Назови новое число.
13. Вычти из произвольного двузначного числа сумму его цифр. Всегда ли разность разделится на 3? А на 9?
И.Г. СУХИН
РАЗДЕЛ 4. ИГРЫ И ФОКУСЫ
И.Г. СУХИН
КАК ВСЕГДА ВЫИГРЫВАТЬ В ПОПУЛЯРНЫХ ИГРАХ МАТЕМАТИЧЕСКОГО СОДЕРЖАНИЯ
ИГРА В ДЕСЯТЬ
По очереди играют двое. Начинающий игру называет 1 или 2. Его товарищ прибавляет в уме к исходному числу 1 или 2 и сообщает сумму партнёру. Последний также увеличивает её на 1 или 2 и называет свой результат. Так игра продолжается, и побеждает тот, кто скажет число 10.
Чтобы выиграть, тебе нужно начать игру и независимо от ответов партнёра называть числа 1, 4, 7. Когда произнесено число 7, противнику приходится назвать 8 или 9. Ты говоришь: «Десять!» – и побеждаешь.
В другом варианте этой игры тот, кто скажет: «Десять», – проигрывает. Чтобы всегда выигрывать, здесь предложи товарищу начать игру. Как бы он ни играл, ты должен называть числа 3, 6, 9. Тут товарищу придётся сказать: «Десять». И снова ты победитель.
ИГРА В ПЯТНАДЦАТЬ
Массовики-затейники часто играют с желающими не в «Десять», а в «Пятнадцать», причём прибавляют также не больше двух. В первом варианте игры (сказавший 15 побеждает) предложи товарищу начать и называй числа 3, 6, 9, 12, 15. Во втором варианте игры (сказавший 15 проигрывает) первое число должно быть твоё. Ты называешь числа 2, 5, 8, 11, 14.
ИГРА В СТО
Играют в эту игру и до 100 (сказавший 100 выигрывает). Здесь первое число должно быть от 1 до 10, затем игроки по очереди прибавляют к предыдущему числу от 1 до 10. Чтобы победить, надо начать игру и называть 1, 12, 23, 34, 45, 56, 67, 78, 89, 100.
Здесь первое число должно быть от 1 до 10, затем игроки по очереди прибавляют к предыдущему числу от 1 до 10. Чтобы победить, надо начать игру и называть 1, 12, 23, 34, 45, 56, 67, 78, 89, 100.
Конечно, можно запомнить все «выигрышные» числа в этих играх, но лучше установи закономерность, чтобы успешно играть не только в «Десять», «Пятнадцать» и «Сто», но и в другие варианты игры до любого числа, набавляя иные числа. Это пригодится тебе при решении заданий из тетради гнома Загадалки. Играй и побеждай!
И.Г. СУХИН
Задания гнома Загадалки
В следующих играх тот, кто скажет последнее число, выигрывает. Ты начинаешь. Какое первое число ты назовёшь, чтобы победить, если:
1. Вы с приятелем играете в «Десять», набавляете от 1 до 3?
2. Играете в «Десять», набавляете от 1 до 5?
3. Играете в «Десять», набавляете от 1 до 6?
Играете в «Десять», набавляете от 1 до 6?
4. Вы с другом играете в «Пятнадцать», набавляете от 1 до 3?
5. Играете в «Пятнадцать», набавляете от 1 до 5?
6. Играете в «Пятнадцать», набавляете от 1 до 6?
7. Играете в «Пятнадцать», набавляете от 1 до 7?
8. Играете в «Пятнадцать», набавляете от 1 до 8?
9. Вы с другом играете в «Сто», набавляете от 1 до 2?
10. Играете в «Сто», набавляете от 1 до 5?
11. Играете в «Сто», набавляете от 1 до 20?
12. Вы с товарищем играете в «Сто», набавляете от 1 до 30?
13. Играете в «Сто», набавляете от 1 до 40?
14. Играете в «Сто», набавляете от 1 до 50?
В следующих играх тот, кто скажет последнее число, проигрывает. Ты начинаешь. Какое первое число ты назовёшь, чтобы победить, если:
Ты начинаешь. Какое первое число ты назовёшь, чтобы победить, если:
15. Вы с приятелем играете в «Десять», набавляете от 1 до 3?
16. Играете в «Десять», набавляете от 1 до 4?
17. Играете в «Десять», набавляете от 1 до 5?
18. Играете в «Десять», набавляете от 1 до 6?
19. Вы с другом играете в «Пятнадцать», набавляете от 1 до 3?
20. Играете в «Пятнадцать», набавляете от 1 до 4?
21. Играете в «Пятнадцать», набавляете от 1 до 5?
22. Играете в «Пятнадцать», набавляете от 1 до 7?
23. Играете в «Пятнадцать», набавляете от 1 до 8?
24. Вы с другом играете в «Сто», набавляете от 1 до 3?
25. Играете в «Сто», набавляете от 1 до 4?
26. Играете в «Сто», набавляете от 1 до 5?
Играете в «Сто», набавляете от 1 до 5?
27. Играете в «Сто», набавляете от 1 до 20?
28. Вы с товарищем играете в «Сто», набавляете от 1 до 30?
29. Играете в «Сто», набавляете от 1 до 40?
30. Играете в «Сто», набавляете от 1 до 50?
ИГРА В ШЕСТЬ ФАНТИКОВ
Ты и твой товарищ выкладываете на столе 2 горизонтальных ряда фантиков, по 3 фантика в каждом ряду. Вместо фантиков могут быть камешки, конфеты, копейки, пуговицы, спички или счётные палочки.
I I I
I I I
Пусть начинает партнёр-товарищ. Он должен взять любое число фантиков из первого или из второго ряда. Нельзя брать фантики одновременно из обоих рядов. Затем ты берёшь фантики – тоже из одного ряда (первого или второго). Так по очереди продолжаете игру. Кто возьмёт последний фантик, тот проиграл.
Так по очереди продолжаете игру. Кто возьмёт последний фантик, тот проиграл.
Условия игры просты, но, чтобы победить, нужно проявить смекалку.
Предположим, противник берёт все 3 фантика из любого ряда. Тогда ты возьмёшь 2 из другого ряда. На столе останется последний фантик.
Партнёр проиграет, ведь пропускать очередь хода нельзя.
Если же первым ходом он возьмёт 2 фантика из одного ряда, то ты выберешь все 3 из другого. Опять твоя победа.
Твоему товарищу лучше всего первым ходом взять 1 фантик. Чтобы не проиграть, ты тоже возьмёшь 1, но из другого ряда. Теперь в обоих рядах останется по 2 фантика. Поражение твоего противника неизбежно.
Ведь если он берёт 2 фантика, то ты возьмёшь 1.
А если он выберет 1, ты возьмёшь 2.
В обоих случаях перед товарищем останется лежать 1 фантик. Победа за тобой.
Победа за тобой.
Запомни: в этой игре тот, кто начинает, проигрывает (при точной игре обоих противников).
ИГРА В ДЕВЯТЬ ФАНТИКОВ
Здесь фантики расположены в 3 ряда. В первом ряду – 1 фантик, во втором – 3, в третьем – 5.
I
I I I
I I I I I
Это расположение можно записать так: 1 3 5.
Условия игры такие же, как и в предыдущей игре.
При безошибочной игре партнёров здесь побеждает тот, кто начинает. Договорись с другом, чтобы первый ход был твоим, и возьми 3 фантика из третьего ряда. Оставшиеся фантики будут расположены так: 1 3 2.
Теперь, если твой товарищ заберёт единственный фантик из первого ряда, то ты возьмёшь 1 фантик из следующего ряда и получится расположение: 2 2, которое мы проанализировали в предыдущей игре. Ход за противником, и он проигрывает.
Ход за противником, и он проигрывает.
Твой партнёр терпит поражение и при других взятиях.
Если он возьмёт все 3 фантика из второго ряда, то ты заберёшь оба из третьего.
Если соперник выберет 2 фантика из второго ряда, ты возьмёшь 1 из третьего и получится положение: 1 1 1. Победа останется за тобой.
Если он возьмёт 1 фантик из второго ряда, ты заберёшь единственный фантик из первого ряда и снова получится выгодное для тебя положение: 2 2.
Если противник заберёт 2 фантика из третьего ряда, ты возьмёшь все 3 из второго.
Если он заберёт 1 фантик из третьего ряда, ты возьмёшь 2 из второго, и снова получится выигрышное для тебя положение: 1 1 1.
Всё, твоя победа, других вариантов нет.
И.Г. СУХИН
Положения для игры в девять фантиков из тетради гнома Загадалки
Представь, что игру начинает твой товарищ и своим ходом в исходном положении 1 3 5 берёт:
31. Единственный фантик из первого ряда: 3 5. Сколько фантиков и из какого ряда сейчас надо взять, чтобы победить?
Единственный фантик из первого ряда: 3 5. Сколько фантиков и из какого ряда сейчас надо взять, чтобы победить?
32. 3 фантика из второго ряда: 1 5. Как выиграть?
33. 2 фантика из второго ряда: 1 1 5. Как сыграть теперь?
34. 1 фантик из второго ряда: 1 2 5. Сколько фантиков из какого ряда ты возьмёшь?
35. Все 5 фантиков из третьего ряда: 1 3. Как победить?
36. 4 фантика из третьего ряда: 1 3 1. Как сыграть?
37. 3 фантика из третьего ряда: 1 3 2. Можно ли тебе избежать поражения?
38. 2 фантика из третьего ряда: 1 3 3. Что делать?
39. 1 фантик из третьего ряда: 1 3 4. Каков твой ответ?
Итак, проанализировав игры в шесть и девять фантиков, мы установили 4 важных расположения, к которым должны стремиться. В них очередь хода за противником, но он неизбежно проигрывает. Запомни их!
В них очередь хода за противником, но он неизбежно проигрывает. Запомни их!
N1: 2 2.
N2: 3 3.
N3: 1 1 1.
N4: 1 2 3.
Чтобы побеждать в этих играх, нельзя забывать: если остался всего один ряд с числом фантиков не менее двух, то своим ходом тебе надо забрать все фантики, кроме одного. А если осталось 2 ряда, в первом из которых находится 1 фантик, а во втором – любое количество фантиков, то нужно взять все фантики из второго ряда.
Всё это пригодится тебе в следующей игре.
ИГРА В ШЕСТНАДЦАТЬ ФАНТИКОВ
Мы постепенно подвели тебя к одной из самых интересных игр на свете, которую иногда называют «Мариенбад».
Здесь фантики расположены в 4 ряда. В первом ряду – 1 фантик, во втором – 3, в третьем – 5, в четвёртом – 7.
I
I I I
I I I I I
I I I I I I I
Это расположение можно записать так: 1 3 5 7.
Условия игры такие же, как и в предыдущих играх.
Проанализировать все варианты игры «Мариенбад» гораздо сложнее, чем для случаев с меньших числом фантиков.
Кроме положений: N1 – N4 своим ходом надо создавать ещё и такие: N5: 4 4, N6: 5 5 (эти 2 положения сводятся к: 2 2), N7: 1 4 5, N8: 2 4 6, N9: 2 5 7, N10: 3 4 7, N11: 3 5 6, N12: 1 1 х х (где х>1), N13: 1 2 4 7, N14: 1 2 5 6, N15: 1 3 4 6.
И наконец N16: 1 3 5 7. То есть в «Мариенбаде»тот, кто начинает, проигрывает!
Итак, если ты хочешь наверняка победить в этой игре, начать её должен твой товарищ. Чтобы быстро не проиграть, ему лучше всего взять один фантик из любого ряда. Теперь у тебя 3 равноценных ответа: надо взять один фантик в любом из трёх остальных рядов, получив расположения N9 – N11 или N13 – N15. Затем партнёр возьмёт фантик в одном из двух рядов, из которых фантики ещё не брали. А ты выберешь фантик из последнего такого ряда, и получится положение N8. Далее в зависимости от хода партнёра ты создашь расположения N1, N4, N5 или N7 и быстро выиграешь.
Далее в зависимости от хода партнёра ты создашь расположения N1, N4, N5 или N7 и быстро выиграешь.
Всё это не так-то уж и трудно. Приобретя игровой опыт, ты убедишься: достаточно помнить 4 важных положения: N4, N7, N8 и N12, чтобы быстро находить лучший ход.
И.Г. СУХИН
Положения для игры в «Мариенбад» из тетради гнома Загадалки
Представь, что игру начинает твой товарищ и своим ходом в исходном положении 1 3 5 7 берёт:
40. 2 фантика из второго ряда: 1 1 5 7. Сколько фантиков и из какого ряда сейчас надо взять, чтобы победить?
41. 3 фантика из второго ряда: 1 5 7. Как выиграть?
42. 2 фантика из третьего ряда: 1 3 3 7. Как сыграть теперь?
43. 3 фантика из третьего ряда: 1 3 2 7. Сколько фантиков из какого ряда ты возьмёшь?
44. 4 фантика из третьего ряда: 1 3 1 7. Как победить?
4 фантика из третьего ряда: 1 3 1 7. Как победить?
45. Все 5 фантиков из третьего ряда: 1 3 7. Как сыграть?
46. 2 фантика из четвёртого ряда: 1 3 5 5. Твой ход?
47. 3 фантика из четвёртого: 1 3 5 4. Что делать?
48. 4 фантика из четвёртого: 1 3 5 3. Каков твой ответ?
49. 5 фантиков из четвёртого: 1 3 5 2. Как сыграть?
50. 6 фантиков из четвёртого: 1 3 5 1. Что делать?
51. Все 7 фантиков из четвёртого: 1 3 5. Каков твой ответ?
ИГРА В ДВАДЦАТЬ ПЯТЬ ФАНТИКОВ
Здесь фантики в пяти рядах. Это расположение можно записать так: 1 3 5 7 9.
Условия игры такие же, как и в предыдущих играх.
Чтобы выиграть, тебе надо начать и первым ходом забрать все 9 фантиков из последнего ряда. Получается игра «Мариенбад», в которой тот, кто начинает, проигрывает.
Получается игра «Мариенбад», в которой тот, кто начинает, проигрывает.
И.Г. СУХИН
ИГРЫ, ГДЕ ВЗЯВШИЙ ПОСЛЕДНИЙ ФАНТИК ВЫИГРЫВАЕТ
В игры с фантиками можно играть и иначе: тот, кто берёт последний фантик, считается победителем. Самое интересное здесь то, что тебе всё равно нужно стремиться в основном к тем же промежуточным положениям, которые мы уже рассмотрели. Т.е. старайся, чтобы после твоего хода создавались положения: N1 – N2, N4 – N16. Если сможешь сделать это, выиграешь. Стратегическое различие проявляется в самом конце. К примеру, если в положении: 2 2 партнёр возьмёт один фантик, то здесь и ты выберешь не два фантика, как в первом варианте игры, а 1 из другого ряда и получится: 1 1, что обеспечит тебе победу. А если соперник возьмёт 2 фантика, то и ты заберёшь оба оставшихся и выиграешь.
Что теперь? Научи товарища правилам игры в такие фантики и обыгрывай. Можешь провести чемпионат класса, турнир во дворе.
Можешь провести чемпионат класса, турнир во дворе.
МАТЕМАТИЧЕСКИЕ ФОКУСЫ
Старинные фокусы из тетради гнома Загадалки
1. Напиши такое трёхзначное число, чтобы первая цифра была по крайней мере на 2 больше, чем третья. Например: 311. Запиши его цифрами в обратном порядке: 113. Из первого вычти второе: получится 198. Это число снова напиши наоборот: 891. И два последние числа сложи.
891 + 198 = 1089.
Удивительное дело: какие бы числа мы ни брали, в ответе всегда будет 1089!
Теперь предложи провести все эти действия с числами кому-то из друзей. Представляешь, как он удивится, когда ты, не спрашивая у него, сколько получилось в результате (как это бывает в других математических фокусах), сам назовёшь ответ! Для эффекта можешь сообщить его не сразу, а через несколько секунд, как-бы что-то подсчитывая в уме.
2. Попроси товарища задумать какое-нибудь двузначное число, вычесть из него сумму его цифр, зачеркнуть в полученном результате одну цифру и сообщить, какое число осталось. После этого ты тотчас скажешь, какая цифра зачёркнута! Для этого ты всего навсего из 9 вычтешь оставшееся однозначное число.
Пример: 97 – 16 = 81, 8 зачёркивается и друг говорит, что осталось 1. Ты выполняешь в уме вычитание и получаешь в результате зачёркнутую цифру: 9 – 1 = 8.
Для информации: СОДЕРЖАНИЕ КНИГИ
Предисловие для учителя
РАЗДЕЛ 1. ГНОМЫ ЗАГАДАЛКА, ПУТАЛКА И ЗАБЫВАЛКА
Знакомство с гномами Математические приключения гномов (в шутку и всерьёз) Говорят гномы Зачёркиваем буквы – получаем числа Задачи из тетради гнома Загадалки Переставляем буквы – получаем числа Задачи из тетради гнома Забывалки Числа прячутся в предложениях Задачи из тетради гнома Загадалки Задачи-шутки из тетради гнома Загадалки
РАЗДЕЛ 2. ЧИСЛА В КЛЕТКАХ
ЧИСЛА В КЛЕТКАХ
Шпаргалка Числовая горизонталь гнома Забывалки (задачи с дополнительными условиями и подсказками) Задачи из тетради гнома Забывалки Задачи на вычитание Задачи на сложение Задачи на умножение Задачи на деление Сочетание арифметических действий Числовая горизонталь гнома Путалки (задачи с дополнительными условиями и подсказками) Задачи из тетради гнома Путалки Математические дорожки Задачи из тетради гнома Забывалки Цифры в буквах Задачи из тетради гнома Забывалки Цифры в цифрах Задачи из тетради гнома Забывалки Волшебные квадраты Задачи из тетради гнома Загадалки
РАЗДЕЛ 3. НЕОБЫЧНЫЕ ЗАДАЧИ И ГОЛОВОЛОМКИ
Подумай и ответь Задачи из тетради гнома Загадалки Натуральные, простые, составные, чётные, нечётные, круглые Шпаргалка Задачи из тетради гнома Загадалки От нуля до девяти (однозначные числа) От нуля до двадцати (однозначные и двузначные числа) От нуля до девяноста девяти (однозначные и двузначные числа) От нуля до тысячи Чётные и нечётные числа Круглые числа Сюжетные задачи Исправление, зачёркивание, превращение, отгадывание цифр и чисел Задачи из тетради гнома Загадалки
РАЗДЕЛ 4. ИГРЫ И ФОКУСЫ
ИГРЫ И ФОКУСЫ
Как всегда выигрывать в популярных играх математического содержания Игра в десять Игра в пятнадцать Игра в сто Задания гнома Загадалки Игра в шесть фантиков Игра в девять фантиков Положения для игры в девять фантиков из тетради гнома Загадалки Игра в шестнадцать фантиков Положения для игры в «Мариенбад» из тетради гнома Загадалки Игра в двадцать пять фантиков Игры, где взявший последний фантик выигрывает Математические фокусы Старинные фокусы из тетради гнома Загадалки
ОТВЕТЫ
ОТВЕТЫ
РАЗДЕЛ 1. ГНОМЫ ЗАГАДАЛКА, ПУТАЛКА И ЗАБЫВАЛКА
МАТЕМАТИЧЕСКИЕ ПРИКЛЮЧЕНИЯ ГНОМОВ
1. Двух. 2. У Забывалки одна, а у Путалки две. 3. У Забывалки две, у Загадалки одна, у Путалки три. 4. По две у Загадалки и Путалки и одна у Забывалки. 5. У Загадалки – 2, у Забывалки – 1, у Путалки – 3 (он 2 носка натянул на одну ногу). 6. За 11 секунд. 7. 12+3+45 = 60. 8. 54+3+2+1 = 60. 9. Одна. 10. Две. 17. Ни одного. 18. Он забил гол в свои ворота. 19. Это был тренер команды соперника. 20. Его товарищи играли за команду «Дырка». 23. Потому что, возвращаясь из магазина, Путалка снова свернул направо. Загадалка и Забывалка пошли по дороге прямо, не сворачивая у перекрёстка. 24. Он перепутал рубашки, надел без колокольчиков. 25. Он забыл надеть рубашку. 26. Забывалка зачитался в доме книгой о Мюнхгаузене и забыл пойти за грибами. 27. Ни от одной. 28. Трое (гномов).
6. За 11 секунд. 7. 12+3+45 = 60. 8. 54+3+2+1 = 60. 9. Одна. 10. Две. 17. Ни одного. 18. Он забил гол в свои ворота. 19. Это был тренер команды соперника. 20. Его товарищи играли за команду «Дырка». 23. Потому что, возвращаясь из магазина, Путалка снова свернул направо. Загадалка и Забывалка пошли по дороге прямо, не сворачивая у перекрёстка. 24. Он перепутал рубашки, надел без колокольчиков. 25. Он забыл надеть рубашку. 26. Забывалка зачитался в доме книгой о Мюнхгаузене и забыл пойти за грибами. 27. Ни от одной. 28. Трое (гномов).
ГОВОРЯТ ГНОМЫ
5. Две и четыре. 6. Нет, 15.
ЗАЧЁРКИВАЕМ БУКВЫ – ПОЛУЧАЕМ ЧИСЛА
1. Нуль. 2. Один. 3. Два. 4. Три. 5. Пять. 13. Тысяча.
ПЕРЕСТАВЛЯЕМ БУКВЫ – ПОЛУЧАЕМ ЧИСЛА
1. Три. 2. Нуль. 3. Сорок. 4. Один. 5. Два. 13-15. Двенадцать. 19. Тридцать. 22. Пятьдесят. 25. Семьдесят. 28. Восемьдесят. 71. Миллиард.
71. Миллиард.
ЗАДАЧИ-ШУТКИ ИЗ ТЕТРАДИ ГНОМА ЗАГАДАЛКИ
1. Один. 2. Двадцать. 3. Нуль, потому что у осла нет рогов. 4. Одна. 5. Ни одного. 6. В норе Кролика. 7. Стон.
НАТУРАЛЬНЫЕ, ПРОСТЫЕ, СОСТАВНЫЕ, ЧЁТНЫЕ, НЕЧЁТНЫЕ, КРУГЛЫЕ
1. Простое. 2. Однозначное. 3. Чётное. 4-7. 0. 8-15. 1. 16-23. 2. 24. 4. 25-26. 7. 27. 8. 28. 1 и 0. 29. 9 и 0. 30. 1 и 2. 31. 3 и 1. 32. 5 и 1. 33. 1 и 7. 34. 8 и 1. 35-36. 9 и 1. 37. 2 и 3. 38-40. 4 и 2. 41. 2 и 5. 42. 6 и 2. 43. 2 и 7. 44. 8 и 2. 45. 3 и 5. 46. 4 и 5. 47-48. 1, 2, 3. 49. 2, 3 и 4. 50. 3, 6 и 2. 51. 2; (9 – 7). 52. 10; (8 + 2). 53. 10; (9 + 1). 54. 11. 55. 18. 56. 1 и 15. 57. 2 и 8. 58. 3 и 5. 59. 3 и 11. 60. 4 и 5. 61. 4 и 8. 62. 5 и 7. 63. 5 и 9. 64. 9 и 6. 65. 8 и 9. 66. 10 и 9. 67. 2, 3 и 6. 68. 6, 3 и 4. 69. 1, 2, 3 и 4. 70. 2, 3, 5, 7. 71. Простых.
156. Четвёрку. 157. 6; (2 + 4). 158. 23 (1 уже был, а 22 упали с неба). 159. 23. 160. 33. 161. А.Пушкин «Сказка о царе Салтане…»; 33. 162. 199. 163. 400. 164. 500. 165. 3, 6, 9. 166. 3, 6, 12. 167. 6, 9, 12.
Четвёрку. 157. 6; (2 + 4). 158. 23 (1 уже был, а 22 упали с неба). 159. 23. 160. 33. 161. А.Пушкин «Сказка о царе Салтане…»; 33. 162. 199. 163. 400. 164. 500. 165. 3, 6, 9. 166. 3, 6, 12. 167. 6, 9, 12.
ИСПРАВЛЕНИЕ, ЗАЧЁРКИВАНИЕ, ПРЕВРАЩЕНИЕ,
ОТГАДЫВАНИЕ ЦИФР И ЧИСЕЛ
1. 1. 2. 6. 3. 7. 4. 8. 5. 22. 6. 23. 7. 47. 8. 59. 9. 89. 10. 95. 11. 153. 12. 942. 13. Да.
РАЗДЕЛ 4. ИГРЫ И ФОКУСЫ
КАК ВСЕГДА ВЫИГРЫВАТЬ В ПОПУЛЯРНЫХ ИГРАХ МАТЕМАТИЧЕСКОГО СОДЕРЖАНИЯ
1. 2. 2. 4. 3-5. 3. 6. 1. 7. 7. 8. 6. 9. 1. 10. 4. 11. 16. 12. 7. 13. 18. 14. 49. 15. 1. 16. 4. 17. 3. 18-19. 2. 20. 4. 21. 2. 22. 6. 23. 5. 24. 3. 25. 4. 26. 3. 27. 15. 28. 6. 29. 17. 30. 48. 31. 2 из последнего ряда. 32. Взять все 5 фантиков из последнего ряда. 33. Забрать 4 из третьего ряда. 34. 2 из третьего. 35. Взять все 3 из второго ряда. 36. Забрать 2 из второго ряда. 37. Нет. 38. Взять 1 фантик из любого ряда. 39. Забрать 2 из третьего ряда. 40. 2 из четвёртого ряда. 41. Взять 3 фантика из последнего ряда. 42. Забрать 6 из четвёртого ряда. 43. Все 7 из четвёртого. 44. Взять 4 из четвёртого ряда. 45. Забрать 5 из последнего ряда. 46. Взять 2 из второго ряда. 47. Взять все 3 фантика из второго ряда. 48. Взять 4 из третьего ряда. 49. Взять все 5 фантиков из третьего ряда. 50. Взять 2 из третьего ряда. 51. Взять 3 из третьего ряда.
37. Нет. 38. Взять 1 фантик из любого ряда. 39. Забрать 2 из третьего ряда. 40. 2 из четвёртого ряда. 41. Взять 3 фантика из последнего ряда. 42. Забрать 6 из четвёртого ряда. 43. Все 7 из четвёртого. 44. Взять 4 из четвёртого ряда. 45. Забрать 5 из последнего ряда. 46. Взять 2 из второго ряда. 47. Взять все 3 фантика из второго ряда. 48. Взять 4 из третьего ряда. 49. Взять все 5 фантиков из третьего ряда. 50. Взять 2 из третьего ряда. 51. Взять 3 из третьего ряда.
О ЛИТЕРАТУРНЫХ ПРИКЛЮЧЕНИЯХ ГНОМОВ МОЖНО ПРОЧИТАТЬ ЗДЕСЬ
ОСНОВНЫЕ РУБРИКИ САЙТА
ЛИТЕРАТУРНЫЕ ЗАТЕИ
Лучшие книги:
«Литературные викторины, тесты и сказки-загадки для дошкольников и младших школьников» (1998) и «Незнайка, Хоттабыч, Карлсон и все-все-все: литературные викторины, кроссворды и чайнворды для детей».
ЗАГАДКИ, ЗАГАДКИ-ШУТКИ, СКАЗКИ-ЗАГАДКИ, ЗАНИМАТЕЛЬНЫЕ ЗАДАНИЯ
Лучшая книга:
«Новые 500 загадок – 70 кроссвордов».
ЛОГОПЕДИЯ И СКОРОГОВОРКИ
Лучшие книги:
«Чистоговорки, наоборотки, запрятки на звук «С» и «Весёлые скороговорки для «непослушных» звуков».
ЗАНИМАТЕЛЬНАЯ МАТЕМАТИКА
Лучшие книги:
«800 новых логических и математических головоломок» и «Весёлая математика: 1500 головоломок для математических олимпиад, уроков, досуга: 1-7 класс».
ШАХМАТЫ ДЛЯ ДЕТЕЙ
Лучшие книги:
«Волшебные фигуры, или Шахматы для детей 2–5 лет» и «Удивительные приключения в Шахматной стране» (для детей 5-–8 лет).
ЗАНИМАТЕЛЬНАЯ БИБЛИОГРАФИЯ
Занимательная библиография
ЧТО УЖЕ РАЗМЕЩЕНО НА САЙТЕ КНИГИ, РУКОПИСИ, СТАТЬИ И.Г.СУХИНА КТО ЗАЩИТИТ АВТОРА, ИЛИ ОХОТА НА ПЛАГИАТОРА ИЗ ПЕРЕПИСКИ С ЧИТАТЕЛЯМИ Калейдоскоп интересных ссылок
НА ГЛАВНУЮ СТРАНИЦУ
mailto:[email protected]
Home Page URL: http://suhin.narod.ru
© 2001-2006 Сухин И.Г. Все права защищены.
Обновление от 13 марта 2006 года.
Сайт управляется системой uCoz
Четные и нечетные числа
Знакомство с четными и нечетными числами обычно происходит в старшем дошкольном возрасте. Если ваше чадо уже умеет считать в пределах двадцати, знает сложение и вычитание, то пришло время объяснить ему, как можно определить, четное число или нет. Это поможет в дальнейшем изучении арифметики и математики.
Это поможет в дальнейшем изучении арифметики и математики.
Содержание:
- Четные числа
- Нечетные числа
- Четность и нечетность: основные свойства
- Таблица четных и нечетных чисел
- 0 – это четное число или нет
- Игровые упражнения
Четные числа
Из школьного курса мы знаем, что четные числа – это те, которые делятся на два нацело. Малыши дошкольного возраста с делением чисел еще не знакомы, им лучше всего объяснять понятие четности и нечетности не в теории, а на примерах с конфетами, яблоками или игрушками.
Возьмите четыре конфеты и предложите ребенку поделить их на две равные кучки – для себя и для мамы. Обратите внимание малыша, что в этом случае каждому достанется по две конфеты.
Попросите малыша сделать то же самое с другими предметами для закрепления понимания. Можно раскладывать, например, карандаши, фишки, кубики и любое другое четное количество вещей.
Нечетные числа
Нечетные числа делятся на два с остатком. Возьмите три яблока и попросите кроху поделить их поровну между вами. Очень скоро малыш придет к выводу, что это невозможно.
Четность и нечетность: основные свойства
Объясните ребенку несколько простых лайфхаков:
- Нечетные и четные числа чередуются. Единица – нечетное, поэтому двойка – четное, тройка – нечетное и так далее.
- Понять, относится двузначное или многозначное число к четным, можно по последней цифре. Она должна быть 0, 2, 4, 6 или 8.
- У нечетных чисел в конце стоит 1, 3, 5, 7 или 9.
Если ребенок уже знаком с арифметикой, ему будет интересно узнать следующие свойства:
- При сложении двух четных чисел получается четное число: 4+2 = 6.
- Если к четному числу прибавить нечетное, то и результат будет нечетным: 2+1 = 3.
- Если умножить четное число на любое другое результат тоже будет четным: 2 х 3 = 6.
- Если умножить два нечетных числа, то получится нечетный результат: 3 х 5 = 15.

Таблица четных и нечетных чисел
Чтобы ребенок мог быстро определять, какое число перед вами, удобно использовать таблицу четных и нечетных чисел. В ней жирным в каждом ряду выделены четные элементы.
Дошкольники обычно умеют уверенно считать в пределах 20. Большая таблица будет их путать.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
Для школьников подойдет таблица от 1 до 100.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 31 | 32 | 33 | 34 | 35 | 36 | 37 | 38 | 39 | 40 |
| 41 | 42 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 |
| 51 | 52 | 53 | 54 | 55 | 56 | 57 | 58 | 59 | 60 |
| 61 | 62 | 63 | 64 | 65 | 66 | 67 | 68 | 69 | 70 |
| 71 | 72 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 |
| 81 | 82 | 83 | 84 | 85 | 86 | 87 | 88 | 89 | 90 |
| 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
0 – это четное число или нет
Математическая теория утверждает, что ноль относится к четным числам. Ребенку этот факт можно объяснить тремя способами:
Ребенку этот факт можно объяснить тремя способами:
- Нечетные и четные числа чередуются, а ноль стоит перед единицей, которая является нечетным числом. Поэтому 0 – четное число.
- Если число оканчивается на ноль, то это признак четности. Соответственно и сам 0 относится к четным.
- Ноль делится на два без остатка. Поэтому его относят к четным числам.
Игровые упражнения
Чтобы закрепить знания, используйте понятия о четных и нечетных числах в играх и задачках. Например, сыграйте в «чет-нечет». Называйте числа и просите малыша хлопать в ладошки, если оно четное. А если вы назовете нечетное, он должен топать ногой.
На прогулке выясняйте у ребенка, четный или нечетный номер дома, автомобиля, городского автобуса или маршрутки. Распечатайте из интернета картинки с воздушными шариками или другими предметами, на которых изображены числа. Попросите закрасить предметы с четными числами синим цветом, а с нечетными – красным.
youtube.com/embed/V0Po-MgLPyg» allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»» loading=»lazy» frameborder=»0″>Рейтинг: 5/5 — 1 голосов
3 четное или нечетное число. Нумерология
- Нечётное число — целое число , которое не делится на без остатка : …, −3, −1, 1, 3, 5, 7, 9, …
Если m чётно, то оно представимо в виде m = 2 k, а если нечётно, то в виде m = 2 k + 1, где k \in \mathbb Z.
История и культура
Понятие чётности чисел известно с глубокой древности и ему часто придавалось мистическое значение. В китайской космологии и натурософии чётные числа соответствуют понятию «инь », а нечётные — «ян » .
В разных странах существуют связанные с количеством даримых цветов традиции. Например в США , Европе и некоторых восточных странах считается, что чётное количество даримых цветов приносит счастье . В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов , у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.
Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли. Например, вполне допустимо подарить даме букет из 12, 14, 16 и т. д. цветов или срезов кустового цветка, имеющих множество бутонов , у которых они, в принципе, не подсчитываются. Тем более это относится к бо́льшему количеству цветов (срезов), даримых в других случаях.
Практика
В высших учебных заведениях со сложными графиками учебного процесса применяются чётные и нечётные недели. Внутри этих недель отличается расписание учебных занятий и в некоторых случаях время их начала и окончания. Такая практика применяется для равномерности распределения нагрузки по аудиториям, учебным корпусам и для ритмичности занятий по дисциплинам с малой аудиторной нагрузкой (1 раз в 2 недели)
В графиках движения поездов применяются чётные и нечётные номера поездов, зависящие от направления движения (прямое или обратное). Соответственно чётностью/нечётностью обозначается направление, в котором проходит поезд через каждую станцию.
С чётными и нечётными числами месяца иногда увязаны графики движения поездов, которые организованы через день.
Напишите отзыв о статье «Чётные и нечётные числа»
Примечания
Ссылки
- Последовательность A005408 в OEIS : нечётные числа
- Последовательность A005843 в OEIS : чётные числа
- Последовательность A179082 в OEIS : чётные числа с чётной суммой цифр в десятичной записи
Отрывок, характеризующий Чётные и нечётные числа
– Так, так, – сказал князь Андрей, обращаясь к Алпатычу, – все передай, как я тебе говорил. – И, ни слова не отвечая Бергу, замолкшему подле него, тронул лошадь и поехал в переулок.
От Смоленска войска продолжали отступать. Неприятель шел вслед за ними. 10 го августа полк, которым командовал князь Андрей, проходил по большой дороге, мимо проспекта, ведущего в Лысые Горы. Жара и засуха стояли более трех недель. Каждый день по небу ходили курчавые облака, изредка заслоняя солнце; но к вечеру опять расчищало, и солнце садилось в буровато красную мглу. Только сильная роса ночью освежала землю. Остававшиеся на корню хлеба сгорали и высыпались. Болота пересохли. Скотина ревела от голода, не находя корма по сожженным солнцем лугам. Только по ночам и в лесах пока еще держалась роса, была прохлада. Но по дороге, по большой дороге, по которой шли войска, даже и ночью, даже и по лесам, не было этой прохлады. Роса не заметна была на песочной пыли дороги, встолченной больше чем на четверть аршина. Как только рассветало, начиналось движение. Обозы, артиллерия беззвучно шли по ступицу, а пехота по щиколку в мягкой, душной, не остывшей за ночь, жаркой пыли. Одна часть этой песочной пыли месилась ногами и колесами, другая поднималась и стояла облаком над войском, влипая в глаза, в волоса, в уши, в ноздри и, главное, в легкие людям и животным, двигавшимся по этой дороге. Чем выше поднималось солнце, тем выше поднималось облако пыли, и сквозь эту тонкую, жаркую пыль на солнце, не закрытое облаками, можно было смотреть простым глазом. Солнце представлялось большим багровым шаром.
Только сильная роса ночью освежала землю. Остававшиеся на корню хлеба сгорали и высыпались. Болота пересохли. Скотина ревела от голода, не находя корма по сожженным солнцем лугам. Только по ночам и в лесах пока еще держалась роса, была прохлада. Но по дороге, по большой дороге, по которой шли войска, даже и ночью, даже и по лесам, не было этой прохлады. Роса не заметна была на песочной пыли дороги, встолченной больше чем на четверть аршина. Как только рассветало, начиналось движение. Обозы, артиллерия беззвучно шли по ступицу, а пехота по щиколку в мягкой, душной, не остывшей за ночь, жаркой пыли. Одна часть этой песочной пыли месилась ногами и колесами, другая поднималась и стояла облаком над войском, влипая в глаза, в волоса, в уши, в ноздри и, главное, в легкие людям и животным, двигавшимся по этой дороге. Чем выше поднималось солнце, тем выше поднималось облако пыли, и сквозь эту тонкую, жаркую пыль на солнце, не закрытое облаками, можно было смотреть простым глазом. Солнце представлялось большим багровым шаром. Ветра не было, и люди задыхались в этой неподвижной атмосфере. Люди шли, обвязавши носы и рты платками. Приходя к деревне, все бросалось к колодцам. Дрались за воду и выпивали ее до грязи.
Ветра не было, и люди задыхались в этой неподвижной атмосфере. Люди шли, обвязавши носы и рты платками. Приходя к деревне, все бросалось к колодцам. Дрались за воду и выпивали ее до грязи.
Князь Андрей командовал полком, и устройство полка, благосостояние его людей, необходимость получения и отдачи приказаний занимали его. Пожар Смоленска и оставление его были эпохой для князя Андрея. Новое чувство озлобления против врага заставляло его забывать свое горе. Он весь был предан делам своего полка, он был заботлив о своих людях и офицерах и ласков с ними. В полку его называли наш князь, им гордились и его любили. Но добр и кроток он был только с своими полковыми, с Тимохиным и т. п., с людьми совершенно новыми и в чужой среде, с людьми, которые не могли знать и понимать его прошедшего; но как только он сталкивался с кем нибудь из своих прежних, из штабных, он тотчас опять ощетинивался; делался злобен, насмешлив и презрителен. Все, что связывало его воспоминание с прошедшим, отталкивало его, и потому он старался в отношениях этого прежнего мира только не быть несправедливым и исполнять свой долг.
Правда, все в темном, мрачном свете представлялось князю Андрею – особенно после того, как оставили Смоленск (который, по его понятиям, можно и должно было защищать) 6 го августа, и после того, как отец, больной, должен был бежать в Москву и бросить на расхищение столь любимые, обстроенные и им населенные Лысые Горы; но, несмотря на то, благодаря полку князь Андрей мог думать о другом, совершенно независимом от общих вопросов предмете – о своем полку. 10 го августа колонна, в которой был его полк, поравнялась с Лысыми Горами. Князь Андрей два дня тому назад получил известие, что его отец, сын и сестра уехали в Москву. Хотя князю Андрею и нечего было делать в Лысых Горах, он, с свойственным ему желанием растравить свое горе, решил, что он должен заехать в Лысые Горы.
Он велел оседлать себе лошадь и с перехода поехал верхом в отцовскую деревню, в которой он родился и провел свое детство. Проезжая мимо пруда, на котором всегда десятки баб, переговариваясь, били вальками и полоскали свое белье, князь Андрей заметил, что на пруде никого не было, и оторванный плотик, до половины залитый водой, боком плавал посредине пруда. Князь Андрей подъехал к сторожке. У каменных ворот въезда никого не было, и дверь была отперта. Дорожки сада уже заросли, и телята и лошади ходили по английскому парку. Князь Андрей подъехал к оранжерее; стекла были разбиты, и деревья в кадках некоторые повалены, некоторые засохли. Он окликнул Тараса садовника. Никто не откликнулся. Обогнув оранжерею на выставку, он увидал, что тесовый резной забор весь изломан и фрукты сливы обдерганы с ветками. Старый мужик (князь Андрей видал его у ворот в детстве) сидел и плел лапоть на зеленой скамеечке.
Князь Андрей подъехал к сторожке. У каменных ворот въезда никого не было, и дверь была отперта. Дорожки сада уже заросли, и телята и лошади ходили по английскому парку. Князь Андрей подъехал к оранжерее; стекла были разбиты, и деревья в кадках некоторые повалены, некоторые засохли. Он окликнул Тараса садовника. Никто не откликнулся. Обогнув оранжерею на выставку, он увидал, что тесовый резной забор весь изломан и фрукты сливы обдерганы с ветками. Старый мужик (князь Андрей видал его у ворот в детстве) сидел и плел лапоть на зеленой скамеечке.
Он был глух и не слыхал подъезда князя Андрея. Он сидел на лавке, на которой любил сиживать старый князь, и около него было развешено лычко на сучках обломанной и засохшей магнолии.
Князь Андрей подъехал к дому. Несколько лип в старом саду были срублены, одна пегая с жеребенком лошадь ходила перед самым домом между розанами. Дом был заколочен ставнями. Одно окно внизу было открыто. Дворовый мальчик, увидав князя Андрея, вбежал в дом.
Алпатыч, услав семью, один оставался в Лысых Горах; он сидел дома и читал Жития. Узнав о приезде князя Андрея, он, с очками на носу, застегиваясь, вышел из дома, поспешно подошел к князю и, ничего не говоря, заплакал, целуя князя Андрея в коленку.
Узнав о приезде князя Андрея, он, с очками на носу, застегиваясь, вышел из дома, поспешно подошел к князю и, ничего не говоря, заплакал, целуя князя Андрея в коленку.
Как мы видели выше, любая подстановка разлагается в произведение транспозиций. Вообще говоря, одну и ту же подстановку можно представить в виде произведения транспозиций многими различными способами. Например, очевидно, что
(формулы (1) и (2) выражают, как легко видеть, один и тот же факт, но в различных обозначениях).
Лемма. Если произведение нескольких транспозиций равно тождественной подстановке, то число этих транспозиций четно.
Мы докажем эту лемму индукцией по числу s различных чисел, входящих в записи данных транспозиций.
Наименьшее возможное значение числа s равно, очевидно, двум. Если , то рассматриваемое произведение является степенью некоторой транспозиции и поэтому равно тождественной подстановке только тогда, когда показатель степени четен (ибо любая транспозиция имеет порядок 2). Таким образом, в случае лемма доказана.
Таким образом, в случае лемма доказана.
Предполагая теперь, что лемма уже доказана для любого произведения транспозиций, записи которых содержат менее s различных чисел, рассмотрим некоторое, равное тождественной подстановке произведение транспозиций
в записи которых входит ровно s различных чисел. Пусть I — одно из этих чисел. Пользуясь соотношением (1) и тем, что независимые транспозиции перестановочны, мы можем «переместить вперед» все транспозиции, в запись которых входит число i, т. е. перейти от произведения (3) к равному произведению вида
в котором все числа отличны от числа l. Если , то, пользуясь соотношением (2) или соотношением
мы можем от произведения (4) перейти к произведению такого же вида, но с меньшим . В результате ряда таких преобразований мы либо полностью уничтожим все транспозиции, в записи которых входит число l, либо получим произведение, содержащее только одну такую транспозицию:
Но это произведение переводит, очевидно, число в число l и потому не может быть тождественной подстановкой. Следовательно, последний случай невозможен. Таким образом, в результате наших преобразований мы получим равное тождественной подстановке произведение транспозиций, записи которых не содержат числа l. Никаких новых чисел записи этих подстановок, очевидно, не содержат. Следовательно, согласно предположению индукции, в это произведение входит четное число транспозиций.
Следовательно, последний случай невозможен. Таким образом, в результате наших преобразований мы получим равное тождественной подстановке произведение транспозиций, записи которых не содержат числа l. Никаких новых чисел записи этих подстановок, очевидно, не содержат. Следовательно, согласно предположению индукции, в это произведение входит четное число транспозиций.
Остается заметить, что при описанных преобразованиях число транспозиций либо не меняется (когда мы пользуемся соотношениями (1), (2)), либо уменьшается на две единицы (когда мы пользуемся соотношением . Поэтому исходное произведение (3) также состоит из четного числа транспозиций. Тем самым лемма полностью доказана.
Пусть теперь некоторая подстановка а двумя способами разложена в произведение транспозиций:
(первое разложение содержит транспозиций, а второе q). Тогда
и, следовательно, по доказанной лемме, число четно.
Таким образом, числа и q либо одновременно четны, либо одновременно нечетны. Другими словами, при всех разложениях подстановки в произведение транспозиций четность числа этих транспозиций будет одна и та же.
Другими словами, при всех разложениях подстановки в произведение транспозиций четность числа этих транспозиций будет одна и та же.
Подстановка называется четной, если она разлагается в произведение четного числа транспозиций, и нечетной — в противном случае. Согласно доказанной теореме, четность подстановки не зависит от выбора ее разложения в произведение транспозиций.
Любая транспозиция, или вообще любой цикл четной длины, является нечетной подстановкой, а любой цикл нечетной длины, в частности любой цикл длины 3, является четной подстановкой. Тождественная подстановка, очевидно, четна.
Разложение подстэновки а в произведение транспозиций, то
откуда следует, что подстановка, обратная — четной подстановке, четна, обратная нечетной — нечетна.
Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.
Например: -24, 0, 6, 38 — все это четные числа.
m = 2k — общая формула написания четных чисел, где k — целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.
Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.
Пример нечетных чисел: 3, 1, 7 и 35.
n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k — целое число.
Сложение и вычитание четных и нечетных чисел
В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.
Операция | Результат | Пример |
Четное + Четное | ||
Четное + Нечетное | Нечетное | |
Нечетное + Нечетное |
Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.
Умножение четных и нечетных чисел
При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.
Операция | Результат | Пример |
Четное * Четное | ||
Четное * Нечетное | ||
Нечетное * Нечетное | Нечетное |
А теперь рассмотрим дробные числа.
Десятичная запись числа
Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.
Например: 3,14; 5,1; 6,789 — это все
С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.
Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.
Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.
А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом — дробную.
Так же десятичные дроби следует округлять.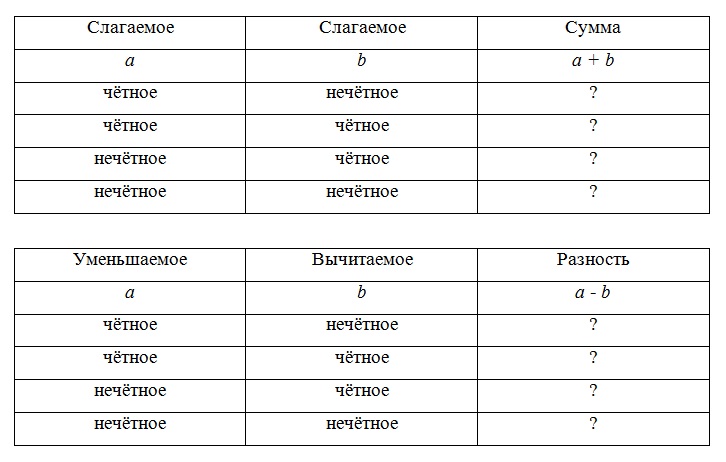 Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Определения
- Чётное число — целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
- Нечётное число — целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …
В соответствии с этим определением нуль является чётным числом.
Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .
В разных странах существуют связанные с количеством даримых цветов традиции.
В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.
Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.
Примечания
Wikimedia Foundation . 2010 .
- Маарду
- Сверхпроводимость
Смотреть что такое «Чётные и нечётные числа» в других словарях:
Нечётные числа
Чётные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Нечётное — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19). … … Википедия
… … Википедия
Нечётное число — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Четные и нечетные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Четные числа — Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Слегка избыточные числа — Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия
Совершенные числа — целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …
Квантовые числа — целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы.… … Большая советская энциклопедия
Книги
- Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна.
 В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
Что означают чётные и нечётные числа в духовной нумерологии. В изучении это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?
Чётные числа
Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.
А что означают чётные числа относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.
У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.
Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Нечётные числа
Нечётные числа
— те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?
Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел , никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.
Возьмём для примера — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.
Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел
надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…
В толковании нечётных чисел
надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…
Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.
Чётные и нечётные числа в нумерологии
Подведём итоги. В чём главное отличие чётных чисел от нечётных?
Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…
Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…
Обратите внимание!
В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом,
а также для заказа книги пройдите по следующей ссылке:
««
Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом,
а также для заказа книги пройдите по следующей ссылке:
««
———————————————————————————————
30 различных чисел четные или. Чётные и нечётные числа
Итак, я начну свою историю с четных чисел. Какие числа четные? Любое целое число, которое можно разделить на два без остатка, считается четным. Кроме того, четные числа заканчиваются на одну из данного ряда цифру: 0, 2, 4, 6 или 8.
Например: -24, 0, 6, 38 — все это четные числа.
m = 2k — общая формула написания четных чисел, где k — целое число. Данная формула может понадобиться для решения многих задач или уравнений в начальных классах.
Есть еще один вид чисел в огромном царстве математики — это нечетные числа. Любое число, которое нельзя разделить на два без остатка, а при делении на два остаток равен единице, принято называть нечетным. Любое из них заканчивается на одну из таких цифр: 1, 3, 5, 7 или 9.
Пример нечетных чисел: 3, 1, 7 и 35.
n = 2k + 1 — формула, с помощью которой можно записать любые нечетные числа, где k — целое число.
Сложение и вычитание четных и нечетных чисел
В сложении (или вычитании) четных и нечетных чисел есть некоторая закономерность. Мы представили ее с помощью таблицы, которая находится ниже, для того чтобы вам было проще понять и запомнить материал.
Операция | Результат | Пример |
Четное + Четное | ||
Четное + Нечетное | Нечетное | |
Нечетное + Нечетное |
Четные и нечетные числа будут вести себя так же, если вычитать, а не суммировать их.
Умножение четных и нечетных чисел
При умножении четные и нечетные числа ведут себя закономерно. Вам заранее будет известно, получится результат четным или нечетным. В таблице ниже представлены все возможные варианты для лучшего усвоения информации.
Операция | Результат | Пример |
Четное * Четное | ||
Четное * Нечетное | ||
Нечетное * Нечетное | Нечетное |
А теперь рассмотрим дробные числа.
Десятичная запись числа
Десятичные дроби — это числа со знаменателем 10, 100, 1000 и так далее, которые записаны без знаменателя. Целую часть отделяют от дробной с помощью запятой.
Например: 3,14; 5,1; 6,789 — это все
С десятичными дробями можно производить различные математические действия, такие как сравнение, суммирование, вычитание, умножение и деление.
Если вы хотите сравнять две дроби, сначала уравняйте количество знаков после запятой, приписывая к одному из них нули, а потом, отбросив запятую, сравните их как целые числа. Рассмотрим это на примере. Сравним 5,15 и 5,1. Для начала уравняем дроби: 5,15 и 5,10. Теперь запишем их, как целые числа: 515 и 510, следовательно, первое число больше, чем второе, значит 5,15 больше, чем 5,1.
Если вы хотите суммировать две дроби, следуйте такому простому правилу: начните с конца дроби и суммируйте сначала (например) сотые, потом десятые, затем целые. С помощью этого правила можно легко вычитать и умножать десятичные дроби.
А вот делить дроби нужно как целые числа, в конце отсчитывая, где надо поставить запятую. То есть сначала делите целую часть, а потом — дробную.
Так же десятичные дроби следует округлять. Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Для этого выберите, до какого разряда вы хотите округлить дробь, и замените соответствующее количество цифр нулями. Имейте ввиду, если следующая за этим разрядом цифра лежала в пределах от 5 до 9 включительно, то последнюю цифру, которая осталась, увеличивают на единицу. Если же следующая за этим разрядом цифра лежала в пределах от 1 до 4 включительно, то последнюю оставшуюся не изменяют.
Что означают чётные и нечётные числа в духовной нумерологии. В изучении это очень важная тема! Чем по своей СУТИ чётные числа отличаются от нечётных чисел?
Чётные числа
Общеизвестно, что чётные числа — те, которые делятся на два. То есть, числа 2, 4, 6, 8, 10, 12, 14, 16, 18 и так далее.
А что означают чётные числа относительно ? Какова нумерологическая суть деления на два? А суть в том, что все числа которые делятся на два, несут в себе некоторые свойства двойки.
У несколько значений. Во-первых, это самая «человечная» цифра в нумерологии. То есть, цифра 2 отражает в себе всю гамму человеческих слабостей, недостатков и достоинств — точнее, то, что в обществе принято считать достоинствами и недостатками, «правильностями» и «неправильностями».
А поскольку данные ярлыки «правильности» и «неправильности» отражают наши ограниченные взгляды на мир, то и двойка вправе считаться самым ограниченным, самым «тупым» числом в нумерологии. Отсюда понятно, что чётные числа гораздо более «твердолобы» и прямолинейны, чем их нечётные собратья, которые на два не делятся.
Это, впрочем, не говорит о том, что чётные числа хуже нечётных чисел. Просто они другие и отражают иные формы человеческого бытия и сознания в сравнении с нечётными числами. Чётные числа в духовной нумерологии всегда подчиняются законам обычной, материальной, «земной» логики. Почему?
Потому что другое значение двойки: стандартно-логическое мышление. И все чётные числа в духовной нумерологии так или иначе, подчиняются определённым логическим правилам восприятия действительности.
Элементарный пример: если камень подбросить вверх, он, набрав определённую высоту, устремится затем к земле. Так «думают» чётные числа. А нечётные числа запросто предположат, что камень улетит в космос; или не долетит, а застрянет где-нибудь в воздухе… надолго, на века. Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Или просто растворится! Чем нелогичнее гипотеза, тем ближе она к нечётным числам.
Нечётные числа
Нечётные числа — те, которые не делятся на два: числа 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21 и так далее. С позиции духовной нумерологии нечётные числа подчиняются не материальной, а духовной логике.
Что, кстати, даёт пищу для размышления: почему число цветов в букете для живого человека нечётное, а для мёртвого — чётное… Не потому ли, что материальная логика (логика в рамках «да-нет») мертва относительно души человека?
Видимые совпадения материальной логики и духовной происходят очень часто. Но пусть это не вводит вас в заблуждение. Логика духа, то есть логика нечётных чисел , никогда в полной мере не прослеживается на внешних, физических уровнях человеческого бытия и сознания.
Возьмём для примера — число любви. Мы разглагольствуем о любви на каждом шагу. Мы признаёмся в ней, мечтаем о ней, украшаем ею свою жизнь и чужую жизнь.
Но что на самом деле мы знаем о любви? О той всепроникающей Любви, которая пронизывает собой все сферы Мироздания. Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Разве мы можем согласиться и принять, что в ней столько же холода, сколько и тепла, столько же ненависти, сколько доброты?! В состоянии ли мы осознать, что именно эти парадоксы составляют высшую, творческую суть Любви?!
Парадоксальность — вот одно из ключевых свойств нечётных чисел. В толковании нечётных чисел надо понимать: не всегда то, что кажется человеку, является действительно существующим. Но в то же время, если что-то кому-то кажется, значит оно уже существует. Есть различные уровни Существования, и иллюзия — один из них…
Кстати, зрелость ума характеризуется способностью воспринимать парадоксы. Поэтому для объяснения нечётных чисел требуется чуть больше «мозгов», чем для объяснения чётных чисел.
Чётные и нечётные числа в нумерологии
Подведём итоги. В чём главное отличие чётных чисел от нечётных?
Чётные числа более предсказуемы (кроме числа 10), основательны и последовательны. События и люди, связанные с чётными числами, более устойчивы и объяснимы. Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…
Вполне доступны для внешних изменений, но только для внешних! Внутренние перемены — область нечётных чисел…
Нечётные числа — взбалмошны, свободолюбивы, неустойчивы, непредсказуемы. Они всегда преподносят сюрпризы. Вот вроде и знаешь смысл какого-то нечётного числа, а оно, это число, вдруг начинает вести себя так, что заставляет тебя заново пересмотреть чуть ли не всю твою жизнь…
Обратите внимание!
В магазины уже поступила моя книга под названием «Духовная нумерология. Язык чисел». На сегодняшний день это самое полное и востребованное из всех существующих эзотерических пособий о смысле чисел. Подробнее об этом, а также для заказа книги пройдите по следующей ссылке: ««
———————————————————————————————
Определения
- Чётное число — целое число, которое делится без остатка на 2: …, −4, −2, 0, 2, 4, 6, 8, …
- Нечётное число — целое число, которое не делится без остатка на 2: …, −3, −1, 1, 3, 5, 7, 9, …
В соответствии с этим определением нуль является чётным числом.
Если m чётно, то оно представимо в виде , а если нечётно, то в виде , где .
В разных странах существуют связанные с количеством даримых цветов традиции.
В России и странах СНГ чётное количество цветов принято приносить лишь на похороны умершим. Однако, в случаях, когда в букете много цветов (обычно больше ), чётность или нечётность их количества уже не играет никакой роли.
Например, вполне допустимо подарить юной даме букет из 12 или 14 цветов или срезов кустового цветка, если они имеют множество бутонов , у которых они, в принципе, не подсчитываются.
Тем более это относится к б́ольшему количеству цветов (срезов), даримых в других случаях.
Примечания
Wikimedia Foundation . 2010 .
Смотреть что такое «Чётные и нечётные числа» в других словарях:
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19). … … Википедия
… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19). … … Википедия
… … Википедия
Чётность в теории чисел характеристика целого числа, определяющая его способность делиться нацело на два. Если целое число делится без остатка на два, оно называется чётным (примеры: 2, 28, −8, 40), если нет нечётным (примеры: 1, 3, 75, −19).… … Википедия
Слегка избыточное число, или квазисовершенное число избыточное число, сумма собственных делителей которого на единицу больше самого числа. До настоящего времени не было найдено ни одного слегка избыточного числа. Но со времён Пифагора,… … Википедия
Целые положительные числа, равные сумме всех своих правильных (т. е. меньших этого числа) делителей. Например, числа 6 = 1+2+3 и 28 = 1+2+4+7+14 являются совершенными. Ещё Евклидом (3 в. до н. э.) было указано, что чётные С. ч. можно… …
Целые (0, 1, 2,…) или полуцелые (1/2, 3/2, 5/2,…) числа, определяющие возможные дискретные значения физических величин, которые характеризуют квантовые системы (атомное ядро, атом, молекулу) и отдельные элементарные частицы. … … Большая советская энциклопедия
… … Большая советская энциклопедия
Книги
- Математические лабиринты и ребусы, 20 карточек , Барчан Татьяна Александровна, Самоделко Анна. В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
212. Какое число получится: чётное или нечётное, если нечётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи три примера, подтверждающих твоё предположение.
При делении нечётного числа на нечётное число результат всегда будет нечётным числом.
45 : 5 = 9 55 : 11 = 5 63 : 7 = 9
213.
Какое число получится: чётное или нечётное, если чётное число делить на нечётное число, при условии, что выполнено деление нацело? Приведи несколько примеров, подтверждающих твоё предположение. Обсуди результат с соседом по парте.
При делении чётного числа на нечётное число результат всегда будет чётным числом.
54 : 9 = 6 50 : 5 = 10 96 : 3 = 32
214.
Можешь ли ты привести пример такого случая деления, когда нечётное число делится нацело на чётное число? Почему? Вспомни, как можно получить делимое из делителя и значения частного.
Делимое можно получить, умножив делитель на значение частного. По условию делитель является чётным числом. Мы знаем, что если чётное число умножить на чётное или нечётное число, то результатом будет всегда чётное число. В нашем же случае делимое должно быть нечётным числом. Это означает, что никакое значение частного в этом случае подобрать нельзя и привести пример такого случая деления невозможно.
215.
Представь число 2873 в виде суммы круглых десятков и однозначного числа. Чётным или нечётным числом является каждое из слагаемых? Чётным или нечётным числом будет значение их суммы? На какую цифру может оканчиваться запись чётного числа? А нечётного?
2873 = 2870 + 3
Первое слагаемое – чётное число, второе слагаемое – нечётное число.
2873 – нечётное число.
Нечётное число 2873 заканчивается на нечётную цифру 3, запись чётного числа 2870 — на чётную цифру 0.
Запись чётного числа может оканчиваться чётными цифрами (0, 2, 4, 6, 8), а запись нечётного числа — нечётными числами (1, 3, 5, 7, 9).
216. Выпиши чётные числа в один столбик, а нечётные — в другой.
2844 57893
67586 9231
10050 9929
217.
Сколько существует чётных двузначных натуральных чисел? А сколько таких же нечётных чисел?
Самое маленькое двузначное чётное число 10, а самое большое – нечётное число 99. Всего их 99 – 10 + 1 = 90. Чётные и нечётные числа в натуральном ряду чередуются, поэтому чётных двузначных чисел столько же сколько и нечётных, то есть 45, поскольку 90 : 2 = 45.
218.
Запиши самое большле чётное шестизначное число.
Нечетные числа — определение, список нечетных чисел
Нечетные числа — это числа, которые нельзя расположить парами. Другими словами, все числа, кроме кратных 2, являются нечетными числами. Давайте узнаем больше о нечетных числах в этой статье.
Другими словами, все числа, кроме кратных 2, являются нечетными числами. Давайте узнаем больше о нечетных числах в этой статье.
| 1. | Что такое нечетные числа? |
| 2. | Список нечетных чисел |
| 3. | Свойства нечетных чисел |
| 4. | Типы нечетных чисел |
| 5. | Часто задаваемые вопросы о нечетных номерах |
Что такое нечетные числа?
Нечетные числа — это те числа, которые нельзя разделить на две равные части. Другими словами, нечетные числа — это положительные целые числа, которые нельзя разделить на группы по два. Например: 1, 3, 5, 7 и т. д. Представим это на примере обуви и вишни. Предположим, что у нас есть обувь в количестве 1, 3, 5 и 7. С другой стороны, у нас есть вишни в парах 2, 4, 6 и 8. Обратите внимание на рисунок, приведенный ниже, чтобы понять, как объединение этих чисел работает.
Здесь следует отметить, что нечетное количество обуви не составляет пару целиком. Один среди всех остается непарным. Наоборот, вишни, которые показывают четные числа, — это те числа, которые можно разделить на две части поровну. Например, 4 вишни можно разделить на 2 пары по 2, 8 вишен можно разделить на 4 пары по 2 и так далее.
Список нечетных чисел
Давайте посмотрим на список всех нечетных чисел от 1 до 200 и попробуем применить полученные знания. Обратите внимание, что ни одно из приведенных здесь чисел не кратно 2. Следует также отметить, что из первых 200 чисел только 100 чисел являются нечетными числами. Посмотрите на список нечетных чисел от 1 до 200, приведенный здесь.
| 1 | 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 |
| 21 | 23 | 25 | 27 | 29 | 31 | 33 | 35 | 37 | 39 |
| 41 | 43 | 45 | 47 | 49 | 51 | 53 | 55 | 57 | 59 |
| 61 | 63 | 65 | 67 | 69 | 71 | 73 | 75 | 77 | 79 |
| 81 | 83 | 85 | 87 | 89 | 91 | 93 | 95 | 97 | 99 |
| 101 | 103 | 105 | 107 | 109 | 111 | 113 | 115 | 117 | 119 |
| 121 | 123 | 125 | 127 | 129 | 131 | 133 | 135 | 137 | 139 |
| 141 | 143 | 145 | 147 | 149 | 151 | 153 | 155 | 157 | 159 |
| 161 | 163 | 165 | 167 | 169 | 171 | 173 | 175 | 177 | 179 |
| 181 | 183 | 185 | 187 | 189 | 191 | 193 | 195 | 197 | 199 |
Определение, которое мы узнали выше, применяется в этой таблице и облегчает нашу работу, не так ли? Обратите внимание на данную таблицу и попытайтесь заметить некоторое сходство между всеми этими числами, приведенными выше.
- Вы заметили закономерность в приведенном выше списке нечетных чисел?
- В списке нечетных чисел цифра на месте единиц всегда остается 1, 3, 5, 7 или 9.
Свойства нечетных чисел
В следующих пунктах перечислены свойства нечетных чисел. Каждое из этих свойств можно подробно объяснить, как показано ниже.
- Сложение нечетных чисел : Сложение двух нечетных чисел всегда дает четное число, т. е. сумма двух нечетных чисел всегда является четным числом. Например, 3 (нечетное) + 5 (нечетное) = 8 (четное).
- Вычитание нечетных чисел : Вычитание двух нечетных чисел всегда дает четное число. Например, 7 (нечетное) — 1 (нечетное) = 6 (четное).
- Умножение нечетных чисел : Умножение двух нечетных чисел всегда дает нечетное число. Например, 3 (нечетное) × 7 (нечетное) = 21 (нечетное).
- Деление нечетных чисел : Деление двух нечетных чисел всегда дает нечетное число.
 Например, 33 (нечетное) ÷ 11 (нечетное) = 3 (нечетное).
Например, 33 (нечетное) ÷ 11 (нечетное) = 3 (нечетное).
Подведем итоги изучения свойств нечетных чисел, используя приведенную ниже таблицу.
| Арифметическая операция | Результат |
|---|---|
| Нечетное число + Нечетное число | Четное число |
| Нечетное число — Нечетное число | Четное число |
| Нечетное число × Нечетное число | Нечетное число |
| Нечетное число ÷ Нечетное число | Нечетное число |
Типы нечетных чисел
Нечетные числа — это список всех чисел, не кратных 2. Так что это похоже на обширный набор чисел. Таким образом, у нас может быть много типов нечетных чисел, начиная с того, есть ли у нечетных чисел делители или нет, в чем разница между двумя нечетными числами, каково их положение на числовой прямой и т. д.
д.
Последовательные нечетные числа
Последовательные нечетные числа — это те нечетные числа, которые перечислены в порядке их следования. Например, если n — нечетное число, то числа n и n + 2 относятся к категории последовательных нечетных чисел. Они всегда имеют разницу в 2 между собой и являются последовательными по своей природе, отсюда и название последовательных нечетных чисел. Например, 3 и 5, 11 и 13, 25 и 27, 37 и 39, 49 и 51 и так далее.
Составные нечетные числа
Составные нечетные числа — это те нечетные числа, которые не являются простыми числами. Эти типы нечетных чисел образованы произведением двух меньших положительных нечетных целых чисел. Составные нечетные числа от 1 до 100: 9, 15, 21, 25, 27, 33, 35, 39, 45, 49, 51, 55, 57, 63, 65, 69, 75, 77, 81, 85, 87. , 91, 93, 95 и 99.
Наименьшее нечетное число
Наименьшее нечетное число равно 1, поскольку нечетные числа начинаются с 1 и записываются как 1, 3, 5, 7, 9, 11 и так далее.
Первые десять нечетных чисел
Первые десять нечетных чисел — это 1, 3, 5, 7, 9, 11, 13, 15, 17 и 19.
Наименьшее нечетное составное число
Наименьшее нечетное составное число — 9. самое маленькое составное число это 4, но это четное число. Следующее составное число — 6, которое снова является четным числом. То же самое относится и к следующему составному числу, которое равно 8. Теперь следующее составное число — это 9, которое является нечетным числом. Итак, это подводит нас к наименьшему нечетному составному числу, которое равно 9..
Советы и рекомендации по нечетным числам
Ниже приведен список нескольких советов и рекомендаций по нечетным числам. Это поможет вам быстрее запомнить понятия.
- Сумма двух нечетных чисел всегда является четным числом.
- Простой способ определить, является ли число четным или нечетным, — это разделить его на 2.
- Если число не делится на 2 полностью, в остатке останется 1, что указывает на то, что число является нечетным числом и не может быть разделено на 2 части без остатка.

- Если число полностью делится на 2, в остатке останется 0, что указывает на то, что это четное число и его можно разделить на 2 части поровну.
- В нечетных числах на месте единиц всегда стоят 1, 3, 5, 7 или 9. В четных числах на месте единиц всегда стоят 0, 2, 4, 6 или 8.
☛ Статьи по теме
- Четные числа
- Реальные числа
- Натуральные числа
- целых чисел
- Рациональные числа
- Иррациональные числа
- Подсчет чисел
- Кардинальные числа
- Нечетные числа от 1 до 1000
- Сумма нечетных чисел
- Рабочие листы с четными и нечетными числами
Примеры нечетных чисел
Пример 1: Определить, является ли 135 нечетным числом.
Решение:
Узнать это можно любым из предложенных двух способов:
Способ 1: Проверить цифру на разряде единиц.
 Разряд единиц числа равен 5, что является нечетным числом. Это показывает, что данное число является нечетным числом. Следовательно, 135 — нечетное число.
Разряд единиц числа равен 5, что является нечетным числом. Это показывает, что данное число является нечетным числом. Следовательно, 135 — нечетное число.Способ 2: Нам нужно проверить делимость числа на 2. При делении заданного числа 135 на 2 мы получаем в остатке 1. Это доказывает, что 135 — нечетное число.
Следовательно, мы знаем, что число 135 — нечетное число.
Пример 2: Сложите данные нечетные числа и узнайте, является ли сумма четным или нечетным числом: 57 + 39
Решение:
Сумма данных нечетных чисел равна 96, что является четным количество.
Пример 3 : Укажите истину или ложь относительно нечетных чисел.
а.) Сумма двух нечетных чисел всегда является четным числом.
б.) Наименьшее нечетное число 5.
Решение:
а) Верно, что сумма двух нечетных чисел всегда является четным числом.
b.) Неверно, наименьшее нечетное число равно 1.
перейти к слайдуперейти к слайду
Разложить сложные концепции с помощью простых визуальных средств.
Математика больше не будет сложным предметом, особенно когда вы понимаете концепции с помощью визуализаций.
Запись на бесплатный пробный урок
Практические вопросы по нечетным числам
перейти к слайдуперейти к слайду
Часто задаваемые вопросы о нечетных номерах
Что такое нечетные числа в математике?
В математике нечетные числа — это числа, не кратные 2. Например, 3, 5, 7, 9 и т. д. Нечетные числа не могут быть расположены парами, а значит, их нельзя разделить на две части поровну.
Какие нечетные числа от 1 до 100?
Список нечетных чисел от 1 до 100: 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37, 39, 41, 43, 45, 47, 49, 51, 53, 55, 57, 59, 61, 63, 65, 67, 69 , 71, 73, 75, 77, 79, 81, 83, 85, 87, 89, 91, 93, 95, 97, 99.
В чем разница между нечетным и четным числом?
Числа, которые можно разделить на две части поровну, называются четными числами. Например, 4, 8, 82 и так далее — четные числа. Тогда как нечетные числа не делятся на равные пары и не делятся на 2. Например, 7, 91, 63 и так далее — нечетные числа.
Что такое последовательные нечетные числа?
Два последовательных нечетных числа — это нечетные числа, разница между которыми равна 2. Например, 3 и 5, 11 и 13 и т. д.
Является ли 0 четным или нечетным числом?
0 — четное число, потому что оно кратно 2. Например, 10, 20, 30 40 и т. д. Следовательно, это нечетное число.
Какое среднее значение первых пяти нечетных чисел?
Чтобы найти среднее значение первых пяти нечетных чисел, нам нужно выполнить шаги, перечисленные ниже:
- Шаг 1: Перечислите первые пять нечетных чисел: 1, 3, 5, 7 и 9.
- Шаг 2: вычислить сумму → 1 + 3 + 5 + 7 + 9 = 25.
- Шаг 3: Примените формулу среднего = Среднее любых n чисел = (Сумма n чисел) ÷ n = 25/5 = 5.

Следовательно, среднее первых пяти нечетных чисел равно 5.
Сколько нечетных чисел находится между 36 и 53?
Список нечетных чисел между 36 и 53: 37, 39, 41, 43, 45, 47, 49, и 51. Следовательно, между 36 и 53 всего 8 нечетных чисел.
Является ли число 1 четным или нечетным?
1 — нечетное число, потому что нечетные числа не делятся полностью на 2. Например, 3, 5 и 7 — это несколько нечетных чисел, которые нельзя разделить поровну на группы по 2.
Какое нечетное число идет после 499?
Нечетное число после 499 — это 501. Число после 499 — это 500, то есть четное число. Итак, 501 — это следующее нечетное число после 499..
Что такое формула нечетных чисел?
Формула нечетных чисел выражается как 2n ± 1, где n ∈ W (целые числа). Мы знаем, что нечетное число всегда выражается на 1 меньше или больше, чем четное число. Четное число выражается как 2n, где n — целое число. Следовательно, формула для нечетных чисел выражается следующим образом: Формула для нечетных чисел = 2n ± 1
Какова HCF двух последовательных нечетных чисел?
Наибольший общий делитель (HCF) любых двух последовательных нечетных чисел всегда равен 1. Например, HCF 13 и 15 равен 1.
Например, HCF 13 и 15 равен 1.
Что такое четные и нечетные числа?
Все целые числа можно разделить на две части: четные и нечетные числа. Четные числа — это те, у которых цифра в единицах измерения равна 0, 2, 4, 6 или 8, а нечетные числа — это те, у которых цифра в единицах измерения равна 1, 3, 5, 7 или 9. Примерами четных чисел являются 2. , 4, 6, 8, 10, 12, 14, 16 и т. д., а примеры нечетных чисел: 1, 3, 5, 7, 9, 11, 13, 15, 17 и т. д.
Какое самое маленькое число Нечетное число?
1 — наименьшее нечетное число, потому что список нечетных чисел начинается с 1, 3, 5, 7 и так далее.
Скачать БЕСПЛАТНЫЕ учебные материалы
Рабочие листы по нечетным числам [PDF]
Что такое четные числа? Определение
Четные числа — это те числа, которые можно разделить на две равные группы или пары и которые точно делятся на 2. Например, 2, 4, 6, 8, 10 и так далее. Эти числа можно сгруппировать в равные пары. Однако эту группировку нельзя выполнить для таких чисел, как 5, 7, 9 или 11. Таким образом, 5, 7, 9 или 11 не являются четными числами. Давайте узнаем больше о четных числах и их свойствах на этой странице.
Таким образом, 5, 7, 9 или 11 не являются четными числами. Давайте узнаем больше о четных числах и их свойствах на этой странице.
| 1. | Что такое четные числа? |
| 2. | Нечетные и четные числа |
| 3. | Свойства четных чисел |
| 4. | Часто задаваемые вопросы о четных числах |
Что такое четные числа?
Четное число — это число, кратное 2. Можно сказать, что любое число, которое полностью делится на 2, является четным числом. Это можно понять с помощью примера. Предположим, у Джона 6 мячей. Если он попытается сгруппировать их, он может соединить все 6 шаров и сформировать 3 пары. Нет шаров, которые остались непарными. Следовательно, он может сделать вывод, что 6 — четное число. Теперь разделим 6 на 2. Получим частное 3, равное количеству образовавшихся пар. Получаем остаток как 0, что равно количеству шаров, которые нельзя спарить. Всякий раз, когда Джон пытается соединить четное количество мячей, он останется без мяча. Другими словами, всякий раз, когда четное число делится на 2, мы всегда получаем в остатке 0,9.0005
Получаем остаток как 0, что равно количеству шаров, которые нельзя спарить. Всякий раз, когда Джон пытается соединить четное количество мячей, он останется без мяча. Другими словами, всякий раз, когда четное число делится на 2, мы всегда получаем в остатке 0,9.0005
Нечетные и четные числа
Целые числа можно разделить на четные и нечетные. Нечетные числа — это те числа, которые не делятся полностью на 2. Тогда как четные числа полностью делятся на 2. Пройдемся по списку всех четных чисел от одной до двухсот. Обратите внимание на числа, указанные ниже. Сможете ли вы найти закономерность или связь между всеми четными числами от одного до двухсот?
| Список четных чисел (1-200) | ||||
|---|---|---|---|---|
| 2 | 4 | 6 | 8 | 10 |
| 12 | 14 | 16 | 18 | 20 |
| 22 | 24 | 26 | 28 | 30 |
| 32 | 34 | 36 | 38 | 40 |
| 42 | 44 | 46 | 48 | 50 |
| 52 | 54 | 56 | 58 | 60 |
| 62 | 64 | 66 | 68 | 70 |
| 72 | 74 | 76 | 78 | 80 |
| 82 | 84 | 86 | 88 | 90 |
| 92 | 94 | 96 | 98 | 100 |
| 102 | 104 | 106 | 108 | 110 |
| 112 | 114 | 116 | 118 | 120 |
| 122 | 124 | 126 | 128 | 130 |
| 132 | 134 | 136 | 138 | 140 |
| 142 | 144 | 146 | 148 | 150 |
| 152 | 154 | 156 | 158 | 160 |
| 162 | 164 | 166 | 168 | 170 |
| 172 | 174 | 176 | 178 | 180 |
| 182 | 184 | 186 | 188 | 190 |
| 192 | 194 | 196 | 198 | 200 |
Выполним сложение различных комбинаций четных и нечетных чисел и посмотрим на результаты. Мы увидим, как числа изменяются от нечетных к четным, когда нечетные и четные числа складываются друг с другом. Записывайте полученные результаты.
Мы увидим, как числа изменяются от нечетных к четным, когда нечетные и четные числа складываются друг с другом. Записывайте полученные результаты.
| Номер 1 | Номер 2 | Число 1 + Число 2 = Сумма |
|---|---|---|
| 4 [четный] | 8 [четный] | 4 + 8 = 12 [четное] |
| 7 [Нечетный] | 3 [Нечетный] | 7 + 3 = 10 [четное] |
| 1 [Нечетный] | 6 [четный] | 1 + 6 = 7 [Нечетное] |
| 2 [четный] | 9 [Нечетный] | 2 + 9 = 11 [Нечетное] |
Подведем итоги.
Последовательные четные числа
Последовательные числа могут быть указаны как 2, 4, 6, 8, 10, 12, 14 и т. д. Последовательные числа — это те числа, которые непрерывно следуют друг за другом в порядке от наименьшего числа к наибольшему. Например, 1, 2, 3, 4 и т. д. — последовательные натуральные числа. Итак, когда нам нужно перечислить последовательные четные числа, мы можем перечислить все четные числа в порядке от наименьшего числа до наибольшего числа. Например, 2, 4, 6, 8, 10, 12, 14 и так далее — последовательные четные числа.
Например, 1, 2, 3, 4 и т. д. — последовательные натуральные числа. Итак, когда нам нужно перечислить последовательные четные числа, мы можем перечислить все четные числа в порядке от наименьшего числа до наибольшего числа. Например, 2, 4, 6, 8, 10, 12, 14 и так далее — последовательные четные числа.
Четные натуральные числа
Четные натуральные числа могут быть указаны как 66, 24, 8, 100 и т. д. Четные числа — это те числа, которые делятся на 2, а натуральные числа — это счетные числа, начинающиеся с 1, 2, 3, 4, 5 и так далее. Итак, если мы выберем все четные числа из списка натуральных чисел, они будут называться четными натуральными числами.
Свойства четных чисел
Давайте посмотрим на различные свойства чисел, такие как сложение, умножение и вычитание, и на то, как ведет себя четное число в таких случаях:
Свойство сложения четных чисел
- Сумма двух четных чисел является четным числом. Например, 14 + 8 = 22 .
- Сумма четного числа и нечетного числа является нечетным числом. Например, 8 + 9 = 17 .
- Сумма двух нечетных чисел является четным числом. Например, 13 + 7 = 20 .

Свойство вычитания четных чисел
- Разница между двумя четными числами является четным числом. Например, 42 — 8 = 34
- Разница между четным числом и нечетным числом является нечетным числом. Например, 22 — 7 = 15 .
- Разница между двумя нечетными числами является четным числом. Например, 35 — 15 = 20 .
Свойство умножения четных чисел
- Произведение двух четных чисел является четным числом. Например, 12 × 4 = 48 .
- Произведение четного числа на нечетное число равно четному числу. Например, 8 × 5 = 40 9029.6
Четные простые числа
Существует только одно четное простое число, равное 2. Все остальные четные числа имеют делители, отличные от 1 и самого числа. Например, множители числа 4 равны 1, 2 и 4. Следовательно, существует только одно четное простое число, равное 2.
☛Статьи по теме
- Составные номера
- Нечетные числа
- Реальные числа
- Натуральные числа
- Целые числа
- Иррациональные числа
- Подсчет чисел
- Кардинальные числа
- Четные и нечетные числа
- Сумма четных чисел
- Четные числа от 1 до 100
- Четные числа от 1 до 1000
- Рабочие листы с четными и нечетными числами
- Рациональные числа
Часто задаваемые вопросы о четных числах
Что такое четные числа в математике?
Числа, которые полностью делятся на 2, называются четными числами . Эти числа при делении на 2 оставляют 0 в остатке. Например, 2, 4, 6, 8 и так далее — четные числа.
Какие четные числа от 1 до 100?
Список четных чисел от 1 до 100 выглядит следующим образом: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36 , 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70,72, 74, 76, 78, 80, 82, 84, 86 , 88, 90, 92, 94, 96, 98, 100.
Какое самое маленькое четное число?
2 — наименьшее четное число. Это также единственное четное простое число.
Все ли четные числа натуральные?
Да, все четные числа, которые полностью делятся на 2, тоже натуральные числа. Например, 14, 18, 22, 24 и т. д.
Что такое формула четных чисел?
Поскольку каждое четное число кратно 2, его формула задается как n = 2k, где ‘k’ — целое число. Если мы заменим «k» на любое число, мы получим четное число. Например, если «k» заменить на 3 в 2k, (2 × 3) = 6. Мы получим 6, которое является четным числом.
Является ли 0 четным или нечетным числом?
Любое число, которое можно разделить на два, чтобы получить еще одно целое число, считается четным. Ноль также является одним из них, потому что когда 0 делится на 2, он дает остаток 0, что означает, что 0 делится на 2. Следовательно, 0 — четное число.
Почему 4 четное число?
Поскольку 4 кратно 2 и может быть разделено на две равные группы, это четное число. Другими словами, это четное число, потому что оно полностью делится на 2.
Другими словами, это четное число, потому что оно полностью делится на 2.
В чем разница между нечетными и четными числами?
Четное число — это число, кратное 2. Например, тогда как нечетное число не кратно 2.
Что такое HCF двух последовательных четных чисел?
HCF двух последовательных четных чисел равен 2. Наибольший общий делитель (HCF) любых двух чисел является их наибольшим общим делителем. Например, 16 и 18 — два последовательных четных числа, и их HCF равен 2.
Как найти четное число?
Чтобы найти четное число, мы должны разделить данное число на 2. Если оно полностью делится на 2 без остатка, то это четное число. Если данное число не делится полностью на 2, то это нечетное число.
Какие четные числа меньше 10?
Четные числа меньше 10 могут быть записаны как 2, 4, 6 и 8. Эти числа полностью делятся на 2 без остатка.
Что такое четные составные числа?
Четные числа — это числа, которые полностью делятся на 2. Например, 2, 4, 6, 8, 10 и т. д. — четные числа. Составные числа — это те числа, у которых делители больше 1 и само число. Например, 4, 6, 9, 15 и так далее. Мы знаем, что все четные числа, кроме 2, имеют делители больше 1 и самого числа. Интересно, что 2 — единственное четное число, которое считается простым числом. Следовательно, кроме 2, все четные числа являются составными числами. Например, 4, 6, 8, 10, 12, 14 и так далее — четные составные числа. Это также показывает, что наименьшее четное составное число равно 4.
Например, 2, 4, 6, 8, 10 и т. д. — четные числа. Составные числа — это те числа, у которых делители больше 1 и само число. Например, 4, 6, 9, 15 и так далее. Мы знаем, что все четные числа, кроме 2, имеют делители больше 1 и самого числа. Интересно, что 2 — единственное четное число, которое считается простым числом. Следовательно, кроме 2, все четные числа являются составными числами. Например, 4, 6, 8, 10, 12, 14 и так далее — четные составные числа. Это также показывает, что наименьшее четное составное число равно 4.
Какое самое большое четырехзначное четное число?
Самое большое 4-значное четное число — 9998. Мы знаем, что самое большое 4-значное число — 9999, значит, первое четное число после этого — 9998.
Какова сумма двух последовательных четных чисел?
Сумма двух последовательных четных чисел всегда является четным числом. Например, 4 + 16 = 20 или 66 + 12 = 78 и так далее.
Четная или нечетная неделя? Определить, четная или нечетная неделя в 2022 году, Великобритания
Эта нечетная неделя имеет номер 37
Календарь этой недели ↓| Пн | ВтWed | Thu | Fri | Sat | Sun | ||
|---|---|---|---|---|---|---|---|
52. even even | 1 | 2 | |||||
| 1. odd | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 2. even | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 3. odd | 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 4. even | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 5. odd | 31 | ||||||
| Mon | Tue | Wed | Thu | Fri | Sat | Sun | |
|---|---|---|---|---|---|---|---|
5. odd odd | 1 | 2 | 3 | 4 | 5 | 6 | |
| 6. even | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 7. odd | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 8. even | 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 9. odd | 28 | ||||||
| Mon | Tue | Wed | Thu | Fri | Sat | Sun | ||||
|---|---|---|---|---|---|---|---|---|---|---|
9. odd odd | 1 | 2 | 3 | 4 | 5 | 6 | ||||
| 10. даже | 7 | 8 | 10 | 11 | 12 | 13 | ||||
| 11. ODD | 111 11. ODD | 9 | 11 11. ODD | 9 161111111111. | 19 | 20 | ||||
| 12. even | 21 | 22 | 23 | 24 | 25 | 26 | 27 | |||
| 13. odd | 28 | 29 | 30 | 31 | ||||||
| Mon | Tue | Wed | Thu | Fri | Sat | Sun | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
13. odd odd | 1 | 2 | 3 | |||||||||||||||||||
| 14. даже | 4 | 5 | 6 | 7 | 8 | 8 | 8 | 0013 | ||||||||||||||
| 15. odd | 11 | 12 | 13 | 14 | 15 | 16 | 17 | |||||||||||||||
| 16. even | 18 | 19 | 20 | 21 | 22 | 23 | 24 | |||||||||||||||
17. odd odd | 25 | 26 | 27 | 28 | 29 | 30 | ||||||||||||||||
| Mon | Tue | Wed | Thu | Fri | Sat | Sun | |
|---|---|---|---|---|---|---|---|
| 17. odd | 1 | ||||||
| 18. even | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 19. odd | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 20. even | 16 | 17 | 18 | 19 | 20 | 21 | 22 |
21. odd odd | 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 22. even | 30 | 31 | |||||
| Mon | Tue | Wed | Thu | Fri | Sat | Sun | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 22. even | 1 | 2 | 3 | 4 | 5 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 23. odd | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 24. even | 13 | 14 | 15 | 16 | 17 | 18 | 19 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.
Четные и нечетные числа Число может быть четным или нечетным. Четные числа — это числа, оканчивающиеся на 0, 2, 4, 6 или 8, и нечетные числа, оканчивающиеся на 1, 3, 5, 7 или 9. Четные и нечетные числа Что такое четные и нечетные числа?Если у вас когда-либо возникал этот вопрос или вы не понимаете, что он означает, вам нужно знать, что число может быть четным или нечетным. Четные числа — это те, которые делятся на 2. То есть, если мы делим число на 2, а остаток от деления равен нулю, это четное число. Число считается нечетным, если оно не делится на 2, то есть если мы делим это число на 2 и получаем остаток, равный 1. В статье ниже см. таблицы четных и нечетных чисел. Свойства четных и нечетных чисел
Четное числоЧисло классифицируется как четное, если оно делится на 2, то есть если мы можем разделить его на две равные части. Например, если есть 6 шариков, их можно разделить между двумя людьми так, чтобы не осталось ни одного, оставив 3 шарика одному человеку и 3 другому. Значит 6 четное число. Пример с четными числами В общем случае четным считается число, единица измерения которого равна 0, 2, 4, 6 или 8. Число 534 четное, так как его единицей измерения является 4. Четные числа меньше 100См. ниже все четные числа меньше 100. Четные числа меньше 100 Нечетные числанечетным, если оно не делится на 2. То есть, разделив это число на 2, мы найдем остаток, равный 1. Например, если мы собираемся разделить 11 шариков между двумя людьми, мы дадим каждому по 5 шариков, и останется 1 шарик. Пример нечетных чисел В общем случае нечетным числом является число, единица которого равна 1, 3, 5, 7 или 9. Смотреть: Число 245 нечетное, так как его единицей измерения является 5. Число 2024 не нечетное, так как его единица измерения равна 4. Нечетные числа меньше 100См. ниже все нечетные числа меньше 100. Нечетные числа меньше 100 Решенные примеры Q1. Ответ: Когда мы складываем нечетные числа два на два, мы находим два четных числа. Когда мы сложим эти два четных числа вместе, мы найдем четное число. Следовательно, сумма четырех нечетных чисел равна четному числу, так как сумма двух нечетных чисел является четным числом, а сумма двух четных чисел является четным числом. Q2. Матеус живет в третьей квартире на 26 этаже дома. Чтобы поговорить с Матеусом, швейцар звонит по номеру 2603, это квартира Матеуса. Анализируя это число, оно четное или нечетное? Ответ: Число 2603 нечетное. Чтобы узнать, нечетное ли оно, просто посмотрите на единицу разряда этого числа, которая равна 3. Числа, оканчивающиеся на 3, всегда нечетные. Самостоятельная практикаQ1. Что такое наименьшее положительное четное число и нечетное число? Ответ: Наименьшие положительные числа, четные и нечетные, равны 2 и 1 соответственно. Q2. Напишите все четные числа от 1 до 50. Ответы: 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50. Советы по четным и нечетным числам, которые помогут учащимся выучить
РезюмеВ статье рассказывается о том, что такое нечетные и четные числа. Четные числа — это те, у которых число два является кратным или, что то же самое, у которых есть совершенная половина. Если мы возьмем четное число и разделим его пополам, то получим две равные части. Это означает, что все четные числа имеют две равные половины. С другой стороны, нечетные числа — это те, которые не имеют равных половин, то есть если их разделить на два, то одна часть будет больше другой, или в их счету будут десятичные дроби. Правила действий для нечетных и четных чиселСформулируем правила сложения, вычитания, умножения и деления четных и нечетных чисел. Вот правила сложения/вычитания четных и нечетных чисел: Чет ± Чет = Чет (например, 2 + 2 = 4; -4 – 2 = -6) Нечетное ± Нечетное = Четное (например, 1 + 1 = 2; -31 – 1 = -32) Четное ± Нечетное = Нечетное (например, 2 + 1 = 3; -12 – 1 = -13) Есть некоторые очень важные наблюдения здесь. Если вы прибавите или вычтете любое количество четных чисел, результат всегда будет четным. Например, -2 + 8 + 20 – 16 = 10 (четное) -2 + 8 + 20 – 16 + 8 – 18 – 2 = -2 (четное) Это можно обобщить как Четный ± Четный ± Четный ….± Четный …. ± четный = всегда четный Если вы прибавите или вычтете нечетное «количество» нечетных чисел, результат всегда будет нечетным. Например, Если вы сложите или вычтете пять (нечетное «количество») нечетных чисел, например 3 + 11 – 19 + 7 + 9 = 11, ответ будет нечетным Аналогично, если вы сложите или вычтете три (нечетное «количество») ‘количество’) нечетные числа, например 3 + 5 – 17 = -9, ответ будет нечетным Однако, если вы прибавите или вычтете четное «количество» нечетных чисел, результат всегда будет четным. Например, Если вы прибавите или вычтете шесть (четное «количество») нечетных чисел, например 3 + 11 – 19 + 7 + 3 + 1 = 6, ответ будет четным. Если вы прибавите или вычтете четыре (четное «количество») нечетных числа, например 3 + 5 – 17 + 7 = -2, ответ будет четным. Это можно обобщить как Нечетное ± Нечетное ± Нечетное ….± Нечетное …. ± Нечетное = Нечетное или Четное (в зависимости от «количества» нечетных чисел, которые добавляются или вычитаются) Вот правила умножения четных и нечетных чисел: Четное × Четное = Четное (например, 2 × 2 = 4) Четное × Нечетное = Четное (например, -2 × 3 = -6) Нечетное × Нечетное = Нечетное (например, 5 × 3 = 15) Опять же, есть несколько очень важных замечаний. Четное число любое другое целое число (четное или нечетное) всегда получается четным. Произведение чисел может быть нечетным только в том случае, если все эти числа нечетны. Например, -2 × 9 × 3 = -54 (четное) 4 × 1 × 3 × 15 × 21 × 33 = 124 740 (четное) Это можно обобщить как Четное × Любое целое число × Любое целое число × Любое целое число…. Нечетное × Нечетное × Нечетное × Нечетное …. × Нечетный ×…. Нечетное = всегда нечетное Вот правила деления четных и нечетных чисел: Четное ÷ четное = четное или нечетное или дробное (например, 100 ÷ 2 = 50, -14 ÷ 2 = -7, 2 ÷ 10 = 0,2) Четный ÷ Нечетный = Четный или дробный (например, 10 ÷ 5 = 2, -20 ÷ 3 = -6,6) Нечетный ÷ Нечетный = Нечетный или дробный (например, 15 ÷ 5 = 3, 9 ÷ 5 = 1,8) Нечетное ÷ Четное = дробь (например, 15 ÷ 2 = 7,5, 21 ÷ 4 = 5,25) Это приводит нас к следующим правилам деления четных и нечетных чисел: При делении четных и нечетных чисел существует множество возможностей. Если есть одно общее правило, которое можно использовать для конкретного случая деления, то оно следующее: Чет/Нечет=Дробь Как и у большинства людей, сдающих GRE, ваши знания по математике могут быть немного заржаветыми. Хорошей новостью является то, что GRE проверяет вас только по математике, которую вы уже выучили в старшей школе. подробнее Стандартное отклонение – важный статистический термин, проверенный на GRE. Это дает вам представление об отклонении или разбросе набора чисел от его среднего значения; следовательно, низкое стандартное отклонение означает, что числа очень близки к среднему, и наоборот…. читать далее Каждое целое число больше 1 является либо простым, либо составным числом. Все составные числа можно представить в виде произведения простых чисел. Например, 6 можно выразить как 2 × 3. Простые делители числа 6 — это 2 и 3. Тогда как выражение 2 × 3 называется… подробнее Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет 100? Настройте диаграмму: 100 Левая колонка Правая колонка 1 100 2 50 4 25 5 20 10 10 Помните правило: как только факторы повторяются (например, 10 и 10), остановитесь. подробнее Вы уже видели прекрасную таблицу множителей — простой способ найти все множители целого числа. Давайте посмотрим, как мы используем диаграмму, чтобы ответить на этот вопрос: сколько положительных факторов имеет число 140? Вопрос касается факторов, поэтому таблица факторов… подробнее Некоторые целочисленные вопросы могут потребовать от вас найти множители целого числа. Таблица множителей — это основной метод нахождения всех множителей любого целого числа. Этот метод также может быть полезен для вопросов о том, сколько множителей имеет конкретное целое число. Техника… подробнее Простые числа играют центральную роль в целочисленных вопросах. Излишняя самоуверенность здесь опасна: в то время как почти каждый может без труда назвать определение простого числа, поле на самом деле изобилует неправильными представлениями. Мы здесь, чтобы убедиться, что вы знаете все. подробнее Начнем с основных определений: Четное: любое целое число, которое делится на 2. Примеры: 2, 4, 14. Нечетное: любое целое число, которое не делится на 2, т. е. оставляет в остатке 1 при делении на 2. Примеры: 1, 3, 5, 7, 9 Пока все хорошо. Рассмотрите этот потенциал… подробнее Найдите остаток от деления 5 142 376 298 на 9? Метод длинного деления точно скажет вам остаток от деления 5 142 376,29.8 на 9, но вы можете себе представить, сколько времени это займет. Хорошая новость заключается в том, что, как и делимость… читать дальше Делится ли 5 142 376 298 на 3? Калькулятор не помешал бы в этом вопросе. К сожалению, калькулятор отображает до восьми цифр. Если число больше восьми цифр, то будет отображаться ERROR. Так как 5 142 376 298 больше, чем восьмерка… читать дальше Четные или нечетные числаФильтр 3 1 класс 4 2 класс 5 3 класс 6 4 класс Сортировка: НовыеСтарыеНазвания (Z — A)Имя (A — Z)Цена (Высокая > Низкая)Цена (Низкая > Высокая) Показать: 15255075100 $4,50 Сортировка четных и нечетных чисел по программе Curriculum for Autism Нечетные или четные числа 1–100 Сортировка для учащихся с аутизмом и особыми образовательными потребностями. )… Уровни классов: 1-й класс, 2-й класс, 3-й класс Цели IEP: Имея до 10 однозначных или двузначных чисел для сортировки, СТУДЕНТ будет сортировать числа по нечетным или четным с точностью 80%, в 4 из 5 возможностей, МЕСЯЦ, ГОД. $3.00 Счет двойками | Группировка по 2 с НЕЧЕТНЫМ количеством объектов TASK BOX FILLER ACTIVITIES by AutismEducators Счет двойками и группировка по 2 с нечетным числом объектов КАРТОЧКА С ЗАДАНИЯМИ набор Task Box Filler для использования в качестве ресурса для раннего вмешательства по математике в вашем классе специального образования, математическом центре или для учащихся, которые переходят в класс общего образования для обучения математике. Уровни классов: 2-й класс, 3-й класс, 4-й класс Цели IEP: Учитывая НЕЧЕТНОЕ количество объектов до 20, (24) СТУДЕНТ сгруппирует объекты попарно и отметит/назовет правильный количество подсчитанных пар с точностью 80% в 4 из 5 возможностей, по МЕСЯЦАМ, ГОДАМ. $3.00 Счет двойками | Группировка по 2 с объектами | Действия по заполнению ящика задач by AutismEducators Счет двойками путем группировки по 2 с предметами КАРТОЧКИ С ЗАДАЧАМИ — задание для заполнения математических навыков. Считайте с помощью изображений предметов, чтобы научиться считать до 2, пропустите счет до 2 или сгруппируйте по 2 для расширенного счета для навыков умножения. Это сопряжение объектов из двух наборов карточек с заданиями соответствует государственным академическим стандартам. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||


 В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…
В наборе: 10 ребусов и 10 математических лабиринтов на темы: — Числовой ряд; — Чётные и нечётные числа; — Состав числа; — Счёт парами; — Упражнения на сложение и вычитание. В комплекте 20…