29 римскими цифрами: 29 римскими цифрами — Calculatio

Как вычислять с римскими цифрами? Способы из книги о средневековой науке

Фрагменты новых книг

© Издательство «Альпина нон-фикшн»

В издательстве «Альпина нон-фикшн» выходит книга историка-медиевиста Себа Фалька «Светлые века». ТАСС публикует отрывок об арифметических операциях с римскими цифрами

Еще в эпоху Возрождения о Средних веках сложилось предубеждение как о времени темном. В «Светлых веках: Путешествии в мир средневековой науки» Себ Фальк его оспаривает. Проводником в этом путешествии служит упомянутый в отрывке английский монах Джон Вествик. Через его биографию Фальк показывает интеллектуальный ландшафт тех времен — как выясняется, совсем не пустынный.

В 1396 году монахи Сент-Олбанса наконец исправили несправедливость длиной в две сотни лет, учиненную Джеффри Горэмом. Когда Джон Вествик родился, поместье Уэствик принадлежало графу Оксфорду, фавориту Ричарда II, но в 1388 году Безжалостный парламент осудил графа Роберта за измену и конфисковал его владения. Восемь лет спустя аббат Сент-Олбанса сговорился о покупке Уэствик-Горэма за 900 марок. Чтобы собрать такую внушительную сумму, пришлось скидываться, и хронист аббатства записал имена монахов и других благодетелей, которые внесли свою лепту. Он аккуратно отметил, какую сумму выделил каждый, — с помощью римских цифр:

«Предмет: получено в порядке дарения от братии и прочих как вспомоществование для покупки владения Уэствик, как то: в дар от владыки Николаса из Редклифа, архидьякона, XL марок. В дар от господина Роджера Хенрида, ризничего, VI фунтов XIII шиллингов IIII пенса. В дар от Томаса Сайдона, слуги аббата, VI фунтов XIII шиллингов IIII пенса…»

Список содержит имена 15 жертвователей и завершается следующими строками:

«В дар от Роберта Транча XI шиллингов & VIII пенсов. Итого: L фунтов II шиллинга VIII пенсов».

Здесь римские цифры используются вперемешку с чем-то довольно близким к позиционной системе счисления: фунтами, шиллингами и пенсами. (Вавилонская позиционная система счисления сложилась на базе единиц такого же типа, приспособившись к измеряемой величине.) В шиллинге было 12 пенсов, а в фунте — 20 шиллингов. Задача усложнялась тем, что деньги считали еще и в марках: одна марка составляла 2/3 фунта, или 13 шиллингов 4 пенса. Николас из Редклифа пожертвовал 40 марок, да и Роджер Хенрид и Томас Сайдон вряд ли намеревались внести в копилку непонятные 6 фунтов, 13 шиллингов и 4 пенса, а скорее всего, выделили круглую сумму в 10 марок. Хронист аббатства суммировал все эти марки, фунты, шиллинги и пенсы и пришел к верному результату (записав его римскими цифрами): 50 фунтов 2 шиллинга и 8 пенсов.

Если такие вычисления кажутся вам каким-то арифметическим подвигом, учтите, что до денежных реформ 1960-х и 1970-х годов школьникам всей бывшей Британской империи приходилось учиться складывать и вычитать двенадцатые и двадцатые доли фунтов, шиллингов и пенсов. (Чуть ли не весь остальной мир перешел на десятичную денежную систему еще в XIX веке. ) Если немного попрактиковаться, сложению и вычитанию римских чисел тоже нетрудно научиться. Для начала можно представить себе X, десятку, как единицу — I, перечеркнутую линией, обозначающей, что перед нами сумма десяти таких единиц. V (пятерка) — это десятка (X), разделенная пополам горизонтально. Элементарное сложение, например VII + XVIII, нетрудно выполнить, записав все цифры рядом и переставив их для удобства местами: VIIXVIII превращается в XVVIIIII, а отсюда легко прийти к верному результату: XXV.

На эту тему

На самом деле подобные примеры можно решать и в уме. Для вычислений посложнее римские цифры переводили в более гибкий формат. В своем знаменитом трактате «Об исчислении времен» живший в VIII веке монах из Нортумбрии Беда Достопочтенный — выдающийся энциклопедист — знакомит читателя с двумя способами сделать это: греческая алфавитная система и метод, который он называл «очень полезным и простым умением счета на пальцах».

Как Беда и другие монахи считали на пальцах в десятичной системе? Вытяните руки перед собой, ладонями от лица. Начинать следует слева, с трех крайних пальцев левой руки. Эти три пальца, выпрямленные или полностью либо частично согнутые, показывают единицы от 1 до 9. Вот почему целые числа назывались digiti, что на латыни означает «пальцы»; отсюда и название цифровых технологий (digital). Степени десяти отсчитывали, по-разному сгибая и скрещивая большой и указательный пальцы (латинское слово «десять» — articuli — означает «костяшки»). За сотни отвечали большой и указательный пальцы правой руки, а за тысячи — средний, безымянный и мизинец. Таким образом, пальцами можно было показать любое число от 0 до 9999. Пальцам присваивалось конкретное разрядное значение — тысячам, сотням, десяткам и единицам было выделено определенное место, поэтому сложение и вычитание больших чисел трудности не представляли, более того, этим способом можно было даже решать простейшие примеры на умножение.

Самые маленькие числа откладывали на пальцах левой руки, и тому было две причины. Во-первых, в этом случае человек, который стоит к вам лицом, читает число как полагается, то есть слева направо. Жестовая арифметика служила не только для счета, но и для коммуникации. Жесты использовали на рынках, где шум и языковой барьер могли помешать разговору, или в монастырях, где нужно было соблюдать тишину. Беда даже предлагал использовать их в качестве алфавитно-цифрового кода, позволяющего передавать тайные сообщения. Во-вторых, если вы в своих вычислениях не выходите за сотню, правая рука остается свободной, и ею можно делать заметки, куда-то указывать или что-то в ней держать. Изумительно практичная система Беды пришла прямиком из классных комнат, где монахи учились использовать руки для запоминания музыкальной грамоты и определения дат или дней солнечного и лунного циклов.

Для простых вычислений было вполне достаточно пальцев, а вот для сложных использовали calculi — камешки или фишки. Джон Вествик учился работать с числами и наверняка мастерски пользовался абаком — счетной доской. Размещение камешков на расчерченной линиями доске представляло собой разложение числа на разряды. Некоторые разновидности абаков позволяли добавить промежуточную позицию для пяти единиц, пяти десятков, пяти сотен и так далее, и тогда фишек для счета требовалось меньше. В других разновидностях сами фишки были пронумерованы цифрами от 1 до 9, и тогда абак был просто рамкой, разделяющей разряды единиц, десятков, сотен и так далее. Монахи рисовали такие рамки в книгах и манускриптах, расчерчивая их на столбцы, которые часто стилизовали под колоннады своей обители, и раскладывали там счетные фишки. В промежутки между колонками они вписывали свои вычисления.

На эту тему

Абаками активно пользовались вплоть до Нового времени, несмотря на широкое распространение других, более совершенных техник счета. В сочинении «Жемчужина философии», популярнейшем учебнике, написанном картезианским монахом Грегором Рейшем и выдержавшем в XVI веке 12 изданий, раздел, посвященный арифметике, начинается с гравюры, иллюстрирующей два подхода к предмету). Слева — Боэций, позднеримский теоретик свободных искусств. Еще один энциклопедист (для средневековой науки всесторонне одаренные люди не редкость), Боэций писал труды по логике, музыке и арифметике, но наибольшую известность ему принесло «Утешение философией», размышление о природе человека. Книга оставила глубокий след в веках: только на английский язык ее переводили Альфред Великий, Джеффри Чосер и Елизавета I. В этом сочинении Боэций, как многие астрономы до и после него, размышлял о необъятности Вселенной, космически малой величине Земли и холоде далеких звезд. Его присутствие на гравюре напоминает читателям, что математика — нечто большее, чем абстрактные величины.

Справа на гравюре изображена фигура равной значимости: это Пифагор. Великий греческий философ выкладывает на счетной доске числа 1241 и 82. Самая дальняя от него линия — это тысячи, следующая — сотни, и так далее, но обратите внимание: между линиями десятков и сотен выделено место для полусотен. Боэций же демонстрирует индо-арабские цифры и их преимущества для записи дробей. Между ними стоит госпожа Арифметика, ее платье украшено степенями двойки и тройки. Хотя в конечном итоге индо-арабские цифры, для операций с которыми достаточно было пера и бумаги, победили (чем они в значительной степени обязаны появлению бухгалтерского учета и сложных банковских операций), счетные доски благодаря своей бесспорной универсальности продолжали применяться и в Новое время. В умелых руках они не уступают электронным калькуляторам. В 1946 году в Токио состоялось захватывающее публичное состязание между японским абацистом и американцем, считавшим на калькуляторе. Победу одержал абацист, который в решении серии сложных математических задач продемонстрировал как невероятную скорость, так и высокую точность вычислений.

На эту тему

Менее опытным пользователям счетная доска могла пригодиться для записи промежуточных результатов вычислений. Средневековые математики знали множество способов упростить вычисления, разбивая задачу на серию операций, которые можно было произвести в уме или с помощью абака. Джон Вествик наверняка владел какими-то из них. Один способ, который называют по-разному: умножением по методу русских крестьян или египетским методом, был придуман независимо в нескольких странах, и ему вполне могли обучать и в Сент-Олбанской школе. Он сводит объемные и сложные примеры на умножение и деление к серии удвоений и делений пополам. Популярность этого метода может объяснить, почему в первых учебниках арифметики, использующей новые индо-арабские цифры, умножению и делению числа на два учили как отдельным операциям — чему-то среднему между сложением и умножением.

Красота метода удвоения и деления пополам — в том, что единственное, что вам нужно знать, — это как прибавить число к самому себе. Пусть вам нужно умножить 43 на 13. Запишите эти числа рядом и начинайте удваивать большее и делить пополам меньшее (отбрасывая остаток). Вот что у вас получится:

43          13

86          6 (отбрасываем остаток)

172        3

344        1 (отбрасываем остаток)

Когда разделить на два больше не получается, вычеркните строчки, в которых число в колонке деления четное (в нашем случае это 86; 6), и сложите числа, оставшиеся в первой колонке. У вас получится 43 х 13 = 43 + 172 + 344 = 559. Немного попрактиковавшись, можно научиться считать очень быстро — и, так как здесь используется устный счет, провернуть этот номер с римскими цифрами не труднее, чем с индо-арабскими. Метод работает, потому что основывается на том, что любое число можно разложить на степени двойки. Например, 43 х 13 = 43 х (1 + 4 + 8).

Мы оставляем только ряды с нечетными числами в колонке деления, потому что именно здесь мы «теряем» остаток, который нужно было бы прибавить в конце. Если вы умножаете на число, которое представляет собой степень двойки (например, 8), остатки не теряются: вы вычеркнете все строки, кроме последней, поскольку умножение на 8 представляет собой простую серию удвоений.

Продолжение

То же и с делением. Скажем, вы хотите разделить 729 на 34 (или DCCXXIX на XXXIV). Просто удваивайте 34 до тех пор, пока не сможете сделать это, не переходя за 729:

XXXIV (1)

LXVIII (2)

CXXXVI (4)

CCLXXII (8)

DXLIV (16) (Удваивать 544 мы не будем, чтобы не перейти за 729. )

Теперь, начиная с нижней линии, складывайте числа (выбирая большие), чтобы подобраться как можно ближе к 729 (придется немного попрактиковаться). Когда вы это сделаете, суммируйте степени двойки, указанные рядом с вашими слагаемыми, и получите ответ. Например:

DXLIV (ряд 16) + СXXXVI (ряд 4) + XXXIV (ряд 1) = DCCXIV.

Итак, 729 / 34 = 16 + 4 + 1= 21 (остаток 15).

И снова результат можно высчитать в уме, но, если бы Джон Вествик считал с помощью абака, он обнаружил бы, что римские числа прекрасно укладываются в его колонки и расшифровать ответ несложно. А вот чтобы записать итог индо-арабскими цифрами, нужно было подумать чуть дольше.

Если рука набита, никакой сложности эти приемы не представляют. Овладев ими и имея счетные доски, монахи не видели необходимости отказываться от системы, которая прекрасно служила их предшественникам. Если же в силу специфики научных интересов и занятий им приходилось то и дело умножать и делить, проще было составить таблицу умножения римских чисел, а не обучаться новой арифметике с нуля. Такие справочные таблицы и счетные доски Джон Вествик всегда держал под рукой в годы учебы в Сент-Олбанской грамматической школе. Они немало ему послужили, прежде чем растущий интерес к астрономии не заставил его перейти на новые цифры и приемы умножения, принятые в индо-арабском «алгорисмусе».

Теги

Фрагменты новых книг

20. Где и как были изобретены римские цифры. Реконструкция подлинной истории [OCR]

20. Где и как были изобретены римские цифры

Считается, что римские цифры возникли задолго до н. э. Во времена «античных римлян». При этом числа, меньшие пятидесяти, записывались с помощью трех значков: I, V, X. Почему именно такие и только такие значки использовались для небольших чисел? Сначала люди оперировали небольшими величинами. Лишь потом в обиход вошли большие числа — сотни и т. п. Тогда и потребовались новые значки, вроде L, C, D, M. Так что значки для небольших чисел были первоначальными, наиболее древними.

Рис. 36. Каменная мельница, обнаруженная в «античных» Помпеях [1268:1], с. 577

Выскажем следующее наблюдение. Когда плотники ставят сруб, а затем переносят его на новое место, они метят бревна топором. Пометки необходимы, чтобы бревна после переноски сложить в том же порядке, поскольку они уже были аккуратно подогнаны друг к другу. Сегодня пометки делаются масляной краской, римскими или арабскими цифрами. Но раньше плотницкие пометки делались только топором и только римскими цифрами. В самом деле, арабские цифры топором не нанесешь. Это очень неудобно. А вот римские цифры как будто специально предназначены, чтобы их легко было вырубить топором на круглом бревне. Поясним.

Плотник, помечающий бревно с помощью топора, должен сделать это засечками. Легко нанести засечку либо поперек волокон бревна, либо под сравнительно небольшим углом к ним. Наносить засечку вдоль волокон очень неудобно.

Это значит, что у плотника есть только три легко различимых знака, которые он может сделать. Это — вертикальная засечка, то есть латинская буква I. Далее, две соединенных друг с другом косых засечки, то есть латинская буква V. Перевернутая буква V не может считаться другим символом, поскольку плотник может подойти к бревну с другой стороны и возникнет путаница. И наконец, две перекрещивающиеся косые черты, то есть латинская буква X. Все остальные символы, изготовляемые топором, должны быть составлены из этих знаков. Или быть близки к ним.

Итак, три основные римские цифры должны были естественно возникнуть именно в плотницком деле. Выходит, что древние римляне почему-то якобы независимо изобрели именно те символы, которые должны были возникнуть у народа, строившего много деревянных срубов (причем при помощи стальных топоров). Но ведь в Италии основное старинное строительство было каменным и кирпичным. Срубы там редкость. Лесов не так уж много. А тем более строевых.

Да и вряд ли русские плотники, среди которых в прежние времена было много необразованных, изучали «древние», якобы, итальянские цифры. Тем не менее, плотники на Руси метили бревна именно «римскими цифрами».

Правда, с одной оговоркой. Правила, что цифра слева вычитается из цифры справа — у них не было. Поскольку в плотницких метках нет понятий «правого» и «левого». Ведь к бревну можно подойти как с одной, так и с другой стороны. Поэтому, например, число 9 писалось как VIIII, а не как IX.

Скорее всего, римские цифры возникли на Руси, но отнюдь не в ученой среде, а среди строителей. На Руси строили много и, в основном, из дерева. Плотников было много, и эта сфера деятельности считалась важной.

Потом, при расширении Империи на запад, «римские плотницкие цифры» занесли и туда, в частности, в Италию. Вначале там тоже были леса, возникло деревянное строительство. Но вскоре итальянские леса в значительной степени вырубили. Ведь Италия сравнительно невелика. Зато здесь оказалось много строительного камня. Как и вообще на юге. А русские плотницкие цифры перешли в ученую среду и их назвали «древне-римскими». И это правильно. Их действительно придумали русские, колонизировавшие Европу в XIV веке.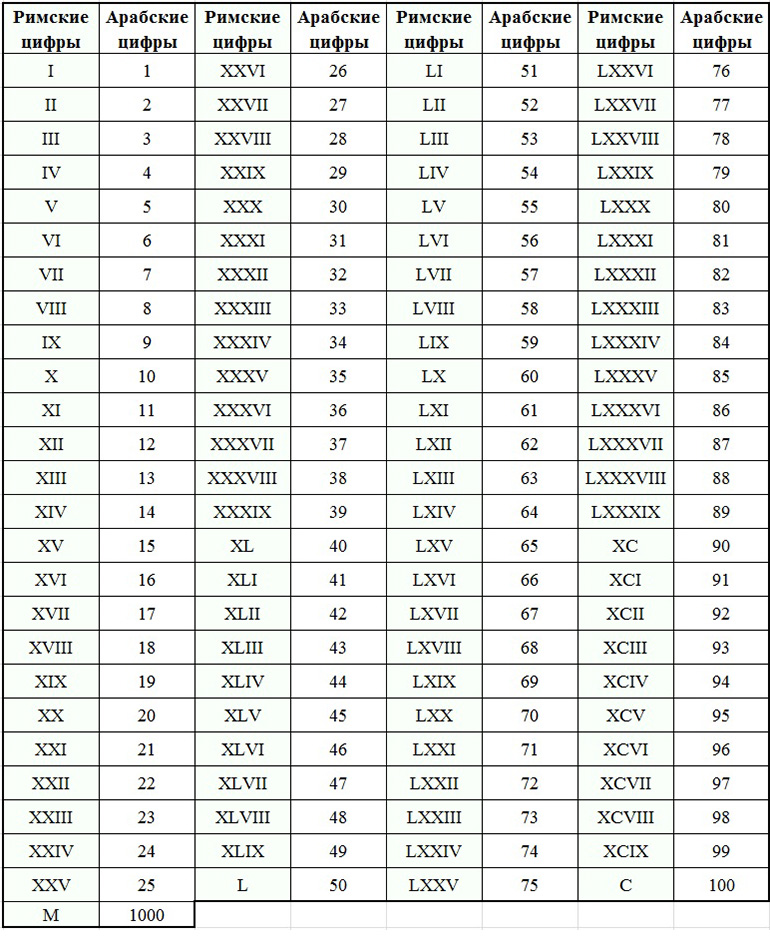

То есть — с точки зрения западных европейцев XVII века — те самые древние римляне, которые и создали Римскую = Ордынскую Империю XIV–XVI веков. Но в XV–XVI веках началось османское завоевание, также исходившее из Руси. Западные европейцы восприняли его как разрушение Древнего Рима и перестали связывать Рим с Русью. Возникла ложная теория, что Древний Рим возник в глубокой древности, в Италии. А «следовательно», именно в Италии будто бы и придумали римские цифры.

Потом, когда римские цифры стали писаться пером на бумаге, конечно, появились обозначения L, M, C, D, необходимые для записи больших чисел. Кстати, если бы римские цифры с самого начала писались на бумаге, то наряду с «пятеркой» = «V», скорее всего, должна была бы появиться и «галочка», то есть «?», перевернутое «V». Эти два символа легко различимы, но только при условии, что определены понятия «низ» и «верх».

Данный текст является ознакомительным фрагментом.

Цифры

Цифры Не многие читатели любят цифры, но для человека, который действительно хочет в чём-то разобраться нет ничего лучше цифр.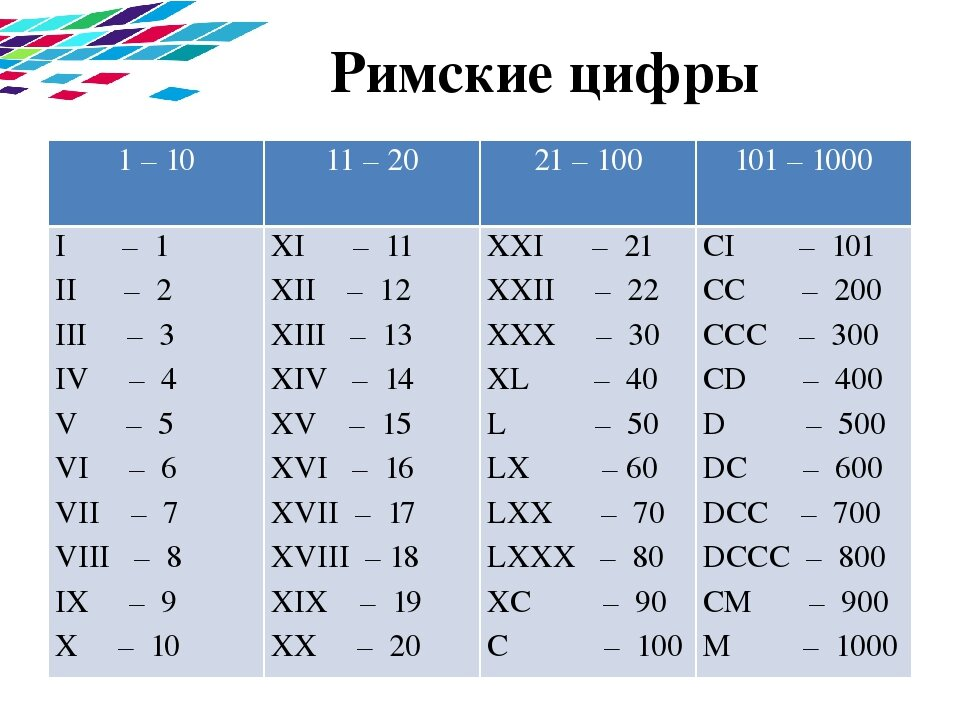 Поэтому я закончу свою работу цифрами самолётного парка Германии и потерь люфтваффе, сведёнными в таблицы, на основании немецких архивных

Под знаком цифры

Под знаком цифры Вернувшись в Ургу, Унгерн в течение двух недель готовится к походу. Одновременно он задумывается об идеологическом обосновании этой акции. В итоге появляется знаменитый впоследствии программный «Приказ № 15». Отпечатанный в большом количестве

Краснохолмские соборы были красивы. «Были» потому, что в настоящее время они почти разрушены

Краснохолмские соборы были красивы. «Были» потому, что в настоящее время они почти разрушены Другой собор — Троицкий. Еще в 1575 году на холме была, кроме Преображенской, церковь Живоначальной Троицы, она была сожжена во времена литовского разорения, охватившего многие

25.

 Как и когда были придуманы арабские цифры

25. Как и когда были придуманы арабские цифры Историк математики В.В. Бобынин писал: «ИСТОРИЯ НАШИХ ЦИФР ПРЕДСТАВЛЯЕТ НЕ БОЛЕЕ КАК РЯД ПРЕДПОЛОЖЕНИЙ, ПЕРЕМЕЖАЮЩИХСЯ С ПРОИЗВОЛЬНЫМИ ДОПУЩЕНИЯМИ, производящими иногда, вследствие предшествующего употребления метода

Глава III. «Славное было время! Были явные поцелуи, были и тайные »{1}

Глава III. «Славное было время! Были явные поцелуи, были и тайные»{1} Сохранились многочисленные свидетельства о том, как приветствовали друг друга хозяева и гости, приглашенные на обед, ужин, вечер или бал.«Теперь я хочу рассказать, каким образом приветствуют друг друга

4. Где и как были изобретены римские цифры?

4. Где и как были изобретены римские цифры? Энциклопедия сообщает: «РИМСКИЕ ЦИФРЫ, цифры древних римлян.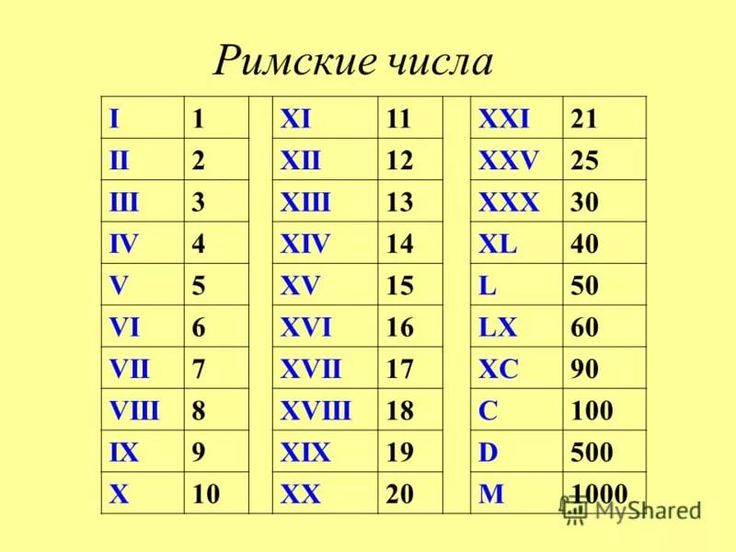 Система Р.ц. основана на употреблении особых знаков для десятичных разрядов I = 1, X = 10, С = 100, М = 1000 и их половин V = 5, L = 50, D = 500. Натуральные числа записываются при помощи

Цифры и факты

Цифры и факты У перестройки есть и положительные моменты. В частности, широкому читателю (хотя какой может быть сегодня «широкий читатель» при тиражах книг в 5—10 тыс.?) предоставлена возможность ознакомиться с уймой фактов, которые кэпээсэсовцы по причине своей тупости

20. Где и как были изобретены римские цифры

20. Где и как были изобретены римские цифры Считается, что римские цифры возникли задолго до н. э. Во времена «античных римлян». При этом числа, меньшие пятидесяти, записывались с помощью трех значков: I, V, X. Почему именно такие и только такие значки использовались для

25.

 Как и когда были придуманы арабские цифры

25. Как и когда были придуманы арабские цифры Историк математики В.В. Бобынин писал: «ИСТОРИЯ НАШИХ ЦИФР ПРЕДСТАВЛЯЕТ НЕ БОЛЕЕ КАК РЯД ПРЕДПОЛОЖЕНИЙ, ПЕРЕМЕЖАЮЩИХСЯ С ПРОИЗВОЛЬНЫМИ ДОПУЩЕНИЯМИ, производящими иногда, вследствие предшествующего употребления метода

ГЛАВА XIX Еще одна причина, почему были забыты римские и салические законы и капитулярии

ГЛАВА XIX Еще одна причина, почему были забыты римские и салические законы и капитулярии Я уже говорил о том, почему салические и римские законы и капитулярии утратили свою силу; прибавлю еще, что широкое распространение доказательства посредством поединка было тому

ГЛАВА XIII О том, что никогда не следует рассматривать законы независимо от цели, ради которой они были созданы. Римские законы о краже

ГЛАВА XIII О том, что никогда не следует рассматривать законы независимо от цели, ради которой они были созданы. Римские законы о краже Когда у римлян вор попадался с поличным, прежде чем успевал спрятать украденное, то кража называлась явною; если же вора обнаруживали лишь

6. ОЧКИ БЫЛИ ИЗОБРЕТЕНЫ В XIII ВЕКЕ. СЛЕДОВАТЕЛЬНО, СТАРИННЫЕ ИЗОБРАЖЕНИЯ «АНТИЧНЫХ» ЛЮДЕЙ В ОЧКАХ ДАТИРУЮТСЯ НЕ РАНЕЕ XIII ВЕКА И ПОКАЗЫВАЮТ НАМ, СКОРЕЕ ВСЕГО, ПЕРСОНАЖЕЙ XIII–XVII ВЕКОВ

6. ОЧКИ БЫЛИ ИЗОБРЕТЕНЫ В XIII ВЕКЕ. СЛЕДОВАТЕЛЬНО, СТАРИННЫЕ ИЗОБРАЖЕНИЯ «АНТИЧНЫХ» ЛЮДЕЙ В ОЧКАХ ДАТИРУЮТСЯ НЕ РАНЕЕ XIII ВЕКА И ПОКАЗЫВАЮТ НАМ, СКОРЕЕ ВСЕГО, ПЕРСОНАЖЕЙ XIII–XVII ВЕКОВ Из истории технологии известно, что очки были изобретены в XIII веке. Считается, правда, что

ЦИФРЫ И ФАКТЫ

ЦИФРЫ И ФАКТЫ  Построен: 1911 год. ТТД: водоизмещение — 46 300 т; длина — 269 м; ширина — 28,2 м; скорость — 25 узлов. Как выглядел: «Титаник» был высотой с 11-этажный дом и длиной в четыре городских квартала.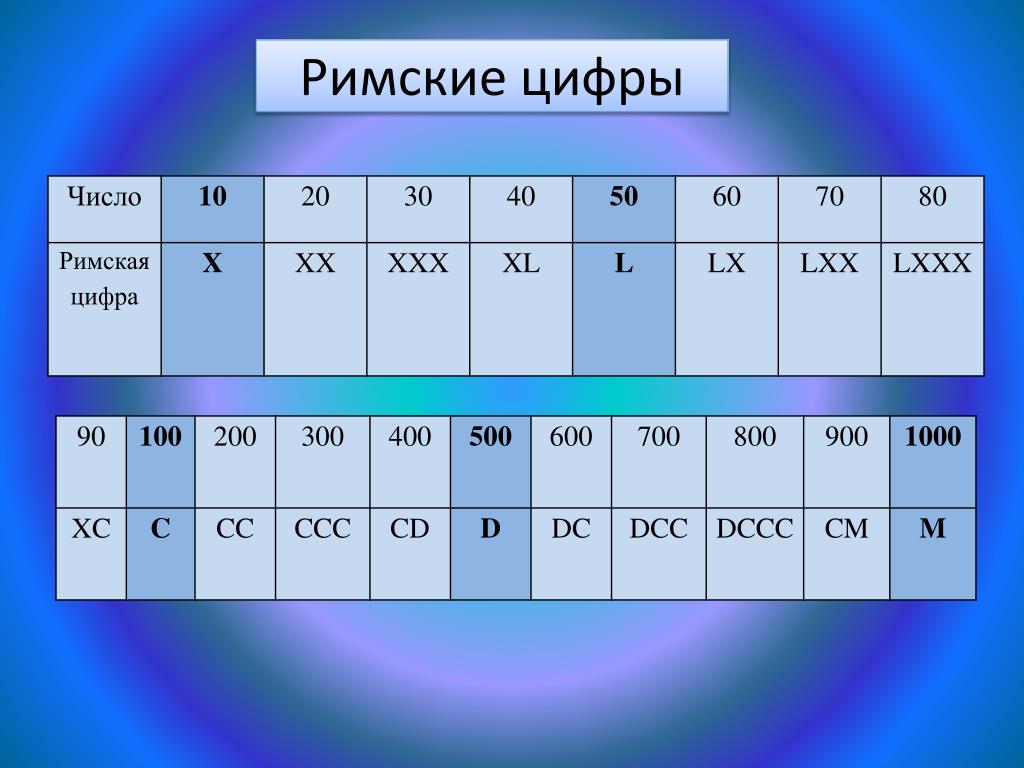  Маршрут: Саутгемптон — Нью-Йорк. Число пассажиров: 2200 человек. Причина

Глава 11. «Чтобы ружья были чисты, тесаки были востры»

Глава 11. «Чтобы ружья были чисты, тесаки были востры» (БЫТ И ПОВСЕДНЕВНАЯ ЖИЗНЬ АРМИИ ПЕТРА I)Медицинское дело в армии было поставлено плохо, это сказывалось на лечении раненых и предупреждении инфекционных заболеваний, в то время как концентрация войск приводила к

29 римскими цифрами — Как написать 29 римскими цифрами?

LearnPracticeDownload

29 римскими цифрами — XXIX. Чтобы преобразовать 29 в римские цифры, запишем 29 в расширенной форме, т.е. 29 = 10 + 10 + (10 — 1), после чего заменив преобразованные числа соответствующими им римскими цифрами, мы получим 29 = X + X + (X — I) = XXIX. В этой статье мы объясним, как правильно преобразовать 29 в римские цифры.

• 29 = 20 + 9
• римских цифр = ХХ + IX
• 29 римскими цифрами = XXIX

1.	Как написать 29 римскими цифрами?
2.	Основные правила
3.	Номера, относящиеся к 29
4.	Часто задаваемые вопросы о 29 римскими цифрами

Как написать 29 римскими цифрами?

Римские цифры для 29 можно получить, используя метод, указанный ниже:
В этом методе мы разбиваем 29 на наименее расширяемую форму, пишем соответствующую им латинскую букву и добавляем/вычитаем их, то есть 29 = 10 + 10 + (10 — 1) = X + X + (X — I) = XXIX.
Следовательно, значение 29 римскими цифрами равно XXIX.

☛ Также проверьте: Калькулятор римских цифр

Основные правила интерпретации римских цифр

• Когда буква большего размера предшествует букве меньшего размера, буквы добавляются. Например: MC, M > C, поэтому MC = M + C = 1000 + 100 = 1100.
• Когда буква меньшего размера предшествует букве большего размера, буквы вычитаются. Например: XL, X < L, поэтому XL = L - X = 50 - 10 = 40.
• Когда буква повторяется несколько раз, они добавляются. Например: ХХХ = Х + Х + Х = 10 + 10 + 10 = 30
• Одну и ту же букву нельзя использовать более трех раз подряд.

Римские цифры могут показаться отличными от цифр, но они похожи. Например, 29 римскими цифрами эквивалентно XXIX. Римские цифры для чисел, связанных с 29приведены ниже:

• ХХ = 20
• ХХI = 20 + 1 = 21
• XXII = 20 + 2 = 22
• XXIII = 20 + 3 = 23
• XXIV = 20 + 4 = 24
• ХХV = 20 + 5 = 25
• ХХVI = 20 + 6 = 26
• XXVII = 20 + 7 = 27
• XXVIII = 20 + 8 = 28
• XXIX = 20 + 9 = 29

29 римскими цифрами Примеры

1. Пример 1. Найдите разницу между 46 и 29 римскими цифрами.

   Решение:

   Решение данной задачи, 46 — 29 = 17
   Для определения значения 46 — 29 римскими цифрами выразим 17 в развернутом виде, т. е. 17 = 10 + 7 = X + VII = XVII.

2. Пример 2: Найдите значение (19 — 30) + 29 римскими цифрами.

   Решение:

   Решение (19- 30) + 29 = -11 + 29 = 18. Теперь запишем ответ, то есть 18 = 10 + 8 = X + VIII = XVIII.

3. Пример 3: Какой остаток при делении XXIX на XVII?

   Решение:

   XVII = 17 и XXIX = 29 в числах.
   При делении 29 на 17 получается остаток 12.
   Итак, 12 = XII
   . Поэтому при делении XXIX на XVII получается остаток XII.

4. Пример 4: Найдите значение 923 — 29.

   Решение:

   Решение данной задачи, 923 — 29 = 894
   Для определения значения 923 — 29 римскими цифрами выразим 894 в развернутом виде, т.е. 894 = 800 + 90 + 4 = DCCC + XC + IV = DCCCXCIV.

перейти к слайдуперейти к слайдуперейти к слайдуперейти к слайду

 

Готовы увидеть мир глазами математика?

Математика лежит в основе всего, что мы делаем. Наслаждайтесь решением реальных математических задач на живых уроках и станьте экспертом во всем.

Запишитесь на бесплатный пробный урок

Часто задаваемые вопросы о 29 римскими цифрами

Что означает 29 римскими цифрами?

Чтобы записать 29 римскими цифрами, сначала выразим 29 в развернутом виде. 29 = 10 + 10 + (10 — 1) = Х + Х + (Х — I) = XXIX. Следовательно, 29 в римских числах записывается как XXIX.

Что нужно добавить к 23, чтобы получить 29? Запишите ответ римскими цифрами.

29 римскими цифрами — XXIX, тогда как 23 — XXIII. 29 — 23 = 6. Следовательно, чтобы получить 29, к 23 нужно прибавить 6. Теперь, чтобы перевести 6 в римские числа, выразим его в развернутом виде, то есть 6 = 5 + 1 = V + I = VI .

Каково значение (2 — 10) + 29 в римских цифрах?

Решение (2 — 10) + 29 = -8 + 29 = 21. Чтобы выразить, (2 — 10) + 29 римскими цифрами, запишем ответ, то есть 21 в развернутом виде. 21 = 10 + 10 + 1 = Х + Х + I = ХХI

Как преобразовать число 29 в римские цифры?

Чтобы преобразовать 29 в римские цифры, преобразование включает разбиение чисел на основе разрядности (единицы, десятки, сотни, тысячи).

• Десятки = 20 = ХХ
• единиц = 9 = IX
• Число = 20 + 9 = ХХ + IX = ХХIX

Почему число 29 римскими цифрами пишется как XXIX?

Мы знаем, что римскими цифрами 9 записывается как IX, а 10 как X. Следовательно, 29 римскими цифрами записывается как 29= 20 + 9 = ХХ + IX = ХХIX.

☛ Статьи по теме:

• 2013 римскими цифрами — MMXIII
• 23 римскими цифрами — XXIII
• 123 римскими цифрами — CXXIII
• 999 римскими цифрами — CMXCIX
• 1400 римскими цифрами — MCD
• 2011 римскими цифрами — MMXI
• 2019 римскими цифрами — MMXIX

Рабочие листы по математике и визуальная программа

Как римскими цифрами записывается число 29?

Почему 29 пишется римскими цифрами как XXIX?

Римские цифры — это древний способ записи чисел, придуманный еще в Древнем Риме.

Он все еще используется сегодня, но в основном для свиданий (например, Super Bowl L для Super Bowl 50) или для фильмов. сериал (Звездные войны IV — Новая надежда).

Вот основные используемые символы:

Основные римские цифры

1	5	10	50	100	500	1000
я	В	Х	л	С	Д	М

Основные комбинации

1	2	3	4	5	6	7	8	9
я	II	III	IV	В	ВИ	VII	VIII	IX

10	20	30	40	50	60	70	80	90
Х	ХХ	ХХХ	XL	л	LX	LXX	LXXX	ХС

100	200	300	400	500	600	700	800	900
С	СС	ССС	CD	Д	DC	ДКК	DCCC	СМ

Большие числа

Для чисел свыше 1000 необходимо поставить тире над римской цифрой для обозначения умножения на 1000.

5000	10 000	50 000	100 000	500 000	1 000 000
В	Х	л	С	Д	М

Как число 29 преобразуется в римские цифры?

Чтобы преобразовать 29 в римские цифры, нам нужно разделить его на разрядные значения (единицы, десятки, сотни и т. д.), например:

Разрядное значение	Номер	Римская цифра
Десятки	20	XX
Один		IX

Обратите внимание, мы пропустили значения места, которые равны 0.